Adaptive Damped Rank-Reduction Method for Random Noise Attenuation of Three-Dimensional Seismic Data

Abstract

Rank-reduction methods are effective for separating random noise from the useful seismic signal based on the truncated singular value decomposition (TSVD). However, the results that the TSVD operator provides are still a mixture of noise and signal subspaces. This problem can be solved using the damped rank-reduction method by damping the singular values of noise-contaminated signals. When the seismic data include highly linear or curved events, the rank should be large enough to preserve the details of the useful signal. However, the damped rank-reduction operator becomes less powerful when using a large rank parameter. Hence, the denoised data contain significant remaining noise. More recently, the optimally damped rank-reduction method has been proposed to solve the extra noise problem as the rank value increases. The optimally damped rank-reduction operator works well for a moderately large rank, but becomes ineffective for a very large rank. We introduce an adaptive damped rank-reduction algorithm to attenuate the residual noise for a very large rank parameter. To elaborate on the proposed algorithm, we first construct a gain matrix by only using the input rank parameter, which we introduce directly into the adaptive singular-value weighting formula to make it more stable as the rank parameter becomes too large. Then, we derive a damping operator based on the improved optimal weighting operator to attenuate the residual noise. The proposed method, which can be regarded as an improved version of the optimally damped rank-reduction method, is insensitive to the input parameter. Examples of synthetic and real three-dimensional seismic data show the denoising improvement using the proposed method.

Article Highlights

• The adaptive damped rank-reduction (ADRR) method is highly stable for the input parameter

• The ADRR method can use a sufficiently large rank to attenuate the random noise in seismic data containing complex structures

• The ADRR method relieves the dependence of RR-based approaches

1 Introduction

Noisy seismic data negatively affect the best characterization of the subsurface. Therefore, removing noise from seismic data becomes an inevitable task in exploration seismology to provide a better quality of data for fundamental processing steps, e.g., post-stack seismic interpretation, seismic imaging and inversion (Kazemi et al. 2016; Li et al. 2020b).

When removing random noise from noisy seismic data, two main concerns require particular caution. First, how much noise can be suppressed, and then how well the signals can be preserved ? Hence, how to get rid of random noise without losing useful information becomes a major problem. Therefore, some researchers have proposed many methods to suppress residual noise effectively. In the group of sparse transforms, signal and noise are separated based on their sparsity difference in the transformed domain. Commonly used sparse transforms include Fourier, Radon (Bracewell and Bracewell 1986; Kabir and Verschuur 1995; Zhai 2014; Xue et al. 2017), curvelet (Beylkin 1987; Neelamani et al. 2008), seislet (Fomel and Liu 2010), and wavelet transforms (Goudarzi and Riahi 2012; Gilles 2013; Mousavi et al. 2016; Chen et al. 2019). Zu et al. (2019) use the dictionary learning-based sparse transform for random noise attenuation. Prediction-based methods use the difference of predictability to separate noise from useful signals. The regularized nonstationary auto-regression (RNA) technique (Liu et al. 2012) combines the hypothesis of stationary and linearity of the signal in the conventional frequency-space (f-x) domain prediction technique. Liu and Chen (2013) introduce an approach called noncausal-RNA for the same task of seismic noise removal. Rank reduction (RR) belongs to another group of denoising methods. The multi-dimensional Cadzow filter (Cadzow 1988; Trickett 2008a), also known as the conventional RR approach (Oropeza and Sacchi 2011), has been broadly used because of its ability to attenuate the random noise. By including the components of seismic data into the Hankel matrix, approaches based on RR assume that seismic data have a low-rank structure in the frequency domain. In the ideal case (seismic data that include linear events), the rank of the seismic matrix corresponds to the amount of dip components (Oropeza and Sacchi 2011). Unfortunately, this assumption is not always valid with field data because of the complex structures. By applying the truncated singular value decomposition (TSVD) operator, the conventional RR method can suppress random noise. However, it becomes less effective when the raw data include a significant amount of random noise. The rank constraint becomes inadequate to further shrink the singular value. Hence, the approximation signal from the TSVD process contains a significant amount of residual noise, which degrades the features of the seismic signal. To restore the useful events effectively, we can apply the RR method on the small time-space window of the seismic data. However, this technique causes another problem in selecting a proper rank value for each local window. The rank value required to reduce the random noise differs from a local window to another. We can therefore understand that a fixed rank value may be large for a local window and small for others.

To solve this problem, it is usually better to select a large rank value to preserve weak and curved energy when recovering the useful events. However, the larger the rank parameter is, the more residual noise the filtered data may contain. Likewise, the denoised data lose useful information when a too small rank is adopted. Thus, how to set the rank parameter properly for each local window to provide a better quality of the seismic signal becomes a common issue. Trickett (2015) discusses how to automatically set the rank of each matrix, enabling the filter to adjust to different situations. The method can achieve a satisfactory balance between noise suppression and signal protection. Aharchaou et al. (2017) improve the well-known singular spectrum analysis method (Trickett 2008b) by shrinking singular values to obtain the best trade-off between noise suppression and signal preservation. Wang et al. (2020a) propose to denoise the seismic signal using an optimal rank selection. This method removes noise based on a rule of rank selection, which can be used in the traditional RR method and other RR-based approaches to further shrink the singular values. On the other hand, the rank can be set based on the ratio of two consecutive singular values (Wang et al. 2020b). A common strategy to remove the extra noise left by the TSVD operation is the nuclear norm minimization techniques (Yang et al. 2013; Kreimer and Sacchi 2013; Li et al. 2017; Zhou and Zhang 2017; Li et al. 2020a; Feng et al. 2021). Such an approach applies a thresholding operator to the low-rank signal matrix to decrease the noise level. However, how to select the thresholding parameter accurately is still challenging. Zhang et al. (2017) investigate multiple constraints for seismic signal estimation using a hybrid rank-sparsity constraint. The approach benefits from the weight of low-rank constraint and sparsity-promoting transforms to further attenuate random noise. Shao et al. (2019) introduce a low-rank matrix approximation method using variational mode decomposition to attenuate the random noise of desert seismic data. Zhang et al. (2020) propose to suppress seismic incoherent noise using a robust low-rank approximation. Cavalcante and Porsani (2022) investigate the CUR matrix decompositions technique to estimate the useful signals matrix from the noisy seismic matrix. The method operates with the columns and rows of the input noisy matrix rather than the singular vector provided by SVD. This process minimizes the necessity for accurate rank by enabling oversampling columns and rows.

Huang et al. (2016) have brought their contribution by improving the TSVD process via a damping operator to make it more adequate to further deal with random noise. The damped truncated singular value decomposition (DTSVD) refers to an improved version of the TSVD operator. The resulting method, called the damped rank-reduction (DRR), demonstrates its ability to attenuate the useful signal from very strong random noise due to the effect of damping (Chen et al. 2016a, b; Huang et al. 2016). However, the DTSVD process becomes less effective when we need to set a large rank value to reduce the random noise accurately. Siahsar et al. (2017) introduce the damped data-driven optimal singular value shrinkage method. In this approach, in addition to the OptShrink strategy (Nadakuditi 2014), the damping factor is used to provide a more robust low-rank approximation compared with TSVD and singular value thresholding. Oboué and Chen (2021) improve the quality of the low-rank matrix by combining the moving-average filter and the arctangent penalty operator into the damped rank-reduction framework. This method aims to remove the extra noise left after the DTSVD process. More recently, Chen et al. (2020) introduce an optimally DRR (ODRR) method to relieve the dependence of these RR-based approaches. The ODRR approach has been confirmed to be effective for random noise attenuation, even when a moderately large rank is needed for complex datasets. However, as the rank value becomes larger, the ODRR operator becomes less effective to further shrink the singular value, thereby attenuating the extra noise.

Following Chen et al. (2020), this work introduces an adaptive damped rank-reduction (ADRR) approach to further fit the singular value even in the condition of strong random noise and complex structures when it is necessary to choose a very large rank parameter to remove the residual noise while preserving the useful signal. To elaborate on the ADRR algorithm, we first formulate a gain matrix only based on the input rank parameter. We introduce this matrix directly into the optimal weighting formula (Nadakuditi 2014) of the singular value to make it more stable when the rank parameter becomes too large. Then, we derive a damping operator by using the improved optimal weighting operator to decrease the level of noise. The ADRR method is highly stable for the input parameter. Therefore, we can select a sufficiently large rank value to attenuate the random noise in seismic data that contain complex structures. The ADRR framework can successfully solve residual noise problem due to the high sensitivity of the rank-reduction methods to the input rank value. It can remove more noise and preserve the useful signal under a very large rank value. This is the benefit of the proposed ADRR method. Different experiments on synthetic and field three-dimensional (3-D) seismic data show the superiority of the adaptive damped rank-reduction method over the traditional RR, DRR, and the ODRR methods.

We first outline the construction of a block Hankel matrix for 3-D seismic data. Then, we provide a brief review of several RR methods and elaborate on our ADRR method for seismic noise attenuation. Next, we conduct several comparisons in terms of both visual and quantitative examination between the traditional RR, DRR, ODRR, and the ADRR methods. We also analyze the sensitivity of each RR method to the input rank parameter in detail. Finally, we draw some conclusions.

2 Theory

2.1 Construction of the Block Hankel Matrix for Three-Dimensional Seismic Data

The main object is a volume of three-dimensional seismic data that we represent in time domain by ${\mathbf {X}}(t, x,y)$ of size $p_t \times p_x \times p_y$. To construct the desired matrix, the rank-reduction algorithm converts ${\mathbf {X}}(t, x,y)$ into ${\mathbf {X}}_{f}(f,x,y)(f=1\cdot \cdot \cdot n_f)$, where t and f correspond to time and frequency components, respectively (Oropeza and Sacchi 2011; Chen et al. 2016a). If we set a frequency $f_0$, the frequency component of ${\mathbf {X}}$ is defined by:

$$\begin{aligned} {{\textbf {X}}}_{f_0}=\begin{bmatrix} {{\textbf {X}}}{(1,1)} &{} {{\textbf {X}}}{(1,2)} &{} ... &{} {{\textbf {X}}}{(1,p_x)}\\ {{\textbf {X}}}{(2,1)} &{} {{\textbf {X}}}{(2,2)} &{} ... &{} {{\textbf {X}}}{(2,p_x)}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{\textbf {X}}}{(p_y,1)} &{} {{\textbf {X}}}{(p_y,2)} &{} ... &{} {{\textbf {X}}}{(p_y,p_x)} \end{bmatrix}. \end{aligned}$$

(1)

For simplification, we omit the argument $f_0$. For each row of ${{\textbf {X}}}$, the rank-reduction algorithm forms a Hankel matrix. The desired matrix ${{\textbf {M}}}_{e}$ for row i of ${{\textbf {X}}}$ corresponds to:

$$\begin{aligned} {{\textbf {M}}}_{e}=\begin{bmatrix} {{\textbf {X}}}{(e,1)} &{} {{\textbf {X}}}{(e,2)} &{} ... &{} {{\textbf {X}}}{(e,l)}\\ {{\textbf {X}}}{(e,1)} &{} {{\textbf {X}}}{(e,2)} &{} ... &{} {{\textbf {X}}}{(e,l+1)}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{\textbf {X}}}{(e,p_x-l+1)} &{} {{\textbf {X}}}{(e,p_x-l+2)} &{} ... &{} {{\textbf {X}}}{(e,p_x)} \end{bmatrix}. \end{aligned}$$

(2)

Then, the Hankelization operator constructs the desired block Hankel matrix ${{\textbf {Q}}}$ in terms of ${\mathbf {M}}_e$ as:

$$\begin{aligned} {{\textbf {Q}}}=\begin{bmatrix} {{\textbf {M}}}_{1} &{} {{\textbf {M}}}_{2} &{} ... &{} {{\textbf {M}}}_{p}\\ {{\textbf {M}}}_{2} &{} {{\textbf {M}}}_{3} &{} ... &{} {{\textbf {M}}}_{p+1}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{\textbf {M}}}_{p_y-p+1} &{} {{\textbf {M}}}_{p_y-p+2} &{} ... &{} {{\textbf {M}}}_{p_y} \end{bmatrix}. \end{aligned}$$

(3)

The size of ${{\textbf {Q}}}$ is $I=(p_x-l+1)(p_y-p+1)$ and $J=pl$. l and p denote the integers selected to bring the matrices ${{\textbf {M}}}_{e}$ and ${{\textbf {Q}}}$ close to square.

The following equation expresses the conversion of the data ${\mathbf {X}}$ into the block Hankel matrix ${\mathbf {Q}}$:

$$\begin{aligned} {\mathbf {Q}}={\mathcal {H}}{\mathbf {X}}, \end{aligned}$$

(4)

where ${\mathcal {H}}$ is the Hankelization operator.

2.2 Rank-Reduction Method

In this section, we describe how to carry out rank reduction of a matrix using the optimally damped method of Chen et al. (2020). Consider an observed data matrix ${\mathbf {Q}}$ modeled as:

$$\begin{aligned} {\mathbf {Q}}={\mathbf {H}} + {\mathbf {E}}, \end{aligned}$$

(5)

where ${\mathbf {H}}$ and ${\mathbf {E}}$ are, respectively, the signal and noise components.

The rank-reduction algorithms assume that the matrices ${\mathbf {Q}}$ and ${\mathbf {E}}$ have complete rank, and the useful signal matrix ${\mathbf {H}}$ has insufficient rank. The size of each matrix is of $J\times I$. Based on this assumption, we can formulate ${\mathbf {H}}$ by:

$$\begin{aligned} {{\textbf {H}}}={{\textbf {U}}}^{{\textbf {H}}}_1{\Sigma ^{{\textbf {H}}}_1}({{\textbf {V}}}^{{{\textbf {H}}}}_1)^\iota , \end{aligned}$$

(6)

and the rank-reduction approach using the conventional TSVD corresponds to:

$$\begin{aligned} \tilde{{{\textbf {Q}}}}={{\textbf {U}}}^{{\textbf {Q}}}_1{\Sigma ^{{\textbf {Q}}}_1}({{\textbf {V}}}^{{{\textbf {Q}}}}_1)^\iota , \end{aligned}$$

(7)

where $\tilde{{{\textbf {Q}}}}$ is the approximated signal. The diagonal matrix $\Sigma ^{{\mathbf {Q}}}_1$ includes the larger singular values. ${\mathbf {U}}^{\mathbf {Q}}_1$, and $({\mathbf {V}}^{\mathbf {Q}}_1)^{{\iota }}$ are the singular vector matrices. The notation $\left[ \cdot \right] ^{{\iota }}$ denotes the conjugate transpose of the matrix.

Combining Eqs. (5)–(7), Chen et al. (2016b) derive the true formulation of $\tilde{{{\textbf {Q}}}}$:

$$\begin{aligned} \tilde{{{\textbf {Q}}}}={{\textbf {H}}}+{{\textbf {U}}}^{{\textbf {H}}}_1{({{\textbf {U}}}^{{\textbf {H}}}_1)}^\iota {{\textbf {E}}}, \end{aligned}$$

(8)

which explains clearly that $\tilde{{{\textbf {Q}}}}$ is still a combination of the signal and noise components. Based on the nuclear-norm minimization strategy (Yang et al. 2013; Zhou and Zhang 2017), the residual noise that still affects the quality of the result can be decreased using the thresholding operator (Donoho 1995):

$$\begin{aligned} {{\textbf {Q}}}={{\textbf {U}}}^{{\textbf {Q}}}_1\mu {(\Sigma ^{{\textbf {Q}}}_1,\tau )}({{\textbf {V}}}^{{{\textbf {Q}}}}_1)^\iota , \end{aligned}$$

(9)

where $\mu$ denotes the thresholding operator, and $\tau$ is its parameter. However, because of the heterogeneity of random noise in each singular value, it is difficult to find a stable threshold parameter to further deal with the residual noise. In the same context, an adaptive singular-value weighting (Nadakuditi 2014) algorithm has been proposed to ease the influence of the rank parameter through the following optimization problem:

$$\begin{aligned} \hat{\varvec{\theta }}=\arg \min _{\varvec{\theta }} \parallel {{\textbf {U}}}^{{\textbf {H}}}_1{\Sigma ^{{\textbf {H}}}_1}({{\textbf {V}}}^{{{\textbf {H}}}}_1)^\iota - {{\textbf {U}}}^{{\textbf {Q}}}_1{{{\theta }}\Sigma ^{{\textbf {Q}}}_1}({{\textbf {V}}}^{{{\textbf {Q}}}}_1)^\iota \parallel _F, \end{aligned}$$

(10)

where ${\theta }$ is a weighting operator introduced to fit ${\Sigma ^{{\textbf {Q}}}_1}$ after the singular value decomposition process. The ith left and right singular vectors correspond to ${{\textbf {U}}}^{{\textbf {H}}}_i$ and ${{\textbf {V}}}^{{\textbf {H}}}_i$, respectively. The solution of Eq. 10 refers to

$$\begin{aligned} \hat{\varvec{\theta }}= diag(\theta _1,\theta _2,...,\theta _N), \end{aligned}$$

(11)

where

$$\begin{aligned} {\theta }_i=\left( -\frac{2}{\alpha ^{{\textbf {Q}}}_i}\frac{{\mathcal {D}}(\alpha ^{{\textbf {Q}}}_i;\varvec{\Sigma })}{{\mathcal {D}}'(\alpha ^{{\textbf {Q}}}_i;\varvec{\Sigma })}\right) . \end{aligned}$$

(12)

$\alpha ^{{\textbf {Q}}}_i$ is the ith diagonal entry of $\Sigma ^{{\textbf {Q}}}_1 (\Sigma ^{{\textbf {Q}}}_1 \in R^{N\times N})$. ${\mathcal {D}}$ corresponds to the ${{\textbf {D}}}$-transform (Chen et al. 2020). $\mathcal {D'}$ is the derivative of ${{\textbf {D}}}$ regarding $\alpha _i$ (Bai et al. 2020; Chen et al. 2020). Equation 11 allows to formulate the approximation signal matrix using the weighting operator as:

$$\begin{aligned} {{\textbf {Q}}}={{\textbf {U}}}^{{\textbf {Q}}}_1\hat{\varvec{\theta }}{\Sigma ^{{\textbf {Q}}}_1}({{\textbf {V}}}^{{{\textbf {Q}}}}_1)^\iota . \end{aligned}$$

(13)

The optimal weighting process specified in Eq. 13 substitutes the traditional TSVD operation used in the rank-reduction method Eq. 7.

Based on Eq. 13, Chen et al. (2020) introduce the optimally damped rank-reduction approach to further attenuate the extra noise as the rank constraint increases. They conclude the ODRR formula for seismic signal enhancement:

$$\begin{aligned} {{\textbf {Q}}}&={{\textbf {U}}}^{{\textbf {Q}}}_1\varvec{\delta }\hat{\varvec{\theta }}{\Sigma ^{{\textbf {Q}}}_1}({{\textbf {V}}}^{{{\textbf {Q}}}}_1)^\iota , \end{aligned}$$

(14)

$$\begin{aligned} \varvec{\delta }&={{\textbf {I}}}-(\Sigma ^{{\mathbf {Q}}}_1)^{-a}{\varvec{{\gamma }}^a}, \end{aligned}$$

(15)

where $\varvec{\delta }$ is the damping operator. ${{\textbf {I}}}$ denotes a unit matrix. $\varvec{{\gamma }}$ includes the maximal element of $\Sigma ^{{\mathbf {Q}}}_2$. a is the damping factor. The damped rank-reduction operator becomes similar to the traditional rank-reduction operator when $a \rightarrow +\infty$.

2.3 Adaptive Damped Rank-Reduction Method

In this section, we describe a novel method to modify the optimally damped rank reduction so that it better handles situations requiring large ranks. Highly linear or curved events influence the weight of the rank value on separating random noise from the useful seismic signals (Chen et al. 2020). Because of the linear events assumption of the conventional rank-reduction approach (Oropeza and Sacchi 2011), it is difficult to select a rank value that can adequately estimate the seismic signals. To estimate the useful signals, we can apply the RR method to the small time-space window of the input noisy data. However, the selection of a proper rank for each local window becomes a major difficulty. The rank value used to attenuate the random noise can be different from a local window to another. It means that a fixed rank value can be high for a local window and small for another. To tackle this difficulty, it is usually better to set a large rank value to preserve the useful events during the denoising process. However, when the rank value becomes large enough, the estimated signals contain significant residual noise. In this context, Chen et al. (2020) suggest selecting a moderately large rank value using the ODRR algorithm. The ODRR strategy aims to further remove the seismic noise as the rank parameter increases. The ODRR method can successfully solve the rank selection problem using the moderate rank values since the signal improvement is much better compared to those of the traditional RR and the DRR method. However, the ODRR operator becomes less stable when a very large rank value is required to deal with noise and signal preservation problems. The very large rank values weaken the performance of the ODRR method since it cannot remove noise at a lower level and preserve the useful signals adequately. We find that the ODRR operator loses its abilities for very large rank values. But it is more important to mention that the ODRR method eases the rank selection compared to the local window strategy. Therefore, we follow Chen et al. (2020) to make the ODRR method more stable under very large rank values. We first formulate a gain matrix only using the input rank parameter. Then, we introduce directly this matrix into the adaptive singular-value weighting formula defined in Eq. 13. We formulate the gain matrix as:

$$\begin{aligned} \varvec{\Phi }=\left[ {{\textbf {I}}}_{(n)}+(-\log (n) + 1){(\Sigma ^{{\textbf {Q}}}_1)^{-1}}\right] ^{k}. \end{aligned}$$

(16)

$\varvec{\Phi }$ is a diagonal matrix denoting the proposed gain matrix. ${{\textbf {I}}}_{(n)}$ corresponds to an identity matrix, and n denotes the input rank parameter. $(\Sigma ^{{\textbf {Q}}}_1)^{-1}$ is the inverse of the diagonal matrix $\Sigma ^{{\textbf {Q}}}_1$ obtained after the singular value decomposition (SVD) process. k is an adaptation factor. It corresponds to the number of factors necessary to provide a good denoising performance. Equation 16 is based only on the input rank parameter. This matrix can be considered as a regulator used to compensate for the formula defined in Eq. 13 to further neglect the influence of the large rank parameter.

Next, we introduce the matrix $\varvec{\Phi }$ directly into Eq. 13 to further shrink the singular values as the rank parameter increases:

$$\begin{aligned} {{\textbf {Q}}}={{\textbf {U}}}^{{\textbf {Q}}}_1\varvec{\Phi }\hat{\varvec{\theta }}{\Sigma ^{{\textbf {Q}}}_1}({{\textbf {V}}}^{{{\textbf {Q}}}}_1)^\iota , \end{aligned}$$

(17)

The introduced gain matrix $\varvec{\Phi }$ makes the adaptive singular-value weighting algorithm more stable. But, to further remove the random noise as the rank value becomes very large, we introduce the damping operator into Eq. 17. To achieve this strategy, we derive a damping operator for the adaptive approximation signal subspace. Consider

$$\begin{aligned} {\mathbf {G}}=\begin{bmatrix} {\mathbf {U}}^{\mathbf {G}}_1 &{} {\mathbf {U}}^{\mathbf {G}}_2\\ \end{bmatrix} \begin{bmatrix} \Sigma ^{\mathbf {G}}_1 &{} 0\\ 0 &{} \Sigma ^{\mathbf {G}}_2\\ \end{bmatrix} \begin{bmatrix} ({\mathbf {V}}^{\mathbf {G}}_1)^{{\mathbf {t}}}\\ ({\mathbf {V}}^{\mathbf {G}}_2)^{{\mathbf {t}}}\\ \end{bmatrix} \end{aligned}$$

(18)

as the SVD of ${\mathbf {G}}$ and

$$\begin{aligned} {\mathbf {U}}^{\mathbf {G}}_1= & {} U^{\mathbf {Q}}_1, \end{aligned}$$

(19)

$$\begin{aligned} \Sigma ^{\mathbf {G}}_1= & {} \varvec{\Phi }\hat{\varvec{\theta }}\Sigma ^{{\mathbf {Q}}}_1, \end{aligned}$$

(20)

$$\begin{aligned} V^{\mathbf {G}}_1= & {} {\mathbf {V}}^{\mathbf {Q}}_1, \end{aligned}$$

(21)

then, Eq. 7 can be regarded as a truncated singular value decomposition of ${\mathbf {G}}$

$$\begin{aligned} \tilde{{{\textbf {G}}}}={{\textbf {U}}}^{{\textbf {G}}}_1{\Sigma ^{{\textbf {G}}}_1}({{\textbf {V}}}^{{{\textbf {G}}}}_1)^\iota . \end{aligned}$$

(22)

Thus, like in Eq. 8, we can rewrite Eq. 22 as follows:

$$\begin{aligned} \tilde{{{\textbf {G}}}}={{{\textbf {Q}}}}=\tilde{{{\textbf {H}}}}+{{\textbf {U}}}^{\tilde{{{\textbf {H}}}}}_1{({{\textbf {U}}}^{\tilde{{{\textbf {H}}}}}_1)}^\iota \tilde{{{\textbf {E}}}}, \end{aligned}$$

(23)

where $\tilde{{{\textbf {H}}}}$ corresponds to the useful signal components of the denoised signal $\tilde{{{\textbf {G}}}}$.

When the rank is large enough, we suppose that the denoised signal contains all useful signal components of the initially noisy data and contains less noise than the noisy data. To further attenuate the residual noise in the denoised signal, we re-examine the matrix ${{{\textbf {Q}}}}$ in detail, and we write the newly denoised signal $\tilde{{{\textbf {G}}}}$ as:

$$\begin{aligned} \tilde{{{\textbf {G}}}}={{\textbf {Q}}}={{\textbf {H}}}+{{\textbf {U}}}^{{\textbf {H}}}_1{({{\textbf {U}}}^{{\textbf {H}}}_1)}^\iota \tilde{{{\textbf {E}}}}, \end{aligned}$$

(24)

where ${{\textbf {U}}}^{{\textbf {H}}}_1{({{\textbf {U}}}^{{\textbf {H}}}_1)}^{\iota }\tilde{{{\textbf {E}}}}$ corresponds to the residual noise subspace after applying the process summarized in Eq. 7. ${{{\textbf {H}}}}$ corresponds to the useful signal components of the newly denoised signal $\tilde{{{\textbf {G}}}}$. As concluded in Chen et al. (2016b), the signal matrix ${{\textbf {H}}}$ can be approximated as:

$$\begin{aligned} {{\textbf {H}}}={{\textbf {U}}}^{{\textbf {G}}}_1{\Sigma ^{{\textbf {G}}}_1}\varvec{\delta }({{\textbf {V}}}^{{{\textbf {G}}}}_1)^\iota , \end{aligned}$$

(25)

where $\varvec{\delta }$ is the damping operator.

If we consider that ${{\textbf {U}}}^{\mathbf {G}}_1={{\textbf {U}}}^{\mathbf {Q}}_1$, $\Sigma ^{{\textbf {G}}}_1=\varvec{\Phi }\hat{\varvec{\theta }}\Sigma ^{{\textbf {Q}}}_1$, ${{\textbf {V}}}^\mathbf {Q}_1={\mathbf {V}}^\mathbf {Q}_1$, Eq. 25 can be formulated as:

$$\begin{aligned} {{\textbf {H}}}={{\textbf {U}}}^{{\textbf {Q}}}_1\varvec{\Phi }\hat{\varvec{\theta }}\varvec{\delta }{\Sigma ^{{\textbf {Q}}}_1}({{\textbf {V}}}^{{{\textbf {Q}}}}_1)^\iota , \end{aligned}$$

(26)

where $\mathbf {{H}}$ corresponds to the estimated signal from the new approach. Equation 26 is the adaptive damped rank-reduction formula. It can be considered as an improved version of the ODRR formula.

The process of obtaining the estimated signal matrix $\mathbf {{H}}$ can be summarized by:

$$\begin{aligned} \mathbf {{H}}={\mathbf {R}}_{ad}{\mathbf {{Q}}}, \end{aligned}$$

(27)

where ${\mathbf {R}}_{ad}$ corresponds to the adaptive damped rank-reduction (ADRR) operator.

Next, we apply the averaging operator ${\mathcal {A}}$ (Oropeza and Sacchi 2011; Chen et al. 2016a, b) to the estimated signal $\mathbf {{H}}$ to recover the filtered data in the following way:

$$\begin{aligned} \hat{\mathbf {X}}={\mathcal {A}}{\mathbf {H}}={\mathcal {A}}{\mathbf {R}}_{ad}{\mathbf {{Q}}}= {\mathcal {A}}{\mathbf {R}}_{ad}{\mathcal {H}}{\mathbf {X}} = f_{ad} {\mathbf {X}}. \end{aligned}$$

(28)

$f_{ad}$ corresponds to the averaging operator and the ADRR filter, respectively.

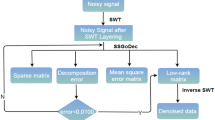
The proposed ADRR algorithm is summarized in the following workflow:

By applying the one-dimensional forward FFT, the ADRR algorithm transforms first the input noisy seismic data ${\mathbf {X}}(t,x,y)$ into ${\mathbf {X}}(f,x,y)$ for a frequency range f. Then, the ADRR algorithm constructs the block Hankel matrix ${\mathbf {Q}}$ by applying the Hankelization operator ${\mathcal {H}}$. Next, the noisy block Hankel matrix ${\mathbf {Q}}$ is transformed via the SVD operation. Afterward, the adaptive damping operator is applied to reduce the rank of the matrix ${\mathbf {Q}}$. The operation allows estimating the signal matrix ${\mathbf {H}}$ as specified in equation (26). The filtered data $\hat{\mathbf {X}}$ are obtained by applying the averaging operator ${\mathcal {A}}$ to the estimated signal ${\mathbf {H}}$. Finally, the denoised data ${\mathbf {X}}(f,x,y)$ obtained in the frequency domain, are converted back into time domain ${\mathbf {X}}(t,x,y)$ through the 1-D inverse FFT. This framework outlines the primary steps of the proposed ADRR method. Similar to the low-rank methods, our ADRR method is augmented with the damped adaptive operator to enhance the denoising performance.

3 Examples

In this section, we apply the RR (Oropeza and Sacchi 2011), DRR (Chen et al. 2016a), ODRR (Chen et al. 2020), and the proposed ADRR methods to three-dimensional synthetic and field seismic data using small and very large rank values. Then, we apply each rank-reduction approach using a very large rank value. In each case, the rank value should be able to deal with noise and signal preservation issues simultaneously. In this work, the small rank corresponds to the value that should be adequate to provide the best results based on the linear events assumption. The very large rank values are selected to further deal with noise and signal preservation issues simultaneously. In each case, we compare the denoising performance of the proposed ADRR method to those of the traditional RR, DRR, and ODRR methods based on the visual examinations of each denoised data and their corresponding frequency-wavenumber spectra. Besides, to further display the denoising performance of each method, we use the local similarity map introduced by Chen and Fomel (2015). The local similarity estimates the damage that the noise attenuation method can cause to the useful signals. The most significant damages are shown by the higher local similarity between the denoised data and the suppressed noise. We conduct several quantitative analyses to compare denoising quality based on the signal-to-noise ratio (SNR) (Chen et al. 2016b) expressed as follows:

$$\begin{aligned} SNR=10\log _{10}\frac{\Vert \mathbf {X^{t}} \Vert ^2_2}{\Vert \mathbf {X^{t}}-\mathbf {X^{d}}\Vert ^2_2}, \end{aligned}$$

(29)

where $\mathbf {X^{t}}$ and $\mathbf {X^{d}}$ show the vectorized true and denoised data, respectively.

These qualitative and quantitative analyses provide a comprehensive demonstration of the effectiveness of the proposed ADRR method on synthetic and field seismic data using different rank values.

3.1 Synthetic Data Examples

This section demonstrates the performance of the proposed ADRR algorithm on one synthetic data containing four planar events and one synthetic data including five curved events. We generate noisy data by adding random noise with a variance of 0.2 to the clean data. The SNR of this noisy data is about $-3.56$ dB. After applying the four rank-reduction methods, we first display the results for synthetic data having planar events. We start the comparison between each approach by displaying the results for a small value of rank ($n = 4$). Figure 1a and b shows the clean and noisy data, respectively. Figure 2a–d is the denoised data from the conventional RR, DRR, ODRR, and the proposed ADRR methods, respectively. The denoised data from the RR method (Fig. 2a) contain a significant amount of residual noise compared to the other three rank-reduction methods. The output SNRs of the RR, DRR, ODRR, and the proposed ADRR approaches are about 7.95 dB, 13.64 dB, 13.89 dB, and 13.91 dB, respectively. This comparison shows that the DRR, ODRR, and the proposed ADRR method can obtain almost the same denoising performance with a smaller value of rank (e.g., rank =4). However, $n = 4$ induces signal leakage because of the high level of smoothing. Therefore, to obtain the best trade-off between random noise attenuation and useful signal preserving, we increase the rank value from 4 to 30, and we conduct another example by applying the four rank-reduction methods to the same noisy synthetic data. We compare the denoising performance in Fig. 2e–h. From Fig. 2h, it is clear that the estimated signal using the ADRR method is much cleaner than those of the other three methods. Figure 3a–d corresponds to the removed noise from the RR, DRR, ODRR, and the proposed ADRR methods, respectively. We find that the proposed ADRR method can remove more noise compared to the RR, DRR, and ODRR methods. To further show the difference between each method, we display their corresponding local similarity maps in Fig. 3e–h. The comparison of the local similarity maps shows the much better denoising performance of the proposed scheme when the rank value increases. The DRR method seems to induce more signal leakage compared to the other three methods. The frequency-wavenumber spectra displayed in Fig. 4c and f vividly confirm the superiority of our approach in terms of random noise attenuation when a very large rank value is selected. The RR, DRR, ODRR, and the ADRR methods provide SNR values of $-0.8$ dB, 6.22 dB, 9.73 dB, and 11.08 dB, respectively. The SNR comparison confirms the visual examination. Then, we subtract the SNR values of this test from the previous to quantify the difference in terms of SNR values. As a result, we obtain 8.75 dB, 7.42 dB, 4.16 dB, and 2.83 dB, respectively, for the RR, DRR, ODRR, and the proposed ADRR approaches. From this analysis, we deduce that while the RR, DRR, and the ODRR methods are influenced by the larger rank value, the ADRR approach seems to be stable. Our approach adapts better to different choices of the rank value.

Fig. 1

Synthetic data with four simple planar events. a and b are from the clean and the noisy data, respectively

Fig. 2

Comparison of denoising performance using different rank values. a–d are from the RR, DRR, ODRR, and the proposed ADRR methods using rank n = 4. e–h are from the RR, DRR, ODRR, and the proposed ADRR methods using rank n = 30

Fig. 3

Removed noise sections and local similarity maps using rank $n=30$. a–d Removed noise sections from the RR, DRR, ODRR, and the proposed ADRR methods, respectively. e–h Local similarity maps from the RR, DRR, ODRR, and the proposed ADRR methods, respectively

Fig. 4

Comparison of denoising performance via the frequency-wavenumber spectra (synthetic data including four simple planar events). a–c show the denoised data from the RR, DRR, ODRR, and the proposed ADRR approaches for rank $n = 4$. d–f plot the denoised data from the RR, the DRR, and the proposed approaches for rank $n = 30$

Then, we carry out some numerical tests to highlight the main difference between the damped rank-reduction method and the adaptive damped rank-reductions algorithm as the noise variance increases. For this case, we select a relatively large value of rank ($n = 10$) to investigate the behavior of each approach under different noise levels. Figure 5a shows the comparison. The plot shows the much better performance of the ADRR algorithm (red line) for different noise variances. As manifested, when the data include significant random noise, the new method still outperforms the DRR method. Then, in the same noise condition, we display a comparison between the ODRR and the proposed ADRR approaches to show their performance under a very large rank value ($n = 30$). Figure 5b plots the difference between both of them in terms of SNRs value. It is clear that the red line, which denotes the new method, is above the green line (ODRR method). The ADRR method provides much better denoising performance compared to the ODRR method. However, it is also clear that as the noise level increases, the contrast between both approaches decreases very slightly.

Fig. 5

Comparison of SNRs diagram (synthetic data having planar events). a Denoising performance from the DRR approach (blue line) and the ADRR approach (red line) for rank $n = 10$. b Denoising performance from the ODRR approach (green line) and the ADRR approach (red line) for rank $n = 30$

We then apply the four aforementioned methods to data with curved events. Here, we add the same noise variance as in the previous examples. First, we apply the RR, DRR, ODRR, and the ADRR methods with rank $n = 15$ to compare the performance. Figure 6a and b shows the clean and the noisy data, respectively. Figure 7a–d shows the denoised data from the conventional RR, DRR, ODRR, and the proposed ADRR approaches, respectively. We find that the denoised data using the RR operator contain significant residual noise compared to the other three methods. The SNR values of the noisy data, the RR, DRR, ODRR, and the proposed ADRR approaches are $-1.17$ dB, 6.94 dB, 11.14 dB, 11.22 dB, and 11.31 dB, respectively. The DRR, ODRR, and the proposed ADRR methods can remove random noise at a lower level. But we find that the result from our denoising framework is much cleaner than those of the other rank-reduction methods. By selecting $n = 15$, the four rank-reduction methods obtain their best performance in terms of SNR and visual observations. However, this rank value causes signal leakage. In the next example, we select a very large rank value (n = 60) to preserve the significant details of the useful signals. Figure 7e–h shows the comparison between the four denoising frameworks. From the visual inspections, it is clear that our denoising workflow can suppress more noise compared to the other rank-reduction methods. Then, we display the removed noise sections (Fig. 8a–d), the similarity maps (Fig. 8e–h), and the frequency-wavenumber spectra (Fig. 9a–f) for further comparison. Here, from the comparison of each subfigure, it is much clear that the RR approach is not effective to handle the residual noise well because of the weakness of the TSVD operator when the rank value increases. The denoised data from the DRR algorithm contain a significant amount of residual. But the improvement is much better than the RR method. The ODRR method can remove more random noise compared to the RR and the DRR methods.

The comparison of each subfigure above mentioned demonstrates that the ADRR approach works better than the RR, DRR, and the ODRR approaches. The lower similarity values (Fig. 8h) demonstrate that the ADRR approach can obtain the best trade-off between random noise attenuation and signal preservation when a large rank value is selected. The frequency-wavenumber spectrum (Fig. 9f) confirms the better denoising performance of the proposed ADRR method in terms of visual observations compared to the other rank-reduction methods. The RR, DRR, ODRR, and the proposed ADRR approaches achieve the denoising performance with SNRs of 1.94 dB, 4.74 dB, 8.64 dB, and 10.18 dB, respectively. The difference in terms of SNRs shows the lower sensitivity of our approach under a very large rank value. This quantitative comparison shows the much better denoising performance of our approach and its adaptability to data containing curved events.

Fig. 6

Synthetic data with curved events. a and b are from the clean and noisy data, respectively

Fig. 7

Comparison of denoising performance for synthetic data having curved events. a–d are from the RR, DRR, ODRR, and the proposed ADRR methods using rank $n = 15$. e–h are from the RR, DRR, ODRR, and the proposed ADRR methods using rank $n = 60$

Fig. 8

Removed noise sections and local similarity maps using rank $n=30$. a–d Removed noise sections from the RR, DRR, ODRR, and the proposed ADRR methods, respectively. e–h Local similarity maps from the RR, DRR, ODRR, and the proposed ADRR methods, respectively

Fig. 9

Comparison of frequency-wavenumber spectra. a–b Frequency-wavenumber spectra of the clean and noisy data, respectively. c–e Frequency-wavenumber spectra using the RR, the DRR, ODRR, and the proposed ADRR approaches using rank n=60

To numerically show the performance of our proposed method on data containing curved events for varying noise levels, we set the rank parameter first at 25. Figure 10a shows the comparison between the DRR and the proposed ADRR approaches. The SNRs of the proposed approach (red line) surpass those of the DRR approach (blue line) for all the noise levels. Based on the distance between both approaches, we find that even though their performance decreases as the random noise becomes significant, our strategy can provide a much better result.

Fig. 10

Comparison of SNR diagram (synthetic data containing curved events). a Denoising performance from the DRR approach (blue line), and the ADRR approach (red line) for rank $n = 25$. b Denoising performance from the ODRR approach (green line), and the ADRR approach (red line) for rank $n = 80$

To evaluate the computation cost of each approach, we test their efficiency on three-dimensional synthetic data with three planar and curved events. The four low-rank methods were performed in MATLAB R2017a on a Linux computer having an Intel Core i7 7th generation and 8 GB RAM. We run the four codes 3 times in the temporal frequencies band of 0 Hz–250 Hz for synthetic data having planar events and 0 Hz–80 Hz for the synthetic data with curved events. We display the average computation time in seconds (s) in Tables 1 and 2, respectively, for data with planar and curved events. From Table 1, we find that the RR, the ODRR, and the proposed ADRR approaches work with almost the same computation time. From Table 2, we find that both the ODRR and the proposed ADRR approaches run at almost the same time to process the synthetic data containing curved events. Here, the RR and the DRR methods take similar running times and are less expensive compared with the ODRR and the proposed ADRR approaches.

3.2 Field Data Examples

This section demonstrates the effectiveness of the proposed ADRR method in practice. We apply the four aforementioned RR methods to three-dimensional field seismic data. Since we do not have the clean data, we cannot make a judgment of the denoising performance by SNR. Therefore, we assess the denoising performance with the visual examination of the spatial coherency of the denoised data and local similarity maps. Figure 11a and b shows the noisy seismic data and the corresponding frequency-wavenumber spectrum. To show the performance of each approach as the rank value increases, we apply the four rank-reduction methods on the same noisy field data by varying the rank value like in the synthetic data examples. First, we apply the denoising methods using rank = 25 to restore the useful signal. Figure 12a–d shows the comparison. Each approach can successfully remove noise using $n = 25$. But this rank value cannot preserve the useful signal energy. Figure 13a–d shows visible signal leakage in the removed noise sections of each approach. The similarity maps (Fig. 14a–d) further confirm that this relatively large rank value is not adequate to preserve the signal energy because of the complexity of the input data. Therefore, after several tests, we adopted a very large rank value (n = 50) to preserve the useful signal during the denoising process. Figure 12e–h shows the denoised data from the RR, DRR, ODRR, and the proposed ADRR methods using rank = 50. The estimated signal using the proposed method (Fig. 12h) is much cleaner than the other three denoising approaches. The removed noise sections (Fig. 13e–h) from each approach contain negligible signal leakage compared to the results using rank = 25. From the local similarity maps, we find that the four RR methods can preserve the signal as the rank value increases. But the proposed method can obtain the best trade-off between noise suppression and signal preservation. To show the difference between each method more clearly, we display the zoomed sections of each data marked by the blue frame boxes (Figs. 11a and 12e–h) in Fig. 15a–e. The zoomed section from our denoising framework (Fig. 15e) is much smoother and cleaner than the other three RR methods (Fig. 15b–d). The proposed ADRR method still removes noise at a lower level when a very large rank value is selected to preserve the useful signal. Finally, we use the frequency-wavenumber spectra (Fig. 16a–d) to compare the quality of the estimated signal from each method using rank n = 50. Here, it is more obvious that the denoised data from the proposed ADRR method (Fig. 16d) contain the least amount of residual noise compared to the other rank-reduction methods (Fig. 16a–c).

Fig. 11

Field data comparison. a Noisy data. b Frequency-wavenumber spectrum from the noisy data

Fig. 12

Field data comparison. a–d Denoised data from the RR, DRR, ODRR, and the proposed ADRR methods ($n = {25}$). a–d Denoised data from the RR, DRR, ODRR, and the proposed ADRR methods ($n = {50}$)

Fig. 13

Field data comparison. a–d Removed noise from the RR, DRR, ODRR, and the ADRR methods using rank n = 25. e–h Removed noise section from the RR, DRR, ODRR, and the ADRR methods using rank n = 50

Fig. 14

a–d Local similarity from the RR, DRR, ODRR, and the ADRR methods using rank $n=25$. e–h Local similarity from the RR, DRR, ODRR, and the ADRR methods using rank $n=50$

Fig. 15

Zoomed section comparison of each data displayed in Fig. 12e–h. a Noisy data. b Denoised data from the RR method. c–e Denoised data from the DRR, the ODRR, and the proposed ADRR approaches, respectively

Fig. 16

Comparison of frequency-wavenumber spectra. a–d Frequency-wavenumber spectra from the RR and DRR, ODRR, and the proposed ADRR approaches using rank $n=50$

4 Discussion

4.1 Comparison of the Sensitivity of Different Rank-Reduction Methods

In this section, we focus on investigating the sensitivity of each rank-reduction approach to the input rank value. By using the synthetic data of the examples section, we display the performance of each approach in terms of SNRs as a function of rank (Figs. 17 and 18). We corrupt the clean synthetic data with a noise level of 0.2, and we apply each approach to analyze their strength and weakness for random noise suppression. From the comparison of the SNR diagrams using the RR approach (blue line) and the DRR method (green line), we find that the DRR operator can obtain higher SNRs than the RR operator. The higher SNRs from the DRR method show the better denoising performance using the damped TSVD operator (Chen et al. 2016b) compared to the traditional TSVD (Oropeza and Sacchi 2011). The remaining noise in the estimated signals from the RR method is mainly caused by the inability of the conventional TSVD process to further shrink the singular value as the rank values increase (Nadakuditi 2014). The DRR method further removes the remaining noise and improves the SNRs because of the introduction of the damping operator just after the TSVD operation. It eases the dependency of the RR method on rank selection since a relatively large rank can be set to improve the SNR of the denoised data by damping the extra noise induced by the TSVD process. We control the damping operator by adjusting a damping factor, which aids in decomposing the noisy seismic section into signal and noise components (Chen et al. 2016b; Huang et al. 2016). However, as shown in Figs. 17 and 18, when the input rank becomes large, the SNR diagrams obtained from the DRR method decrease significantly. But the SRNs using the ODRR approach (green lines) outperform those using the traditional RR and the DRR methods as already demonstrated by Chen et al. (2020) and Bai et al. (2020). This comparison underlines the shortcoming of the damped TSVD when we need to select large rank values to improve the quality of the useful signals. The ODRR method compensates for the DRR method by using an optimally damped TSVD, which relieves the dependence of most RR-based approaches. From the smaller values to the relatively larger values of the input rank value, the ODRR and the proposed ADRR approaches (red line) obtain almost the same SNRs. However, it is clear that as the rank value becomes very large, the SNR diagram from the ADRR approach surpasses those of the other low-rank methods including the ODRR algorithm. It means that by introducing the gain matrix into the ODRR formula, we can obtain a much better result (red line) compared to the former (green line) when the rank parameter increases gradually.

For the synthetic data having linear events, it is obvious that the SNRs obtained by the proposed ADRR method are almost consistent for the rank values ranging from 3 to 20. The SNR decreases slightly above $n = 20$ (Fig. 17). For data containing curved events, the SNR values seem to be slightly consistent as the rank value increases from $n = 15$ to $n= 40$ (Figure 18). Based on the smaller SNRs value, we find that the lower value of n (1 and 2) is not suitable to provide better results (see Fig. 17). The result obtained from such rank value contains a significant amount of residual noise. However, all values of n selected above 2 can obtain much better denoising performance. The SNR using the traditional RR method is the highest when we select ranks 1 and 2 because the estimated signal is not too smooth compared to those of the DRR, ODRR, and the proposed ADRR methods. We find that the smoothing degree of the damping factor induces much signal leakage, which negatively influences the SNR of the estimated signal when the rank is defined as 1 and 2. As shown in Fig. 18, smaller values of n are not appropriate for data containing curved events or complex structures. We need to select a sufficiently large rank value to reach better denoising performance (Cadzow 1988; Trickett 2008a; Oropeza and Sacchi 2011). When data contain linear or curved events, we find that the proposed algorithm is less sensitive to the very large rank constraint compared to the other algorithms. The ADRR approach adapts better when the rank increases.

Fig. 17

SNR diagram of different rank-reduction methods for the selected rank parameters concerning synthetic data having simple linear events. The black and blue lines are from the RR and the DRR methods, respectively. The green and red lines correspond to the ODRR and the ADRR methods, respectively

Fig. 18

SNR diagram of different rank-reduction methods for the selected rank parameters concerning synthetic data containing curved events. The black and blue lines are from the RR and the DRR methods, respectively. The green and red lines correspond to the ODRR and the ADRR methods, respectively

4.2 Signal Improvement Under Different Frequency Bands

Using the noisy synthetic data of the first example, we compare the SNR values among the RR, DRR, ODRR, and the proposed ADRR methods using rank $n=30$ under different frequency bands. Table 3 shows the comparison. We find that SNR values change with frequency for the four rank-reduction methods. As the frequency band becomes large, the SNR values increase. But the distance between the proposed method and the other rank-reduction methods is still obvious. It is clear that our denoising framework can improve the quality of the useful signal in different frequency bands under a very large rank value.

4.3 Signal Preservation of the ADRR Method

Preserving the useful signal features when attenuating the residual noise is one of the most important aims in seismic data processing. Therefore, we analyze the effects of the rank parameter on the quality of the estimated signal. From Fig. 3h, the local similarity demonstrates that the proposed ADRR method can effectively attenuate random noise and preserve the significant signal features when we select a large rank parameter ($n = 30$). The different rank-reduction operators can further shrink the singular value and obtain a better quality of the denoised data using rank $n=4$ as shown in Fig. 2a–d. But the ADRR operator (Eq. 26) can achieve this task even better compared with the RR and the DRR methods. The rank parameter $n = 4$ corresponds exactly to the number of dip components in the first synthetic data. As shown in Fig. 17, this rank parameter produces a higher SNR for the proposed approach. Therefore, we understand that like the RR-based methods, the proposed ADRR method also relies on the linear events assumption (Oropeza and Sacchi 2011). As shown in Fig. 17, when we select a moderately rank parameter $n = 10$, the SNRs of both the RR and the DRR methods decrease considerably because of the sensitivity of their operator to the input rank value. Furthermore, we find that the RR and the DRR methods induce more signal leakage because of the inadequacy of the TSVD and the DTSVD processes to preserve the useful features of the estimated signal when a relatively larger rank value is selected for removing the residual noise. In contrast, by using $n=10$, the ADRR operator produces almost the same SNR because of its insensitivity to the input rank parameter. The local similarity map plotted in Fig. 8h shows that the ADRR process can preserve the signal energy while removing the residual noise when a very large value is selected ($n=60$). As shown in Figs. 14h, 15e and 16d, the ADRR method can attenuate the residual noise while keeping the useful signal features using a very large rank parameter ($n=50$) in practice.

4.4 Main Contribution

When implementing the proposed ADRR algorithm, we introduced a gain matrix (Eq. 16) to make the new rank-reduction formula (Eq. 26) less sensitive to the input rank parameter, and thus to further deal with strong random noise while preserving the properties of the estimated seismic signal. From Tables 1 and 2, both the ODRR and the proposed ADRR approaches perform with similar running time. Therefore, the introduced gain matrix does not negatively affect the computing time of the ODRR method. This is very competitive for the processing of multi-dimensional seismic data.

Chen et al. (2020) introduce the damping operator (Chen et al. 2016a, b; Huang et al. 2016) into the optimal weighting (Nadakuditi 2014) formula (Eq. 13) to propose the ODRR method. It is clear that, in the ODRR framework, it is the damping operator that makes the optimal weighting operator more robust to further remove random noise as the rank value increases. However, when we select a very large value, the damping operator loses its ability to further attenuate the extra noise. We find that the damping factor only is not enough to further shrink the singular values when the input rank becomes too large. Therefore, we first develop a gain matrix (Eq. 13) into the optimal weighting operator (Eq. 17) to further shrink the singular values as the rank increases. The gain matrix improves the performance of the adaptive singular-value weighting method (Nadakuditi 2014) since the resulting algorithm becomes more stable as the rank value increases. However, the estimated signal contains a significant amount residual noise. To solve the residual noise problem as the rank value becomes very large, we introduce the damping operator into Eq. 17. We find that the proposed ADRR framework succeeds for a very large rank because of the gain matrix. The proposed gain matrix has been developed in this paper to further fit the singular values of the noisy data when it is necessary to select a very large rank parameter to restore the whole features of the useful signal. We have adopted the formula of $\varvec{\Phi }$ after several tests conducted on different datasets. In this matrix, the term k is the adaptation factor. The value of k may vary depending on the type of data to be processed. In this paper, we have adopted $k = 8$ when dealing with all types of data because it provides the best quality of results.

The window size is a trade-off between ensuring the planar-event assumption and maximizing the feature extraction ability. It is known that the smaller the window, the better suitability of rank-reduction methods due to more planar events in the smaller windows. However, if the window is too small, it fails to include some locally complex structures of the nonstationary seismic data. As a result, a window that is too small cannot be applied in complicated situations. Since the window size cannot be too small, even for the smallest windows that are allowed to maintain the structural complexity in the data, the rank could vary greatly across all windows. Our approach provides a solution to those cases where seismic data are extremely complex and ranks across windows vary dramatically.

A crucial problem in seismic noise attenuation using RR-based approaches is the choice of the rank value (Bai et al. 2020; Chen et al. 2020). Since the proposed ADRR approach is highly insensitive to the rank parameter, we can choose a sufficiently large rank to attenuate the random noise in seismic data containing complex structures, which is the primary advantage of the proposed ADRR method.

Table 1 Computation time comparison in seconds for the synthetic data, including simple linear events. We execute the three codes in MATLAB R2017 on a Linux computer having an Intel Core i7 7th generation and 8 GB RAM in a temporal frequencies band $0 - 250$ Hz

Table 2 Computation time comparison in seconds for the synthetic data, including curved events. We execute the three codes in MATLAB R2017 on a Linux computer having an Intel Core i7 7th generation, and 8 GB RAM in a temporal frequencies band $0 - 80$ Hz

Table 3 Comparison of S/N values among the RR, DRR, ODRR, and the proposed ADRR methods using rank $n=30$ under different frequency bands

5 Conclusions

Based on the special features of the optimal weighting operator, the proposed gain matrix, and the damping operator, we introduce an adaptive damped rank-reduction (ADRR) approach for denoising of 3-D seismic data. The ADRR framework is proposed to solve the residual noise problem due to the high sensitivity of the low-rank methods to the input rank parameter. As demonstrated in our analysis, the denoised data produced by the ADRR method are smoother and cleaner. Compared with the conventional rank-reduction, the damped rank-reduction, and the optimally damped rank-reduction methods, the proposed ADRR method has been verified to be more competitive to decompose the 3-D synthetic and real seismic data into signal and noise subspaces even when a very large rank parameter is used.