Introduction

Random noise has always been one of the important factors affecting the quality of seismic data. One of the main tasks of seismic data processing is to attenuate it. Many scholars have put forward and developed numerous effective approaches for random noise attenuation such as predict filter (Canales 1984; Liu and Liu 2011; Liu et al. 2012; Naghizadeh and Sacchi 2012), median filter (Liu et al. 2006; Zheng et al. 2017), empirical mode decomposition (EMD) (Cai et al. 2011; Chen et al. 2017; Liu et al. 2018), edge-preserving filtering (Yuan et al. 2018b) and some methods based on transform including the wavelet transform (Yang et al. 2017), the seislet transform (Fomel and Liu 2010) and sparsity dictionary (Beckouche and Ma 2014).

Singular value decomposition (SVD) filtering is a simple and powerful tool in random noise attenuation based on extracting the essential coherency components. Its performance of removing background noise is better than other denoising methods in seismic data with continuous unconflicting events (Bekara and Mirko 2007). Freire (1988) used it in the time-space (t-x) domain to separate noise with the upgoing and downgoing waves especially when the events are horizontal. Cadzow filtering (Trickett 2002; Trickett et al. 2003) can separate linear dipping coherent events from random noise because the rank of the Hankel matrix which is built from each frequency slice of linear events in the frequency-space (f-x) domain is equivalent to the number of their different slopes. Cadzow filtering is expanded to multiple dimensions (Oropeza and Sacchi 2011; Naghizadeh and Sacchi 2013, ), called multichannel singular spectrum analysis (MSSA), via embedding–deducting and restructuring the Hankel matrix in the f-x domain for 3D seismic volumes. Kreimer and Sacchi (2012) represented the spatial data at one frequency slice by a high-order tensor for denoising and interpolating of curved events. Huang et al. (2015) developed the MSSA algorithm by a damping factor controlling the degree of residual noise attenuation. However, the frequency-space (f-x) domain SVD methods, such as Cadzow filtering and MSSA, need to fit the assumption of a few linear events. To meet approximately linear and denoise effectively, Yuan and Wang (2011) presented that the seismic data in the t-x domain are preprocessed with a sliding window before using Cadzow filtering (called local Cadzow filtering). The denoising performance of the method is affected by the parameter of window length which is set more subjectively and experientially.

Local SVD (LSVD) (Bekara and Mirko 2007) is utilized by laterally aligning all coherent signal along dip direction within t-x domain local window. The method is not limited by the linear assumption. A structure-oriented SVD approach (SOSVD) (Gan et al. 2015) can enhance useful reflections via flattening predicted seismic events according to the estimated local dips. Although the structure-oriented-type approach requires prior flattening, which complicates the process, it has two advantages. First, both rank reduction of SVD and stacking can reduce noise. Second, without the limit of a uniform slope in processed windows, it is more effective in handling hyperbolic events and complex structures. However, the design that the rank of the estimated signal is fixed limits the denoised performance of SOSVD. If it can be adjusted according to the signal-to-noise ratio of the data, the effect of noise reduction will be improved.

In this paper, we propose a structure-oriented adaptive SVD (named SOASVD) approach for random noise attenuation. Firstly, we review the theory of SVD, analyze the distribution of singular values corresponding to random noise and put forward the concept of adjacent singular value increment and the method of adaptively choosing the rank of estimated signal. Then, we introduce the prediction of plane waves and combine it with ASVD for random noise attenuation of seismic data. Finally, we use the synthetic and field examples to compare the proposed algorithm with f-x deconvolution, f-x EMD, LSVD and local Cadzow filtering, and draw some conclusions.

Theory

SVD

Seismic data \({\mathbf{D}}\) consist of useful signal \({\mathbf {S}}\) and random noise \({\mathbf {N}}\), which is:

$$\begin{aligned} {\mathbf {D}}={\mathbf {S}}+{\mathbf {N}} \end{aligned}$$
(1)

where the size of matrixs \({\mathbf {D}}\), \({\mathbf {S}}\) and \({\mathbf {N}}\) is \( N \times M \), \( M \) represents the number of seismic traces and \( N \) represents the number of time samples in the processed window. The SVD of matrix \({\mathbf {D}}\) can be expressed as (Vrabie et al. 2004):

$$\begin{aligned} {\mathbf {D}}= {\mathbf {U}}{\sum }{\mathbf {V}}^{T}=\sum \limits _{\mathbf {k=1}}^{R}\sigma _{k}{\mathbf {u}}_{k}^{T} \end{aligned}$$
(2)

where \({\mathbf {U}} =[{\mathbf {u}}_1,{\mathbf {u}}_2,...,{\mathbf {u}}_k,...,{\mathbf {u}}_R], \)\({\mathbf {V}} =[{\mathbf {v}}_1,{\mathbf {v}}_2,...,{\mathbf {v}}_k,...,{\mathbf {v}}_R] \), \({\mathbf {u}}_k\) and \({\mathbf {v}}_k\) are the eigenvectors, the matrix \({\mathbf {u}}_k{\mathbf {v}}_k^T \) is the eigenimages of \( {\mathbf {D}}{\mathbf {D}}^T\), \(\varvec{\sum } =diag[\sigma _1,\sigma _2,...,\sigma _k,...,\sigma _ R ]\), \(\sigma _1\ge \sigma _2\ge ...\sigma _k\ge ...\ge \sigma _{ R }\), \(\sigma _k\) is the singular value and \( R \) is rank of \({\mathbf {D}}\). Equation (2) means that seismic data \({\mathbf {D}}\) include \( R \) eigenimages weighted by the corresponding singular values. Equation (2) can be also represented as (Freire 1988; Lu 2006) :

$$\begin{aligned} {\mathbf {D}}=\sum \limits _{k=1}^r\sigma _ku_kv_k^T+\sum \limits _{k=r+1}^ R \sigma _ku_kv_k^T \end{aligned}$$
(3)

where \( r \) is the rank of estimated seismic signal. Therefore, seismic data can be approximately divided into the seismic signal and random noise.

To effectively attenuate noise in seismic data using SVD method, we need to solve two problems. Firstly, we should obtain the events as horizontal as possible in processed windows. Secondly, the rank \( r \) needs to vary with the SNR of the seismic section. It is often set as 1 or 2 (Bekara and Mirko 2007), but it is only suitable for a single horizontal event with the fixed SNR. Lu (2006) suggests that it is given via the ratio of the stacking energy to the energy of the whole data. Freire (1988) refers that an abrupt change in the signal eigenvalues magnitude is easily distinguished from more gradual change in those of noise. However, the assumption is not proved and how to choose \( r \) based on the assumption is not given.

Singular value distribution of random noise

Assuming that the mean of random noise \({\mathbf {N}}\) is zero and its variance is \(\sigma ^2\), normally, it is considered that all singular values \(\sigma _{ni}\) for \({\mathbf {N}}\) are equal to \(\sqrt{N}\sigma \). However, the singular value of noise \(\sigma _{ni}\) is also calculated by the equation:

$$\begin{aligned} {\mathbf {n}}{\mathbf {n}}^T\simeq \left[ \begin{array}{ccccc} \sum \limits _{j=1}^Nn_{1,j}^2 &{}0 &{}\cdots &{}\cdots &{}0\\ 0&{}\ddots &{}0 &{} \cdots &{} 0 \\ \vdots &{}0 &{}\sum \limits _{j=1}^Nn_{i,j}^2 &{} 0&{} \vdots \\ 0&{}\cdots &{} 0&{}\ddots &{}0 \\ 0&{}\cdots &{} \cdots &{}0 &{}\sum \limits _{j=1}^Nn_{M,j}^2 \\ \end{array} \right] \end{aligned}$$
(4)

where \({\sigma _{n1}^2,\cdots ,\sigma _{ni}^2,\ldots ,\sigma _{nM}^2 }\) is the descending order of the collection \(\left\{ \sum \nolimits _{j=1}^Nn_{1,j}^2,\ldots ,\sum \nolimits _{j=1}^Nn_{i,j}^2,\ldots ,\sum \nolimits _{j=1}^Nn_{M,j}^2\right\} \) Defining a statistic variable \(X=\sum \nolimits _{j=1}^Nn_{i,j}^2/{\sigma ^2}\), \( \,X \,\) yields \(\,\chi ^2\,\) distribution with the degree of freedom of \( N. \) When \( N \) is relatively large, then X approximately yields a normal distribution with the mean of \( N \) and variance of \(\,2 N \). Taking \(Y=(X-N)/2N\), Y yields a standard normal distribution. If p denotes probability, \( u _p\) and \( u _a\) denote the quantile and upper quantile of Y. The relationship between \( u _p\) and \( u _a\) can be described as:

$$\begin{aligned} u _p= {\left\{ \begin{array}{ll} - u _a &{} 0< p< 0.5,\,p=a\\ 0&{} p=0.5\\ u _a &{} 0.5< p < 1,\,p=1-a\\ \end{array}\right. } \end{aligned}$$
(5)

According to Yamauchi approximation, we have

$$\begin{aligned} u _a\approx \sqrt{z(2.0611786-5.7262204/(z+11.640595)} \end{aligned}$$
(6)

where \(z=-ln(4a(1-a))\). Therefore, the relationship between \( u _{xp}\) and p can be written as:

$$\begin{aligned} u _{xp}=\sqrt{2N} u _{p}+N \end{aligned}$$
(7)

where \( u _{xp}\) represents the quantile of X and the relationship between \( u _{np}\) and p can be written as:

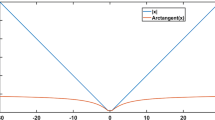
$$\begin{aligned} u _{np}=\sigma \sqrt{\sqrt{2N} u _{p}+N} \end{aligned}$$
(8)

where \( u _{np}\) represents the quantile of \(\sigma _{ni}\). Equations (5), (6) and (8) describe the relationship between \(\, u _{np}\) and p. It is equivalent to the relationship between \(\sigma _{ni}\) and the index i. We plot the curve of \( u _{np}\) with p ( \( N =100\) and \(\sigma =0.1778\)) in Fig. 1. It indicates that: 1) All singular values \(\sigma _{ni}\) are larger than zero and the mean value is about \(\sqrt{ N }\sigma \). 2) \( u _{np}\) is approximately linear with p from 0.1 to 0.9; in other words, the slope of \( u _{np}\) can be regarded as a constant. Therefore, the difference of adjacent singular values of \({\mathbf {N}}\) can be considered as a constant. 3) Both the slope of \( u _{np}\) and the mean of \(\sigma _{ni}\) increase with \(\sigma \) and \( N \). So we define the difference between two adjacent singular values as the singular value increment:

$$\begin{aligned} \Delta \sigma _i=\sigma _i-\sigma _{i+1} \end{aligned}$$
(9)

Then, we have the following equation:

$$\begin{aligned} \Delta {\overline{\sigma }}_{ni}\approx (\sigma _{n1}-\sigma _{nN})/(N-1)<\sigma _{n1}/(N-1) \end{aligned}$$
(10)

where \(\Delta {\overline{\sigma }}_{ni}\), \(\sigma _{n1}\) and \(\sigma _{nN}\) are the mean of adjacent singular value increments, the maximum singular value and the minimum singular value corresponding to random noise, respectively.

Adaptive SVD

Different from random noise, seismic signal may be reconstructed from only a few of the first eigenimages because of their high correlation. The high correlation has been commonly utilized to seismic data processing (Yuan et al. 2018a; Ma et al. 2018; Shi et al. 2018). Increments of adjacent singular values corresponding to seismic signal can be characterized by the following equation:

$$\begin{aligned} \Delta \sigma _{sm}>\sigma _{s1}/(N-1) \end{aligned}$$
(11)

where \(\triangle \sigma _{sm}\) and \(\sigma _{s1}\) are the maximum adjacent singular value increment and the maximum singular value corresponding to seismic signal, respectively. Comparing Eqs. (10) and (11), it is derived:

$$\begin{aligned} \Delta \sigma _{sm}/\Delta {\overline{\sigma }}_{ni}>\sigma _{s1}/\sigma _{n1} \end{aligned}$$
(12)

Equation (12) indicates that the seismic events can be better separated from noise by choosing the rank \( r \) by the singular value increments than the singular values. The \( r \) is varied with the singular value increments corresponding to seismic signal and noise using ASVD algorithm. The main flowchart of ASVD is as follows:

  1. 1.

    Determine a threshold by the mean of singular value increments corresponding to noise;

  2. 2.

    Determine the rank \( r \) through comparing the first few singular value increments with the threshold.

Prediction of plane waves

The input matrix of ASVD algorithm should be adjusted as horizontal as possible, so we apply the prediction of plane waves to it. The local plane differential equation is expressed as:

$$\begin{aligned} \dfrac{\partial D}{\partial x}+\alpha \dfrac{\partial D}{\partial t}=0 \end{aligned}$$
(13)

where \(\alpha \) is the local seismic dip. The solution of Eq. (13) can be given as (Fomel 2002; Liu et al. 2015):

$$\begin{aligned} {\mathbf {d}}_{(x+1)}={\mathbf {d}}_{(x)}{\mathbf {p}}_{(x\rightarrow {x+1})} \end{aligned}$$
(14)

where \({\mathbf {d}}_{(x)}\) is the data of trace x. \({\mathbf {p}}_{(x\rightarrow {x+1})}\) represents a prediction matrix from trace x to trace \(x+1\) and is a function of \(\varvec{\alpha }\). The local seismic dip \(\varvec{\alpha }\) is optimized by solving the following least-squares minimization problem:

$$\begin{aligned} \tilde{\varvec{\alpha }}= \mathop {\arg min}\Vert {\mathbf {W}}(\varvec{\alpha }){\mathbf {D}}\Vert _2^2 \end{aligned}$$
(15)

where \({\mathbf {W}}(\varvec{\alpha })=\left[ \begin{array}{ccccc} {\mathbf {I}} &{} 0&{} 0&{} \cdots &{} 0\\ -{\mathbf {p}}_{(1\rightarrow {2})} &{} {\mathbf {I}}&{} 0&{} \cdots &{} 0\\ 0 &{} -{\mathbf {p}}_{(2\rightarrow {3})}&{}{\mathbf {I}}&{} \cdots &{} 0\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ 0 &{} 0&{} 0&{}-{\mathbf {p}}_{(N-1\rightarrow {N})}&{}{\mathbf {I}}\\ \end{array} \right] \) , \({\mathbf {I}}\) is the identity matrix. Let \(\tilde{{\mathbf {D}}}_1\) represent a collection of predicted traces from the reference trace \({\mathbf {d}}_1\), \(\tilde{{\mathbf {D}}}_1\) can be calculated (Fomel 2002):

$$\begin{aligned} \tilde{{\mathbf {D}}}_1^T={\mathbf {P}}_{(1\rightarrow {i})}^T{{\mathbf {d}}_1} \end{aligned}$$
(16)

where \(\tilde{{\mathbf {D}}}_1=[\tilde{{\mathbf {d}}}_{(1\rightarrow {1})},\tilde{{\mathbf {d}}}_{(1\rightarrow {2})},\tilde{{\mathbf {d}}}_{(1\rightarrow {3})},\cdots ,{\tilde{{\mathbf {d}}}_{(1\rightarrow {N})}}]\) and \({\mathbf {P}}_{(1\rightarrow {i})}=[{\mathbf {I}},{\mathbf {p}}_{(1\rightarrow {2})},{\mathbf {p}}_{(1\rightarrow {3})},\cdots ,{{\mathbf {p}}_{(1\rightarrow {N})}}]\). Then, we can predict \(\tilde{{\mathbf {D}}}_i\) from a reference trace i\((i=1,2, \cdots ,N\)). Therefore, a 3D predicted volume from a 2D seismic data is created. A 2D profile of the 3D predicted volume is composed of predicted traces \(\tilde{{\mathbf {d}}}_{(1\rightarrow {x})},\tilde{{\mathbf {d}}}_{(2\rightarrow {x})},\tilde{{\mathbf {d}}}_{(3\rightarrow {x})},\cdots ,{\tilde{{\mathbf {d}}}_{(N\rightarrow {x})}}\), which have high similarity with the primitive trace x.

SOASVD denoising

The ASVD is applied to the 2D profile with approximate flat events. It is a structure-oriented ASVD ( SOASVD ) denoising approach. The detailed steps are shown below:

  1. 1.

    Estimate dominant local slopes.

  2. 2.

    Predict other traces from a reference trace i\((i=1,\ldots ,N)\) by applying plane-wave destruction filter which are designed by using the estimated slope. A 3D seismic volume is composed of all predict traces.

  3. 3.

    Apply ASVD filter to a 2D profile of the 3D seismic volume for denoising.

  4. 4.

    Stack the output of step 3).

  5. 5.

    Repeat steps 3) and 4) until all 2D profiles are processed and stacked.

Figure 2 demonstrates the process of SOASVD. Figure 2a is the original noisy model. Figure 2b is the estimated dip field of noisy model. A front view of Fig. 2c is the predicted traces from a reference trace applying the plane-wave destruction filter, and a profile view of Fig. 2c is the prediction of a primitive trace from all reference traces. Figure 2d is the partial profile view which is close to the primitive trace. Figure 2e is the denoised result of Fig. 2d using ASVD method. Figure 2f is the final denoised result of Fig. 2a, and every trace in the figure is formed by the stacked trace of a denoised 2D profile.

Fig. 1
figure 1

The relationship between \( u _{np}\) and p

Full size image
Fig. 2
figure 2

Demonstration for SOASVD method

Full size image
Fig. 3
figure 3

Hyperbolic-events synthetic seismic example

Full size image
Fig. 4
figure 4

Comparison of denoised data for the hyperbolic-events synthetic example

Full size image
Fig. 5
figure 5

Comparison of removed noise for the hyperbolic-events synthetic example

Full size image
Fig. 6
figure 6

Cross-correlation of denoised data and, respectively, removed noise for the hyperbolic-events synthetic example

Full size image
Fig. 7
figure 7

Conflicted linear synthetic seismic profile

Full size image
Fig. 8
figure 8

Comparison of denoised data for the conflicted linear synthetic example

Full size image
Fig. 9
figure 9

Comparison of removed noise for the conflicted linear synthetic example

Full size image
Fig. 10
figure 10

Cross-correlation of denoised data and, respectively, removed noise for the conflicted linear synthetic example.

Full size image
Fig. 11
figure 11

SOASVD orthogonalization for the conflicted linear synthetic example

Full size image
Fig. 12
figure 12

Comparison of denoised results for field data

Full size image
Fig. 13
figure 13

Comparison of denoised results for field data

Full size image

Examples

Synthetic examples

To test the performance of the proposed algorithm, we use two synthetic examples in this section. The first example is a simple seismic profile including five hyperbolic events. The data consist of 81 traces with a sampling rate of 4 ms. The total time is 1.5 s. The slopes of five events become gradually smaller from the top to the bottom. The amplitudes of five events are 3, 2.5, 2, 1.5 and 0.8 from the top to the bottom, respectively. The clean data and noisy data with SNR of −4.074 dB are shown in Fig. 3. For f-x deconvolution, f-x EMD and local Cadzow filtering, the range of frequency is set from 2 Hz to 75 Hz. For local Cadzow filtering, LSVD and LASVD, we use the sliding window consisting of 20 traces and 50 time samples. For local Cadzow filtering and LSVD, we set the rank r to be 2. For LASVD and SOASVD, we set the threshold as \(4\triangle {\overline{\sigma }}_{ni} \). The denoised results using f-x deconvolution, f-x EMD, LSVD, local Cadzow filtering, LASVD and SOASVD algorithm are shown in Fig. 4. We can see that the denoised result using f-x deconvolution (Fig. 4a) has obvious residual noise. Compared with local Cadzow filtering, LSVD, f-x EMD and f-x deconvolution, LASVD and SOASVD are more effective in removing noise. The removed noise sections are displayed in Fig. 5. We can also observe five hyperbolic leakage events from the removed noise section using f-x deconvolution in Fig. 5a and some visible leakage energy to the high slope event for LSVD (Fig. 5c) and local Cadzow filtering (Fig. 5d). There are little visible events using f-x EMD (Fig. 5b), LASVD (Fig. 5e) and SOASVD approach (Fig. 5f). To measure the leakage energy, we evaluate the cross-correlation sections between the denoised data and the corresponding removed noise shown in Fig. 6. The cross-correlation section in Fig. 6f illustrates that the leakage energy using SOASVD approach is least. For numerically comparing the denoising performances of these approaches, we evaluate the SNR of results processed with five approaches and list them in Table 1. The SNR of input noisy data in experiment one is −4.074 dB. The SNR using f-x deconvolution, f-x EMD, LSVD, local Cadzow filtering, LASVD and SOASVD approaches is 5.780 dB, 6.634 dB, 6.542 dB,7.237 dB, 9.709 dB and 12.047dB, respectively. The SNR of input noisy data in experiment two is −6.974 dB, and the SNR after processing using these approaches is 4.785 dB, 4.75 dB, 4.897 dB, 5.785 dB, 7.741 dB and 9.238 dB, respectively. SOASVD approach yields the best result for noise attenuation.

The second synthetic example contains conflicting linear events. The clean data (Fig. 7a) include one horizontal event and two dipping events. The noisy data are shown in Fig. 7c after adding random noise (Fig. 7b). Figures 8,  9 and  10 show the denoised results, the removed noise sections and their corresponding cross-correlation sections. The denoised results (Fig. 8a–d) by using f-x deconvolution, f-x EMD, LSVD and local Cadzow filtering are still contaminated by a certain amount of noise. Compared with them, Fig. 8e, f shows that random noise is largely suppressed. The removed noise (Fig. 9a–c) still has visible coherent events. From Figures 8f,  9f and  10f, it can be observed that SOASVD has the best performance in removing noise and preserving the useful signal except leaking a little energy in conflicted point of events. The processed result using the local orthogonalization method (Fomel 2007; Chen and Fomel 2015) is shown in Fig. 11. Comparing Fig. 11b, c with Figs. 9f,  10f illustrates that the leaked useful signal in conflicted point is effectively retrieved.

Table 1 Comparison of SNR using different approaches
Full size table

Field data example

To further demonstrate the performance of SOASVD in practice, we choose the 2D profile (Fig. 12a) from western China. There are 57 traces with a sampling rate of 1 ms. It can be observed that strong random noise is present in data. After applying f-x deconvolution, f-x EMD, LSVD, local Cadzow filtering and SOASVD methods, the denoised result and the removed noise are shown in Figs. 12 and  13, respectively. Random noise around at about 0.2 s is effectively attenuated by using f-x deconvolution, f-x EMD, LSVD and local Cadzow filtering approaches, while their performance is poor at about 0.3 s–0.5 s. Figures 12f and  13e show the information of events is well preserved and noise is suppressed using SOASVD method. It is noted that the dominant local slopes are estimated from Fig. 12b.

Limitations and future work

The SOASVD approach has its own limitations. The main limitation is that seismic events are attenuated or distorted at the crossed points because the predicted traces have lower similarity with the primitive trace in the region of the crossed points. Although the performance has improved by using the local orthogonalization, the investigation of noise attenuation regarding crossed points may be the subject of our future work.

Conclusions

We put forward a approach to attenuate random noise using structure-oriented adaptive singular value decomposition (SOASVD). With the approach, each trace is extended to a flat 2D profile via predicting the trace from its neighboring traces. After noise is attenuated, the predicted 2D profile is stacked as one trace. Random noise of the predicted flat 2D profile is attenuated by using ASVD filter which can adaptively choose the rank of the estimated signal according to the adjacent singular value increment and the SNR of processed windows. Synthetic and field data examples demonstrate that, compared with f-x deconvolution, f-x EMD, LSVD and local Cadzow filtering, the proposed approach can obtain the best performance in suppressing random noise and preserving the useful signals for the low SNR data with dipping and hyperbolic events .