Density interface topography recovered by inversion of satellite gravity gradiometry observations

Abstract

A radial integration of spherical mass elements (i.e. tesseroids) is presented for evaluating the six components of the second-order gravity gradient (i.e. second derivatives of the Newtonian mass integral for the gravitational potential) created by an uneven spherical topography consisting of juxtaposed vertical prisms. The method uses Legendre polynomial series and takes elastic compensation of the topography by the Earth’s surface into account. The speed of computation of the polynomial series increases logically with the observing altitude from the source of anomaly. Such a forward modelling can be easily applied for reduction of observed gravity gradient anomalies by the effects of any spherical interface of density. An iterative least-squares inversion of measured gravity gradient coefficients is also proposed to estimate a regional set of juxtaposed topographic heights. Several tests of recovery have been made by considering simulated gradients created by idealistic conical and irregular Great Meteor seamount topographies, and for varying satellite altitudes and testing different levels of uncertainty. In the case of gravity gradients measured at a GOCE-type altitude of $\sim$300 km, the search converges down to a stable but smooth topography after 10–15 iterations, while the final root-mean-square error is $\sim$100 m that represents only 2 % of the seamount amplitude. This recovery error decreases with the altitude of the gravity gradient observations by revealing more topographic details in the region of survey.

1 Introduction

Gravity gradiometry has been mainly used to image sub-surface geology to aid hydrocarbon and mineral exploration. Being more sensitive to the surface contrast of density and with higher acuity, the gravity gradiometry is better able to discern and locate mineral deposits and small-scale near surface geologic features. The detection of such buried structures requires accurate computation of the second derivatives of the potential (i.e. the six independent coefficients of the gravity gradient matrix) with respect to the three spatial coordinates of the chosen reference system.

Compared to the first derivatives of the gravitational potential, the spectral power of the gravity gradient components concern higher spatial frequencies. This makes the gravity gradient components (proportional to the inverse of the cube of the distance between the observation and the sources points) more localized than gravity anomaly vector components, and thus more sensitive to deeper masses.

Numerical methods to compute the gravity gradients were obtained by differentiating the gravity potential twice with respect to spatial coordinates. Except of the cases of mass volumes of simple shapes in polyhedral modelling (Roy 2008, Chap. 3), this operation requires discretization of the mass distribution by decomposing the Earth’s surface layer into elementary solid bodies.

Representation of mass sources in rectangular prisms was earlier explored by Talwani and Ewing (1960), Nagy (1966), Paul (1974), Plouff (1976), Ku (1977), and more recently Nagy et al. (2000), with exact analytical expressions for estimating gravity anomalies. Some of these approaches rely on Taylor series expansion of the potential integral kernel as they were inspired by MacMillan (1930) who developed the theory of rectangular-shaped mass elements.

Alternative computational methods were proposed to evaluate the gravitational effects of spherical prisms (or tesseroids). As there is no direct analytical expression providing the gravity effects of such a distribution of tesseroids, approximate methods of integration have to be considered. Ku (1977) and von Frese et al. (1981a, b) considered the spherical Earth approximation to locate points of mass through Gauss-Legendre Quadrature (GLQ) decomposition for solving the potential integrals. By minimizing the residuals between modelled and observed values following the least-squares criteria, these authors estimated the spatial positions of mass sources and use them as equivalent masses to model gravity anomalies for any arbitrary mass distribution. Later, Wild-Pfeiffer (2008) used GLQ decomposition to model gravity potential and to deduce its first derivatives. Petrović (1996) and Tsoulis (2012) proposed analytical expressions for polyhedral bodies using line integrals. It has been proved that sets of spherical prisms are the most accurate representations to evaluate gravity gradients with acceptable computational time (Heck and Seitz 2007; Wild-Pfeiffer 2008). In particular, Heck and Seitz (2007) considered a third-order Taylor expansion at the centres of the tesseroids to evaluate the gravity potential and its first radial derivatives, and finally Wild-Pfeiffer (2008) extended this method of integration to the second derivatives (i.e. all the components of gravity gradient). These authors proposed a semi-analytical strategy to solve 1D and then the remaining 2D integrals of the gravity potential by quadrature. This method was inspired by Tsoulis et al. (2003) who considered an arbitrary shape body and smooth mass sources. Grombein et al. (2013) proposed an optimal expression of the integral kernels where Cartesian coordinates replace spherical ones to decrease computational time. Lately, Roussel et al. (2015) proposed to use an ellipsoidal prisms representation and GLQ for integration of mass elements.

Spectral representations have been also developed to estimate the Fourier (or spherical harmonic) coefficients of gravity potential from the surface topography ones in a flat (or spherical, respectively) Earth approximation. Parker (1972) has originally proposed to estimate the gravity potential anomaly related to material interface variations by simply summing the Fourier transforms of the successive powers of the plane 2D topography limiting two media of different densities.

A number of algorithms have been developed to estimate the gravity gradients created by an interface separating two media of different densities; these techniques are exclusively based on fast 2-D Fourier transform in a planar approximation (Tziavos et al. 1988; Schwarz et al. 1990). Jekeli and Zhu (2006) assumed the topography consisting of rock columns of constant density but irregular heights, and computed the corresponding gradiometric anomaly by rectangular numerical integration. These authors showed that Fourier Transform techniques generate oscillations due to spectrum truncation (i.e. Gibbs effects). Moreover, more and more high-order terms in the Fourier expansion are required to reach the accuracy of 1 Eötvös $(10^{-9}\, \hbox {s}^{-2})$. These algorithms based on the flat-Earth approximation remain fast but inadequate to model gravity gradients in the case of large-scale sources that a 300-km altitude satellite such as GOCE (Gravity field and steady-state Ocean Circulation Explorer) mission would detect (Bouman et al. 2013). However Ramillien (2002) extended the Parker’s formula for modelling spherical harmonics of the gravity potential due to the topography of a shell density interface. Eshagh and Sjöberg (2009a, b) derived the forward expressions in spherical harmonics to estimate the GOCE-based gravity gradients. From a given geometry of mass density distribution, static gravitational effects of the topographic and atmospheric masses reach the level of tens of mGal and some units of E (mE) (Novák and Grafarend 2006). Eshagh and Sjöberg (2009a) proposed a method to evaluate the coefficients of the Earth’s topographic (and atmosphere) effects that were used to reduce the satellite gravimetry data in the local north-oriented instead of geocentric frames (Novák and Grafarend 2006) and applied it to the Fennoscandia and Iran regions. More recently, Eshagh and Sjöberg (2009b) have proposed non-singular expressions for gravity gradients based on the sums of spherical harmonics (defined on the entire sphere) by considering constant and laterally-varying topographic densities. This study was done in the perspective of the treatment of the ESA (European Space Agency) GOCE satellite mission measurements, since this mission was the first low-altitude geodetic mission carrying a 3-axis gradiometre to reach a spatial resolution of $\sim$100 km on the entire Earth excepting polar gaps (Floberghagen et al. 2011).

Martinec (2014) provides the spherical harmonic forms of the tensor Green’s functions to analyse GOCE-based gravitational gradients created by crustal and lithospheric anomalies in cartesian and spherical coordinate systems and shows that band-limited omission error for GOCE does not exceed 1 % in amplitude compared to the full spectrum mass density Green’s functions. It is also possible to evaluate the gravitational potential of topographic masses by introducing Legendre functions of the first and second kinds with imaginary variable expanded in Laurent series in a spherical geometry (Wang and Yang 2013). Šprlák et al. (2014) derived spatial and spectral forms for isotropic kernels of gravity gradients to solve analytically the spherical gradiometric boundary value problem.

Recently, different operators decomposed into azimuthal and isotropic parts in a local north-oriented reference frame were proposed to evaluate third-order disturbing gravitational tensor from density distribution (Šprlák and Novák 2015).

Except for localizing equivalent-mass points (Ku 1977; von Frese et al. 1981a, b), so far no inverse method has been proposed to estimate medium and long wavelengths of hundreds of kilometres of density interface topography from satellite-based (and airborne) gravity gradients in a spherical Earth approximation.

In the present article, new forward and inverse approaches to calculate the potential, the vector anomaly and second derivatives of gravity anomaly caused by the presence of a compensated topography for the spherical Earth are proposed. As gravity gradiometry technique is more suitable for catching the gravitational signature of an interface lying on a shell, we propose here to model and invert unevenly distributed gravity gradient data for the shape of an interface described by a set of infinitesimally narrow columns of constant density. As considering spherical (or ellipsoidal) tesseroids is the most accurate representation (see Heck and Seitz 2007; Wild-Pfeiffer 2008), it is adopted in the present study to derive the gravity gradients expressions for infinitesimally thin vertical column of constant density obtained by integration of elementary spherical elements in the radial direction from the Earth’s centre. Gravity gradients due to the presence of a topography can be evaluated by summing the individual contributions of rock columns of constant density.

In the first part of the article, the theoretical aspects of the computation are derived from the series of per-degree Legendre polynomials. One of the advantages of these series enables to introduce elastic Love numbers to take elastic compensation of the Earth’s surface into account, as this phenomena of compensation may occur at regional scales. The results of this forward method are confronted to the ones obtained by applying the Jekeli and Zhu (2006) approach based on the “planar approximation”, in the simple case of a single column of rock of constant density. An iterative least-squares inversion of satellite (or airborne) gravity gradient observations is proposed to estimate the corresponding topography of the interface, given the uncertainties on both the gravity gradients observations and modelled topographic heights. In the second part of the article, numerical validation of inversion consists of recovering the simple shape of a conical seamount by input of different data altitudes and a priori uncertainties for discussion. The method of estimation is finally used for retrieving the irregular seafloor topography around the 5000-m Great Meteor seamount [$29{^{\circ }}57^{\prime }10.6^{\prime \prime }$N; $28{^{\circ }}35^{\prime }31.3^{\prime \prime }$W], located in the North Atlantic Ocean by considering simulated along-track GOCE satellite measurements, and lower altitude airborne data.

2 Method

2.1 Model geometry

In the fixed-Earth reference frame, the surface topography of a spheroid is assumed to consist of a collection of vertical prisms of rectangular sections, inside a geographical region. The centre of the Earth is the centre of this orthogonal reference frame formed by the three unit vectors $\varepsilon _1$, $\varepsilon _2$ and $\varepsilon _3$. The $\varepsilon _3$-axis is along the rotation axis passing through the North and South poles, $\varepsilon _1$ and $\varepsilon _2$ axis are perpendicular to each other and they are contained in the equatorial plane. These $\varepsilon _1$ and $\varepsilon _2$ axis point across the Gulf of Guinea and the Pacific Ocean, respectively. Each element of a column is located at a radial distance r from the centre of the Earth $\Omega$ and has a thickness of dr and a constant density $\rho$, and thus its mass is:

$$\begin{aligned} dm=\rho \Delta \lambda \Delta \theta \cos \theta r^{2}dr \end{aligned}$$

(1)

where $\lambda$ and $\theta$ are the longitude and latitude of the considered mass element, and $\Delta \lambda$ and $\Delta \theta$ are its extensions in the geographical directions. The mass element is observed at satellite position at a radius a (Fig. 1). The angular and the Cartesian distances between the mass element and the observation point are $\psi$ and $\xi$, respectively.

Fig. 1

Schematic view of the surface rock column (as a particular element of the topography) having a gravity attraction measured at an external point (e.g. an artificial satellite)

2.2 Gravitational potential created by a compensated topography

The gravitational potential created by such a mass element is:

$$\begin{aligned} dV(a,\psi )=\frac{G}{\xi }dm=\frac{G}{\xi }\rho \Delta \lambda \Delta \theta \cos \theta r^{2}dr \end{aligned}$$

(2)

where G is the gravitational constant $({\sim }6.67\,\times \,10^{-11} \hbox {m}^{3}\,\hbox {kg}^{-1}\,\hbox {s}^{-2})$, and $\xi$ the distance between the mass element and the observing satellite. The inverse of this distance can be expanded into Legendre polynomials $P_n$ of degree n:

$$\begin{aligned} \frac{1}{\xi }=\frac{1}{a}\sum _{n=0}^\infty {\left( \frac{r}{a}\right) ^{n}P_n (\cos \psi )} \end{aligned}$$

(3)

Equation 2 can be integrated with respect to the radial distance and taking Eq. 3 into account, to obtain the potential created by a column of rock of length r from $\Omega$ (i.e. $r=0$) :

$$\begin{aligned} V(a,t)=\frac{G\rho \Delta \lambda \Delta \theta \cos \theta }{a}\sum _{n=0}^\infty {P_n (t)\left( \frac{r}{a}\right) ^{n}\frac{r^{3}}{n+3}} \end{aligned}$$

(4)

and defining the angular parameter: $t=\cos \psi$.

For taking elastic compensation of the Earth’s surface into account, a linear factor containing the per-degree Love numbers $k_n$ is simply added into Eq. 4:

$$\begin{aligned} V(a,t)= & {} \frac{G\rho \Delta \lambda \Delta \theta \cos \theta }{a}\sum _{n=0}^\infty P_n (t)(1+k_n )\left( \frac{r}{a}\right) ^{n}\nonumber \\&\times \frac{r^{3}}{n+3} \end{aligned}$$

(5)

A list of the first load Love numbers is provided by Wahr et al. (1998). These values were previously computed following the method of Dazhong and Wahr (1995) and using the Preliminary Reference Earth Model (PREM) (Dziewonski and Anderson 1981).

2.3 Gravity anomaly components

The components of the gravity anomaly vector $\Gamma _\alpha =(\nabla V)_\alpha$ are the first derivatives of the potential measured by the onboard instruments with respect to the one of the spatial coordinates $\alpha$ of the observation point, which can be $X_1$, $X_2$ or $X_3$ in the geocentric reference frame defined in Sect. 1.1, so that:

$$\begin{aligned} \frac{\partial V}{\partial \alpha }=\frac{\partial V}{\partial a}\frac{\partial a}{\partial \alpha }+\frac{\partial V}{\partial t}\frac{\partial t}{\partial \alpha } \end{aligned}$$

(6)

If the Cartesian coordinates of the top of the rock column are $x_1 ,x_2 ,x_3$ in the same reference frame and using Eq. 5, we have:

$$\begin{aligned} \frac{\partial V}{\partial a}= & {} -\frac{G\rho \Delta \lambda \Delta \theta \cos \theta }{a^{2}}\sum _{n=0}^\infty {(1+k_n )(n+1)} \left( \frac{r}{a}\right) ^{n}P_n (t)\nonumber \\&\times \frac{r^{3}}{n+3} \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial V}{\partial t}= & {} \frac{G\rho \Delta \lambda \Delta \theta \cos \theta }{a}\sum _{n=0}^\infty {(1+k_n )\left( \frac{r}{a}\right) ^{n}} \frac{dP_n (t)}{dt}\frac{r^{3}}{n+3}\nonumber \\\end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial a}{\partial \alpha }= & {} \frac{\alpha }{a}\end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial t}{\partial \alpha }= & {} \frac{\partial t}{\partial X_i }=-\frac{X_i t}{a^{2}}+\frac{x_i }{ar} \end{aligned}$$

(10)

where $\frac{dP_n (t)}{dt}$ is the first derivative of the Legendre function $P_n (t)$ with respect to the angular parameter t.

Fig. 2

Convergence of the Legendre polynomial expansion to compute the components of the gravity gradient, with respect to the number of terms of the series and the ratio of the radial distances. The convergence of the series is particularly fast for important satellite altitudes, as it requires less terms to be reached completely. The bottom graph is zoomed in to illustrate the slow convergence of the Legendre polynomial series that is completed for at least 20,000 terms

Fig. 3

Geographical maps of the six independent components of the gravity gradient anomaly created by an uncompensated 2-km height rock column located at x = 0 and y = 0 and having a density of $2600\,\hbox {kg/m}^{3}$ and measured at 10 m above the summit. The size of the section of each infinitesimally thin column is 10 m $\times$ 10 m, and the total number of juxtaposed columns is 40,000

Fig. 4

Maps of the gravity gradient components due to a simple 2 km $\times$ 2 km $\times$ 2 km cubic topography having a constant density of $2600\,\hbox {kg/m}^{3}$ as it is observed at an airborne-type altitude of 4000 m above the summit (to be compared with the previous figure)

2.4 Gravity gradient components

The elements of the symmetric gravity gradient $\Gamma _{\alpha ,\beta } =(\nabla \nabla V)_{\alpha ,\beta }$ are the second derivatives of the potential function with respect to the pair of spatial coordinates $\alpha$ (i.e. $X_1$, $X_2$ or $X_3$), and $\beta$ (i.e. $X_1$, $X_2$ or $X_3$):

$$\begin{aligned} \frac{\partial ^{2}V}{\partial \alpha \partial \beta }= & {} \frac{\partial V}{\partial a}\frac{\partial ^{2}a}{\partial \alpha \partial \beta }+\frac{\partial V}{\partial t}\frac{\partial ^{2}t}{\partial \alpha \partial \beta }+\frac{\partial ^{2}V}{\partial a^{2}}\frac{\partial a}{\partial \alpha }\frac{\partial a}{\partial \beta }\nonumber \\&+\frac{\partial ^{2}V}{\partial t^{2}}\frac{\partial t}{\partial \alpha }\frac{\partial t}{\partial \beta }+\frac{\partial ^{2}V}{\partial a\partial t}\left( \frac{\partial a}{\partial \alpha }\frac{\partial t}{\partial \beta }+\frac{\partial a}{\partial \beta }\frac{\partial t}{\partial \alpha }\right) \end{aligned}$$

(11)

with:

$$\begin{aligned} \frac{\partial ^{2}V}{\partial a^{2}}= & {} \frac{G\rho \Delta \lambda \Delta \theta \cos \theta }{a^{3}}\nonumber \\&\times \sum _{n=0}^\infty {(1+k_n )(n+1)(n+2)P_n (t)}\nonumber \\&\times \left( \frac{r}{a}\right) ^{n}\frac{r^{3}}{n+3} \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial ^{2}V}{\partial t^{2}}= & {} \frac{G\rho \Delta \lambda \Delta \theta \cos \theta }{a}\sum _{n=0}^\infty {(1+k_n )\frac{d^{2}P_n (t)}{dt^{2}}}\nonumber \\&\times \left( \frac{r}{a}\right) ^{n}\frac{r^{3}}{n+3} \end{aligned}$$

(13)

$$\begin{aligned} \frac{\partial ^{2}V}{\partial a\partial t}= & {} \frac{\partial ^{2}V}{\partial t\partial a}=-\frac{G\rho \Delta \lambda \Delta \theta \cos \theta }{a^{2}}\nonumber \\&\times \sum _{n=0}^\infty {(1+k_n )(n+1)} \frac{dP_n (t)}{dt}\left( \frac{r}{a}\right) ^{n}\frac{r^{3}}{n+3}\nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial ^{2}a}{\partial X_i \partial X_j }= & {} \frac{\partial ^{2}a}{\partial X_j \partial X_i }=\frac{\delta (i,j)}{a}-\frac{X_i X_j }{a^{3}} \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial ^{2}t}{\partial X_i \partial X_j }= & {} \frac{\partial ^{2}t}{\partial X_j \partial X_i }=-\frac{t}{a^{2}}\delta (i,j)\nonumber \\&+\frac{3X_i X_j t}{a^{4}}-\left( \frac{X_i x_j +X_j x_i }{a^{3}r}\right) \end{aligned}$$

(16)

where $\delta (i,j)$is the Kronecker delta symbol that equals one if $i=j$ and zero elsewhere, and $\frac{d^{2}P_n (t)}{dt^{2}}$ is the second derivative of the Legendre function with respect to the parameter t.

From the equations for computing potential, gravity vector and gradients, it is clear that the speed of the convergence of the polynomial series decreases as the ratio r / a approaches unity. Consequently, the number of terms to reach the exact gravity gradient component values must increase for low altitudes, as more degree n terms from Eq. 3 are required to reach stable estimates (Fig. 2). The speed of convergence of each $\Gamma _{\alpha ,\beta }$ is different. For the diagonal tensor elements, stable values are reached faster than the non-diagonal ones. The magnitudes of the gravity gradient components decrease with observation altitude, and these magnitudes tend to the same order as the observer is closer to the density source, e.g. of several hundreds of E at 4 km below the top of the relief (see the bottom graph of Fig. 2).

2.5 Case of surface topographic heights

The compensated potential, gravity anomaly and gravity gradients created by a vertical rock column which basis and top surfaces are located at the radial distances $r=r_{\min }$ and $r=r_{\max }$, respectively, from the centre of the Earth are the differences (Fig. 1):

$$\begin{aligned} V(r_{\min } ,r_{\max } )= & {} V(r=r_{\max } )-V(r=r_{\min } ) \end{aligned}$$

(17)

$$\begin{aligned} \Gamma _\alpha (r_{\min } ,r_{\max } )= & {} \Gamma _\alpha (r=r_{\max } )-\Gamma _\alpha (r=r_{\min } ) \end{aligned}$$

(18)

$$\begin{aligned} \Gamma _{\alpha ,\beta } (r_{\min } ,r_{\max } )= & {} \Gamma _{\alpha ,\beta } (r=r_{\max } )-\Gamma _{\alpha ,\beta } (r=r_{\min } ) \end{aligned}$$

(19)

For a set of juxtaposed rock columns inside a region, the gravity potential, anomaly or gradient observed at satellite altitude a and angular parameter t (see Eq. 4 in Sect. 2.1) is simply the sum of all the gravity attractions of the $k=1,2,\ldots K$ topographic heights. For example, for computing the gravity gradient components created by a collection of constant density rock prisms, we use:

$$\begin{aligned} \Gamma _{\alpha ,\beta } =\sum _{k=1}^K {\Gamma _{\alpha ,\beta } (r=r_{k,\max } )-\Gamma _{\alpha ,\beta } (r=r_{k,\min } )} \end{aligned}$$

(20)

Figures 3 and 4 present the results of the computation of the gravity gradient components in the case of a very simple topography formed by a 2 km $\times$ 2 km $\times$ 2 km cube composed by juxtaposed radial columns which horizontal section dimensions of each column are 10 m $\times$ 10 m, and depending upon the altitude of observation (i.e. the vertical distance from the base of this relief 10 m and 4 km, resp.). Note that non-diagonal gravity gradient components are smaller than the diagonal ones in Fig. 3 (case of the bottom graph in Fig. 2 for a 4-km observation altitude), they are simply multiplied by a factor 2 for easing graphical representation. Note that decreasing the altitude down to tens of metres above the summit enables to locate the sharp edges and faces of the source better. This sensitivity illustrates one the superiority of using gravity gradiometry instead of considering less recent potential methods for detecting the shapes of small objects (see Pajot 2007).

Fig. 5

Profiles of the gravity gradient components created by a 2 km $\times$ 2 km $\times$ 2 km block of constant density $2600\, \hbox {kg/m}^{3}$ in the horizontal x-axis direction (top, where $\Gamma _{xy} =\Gamma _{yz} )$ following the proposed spherical tesseroids method, and in the diagonal direction between the x and y axis (bottom, where $\Gamma _{xx} =\Gamma _{yy}$ and $\Gamma _{yz} =\Gamma _{zx} )$

Fig. 6

Differences between the 2 km $\times$ 2 km $\times$ 2 km block simulations made using the Fourier-based method proposed by Jekeli and Zhu (2006) and applying our “spherical” approach. Differences are less than $10^{-4}$ E, this values corresponds to 0.1 % of the amplitude above the source of anomaly

Fig. 7

Error analysis on the evaluation of the gravity gradient derivatives with respect to the topographic parameter dh from Eq. 23, in the case of a 2 km $\times$ 2 km $\times$ 2 km block of constant density $2600\,\hbox {kg/m}^{3}$ observed at an altitude of 4000 m (same configuration as Fig. 4). An acceptable precision on the values of the derivatives are reached for dh < 0.1 – 1 metre

2.6 Numerical validation of the gravity gradients

The estimates obtained by the method proposed for the spherical case (Eq. 20) need to be confronted to the predicted ones using the computational scheme earlier proposed by Jekeli and Zhu (2006) for the local case. For this purpose, the simple case of the gravity gradient components observed at several altitudes created by a 2000-m rock column of constant density $2600\,\hbox {kg/m}^{3}$ is considered. To simplify this numerical test, this rock column is centred at zero longitude and latitude, and its top surface is $1{^{\circ }}$ by $1{^{\circ }}$ that represents around 111 km $\times$ 111 km at equatorial latitudes. Figure 5 presents on-axis and diagonal profiles of the six gradiometric components with respect to the distance from the centre of the rock column. In both cases of applying separately Jekeli and Zhu (2006) method and our spherical approach, the amplitudes computed per gravity gradient component, within ${-}0.2$ to ${+}$0.4 E, remain very comparable. The per-component differences do not exceed $10^{-4}$ E at the summit of the column and decreases with the distance according to Fig. 6. Thus, the forward spherical approach provides consistent estimates of the gravity gradient elements. These residuals represent $10^{-4}$ E for each component of the gravity gradient for a volume of rock, and these tiny differences correspond to the small region of 2-by-2${^{\circ }}$ we consider where the geometrical distortion between “pure planar” and spherical terrestrial surface approximations remains insignificant. The differences are important when the Earth’s curvature cannot be neglected for large geographical areas. Spectral methods can be only applied to small regions where the planar approximation remains valid. Alternatively, the strategy of decomposing a large area into overlapped planar tiles of a few degrees in longitude and latitude each, have to be applied for predicting seafloor topography from radar altimetry data, e.g. in entire oceanic basins (Ramillien 1998).

Fig. 8

Recovery of a conical 2000-m amplitude seamount from simulated gravity gradients at several iteration steps. The altitudes of observation are of 100 km (left) and 300 km (right)

3 Inverse problem: estimating topographic height from gravity gradients

A set of topographic heights separating media of different densities can be recovered from satellite / airborne gravity gradient observations $\Gamma _{\alpha \beta }$ with ${ i=1,{\ldots } 6 \times N}$, by considering the six independent component of the gravity gradient matrix for each observation point. Density of the topographic columns to retrieve is assumed to be constant. As the operator relating the topographic heights to the observations is not linear, an iterative strategy for approximating progressively the optimal topography solution needs to be applied. The Gauss-Newton steepest descent algorithm proposed earlier by Tarantola (1987) (see Sect. 4.5, p. 244) is the easiest estimation procedure to implement in our case. This simple gradient search gives the vector $H_k$ containing the j = 1,... M topographic heights $h_j$ at the iteration number k from the vector $H_{k-1}$ of the previous iteration $k-1$:

$$\begin{aligned} H_k= & {} H_{k-1} +\left[ {F_{k-1}^T C_D^{-1} F_{k-1}^ +C_H^{-1} } \right] ^{-1}\nonumber \\&\times \left\{ {F_{k-1}^T C_D^{-1} (f_{OBS} -f_{k-1} )+C_H^{-1} (H_{k=0} -H_{k-1} )} \right\} \nonumber \\ \end{aligned}$$

(21)

The superscripts “T” and “−1” indicate the transpose and the inverse matrices, respectively. $f_{OBS}$ is the vector containing the N gradiometry data observations, $f_k$ is the one of the gradiometric values computed at the k-th iteration from the set of M topographic heights $H_k$ to be recovered using the forward modelling equations of the previous Sect. 2. $F_k$ represents the matrix of the first derivatives of $f_k$ for each topographic height that can be approximated by:

$$\begin{aligned} F_{ij} \approx \frac{f_i (h_j +\delta h/2)-f_i (h_j -\delta h/2)}{\delta h} \end{aligned}$$

(22)

and numerical tests have shown that the topographic parameter $\delta h$ should be smaller than $\sim$1 m (0.1 m was used for a level of accuracy of $10^{-5 }$% in all gravity gradient simulations) (see Fig. 7, where the computational errors on the derivatives obtained for different distances between the observation point and the density relief show similar simple shapes. They are flat from $\delta h \sim$1 to $\sim$10 m for distances of 4 km and 10 km, respectively, and the errors suddenly increase from these values). The condition for a relative error less than 0.01 % is reached at $\delta h = 50\,\hbox {m}$ as the altitude is 4000 m above the summit, and at $\delta h = 5000\,\hbox {m}$ when the altitude of observation is 300 km. The 0.01 %-error limit for this topographic parameter increases with the smoothness of the gravity gradient signals, thus with the distance between the observation point and the mass sources. $C_D$ is the a priori error covariance matrix of the observations of dimension 6Nx6N which can be simply modelled in the case of independent gravity gradient observations by:

$$\begin{aligned} C_D =\sigma _D^2 I \end{aligned}$$

(23)

where $\sigma _D^2$ is the a priori variance of the gradiometric observations and I represents the identity matrix, and thus it is purely diagonal. $C_H$ is the a priori error covariance matrix of the topographic heights of dimension MxM that can be modelled with the input of the spatially isotropic correlations between the topographic heights into account by imposing its elements to be (Hirvonen 1962):

$$\begin{aligned} \{C_H \}_{ij} =\frac{\sigma _H^2 }{1+(\varphi _{ij} /\varphi _0 )^{2}} \end{aligned}$$

(24)

where $\sigma _H^2$ is the a priori variance of the topographic errors. $\varphi _{ij}$ represents the spherical distance between the rock columns numbers i and j, and $\varphi _0$ the length of correlation between the topographic heights. In the following numerical tests, these priori variances, and the length of correlation, were tested in the iterative inversion (Eq. 21) for different cases of recovery.

Fig. 9

Recovery errors for the case of the conical seamount with respect to the a priori uncertainty on the unknown topographic heights $\sigma _H$ and the length of their spatial correlation $\varphi _0$

4 Inversion of simulated gradiometric data of a simple relief

The main advantage of using simulated topography data and observations is to consider them as a reference and thus to quantify the recovery error easily. For validation of the proposed inverse method, we try to retrieve the shape of a 2000-m high conical seamount of density $2600\,\hbox {kg/m}^{3}$ as accurately as possible. The density of the surrounding sea water is assumed to be $1000\,\hbox {kg/m}^{3}$. The base of the seamount is located at a constant radial distance, which corresponds to the mean Earth’s radius. Simulation of the six independent components of the gravity gradient matrix due to the presence of this simple relief is made on a 1/5-degree grid at altitude h above the base of the seamount, by applying the forward problem equations from Sect. 2.4.

Fig. 10

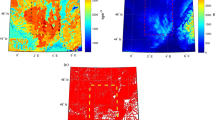
Reference bathymetry in the region of the Great Meteor seamount extracted from the ETOPO-5 database and spatially re-sampled at $0.04{^{\circ }}$ (left), and three months of GOCE satellite tracks over the same oceanic region (right). The rectangular frame indicates the limits of the inner region where the topographic heights are adjusted, while the positions of the gravity data used in the inversion are taken in the larger area

Fig. 11

Seafloor topography in the Great Meteor seamount region estimated by using the proposed spherical approach and after 15 iterations, considering $N=300$ Legendre polynomial terms, $\varphi _0 =0.2{^{\circ }}$, as well as different durations of 300-km altitude observations and a priori gravity gradient data accuracy

Fig. 12

Final estimation of the topography of the Great Meteor seamount a after 15 iterations of inversion, considering gravity gradient observations at an altitude of 10 km, with $\varphi _0 =0.2{^{\circ }}$, $\sigma _D =0.1$ E and $\sigma _H =5000$ m, as well as associated recovery errors (b)

Following the proposed inversion procedure of Eq. 21, the parameter vector formed by the topographic heights to recover is progressively constructed as a linear combination of the gravity gradient observations with optimal coefficients from least-squares adjustment and converges to a stable solution. Figure 8 illustrates the progressive construction of the topographic solution for several iterations in two cases of observation levels above the sea floor: (i) altitude of 100 km considering $N=1000$ terms in the polynomial series, and (ii) GOCE satellite-type altitude of 300 km keeping $N=300$ terms only. As short-wavelength details of the density source are damped with altitude, the recovery of the shape of the seamount is more precise in the first case where final errors less than 50 m root mean square (r.m.s) after having completed a total of 50 iterations, whereas the summit and the flanks of the structure are not well retrieved in the second case (with final errors of $\sim$100 m r.m.s.). A stable topographic solution is reached after 15–20 iterations in both cases (i) and (ii). The r.m.s. differences consecutive solutions is less than 10 metres after the iteration number 20–25 (see last iterations presented in Fig. 8).

In order to reach the most precise solution, the inversion parameters (i.e. a priori uncertainties $\sigma _D$ and $\sigma _H$ on observations and topographic heights, respectively, and the correlation length $\varphi _0)$ can be tuned in the inversion. The best results have been obtained when $\sigma _D = 10^{-5}$ – $10^{-3}$ E for very accurate gravity gradient observations and $\sigma _H = 700 - 900$ m (Fig. 9). Smaller values of this latter parameter lead to a slow convergence to a stable estimate, while important values yield oscillating solutions (no convergence). When the observations are considered as not accurate enough ($\sigma _D> 0.1$ E), the recovered topography is smooth, whereas the process diverges due to numerical instabilities if $\sigma _D < 10^{-6}$ E. As in Fig. 9, a length of spatial correlation of $\sim 0.2 {^{\circ }}$ provides less error in the final topographic solution.

5 Case of an irregular topography: the Great Meteor seamount

The region of the Great Meteor seamount in the North Atlantic Ocean is the perfect example of an irregular topography, so that it represents a good test for challenging the proposed method of inverting gravity gradient components due to the seafloor interface and measured by a low-altitude gradiometer such as GOCE satellite. Seafloor topography in this region is provided by the ETOPO-5 database (1988) and linearly re-interpolated onto a grid sampled at $0.02 {^{\circ }}$ in the longitude and latitude directions. In other words, the topographic heights to be recovered consist of rock columns of $0.02 {^{\circ }} x\,0.02{^{\circ }}$, and the density contrast with respect to the surrounding seawater is assumed to be $1700\,\hbox {kg/m}^{3}$. The base of the Great Meteor seamount is located at a depth of $\sim$5000 m below the sea surface (Fig. 10).

The positions of the GOCE satellite for a period of 3 months are from the kinematic orbits computed by the Institute of Theoretical Geodesy and Satellite Geodesy (ITSG) at the University of Graz, Austria (website: ftp.tugratz.at/outgoing/ITSG/tvgogo/orbits), where the satellite positions are computed at a 5 second-sampling rate. From these positions and the ETOPO 5-derived topography in the region, the six components of the gravity gradients are computed using the forward equations given in Sect. 2.4. According to the numerical tests presented in the previous section, choosing $N=300$ is enough to ensure the convergence of the series of Legendre polynomials at the GOCE satellite altitude due to less sensitivity of the satellite observations to upward continuation. Alternatively, at least $N \sim 8000$ terms are required to compute the gravity gradient components at low (airborne) altitude (as the number of terms increases to reach the convergence as the ratio r / a gets closer to 1, see Fig. 2). Then, Eq. 21 is applied to estimate the topographic heights starting by the zero solution (i.e. no information on the starting topographic heights, $H_{k=0}=0)$.

Figure 11 shows the solutions obtained after 15 iterations when considering different combination of parameters like the duration of observation (i.e. satellite data coverage) and a priori uncertainties $\sigma _D$ and $\sigma _H$. The final solutions are relatively smooth for a 300-km GOCE-type altitude, but the location and amplitude of the Great Meteor seamount are quite well retrieved. Convergence remains slow if $\sigma _H < 2000\,\hbox {m}$, optimal speed or number of iterations is found for $\sigma _H = 5000\,\hbox {m}$, as lower values of this a priori parameter yield slower convergence (see Sect. 4). Absolute errors are in the range of 6 – 8 m r.m.s. Less error in the final solution is obtained for small values of the a priori variance on the gravity gradient observations (${<}10^{-4}$ E) than for three time denser coverage of 3 months of the satellite tracks. To confirm that the altitude of the observations is the most sensitive parameter in the recovery process, airborne-type gravity gradient observations were simulated for an altitude of 10 km and inverted by still following Eq. 21. The final solution and the corresponding absolute errors represented by short wavelengths of 3.5 m r.m.s. with a maximum of 1135 m on the northern flank of the main Great Meteor structure are presented on Fig. 12. It shows a gain of topographic details; in particular, the smaller seamount is detected in the southwest part. Residual errors are located on the slopes of the three seamounts of the region where the topographic gradient is important, while the peaky tops of the small reliefs are underestimated because the topographic solution remains smooth, as it is the same case for the simple conical seamount (see Sect. 4 and Fig. 8).

Next step would be to invert real gradiometry data provided by the GOCE mission. However, the use of such real satellite gravity gradient observations is difficult because of: (i) the presence of coloured noise, (ii) the fact that GOCE gradiometer provides only four accurate measurements, and (iii) the fact that the observations are a mixing of gravitational effects of many possible density interfaces inside Earth. Efficient band-pass pre-filtering for isolating the unique signature of a surface topography remains another problem to be solved before inverting real GOCE gravity gradient measurements. Unfortunately, these observations are a mixing of all possible gravitational effects created by deeper density interfaces, and thus difficult to be interpreted in terms of interface topography only.

6 Conclusions and recommendations

A forward approach for computing gravity anomaly data, including the six components of the gravity gradient matrix, due to a compensated interface topography has been developed for a spherical Earth surface. In particular, for regions where the planar approximation remains valid, it provides estimates that are consistent to the ones obtained by the method earlier proposed by Jekeli and Zhu (2006). The approach could be used to reduce regional airborne (or satellite) observations from the effects of the surface topography or any other density interface. An iterative inverse strategy is also proposed to demonstrate the possibility of recovering a set of topographic heights on a spherical surface given the associated gravity gradient observations. The most critical parameter in the inversion process is the distance between the positions of the sources of mass and the observations, as more details of the topography can be adjusted for accurate measurements. Numerical experiments suggest that noise-free accurate gravity gradient data are the ideal case by considering very small values for a priori uncertainty on gravity gradient observations $\sigma _D$, besides divergence of the estimation process is avoided when $\sigma _D$ is greater than $10^{-5}$ E. In terms of optimal a priori uncertainty parameters, the convergence is fast when a priori uncertainty on topographic heights $\sigma _H$ is of order of the expected amplitude of the topography to be recovered. In this case, a length of correlation of $0.2{^{\circ }}$ provides the less recovery errors. Recovering undersea relief of irregular shape, such as the one of the Great Meteor seamount, would be also possible by inverting gravity gradient data. The numerical studies presented here are based on simulated gravity gradient data; the next step would be how the proposed method perform with inversion of actual GOCE products, e.g. to map seafloor topography in remote regions of the Southern oceans that are not covered by ship tracks, or to estimate density and thickness variations of the oceanic lithosphere. However, the forward modelling of gravity gradient quantities in the spherical case derived in this study would be of great help for data reduction, as previously mentioned by Heck and Seitz (2007).