1 Introduction

A large number of research has been dedicated to study the failure due to ductile and brittle fracture under various loading conditions, which causes different modes of fracture. One of the modes of fracture which has recently been considered by various researchers is the third mode of fracture and its combination with the first mode of fracture. On the other hand, mixed mode failure conditions can be seen more in sandwich structures and adhesive joints between constitutive layers of the structures. Hence, designing an efficient testing configuration, in order to examine fracture resistance of specimens under different combinations of fracture modes I and III, is needed for these kinds of investigations on structures.

Numerous fixtures and test specimens have been used by researchers for experimental studies of mixed mode I + II fracture (see, for example, Richard and Benitz 1983; Shetty et al. 1987; Williams and Ewing 1972; Papini et al. 1994; Xeidakis et al. 1996; Szekrényes 2006; Ayatollahi and Aliha 2009; Ayatollahi et al. 2011; Aliha and Ayatollahi 2013, 2014; Shimamoto et al. 2016; Vaishakh and Narasimhan 2019; Ajdani et al. 2020). Among the studies about the mixed mode I + II fracture, some researchers focus on Mixed Mode Bending (MMB) test configuration for the combination of mixed mode I/II loading. For instance, Ducept et al. (2000) compare mixed mode initiation failure criteria for delamination of a glass/epoxy composite and its composite/composite bonded joint by using DCB, ENF, and MMB test configurations. Also, Khoo and Kim (2011) investigate the effect of bond-line thickness on the critical strain energy release rate of Aluminium adherends and an epoxy adhesive under mixed mode loading I + II. In addition, Stamoulis et al. (2014) investigate the fracture properties of adhesively bonded joints by single-component epoxy adhesive under mode I and mixed-mode I + II loadings (by using MMB experimental fixture), in order to obtain the full fracture envelope.

On the other hand, the Compact Mixed Mode (CMM) (Pang 1995) and bonded Compact Tension Shear (CTS) specimen (Madhusudhana and Narasimhan 2002; Pirondi and Nicoletto 2002) have been adapted to test mixed mode loaded bonded joint. They use a calibration factor that compares the Stress Intensity Factor (SIF) of an adhesive joint to that of a homogenous specimen. The calibration factor is extracted from FE analyses for each mode and depends on the geometry of the specimen (Högberg and Stigh 2006).

Sørensen et al. (2006) and Sørensen and Jacobsen (2009) have represented a fixture to characterize fracture of adhesive joints in mixed modes I and II fracture. In the designed test configuration in their study, the state of the stress at the crack tip of the specimens can be varied from pure mode I to pure mode II by varying the ratio between two uneven moments applied to a double cantilever specimen. One of the advantages of the represented fixture in the studies of Sorensen is the ability to apply direct moment to the test specimens.

Compared to the mixed mode I + II fracture, fewer test specimens and configurations have been represented for experimental studies of mixed mode I + III fracture in prior investigations. A number of outstanding examples of mixed mode I + III fracture can be mentioned; e.g., the compact tension (CT) specimen with an angled crack (Kamat et al. 1998), the circumferentially notched round bar (Chang et al. 2006), the single edge cracked specimen (Lan et al. 2006) and the three-point bend specimen with asymmetrically oriented crack (Lin et al. 2010; Pham and Ravi-Chandar 2014). Some studies (Ayatollahi and Saboori 2015; Berto et al. 2016; Akhavan-Safar et al. 2020) have suggested a loading fixture for edged crack rectangular plate specimens for mixed-mode I + III fracture toughness investigations. Another test configuration was designed by Aliha et al.(2015, 2016) and Bahmani et al. (2021) called the edge notched disc bend (ENDB) specimen which is a circular disc that contains a straight edge crack through the disc side and is subjected to three-point bend loading. Davidson and Sediles (2011) and Johnston et al. (2014) proposed a new shear-torsion-bending (STB) test which is capable of providing any ratio of the mode I, II, and III loading to determine fracture toughness in testing. They have superposed a mixed-mode bending (MMB) type arrangement for modes I and II (ASTM D6671_D6671M-06 2006) with a modified split cantilever beam (MSCB) arrangement for mode III (Robinson and Song 1992; Sharif et al. 1995) in their testing configuration. However, carrying out STB tests requires 4 individual actuators for creating different modes of loading and 5 sensors and load cells for measuring the applied loads, which makes it very difficult to simultaneously control all of them.

Brittle fracture occurs at the fully constrained loading conditions where the small scale yielding condition is not violated. However, in the unconstrained loading conditions where fracture process zone is larger than K-dominated zone (Kanninen et al. 1988), ductile fracture happens in the material. In an intermediate situation, similar to the one represented in this paper, failure prediction requires the modelling of the fracture process zone (Sørensen and Jacobsen 2003). Cohesive zone modelling is one of the most applicable models that is recently being used for this purpose in various studies.

This model assumes that the stress across the fracture process zone (\(\sigma \)) is a function of the local opening of the crack tip (\(\delta \)) and represents a relationship between these parameters. Based on the cohesive law approach, cohesive stress vanishes where the crack tip opening reaches a critical value. The failure of concrete structures (Li et al. 1994) and crack bridging on ceramic matrix composites (Cox and Marshall 1991) can be mentioned as the first examples of large scale process zone problems which have been analysed by cohesive zone modelling (CZM). A lot of investigations have been conducted to predict the strength of the specimens and components based on idealized cohesive laws (e.g. see Suo et al. 1993; Gu 1993; Wei and Hutchinson 1998; Kafkalidis and Thouless 2002). Most studies use an indirect method for determining cohesive laws wherein a trial on the prediction of the cohesive law parameters has been done by comparing the behaviour of the component (e.g. experimental load–displacement curve) with the resulting data from the corresponding simulations based on guessed cohesive law parameters (Yang and Thouless 2001). Hence, this method requires massive computational modelling to extract cohesive law parameters. Several studies have represented direct methods for the determination of the cohesive law parameters. Measuring the crack opening profile of a crack subjected to monotonic loading and then back-calculating the cohesive stresses using the fracture mechanics modelling in a way that the crack opening profile obtained from the calculation and the experiment agree with each other is one of the direct methods (Cox and Marshall 1991). However, in this method, it is challenging to introduce a test configuration that provides a stationary (stable) crack wherein the crack end opening exceeds its critical value so that the cohesive zone is fully developed and the entire cohesive law is in play, due to the crack growth at this situation (Sørensen and Jacobsen 2003).

The direct tensile test can be mentioned as another direct approach for determining the cohesive law parameters represented by Brenet et al. (1996). In this method, the opening of the cohesive law has been given by subtracting the elastic deformation from the measured displacement between two points of the tensile test specimen. However, it is usually hard to achieve a uniform damage evolution across the width of the specimen. Li and Ward (1989) measured the J-integral and end opening of the cohesive zone in compact tension specimens and derived the cohesive law parameters from the resulted data. Sørensen and Jacobsen (2003) and Joki et al. (2020) applied the same approach to double cantilever beam specimens and extended the method to deal with mixed mode I + II fracture. The first pioneering research to measure the fracture energies of adhesively bonded joints under mixed-mode I + III loading has been published by Chai (1992, 2021). Recently, following the idea of Chai, Loh and Marzi (2018a, b, 2019) studied the fracture of adhesive joints by designing a new test setup which is called the mixed-mode controlled double cantilever beam (MC-DCB) test, based on superimposing peel mode I and out-of-plane shear mode III. In this setup, an adhesively bonded DCB specimen is loaded by the combination of a force in mode I and a moment in mode III of fracture (Bödeker and Marzi 2020).

In this paper, firstly, theoretical backgrounds of the cohesive zone model and a method to calculate the J-integral in double cantilever beam specimens under uneven bending moments applied using the fixture, have been represented. Afterward, a new fixture and test specimen, inspired by the represented test configuration by Sørensen et al. (2006) and Sørensen and Jacobsen (2009) for mixed mode I + II fracture, have been designed for the experimental studies of mixed-mode I + III fracture resistance of specimens where it can provide loading conditions from pure mode I to pure mode III. A double cantilever beam specimen loaded with two pure bending moments which is named dual bending moment double cantilever beam (DBM-DCB) has been proposed to study the mixed mode I + III fracture resistance. The proposed DBM-DCB test configuration provides one of the few exceptions in which \({J}_{ext}\) can be obtained analytically due to the pure bending moments applied to the DCB specimens (Sørensen and Jacobsen 2003). This feature of the DBM-DCB test configuration can be considered as the major advantage of this fixture upon the prior testing configurations like the STB test or the one represented by Loh and Marzi (2018a, b, 2019) for studying the adhesive delamination.

Afterward, a section of the paper is dedicated to evaluation of the application of the fixture in providing pure mode I, pure mode III and two different combinations of these modes of fracture. For this purpose, linear elastic FE simulations of the fixture and the DCB specimen has been conducted without considering the adhesive layer in the specimens and different modes of the stress intensity factor have been calculated at the crack tip. It is concluded that the entire mode mixity range from pure mode I to pure mode III can be obtained by the same specimen geometry by applying direct bending moments to the specimens.

The final part of the paper is related to the determination of the cohesive law parameters of the Araldite 2015 adhesive using the proposed test configuration. A series of double cantilever beam specimens have been examined in different combinations of modes I and III and J-integral and crack opening displacement data have been obtained using recorded data. Cohesive law parameters have been determined from the numerical differentiation of the J-integral with respect to the crack opening displacement data. Eventually, the obtained cohesive law parameters have been implemented in FE simulations to calibrate the cohesive elements and model the crack initiation and propagation in different setups of the testing situation. Comparing the force-COD (crack opening displacement) curves resulting from the FEM simulations and the experimental data demonstrates the accuracy of the cohesive zone model (CZM) in predicting the strength of the adhesives in mixed mode I + III fracture.

2 Theoretical background

2.1 Cohesive law parameters determination

Since CZM and J-integral approach were reported in prior studies to work well for the determination of the cohesive law in mode I and mixed mode I + II fracture, it is convincing to develop a similar approach for simulating cracking problems in mixed mode I + III fracture. As it is illustrated in Fig. 1, an integration path extended ahead of the crack tip (\({\Gamma }_{\mathrm{loc}}\)) can be considered for analysing J-integral of cohesive zone problems. The resulting locally calculated J-integral along this path can be expressed as Eq. (1) (Sørensen and Jacobsen 2003).

Fig. 1
figure 1

HIntegration path locally around the cohesive zone

Full size image
$${J}_{loc}={\int }_{0}^{{\delta }_{n}^{*}}{\sigma }_{n}\left({\delta }_{n},{\delta }_{t}\right)d{\delta }_{n}+{\int }_{0}^{{\delta }_{t}^{*}}{\sigma }_{t}\left({\delta }_{n},{\delta }_{t}\right)d{\delta }_{t}$$
(1)

where in Eq. (1) \({\sigma }_{n}\) and \({\sigma }_{t}\) are normal and transversal (shear) stresses and \({\delta }_{n}\) and \({\delta }_{t}\) are normal and transversal crack openings along the integration path. \({\delta }_{n}^{*}\) and \({\delta }_{t}^{*}\) indicate the crack opening in normal and transversal directions at the end of the cohesive zone. Cohesive stresses have been assumed to be independent of opening history and derived from a potential function as Eq. (2)

$${\sigma }_{n}\left({\delta }_{n},{\delta }_{t}\right)=\frac{\partial \phi \left({\delta }_{n},{\delta }_{t}\right)}{\partial {\delta }_{n}} \quad \quad {\sigma }_{t}\left({\delta }_{n},{\delta }_{t}\right)=\frac{\partial \phi \left({\delta }_{n},{\delta }_{t}\right)}{\partial {\delta }_{t}}$$
(2)

Considering \(\phi \left(\mathrm{0,0}\right)=0\), Eq. (1) can be rewritten as Eq. (3) (Sørensen and Jacobsen 2003).

$${J}_{loc}=\phi \left({\delta }_{n}^{*},{\delta }_{t}^{*}\right)$$
(3)

By increasing the loads, the crack starts to grow when J-integral at the crack tip reaches a specific value. J-integral during the crack propagation can be denoted as \({J}_{R}\) (fracture resistance). \({J}_{R}\) increases by crack propagation and reaches a steady-state value when total crack opening reaches a critical value. Therefore, cohesive stresses can be obtained as Eq. (4) by replacing \({J}_{loc}\) with \({J}_{R}\) in Eq. (3) (Sørensen and Jacobsen 2003).

$${\sigma }_{n}\left({\delta }_{n}^{*},{\delta }_{t}^{*}\right)=\frac{\partial {J}_{R}\left({\delta }_{n}^{*},{\delta }_{t}^{*}\right)}{\partial {\delta }_{n}^{*}} \quad \quad {\sigma }_{t}\left({\delta }_{n}^{*},{\delta }_{t}^{*}\right)=\frac{\partial {J}_{R}\left({\delta }_{n}^{*},{\delta }_{t}^{*}\right)}{\partial {\delta }_{t}^{*}}$$
(4)

Eventually, according to Eq. (4) cohesive stresses can be determined by calculating \({J}_{R}\) and recording normal and transversal crack end opening (\({\delta }_{n}^{*}\) and \({\delta }_{t}^{*}\)) during the experimental tests. The process of calculating J-integrals has been represented in the next section. In this paper, a numerical differentiation on the resulting J-COD curves gives the traction–separation data, which defines the cohesive laws for the introduced DCB specimens.

2.2 J-integral analysis of the test specimen

In the proposed test configuration, loads are applied as pure bending moments at two beams of a double cantilever beam specimen as shown in Fig. 2a. The usual assumptions of small displacements, small strains, small rotations and a small-scale fracture process zone have been used to analyse the test specimen.

Fig. 2
figure 2

The double cantilever beam specimen loaded with the two components of the applied moment: a Overview; b pure mode I; c pure mode III

Full size image

Due to the integral path independency of the J-integral, \({J}_{loc}\) is equal to \({J}_{ext}\) which its integration path is defined on the peripheral boundary of the DCB specimen. In this study, a new equation has been represented in order to calculate J-integral around the crack tip of the DCB specimens subjected to mixed mode I + III loading state.

The fracture state at the crack tip of test specimens can be obtained by superposition of two separated pure mode I and III specimens, as shown in Fig. 2b and c. Therefore, total \({J}_{ext}\) can be calculated as the summation of J-integral in different fracture modes I and III (\({J}_{ext}={J}_{ext}^{I}+{J}_{ext}^{III}\)), separately. \({J}_{ext}^{I}\) can be calculated by integrating the equation of the J-integral represented by Rice (Rice 1968) along the peripheral boundary of the specimen where the only none zero contribution of the J-integral occurs at the two ends of the beams where moments are applied as the only none zero component of the stress tensor is \({\sigma }_{11}\) parallel to the direction of the crack. This integration has been done by Sørensen et al. (2006) for the same test configuration (Fig. 2b) in mode I fracture by assuming the fracture process zone to be very smaller than the characteristic length of the beam specimens and Eq. (5) has been represented for plane stress situation.

$${J}_{ext}^{I}=12\frac{{M}_{I}^{2}}{{B}^{2}{H}^{3}E}$$
(5)

In Eq. (5), \({M}_{I}\) indicates the bending moment applied to the end of the beam specimen as shown in Fig. 2a which causes mode I fracture. \(B\) and \(H\) have defined the geometry of the transversal rectangular cross-section of the beam.

Loh and Marzi (2018a, b, 2019) represented a solution for calculating Rice’s J-integral around the peripheral boundary of the DCB specimen under pure bending moment loading creating a mode III loading state at the crack tip (Fig. 2c). Based on their studies \({J}_{ext}^{III}\) can be determined from Eq. (6).

$${J}_{ext}^{III}=12\frac{{M}_{III}^{2}}{{B}^{4}HE}$$
(6)

where in Eq. (6) \({M}_{III}\) is the bending moment creating mode III deformation as shown in Fig. 2c, \(B\) is the thickness of the beam specimen and \(E\) is the Young’s modulus of the aluminium beams.

As mentioned earlier, the loading state at the crack tip of the represented double cantilever beam specimen can be obtained by the superposition of a pure mode I specimen and pure mode III specimen. Therefore, the amount of J-integral for this specimen in the mixed mode situation can be calculated by the summation of separated pure mode I and pure mode III loading conditions as Eq. (7).

$${J}_{ext}=12\frac{{M}_{I}^{2}}{{B}^{2}{H}^{3}E} + 12\frac{{M}_{III}^{2}}{{B}^{4}HE}$$
(7)

In summary, the J-integral can be calculated from Eq. (7) in the represented test configuration by recording the applied moments during the experimental examinations. Furthermore, by recording the crack end openings \({\delta }_{n}^{*}\) and \({\delta }_{t}^{*}\) during the tests, the corresponding \(J\)–\({\delta }_{n}^{*}\) and \(J\)–\({\delta }_{t}^{*}\) curves can be obtained. Finally, the mixed mode cohesive laws can be determined by the numerical differentiation of the obtained J-integral curves with respect to the crack end openings \({\delta }_{n}^{*}\) and \({\delta }_{t}^{*}\) as Eq. (4).

3 (DBM-DCB) fixture and test configuration

3.1 Design and manufacturing fixture and test specimens

As mentioned earlier, the idea of the designed fixture has been built upon the earlier fixture represented by Sørensen et al. (2006) for mixed-mode I + II testing. Figure 3 shows the fixture’s setup, attached by two rectangular steel plates to the Zwick z100 tensile testing machine. Two springs have been installed on the top plate in order to out-balance the weight of the transverse arms, which have been used to apply moments. The uncracked end of the specimen is restricted from rotation in any direction and it can freely move just in the vertical direction tangent to the considered roller bearings shown in Fig. 3.

Fig. 3
figure 3

DBM-DCB fixture attached to the tensile testing machine using two rectangular steel plates

Full size image

The process of creating applied moments to the cracked end of the beam specimens has been done using identical forces obtained from a wire arrangement. As it is shown in Fig. 4, a towing wire with a diameter of 1.5 mm goes through a path around six pulleys which two of them are mounted on the upper plate and two pulleys are mounted to each transverse arm. An S-Type 2.5 kN load-cell is mounted to one end of the wire to record the created tensile force in the wire. By moving the upper grip of the tensile testing machine upwards, the resulting force in the wire creates a coupling in each arm of the fixture as Eq. (8).

Fig. 4
figure 4

Schematic of the represented testing configuration and wire arrangement

Full size image
$$M=P.l$$
(8)

In Eq. (8) \(l\) indicates the summation of the distance between the centers of two pulleys and the radius of each pulley of the arm and \(P\) is the created force through the wire, which is measured by the load-cell. It’s worth saying that owing to the small rotation of the transverse arm, the radius of the pulleys should be taken into consideration. This was explained in more detail by Sørensen et al. (2006). The resulting moment from this equation is the total moment applied to each beam of the cracked end of the double cantilever beam specimen. This moment can be decomposed into two components depending on the angle (\(\theta \)) (Fig. 4) that each transverse arm creates with the longitudinal symmetry plane of the testing specimen, where one component of the moment creates mode I and the other component creates mode III loading state at the crack tip.

Two quarter circle steel components; each fixed with two steel pins to the grip components; are designed to create different ratios of mode I and III by varying the angle of applied moments to the specimens. As shown in Fig. 4, four rows of holes have been considered to connect the transverse arm to this component in order to create various combinations of mode I and III testing situations from pure mode I to pure mode III. The center line of each row of holes creates 0°, 30°, 60°, and 90° angles to the longitudinal symmetry plane of the test specimens as shown in Fig. 4. The designed grip components provide an easy way to attach and detach test specimens to the fixture without changing the test setup as shown in Fig. 4.

The test specimens have been manufactured from Aluminium alloy AL-alloy 2024-T3 by joining two rectangular Aluminium bars using Araldite 2015 adhesive with dimensions shown in Fig. 5. Rectangular bars have been cut out from the Aluminium sheet and could be fitted in the grip components of the fixture and mounted on it by two steel pins. Before performing the bonding process, specimens have been polished using three grades of sandpapers and washed in the distilled water to create standard roughness for the bonding. Two steel spacers with a thickness of 1 mm have been placed at each end of the specimens between the bars to create the intended thickness of the adhesive. Teflon coated razor blade with the length of 5 mm has been used at the middle of the adhesive part to create a sharp pre-crack. Finally, the curing process has been done at room temperature by putting the specimens under the pressure of two heavy plates to remove the possible bubbles and extra adhesive.

Fig. 5
figure 5

Geometry and dimensions (mm) of the testing specimens

Full size image

3.2 Conducting mixed mode separation tests

Two dial indicators were fixed to the specimens as shown in Fig. 6a, near the crack tip, in order to measure the distancing between two surfaces of the beams along mode I and III directions and recording the crack end opening in normal (\({\delta }_{n}^{*}\)) and transversal (\({\delta }_{t}^{*}\)) directions. A digital monitor has been calibrated and connected to the load-cell to display the force in the wire. During the test, two cameras have been set in front of the fixture in a way to record the amounts shown in the digital monitor and both dial indicators which are able to determine the instantaneous relative amounts of the displacements, and forces. The loading has been applied by the continuous displacement-controlled upward movement of the upper steel plate, which is attached to the upper grip of the testing machine. The upper grip of the testing machine has been displaced with 0.5 mm/min speed to create quasi-static monotonic loading conditions.

Fig. 6
figure 6

View of DBM-DCB fixture, a installation of two dial indicators, b opening of the crack during the experimentations

Full size image

The recorded videos by the cameras have been used to extract and synchronize the loads measured by the load-cell (displayed by the digital monitor) and the crack end displacements measured by the dial indicators, frame by frame, through the experiments. Figure 6b shows the deformation of the specimen in the mixed mode I + III loading condition during the testing process.

Typical fracture surfaces of the tested specimens under different loading modes are illustrated in Fig. 7. As it can be seen, an acceptable bonding exists between the adhesive and the substrates, and a cohesive type fracture was occurred. For mode I dominant cases we have a rough and pitted fracture surface due to the locally elevated tensile stress which indicates cleavage fracture.

Fig. 7
figure 7

Fracture surfaces of tested specimen under loading conditions of, a pure mode I, b mixed mode 30°, c mixed mode 60°, d pure mode III

Full size image

For mode III dominant cases, a smoother failure surface is observed due to out of plane sliding mode of the loading. In these cases, adhesive layer shows more tendency for transition from cohesive type failure to the adhesive type, but it doesn’t occur at the beginning of the crack propagation where the cohesive parameters were calculated.

3.3 Finite element simulation of the test configuration

Finite element simulations of the fixture and specimen under considered loading conditions have been conducted to evaluate the represented test configuration by calculating mode I, mode II and mode III stress intensity factors for each loading condition and examine the ability of the DBM-DCB fixture in creating different loading states from pure mode I to pure mode III. As it is mentioned earlier, the adhesive layer has not been considered in the FE simulations of this section in order to be able to follow the LEFM assumptions. However, the adhesive layer of the specimens would be modelled by cohesive elements in the next sections where the fracture of the bonded DCB specimens has been studied.

As shown in Fig. 8, three-dimensional finite element models of the fixture and test specimen have been simulated in different testing conditions using various elements (mostly cubic 8 node brick elements) in Ansys commercial FE code. A total number of 1,395,880 elements have been chosen to mesh the test configuration through a performed convergence study. All the materials have been assumed to be homogeneous and isotropic with linear elastic behavior. Mechanical properties of the materials used in the FE simulations have been represented in Table 1.

Fig. 8
figure 8

Represented mesh of the fixture and specimen with a refined mesh at the crack tip for numerical analyses

Full size image
Table 1 Mechanical properties of the AISI 4140, Aluminum 2024-T3
Full size table

As it can be seen in Fig. 8, a number of simplifications have been done during modeling the fixture in order to reduce the time and memory costs of the simulations. As it is shown in this figure, the pulleys of the transverse arms have not been included in the simulation, and they are replaced by corresponding created forces in the wire. Since the material used in the manufacturing of the fixture is stiffer than the specimens, this simplification would not considerably affect the results of the simulations.

Another simplification in this simulation is the modelling of the connections between different parts of the fixture using contact elements between the surfaces of the components instead of modelling the steel pins. For example, the transverse arms of the fixture and the quarter circle components are fixed (bonded) to each other by creating contact elements between the jointed surfaces of the two parts. Such a method has been used to model the joints between the specimens and the fixture. Figure 8 shows the mesh around the crack tip; as it can be seen, finer mesh is used in this area. This region was meshed using 9 rings of cylinders, each consists of 24 cubic elements in the circumferential direction and 36 elements through the thickness of the crack tip.

According to Fig. 8, in the FE model the specimen end is constrained in the lateral directions (X and Z directions) just like in the practice in which roller supports were used at the end. Instead of the wire loads, downward and upward displacements in the Y direction were applied to the side faces of the transverse arms. The distance between two opposite forces, which act in each transverse arm, is equal to the distance of the wire \((l)\) in the fixture. This kind of loading can create the same loading condition in the experiments. Also, the other end of the specimen and grip components, quarter circle and transverse arm were bonded where they were in contact as explained above. These boundary conditions provide a circumstance to solve a static model in the used software.

Figure 9 shows the calculated normalized stress intensity factors (SIFs) from FEM simulation for all modes of fracture (\({K}_{I}\),\({K}_{II}\) and \({K}_{III}\)) through the crack front in the double cantilever specimen under different loading conditions at a reference wire load of 145 N. \({K}_{Im}\) in all the graphs indicates the maximum value of the mode I stress intensity factor through the crack front that occurs in the midpoint, and it is used for normalizing the stress intensity factors. A normalized parameter (\(z/Z\)) was defined to show the variation of SIFs on the crack front (\(Z\) is the half of specimens thickness (\(Z= B/2\)) equal to 4.5 mm and \(z\) is the distance of the considered point on the crack front to the midpoint), whereas \(z/Z=\) − 1, 1 indicates free surfaces of the crack front and \(z/Z=\) 0 corresponds to the midpoint. Figure 9 shows the contribution of all fracture modes and their stress intensity factor distribution through the crack front. According to Fig. 9a, when the transverse arm was located at the \(\theta =\) 0° position, both shear components of the stress intensity factor (\({K}_{II}\) and \({K}_{III}\)) are zero through all the crack front where \({K}_{I}\) is nonzero that demonstrates the specimen is subjected to the pure mode I loading condition. It can be seen from Fig. 9a, \({K}_{I}\) varies through the crack front in a way that it meets its maximum value at the midpoint (\(z=\) 0) and reduces (up to about 20%) at the free surfaces (\(z/Z =\) − 1, 1). This issue has also been reported in other studies such as investigations of Aliha et al. (2015), Sukumar et al. (2000) and (Aliha and Saghafi 2013).

Fig. 9
figure 9

Distribution of the three components of the normalized stress intesity factor through the crack front in different loading conditions

Full size image

Figure 9b and c represent the distribution of the stress intensity factors through the crack front in mixed mode loading conditions. As it can be seen from these figures, shear components of the stress intensity factor (\({K}_{II}\) and \({K}_{III}\)) have noticeable values, especially near the free surfaces. In both graphs \({K}_{III}\) is much bigger than \({K}_{II}\), especially in the range \(- 0.8< z/Z <0.8\), where \({K}_{II}\) tends to zero near the midpoint, and is almost negligible compared to other modes of the stress intensity factor. It should be mentioned that based on Bažant and Estenssoro (1979), Aliha et al.(2015), and Razavi and Berto (2019) the stress singularities near the edges and free surfaces differ from prevailing definitions of the crack tip stress field and classical stress intensity factor. So, the results of the finite element study next to the surface of the DBM-DCB specimen (for the \(z/Z>0.8\)) should be ignored. Therefore, the mode III stress intensity factor is the dominant component between the shear components of the stress intensity factors which means the crack tip is subjected dominantly to mixed mode I + III fracture (at \(\theta =\) 30 and 60) in the DBM-DCB fixture. It is observed from comparing Fig. 9b and c that \({K}_{I}\) and \({K}_{III}\) are decreasing and increasing respectively, by increasing the angle of the transverse arm from pure mode I to pure mode III loading state.

The variation of the stress intensity factor through the crack front for loading angle \(\theta =\) 90° has been represented in Fig. 9d. This figure indicates that except a region near the free surfaces of the crack front in a wide central region through the crack front \({K}_{I}\) and \({K}_{II}\) tend to be zero and are negligible compared to \({K}_{III}\). Therefore, in this configuration of the fixture \({K}_{III}\) is the dominant component of the stress intensity factor in the crack front and it can be assumed that the crack tip is subjected to pure mode III fracture. Consequently, FEM results represented in Fig. 9 demonstrates that the designed testing configuration can provide pure mode I, mixed mode I + III and pure mode III fracture by changing the angle of the applied moment (\(\theta \)). Moreover, the loading condition varies from pure mode I to pure mode III by increasing the angle of the transverse arms from 0 to 90°.

Figure 10 represents each normalized stress intensity factor (\({K}_{I}/{K}_{Im}\), \({K}_{II}/{K}_{Im}\) and \({K}_{III}/{K}_{Im}\)) separately in different angles of transverse arm (\(\theta \)) and different loading conditions. As it is seen in Fig. 10a, the mode I stress intensity factor decreases by increasing the angle of the applied moment (\(\theta \)) on the specimen that means the dominance of the first mode of fracture decreases. It should be noted that all the curves in this figure meet their maximum values in the midpoint through the crack front. Figure 10b illustrates the variation of the mode II stress intensity factor through the crack front in different loading conditions. Except near the free surfaces, \({K}_{II}\) is negligible and tends to zero in the central areas. Therefore, the effect of mode II fracture in the represented testing configuration and fixture can be ignored. Finally, Fig. 10c shows that mode III of stress intensity factor increases by increasing the angle of the loading (\(\theta \)) in the fixture and reaches its maximum where the fixture is set in pure mode III loading condition, which is the desired purpose of the designed testing configuration.

Fig. 10
figure 10

Distribution of the a first, b second, c third mode of the stress intenstiy factor through the crack front in different loading conditions

Full size image

4 Determination and validation of cohesive laws

4.1 Determination of cohesive laws in different loading conditions

Based on the previous section, the fixture introduced in this study can provide various loading states at the crack tip from pure mode I to pure mode III. In specimens similar to the represented DCB specimen in this study, the fracture process zone would elongate through the adhesive along the direction of the crack which is a suitable case to be modelled by CZM (Sørensen and Jacobsen 2003).

During the experimentations to create different combinations of fracture modes of I and III in the represented DCB specimens, the instantaneous applied forces in the wire and corresponding crack end opening data in both normal and transversal directions are measured. J-COD curves are plotted based on the resulting data from the experimental tests using Eq. (7) for each test. The amount of moments in Eq. (7) can be calculated by multiplying the value of the force in the wire to the length of the coupling arm in the transverse arms as Eq. (9).

$${M}_{I}=Plcos(\theta)\, {M}_{III}=Plsin(\theta )$$
(9)

In Eq. (9) \({M}_{I}\) and \({M}_{III}\) represent the corresponding moments to the mode I and the mode III loading conditions, and \(P\) and \(l\) are the force and arm length, respectively. \(\theta \) indicates the angle of the transverse arm with the specimen that varies from 0° to 90°. Angle value of 0° creates pure mode I loading situation at the crack tip and in 90° the loading state of the crack tip changes to pure mode III. After calculating \({M}_{I}\) and \({M}_{III}\) from Eq. (9) by using geometrical parameters and Young’s modulus of the adherents for each test condition, J-integral in the manufactured DCB specimens in this study can be obtained from Eq. (7) even in the presence of the adhesive layer. It should be noted that the Eq. (7) has been represented for calculating the J-integral in the DCB specimens without considering the effect of the adhesive layer. However, this equation can be used for calculating the J-integral in the sandwich DCB specimens, since the thickness (and stiffness) of the adhesive layer is considerably smaller than the thickness (and stiffness) of the beams. The adhesive layer causes negligible strain energy compared to the beams. More specific explanations have been represented by Sørensen et al. (2006) for similar conditions under mixed mode I–II. Figure 11 shows the \(J\)–\({\delta }^{*}\) curves resulting from the averaging of three tests for each angle of the applied moment. The represented error bars for each \(J\)–\({\delta }^{*}\) curve provide upper and lower bounds where the resulting experimental data vary between them. For mixed mode testing situations \({\delta }^{*}\) represents the vector magnitude of the crack end opening and transversal displacements. It is calculated based on Eq. (10) using the recorded normal (\({\delta }_{n}^{*}\)) and transversal (\({\delta }_{t}^{*}\)) crack end displacements during the experiments (Sørensen et al. 2006).

Fig. 11
figure 11

Resulting experimental \(\mathrm{J}\)–\({\updelta }^{*}\) curves for different combinations of fracture modes I and III

Full size image
$${\delta }^{*}=\sqrt{{{\delta }_{n}^{*}}^{2}+{{\delta }_{t}^{*}}^{2}}$$
(10)

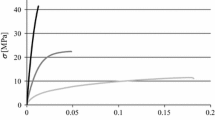
Figure 11 illustrates that the fracture resistance (\({J}_{R}\)) increases in all loading conditions by opening the crack end and reaches a stable value (\({J}_{ss}\)). This stable value indicates that cohesive stresses at the end of the cohesive zone vanish. This figure also shows, as the loading state at the crack tip of the DCB specimen varies from pure mode I to pure mode III, \({J}_{ss}\) and corresponding crack end opening increase in Araldite 2015 adhesive.

As mentioned earlier, cohesive law parameters are defined by traction–separation curves resulting from differentiation of the obtained \(J\)–\({\delta }^{*}\) data from experimental examinations. In this paper, numerical differentiations have been conducted to obtain the traction–separation curves. It should be noted that for pure mode I and mode III tests, \({\delta }^{*}\) represents the opening value of the crack end in one direction and equals to \({\delta }_{n}^{*}\) or \({\delta }_{t}^{*}\) respectively, hence, the traction–separation curves can be obtained from differentiation of the corresponding \(J\)–\({\delta }_{n}^{*}\) or \(J\)–\({\delta }_{t}^{*}\) data. However, in mixed mode testing situations \({\delta }^{*}\) indicates the magnitude of total crack end opening and found from vector summation of the \({\delta }_{n}^{*}\) and \({\delta }_{t}^{*}\) as Eq. (10). Therefore, since the \({\delta }_{n}^{*}\) and \({\delta }_{t}^{*}\) have been recorded separately during the experimental tests, two separate \(J\)–\({\delta }_{n}^{*}\) and \(J\)–\({\delta }_{t}^{*}\) curves can be plotted for each mixed mode condition as Fig. 12. Eventually, mixed mode cohesive laws can be determined from these separate curves in two different directions as Eq. (4).

Fig. 12
figure 12

Comparing the relationship of the J-integral with both a normal and b trasversal crack end opening in mixed mode I + III loading conditions

Full size image

The traction–separation curves for each loading condition have been plotted in Fig. 13. These curves have been used to model the traction–separation behaviour of the cohesive elements in FEM simulations to conduct CZM in mixed mode I + III fracture in Araldite 2015 adhesive.

Fig. 13
figure 13

Resulting traction–separation curves from experimental tests on DCB specimens in different loading states

Full size image

4.2 Finite element simulation of the cohesive zone model

In order to use a cohesive zone model in FEM simulations, interface elements should be considered in a probable crack growth region. In this paper, cohesive elements have been used to model the adhesive layer of the DCB specimens in Ansys commercial FE code. In this software, there are two types of presumed traction–separation curves for defining cohesive laws in the cohesive elements; exponential and bilinear curves. In this study, the bilinear traction–separation curves have been used to define the cohesive laws. Four different parameters must be defined in order to use the bilinear traction–separation curves for modeling the cohesive laws of the cohesive elements; maximum normal stress, critical normal crack opening (\({\delta }_{n}^{c}\)) corresponding to the value of the crack opening in the normal direction where normal cohesive stress vanishes, maximum transversal stress (shear stress), critical transversal crack opening (\({\delta }_{t}^{c}\)) corresponding to the value of the crack opening in the transversal direction where shear cohesive stress vanishes as shown in Fig. 14.

Fig. 14
figure 14

Bilinear traction–separation model

Full size image

The plotted bilinear traction–separation curves in Fig. 14 can be obtained by considering the resulting traction–separation curves from the numerical differentiation of the \(J\)–\({\delta }^{*}\) curves calculated from the experimental data. Figure 15 shows the resulting traction–separation curves from the experimental data obtained from the represented DCB testing configuration and modelled bilinear traction–separation curves for mixed mode (\(\theta \) = 60) loading conditions in normal and transversal crack opening directions. The parameters of the bilinear curves have been obtained by assuming that the area of the created triangle equal to the underlying area of the real traction–separation curves, which can be considered as the converged value of the \(J\)-\({\delta }^{*}\) curves. On the other hand, as it is shown in Fig. 15 the maximum shear and normal stresses and the corresponding crack opening of them have been defined as their values in the real traction separation curves. Therefore, critical crack opening (\({\delta }^{c}\)) in the bilinear traction–separation curves can be calculated as Eq. (11). The described procedure has been conducted to determine the bilinear traction–separation curves and cohesive laws in different crack tip loading states.

Fig. 15
figure 15

Modeled Bilinear traction–separation curves based on the experimental data of a Mixed mode (\(\uptheta \) = 60°) in normal direction and b Mixed mode (\(\uptheta \) = 60°) in transversal direction

Full size image
$${J}_{ss}=\frac{1}{2}{\sigma }^{max}\times {\delta }^{c}\to {\delta }^{c}=\frac{2 {J}_{ss}}{{\sigma }^{max}}$$
(11)

In order to predict the fracture load from the cohesive zone modelling, the finite element model shown in Fig. 8 was used except that instead of the adhesive, zero thickness cohesive zone elements were employed between the Aluminium substrates of the DCB specimens. Displacement control simulations (as shown in Fig. 8) were conducted to obtain the fracture load at different combination of mode I and mode III. The accuracy of the CZM in pure modes I and III and mixed mode I + III fracture is validated by comparing the F–\({\delta }^{*}\) curves resulting from the FEM simulations and the experimental examinations on the DCB specimens using the represented fixture and shown in Fig. 16, where in this figure F is the instantaneous tensile loads of the wire recorded by the load cell and \({\delta }^{*}\) is the total crack end opening.

Fig. 16
figure 16

Comparison of resulting experimental and numerical F-COD curves

Full size image

It is necessary to emphasize that in Ansys or other commercial software, only the pure modes cohesive parameters (i.e. mode I and mode III here) are necessary to implement the simulation in the mixed modes. However, in Fig. 16, the cohesive parameters obtained from pure modes and the parameters obtained from the mixed modes have been used for comparison purposes.

As it can be seen from Fig. 16, the resulting curves from the examinations and numerical simulations show a good coincidence, indicating the accuracy and validity of the cohesive zone model and the represented calculation for J-integral in predicting mixed mode I + III fracture of the DCB specimens.

4.3 Comparison to results of DCB and ENF-tests and fracture envelope

The DCB (Lopes Fernandes et al. 2019; Sadeghi et al. 2021) and ENF (da Silva et al. 2010; Figueiredo et al. 2018) tests have been used in the prior investigations to study the fracture strength or the critical strain energy release rate of the bonded joints under pure mode I and pure mode II loading conditions at different thickness of the adhesive. This research shows that the fracture resistance of Araldite 2015 adhesive joints increases by increasing the thickness of the adhesive layer up to 1 mm, and it stabilizes and decreases over this thickness (\({t}_{A}=1 {\text{mm}}\)). Teixeira et al. (2018) have worked on the strength of the DCB specimens bonded with Araldite 2015 adhesive with 1 mm thickness. Their tests have shown that the value of the tensile critical strain energy release rate (\({G}_{IC}\)) is between 0.75 and 1.26 N/mm which has a good agreement with the resulting mode I fracture resistance for this adhesive in this paper.

Figueiredo et al. (2018) have studied the fracture resistance of Araldite 2015 adhesive subjected to a pure mode II loading state using ENF tests. The results of this study show that \({G}_{IIC}\) is in the range of 9.55–10.5 N/mm for an adhesive layer thickness of 1 mm. The fracture resistance of the Araldite 2015 adhesive under pure mode III and mixed mode I + III loading conditions has not been examined, but due to the shear nature of both modes II and III, \({G}_{IIIC}\) can be estimated to some extent with \({G}_{IIC}\). As it can be seen, the results of the present research for pure mode III have a good agreement with the results of Figueiredo et al. study (2018), which was mentioned above.

The critical strain energy release rate results for repetition of the DBM-DCB fixture fracture tests under different loading conditions can be summarized as the fracture envelope presented in Fig. 17. The results show good repeatability of the mixed mode test using the proposed fixture. The fracture envelope shows that the fracture resistance is increasing with an almost constant slope, with increasing \(\theta \) up to \(\theta ={60}^{^\circ }\), where the fracture resistance is 2.6 times of this parameter in pure mode I. Figure 17 shows that with further increasing \(\theta \) to \({90}^{^\circ }\), fracture resistance of pure mode III increases rapidly to 6.3 times of \({J}_{Iss}\). Similar behavior can be observed from the results of other investigations in the literature (Loh and Marzi 2019).

Fig. 17
figure 17

Fracture envelope of DBM-DCB fixture for mixed-mode I + III

Full size image

5 Summary and conclusions

The proposed double cantilever beam specimen and DBM-DCB fixture in this paper has advantages compared to other test specimens and fixtures, which make this testing configuration more suitable for mixed-mode I + III fracture investigations. The simple geometry of the test specimens and the ability to use different dimensions in manufacturing the specimen with various initial lengths of the crack make this testing configuration very useful. On the other hand, the manufacturing procedure of the test specimens is so simple and there is no need for complex machining in preparing test specimens. In this testing configuration and proposed fixture, specimens are subjected to direct moment loading, which is different from prior represented mixed mode I + III test configurations such as three-point bending specimens which are mostly subjected to axial forces. The proposed fixture also enables us to use the available solutions for calculating J-integral.

As concluded from FEM simulations, this testing configuration can create different loading states at the crack tip from pure mode I to pure mode III. The represented testing configuration can provide a full range of mixed-mode I + III fracture States, despite most of the previously available fixtures. For example, most of the previous configurations (Liu et al. 2004; Rao et al. 2008; Seifi and Omidvar 2013) could not produce pure or dominant mode III deformation and the available ratio of the \({K}_{III}/{K}_{I}\) in the mode III loading situation was about 1. However, the represented numerical results in this paper indicate the capability of the proposed testing configuration in producing pure mode III deformations, where \({K}_{I}\) and \({K}_{II}\) are very small and negligible comparing to \({K}_{III}\), and the state of the loading at the crack tip can surely be considered as pure mode III. Therefore, a full combination of the fracture modes I and III from pure mode I to pure mode III can be created using this fixture by changing the angle of the applied moment.

On the other hand, in this paper, a solution for calculating J-integral in mixed mode I + III loading state has been represented for DCB specimen under pure bending moment loading. The represented J-integral formula has been used for determining cohesive laws in different combinations of the modes I and III fracture by calculating the traction–separation curves from numerical differentiation of the obtained J-integral from experimental data with respect to the crack end opening. The resulting traction–separation curves define cohesive laws of the Araldite 2015 adhesive with 1 mm thickness in different loading states, which can be used in the future research (see Figs. 13 and 17). The obtained cohesive laws have been implemented in the FEM simulations to define the behaviour of the adhesive under mixed mode I + III loading states. Finally, the resulting data from FEM simulations for applied force in the wire of DBM-DCB fixture and corresponding total crack end opening have been compared with the experimental results. This comparison indicates that F–\({\delta }^{*}\) curves in the experimental tests and FEM simulations show a satisfying fit, which implies the accuracy and validity of the cohesive zone model in predicting the fracture in mixed mode I + III loading states.