Keywords

1 Introduction

Fracture mechanics methodology was developed and experimentally demonstrated for the prediction of the growth of bond-line flaws in an adhesively bonded structure that has been with success applied to several engineering problems in recent years. The damage tolerance design concept, originally adopted in the aircraft industry, was based mainly on the well-established concept of linear elastic fracture mechanics (LEFM), and it has gradually gained ground in other engineering fields. Many studies dealing with adhesive joints use the strain energy release rate (SERR), G, and respective critical value or fracture toughness, G C, instead of stress intensity factors because these are not easily determinable when the crack grows at or near to an interface. Linear elastic fracture mechanics (LEFM) has proven to be an efficient tool for analysis of the criticality and propagation rate of an interlaminar defect for a given structural component and service conditions [1]. The scalar quantities which are in use to characterize the resistance of an interlaminar interface to crack propagation are: (a) fracture toughness under static loading for principal loading modes and (b) Paris law parameters and thresholds for cyclic loading [2]. Cohesive zone models (CZMs) can be considered to model the interfacial fracture behavior based on the concept of local stresses and fracture mechanics using continuum approach of either equally or differentially oriented plies in stacked composites or the adhesive/adherend interface to simulate adhesive failure [3].

Interlaminar fracture toughness tests were conducted under pure mode-I, pure mode-II, and mixed-mode-I+II loading [4]. Test data were used for development of numerical simulations and their validation [4]. Mode-I, mode-II and mixed-mode-I+II fracture toughness tests are conducted as per ASTM D5528, ASTM D7805, and ASTM D6671 [5,6,7]. The test procedure and fracture toughness calculations are not presented in current work since it is well defined in the open literature. However, a brief detail of all tests and measured fracture toughness is presented, and this detail can be found in the literature [4, 8]. Cohesive zone models are based on interface elements where propagation occurs without any user intervention which has the ability to simulate crack initiation and crack propagation [9,10,11]. From Benzeggagh–Kenane (B–K) law [12] the measured fracture toughnesses G IC = 325 J/m2, G IIC = 2492 J/m2. These data are used for development and validation of numerical simulation for ENF and MMB test. A bilinear traction–separation description of a cohesive zone model was employed to simulate progressive damage in the adhesively bonded joints [13]. The single lap joint has been modeled and analyzed using the geometrically nonlinear finite element method [14]. A damage law used was able to simulate damage evolution prior to crack growth using power law relationship to define damage rate [15]. Mode-II cohesive zone parameters were used directly from the previously determined mode-I parameters [4] to predict the fracture and deformation of mixed-mode geometries [8].

1.1 Scope of the Work

Adhesive bonded joints are ideal for joining parts in highly contoured, low-observable composite structures for aerospace structural applications; it is also critical in certifying the repaired bonded joints in assemblies [3]. In view of above-said scientific problems, there is a need to understand the behavior of adhesively bonded joints under complex bilateral loading conditions, which includes statics and dynamics. This research will address the durability damage and fracture development in adhesive composite joints.

The delamination process is frequently met in composite materials, and in most cases it results from mode-I, mode-II, or mixed-mode-I+II delamination. The present study concerns the simulation of delamination initiation and propagation in the mode-II and mixed-mode loadings.

Cohesive zone model (CZM) was developed in a continuum damage mechanics framework and made use of fracture mechanics concepts to improve its applicability [2]. The advantage of using CZM is their ability to simulate onset and growth of damage without the requirement of an initial flaw, unlike classical fracture mechanics approach. CZM fits seamlessly into available FE tools to model the fracture behavior of adhesively bonded joints and thus opening a scope and possibilities to carry out the research problem.

2 Approach

The aim of this investigation is to study types of damages and their propagations in SLJs to establish simplicity in design and to increase service efficiency. Presently large amount of databases has been archived on experimental methods to understand SLJ and always been the subject of considerable research. In-line to this finite element method will play a significant role in SLJ structural analysis and are capable of solving problems with various types of damages in adhesively bonded joints; combining with the concepts of linear elastic fracture mechanics based CZM provides a practical and convenient means of studying the damage propagation in adhesively bonded joints. The damage modes in SLJ and the damage propagation were studied and presented in this paper as a nonlinear finite element analysis.

The CZM is an advanced numerical analysis technique in the area of fracture mechanics to understand the separation of the surfaces involved in crack propagation across an extended crack tip or cohesive zone. The limitation of CZM is restricted by cohesive tractions. The CZM formulation brings out robustness, stability, and integrity of FE model by evaluating cohesive parameters (penalty factor and δ ratio). CZM implicitly represents traction–separation laws to model interfaces or finite elements. The analyzed results will be used to demonstrate the use of cohesive zone approaches for the design of adhesively bonded SLJ and to validate approaches for determining the relevant properties to define mixed-mode (tension and shear) interaction in SLJ [16]. An eight-nodded cohesive element for modeling delamination was used between shell elements on the basis of a 3D cohesive element previously developed by authors [4, 10] is proposed.

In addition to mode-II analysis, this paper also focuses on different ratios of G II/G T MMB modals to show good agreement with assumptions and boundary conditions in literature [10, 16]. The quadratic interaction between the tractions is proposed to predict delamination propagation for the mixed-mode fracture toughness. In post-processing ABAQUS/Standards, the validation part will reproduce load–displacement response of (i) ENF and (ii) MMB from literature [8]. Finally, SLJ will be modeled in 2D to show cohesive element for shells which can be used to represent the onset propagation of delamination in composite structures.

2.1 Fracture Mechanics Approach

2.1.1 Cohesive Zone Modeling

A relatively effective method for prediction of delamination and growth within the framework of damage mechanics is cohesive zone model (CZM). CZM can be used to predict both the initiation of a new crack and growth of an existing crack [8]. CZM is widely used in finite element tools for interfacial failure or disbond/delamination modeling. The increased application of cohesive element with ABAQUS has both standard (implicit) and explicit solution procedures enabling the user to model a defined plane of finite or zero thickness where the crack is expected to develop in the structure. The interface response in cohesive element modeling is defined by parameters such as fracture energy is obtained from fracture toughness test. The constitutive response of these elements depends on the specific model and certain assumptions about the deformation and 3D stress vectors.

2.1.2 Bilinear Traction Separation Law

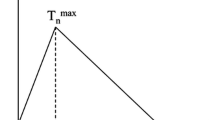
The law states that cohesive elements should follow linear path governed by its elastic parameters such as K NN, K SS, and K TT. Once the traction reaches the nominal value of N max, S max, and T max the stiffness of the element reduces gradually. Traction–separation based modeling is opted for these simulation(s) [8]. Response of the traction–separation law is defined within the base framework of CZM [10]. The element follows a linear (or exponential) degradation post-initiation response.

The work done to completely degrade the cohesive element stiffness to approximate zero is called fracture energy G C. Further degraded cohesive element acts only as a contact region to deny any physically impermissible crossover of the two base structures close to overlap zone. The element fails completely with final displacement δ fail (Fig. 1).

Fig. 1
figure 1

Traction–separation law for cohesive elements

Full size image

All the above cohesive element parameters are material dependent as shown in the equations

$$ N_{\hbox{max} } = 2 \frac{{{\text{G}}_{\text{IC}} }}{{\delta_{\text{fail}} }} $$
(1)
$$ S_{\hbox{max} } = T_{ \hbox{max} } = 2 \frac{{G_{\text{IIC}} }}{{\delta_{\text{fail}} }} $$
(2)
$$ {\text{K}}_{\text{NN}} = 2 \frac{{G_{\text{IC}} }}{{\delta_{\text{ratio}} { \times }\delta_{\text{fail}}^{2} }} $$
(3)
$$ K_{\text{SS}} = K_{\text{TT}} = 2\frac{{G_{\text{IIC}} }}{{\delta_{\text{ratio}} { \times }\delta_{\text{fail}}^{2} }} $$
(4)

where penalty factor = δ fail/ΔL c and δ ratio = δ init/δ fail. G IC and G IIC are the fracture energies measured from mode-I and mode-II fracture toughness tests experimentally, in this case from literature [4]. G IIIC is assumed to be equal to G IIC. ΔL c is decided by the over meshing factor (OMF). OMF is the ratio of structural mesh to cohesive zone mesh. The cohesive zone mesh need to finer than the surrounding structural mesh based on modeling experience by the authors [8].

2.1.3 Benzeggagh and Kenane (B–K) Law

In the analyses presented herein, energy-based Benzeggagh and Kenane (B–K) law was used for damage evolution criterion as shown in Eq. (5). In general, each load case is a combination of mode-I/II thus bringing the mixed-mode B–K criterion to play vital role for damage evolution. Interface failure is expected for a given mixed-mode ratio G II/G T, when G T exceeds the G C.

$$ G_{\text{IC}} + \left( {G_{\text{IIC}} - G_{\text{IC}} } \right)\left( {\frac{{G_{\text{II}} }}{{G_{\text{T}} }}} \right)^{\eta } = G_{\text{T}} $$
(5)

It is assumed that the onset of damage can be predicted by quadratic normal stress criterion. Damage is assumed to initiate when nominal stress ratios reaches a value of 1 given in Eq. (6).

$$ \left( {\frac{N}{{N_{ \hbox{max} } }}} \right)^{2} + \left( {\frac{S}{{S_{ \hbox{max} } }}} \right)^{2} + \left( {\frac{T}{{T_{ \hbox{max} } }}} \right)^{2} = 1 $$
(6)

3 Simulation and Validation

It is important to use proper stiffness definition of cohesive elements in numerical simulation of delamination or disbond [8]. Cohesive element poses numerical convergence issues if softening constitutive model stiffness is not optimized. Furthermore, cohesive parameters like penalty factor and δ ratio affect computation time, accuracy of results and output file size. The stress and stiffness for cohesive elements in opening mode were calculated from the fracture toughness measured from test data using Eqs. (1–4).

3.1 Parametric Study of Cohesive Elements from Simulation of ENF and MMB Tests

Using the ABAQUS/CAE (Pre-processor), the finite element model of ENF specimen was modeled. The model is composed of two sub-laminates, each of 1.8 mm thick. The initial crack length a o is 41 mm, and total laminate length (L) is 120 mm and width (w) is 25 mm. Each sub-laminate has a stacking sequence of [010]. The material properties and dimensions of ENF specimen used in modeling are mentioned in Table 1 and Fig. 2, respectively. The laminate consists of 20 plies (all 0° orientation), with the initial delamination at the midplane. Figure 2 shows the configuration of the specimen along with the boundary conditions applied [8].

Table 1 Material properties of IMA/M21 prepreg
Full size table
Fig. 2
figure 2

Schematic of ENF specimen model

Full size image

Each sub-laminate was modeled with four-noded shell elements (S4R) and a layer of eight-noded cohesive element (COH3D8) was modeled at mid plane next to the pre-crack region to simulate progressive damage growth under mode-II loading. Tie constraints were used to tie the top and bottom faces of cohesive element layer to the shell elements. The thickness of cohesive elements was taken as 0.01 mm. In order to aid the convergence of simulation in the nonlinear region, viscosity parameter of 1 × 10−5 was used for cohesive elements [8]. OMF of five has been used as found in Diehl’s work [10]. A mesh convergence study was conducted while assuming penalty factor and δ ratio of 0.08 and 0.5, respectively (Table 2).

Table 2 Optimized cohesive element parameters
Full size table

Using above-said parameters and properties, MMB specimen has been modeled. The specimen was composed of two sub-laminates each of 1.67 mm thick. The initial crack length (a o) is 27.5 mm, and the total specimen length (L) is 100 mm and width (w) is 25 mm. Each sub-laminate has a stacking sequence of [010].

In MMB test, the failure is assumed in the specimen once crack growth initiates and crack growth leads to unstable. The cohesive element layer was modeled only up to 10 mm from crack tip along the length of specimen. Different G II /G T ratios (literature [8]) were simulated by applying different displacement boundary conditions using kinematic coupling feature available in ABAQUS/standard.

The advantage of kinematic coupling is that different mode ratios can be simulated simply by changing the length C of loading lever. A schematic of the developed numerical model (specimen, interface elements and applied boundary conditions) is shown in Fig. 3. The green line in Fig. 3 represents loading lever which is connected to the specimen with hinged boundary conditions. Loading lever transferred only load without generating any moment at the connection.

Fig. 3
figure 3

Schematic view of MMB specimen model

Full size image

4 Results and Discussion

The model of ENF specimen uses 9600 structural (S4R) elements of 1 mm × 1 mm size and 6900 cohesive elements (COH3D8) of size 0.2 mm × 0.2 mm. The numerical simulation of ENF test typically takes about 7 h of CPU time and generates an output file size of about 4 GB.

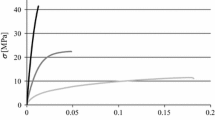
The global response of the tested ENF specimens in terms of load (RF2) versus displacement (U2) curves is depicted from numerical simulation, and it was observed that accurate results were obtained by comparing it with the model from literature [4]. From Fig. 4, we can observe that a good repeatability of the results exhibits an initially linear response, followed by increasing nonlinearities, as the crack begins to propagate. The crack propagated in a stable manner during the displacement control fracture testing of models.

Fig. 4
figure 4

Comparison of reaction load versus applied displacement for simulation of ENF test with literature

Full size image

In similar way, the model of MMB specimen uses 5000 structural (S4R) elements and 62,500 cohesive elements (COH3D8). The plot of reaction load (RF2) versus applied displacement (U2) for different mode ratios was generated from numerical simulation for all load cases and compared with reference data from literature. Figure 5 shows the load–displacement data which show good agreement with reference data. The FE analysis were forcefully terminated once crack start to grow due to a fact that numerical simulation faces convergence issues for simulation of sudden drop in stiffens and requires high computation time.

Fig. 5
figure 5

Comparison of reaction load versus applied displacement for simulation of MMB test with literature

Full size image

The numerical simulation of MMB test typically takes about 50 h of CPU time and generates an output file size of about 11 GB.

By validating ENF and MMB numerical simulations, the model is comparable with literatures with optimized parameters and properties. Henceforth, same methodology has been taken to develop a single lap joint mixed-mode analysis in next section.

5 Numerical Modeling of SLJ

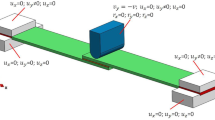
The standard single lap joint was modeled by two laminates of size 175 × 125 mm (approximately) as shown in Fig. 6 and bonded together alongside the components. As the surface preparation plays important role on adhesive strength, the component and traveler panel shall undergo the same treatment and at the same time.

Fig. 6
figure 6

Dimensional panel for modeling bonded assembly

Full size image

For the SLJ, the finite element model of the mixed-mode specimen was developed in preprocessor ABAQUS/CAE. The specimen is composed of two sub-laminates, each of 1.80 mm thick with four-noded plane stress shell elements (S4R) were used for the substrates and to study the progressive damage in the adhesive, one layer of eight-noded cohesive elements (COH3D8) with the bilinear traction–separation descriptions as defined in earlier sections were utilized.

Cohesive element was modeled at mid plane and placed between two laminates with (12.5 + 0.2) distance from each lamina. Moreover, one end of the substrate was constrained by an encastre constraint (u 1 = u 2 = u 3 = 0), while the transverse displacement and rotation about the out of plane axis of the other end were constrained (u 1 = 10 mm, u 2 = u 3 = 0) as shown in Fig. 7.

Fig. 7
figure 7

Boundary conditions for the single lap joint assembly

Full size image

Top and bottom faces of cohesive element layer were tied to the shell elements using tie constraints. The thickness of cohesive element was taken as 0.01 mm. From the previous analysis, penalty factor and δ ratio are assumed to be 0.05 and 0.5 in order to avoid mesh convergence issues. The quadratic stress criterion was used to predict damage initiation in the cohesive elements. A higher mesh density was used near the cohesive elements to obtain more accurate results (Fig. 7). It is assumed that there is no friction between the cohesive and the laminates during the test, so that we use frictionless interaction property in this case.

The number of elements used in model is 70,525 (55,125 linear hexahedral elements of type COH3D8 and 15,400 linear quadrilateral elements of type S4R), and the number of nodes is 167,180. The reaction force for above model is plotted against applied displacement (Fig. 8). The main output parameters include QUADSCRT and SDEG. QUADSCRT indicates whether the maximum nominal stress damage initiation criterion has been satisfied at a material point. When QUADS reaches 1.0, it means that the damage initiates. SDEG is the overall value of the scalar damage variable. The parameter SDEG increases from 0.0 to 1.0, which stands for the damage evolution, and the evolution is finished when SDEG equals to 1.0, which means that the cohesive element is fully damaged and therefore a crack is formed.

Fig. 8
figure 8

Load versus applied displacement curve for single lap joint mixed mode test

Full size image

The numerical simulation of mixed-mode model typically takes about 168 h of CPU time and generates an output file size of about 15 GB. Figure 8 shows the load versus displacement response for SLJ, and the plot shows failure near to 5 mm displacement for the applied displacement of 10 mm.

6 Conclusion

A pure mode-II and mixed-mode cohesive zone model has been used to simulate the propagation of adhesively bonded specimen loaded by three-point bending and mixed-mode bending. The material properties required to define traction separation law, i.e., strength and stiffness were calculated using refined cohesive element parameters.

A quadratic normal stress criterion is used for onset of delamination and subsequently B–K law is used for damage evaluation in numerical simulations. Cohesive element parameters δ ratio and penalty factor are refined for optimum solution by ENF test and MMB test. The characteristic strength for the mode-II traction separation law was essentially identical to the cohesive strength of the interface. The reaction forces on a single lap joint (SLJ) subjected to 3ENF test using the parameters described in above sections are shown in Fig. 8. A method is presented for the prediction of crack growth in specimens under pure mode-II and mixed-mode tests using ABAQUS cohesive elements. Table 3 gives a brief detail about testing procedures for various models simulated for analysis. Numerical predictions for the reaction loads versus displacements are obtained using cohesive zone modeling. In order to capture the unstable onset of delamination growth in the simulation, displacement and time period of the simulation had been resolved with convergence issues. The proposed mixed-mode criteria for SLJ can predict the strength of composite structures that exhibit progressive delamination.

Table 3 Output database
Full size table

7 Future Scope of Work

Numerical results will be validated with the experimental test data for better understanding of the crack propagation, and acoustic emission testing will be carried out to characterize the fracture initiation and damage propagation.