Further examination of the criterion for crack initiation under mixed-mode I+III loading

Abstract

Mixed-mode fracture presents spectacular, scale-independent, pattern formation in nature and engineering applications. The criteria for crack initiation and growth under such mixed mode loading, however, are not well established. This work is aimed at exploring the failure criteria and the pattern formation under combined modes I and III. Specific designs of specimens based on boundary element simulations are considered with the aim of examining crack path selection at nucleation, threshold behavior of crack front fragmentation and, spacing of fragmentation. Experimental investigations with these specially designed geometries show that there does not exist a threshold ratio of $K_{III}^{\infty }/K_{I}^{\infty }$ below which a crack will propagate smoothly without fragmenting into facets. The crack front is shown to fragment immediately as soon as it is perturbed by a small amplitude mode III loading. The experimental results show further that spacing of the fragmentation is set not by any intrinsic length scale of the material, but by the characteristic dimension of the driving crack and the global loading.

1 Introduction

The question of an appropriate criterion for fracture, although originally raised by Griffith nearly one century ago, is still being discussed, even within the restricted setting of linearly elastic materials, exhibiting a small-scale (nonlinear) fracture process zone. Griffith’s criterion, as originally stated, is itself quite remarkable in its generality; subsequent attempts have only provided simplified implementations of this idea such as to permit applications to specific conditions of loading symmetries. For completeness, we quote the theory of rupture postulated by Griffith:

“...the problem of the rupture of elastic solids has been attacked from a new standpoint. According to the well-known ‘theorem of minimum energy’, the equilibrium state of an elastic solid body, deformed by specified surface forces, is such that the potential energy of the whole system is a minimum. The new criterion of rupture is obtained by adding to this theorem the statement that, the equilibrium position, if equilibrium is possible, must be one in which rupture of the solid has occurred, if the system can pass from the unbroken to the broken condition by a process involving a continuous decrease in potential energy. In order, however, to apply this extended theorem to the problem of finding the breaking loads of real solids, it is necessary to take account of the increase in potential energy which occurs in the formation of new surfaces in the interior of such solids.” ...A.A. Griffith (1920).

In principle, this criterion should be able to predict arbitrary evolution of the crack(s), if such evolution is possible quasi-statically.¹ The total energy of the system is written as: $E=\Pi +U_{s}$ where $U_{s}$ is the surface energy and $\Pi =-W_{\partial R} +U_{R}$ is the potential energy of the mechanical system. Griffith’s postulated fracture criterion is then: ${E}^{\prime }(a)=0$ where $a$ represents the equilibrium crack length. Griffith’s example was a crack loaded with an opening mode symmetry with the consequence of a straight extension of the crack and he equated the fracture energy to the surface energy (surface tension), but the theory itself corresponds to the standard idea of energy minimization, and has no such restrictions. In principle, when considering ${E}^{\prime }\left( a\right) =0$, all possible crack configurations must be considered, and all possible source of dissipation that occur prior to generation of failure could be introduced into $U_{s}$, not just the surface energy. Therefore, the criterion for selection of the crack path (or nucleation of a crack) is embedded in Griffith’s postulate; the main hurdle is that it is extremely difficult to extract the path corresponding to this minimization unless special methods are introduced to permit crack surface evolution! The change in the mechanical potential energy (outside of the crack surface energy) $-d\Pi /da=G$ is labeled the elastic energy release rate.

Practical fracture criteria (note plural) have been introduced since the time of Irwin (1957), that, while still based on the Griffith theory, are of limited validity. Nevertheless, such criteria are of enormous practical significance since they permit the design of fracture critical structures, determination of residual strength of structural components in the presence of cracks, and assessment of structural integrity in a large number of applications. The separation of the global loading into the three symmetries—opening mode (mode I), in-plane shearing mode (mode II) and anti-plane shear mode (mode III)—is an extremely useful exercise that decouples the problem of crack path selection from the energy balance equation, at least for mode I. Since mode I loading is perhaps the most prevalent in structural applications, such decoupling has permitted successful development of a practical fracture theory.

For mode I, based on the Williams (1952) and Irwin (1957) estimate of the singular crack tip stress field, $\sigma _{\alpha \beta } =K_{I}^{\infty } \left( {2\pi r}\right) ^{-1/2}f_{\alpha \beta }\left( \theta \right)$, where $K_{I}^{\infty }$ is the mode I stress intensity factor (SIF), and $f_{\alpha \beta }^{I} \left( \theta \right)$ is a known angular distribution, the connection to the Griffith criterion can be written as $G=\left( {1-\nu ^{2}} \right) \left( {K_{I}^{\infty }}\right) ^{2}/E$. The Griffith fracture criterion can be written as $K_{I}^{\infty }=K_{IC}$ at onset of crack growth, where $K_{IC}$ is the fracture toughness and is related to the fracture energy per unit area $G_{c}$ by $\sqrt{EG_{c}}\equiv K_{IC}$. This should be considered to be a solved problem, apart from the search for numerical methods that can implement this in a robust calculation.

For problems involving coupled in-plane modes I+II, the stress field in the vicinity of the crack tip is written as: $\sigma _{\alpha \beta } =K_{I}^{\infty }\left( {2\pi r}\right) ^{-1/2}f_{\alpha \beta }^{I} \left( \theta \right) +K_{II}^{\infty }\left( {2\pi r} \right) ^{-1/2}f_{\alpha \beta }^{II} \left( \theta \right)$, where $K_{II}^{\infty }$ is the mode II stress intensity factor, $f_{\alpha \beta }^{II} \left( \theta \right)$ is another known angular distribution, and the connection to the Griffith criterion can be written formally as: $G=\left( {1-\nu ^{2}}\right) \left( \left( K_{I}^{\infty }\right) ^{2}+\left( {K_{II}^{\infty }}\right) ^{2}\right) /E$. However, it must be noted that this estimate of the energy release rate is strictly valid only for a straight line extension of the crack; however, it is expected that due to the asymmetry in the loading under combined modes I+II, that the crack will in general experience a curved or kinked crack evolution, depending on the magnitude of the asymmetry that is dictated by the ratio: $K_{II}^{\infty }/K_{I}^{\infty }$. At least three different formulations of the failure criterion have been used in the literature: (i) Griffith—crack grows in the direction of the maximum energy release, when this attains the fracture energy, $G_{c}$. Calculation and implementation of this criterion has been difficult and awaits the development of numerical or other methods—such as the phase field method—for determining this path. (ii) Maximum hoop stress criterion—crack grows in the direction perpendicular to which the hoop stress reaches a maximum; of course, the energy released in this direction will be a function of the stress intensity factors; therefore, this criterion can be written as: $F\left( {K_{I}^{\infty },K_{II}^{\infty }}\right) =0$. (iii) Principle of local symmetry (PLS): consider an infinitesimal extension of the main crack along some direction, $\gamma$, and denote the stress intensity factors at the tip of such extension as $\left( {k_I (\gamma ), k_{II} (\gamma )}\right)$; the crack will grow in the direction $\gamma _{c}$ in which the local mode II stress intensity factor vanishes: $k_{II} (\gamma _{c})=0$, when $k_{I} (\gamma _{c})=K_{IC}$. The scatter in the available experimental data prevents a positive discrimination between the predictions of the maximum hoop stress criterion and the principle of local symmetry; within these limits, both the PLS and the maximum hoop-stress criterion appear to provide acceptable predictions of crack path and growth. Combined modes I+II also represents a nearly solved problem; additional investigations could be fruitful if directed towards design of suitable experiments that could discriminate between the different failure criteria and towards development of robust numerical methods for implementation of these failure criteria.

For problems involving mixed modes I+III, the situation is much less developed for many different reasons. First, there have been limited attempts, some experimental and others analytical, to extract/elucidate the appropriate failure criterion. Second, the available experimental investigations have been clouded somewhat by uncertainties associated with the actual loading/boundary conditions that bring to question the mode mix really responsible for crack initiation/growth. Lastly, while the anti-plane shear problem for deformation is governed by Laplace’s equation in two-dimensions, the corresponding fracture problem must include additional specification of the nature of the failure process before the need for three-dimensional analysis can be determined; thus, on the one hand, if failure is taken to be caused by slip along planes of maximum shear (as in the work of Barenblatt and Cherepanov 1961), the mode III problem remains two-dimensional, and such “shear cracks” can propagate with the normal to the crack surface remaining in the plane and maintaining the anti-plane symmetry. In fact, in this case, the mode III problem is fully decoupled from the in-plane modes I+II. Barenblatt and Cherepanov (1961) used this criterion to solve a number of different crack problem in pure mode III. On the other hand, if one considers that failure is caused by opening stresses, one must abandon the assumption that the solutions retain anti-plane symmetry; the fracture problem is then inherently three dimensional, and indicates possibly discontinuous evolution of the crack that make analysis difficult. This distinction has not always been maintained clearly in the literature, with most analyses of the problem implicitly assuming failure by opening stresses.

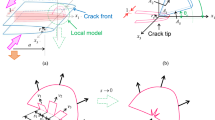
One generalization of the PLS was proposed by Goldstein and Salganik (1974) is the following postulate: $k_{II} (\gamma _{c})=0$, with $f\left( {k_{I}, k_{III}}\right) =0$; here $k_{III}$ represents the mode III SIF at the extension of the main crack along the orientation $\gamma _{c}$. As with the criterion posed by Barenblatt and Cherepanov (1961), this is a possible criterion and its implications must be evaluated for specific mixed mode loading conditions to determine its suitability. In order to explore the predictions of this criterion, we use the perturbation estimates of Leblond (1999) to express the fracture criterion in terms of the SIF on the original crack faces. Consider a local region of a curved crack front (CF), with the position along the crack indicated by the arc length $s$ as shown in Fig. 1. The unit vector $\mathbf{t}(s)$ is tangent to the CF, the unit vector $\mathbf{n}(s)$ is normal to the original crack plane (CP) and the unit vector $\mathbf{b}(s)$ indicates the normal to the CF and completes the triad of unit vectors at the point $s$. The cracked solid is subjected to arbitrary loading such that the crack tip experiences a combined mode I+II+III loading indicated by $\left( {K_{I}^{\infty }(s),K_{II}^{\infty } (s),K_{III}^{\infty } (s)}\right)$ along the $\left( {\mathbf{n}(s),\mathbf{b}(s),\mathbf{t}(s)}\right)$ directions, respectively. Leblond (1999) established that for a perturbation of the crack that evolves continuously from the original crack font, that $k_{p} (\gamma )=F_{p,i} K_{i}^{\infty }$, where $p$ and $i$ take the values I,II,III, (summation over repeated index is implied, but the comma is used simply to separate the two subscripts) and $\gamma$ is the tilt angle with respect to the $\mathbf{t}(s)$ axis. Using symmetry arguments Leblond (1999) suggests that $F_{i,p} =0$ when either $p$ or $i$ takes the value III; this results in a complete decoupling of the in-plane $(\mathbf{b}\times \mathbf{n})$ loading modes from the anti-plane modes.² The consequences of this decoupling are examined in the following; the fracture criterion according to the PLS can now be written as

$$\begin{aligned}&k_{II} (\gamma )=F_{II,I} (\gamma )K_{I}^{\infty }+F_{II,II} (\gamma )K_{II}^{\infty } =0 \nonumber \\&k_{III} (\gamma )=F_{III,III} (\gamma )K_{III}^{\infty }\nonumber \\&f\left[ F_{I,I} K_{I}^{\infty }+F_{I,II} K_{II}^{\infty },F_{II,I} K_{I}^{\infty }\right. \nonumber \\&\qquad \left. +F_{II,II} K_{II}^{\infty },F_{III,III} K_{III}^{\infty } \right] =0 \end{aligned}$$

(1)

The first equation above dictates the direction of crack extension $\gamma _{c}$: setting $k_{II} (\gamma _{c})=0$ yield indicates that the direction of crack extension is influenced only by the ratio of $K_{II}^{\infty }(s)/K_{I}^{\infty }(s)$, the second equation provides the value of $k_{III} (\gamma )$, while the third is the energy balance equation; note that $K_{III}^{\infty }(s)$ contributes only to the energy released or equivalently the crack initiation load level, but does not influence the crack path. This situation is clearly of limited validity: for example, consider a half-plane crack with a straight crack front subjected to a constant initial SIF: $\left( {K_{I}^{\infty }(s)=a,K_{II}^{\infty }(s) =b,K_{III}^{\infty }(s)=c}\right)$. The PLS criterion suggests that the angle $\gamma _{c}$ is dictated only by the ratio $b/a$ and is completely independent of $c$. If we take $b=0$, thereby considering a pure mode I crack, the PLS failure criterion as postulated above predicts crack extension along $\gamma _{c}=0$ for all values of $c$. Experiments, going all the way back to Smekal (1953) have shown that even a small magnitude of $c$ in a dominant mode I problem will nucleate new crack fragments along the CF that are inclined at an angle so as to eliminate $k_{III}$. The insistence on continuous evolution of the crack that is inherent in this criterion makes it applicable only when $K_{III}^{\infty }$ is small; this raises one fundamental question of whether there exists a threshold ratio $K_{III}^{\infty }/K_{I}^{\infty }$ below which continuous extension of the crack may occur. Such a threshold will place a limit on the applicability of the PLS criterion.

Fig. 1

Schematic diagram of a three dimensional crack front. CF and CP represent the crack front and crack plane, respectively. $\left( {\mathbf{b,n,t}}\right)$ represent the directions normal to CF, normal to CP, and tangent to the CF respectively

Since we know that mode III loading is important in crack front evolution, we seek a different generalization of the PLS: if in-plane cracks evolve so as to eliminate shear, the natural generalization would be to insist that 3D cracks also evolve so as to eliminate shear. Based on the experiments of Sommer (1969), Knauss (1970), Cooke and Pollard (1996), and Lin et al. (2010), we revisit the criterion that eliminates all shear induced SIF and postulate that the crack will propagate along the direction $\left( {\gamma _{c},\phi _{c}}\right)$ when $k_{I} (\gamma _{c}, \phi _{c})=K_{IC}$, $k_{II} (\gamma _{c},\phi _{c})=0$, $k_{III} (\gamma _{c},\phi _{c})=0$. A simple interpretation of this criterion is that the first provides the condition of criticality, while the second and third dictate the rotation angle $\gamma _{c}$ of the crack normal about the $\mathbf{t}(s)$ and angle $\phi _{c}$ about the $\mathbf{b}(s)$ axes—the tilt and twist, respectively. However, crack twisting cannot be achieved by a continuous evolution of the crack front; this requires the crack front to fragment—through the generation of crack nuclei—immediately upon application of a nonzero $K_{III}$. This raises the second fundamental question: what, if any, sets the intrinsic scale for the spacing between the nucleated crack front fragments. Since linear elastic fracture theory does not provide an intrinsic length scale, this length must arise from other geometrical features of the problem—either an intrinsic process zone or a macroscopic length scale.

The focus of this article is on the initiation of mode I+III cracks, addressing the two fundamental questions raised above. We examine the initiation of mixed mode I+III cracks through a systematic variation of specimen design that enables addressing the issue of the existence of a threshold as well as an intrinsic length scale for the fragmentation of the crack front. This article is organized as follows: recent work on mixed-mode I+III cracks is reviewed in Sect. 2. The design of specimens aimed at revealing the underlying reasons for crack front fragmentation are discussed in Sect. 3. The results are discussed in Sect. 4, with particular attention to the question of the existence of a threshold for the occurrence of fragmentation along the crack front, and the question of pattern formation from the resulting crack initiation. The main outcomes and their implication on fracture modeling are summarized in Sect. 5.

2 Background for the mode I+III problem

We assume that fragmentation of the crack front into facets of new cracks is an important aspect of mixed mode I+III crack initiation and address two main questions: (i) is there a threshold level of $K_{III}^{\infty }$, below which continuous evolution of the crack front is possible, and (ii) what sets the length scale of fragmentation? The relevant literature is reviewed in this section.

It has long been postulated that the crack will propagate in a direction perpendicular to the maximum principal stress (see Sommer 1969; Knauss 1970); under this criterion, the orientation for conditions of plane strain is given by Cooke and Pollard (1996):

$$\begin{aligned} \left( {\frac{1}{2}-\nu }\right) \tan \left( {2\phi _{c}}\right) =\frac{K_{III}^{\infty }}{K_{I}^{\infty }} \end{aligned}$$

(2)

Experimental observations support the above postulate for crack initiation (see Knauss 1970; Yates and Miller 1989; Cooke and Pollard 1996; Lazarus et al. 2008; Lin et al. 2010); in particular, the pure mode III experiment of Knauss (1970) indicates an angle of the cracks to be $\pi /4$ in agreement with the prediction of Eq. (2). Cooke and Pollard (1996) showed that this criterion is equivalent to $k_{III} =0$ and maximum $k_{I}$ criterion; both these criteria indicate that $\phi _{c}\rightarrow \pi /4$ as ${K_{III}^{\infty }}/{K_{I}^{\infty }}\rightarrow \infty$. Cooke and Pollard (1996) also considered the maximum energy release rate criterion; this was evaluated by a simple perturbation analysis where the SIFs on the twisted cracks were obtained by imposing the stress from the parent crack; for values of ${K_{III}^{\infty }}/{K_{I}^{\infty }}>1.4$ (for $\nu =0.38$), the predictions of this criterion deviated from that of the maximum principal stress criterion with two branches, tending towards $\phi _{c}\rightarrow 0$ or $\phi _{c}\rightarrow \pi /2$ as ${K_{III}^{\infty }}/{K_{I}^{\infty }}\rightarrow \infty$. Clearly, the pure mode III results of Knauss (1970) indicate that $\phi _{c}\rightarrow \pi /4$ as ${K_{III}^{\infty }}/{K_{I}^{\infty }}\rightarrow \infty$ and contradict the predictions based on energy release. Nevertheless, one cannot discard the maximum energy release rate criterion since it is obtained from a fundamental principle; it would appear that the perturbation estimate for the energy release rate requires additional investigation. In the following, we shall assume that the crack will develop fragments in agreement with the orientation predicted by the maximum principal stress criterion in Eq. (2).

Sommer (1969) examined the role of superposed mode III loading on a crack growing under a dominant mode I loading. The lateral surface of a cylindrical glass rod was subjected to fluid pressure; the fluid penetrated to the inside through surface flaws and then generated an opening mode interior crack perpendicular to the axis of the rod. By superposing a small torque on the rod, the fluid pressure driven crack was then subjected to a small additional mode III loading. In this case, Sommer observed a transition from a smooth to faceted fracture surface; such a transition had been observed earlier by Smekal (1953), who called the fragments “fracture lances” and associated this transition with the competition of mode III and mode I. In Sommer’s experiments, mode III is negligibly small when the crack is in the central portion of the rod but increases as it grows towards the outer surface. The experiments were performed at three levels of torsion and the radius and crack tilt angle at the location of the initiation of faceted cracks were measured. Based on the experimental data, Sommer postulated that for lance initiation (fragmentation), a minimum angle of twist of the principal axis was necessary. This minimum angle is presumably dictated by intrinsic material properties and was measured to be $3.3^{\circ }$ with respect to the nominal crack plane for the AR-glass tested. The existence of the minimum twist angle of the crack is equivalent to a threshold ratio ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ above which the crack front will fragment into facets and below which the crack surface will exhibit smooth undulations.

Recently, Pons and Karma (2010) studied the instability of helical crack-fronts under mixed mode loading using a continuous phase-field method that permitted the evolution of the crack front to be examined. In their notation, the $\left( {\mathbf{b,n,t}}\right)$ directions at a local point on the CF are denoted as $\left( {x,y,z}\right)$. Mixed mode I+III loading was imposed by choosing the initial opening and out-of-plane sliding displacements in $y$ and $z$ directions, respectively. The crack front was perturbed helicoidally; the perturbation amplitude also changes exponentially in time (or crack extension along $x$) and was parameterized in the form:

$$\begin{aligned}&\delta x_{front} \left( {z,t}\right) +i\delta y_{front} \left( {z,t}\right) \nonumber \\&\quad =A_{0} \exp \left[ {-ikz+\frac{\sigma (k)t}{\tau }} \right] \end{aligned}$$

(3)

Based on this parameterization, the variation of the perturbation amplitude versus time for simulations with different wave number $k$ and ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ were obtained and used to extract the linear stability spectrum $\sigma \left( k\right)$. The simulated data was fitted to the form $\sigma \left( k\right) =ak-bk^{2}$. The spectrum is characterized by the fastest-growing wavelength $\Lambda _{\max } =2\pi /k_{\max }$, where $\sigma \left( {k_{\max } }\right)$ reaches the peak value, and the marginally stable wavelength $\Lambda _{stable} =2\pi /k_{stable}$, where $\sigma \left( {k_{stable} }\right)$ vanishes and $\Lambda _{\max } \approx 2\Lambda _{stable}$. Then a relation between $\Lambda _{stable}$ and ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ and a “process zone” length scale $\xi$ was developed by equating the configurational force with the cohesive force and imposing the maximum fracture energy release rate criterion. This yields an approximate relation for the maximally unstable wavelength:

$$\begin{aligned} \Lambda _{\max } \approx 2\Lambda _{stable} \approx 4\pi \xi \left( {\frac{K_{I}^{\infty }}{K_{III}^{\infty }}}\right) \end{aligned}$$

(4)

Based on this result, the authors postulated that the initial instability wavelength depends solely on the stress intensity factors for modes I+III and the process zone scale. It should be noted that a threshold behavior is not predicted by this analysis; for each loading condition, ${K_{III}^{\infty }}/{K_{I}^{\infty }}$, there exists a critical wavelength of fragmentation. Following on this numerical effort, Leblond et al. (2011) derived an analytical expression of the variation of the SIF near a helicoidally perturbed crack front using the results of Movchan et al. (1998). They used this expression in linear stability analysis and identified that helicoidal perturbations are unstable beyond a critical ratio of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ that depends on the Poisson’s ratio:

$$\begin{aligned} \left( {\frac{K_{III}^{\infty }}{K_{I}^{\infty }}}\right) _{\mathrm{cr}} =\sqrt{\frac{\left( {1-\nu }\right) \left( {2-3\nu } \right) }{3\left( {2-\nu }\right) -4\sqrt{2}\left( {1-2\nu }\right) }} \end{aligned}$$

(5)

For a Poisson’s ratio of $\nu =0.22$ and $\nu =0.34$, corresponding to glass and Homalite-100,³ respectively, the critical values are 0.69 and 0.45. However, Sommer’s experimental results indicate that fragmentation occurs when the ratio ${K_{III}^{\infty }}/{K_{I}^{\infty }}\sim 0.03$; this observation suggests that there is possibly another mode of instability that intervenes prior to reaching the helocoidal instability with a continuous evolution of the crack front.

Lin et al. (2010) suggested a generalization of the PLS criterion. They impose that both local shear SIFs vanish on the incipient crack, and that the local opening mode SIF approaches the critical value for the material:

$$\begin{aligned} k_{I} =K_{IC},\,k_{II} =0,\,k_{III} =0, \end{aligned}$$

(6)

This criterion requires the crack front to fragment into new faceted cracks as soon as a small amount of mode III loading is applied. The plane of the prospective crack (twist angle $\phi _{c}$) is dictated by the Eq. (2). The cross-section perpendicular to the original crack surface exhibits a “factory roof” profile (see Fig. 2). There are two types of cracks corresponding to the two twist angles in this factory-roof pattern: cracks of type $A$ (en echelon cracks) are formed by opening mode I, and cracks of type $B$ which are not favorably oriented with respect to local opening mode I. Therefore, type $B$ cracks cannot form concurrently with the type $A$ cracks. Based on experimental observation of the dynamic crack growth, Lin et al. (2010) proposed that type $A$ cracks form first, but the region between them (bridging region) is either uncracked or breaks later. The energy penalty associated with the bridging region must be paid as the type $A$ cracks develop. By balancing the local energy dissipation per unit crack extension with the global dissipation, Lin et al. (2010) developed a relationship between the twist angle and the space of new crack fronts:

$$\begin{aligned} \Gamma d\sec \phi _{c}+\gamma _s \alpha d\tan \phi _{c}=\tilde{\Gamma }\left( {\frac{K_{I}^{\infty }}{K_{III}^{\infty }}}\right) b \end{aligned}$$

(7)

where $b,d$ and $\phi _{c}$ are defined in Fig. 2. $\Gamma$ is the energy penalty per unit area for type $A$ cracks. $\tilde{\Gamma }$ is the global fracture energy corresponding to the appropriate ratio of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$. $\gamma _s ,\alpha$ are the energy penalty per unit volume and the characteristic width associated with the bridging region. Based on Eq. (7), they postulated that there exists an intrinsic length scale $b$ (the scale of nonlocality) which is set by material properties. Experimental data on $d$ and twist angle $\phi _{c}$ of the fracture surface from three point bending specimens with slant crack at the center was collected. Fitting the data to the model, they were able to extract the scale of nonlocality $b$ and the energy penalty associated with the bridging region $\gamma _{s}$.

Fig. 2

a Geometry of the “factory roof” profile in a plane perpendicular to the crack propagation direction; the red lines indicate type A cracks inclined at an angle $\phi$ with respect to the nominal crack plane and the black dashed lines indicate type B cracks; b “Hand-shaking” mode of linking of the type A cracks; c Bridging cracks linking type A cracks, formed after rearrangement of the stress field; d Representation of bringing regions R that connect the type A cracks and provide energy penalty for the overall extension of the crack. (reproduced from Lin et al. 2010)

Recently, Goldstein and Osipenko (2012) examined this problem by performing and interpreting experiments on gypsum and cheese; their specimen, shown in Fig. 3, experiences dominant mode I, with a superposed mode III loading. They calculated the stress intensity factor at the fragmented crack approximately and explored the reasons for the coarsening of the crack fragments; we will examine this configuration in greater detail in this work. An important outcome of their work is the demonstration (see Fig. 3) that type $B$ cracks are not formed at the same time as the type $A$ cracks. Coarsening of the spacing between the fragmented cracks was also observed, but we will not consider this aspect in the present work. Lazarus et al. (2008) had examined this issue earlier in PMMA specimens subjected to fatigue cyclic loading and demonstrated the absence of type $B$.

Fig. 3

a The specimen configurations used by Goldstein–Osipenko b schematic representation of sections of the specimen at different distances from the notch and c images of similar sections from the notch on cheese specimens indicating (i) the absence of type $B$ cracks and (ii) the coarsening of the fractures (reproduced with permission from Goldstein and Osipenko 2012)

3 Specimen design

As discussed above, different specimen geometry and loading configurations have been explored in the literature in order to elucidate initiation and growth of fracture under mixed mode I+III conditions. However, controlling the exact combination of mixed mode loading is quite difficult; in particular, while the primary interest is in the combination of modes I+III, it is extremely difficult to eliminate mode II loading, except in some special cases, such as the internal pressure combined with superposed torsion. In the present work, we begin with the geometry and loading considered by Goldstein and Osipenko (2012) shown in Fig. 3. Then, we consider modifications to this geometry and loading in order to control the crack tip state; specific designs of specimens were based on accurate calculations of the stress intensity variations using a boundary element technique, and are aimed at examining crack path selection at nucleation, threshold behavior of crack front fragmentation, and the spacing of fragmentation. Using these variants of the Goldstein–Osipenko geometry, we are able to expand the range of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ that can be examined.

3.1 Goldstein–Opisenko geometry and variants

We performed a number of simulations to calculate the SIFs using a Symmetric Galerkin Boundary Element code (Li and Mear 1998; Li et al. 1998). First, the Goldstein–Osipenko geometry shown in Fig. 3 was simulated with the following dimensions: $H=2.0$, $w=1.0$, $\gamma =15^{\circ }$ and $a=0.25w$. The variation of the mode I, II and III SIFs for this geometry along one of the cracks is shown in Fig. 4;⁴ it is clear that the mode I SIF is negative, indicating crack closure/contact for sharp cracks, and that the mode III SIF reaches very large values. We note that the simulations considered an ideally sharp crack, while the experimental crack would have some bluntness arising from the fabrication process. At the central portions of the crack front, this combined mode I+III SIF will cause crack initiation with an angle $\phi _{c}$ with respect to the main crack plane and possibly trigger crack front fragmentation. However, in addition to these two modes, it can be identified readily that the mode II SIF is singular at the surface where the crack intersects the free surface and varies monotonically across the specimen. Such variation of $K_{II}^{\infty }$ was pointed out by Lin et al. (2010) for the bending specimen. The role of this $K_{II}^{\infty }$ is to kink the crack to attain local mode I conditions; in brittle materials such as glass and H-100, the effect of mode II is very strong and causes the crack to follow a tortuous surface under all three modes. Therefore, we sought a modification to the Goldstein–Osipenko geometry that would eliminate the mode II SIF.

Fig. 4

The variation of the stress intensity factors $K_{I}^{\infty }(s),K_{II}^{\infty }(s),K_{III}^{\infty }(s)$ along the crack front in the Goldstein–Osipenko configuration with slant cracks with $\gamma =15^{\circ }$

3.2 Calculation of stress intensity factors

In the second set of simulations, the geometry was modified with a design of a part-through crack as shown in Fig. 5; for the loading configurations considered, the part through crack is not expected to generate a mode II stress intensity factor at the point where the crack meets a free surface. Two interesting specimen types were found, Type I that introduces predominantly mode I+III loading, while Type II generates negative mode I along most of the pre-crack front.

Fig. 5

Geometry of modified Goldstein–Opisenko configurations. The crack fronts are curved and break the surface on planes $y=\pm D/2$. Specimen Type II is obtained merely by flipping the loading about the $xy$-plane. a Specimen Type I. b Specimen Type II. c Specimen Type III

Specimen Type I: The geometry is shown in Fig. 5a. The specimen is loaded from the top and supported at the bottom of two pre-cracks. The specific dimensions used are as follows: $L=3.0$, $H=2.0$, $d=2.25$, $a=0.186$, $b=0.2$, $r=1.5$, $\gamma =26.6^{\circ }$, and $D=0.5$ for H-100 and $D=0.75$ for glass. The variation of the stress intensity factors for all three modes along the curved crack front are shown in Fig. 6. There exist some interesting characteristics to the variation of the SIFs along the crack front that are useful in mixed-mode I+III investigations. $K_{I}^{\infty }$ is positive and dominates the loading with a very large amplitude. $K_{II}^{\infty }$ is very small in the central regions of the CF $0.4s-1.0s$; it should also be noted that, as expected, it goes to zero at $s=0$ and $s=1$, where the crack pierces to the free surface. $K_{III}^{\infty }$ is large over some portion of the crack front, but only in locations where $K_{I}^{\infty }$ is small. The most interesting part is that $K_{III}^{\infty }$ switches sign along the pre-crack front; at $s=0.82\,K_{I}^{\infty }$ reaches the maximum value, and both $K_{II}^{\infty }$ and $K_{III}^{\infty }$ nearly vanish; (we will refer to this location as the transition point). The importance of this specimen design is that it can provide a critical test to the existence of a threshold for the fragmentation of the crack front. First, according to the criterion postulated by Lin et al. (2010), we expect the initiation of crack growth to occur at the transition point, where $K_{I}^{\infty }$ approaches the critical value $K_{IC}$, while $K_{II}^{\infty }$ and $K_{III}^{\infty }$ both vanish; the principle of local symmetry would also suggest crack initiation at this location. Based on Eq. (2), we would also expect to see the twist angle on either side of the transition point to be of opposite signs. However, if there exists a threshold ratio of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ where the fragmentation does not occur, we should observe a continuous evolution of the crack front without fragmentation in region around the transition point. The extent of this region can be estimated from the Sommer’s results (Sommer 1969); if a minimum twist angle of $3.3^{\circ }$ is necessary for fragmentation to occur in glass, based on Eq. (2), this yields a threshold ratio of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ equal to 0.029 for glass assuming $\nu =0.25$. From the simulation result for the SIFs, one should observe a flat portion of normalized length 0.042 (equivalent to 2.044 mm for the specimen dimensions indicated earlier) around the transition point. We will address this through experiments on glass and H-100.

Fig. 6

The variation of the stress intensity factors $K_{I}^{\infty }(s),K_{II}^{\infty }(s),K_{III}^{\infty }(s)$ along the crack front for specimen type I. The origin of $s$ is located at the top of the specimen. Elastic properties of glass have been assumed in the simulations. The specimen redesign has eliminated the concentration of mode II stress intensity factor where the crack meets a free surface $(\gamma =26^{\circ })$

Specimen Type II: Specimen Type I has a very large mode I stress intensity factor. As a result, when crack initiation occurs (particularly in the somewhat blunted specimens that were manufactured), further growth is extremely dynamic and interpretation of the fracture surface beyond the onset of crack initiation becomes quite difficult. In an effort to modify the stability of crack growth in the specimen, we flipped the orientation of the specimen with respect to the loading direction for specimen Type I as shown in Fig. 5b, making it close to the Goldstein–Osipenko specimen geometry, with the exception of the curved crack fronts. The variation of the three stress intensity factors along the crack front is shown in Fig. 7. In contrast to the Type I specimen, $K_{I}^{\infty }$ is negative over most of the crack front except for the portion close to the bottom of the specimen; the largest compressive values of $K_{I}^{\infty }$ occur in the same region where $K_{III}^{\infty }$ is also large; $K_{II}^{\infty }\sim 0$ in this segment, indicating that we have a segment over which crack initiation will be governed by $K_{III}^{\infty }$ and $K_{I}^{\infty }$, but with tilt angles that are opposite to that expected in Type I specimens. The nucleation should occur first in the central regions and the cracks may grow in a stable manner until nucleation occurs in the region of positive $K_{I}^{\infty }$.

Fig. 7

The variation of the stress intensity factors $K_{I}^{\infty }(s),K_{II}^{\infty }(s),K_{III}^{\infty }(s)$ along the crack front for specimen type II. The origin of $s$ is located at the top of the specimen. Elastic properties of Homalite-100 have been assumed in the simulations $(\gamma =26^{\circ })$

Other variants of the Goldstein–Osipenko geometry were considered; for example, in order to prevent the possible nucleation of cracks from the positive $K_{I}^{\infty }$ in specimen Type II, a compressive stress was applied on the two vertical surfaces as indicated in Fig. 5c; The resulting variation of the three stress intensity factors is shown in Fig. 8. This geometry provides a nice symmetry in the loading; compressive , nearly negligible $K_{II}^{\infty }$, and a large $K_{III}^{\infty }$ are observed. However, the large compression in the vicinity of the maximum shear makes it difficult to initiate crack growth in this geometry. Preliminary experiments indicated that prior to crack initiation from the machined crack tips, cracks nucleated from other defects near the free surfaces of the specimen under mode I conditions and grew dynamically. Tabulated values of the stress intensity factor variation for the Goldstein–Osipenko geometry and its three variants considered here are given in the “Appendix”.

Fig. 8

The variation of the stress intensity factors $K_{I}^{\infty }(s),K_{II}^{\infty }(s),K_{III}^{\infty }(s)$ along the crack front for specimen type III. The origin of $s$ is located at the top of the specimen. Elastic properties of Homalite-100 have been assumed in the simulations $(\gamma =26^{\circ })$

4 Experimental results

Parallelopipedic specimens $50.8\times 76.2$ mm ($2\times 3$ in; $\hbox {height} \times \hbox {length}$;) were machined from 12.7 mm (0.5 in) thick H-100 and 19 mm (0.75 in) thick glass sheets. The cracks were cut according to the specimen design of types I and II, using a diamond blade with radius 38.1 mm (1.5 in) and thickness 0.178 mm (0.007 in). Although an extremely thin diamond blade was used to machine the crack, the pre-crack front is far from the idealized sharp crack front. There also exist many groove lines along the blunt pre-crack front that are caused by the hard particles that form the diamond-coated cutting blade. The experiments were performed under displacement control in an Instron Model 4482 testing machine. The load vs load-point displacement was monitored. However, in all the tests performed, the response was linear until abrupt and unstable fracture initiation. The critical load varied significantly from test to test due to the fact that there were variations in crack tip state; however, the geometric aspects of the response were repeatable to permit interpretation of the threshold behavior, fragment spacing etc.

4.1 Threshold behavior

The main objective of the tests performed with specimen of Type I was to examine the response of the crack when $K_{III}^{\infty }$ passes through zero. Therefore, the fracture surface of the glass and H-100 specimens of Type I were examined using a scanning electron microscope (SEM) (Model Quanta 650 FEG) at different magnifications. The fracture surface was coated with a very thin layer of Pd/Pt material before performing SEM observations to prevent charging of the specimens from the electron beam. Figures 9 and 10 show the detailed fractography of the H-100 and glass specimens, respectively. The fracture surfaces of these materials exhibit many similar features at the early state of the crack growth. First, it appears that initiation of the crack occurred on the pre-crack front very close to the transition point identified through the analysis presented in Sect. 3.2. The fact that nucleation occurs at the transition point is not surprising; either fracture criterion under consideration would indicate such initiation. The key difference is in the prediction of the onset of fragmentation of the crack front. Second, the fragmentation of the crack front into multiple facets is immediate! This is clearly observed by noting that in the neighborhood of the transition point there does not exist a flat area where pre-crack front grows without fragmentation. For the glass specimen, if the threshold twist angle of $3.3^{\circ }$ indicated by Sommer (1969) is to hold, a straight extension of the crack front is expected over a length of about 2.044 mm, but it is seen that fragments appear within the distance of $100~\upmu \hbox {m}$ from the transition point. Within this distance the value of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ is only marginally different from zero. The same behavior is also observed in Fig. 9 in H-100, with immediate fragmentation of the crack over a length that is nearly the same as in the glass specimen. Taken together, these observations suggest that there appears to be no threshold value of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ required for fragmentation of the crack front; a crack front will fragment immediately as soon as it is perturbed by mode III. It remains to identify the scale on which such fragmentation is observed and we will consider some aspects of this problem in the next section. Finally, beyond the initiation of crack growth at the transition point, further crack growth occurred dynamically, dominated by mode I loading. This specimen design was not suitable for examining continued crack growth, if any, under the combined mode loading

Fig. 9

Fractograph of Homalite H-100 specimen type I, showing the region near the transition point. b Shows a magnification of the boxed region in a

Fig. 10

a Fractograph of glass specimen type I, showing the region near the transition point. (a1) Shows a magnification of the boxed region in a; (a2) Shows a magnification of the boxed region in a1. b Identifies the region of interest (near the transition point) where there is a transition from positive $K_{III}^{\infty }$ to negative $K_{III}^{\infty }$

4.2 Intrinsic length scale

While the specimen Type I was well suited for considering the possible threshold behavior, continued growth was dominated as indicated above by mode I. Therefore, experiments were performed on H-100 with specimen Type II, where it was anticipated that as a result of the negative $K_{I}^{\infty }$, the nucleated fragments along the crack front may get arrested. However, cracks initiated along the region of the positive $K_{I}^{\infty }$ on the pre-crack front (see Fig. 7, between 0.9 and 1.0 $s$), grew faster than the cracks nucleated in other regions, and quickly reached an unstable state, popping across the entire specimen dynamically. Nevertheless, the unstable cracks deviated away from the machined crack fronts, and left parts of specimen containing “unbroken” portions of the pre-crack that could be examined to evaluate the nucleation of fragments from the machined pre-crack. These unbroken portions were recovered, polished to extremely thin sections on planes above and below the pre-crack surface and imaged by an optical microscope with magnification of 100$\times$, 200$\times$ and 300$\times$; these images are shown in Fig. 11. It is worth emphasizing that fragmentation spacing can be observed at three different length scales in these specimens. The third level, the largest scale observed, is shown in Fig. 11a. The pre-crack front is identified by an arrow; the width of the crack is dictated by the blade used to cut the crack and as indicated earlier, this is on the order of 175–$200~\upmu \hbox {m}$. At this level, the nucleated cracks are easily observed, and are indicated in Fig. 11a, b; they appear to form a nice nearly periodic pattern with a spacing of about two pre-crack thicknesses, but also indicate significant fluctuations. There exists a smaller length scale—the second level—that is associated with the width of the groove lines on the pre-crack front. As indicated earlier, in addition to the thickness of the blade that dictates the thickness of the pre-crack, the crack front is decorated with grooves that arise from the size of the cutting particles that are part of the cutting blade. These grooves are on the order of a few tens of microns in size and run along the entire crack front. Nucleation of fragments that occur at these grooves results in fragments with a spacing of a few tens of microns. Finally, fragmentation at the smallest length scale—the first level—was discovered along natural crack front (Fig. 11c, d). The thickness of a naturally formed crack is typically much smaller than the machined cracks and is of the order of the fracture process zone. Therefore, one expects the lower bound of the fragment spacing to be dictated by this microstructural scale, as indicated by the results of Lin et al. (2010). Indeed, fragments that were nucleated from a natural crack exhibited a much smaller fragmentation spacing in comparison to the machined cracks; optical microscopy resolved this spacing to be about $10~\upmu \hbox {m}$, but there could be much smaller features that are not resolved optically.

Fig. 11

Cascading length scales of fragmentation spacing. a Nucleation along the pre-crack front on the scale of the thickness of the machined crack. A high magnification image covering a longer length along the crack front is provided as Supplementary Material. b Nucleation along the pre-crack front influenced by the width of the groove lines in the machined crack. c Nucleation along a natural crack front. (d) A magnified view of the boxed region $(100~\upmu \mathrm{m} \times 500~\upmu \mathrm{m})$ indicated in c

The SEM images for glass specimen discussed in Sect. 4.1 (Fig. 10a2) also manifest the cascading length scale of fragment spacing. The larger spacing in Fig. 10a is associated with the width of the machined pre-crack. But in Fig. 10a2 a small region along the natural crack front captured at extremely high magnification is shown. It is worth emphasizing that the fragmentation spacing of a natural crack front is of the order of 0.5–$1.0~\upmu \hbox {m}$ which is much smaller than the fragmentation spacing for the machined crack front for glass.

For the specimens used in Sect. 4.1, over the distance of $100~\upmu \hbox {m}$ near the transition point, the ratio of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ is nearly the same for both the glass and H-100 specimens $({K_{III}^{\infty }}/{K_{I}^{\infty }}\sim 0.001)$. Based on the dependence of the fragmentation spacing on the fracture process zone predicted by the stability analysis of Pons and Karma (2010) (Eq. 4) one would expect differences between glass and H-100, because the fracture process zone size in H-100 is about two orders of magnitude larger than that of glass. But it can be observed clearly that the fragmentation spacing is approximately of the order $30~\upmu \hbox {m}$ for both materials (see Figs. 9, 10).

Together, these observations indicate that an intrinsic length scale for the crack front fragmentation spacing does not exist, but that the spacing depends on the characteristic dimension of the driving crack (thickness of the crack). This provides an explanation for the fact that fragmentation of the crack front has been observed in scales ranging from the microscale to the geological scale where the fragmentation space may be on the order of meters. In the following, we will explore the effect of the stress field shielding from one nucleated crack front on the neighborhood of this nucleus.

4.3 Shielding along the crack front resulting from nucleation of a fragment

As discussed in Sects. 1 and 2, there have been many attempts at understanding the initiation of cracks under mixed mode I+III. Almost without exception, these investigations have used the approach of getting the stress intensity factor using a perturbation approach in which a continuous (smooth) evolution from the “parent” crack was considered. Linear stability analysis was then considered on the basis of the PLS criterion; as discussed earlier, the predictions of such analysis, for example by Leblond et al. (2011), indicate that the crack path is stable for much larger values of ${K_{III}^{\infty }}/{K_{I}^{\infty }}$ than observed experimentally. However, if the PLS generalization in Eq. (6) is used, we expect crack front to fragment into multiple cracks; we explore the possible origins of the fragment spacing under this criterion through a series of numerical simulations. In order to explore the changes in the SIF that is triggered by the nucleation of crack front fragments, we introduce a fragmented crack in the middle of the parent crack; we shall call this the “daughter” crack. Because of limitations in the BEM code in representing intersecting cracks, the following strategy was adopted. The parent crack was represented as a sharp crack in a large block of size $\left( {a\times b\times c}\right)$. The specimen was subjected to boundary loading that generated a mixed mode loading $\left( {K_{I}^{\infty },K_{III}^{\infty }}\right)$ along the straight crack front. The daughter crack was represented by a three-dimensional geometrical feature: the daughter crack was idealized as a disk-like geometrical feature with a “crack tip radius” $r_{\mathrm{micro}}=12.7~\upmu \hbox {m}$, with a circular crack of radius $a_{\mathrm{micro}}=\alpha r_{\mathrm{micro}}$, and $\alpha \in \left[ {5,50}\right]$. The nucleated crack was taken to be orientated at an angle $\phi _{c}$, as dictated by Eq. (2). The system of the parent-daughter cracks is shown in Fig. 12a. The variation of the stress intensity factors $\left( {k_{I}, k_{II}, k_{III}}\right)$ along the original crack front that results from nucleation of the daughter crack was calculated from the boundary element simulation. This variation is shown in Fig. 12b, where the stress intensity factors are normalized by $K_{I}^{\infty }$ and the distance along the crack front from the daughter crack is normalized by the radius of the daughter crack. The results shown correspond to${K_{III}^{\infty }}/{K_{I}^{\infty }}=0.42$, resulting in $\phi _{c}=35^{\circ }$, and for $\alpha \in \left[ {5,50}\right]$, corresponding to a daughter crack of radius $a\in \left[ {63.5,635} \right] ~\upmu \hbox {m}$. The shielding effect of the nucleated crack on either side of the daughter crack is evident: the stress intensity factors for modes I and III on the parent crack drop in the immediate vicinity of the microcrack; with distance away from the site of the daughter crack, the stress intensity factors along the parent crack gradually return to the far-field values that correspond to the imposed uniform values, with a small peak at about one radius from the daughter crack. A local fluctuation in the mode II stress intensity factor is also introduced, indicating the inherent coupling of all three modes. It is clear that any crack nucleation that occurs along the crack front will shield—by elastic unloading—a neighborhood whose size depends on $\phi _{c}$ and $\alpha$. In order to obtain a quantitative measure of this shielding, we need to identify the location at which the next crack may nucleate: this could be at the site of maximum $k_{I}$ located at a distance $b_{1}$ from the nucleation point. However, there is a significant amount of $k_{III}$ at this location; nucleation could also occur at the location of minimum $k_{III}$, which is located at a distance $b_{3}$ from the nucleation point. The distances $b_{1}$ and $b_{3}$ could be considered to indicate the spacing between the nucleated cracks corresponding to any twist angle $\phi _{c}$ and crack size $\alpha$. These simulations were repeated for values of $\phi _{c}\in \left[ {10,35}\right]$ at fixed $\alpha =20$ and the results of mode I and III stress intensity factors, $\left( {k_I /K_{I}^{\infty },k_{III} /K_{III}^{\infty }}\right)$ were obtained. From these results, the dependence of the distances $b_{1}$ and $b_{3}$ on $\phi _{c}$ were extracted and are plotted in Fig. 13. From these results, it is seen that $b_{1}$ increases with $\phi _{c}$ while $b_{3}$ indicates a decrease with an increase in $\phi _{c}$; the latter trend is similar to that indicated in the experimental results of Lin et al. (2010) (see Fig. 7c of that reference). The implication of this result is that the shielded length (and therefore the fragment spacing) depends on the size of the daughter crack, which in turn, would depend on the characteristic thickness of the parent crack that drives the nucleation. We conclude this discussion by pointing out that we have only considered the nucleation of the crack fragments and not its further evolution. Upon further loading, the nucleated population of daughter cracks will interact with each other, and create a quite complex state of local mode mix. The further evolution of the daughter cracks follows one of two possible paths: if the global loading is dominant $K_{I}^{\infty }$, the daughter cracks will eventually coalesce into each other and rotate the crack so as to eliminate $K_{III}^{\infty }$. On the other hand, if the global loading is dominant $K_{III}^{\infty }$, within a compressive field (negative $K_{I}^{\infty }$), the fragments may continue to grow as independent cracks as indicated in the experiments of Goldstein and Osipenko (2012) and in the type II specimens reported in the present work.

Fig. 12

a Schematic diagram indicating the parent crack under a mixed mode loading, with a daughter crack that nucleated at the center. b Change in crack tip SIFs with daughter cracks size $a_{\mathrm{micro}}= \alpha r_{\mathrm{micro}}$. The daughter crack tip was idealized by a rounded geometrical feature $r_{\mathrm{micro}}=12.7\,\upmu \hbox {m}$ in the simulations. The parent crack is loaded such that ${K_{III}^{\infty }}/{K_{I}^{\infty }}=0.42$ (to produce the twist angle $\phi =35^{\circ })$. The distance along the parent crack front from the daughter crack is normalized by $a_{\mathrm{micro}}$

Fig. 13

Location $b_{1}$ of maximum $k_{I}$ and $b_{3}$ of minimum $k_{III}$ for different daughter cracks angles $\phi$. The daughter crack tip was idealized by a rounded geometrical feature $r_{\mathrm{micro}}=12.7\,\upmu \hbox {m}$, with crack size $a_{\mathrm{micro}}=\alpha r_{\mathrm{micro}}$; $\alpha =20$ in these simulations

5 Conclusion

The criterion for initiation of cracks under mixed-mode I+III loading has been examined further. Following on the geometry suggested for such investigations by Goldstein and Osipenko (2012), we explored alternative geometries that can be tailored to address specific questions related to the initiation of cracks. All designs were supported with calculation of the stress intensity factors using a boundary element code (Li et al. 1998). With the first design, mode II was nearly completely eliminated, and the value of the mode III stress intensity factor experienced a change of sign from negative to positive in the location where the mode I stress intensity factor attained a maximum. This allowed examination of the question of existence of a threshold for crack front fragmentation. The second design, in which the mode I stress intensity factor was negative caused crack that nucleated to be arrested, permitting examination of the spacing between the nucleated crack front fragments. Experiments were performed on two materials: glass and H-100, both of which exhibit brittle or quasi-brittle fracture behavior. Recovered specimens were examined to reveal the geometry of the nucleated crack front fragments. From this study, two major conclusions are reached:

• i. Cracks subjected to combined modes I+III loading cause fragmentation of the crack front without any threshold; perturbations as small as ${K_{III}^{\infty }}/{K_{I}^{\infty }}\sim 0.001$ cause nucleation of fragmented daughter cracks.

• ii. The distance between the fragments is dictated by the length scale corresponding to the decay of the elastic field; this decay depends on the thickness dimension of the parent crack from which the daughter fragments are nucleated. The thickness of the parent crack is governed either by the microstructural scale of the fracture process zone for a natural crack, or by the local radius of curvature of grooves for a machined crack.

The continued growth or coalescence of the nucleated crack fragments, which themselves could be subjected to further mixed mode loading, would depend on the global loading imposed and will been examined in a future contribution.

Appendix: Tables of stress intensity factors for part-through cracks for specimen types I, II and III

The variation of the stress intensity factor along the crack front for the original Goldstein–Osipenko geometry and its variants used in this work, labeled Type I, II and III specimens are provided here; the stress intensity factors were calculated using a boundary element code developed by Li et al. (1998).

See Tables 1, 2 and Fig. 14.

Fig. 14

a Mesh discretization of Goldstein–Osipenko configurations. b Typical mesh discretization for part-through crack configurations

Table 1 Stress intensity factors for Goldstein–Opisenko configurations

Table 2 Stress intensity factors for part-through cracks for types I, II and III