Multiaxial ductile fracture criteria coupled with non-quadratic non-prismatic yield surface in the predictions for a naturally aged aluminium alloy

Abstract

The ductile fracture has been one of the most important topics in various branches, such as the automotive, maritime or energy industry. Many approaches have been developed under certain assumptions. The present work focuses on bringing together the microstructural- and phenomenological-based ductile fracture modelling under large plastic deformations, room temperature and quasi-static monotonic loading. The complex yield criterion dependent on three stress invariants with a deviatoric associated flow rule was coupled with several advanced multiaxial ductile fracture criteria. The models were calibrated for the 2024-T351 aluminium alloy and implemented within the commercial explicit finite element code of Abaqus. Two additional tests, which were not covered within the calibration procedure, were simulated to demonstrate good predictability of the onset of cracking and its propagation, modelled by the element deletion technique. It was a small punch test and a three-point bending test of a randomly notched bar.

1 Introduction

Failure predictions aim to increase the safety of machine elements, optimize manufacturing processes or investigate the behaviour of structures in accidents (Cerik et al. 2019; Talemi et al. 2019). Non-destructive testing has to be employed for the inspection of parts, when inner flaws occur, while numerical simulations are an effective tool in predicting those discontinuities. Manufacturing costs can decrease when metal forming operations are optimized (Gachet et al. 2015). Apart from the products, the tools can also be analysed (List et al. 2012). However, cracking can also be optimized in processes such as machining or cutting, where it is intended (Wang and Liu 2016). The computations may be useful when there is a shortage of material available or the material is vintage or hazardous, such as irradiated. The design of a new material and its application in various services, such as ballistic protection (Xiao et al. 2019b), may also be of interest. Immediate cost savings are apparent, but future liability problems can be avoided with the help of numerical simulations as well. Nevertheless, it should be noted that the computations cannot ever fully replace the experiments.

Another step forward was the use of digital image correlation (Erice et al. 2018). It is useful in the calibration and verification stage (Park et al. 2018). It should be noted that utilization is mainly in sheet metal applications with the biaxial stress state and major strains observable on the material surface (Mu et al. 2020). However, cracks often initiate inside the material in many cases, so another option has to be sought, such as computed tomography (Roth et al. 2018).

Isotropic hardening is often utilized in ductile fracture, while it is generally insufficient to predict the springback (Lin et al. 2020). In addition to kinematic hardening, directional distortional hardening may be used (Lee et al. 2019). Another approach may be crystal plasticity (Scherer et al. 2019) or probabilistic modelling (Tancogne-Dejean et al. 2019).

The first influence on the ductile fracture was attributed to the stress state conventionally represented by the first principal stress. Proposed criteria were quite simple and usually one-parametric as proposed by Ko et al. (2007). Although the criteria were usually dimensionless, the use of stress triaxiality has started to prevail as published by Bao and Wierzbicki (2004), who also concluded that there is a cut-off stress triaxiality $\eta_{c} = - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$, below which the damage parameter does not accumulate and, therefore, there is no fracture. It is probably a correct assumption, but it was proved that the value is material dependent and can be lower than $- {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}$ (Tutyshkin et al. 2014). Finally, the complex dependency on the stress triaxiality was just one step before the Lode dependency was acknowledged. Wilkins et al. (1980) proposed a criterion depending not only on the hydrostatic pressure but also on the deviatoric stress state, assuming that the fracture strain decreased with increasing shear load. However, it took much longer before the Lode dependency was widely accepted within the ductile fracture community. Then it even took its place within the porosity-based models (Xue 2008). Moreover, the lowest ductility at generalized shear also implies that the cut-off plane should be convex, which has not been much regarded in the literature yet. It will be further addressed accordingly. Bai and Wierzbicki (2010) later proposed a more sophisticated (extended Mohr–Coulomb) criterion with a low number of material parameters related to fracture. Lou et al. (2014) introduced a criterion with a changeable cut-off inspired by the criterion proposed by Cockroft and Latham (1968). Kubík et al. (2018) introduced a slight modification to this criterion independently and simultaneously with Xiao et al. (2018), which considered the fixed material parameter (causing the cut-off plane shape to be fixed) as another material parameter used for fitting. Finally, Lou et al. (2017) introduced another material parameter into the cut-off in order to better govern the dependence on the deviatoric stress state measure. Although the material parameters were already calibrated altogether, there was still a prescribed restriction on the cut-off stress triaxiality. Therefore, the material parameter can still be regarded as fixed or semifixed in such a case. Roth and Mohr (2014) proposed a (Hosford–Coulomb) criterion in a way similar to that of Bai and Wierzbicki (2010). Last but not least, the significant influence of plasticity non-associativity on the ductile fracture was demonstrated by Vobejda et al. (2022).

The foundation of continuum damage mechanics was laid by Kachanov (1958), who formulated the concept of effective stress and introduced the weakening function, which is zero at the moment of fracture and unity for the undamaged material. Lemaitre (1985) formulated the coupling within the framework of the thermodynamics of irreversible processes and introduced the damage strain energy release rate. Chaboche (1981) introduced anisotropic damage, for which Murakami and Ohno (1981) proposed a procedure for symmetrizing the effective stress. Based on that, Chow and Wang (1987) proposed an anisotropic model in the scope of approach proposed by Lemaitre (1985), later followed within the thermodynamically consistent framework by Brünig (2002) or Besson (2010). Kattan and Voyiadjis (2001) decomposed the damage into two parts related to voids and cracks, respectively. Xue (2007) assumed that the flow stress of a matrix is greater than the conventional flow stress of the material containing flaws and introduced the weakening exponent in order to relate the micro and macro behaviour. In addition to that, Xue (2007) also proposed a non-linear damage accumulation and symmetric ductile fracture criterion.

The so-called post-initiation softening is another technique when the damage is partially coupled with elastic–plastic behaviour, which means that damage accumulation is driven by plastic deformation, and in turn, the elastic behaviour and constitutive law is influenced by the amount of damage after some threshold (Li and Wierzbicki 2010; Paredes et al. 2018; Keim et al. 2020). It was introduced because it is challenging to reproduce the slant fracture with the phenomenological ductile fracture criteria, which are uncoupled. It should be noted that all described solutions are mesh dependent. Moreover, the loss of ellipticity and subsequent localization occur when coupled models are employed. This may be solved by nonlocal regularization (Seidenfuss et al. 2011; Andrade et al. 2011; Baltic et al. 2020).

2 Material testing

The whole experimental campaign was carried out on the wrought aluminium alloy 2024-T351. Heat treatment designates that the material was solution heat-treated, stress-relieved and then naturally aged (the influence of aging on plasticity and ductile fracture was investigated by Jung et al. (2022) for a different aluminium alloy), while stress relief was achieved by stretching the metal by 1.5 to 3.0% of deformation. There was no straightening after stretching. Although this aluminium alloy with the face-centred cubic structure does not exhibit extensive necking, many tests have been conducted in the scope of ductile fracture (Papasidero et al. 2014; Hartlen and Doman 2019). Each batch is unique and the results may vary significantly. Flow curves from various sources with considerable scatter even in such a limited range are plotted in Fig. 1, where $\overline{\sigma }$ is the equivalent stress and $\overline{\varepsilon }_{p}$ is the equivalent plastic strain. To avoid combining data from various sources as in Khan and Liu (2012), Li et al. (2021), Quach et al. (2020), and to eliminate the influence of microstructure or even to misinterpret the behaviour of the real material, the experimental campaign has been set up and the material was supplied by Feropol as a cold-rolled plate with dimensions of 1500 × 1000 × 20 mm.

Fig. 1

Scatter in flow curves published by Bai et al. (2006), Wierzbicki et al. (2005), Seidt and Gilat (2013), Papasidero et al. (2015) and Xiao et al. (2019a)—for the reference strain rate and room temperature

The chemical composition given in Table 1 is the result of three repeated measurements using Spectrumat GDS 750 obtained by glow discharge optical emission spectroscopy (Šebek et al. 2018).

The reference block of material was cut from the plate and the weight was measured using the analytical balance with 1 mg readability, resulting in a density of 2770 kg × m^–3. The block was used for non-destructive measurement of the wave velocity by the OLYMPUS 38DL PLUS ultrasonic thickness gauge with M110 contact transducer. The Poisson’s ratio of 0.34 was calculated knowing Young’s modulus (72,500 MPa from the standard tensile tests performed further) and the average wave velocity of 6347 m × s^–1 (Šebek et al. 2018).

The level of anisotropy was low from a macroscopic point of view in such a bulk material, as demonstrated by the final shape of the post-mortem sample from the transverse direction after the tensile test (Fig. 2), which was obtained using the SEM Tescan LYRA3 XMH (Šebek et al. 2019). Therefore, the material was considered isotropic for the finite element modelling and all specimens were manufactured in the same direction, which showed minimal scatter in the displacements to fracture (Fig. 2). Furthermore, a moderate Portevin–Le Chatelier effect was observed in the tensile tests between 5 and 6 mm of elongation (Fig. 2).

Fig. 2

Results of 5 standard tensile tests in the transverse direction (left) and post-mortem specimen showing minimum ellipticity (right) (Šebek et al. 2019)

The crack was initiated either on the surfaces of the specimens or inside the specimens within this study, as discussed further. However, all specimens had the process zone, where the crack appeared sooner or later, prepared in the same quality. The surface roughness of 0.4 µm was prescribed in the detailed drawings, but much lower values between 0.078 and 0.102 µm were measured on a representative specimen using the BrukerContourGT-X8 Non-Contact 3D Optical Profiler. Therefore, the surfaces of the process zones were prepared very carefully so that the surface roughness could not influence the results.

All tests were performed under quasi-static loading. There were conducted 5 tensile tests of smooth (strain rate approximately from $0.000\overline{5}$/s to $0.00\overline{1}$/s on 30 mm gauge length) and 3 notched (strain rate approximately of 0.0005/s on 30 mm gauge length) cylindrical specimens, 3 tensile (strain rate approximately of $0.000\overline{5}$/s on 30 mm gauge length) and 3 torsional (strain rate approximately of $0.001$ rad/s for 646 Hydraulic Collet Grip—the stiffness of the system influenced the torque response as discussed further) tests of notched tubular specimens and 2 compression tests of notched cylinders (strain rate approximately of $0.0009$/s on height 18 mm). The detailed description of all experiments can be found in Kubík et al. (2018) and is not repeated within the present study, as it is in the rest of the article, where only new information is presented unless otherwise stated.

3 Material modelling

All computations were performed in Abaqus 2019. The mesh dependency was treated using the same element size of 0.075 mm within the gauge section in all numerical simulations. The mapped mesh was created as depicted in Fig. 3, where the smooth cylindrical specimen is omitted because the mesh layout is obvious, when a 3 × 15 mm was modelled. All tests were modelled using axial symmetry with CAX4R four-node bilinear quadrilateral elements with reduced integration and hourglass control, apart from torsion and compression, which were modelled in three dimensions with C3D8R eight-node linear brick elements with reduced integration and hourglass control. The upper tubular part of the torsional specimen, which did not undergo any deformation, was meshed with elements of a size of 0.2 mm so as the parts of the notched cylinder, modelled with respect to the vertical and horizontal planes of symmetry, at a distance of 1.5 mm from the notch. Furthermore, R3D4 four-node bilinear quadrilateral rigid elements with the size of 0.2 mm were used for the tool in the upsetting test, where the friction coefficient of 0.05 was applied (the punch is not shown in Fig. 3). The friction coefficient was identified on the basis of deformation—barrelling and stick and slip regions. Duration of the simulated tests was shortened to 0.1 s and the mass scaling with the time increment of 1 × 10^–7 s was used for torsion and compression to speed up the calculations, while the kinetic energy was checked to be negligible compared to the total energy.

Fig. 3

Meshed specimen with highlighted crack initiation location: a cylindrical with R13 notch for tension (largest diameter of 16 mm), b cylindrical with R6.5 notch for tension (largest diameter of 16 mm), c cylindrical with R4 notch for tension (largest diameter of 16 mm), d cylindrical with notch for compression (largest diameter of 12 mm), e tubular with R4 notch for tension (largest diameter of 16 mm), f tubular with R4 notch for torsion (largest diameter of 15 mm)—not in a mutual scale

3.1 Model of elasticity

The isotropic elastic model of the material was adopted, as mentioned earlier. The material parameters used for the computations are given in Table 2 along with the physical property needed for the calculations within the explicit finite element method, which was utilized due to its conditional stability allowing crack initiation and propagation by means of element deletion. In such a case, the implicit algorithm would not be capable of convergence.

Table 1 Chemical composition of 2024-T351 (Šebek et al. 2018)

Table 2 Elastic characteristics and specific mass utilized within computations (Šebek et al. 2018)

3.2 Model of plasticity

The isotropic plastic behaviour was assumed, as discussed earlier. All parts of the plasticity model are introduced in the following subsections.

3.2.1 Isotropic hardening law

All the following yield criteria will share the same hardening law at the axisymmetric tension condition. The flow curve was identified with the standard tensile test of a smooth cylindrical specimen. First, engineering strains and stresses were recalculated in true quantities up to the ultimate tensile strength (Fig. 4). Beyond that, the curve was extrapolated and the inverse calibration was employed until the satisfying match between the average experiment and computation was achieved. The calibrated multilinear flow curve is depicted in Fig. 4 and is named as conventional. There is also a flow curve of the matrix, which will be introduced later within this section as a result of the adopted plasticity damage approach.

Fig. 4

Engineering and true stress–strain curves with highlighted necking point (left) and calibrated (extrapolated) conventional multilinear flow curve (right)

3.2.2 Von Mises yield criterion with associated flow rule

The yielding occurs when the second invariant of deviatoric stress tensor reaches a critical value. The yield function may be written as

$$ f = \overline{\sigma } - \sigma_{y} , $$

(1)

where $\sigma_{y}$ is the yield stress. Equivalent stress is defined as

$$ \overline{\sigma } = \sqrt {\frac{3}{2}\left( {\underline {s} :\underline {s} } \right)} , $$

(2)

where $\underline {s}$ is the deviatoric stress tensor and $:$ is the double dot product. The associated flow rule is given by

$$ \frac{\partial f}{{\partial \underline {\sigma } }} = \frac{3}{2}\frac{{\underline {s} }}{{\overline{\sigma }}}, $$

(3)

where $\underline {\sigma }$ is the stress tensor. It should be noted that the outward normal is not unity when the above formulation is adopted. Finally, the increment of the plastic multiplier is explicitly written as

$$ \Delta \lambda = \frac{{\sigma_{t} - \sigma_{y} }}{3G + H}, $$

(4)

where $\sigma_{t}$ is the trial stress, $G$ is the shear modulus and $H$ is the plastic modulus.

3.2.3 Kroon–Faleskog yield criterion with associated flow rule

Kroon and Faleskog (2013) proposed a yield function (Kroon–Faleskog hereinafter), which was dependent on the second and third invariants of deviatoric stress tensor. The yield function is formulated as follows

$$ f = \overline{\sigma } - k\sigma_{y} , $$

(5)

where $k$ is the yield function correction

$$ k = 1 - \mu \left( {1 - \xi^{2} } \right)\left( {\frac{{1 + \xi_{0}^{\frac{1}{a}} }}{{\left[ {1 - \xi^{2} } \right]^{\frac{1}{a}} + \xi_{0}^{\frac{1}{a}} }}} \right)^{a} = 1 - \mu \sin^{2} \left( {3\theta_{L} } \right)\left( {\frac{{1 + \xi_{0}^{\frac{1}{a}} }}{{\sin^{\frac{2}{a}} \left( {3\theta_{L} } \right) + \xi_{0}^{\frac{1}{a}} }}} \right)^{a} , $$

(6)

where $\mu$, $\xi_{0}$ and $a$ are the material parameters and $\xi$ and $\theta_{L}$ are the normalized third invariant of deviatoric stress tensor and Lode angle defined in Appendix 1. The associated flow rule is given by the derivative of the yield function as

$$ \frac{\partial f}{{\partial \underline {\sigma } }} = \frac{3}{2}\frac{{\underline {s} }}{{\overline{\sigma }}} - 3\frac{{\frac{{{\text{d}}k}}{{{\text{d}}\xi }}}}{k}\left( {2\frac{3}{2}\frac{{\underline {s} }}{{\overline{\sigma }}} \cdot \frac{3}{2}\frac{{\underline {s} }}{{\overline{\sigma }}} - \underline {I} - \xi \frac{3}{2}\frac{{\underline {s} }}{{\overline{\sigma }}}} \right), $$

(7)

where $\cdot$ is the dot product and $\underline {I}$ is the identity matrix and the derivative is

$$ \frac{{{\text{d}}k}}{{{\text{d}}\xi }} = \frac{{2\mu \left( {1 + \xi_{0}^{\frac{1}{a}} } \right)^{a} \xi_{0}^{\frac{1}{a}} \xi }}{{\left( {\left[ {1 - \xi^{2} } \right]^{\frac{1}{a}} + \xi_{0}^{\frac{1}{a}} } \right)^{a + 1} }}. $$

(8)

Note that the first term in Eq. (7) is analogical to Eq. (3). Furthermore, the Kroon–Faleskog yield criterion is symmetric with respect to generalized shear $\left( {\xi = 0} \right)$, which implies that the yield correction function is an even function, so $k\left( \xi \right) = k\left( { - \xi } \right)$. It simplifies to the von Mises yield criterion when $\mu = 0$ and roughly approaches the Tresca yield criterion when $\mu = 1 - {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-\nulldelimiterspace} 2}$, yet with round corners, unlike the Tresca yield criterion exhibiting a singularity. The plastic multiplier increment was calculated similarly to Eq. (4) according to the following expression

$$ \Delta \lambda = \frac{{\sigma_{t} - k\sigma_{y} }}{3G + kH}, $$

(9)

containing only the yield correction function additionally. The yield criterion was implemented into Abaqus using the Vectorized User MATerial (VUMAT) subroutine. Then, the inverse calibration was used towards the experiments in generalized shear (tension and torsion of the notched tube). Calibrated material parameters are given in Table 3 with the yield locus depicted in Fig. 5 compared to the von Mises one, where $\sigma_{{\text{I}}}$, $\sigma_{{{\text{II}}}}$ and $\sigma_{{{\text{III}}}}$ are the principal stresses not ordered according to the magnitude.

Table 3 Calibrated material parameters for Kroon–Faleskog yield criterion (Šebek et al., 2018)

Fig. 5

Calibrated Kroon–Faleskog yield criterion in Haigh–Westergaard space (right) and compared to von Mises one on deviatoric plane (left) (Šebek et al., 2018)

The curvature was checked to ensure that the yield surface is convex according to the expression for polar coordinates in the form

$$ \kappa = \frac{{r^{2} + 2\left( {\frac{{{\text{d}}r}}{{{\text{d}}\theta_{L} }}} \right)^{2} - r\frac{{{\text{d}}^{2} r}}{{{\text{d}}\theta_{L}^{2} }}}}{{\left( {r^{2} + \left( {\frac{{{\text{d}}r}}{{{\text{d}}\theta_{L} }}} \right)^{2} } \right)^{\frac{3}{2}} }} > 0, $$

(10)

where $r$ is the radial coordinate of the cylindrical coordinate system dependent on the Lode angle through the yield correction function as

$$ r = k\sqrt{\frac{2}{3}} \sigma_{y} . $$

(11)

The respective derivatives are

$$ \frac{{{\text{d}}r}}{{{\text{d}}\theta_{L} }} = \frac{{{\text{d}}k}}{{{\text{d}}\theta_{L} }}\sqrt{\frac{2}{3}} \sigma_{y} = - 3\mu \frac{{\left( {1 + \xi_{0}^{\frac{1}{a}} } \right)^{a} \xi_{0}^{\frac{1}{a}} }}{{\left( {\sin^{\frac{2}{a}} \left( {3\theta_{L} } \right) + \xi_{0}^{\frac{1}{a}} } \right)^{a + 1} }}\sin \left( {6\theta_{L} } \right)\sqrt{\frac{2}{3}} \sigma_{y} , $$

(12)

$$ \frac{{{\text{d}}^{2} r}}{{{\text{d}}\theta_{L}^{2} }} = \frac{{{\text{d}}^{2} k}}{{{\text{d}}\theta_{L}^{2} }}\sqrt{\frac{2}{3}} \sigma_{y} = 9\mu \frac{{\left( {1 + \xi_{0}^{\frac{1}{a}} } \right)^{a} \xi_{0}^{\frac{1}{a}} }}{{\left( {\sin^{\frac{2}{a}} \left( {3\theta_{L} } \right) + \xi_{0}^{\frac{1}{a}} } \right)^{a + 1} }}\left( {\frac{a + 1}{a}\frac{{\sin^{\frac{2}{a}} \left( {3\theta_{L} } \right)}}{{\sin^{\frac{2}{a}} \left( {3\theta_{L} } \right) + \xi_{0}^{\frac{1}{a}} }}4\cos^{2} \left( {3\theta_{L} } \right) - 4\cos^{2} \left( {3\theta_{L} } \right) + 2} \right)\sqrt{\frac{2}{3}} \sigma_{y} . $$

(13)

Finally, the curvature was modified for easier plotting according to Kroon and Faleskog (2013) as

$$ \overline{\kappa } = \frac{{\ln \left( {1 + \sqrt{\frac{2}{3}} \sigma_{y} \kappa } \right)}}{\ln \left( 2 \right)}. $$

(14)

The smoothness of the yield surface is ensured when the curvature is finite, which is satisfied as well.

3.2.4 Bai–Wierzbicki yield criterion with deviatoric associated flow rule

Bai and Wierzbicki (2008) proposed a yield criterion dependent on the stress triaxiality $\eta$ (defined in Appendix 1) and the normalized third invariant of deviatoric stress tensor. Due to easier implementation, the yield correction function was introduced as in the case of Kroon–Faleskog yield criterion as

$$ k = \left( {1 - c_{\eta } \left[ {\eta - \eta_{0} } \right]} \right)\left( {c_{s} + \left[ {c_{a} - c_{s} } \right]\left[ {\gamma - \frac{{\gamma^{m + 1} }}{m + 1}} \right]} \right), $$

(15)

where $\eta_{0}$ is the initial stress triaxiality (serving as another material parameter), $c_{\eta }$, $c_{s}$ and $m$ are the material parameters and $\gamma$ is the function of the deviatoric stress tensor as

$$ \gamma = \frac{\sqrt 3 }{{2 - \sqrt 3 }}\left( {\sec \left( {\frac{1}{3}\arcsin \left[ \xi \right]} \right) - 1} \right) = \frac{\sqrt 3 }{{2 - \sqrt 3 }}\left( {\sec \left( {\frac{{\uppi }}{6} - \theta_{L} } \right) - 1} \right). $$

(16)

It should be noted that the secant is an even trigonometric function. Therefore, Bai and Wierzbicki (2008) used $\sec \left( {\theta_{L} - {{\uppi } \mathord{\left/ {\vphantom {{\uppi } 6}} \right. \kern-\nulldelimiterspace} 6}} \right)$. Finally, $c_{a}$ is the function distinguishing between the tension and compression as

$$ c_{a} = \left\{ {\begin{array}{*{20}c} {c_{t} \;{\text{if}}\;\xi \ge 0} \\ {c_{c} \;{\text{if}}\;\xi < 0} \\ \end{array} } \right., $$

(17)

where $c_{t}$ and $c_{c}$ are the material parameters. It should be noted that Vershinin (2017) pointed out that Bai and Wierzbicki (2008) calibrated material parameters, which do not satisfy the convexity condition, and mistakenly assumed that $\overline{\sigma } = \sigma_{y}$, which is not the case for the yield criteria dependent on the stress triaxiality and/or deviatoric stress tensor. The original yield criterion was later corrected by Ghazali et al. (2020) as well. Nevertheless, the deviatoric associated flow rule is given by Bai and Wierzbicki (2008) using the chain rule as

$$ \frac{\partial f}{{\partial \underline {\sigma } }} = \frac{{\partial \overline{\sigma }}}{{\partial \underline {\sigma } }} + \sigma_{y} c_{\eta } \left( {c_{s} + \left[ {c_{a} - c_{s} } \right]\left[ {\gamma - \frac{{\gamma^{m + 1} }}{m + 1}} \right]} \right)\frac{\partial \eta }{{\partial \underline {\sigma } }} - \sigma_{y} \left( {1 - c_{\eta } \left[ {\eta - \eta_{0} } \right]} \right)\left( {c_{a} - c_{s} } \right)\left( {1 - \gamma^{m} } \right)\frac{\partial \gamma }{{\partial \underline {\sigma } }}, $$

(18)

where the first derivative is analogous to the one in Eq. (3)

$$ \frac{{\partial \overline{\sigma }}}{{\partial \underline {\sigma } }} = \frac{3}{2}\frac{{\underline {s} }}{{\overline{\sigma }}}, $$

(19)

$$ \frac{\partial \eta }{{\partial \underline {\sigma } }} = \frac{1}{3}\frac{{\underline {I} }}{{\overline{\sigma }}} - \frac{3}{2}\frac{{\underline {s} }}{{\overline{\sigma }^{2} }}\eta , $$

(20)

$$ \frac{\partial \gamma }{{\partial \underline {\sigma } }} = \frac{3\sqrt 3 }{{2 - \sqrt 3 }}\frac{{\tan \left( {\frac{1}{3}\arcsin \left[ \xi \right]} \right)}}{{\cos \left( {\frac{1}{3}\arcsin \left[ \xi \right]} \right)}}\frac{1}{{\overline{\sigma }\sqrt {1 - \xi^{2} } }}\left( {\frac{3}{2}\frac{{\underline {s} \cdot \underline {s} }}{{\overline{\sigma }^{2} }} - \frac{{\underline {I} }}{3} - \frac{{\xi \underline {s} }}{{2\overline{\sigma }}}} \right). $$

(21)

It should be noted that the equivalent plastic strain increment is perpendicular to the yield loci in the deviatoric (octahedral) plane only, so it is different from the yield surface outward normal. Therefore, it is named as the deviatoric associativity of the flow rule. This may be assumed when the plastic dilatancy is negligible and the plastic incompressibility is desired. It is achieved when the first term is eliminated from Eq. (20). The yield criterion simplifies into the von Mises one when either $c_{\eta } = 0$ and $c_{t} = c_{s} = c_{c} = 1$ or $m = 0$. It becomes the yield criterion proposed by Drucker and Prager (1952) when $c_{\eta } \ne 0$ while either $c_{t} = c_{s} = c_{c} = 1$ or $m = 0$. Finally, it closely approaches the Tresca yield criterion when $c_{\eta } = 0$, $c_{s} = {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-\nulldelimiterspace} 2}$, $c_{t} = c_{c} = 1$ and $m \to \infty$. The plastic multiplier was calculated according to the same equation, as in the case of the previous yield criterion, Eq. (9). The yield criterion was implemented in Abaqus using the VUMAT as in the previous case. Then, the inverse calibration was used for all experiments. Calibrated material parameters are in Table 4, while the yield locus is depicted in Fig. 6 and compared to the von Mises one.

Table 4 Calibrated material parameters for Bai–Wierzbicki yield criterion (Kubík et al., 2018)

Fig. 6

Calibrated Bai–Wierzbicki yield criterion in Haigh–Westergaard space (right) and compared to the von Mises one on deviatoric plane (left) (Kubík et al., 2018)

The convexity of the yield surface depends on four material parameters $c_{t}$, $c_{s}$, $c_{c}$ and $m$, and not just the first three, as stated by Bai and Wierzbicki (2008), who used a set of material parameters that do not satisfy the convexity condition. Lian et al. (2013) derived a simple criterion for convexity, ${{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } 2}} \right. \kern-\nulldelimiterspace} 2} \le {{c_{s} } \mathord{\left/ {\vphantom {{c_{s} } {c_{a} }}} \right. \kern-\nulldelimiterspace} {c_{a} }} \le 1$, which is independent of the material parameter $m$, which should be a positive integer. For full control, the curvature was calculated and checked again according to Eqs. (10) and (11) with the following derivatives

$$ \begin{array}{*{20}c} {\frac{{{\text{d}}r}}{{{\text{d}}\theta_{L} }} = \frac{{{\text{d}}k}}{{{\text{d}}\theta_{L} }}\sqrt{\frac{2}{3}} \sigma_{y} = }{\left( { - 1 + c_{\eta } \left[ {\eta - \eta_{0} } \right]} \right)\left( {c_{a} - c_{s} } \right)\frac{{\sin \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)}}{{\left( {\sqrt 3 - 2} \right)^{2} \cos^{2} \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)}}\sqrt{\frac{2}{3}} \sigma_{y} } \\ {}{ \times \left( {2\sqrt 3 - 3 + \left( {3^{{\frac{m}{2} + 1}} - 2 \times 3^{{\frac{m}{2} + \frac{1}{2}}} } \right)\left[ {\frac{{ - 1 + \cos \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)}}{{\left( {\sqrt 3 - 2} \right)\cos \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)}}} \right]^{m} } \right)} \\ \end{array} , $$

(22)

$$ \begin{array}{*{20}c} {\frac{{{\text{d}}^{2} r}}{{{\text{d}}\theta_{L}^{2} }}}{ = \frac{{{\text{d}}^{2} k}}{{{\text{d}}\theta_{L}^{2} }}\sqrt{\frac{2}{3}} \sigma_{y} } \\ {}{ = \frac{{\left( {1 - c_{\eta } \left[ {\eta - \eta_{0} } \right]} \right)\left( {c_{a} - c_{s} } \right)}}{{\left( {\sqrt 3 - 2} \right)^{2} \cos^{3} \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)}}\left( {\left[ {\left( {3^{{\frac{m}{2} + 1}} - 2 \times 3^{{\frac{m}{2} + \frac{1}{2}}} } \right)\left[ {m - \cos \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)} \right]\cos \left( {\frac{{\uppi }}{6} - \theta_{L} } \right) + 6 \times 3^{\frac{m}{2}} } \right.} \right.} \\ {}{\left. {\left. { + \left( { - 2m - 4} \right)3^{{\frac{m}{2} + \frac{1}{2}}} + m3^{{\frac{m}{2} + 1}} } \right]\left[ {\frac{{ - 1 + \cos \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)}}{{\left( {\sqrt 3 - 2} \right)\cos \left( {\frac{{\uppi }}{6} - \theta_{L} } \right)}}} \right]^{m} - 2\left( {\sqrt 3 - \frac{3}{2}} \right)\left[ {\cos^{2} \left( {\frac{{\uppi }}{6} - \theta_{L} } \right) - 2} \right]} \right)\sqrt{\frac{2}{3}} \sigma_{y} .} \\ \end{array} $$

(23)

The requirement on the finite curvature was satisfied, so the yield surface is smooth.

3.2.5 Comparison of calibrated yield criteria

The modified curvatures of all calibrated yield criteria are compared in Fig. 7. All computations have been performed using the conventional flow curve (Fig. 4) so far. Responses from all standard tensile tests are depicted in Fig. 8. As expected, all predicted force responses were almost identical for the standard tensile test, which was utilized for estimating the conventional flow curve. Only the Bai–Wierzbicki yield criterion with deviatoric associated flow rule produced slightly lower responses, although $c_{t} = 1.00$ (Table 4). However, the deterioration is negligible overall, because the yield criterion improved the remaining tensile tests of notched cylindrical specimens (Fig. 9) and had globally the lowest error (Table 5). It was 16% compared to 21% for Kroon–Faleskog and 43% for von Mises yield criteria with associated flow rules. Therefore, the Bai–Wierzbicki yield criterion with deviatoric associated flow rule, which is the most complex one, will be utilized within further computations.

Fig. 7

Modified curvature of calibrated yield criteria

Fig. 8

Force responses for the standard tensile test and simulations with all plasticity models considered (Kubík et al. 2018)

Fig. 9

Force responses for experiments and simulations with all plasticity models considered, except for the standard tensile test (Kubík et al. 2018)

Table 5 Deviations between experiments and simulations with all plasticity models considered (Kubík et al. 2018)

The errors were computed according to

$$ 100\sum {\frac{{\left| {F_{e} - F_{c} } \right|}}{{F_{e} }}} , $$

(24)

where $F_{e}$ and $F_{c}$ are the forces from the experiment and the computation, respectively, while all responses were sampled with 200 points. All errors are summarized in Table 5, while all remaining responses are depicted in Fig. 9. It should be noted that unfortunately no sensor was used for torsion, which resulted in a slightly different elastic range in Fig. 9f due to the stiffness of the gripping system.

3.3 Model of damage

The nonlinear damage accumulation is one of the key features to the possible solution of the problems with non-proportional loading, although there have been some doubts (Park et al. 2020) or other modelling approaches (He and Huo 2018; Fincato and Tsutsumi 2019). Lemaitre and Dufailly (1987) described eight different methods of measuring damage by destructive and non-destructive methods covering the fractography and variation of the following quantities: density, ultrasonic wave propagation, cyclic plasticity response, tertiary creep response, microhardness, electrical potential and finally, the variation of Young’s modulus, which is employed in the article. Other methods of investigating the evolution of damage lie in non-proportional tests, usually conducted on notched tubular or cylindrical specimens under biaxial loading (tension–torsion) and following numerical analysis (Papasidero et al. 2015; Derpenski et al. 2018). The problem is that damage accumulates at one material point when the specimen is pulled, but once the specimen is twisted, damage accumulation continues at a different location, which is not critical in the first stage of loading during tension. Theoretically, better results could be obtained by two-step tests (Basu and Benzerga 2015; Thomas et al. 2016), which consist of pulling the specimen from one geometry until the fracture and then the same specimen until a prescribed deformation. Once the test is interrupted at this deformation, the specimen is machined into a new geometry, resulting in a different stress state, and pulled until the fracture. Cortese et al. (2016) incorporated fracture strain into the damage accumulation power law, which is micromechanically questionable, as completely different damage accumulation behaviour may occur in very close locations. The exponent may be greater than one in one location and lower than one in the other (for a notched cylindrical specimen, for example), therefore, the damage accumulation would be decelerating in one location while rapidly accelerating in the other, which could be quite close to each other. However, the most promising appears to be the biaxial loading of a cruciform specimen (Gerke et al. 2019; Brünig et al. 2022). When carefully prepared, there is no problem with migrating critical location or with machining between the two steps, which may introduce undesirable effects.

As mentioned above, Young’s modulus degradation served to calibrate the following nonlinear damage accumulation (Šebek et al. 2018)

$$ D = q_{1} \int\limits_{0}^{{\overline{\varepsilon }_{D} }} {\frac{{{\text{d}}\overline{\varepsilon }_{p} }}{{C_{m} + \overline{\varepsilon }_{f} }}} + q_{2} \left( {1 - q_{1} } \right)\int\limits_{0}^{{\overline{\varepsilon }_{D} }} {\left( {\frac{{\overline{\varepsilon }_{p} }}{{C_{m} + \overline{\varepsilon }_{f} }}} \right)^{{q_{2} - 1}} \frac{{{\text{d}}\overline{\varepsilon }_{p} }}{{C_{m} + \overline{\varepsilon }_{f} }}} , $$

(25)

where $q_{1}$ and $q_{2}$ are material parameters (related to the double damage curve), while $q_{2} > 0$ must always be satisfied, $C_{m}$ is the additional material parameter relating the micro and macro perspective of the damage indication, $\overline{\varepsilon }_{D}$ is the accumulated equivalent plastic strain for a given loading path, $\overline{\varepsilon }_{p}$ is the accumulated equivalent plastic strain (not to be confused with its instantaneous variant) and $\overline{\varepsilon }_{f}$ is the fracture strain, which may be dependent on the stress state measures. The non-linear law degenerates into linear, when either $q_{1} = 1$ or $q_{2} = 1$ and becomes polynomial, as the law proposed by Xue (2007) when $q_{1} = 0$. The damage accumulation rate may be decelerating when either $0 < q_{1} < 1$ and $0 < q_{2} < 1$ or $q_{1} > 1$ and $q_{2} > 1$, or accelerating, when $0 < q_{1} < 1$ and $q_{2} > 1$ or $q_{1} > 1$ and $0 < q_{2} < 1$ (Šebek et al. 2018).

All simulations have been performed with the conventional flow curve (Fig. 4) up to this point. From now on, the multilinear flow curve of the matrix was deployed in the following form (Šebek et al. 2018)

$$ \tilde{\sigma } = \left( {1 + \overline{\varepsilon }_{p} } \right)\sigma_{y} , $$

(26)

so that finally, the yield function was used in the following form

$$ f = \overline{\sigma } - \left( {1 - D^{\beta } } \right)\left( {1 + \overline{\varepsilon }_{p} } \right)k\sigma_{y} , $$

(27)

where $\beta$ is the weakening exponent in the term, which is responsible for the material softening within the approach of continuum damage mechanics. All damage-related parameters are summarized in Table 6, while detailed information is given in Šebek et al. (2018), including the experiments and calibration procedure. Finally, the points for ductile fracture criteria calibration were obtained through integration with respect to non-linear damage accumulation, which is summarized in Kubík et al. (2018) and is not given here in detail, as it is not a primary goal of this article.

Table 6 Calibrated damage-related parameters (Šebek et al., 2018)

3.4 Model of failure

Three ductile fracture criteria were selected so that a broad range of possibilities could be examined. The first was the extended Mohr–Coulomb criterion (Bai and Wierzbicki 2010) using directly the Bai–Wierzbicki yield criterion (the full version was therefore considered), then the model proposed on a different basis by Lou et al. (2017), and finally the KHPS2 criterion (Šebek et al. 2018). The minimum of constrained nonlinear multivariable target function was found using the created optimization problem structure that included the initial guess of material parameters and their lower and upper bounds, where appropriate.

3.4.1 Extended Mohr–Coulomb criterion

The following polynomial law inspired by the Hollomon one may be adopted as

$$ \overline{\sigma }_{f} = kK\overline{\varepsilon }_{f}^{n} , $$

(28)

where $\overline{\sigma }_{f}$ is the fracture stress, $K$ is the strength coefficient and $n$ is the strain hardening exponent. Then, the extended Mohr–Coulomb criterion will be the one proposed by Bai and Wierzbicki (2010) and slightly modified by Kubík et al. (2018) as

$$ \overline{\varepsilon }_{f} = \left[ {\frac{K}{{M_{2} }}k\left( {\sqrt {\frac{{1 + M_{1}^{2} }}{3}} \cos \left( {\frac{1}{3}\arcsin \left[ \xi \right]} \right) + M_{1} \left[ {\eta + \frac{1}{3}\sin \left( {\frac{1}{3}\arcsin \left[ \xi \right]} \right)} \right]} \right)} \right]^{\frac{1}{n}} , $$

(29)

where $M_{1}$ and $M_{2}$ are the material parameters. It is slightly different from what was proposed by Bai and Wierzbicki (2010), because it uses the yield correction function exactly without any simplifications. Moreover, Eq. (29) is not formally correct, as the stress–strain relationship is used in the multilinear form with respect to Eq. (26) and not according to the form based on Hollomon’s power law used for the conversion from the stress-based space to the strain-based one. Finally, the cut-off stress triaxiality is

$$ \eta_{c} = - \frac{1}{{M_{1} }}\sqrt {\frac{{1 + M_{1}^{2} }}{3}} \cos \left( {\frac{1}{3}\arcsin \left[ \xi \right]} \right) - \frac{1}{3}\sin \left( {\frac{1}{3}\arcsin \left[ \xi \right]} \right). $$

(30)

The first constraint $\eta_{c} - \eta_{a} < 0$, where $\eta_{a}$ is the average stress triaxiality used for the calibration, ensures that there is no negative fracture strain, which is physically unreal and common to all criteria utilized within this article. The second constraint $M_{1} > 0$ ensures that the cut-off plane will be convex. The strength coefficient may even be omitted (set equal to unity) and the strain hardening exponent may be considered as another material parameter for calibration along with $M_{1}$ and $M_{2}$, which gives more flexibility to the criterion (Šebek et al. 2016, 2018). Nevertheless, such an approach was not pursued in the present article. It should be noted that it does not seem to be of importance when two material parameters remain to be calibrated.

Equation (28) was fitted to the conventional flow curve, so the approach is consistent as all simulations for calibration were done using that constitutive law, while the fracture stress was considered an equivalent stress, the yield correction function equal to one and the fracture strain an equivalent plastic strain. Calibrated material parameters are altogether given in Table 7. It may be pointed out that even the simplest polynomial law is often capable of a good fit. Therefore, more complicated formulas (Fig. 1) are not necessary.

Table 7 Calibrated material parameters for the extended Mohr–Coulomb criterion

3.4.2 Lou–Huh criterion

The Lou–Huh criterion is the one proposed by Lou et al. (2017) in the form that reads

$$ \overline{\varepsilon }_{f} = K_{3} \left( {\frac{2}{{\sqrt {3\left[ {1 + \tan^{2} \left( { - \frac{1}{3}\arcsin \left[ \xi \right]} \right)} \right]} }}} \right)^{{ - K_{1} }} \left\langle {\frac{3}{{1 + 2K_{4} + 3K_{5} }}\left( {\eta + K_{4} \frac{{\sqrt 3 - \tan \left( { - \frac{1}{3}\arcsin \left[ \xi \right]} \right)}}{{3\sqrt {1 + \tan^{2} \left( { - \frac{1}{3}\arcsin \left[ \xi \right]} \right)} }} + K_{5} } \right)} \right\rangle^{{ - K_{2} }} , $$

(31)

where 〈 〉 are the Macaulay brackets and $K_{1} , \ldots ,K_{5}$ are the material parameters with a condition that

$$ K_{4} \ne - \frac{1}{2} - \frac{3}{2}K_{5} . $$

(32)

Furthermore, the cut-off stress triaxiality is

$$ \eta_{c} = - K_{4} \frac{{\sqrt 3 - \tan \left( { - \frac{1}{3}\arcsin \left[ \xi \right]} \right)}}{{3\sqrt {1 + \tan^{2} \left( { - \frac{1}{3}\arcsin \left[ \xi \right]} \right)} }} - K_{5} . $$

(33)

The correct calibration is enforced by the constraint $\eta_{c} - \eta_{a} < 0$ and the convexity of the cut-off plane, discussed further, is reached by the condition $K_{4} > 0$.

The constraint $\eta_{c} = - 0.5$ at $\xi = - 1$ was posed in order to obtain the cut-off in a reasonable range, as the criterion is too flexible without that condition. It is a similar approach to the one presented by Lou et al. (2017) or Lou and Yoon (2017). Finally, all material parameters are presented in Table 8.

Table 8 Calibrated material parameters for the Lou–Huh criterion

3.4.3 KHPS2 criterion

The KHPS2 criterion proposed by Šebek et al. (2018) has a hyperbolic shape, while the foci of rectangular hyperbolas obey a quadratic dependency on the normalized third invariant of deviatoric stress tensor. The fracture strain reads

$$ \overline{\varepsilon }_{f} = \left[ {\frac{1}{2}\left( {\frac{{G_{4} }}{{\left\langle {\eta - \eta_{c} } \right\rangle }} + \frac{{G_{5} }}{{\left\langle {\eta - \eta_{c} } \right\rangle }}} \right) - \frac{{G_{6} }}{{\left\langle {\eta - \eta_{c} } \right\rangle }}} \right]\xi^{2} + \frac{1}{2}\left( {\frac{{G_{4} }}{{\left\langle {\eta - \eta_{c} } \right\rangle }} - \frac{{G_{5} }}{{\left\langle {\eta - \eta_{c} } \right\rangle }}} \right)\xi + \frac{{G_{6} }}{{\left\langle {\eta - \eta_{c} } \right\rangle }}, $$

(34)

where $G_{1} , \ldots ,G_{6}$ are the material parameters. The parabolic cut-off stress triaxiality is

$$ \eta_{c} = - \left( {G_{3} + \frac{{G_{1} - G_{3} }}{2} - G_{2} } \right)\xi^{2} - \frac{{G_{1} - G_{3} }}{2}\xi - G_{2} . $$

(35)

The first three material parameters, $G_{1} , \ldots ,G_{3}$, are the additive inverses of the cut-off plane distance in the stress triaxiality, as illustrated in Fig. 10. The last three material parameters have to be positive, $G_{4} , \ldots ,G_{6} > 0$, because those influence the vertices of rectangular hyperbolas (highlighted by red circles in Fig. 10). To properly calibrate the criterion, the constraint $\eta_{c} - \eta_{a} < 0$ has to be satisfied along the convexity of the cut-off stress triaxiality required by the condition posed on the signed curvature in the Cartesian coordinates as

$$ \kappa = \frac{{\frac{{{\text{d}}^{2} \eta_{c} }}{{{\text{d}}\xi^{2} }}}}{{\left( {1 + \left( {\frac{{{\text{d}}\eta_{c} }}{{{\text{d}}\xi }}} \right)^{2} } \right)^{\frac{3}{2}} }} = \frac{{ - \left( {G_{1} - 2G_{2} + G_{3} } \right)}}{{\left( {1 + \left( {\left[ {G_{1} - 2G_{2} + G_{3} } \right]\xi + \frac{{G_{1} - G_{3} }}{2}} \right)^{2} } \right)^{\frac{3}{2}} }} > 0. $$

(36)

This can be solved more easily using the second derivative of a function. Therefore, the cut-off is convex if

$$ \frac{{{\text{d}}^{2} \eta_{c} }}{{{\text{d}}\xi^{2} }} = - \left( {G_{1} - 2G_{2} + G_{3} } \right) > 0, $$

(37)

which is consistent with Eq. (36). It was discussed earlier that this cut-off shape is more natural when expecting lower ductility for generalized shear $\left( {\xi = 0} \right)$ than for axisymmetric tension or compression. Nevertheless, this is contrary to how it is used sometimes (Gao et al. 2010; Lou and Yoon 2017).

Fig. 10

Graphical representation of individual material parameters of the KHPS2 criterion

All calibrated material parameters are summarized in Table 9.

Table 9 Calibrated material parameters for the KHPS2 criterion

3.4.4 Comparison of calibrated ductile fracture criteria

The fracture strains predicted by all calibrated ductile fracture criteria are compared to the fracture strains used for fitting (obtained by a hybrid experimental–computational method) in Fig. 11. All criteria resulted in similar prediction in general. It is surprising that the extended Mohr–Coulomb criterion, which has only two material parameters, performed comparable to other criteria. However, the performance of the Lou–Huh criterion with five material parameters could have been slightly better if the negative cut-off stress triaxiality had gone into the thousands, which was omitted in the end as it was probably unrealistic. The circles represent the tensile notched cylindrical specimens, the squares represent the upsetting notched cylindrical specimen, the hexagrams represent the tensile notched tubular specimen and the diamonds represent the torsional notched tubular specimen in Figs. 11, 12, and 13.

Fig. 11

Comparison of the predicted and observed fracture strains for all calibrated ductile fracture criteria

Fig. 12

Comparison of the plane stress states and cut-off stress triaxialities with points used for fitting and calibrated fracture criteria

Fig. 13

Calibrated ductile fracture criteria with the points used for fitting

The states of plane stress and cut-off stress triaxialities are compared in Fig. 12, where $\sigma_{1}$, $\sigma_{2}$ and $\sigma_{3}$ are the first (maximum), the second (middle) and the third (minimum) principal stresses. The regions of plane stress with the corresponding zero principal stresses are highlighted in Fig. 12 too.

All calibrated ductile fracture criteria with respective calibration points are depicted in Fig. 13. It can be seen that both the extended Mohr–Coulomb and Lou–Huh criteria have more flat cut-off planes than the KHPS2 criterion. Furthermore, the extended Mohr–Coulomb criterion has a cut-off plane further in the negative stress triaxiality.

4 Application

The material model developed above is applied to small punch testing and three-point bending to reveal predictability. These two experiments were not included in the calibration procedure. The quantitative and qualitative assessments were carried out.

4.1 Small punch testing

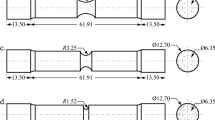
Three small punch test (Šebek et al. 2019) was prepared mainly in accordance with the ASTM standard (E3205 2020), although it was carried out prior to the first publication of the standard. Testing was carried out using the Zwick Z250 Allround-Line, tCII, with the Zwick multiXtens extensometer and a loading rate of 1 mm/min. The detailed drawing of the apparatus with the specimen penetrated by a cemented carbide ball is given in Fig. 14a–e. The responses are given in Fig. 14f (Šebek et al. 2019).

Fig. 14

Small punch testing: a punch, b clamping die, c ball, d specimen, e receiving die, f force responses

The long cylindrical rod with a diameter of $8 \pm 0.02$ mm was machined with a surface roughness of 0.4 µm. Discs of $0.6 \pm 0.02$ mm thickness were cut from that rod by electrical discharge machining. Then, grinding was applied using sandpapers with roughness of P600, P1200 and P2000. Finally, polishing with 3 and 1 µm grain-sized diamond paste was used until the required thickness of $0.5 \pm 0.005$ mm was achieved (Šebek et al. 2019).

The simulation time was 0.1 s, while the mass scaling was introduced with the time increment of $1 \times 10^{ - 7}$ s to save some computational time of explicit finite element analysis. The kinetic energy was negligible when compared to the total one, so the quasi-static loading was maintained. The specimen was discretized with C3D8R elements having a size of 0.075 mm in the central zone (Fig. 15). The ball and tools were meshed with R3D4 elements with the size of 0.025 mm. The friction coefficient of 0.1 was used after the numerical analysis of its role.

Fig. 15

Finite element mesh layout for the small punch test specimen

The experimental and computational responses (Fig. 16) represent a quantitative measure. The Lou–Huh criterion with the material parameters given in Table 8 overpredicted the force response. Therefore, it was recalibrated with a constraint $\eta_{c} = - 1$ at $\xi = - 1$, which was different from the one applied in Sect. 3.4.2. Unfortunately, it led to a severely overpredicted force response. An even worse result was achieved when the recalibration was performed again, but without any constraints this time. This recalibration yielded in an unreal cut-off stress triaxiality around $- 8 \times 10^{4}$ (this is why the constraints have to be applied), but quite surprisingly in a fit better approximately by 10% in total. Therefore, the material parameters were finally kept as originally calibrated (Table 8). Unlike the Lou–Huh criterion, the extended Mohr–Coulomb and KHPS2 criteria underestimated the maximum force. Finally, more compliant responses were obtained from experiments, which can be attributed to the stiffness of the measuring chain (similarly as in the case of torsion in Fig. 9). No contact sensor was used for torsion, while the extensometer was some distance from the specimen in the case of small punch testing. Therefore, it may be more convenient to use a measuring rod under the specimen as suggested by the ASTM standard (E3205 2020).

Fig. 16

Experimental and computational force responses for small punch testing up to the largest displacement

The fracture surfaces in Fig. 17 correspond to the three specimens that were tested. The observations were made after performing the tests with the use of the field emission SEM ZEISS Ultra Plus equipped with an auto-emission cathode (Šebek et al. 2019). All computational fracture surfaces were obtained from three different moments corresponding to the respective punch displacements. The extended Mohr–Coulomb and KHPS2 criteria performed in a similar manner. The Lou–Huh criterion predicted more radial cracks and late cracking, which is especially apparent for a punch displacement of 0.752 mm (Fig. 17). A similar amount of elements was removed by all criteria.

Fig. 17

Damage parameter fields from computations for all ductile fracture criteria compared to the experimentally obtained micrographs

4.2 Three-point bending

The three-point bending was another test for the validation of calibrated criteria. Zwick Z250 Allround-Line, tCII, with the Zwick multiXtens extensometer and a loading rate of 2 mm/min were used. The specimen had several randomly located notches, which caused an asymmetrical deflection. The detailed drawing is in Fig. 18 together with the force responses of the two specimens. The punch had a radius of 5 mm. The supports had a span of 160 mm and the same radius as the punch. The specimens were placed on the supports so that the largest hole was centred (Kubík et al., 2019).

Fig. 18

Detailed drawing of the specimen (left) and force responses of the three-point bending test (right)

The first sensor arm was stationary and touched the fixed test machine frame, while the second sensor arm was placed on the edge of the surface notch closer to the larger hole, as highlighted in Fig. 18. A bounce of the sensor arm was observed on the force–displacement responses (Fig. 18). It occurred immediately after the rupture, when the energy was released and the crack propagated. The bounce can be recognized by the part of the response where the displacement is decreasing, which would otherwise be irrational. It should be noted that the bouncing of the sensor arm was captured by the optical measurement described later as well.

The crack initiated at the notch surface location I, as depicted in Fig. 19. It propagated laterally and inward along the path II until the first section failed. After some additional loading, the secondary cracking initiated at the notch surface location III and propagated the same way as in the case of the first cracking. The lateral rupture was finalized with shear lips (Fig. 19).

Fig. 19

Fractured specimen after the three-point bending test (Kubík et al. 2019)

Again, the C3D8R element was deployed with a size of 0.075 mm in the regions of potential cracking. These regions with mapped mesh were surrounded by a free mesh with an element size of 0.2 mm, which finally transformed into the structured coarse mesh of 2 mm element size in the remote areas (Fig. 20). The element size of 0.075 mm was along the width everywhere. The punch and supports were modelled as rigid bodies with R3D4 elements. The punch had a size of 0.075 mm and the supports had the same size along the width, but 0.5 mm in the circumferential direction. There were approximately two million nodes in total. The simulation time was 0.1 s. There was a sudden drop in force for this bi-failure test, which could lead to some oscillations. In order to avoid excessive vibrations, the time increment of $5 \times 10^{ - 8}$ s was enforced—that is twice lower than in other simulations where the mass scaling was deployed, but still providing a sufficient decrease of the computational time, which was several weeks using the standard personal computer. The punch had a prescribed velocity, contrary to other simulations, where the displacements and rotations were exploited. It should be noted that no symmetry was used, as in the case of small punch testing.

Fig. 20

Assembly (top) and detail (bottom) of the notched meshed block for the three-point bending test

The force responses are compared in Fig. 21. It is clear that the extended Mohr–Coulomb criterion predicted the failure of the first section slightly earlier, but the onset of the second one accurately, which is contrary to the Lou–Huh and KHPS2 criteria. However, all criteria predicted very slow secondary crack growth, while it was rapid in experiments similar to the first failure. Moreover, the shocks may be spotted in the responses occurring after the first cracking, when a sudden drop of force appeared. These are due to the dynamic nature of the crack propagation and its representation by the explicit finite element calculation algorithm. The sudden change from quasi-static behaviour to the dynamic propagation is followed by parasitic oscillations, which could be treated only at the expense of much higher computational demands. This with secondary cracking was better captured by Hu et al. (2021) using the variational phase-field model with coalescence dissipation. On the other hand, Hu et al. (2021) did not predict shear lips.

Fig. 21

Three-point bending force responses from experiments and computations with all ductile fracture criteria

The fracture surfaces from the experiment and numerical simulations are shown in Fig. 22. All criteria predicted a small slant fracture, but only in the first stage of cracking. Furthermore, the computationally predicted shear lips were smaller than those observed experimentally. Additionally, Lou–Huh and KHPS2 criteria exhibited some unusual crack propagation in the final stage, forming a shallow groove.

Fig. 22

Fracture surfaces from experiments compared to those obtained computationally with all ductile fracture criteria, where the field of damage parameter is displayed

There is a significant difference compared to Kubík et al. (2019), who used a simpler plasticity model—Kroon–Faleskog yield criterion—with almost the same fracture criteria (there are slight differences in the formulation of the extended Mohr–Coulomb and Lou–Huh criteria) and reported very pronounced shear lips closer to reality and even in the second stage of cracking. On the other hand, it seems to be a trade-off, since the accuracy in force response was worse, probably given by a less accurate plasticity model (Kroon–Faleskog), which probably influenced the appearance of fracture surfaces extensively, while still not being that different from Bai–Wierzbicki yield criterion (Table 5).

Finally, the digital image correlation was done to evaluate the performance of the model. The test was recorded with the mono digital camera Basler acA2000-165um with a resolution of 2048 × 1088 px. The images were captured with a frame rate of 10 fps. A speckle pattern was created on the surface by spraying black on the white background so that the displacements could be calculated with Mercury RT × 64 2.6. The grid spacing was 3 px, while the size of 1 px was 0.058 mm. This validation concerns mainly the plasticity as it was executed prior to the fracture. The contours may look the same for all cases in Fig. 23, but there are minor differences due to the coupled approach, where damage and plasticity mutually influence each other. There was a good conformity between the experimental observation and calculations for the instant corresponding to the deflection of 4.5 mm (highlighted by the vertical black dashed line in Fig. 21).

Fig. 23

Field of horizontal strain component in percent obtained using the digital image correlation from the experiment compared to the numerical simulations with all ductile fracture criteria

In addition to digital image correlation, the horizontal strain component was plotted in Fig. 24 along three paths highlighted in Fig. 20 to quantitatively compare the simulations with the experiment. The biggest difference was for path B (primary cracking), while path C exhibited the best conformity with experiment (Fig. 24) for the KHPS2 criterion. The strains were computationally overpredicted because the concentration was probably not sufficiently captured by the optical method. It could be due to a poor adhesion of the pattern in the instant close to the metal failure (large strains).

Fig. 24

Horizontal strain component in percent from simulation with the KHPS2 criterion for three normalized paths compared to the result obtained using the digital image correlation from the experiment

5 Conclusions

The present paper deals with the ductile fracture under quasi-static monotonic loading and room temperature. The aluminium alloy 2024-T351 from one heat (melt) was studied. It was found that it is pressure and Lode dependent for both plasticity and failure. Two Lode-dependent plasticity yield criteria were calibrated, but the one with pressure dependency resulted in better responses when compared to the experiments. Then, the non-linear damage accumulation law was calibrated by means of loading–unloading (semi-cyclic) tests of smooth cylindrical specimens. Finally, three ductile fracture criteria were calibrated to six experiments that covered tensile notched cylindrical specimens, tensile and torsional notched tubular specimens and upsetting notched cylindrical specimen. The final part of this work focuses on a successful application of calibrated models to two distinct tests. It is composed of small punch testing and three-point bending. Computation of the first test revealed a good conformity with the experiments regarding both quantitative and qualitative measures. The latter of the two validation tests was more complicated as it exhibited a bi-failure mode of rupture. The force responses of the three-point bending were in a very good correspondence with the experimental observation, as well as the fracture surfaces and the strains evaluated by the digital image correlation on the specimen surface prior to the first cracking onset.

Appendix 1: Characterization of the stress state

A geometrical representation may be realized within the Cartesian coordinate system of principal stresses not ordered according to the magnitude – the Haigh–Westergaard space. The space cannot be formed with principal stresses ordered according to the magnitude, as $\sigma_{1} = \sigma_{2} = 0$ MPa and $\sigma_{3} = 1$ MPa are inadmissible, for example. Otherwise, only one sextant would be needed in the deviatoric plane. The Cartesian coordinate system is illustrated together with cylindrical $\left( {r,\theta_{L} ,z} \right)$ and spherical $\left( {\rho ,\theta_{L} ,\varphi } \right)$ coordinate systems in Fig. 25, where $z$ is the axial coordinate, $\rho$ is the radial coordinate of the spherical coordinate system and $\varphi$ is the polar angle.

First, stress triaxiality ranging $-\infty <\eta <\infty$ is defined as

$$ \eta = \frac{{I_{1} }}{{3\sqrt {3J_{2} } }}, $$

(38)

where $I_{1}$ is the first invariant of stress tensor and $J_{2}$ is the second invariant of deviatoric stress tensor. Then, the polar angle ranging $0<\varphi< {\uppi}$ can be written as

$$ \varphi = {\text{arccotan}}\left( {\frac{3}{\sqrt 2 }\eta } \right). $$

(39)

The deviatoric or octahedral plane is any plane perpendicular to the axis of the first and seventh octants (perpendicular to the hydrostatic axis where $\sigma_{{\text{I}}} = \sigma_{{{\text{II}}}} = \sigma_{{{\text{III}}}}$). A special case of such a plane is the rendulic or ${\uppi }$ plane, which above the perpendicularity to the hydrostatic axis also contains the origin of the Haigh–Westergaard space (Fig. 25). The normalized third invariant of deviatoric stress tensor ranging $-1\leq\xi\leq 1$ can be defined as

$$ \xi = \frac{{\sqrt {27} }}{2}\frac{{J_{3} }}{{J_{2}^{\frac{3}{2}} }}, $$

(40)

where $J_{3}$ is the third invariant of deviatoric stress tensor. Then, other deviatoric state variables may be defined. The Lode angle ranging $0 \le \theta_{L} \le {{\uppi } \mathord{\left/ {\vphantom {{\uppi } 3}} \right. \kern-\nulldelimiterspace} 3}$ is

$$ \theta_{L} = \frac{1}{3}\arccos \left( \xi \right). $$

(41)

Fig. 25

Geometrical representation of the stress state with various variables in the Haigh–Westergaard space

Fig. 26

Graphical representation of the measures of the deviatoric stress state

Then, a similar measure is the azimuth angle written as

$$ \theta_{A} = \theta_{L} - \frac{{\uppi }}{6}, $$

(42)

ranging $- {{\uppi } \mathord{\left/ {\vphantom {{\uppi } 6}} \right. \kern-\nulldelimiterspace} 6} \le \theta_{A} \le {{\uppi } \mathord{\left/ {\vphantom {{\uppi } 6}} \right. \kern-\nulldelimiterspace} 6}$. The azimuth angle can be normalized as

$$ \overline{\theta } = - \frac{{6}}{{\uppi }}\theta_{A} , $$

(43)

so the range is $- 1 \le \overline{\theta } \le 1$. Then, the Lode parameter has the same range as the normalized Lode angle $- 1 \le L \le 1$, with the following definition

$$ L = \sqrt 3 \tan \left( { - \frac{{\uppi }}{{6}}\overline{\theta }} \right). $$

(44)

Finally, all deviatoric stress state measures are graphically represented in Fig. 26 under the condition of plane stress, where $\sigma$ is the stress.