Numerical implementation of a $J_2$- and $J_3$-dependent plasticity model based on a spectral decomposition of the stress deviator

Abstract

A new plasticity model with a yield criterion that depends on the second and third invariants of the stress deviator is proposed. The model is intended to bridge the gap between von Mises’ and Tresca’s yield criteria. An associative flow rule is employed. The proposed model contains one new non-dimensional key material parameter, that quantifies the relative difference in yield strength between uniaxial tension and pure shear. The yield surface is smooth and convex. Material strain hardening can be ascertained by a standard uniaxial tensile test, whereas the new material parameter can be determined by a test in pure shear. A fully implicit backward Euler method is developed and presented for the integration of stresses with a tangent operator consistent with the stress updating scheme. The stress updating method utilizes a spectral decomposition of the deviatoric stress tensor, which leads to a stable and robust updating scheme for a yield surface that exhibits strong and rapidly changing curvature in the synoptic plane. The proposed constitutive theory is implemented in a finite element program, and the influence of the new material parameter is demonstrated in two numerical examples.

1 Introduction

Polycrystalline materials can often be taken to be isotropic at the meso- and macroscopic levels, and plastic yield criteria for ductile polycrystalline materials are, in general, formulated in terms of three invariants of the (macroscopic) stress state. The principal stresses, $\sigma _1$, $\sigma _2$, and $\sigma _3$, constitute such a set of invariants. An infinite number of invariants may be constructed on the basis of the principal stresses. Three such invariants, commonly used in plasticity theory, are $I_1$, $J_2$ and $J_3$, where $I_1$ is the trace of the stress tensor, and $J_2$ and $J_3$ are the two non-trivial invariants of the deviatoric stress tensor.

The von Mises [1] and Tresca [2] yield criteria are widely used in computational plasticity, and these models are, in many cases, well suited for modelling plastic yielding of ductile, polycrystalline metals [3]. In the von Mises model, it is assumed that plastic yielding only depends on $J_2$, whereas the Tresca model includes a dependence on $J_3$. The Drucker-Prager [4] and Coulomb-Mohr [5, 6] criteria—often employed to model polymers, rock and soil [7–10]—include a dependence on $I_1$ as well, and may therefore be seen as extensions of the von Mises and Tresca criteria, respectively.

Plastic deformation of ductile metals is mainly governed by shear stresses, and this is the reason for the success of the von Mises model. However, it has been recognized in both experimental investigations and theoretical examinations, that the plastic yield behaviour of metals may depend not only on $J_2$, but also on $I_1$ (e.g., [11–16]) as well as on $J_3$ (e.g., [17–25]). In the present study, we focus on metals whose yielding behaviour may be considered to be independent of $I_1$, but shows a dependence on $J_3$. Yield functions for such materials may be formulated either in terms of the invariants $J_2$ and $J_3$ or in terms of the differences between the principal stresses, i.e. $\sigma _1-\sigma _2$, $\sigma _1-\sigma _3$, and $\sigma _3-\sigma _2$, since these differences are independent of $I_1$. One early $J_2$,$J_3$-based yield criterion was proposed by Drucker [26], i.e.

$$\begin{aligned} f = J_2^3 - aJ_3^2 - b = 0, \end{aligned}$$

(1)

where $a$ and $b$ are material constants. Other closely related models have followed, e.g. Hosford and Allen [27], Cazacu and Barlat [28], Brünig et al. [29], and Hu and Wang [30], where one or several $J_3$-dependent terms are added to the yield criterion. An early model based on a principal stress formulation is the Hershey–Hosford model [31, 32], in which the yield surface is given by

$$\begin{aligned} f \!=\! |\sigma _1\!-\!\sigma _2|^n \!+\! |\sigma _2\!-\!\sigma _3|^n \!+\! |\sigma _3\!-\!\sigma _1|^n \!-\! 2\sigma _0^n \!=\! 0, \end{aligned}$$

(2)

where $\sigma _0$ is the yield stress in uniaxial tension. Hence, for $n=2$, the von Mises criterion is restored, and for $n\rightarrow \infty$, the Tresca criterion is approached.

Other models with a similar type of behaviour exist. One example is the model proposed by Zhu and Leis [33, 34], in which an average shear stress is introduced as the weighted average of the maximum shear stress (Tresca) and the effective von Mises shear stress. Other examples include the models proposed by Racherla and Bassani [35], Bai and Wierzbicki [36], and Gao et al. [37], who introduce new equivalent stress entities that depend not only on the von Mises stress (i.e. $J_2$), but also on $J_3$ (and $I_1$).

In the present paper, we propose a new $J_2$- and $J_3$-dependent yield function for ductile metals that is able to model yield behaviour between the Tresca surface and the von Mises surface and that is well suited for numerical implementation into a finite element framework. The domain in stress space between the Tresca and von Mises yield surfaces is parametrized by a material parameter $\mu$ and a $J_3$-dependent invariant introduced by Nahshon and Hutchinson [38]. In the numerical implementation, we use a spectral decomposition of the stress tensor, which greatly facilitates the stress updating procedure. Hence, in Sect. 2, the new plasticity model is presented, and in Sect. 3, we describe its numerical implementation. In Sect. 4, we provide some numerical examples in the form of simulations of tensile testing of two different test specimens. Finally, the results are discussed and put in some perspective in Sect. 5.

2 A new $J_2$- and $J_3$-dependent yield criterion

2.1 Preliminaries

The strain tensor ${\varvec{\epsilon }}$ is defined as

$$\begin{aligned} {\varvec{\epsilon }}= \mathrm{sym}\left( \frac{\partial \mathbf{u}}{\partial \mathbf{x}}\right) , \end{aligned}$$

(3)

where $\mathbf{u}$ and $\mathbf{x}$ are the displacement and position vectors, respectively. The strain tensor may be additively decomposed according to

$$\begin{aligned} {\varvec{\epsilon }}= {\varvec{\epsilon }}^\mathrm{p} + {\varvec{\epsilon }}^\mathrm{e}, \end{aligned}$$

(4)

where ${\varvec{\epsilon }}^\mathrm{p}$ and ${\varvec{\epsilon }}^\mathrm{e}$ denote the plastic and elastic strain tensors, respectively. The Cauchy stress tensor is denoted by $\varvec{{\sigma }}$, and is obtained as

$$\begin{aligned} \varvec{{\sigma }}= \mathbf{D}:{\varvec{\epsilon }}^\mathrm{e} = \mathbf{D}:({\varvec{\epsilon }}-{\varvec{\epsilon }}^\mathrm{p}), \end{aligned}$$

(5)

where $\mathbf{D}$ is the stiffness tensor (Hooke’s law on tensor form).

The deviatoric stress tensor, $\mathbf{s}$, is defined as $\mathbf{s}=\varvec{{\sigma }}-I_1\mathbf{I}/3$, where $I_1=\varvec{{\sigma }}:\mathbf{I}$ is the first invariant of the stress tensor, and $\mathbf{I}$ is the identity tensor. The invariants of the stress deviator $\mathbf{s}$ are defined as

$$\begin{aligned} J_1&= \mathbf{s}:\mathbf{I}\equiv 0, \quad J_2 = \frac{1}{2}(\mathbf{s}\cdot \mathbf{s}):\mathbf{I}, \quad J_3 = \mathrm{det}\mathbf{s}. \end{aligned}$$

(6)

When a dependence on $J_3$ is to be incorporated into the yield criterion, it is convenient to introduce modified $J_3$-dependent invariants. Hence, the Lode parameter, $L$, is defined as

$$\begin{aligned} L = \frac{2\sigma _2 - \sigma _1 - \sigma _3}{\sigma _1 - \sigma _3}, \quad -1 \le L \le 1. \end{aligned}$$

(7)

Furthermore, the Haigh-Westergaard coordinates $\rho$ and $\vartheta$ may be used to characterise the stress state in the synoptic plane (see Fig. 2), where

$$\begin{aligned} \rho = \sqrt{2J_2}, \quad \cos 3\vartheta = \frac{27J_3}{2\sigma _\mathrm{e}^3} = \xi , \quad -1 \le \xi \le 1, \end{aligned}$$

(8)

where $\sigma _\mathrm{e}=\sqrt{3J_2}$ is the equivalent von Mises stress. The invariants $\xi$ and $L$ relate according to

$$\begin{aligned} \xi = \frac{L(L^2-9)}{(3+L^2)^{3/2}}. \end{aligned}$$

(9)

An additional $J_3$-dependent invariant was introduced by Nahshon and Hutchinson [38]:

$$\begin{aligned} \omega = 1 - \xi ^2 = \sin ^23\vartheta , \quad 0 \le \omega \le 1. \end{aligned}$$

(10)

2.2 Yield criterion

We propose a yield function on the form

$$\begin{aligned} f(\varvec{{\sigma }})&= \sigma _\mathrm{e} - \sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p}) h(\omega ), \nonumber \\ h(\omega )&= 1 - \mu \omega \left( \frac{1+\omega _0^{1/p}}{\omega ^{1/p}+\omega _0^{1/p}}\right) ^p, \end{aligned}$$

(11)

where $\sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p})$ is the yield stress in uniaxial tension, $\epsilon _\mathrm{e}^\mathrm{p}$ is the equivalent plastic strain, and $\mu$, $\omega _0$ and $p$ are material constants. The function $h(\omega )$ fulfills $1-\mu \le h(\omega )\le 1$, and the functional form of the second term in the expression for $h$ is illustrated in Fig. 1. The resulting yield function $f$ is illustrated in Fig. 2 for different values of $\mu$. For $\mu =0$, the yield behaviour simplifies to standard von Mises plasticity. For a suitable choice of model parameters, the yield function in Eq. (11) approaches the Tresca yield criterion ($\mu \rightarrow 1-\sqrt{3}/2\approx 0.1340$). The influence of the third stress invariant is accounted for by $\omega =1-\xi ^2$, where $\xi$ takes on the values 1 in uniaxial tension, 0 in pure shear, and -1 in biaxial tension.

Fig. 1

Function adopted for modelling the influence of $\xi$ on the yield behaviour ($\omega _0 = 0.18$ and $p=4$)

Fig. 2

Yield surfaces for $\mu =0$, 0.06, and 0.12345 ($p=4$ and $\omega _0=0.18$)

The proposed yield function $f$ is smooth, i.e. the curvature is continuous, and for a suitable choice of the model parameters $\mu$, $\omega _0$ and $p$, it will also be convex.

2.3 Flow rule

The plastic flow potential is denoted by $g=g(\varvec{{\sigma }})$, and an associated flow rule is adopted such that $g\equiv f$. The plastic strain increment tensor, $\dot{{\varvec{\epsilon }}}^\mathrm{p}$, is given by

$$\begin{aligned} \dot{{\varvec{\epsilon }}}^\mathrm{p}&= \dot{\lambda }\frac{\partial f}{\partial \varvec{{\sigma }}} = \dot{\lambda }\mathbf{M}, \end{aligned}$$

(12)

$$\begin{aligned} \mathbf{M}&= \mathbf{n}- 3\gamma \mathbf{m}, \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{n}&= \frac{3\mathbf{s}}{2\sigma _\mathrm{e}}, \quad \mathbf{m}= 2\mathbf{n}\cdot \mathbf{n}- \mathbf{I}- \xi \mathbf{n}, \end{aligned}$$

(14)

where $\dot{\lambda }$ is the plastic multiplier, $h^{\prime }=\mathrm{d}h/\mathrm{d}\xi$, and $\gamma =h^{\prime }/h$. Note that the inclusion of $J_3$ in the yield criterion introduces a quadratic dependency on $\mathbf{s}$ in the flow rule. However, the tensors $\dot{{\varvec{\epsilon }}}^\mathrm{p}$, $\mathbf{s}$, $\mathbf{M}$, $\mathbf{n}$, and $\mathbf{m}$ all share the same set of principal directions, $\mathbf{N}_i$ ($i=1,2,3$), such that

$$\begin{aligned} \dot{{\varvec{\epsilon }}}^\mathrm{p}&= \sum _{i=1}^3 \dot{\epsilon }^\mathrm{p}_i \mathbf{N}_i\otimes \mathbf{N}_i, \quad \mathbf{s}= \sum _{i=1}^3 s_i \mathbf{N}_i\otimes \mathbf{N}_i, \nonumber \\ \mathbf{n}&= \sum _{i=1}^3 n_i \mathbf{N}_i\otimes \mathbf{N}_i, \quad \mathbf{m}= \sum _{i=1}^3 m_i \mathbf{N}_i\otimes \mathbf{N}_i, \end{aligned}$$

(15)

where $(\bullet )_i$ ($i=1,2,3$) denotes principal values and directions of the tensors. The principal values are related according to

$$\begin{aligned} \dot{\epsilon }^\mathrm{p}_i = \dot{\lambda }M_i = \dot{\lambda }\left( n_i \!-\! 3\gamma m_i\right) , \quad m_i&= 2n_i^2 \!-\! 1 \!-\! \xi n_i. \end{aligned}$$

(16)

The principal values of $\mathbf{n}$ may in turn be expressed as

$$\begin{aligned} n_1&= \cos \vartheta , \nonumber \\ n_2&= \cos (\vartheta -2\pi /3), \\ n_3&= \cos (\vartheta +2\pi /3), \nonumber \end{aligned}$$

(17)

where $\vartheta$ is the angle defined in the synoptic plane, as illustrated in Fig. 2.

2.4 Equivalent plastic strain

The yield stress, $\sigma _\mathrm{y}=\sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p})$, is a function of the equivalent plastic strain, $\epsilon _\mathrm{e}^\mathrm{p}$, which is taken to be the plastic work conjugate of the von Mises stress, $\sigma _\mathrm{e}$. The plastic work rate per unit volume, $\dot{w}_\mathrm{p}$, is defined as

$$\begin{aligned} \dot{w}_\mathrm{p} = \sigma _\mathrm{e}\dot{\epsilon }_\mathrm{e}^\mathrm{p} = \varvec{{\sigma }}:\dot{{\varvec{\epsilon }}}^\mathrm{p} = \dot{\lambda }\mathbf{s}:(\mathbf{n}-3\gamma \mathbf{m}) = \ldots = \sigma _\mathrm{e}\dot{\lambda }, \end{aligned}$$

(18)

i.e. $\dot{\epsilon }_\mathrm{e}^\mathrm{p}\equiv \dot{\lambda }$. In the following sections, $\epsilon _\mathrm{e}^\mathrm{p}$ and $\lambda$ will be used interchangeably.

Just like in standard $J_2$-plasticity, the plastic multiplier $\dot{\lambda }$ is identical to the increment in equivalent plastic strain, $\dot{\epsilon }_\mathrm{e}^\mathrm{p}$. Furthermore, by double-contracting $\dot{{\varvec{\epsilon }}}^\mathrm{p}$ with itself, the increment in equivalent plastic strain can also be related to the increments of the plastic strain components, i.e.

$$\begin{aligned} \dot{\epsilon }_\mathrm{e}^\mathrm{p} = \frac{\displaystyle \sqrt{\frac{2}{3}\dot{{\varvec{\epsilon }}}^\mathrm{p}:\dot{{\varvec{\epsilon }}}^\mathrm{p}}}{\sqrt{1+9\gamma ^2\omega }}. \end{aligned}$$

(19)

The double-contraction of $\mathbf{M}$ with itself yields $\mathbf{M}:\mathbf{M}=\mathbf{n}:\mathbf{n}+9\gamma ^2\mathbf{m}:\mathbf{m}=3(1+9\gamma ^2\omega )/2$, because the cross-terms $\mathbf{n}:\mathbf{m}$ vanish ($\mathbf{n}$ and $\mathbf{m}$ are orthogonal). Thus, with regard to the definition of the equivalent plastic strain, the present theory deviates from standard $J_2$-theory, since the square-root expression in the denominator of Eq. (19) would be unity in standard $J_2$-theory. However, for the special stress states of axisymmetry ($\omega =0$) and shearing ($\omega =1$), the denominator simplifies to unity. This is of relevance to the experimental determination of the hardening function and the parameter $\mu$, which will be further elaborated on in Sect. 5.

2.5 Convexity and smoothness of yield function

Figure 2 displays the synoptic plane, in which the radial coordinate $\rho =\sqrt{\mathbf{s}:\mathbf{s}}$ and the angular coordinate $\vartheta =1/3\cdot \arccos \xi$ may be defined. The curvature of the yield function in the synoptic plane, $\kappa (\vartheta )$, may be expressed as

$$\begin{aligned} \kappa (\vartheta ) = \frac{\displaystyle \rho ^2+2\left( \frac{\mathrm{d}\rho }{\mathrm{d}\vartheta }\right) ^2- \rho \frac{\mathrm{d}^2\rho }{\mathrm{d}\vartheta ^2}}{\displaystyle \left( \rho ^2+\left( \frac{\mathrm{d}\rho }{\mathrm{d}\vartheta }\right) ^2\right) ^{3/2}}. \end{aligned}$$

(20)

Convexity of $f$ implies that $\kappa \ge 0$ for all $\vartheta$, whereas smoothness of $f$ requires that $\kappa$ is finite for all $\vartheta$.

In the synoptic plane, see Fig. 2, the yield surfaces may be expressed as a function $\rho (\vartheta )$, where $\rho =\sqrt{2/3}\sigma _\mathrm{e}$. Provided that $\cos 3\vartheta =\xi$, the yield function given in Eq. (11) may be expressed as

$$\begin{aligned} \rho (\vartheta ) = \sqrt{\frac{2}{3}}\sigma _\mathrm{y} h(\xi ). \end{aligned}$$

(21)

Thus, we have

$$\begin{aligned}&h = 1 - \mu \omega \left( \frac{1+\omega _0^{1/p}}{\omega ^{1/p}+\omega _0^{1/p}}\right) ^p, \nonumber \\&\frac{\mathrm{d} h}{\mathrm{d} \vartheta } = -3\mu \frac{\left( 1+\omega _0^{1/p}\right) ^p\omega _0^{1/p}}{\left( \omega ^{1/p}+\omega _0^{1/p}\right) ^{p+1}}\sin 6\vartheta , \\&\frac{\mathrm{d}^2 h}{\mathrm{d} \vartheta ^2} = 9\mu \frac{\left( 1+\omega _0^{1/p}\right) ^p\omega _0^{1/p}}{\left( \omega ^{1/p}+\omega _0^{1/p}\right) ^{p+1}} \nonumber \\&\qquad \qquad \cdot \left[ \frac{p+1}{p}\frac{\omega ^{1/p}}{\omega ^{1/p}+\omega _0^{1/p}} 4(1-\omega )+2(2\omega -1)\right] . \nonumber \end{aligned}$$

(22)

The curvature function $\kappa (\vartheta )$ may now be evaluated by substituting the expressions in Eq. (22) into Eq’s. (21) and (20). The curvature will be positive and the yield function convex for certain combinations of the parameters $\mu$, $\omega _0$, and $p$. The admissible domains for $\omega _0$ and $p$ are shown in Fig. 3a for several levels of $\mu$, where it can be observed that the domain that allows for $\mu \ge 0.12$ is rather limited in $p\,-\,\omega _0$ space. The dashed line defines the value of $\omega _0$ that—for a given value of $p$—enables the highest value of $\mu$ (while still maintaining a convex yield surface). The associated values of $\mu$, denoted $\mu _\mathrm{max}$, are plotted versus $p$ in Fig. 3b, where the Tresca limit is included as a reference. The Tresca limit is slightly out of reach of the present model.

Fig. 3

a Convexity limits for different parameter combinations; b maximum value of $\mu$ versus exponent $p$

The black dot in Fig. 3a represents the point $p = 4$ and $\omega _0 = 0.18$, which will furnish a convex yield surface provided that $\mu \le 0.12345$. This parameter combination will be further explored in this study, and in Fig. 4, a curvature plot for this set is shown. For the sake of clarity, the entity $\ln (1+\sqrt{3/2}\sigma _\mathrm{y}\kappa (\vartheta ))/\ln 2$ is plotted, where $\sigma _\mathrm{y}\kappa (\vartheta )$ is a dimensionless entity.

Fig. 4

Curvature of the yield function for $\mu =0$ (blue line), $\mu =0.06$ (green line), and $\mu =0.12345$ (red line). In all cases, $p=4$ and $\omega _0=0.18$ have been applied. (Color figure online)

It is clear from Fig. 2 that the curvature of the present yield function will exhibit peaks when $\vartheta$ approaches multiples of $\pi /3$. Hence, $\kappa (\vartheta )$ increases dramatically in the vicinity of these angles. However, the curvature remains finite, and for multiples of $\pi /3$, it can be shown that the curvature takes on the value

$$\begin{aligned} \begin{array}{c}\mathrm{lim} \\ _{\vartheta \rightarrow k\pi /3} \end{array} \sqrt{\frac{3}{2}}\sigma _\mathrm{y}\kappa (\vartheta ) = 1 + 18\mu \frac{1+p}{p}\frac{(1+\omega _0^{1/p})^p}{\omega _0}, \end{aligned}$$

(23)

where $k$ is an integer. For example, for the most Tresca-like curve ($\mu =0.12345$), we get $\ln (1 + \sqrt{3/2}\sigma _\mathrm{y}\kappa )/\ln 2\rightarrow 6.55$ as $\vartheta \rightarrow k\pi /3$.

3 Numerical implementation

3.1 Prerequisites

In this section, the components of a numerical implementation of the proposed plasticity model are derived. Hence, we assume that at time step $t^{n}$, all field variables and internal variables are known, and the updated variables at time $t^{n+1}$ are to be computed. Hence, for a given updated strain tensor ${\varvec{\epsilon }}^{n+1}$, the updated stress tensor $\varvec{{\sigma }}^{n+1}$, the updated equivalent plastic strain $\epsilon _\mathrm{e}^{\mathrm{p},n+1}$ (or $\lambda ^{n+1}$), and the algorithmic stiffness tensor $\mathbf{D}_\mathrm{alg}^{n+1}=\partial \varvec{{\sigma }}^{n+1}/\partial {\varvec{\epsilon }}^{n+1}$—all entities associated with a backward Euler scheme—are to be computed.

In the following derivation, we assume the existence of a Cartesian coordinate system with basis vectors $\mathbf{e}_i$ ($i=1,2,3$), such that second order tensors may be expressed as

$$\begin{aligned} (\bullet ) = (\bullet )_{ij} \cdot \mathbf{e}_i\otimes \mathbf{e}_j, \end{aligned}$$

(24)

where $(\bullet )_{ij}$ denotes the matrix components of the second order tensor in question. First and higher order tensors are represented in analogous ways. Hence, the stiffness tensor associated with Hooke’s law may be expressed on component form as

$$\begin{aligned} D_{ijkl} = 2G\left( I_{ijkl}-\frac{1}{3}\delta _{ij}\delta _{kl}\right) + K\delta _{ij}\delta _{kl}, \end{aligned}$$

(25)

where

$$\begin{aligned} I_{ijkl} = \frac{1}{2}\left( \delta _{ik}\delta _{jl} + \delta _{il}\delta _{jk}\right) , \end{aligned}$$

(26)

$\delta _{ij}$ is Kronecker’s delta function, and $G$ and $K$ are the shear and bulk moduli, respectively.

3.2 Integration of stresses

The flow rule adopted is

$$\begin{aligned} \dot{\epsilon }_{ij}^\mathrm{p}&= \dot{\lambda }M_{ij} = \dot{\lambda }\left( n_{ij} - 3\gamma m_{ij}\right) , \end{aligned}$$

(27)

where

$$\begin{aligned} n_{ij} = \frac{3s_{ij}}{2\sigma _\mathrm{e}}, \quad m_{ij} = 2n_{ik}n_{kj} - \delta _{ij} - \xi n_{ij}. \end{aligned}$$

(28)

Stresses are integrated according to

$$\begin{aligned} \sigma _{ij}^{n+1}&= \sigma _{ij}^{n} + \int _{n}^{n+1}D_{ijkl}\mathrm{d}\epsilon _{kl}^\mathrm{e} = \sigma _{ij}^{n} + D_{ijkl}\Delta \epsilon _{kl}^{\mathrm{e}} \nonumber \\&= \sigma _{ij}^{n} + D_{ijkl}(\Delta \epsilon _{kl} - \Delta \epsilon _{kl}^{\mathrm{p,}}) \nonumber \\&\approx \sigma _{ij}^* - 2G\Delta \lambda M_{ij}^{n+1}, \end{aligned}$$

(29)

where $(\bullet )^n$ and $(\bullet )^{n+1}$ denote entities at times $t^{n}$ and $t^{n+1}$, respectively, $\Delta \epsilon _{ij}^{\mathrm{e}}$, $\Delta \epsilon _{ij}=\epsilon _{ij}^{n+1}-\epsilon _{ij}^{n}$, and $\Delta \epsilon _{ij}^{\mathrm{p}}$ are the elastic, total, and plastic strain increments, respectively, $\sigma _{ij}^*$ is the trial stress (elastic predictor), and $\Delta \lambda =\lambda ^{n+1}-\lambda ^{n}$. In the following, the index $(\bullet )^{n+1}$ is understood unless otherwise indicated.

Equtaion (29) may be recast into

$$\begin{aligned} \sigma _{ij}^* = \sigma _{ij} + 2G\Delta \lambda M_{ij}. \end{aligned}$$

(30)

The hydrostatic stress is defined as $\sigma _\mathrm{h}=\sigma _{kk}/3$. Since $M_{ij}$ is purely deviatoric ($M_{ii}=0$), it follows that the hydrostatic components of $\sigma _{ij}^*$ and $\sigma _{ij}$ are identical, i.e. $\sigma _\mathrm{h}^*=\sigma _\mathrm{h}$, which implies that

$$\begin{aligned} s_{ij}^* = \sigma _{ij}^* - \sigma _\mathrm{h}^*\delta _{ij} = s_{ij} + 2G\Delta \lambda M_{ij}. \end{aligned}$$

(31)

As discussed previously, $s_{ij}$ and $M_{ij}$ share the same set of principal directions $\mathbf{N}_i$, and the equations in Eq. (31) may therefore be reduced to three equations for the principal values, i.e.

$$\begin{aligned} s_{i}^* = s_{i} + 2G\Delta \lambda M_i, \quad i = 1,2,3. \end{aligned}$$

(32)

The principal values $s_{i}^*$ and the principal directions $\mathbf{N}_i$ may be computed from the known tensor $s_{ij}^*$. Furthermore, $s_{i}$ may be expressed as

$$\begin{aligned} s_{i} = \frac{2\sigma _\mathrm{e}}{3}n_i = \frac{2\sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p})h(\omega )}{3}n_i(\vartheta ), \quad i = 1,2,3, \end{aligned}$$

(33)

where $\xi =\cos 3\vartheta$ and $\omega =1-\xi ^2=\sin ^2 3\vartheta$. Since Eq. (31) is purely deviatoric, there are, in fact, only two independent relations in Eq. (32), and the equation for $i=3$ may therefore be ignored. Hence, based on the two relations for $i=1$ and 2 in Eq. (32), we define a residual vector function $\mathbf{q}=\mathbf{q}(\vartheta ,\Delta \lambda )$ according to

$$\begin{aligned} \mathbf{q}(\vartheta ,\Delta \lambda ) = \left[ \begin{array}{c} 2\sigma _\mathrm{y}hn_1 + 6G\Delta \lambda M_1 - 3s_1^* \\ 2\sigma _\mathrm{y}hn_2 + 6G\Delta \lambda M_2 - 3s_2^* \end{array} \right] = {\mathbf{0}}, \end{aligned}$$

(34)

where $\sigma _\mathrm{y}$ is evaluated for the updated value of $\epsilon _\mathrm{e}^\mathrm{p}=\lambda =\lambda ^n+\Delta \lambda$, i.e. $\sigma _\mathrm{y}=\sigma _\mathrm{y}(\lambda ^n+\Delta \lambda )$. Expressions for $n_1(\vartheta )$ and $n_2(\vartheta )$ were provided in Eq. (17), and $M_1(\vartheta )$ and $M_2(\vartheta )$ may be expressed as

$$\begin{aligned} M_1(\vartheta )&= \cos \vartheta - 3\gamma \sin 3\vartheta \sin \vartheta , \end{aligned}$$

(35)

$$\begin{aligned} M_2(\vartheta )&= \cos (\vartheta -2\pi /3) - 3\gamma \sin 3\vartheta \sin (\vartheta -2\pi /3). \nonumber \\ \end{aligned}$$

(36)

The functions in Eq. (34) are strongly non-linear and they need to be solved for $\vartheta$ and $\Delta \lambda$ using an iterative solution procedure. The eigenvalues $s_i^*$ are sorted such that $s_1^*\ge s_2^*\ge s_3^*$ holds, which implies that the true solution for $\vartheta$ (i.e. the solution that fulfills the physical requirement $\Delta \lambda >0$) is to be found in the interval $\vartheta \in [0,\pi /3]$.

Once $\vartheta$ and $\Delta \lambda$ have been determined on the basis of Eq. (34), the principal values $s_{i}$ may be computed by use of Eq. (33). The eigenvectors $\mathbf{N}_i$ were computed from $s_{ij}^*$, and the components of the updated stress deviator tensor $s_{ij}^{n+1}$ may then be established by use of Eq. (15)$_2$. The updated stress tensor is then computed as $\sigma _{ij}^{n+1}=s_{ij}^{n+1}+\sigma _\mathrm{h}^*\delta _{ij}$.

3.3 Algorithmic tangent stiffness

To establish the stiffness tensor, we start by differentiating Eq. (29), yielding

$$\begin{aligned} \mathrm{d}\sigma _{ij} = D_{ijkl}\mathrm{d}\epsilon _{kl} - 2G[\mathrm{d}(\Delta \lambda )M_{ij}+\Delta \lambda \mathrm{d}M_{ij}]. \end{aligned}$$

(37)

Hence, in order to attain a relation between $\mathrm{d}\sigma _{ij}$ and $\mathrm{d}\epsilon _{ij}$, we need to express $\mathrm{d}(\Delta \lambda )$ and $\mathrm{d}M_{ij}$ in terms of $\mathrm{d}\sigma _{ij}$ and $\mathrm{d}\epsilon _{ij}$. As before, the index $(\bullet )^{n+1}$ is understood but left out for the sake of clarity.

If Eq. (30) is double-contracted with $n_{ij}$, $\Delta \lambda$ may be expressed as

$$\begin{aligned} \Delta \lambda = \frac{(\sigma _{ij}^*-\sigma _{ij})n_{ij}}{3G}. \end{aligned}$$

(38)

We note that $\mathrm{d}\sigma _{ij}^*=D_{ijkl}\mathrm{d}\epsilon _{kl}$ and $n_{ij}D_{ijkl}=2Gn_{kl}$, and differentiation of Eq. (38) leads to

$$\begin{aligned} \mathrm{d}(\Delta \lambda ) = \frac{2}{3}n_{ij}\mathrm{d}\epsilon _{ij} - \frac{1}{3G}n_{ij}\mathrm{d}\sigma _{ij} + \frac{2\Delta \lambda }{3}M_{ij}\mathrm{d}n_{ij}. \end{aligned}$$

(39)

The differential of $n_{ij}$ is

$$\begin{aligned} \mathrm{d}n_{ij}&= \mathrm{d}\left( \frac{3s_{ij}}{2\sigma _\mathrm{e}}\right) = \frac{3}{2\sigma _\mathrm{e}}\mathrm{d}s_{ij} - \frac{3s_{ij}}{2\sigma _\mathrm{e}^2}\mathrm{d}\sigma _\mathrm{e} \nonumber \\&= \frac{3}{2\sigma _\mathrm{e}}\frac{\partial s_{ij}}{\partial \sigma _{kl}}\mathrm{d}\sigma _{kl} \nonumber \\&- \frac{3s_{ij}}{2\sigma _\mathrm{e}^2}\left( H\mathrm{d}(\Delta \lambda )h + \sigma _\mathrm{y}h^{\prime }\frac{\partial \xi }{\partial \sigma _{ij}}\mathrm{d}\sigma _{ij}\right) \nonumber \\&= \frac{1}{2\sigma _\mathrm{e}}\left( 3I_{ijkl} - \delta _{ij}\delta _{kl} - 6\gamma n_{ij}m_{kl}\right) \mathrm{d}\sigma _{kl} \nonumber \\&- \frac{H}{\sigma _\mathrm{y}}n_{ij}\mathrm{d}(\Delta \lambda ) = P_{ijkl}\mathrm{d}\sigma _{kl} - \frac{H}{\sigma _\mathrm{y}}n_{ij}\mathrm{d}(\Delta \lambda ), \end{aligned}$$

(40)

where $H=\mathrm{d}\sigma _\mathrm{y}/\mathrm{d}\epsilon _\mathrm{e}^\mathrm{p}=\mathrm{d}\sigma _\mathrm{y}/\mathrm{d}(\Delta \lambda )$. Substitution of the expression for $\mathrm{d}(\Delta \lambda )$ in Eq. (39) into Eq. (40) yields

$$\begin{aligned}&\underbrace{\left( I_{ijkl} \!+\! \frac{2H\Delta \lambda }{3\sigma _\mathrm{y}}n_{ij}M_{kl}\right) }_{\displaystyle \varLambda _{ijkl}}\mathrm{d}n_{kl} \nonumber \\&\quad = \underbrace{\left( P_{ijkl}\!+\!\frac{H}{3G\sigma _\mathrm{y}}n_{ij}n_{kl}\right) }_{\displaystyle R^*_{ijkl}}\mathrm{d}\sigma _{kl} \!-\! \underbrace{\frac{2H}{3\sigma _\mathrm{y}}n_{ij}n_{kl}}_{\displaystyle Q^*_{ijkl}}\mathrm{d}\epsilon _{kl}, \end{aligned}$$

(41)

from which we deduce

$$\begin{aligned} \mathrm{d}n_{ij}&= \varLambda _{ijmn}^{-1}\left( R^*_{mnkl}\mathrm{d}\sigma _{kl} - Q^*_{mnkl}\mathrm{d}\epsilon _{kl}\right) \nonumber \\&= R_{ijkl}\mathrm{d}\sigma _{kl} - Q_{ijkl}\mathrm{d}\epsilon _{kl}. \end{aligned}$$

(42)

This expression may now be substituted back into Eq. (39), yielding

$$\begin{aligned} \mathrm{d}(\Delta \lambda )&= \ldots = \left( \frac{2}{3}n_{ij} - \frac{2\Delta \lambda }{3}M_{kl}Q_{klij}\right) \mathrm{d}\epsilon _{ij} \nonumber \\&\qquad \quad + \left( \frac{2\Delta \lambda }{3}M_{kl}R_{klij}-\frac{1}{3G}n_{ij}\right) \mathrm{d}\sigma _{ij} \nonumber \\&= Y_{ij}\mathrm{d}\epsilon _{ij} + V_{ij}\mathrm{d}\sigma _{ij}. \end{aligned}$$

(43)

Next we consider the differential of $M_{ij}$:

$$\begin{aligned} \mathrm{d}M_{ij} = \mathrm{d}n_{ij} - 3\mathrm{d}\gamma m_{ij} - 3\gamma \mathrm{d}m_{ij}, \end{aligned}$$

(44)

where $\mathrm{d}n_{ij}$ is given in Eq. (42), and the additional differentials are

$$\begin{aligned}&\mathrm{d}\gamma = \left( \frac{h^{\prime \prime }}{h}-\gamma ^2\right) \frac{\partial \xi }{\partial \sigma _{ij}}\mathrm{d}\sigma _{ij} \nonumber \\&\qquad = \left( \frac{h^{\prime \prime }}{h}-\gamma ^2\right) \frac{3}{\sigma _\mathrm{e}}m_{ij}\mathrm{d}\sigma _{ij} = B_{ij}\mathrm{d}\sigma _{ij}, \end{aligned}$$

(45)

$$\begin{aligned}&\mathrm{d}m_{ij} = \left( \delta _{ik}n_{jl} + \delta _{il}n_{jk} + \delta _{jl}n_{ik} + \delta _{jk}n_{il} - \xi I_{ijkl}\right) \mathrm{d}n_{kl} \nonumber \\&\qquad \qquad -\frac{3}{\sigma _\mathrm{e}}n_{ij}m_{kl}\mathrm{d}\sigma _{kl} = S_{ijkl}\mathrm{d}n_{kl} - W_{ijkl}\mathrm{d}\sigma _{kl}. \end{aligned}$$

(46)

Substitution of the expressions in Eqs. (45), (46), and (42) into Eq. (44) yields

$$\begin{aligned} \mathrm{d}M_{ij}&= \left( I_{ijkl}-3\gamma S_{ijkl}\right) \mathrm{d}n_{kl} \nonumber \\&+ \left( 3\gamma W_{ijkl}-3m_{ij}B_{kl}\right) \mathrm{d}\sigma _{kl} \nonumber \\&= U_{ijkl}\mathrm{d}n_{kl} + X_{ijkl}\mathrm{d}\sigma _{kl} \nonumber \\&= \left( U_{ijmn}R_{mnkl}+X_{ijkl}\right) \mathrm{d}\sigma _{kl} \nonumber \\&- U_{ijmn}Q_{mnkl}\mathrm{d}\epsilon _{kl} \nonumber \\&= T_{ijkl}\mathrm{d}\sigma _{kl} - A_{ijkl}\mathrm{d}\epsilon _{kl}. \end{aligned}$$

(47)

Substitution of the expressions for $\mathrm{d}(\Delta \lambda )$ and $\mathrm{d}M_{ij}$ in Eqs. (43) and (47), respectively, into Eq. (37) yields

$$\begin{aligned} \mathrm{d}\sigma _{ij}&= \underbrace{\left( D_{ijkl}-2GM_{ij}Y_{kl}+2G\Delta \lambda A_{ijkl}\right) }_ {\displaystyle Z_{ijkl}}\mathrm{d}\epsilon _{kl} \nonumber \\&- 2G\left( M_{ij}V_{kl} + \Delta \lambda T_{ijkl}\right) \mathrm{d}\sigma _{kl}, \end{aligned}$$

(48)

$$\begin{aligned}&\Rightarrow \underbrace{\left( I_{ijkl} + 2GM_{ij}V_{kl} + 2G\Delta \lambda T_{ijkl}\right) }_ {\displaystyle F_{ijkl}}\mathrm{d}\sigma _{kl} \nonumber \\&= Z_{ijkl}\mathrm{d}\epsilon _{kl}, \end{aligned}$$

(49)

$$\begin{aligned}&\Rightarrow \mathrm{d}\sigma _{ij} = F_{ijmn}^{-1}Z_{mnkl}\mathrm{d}\epsilon _{kl} = D_{ijkl}^\mathrm{alg}\mathrm{d}\epsilon _{kl}, \end{aligned}$$

(50)

where $D_{ijkl}^\mathrm{alg}$ are the components of the algorithmic stiffness tensor.

3.4 Computational schemes

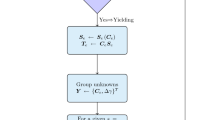
When integrating the stress state, the most challenging part is to solve the non-linear functions in Eq. (34) for the two unknowns $\vartheta$ and $\Delta \lambda$. It should be noted that it is, in general, not possible to solve Eq. (34) directly by use of, for example, the Newton-Raphson method, unless the initial guess is relatively close to the correct solution. Hence, a robust solution procedure is established in the following way: First, the hardening function is linearised such that $\sigma _\mathrm{y}(\lambda ^n+\Delta \lambda )\approx \sigma _\mathrm{y}^n+H\Delta \lambda$, where $H=\mathrm{d}\sigma _\mathrm{y}/\mathrm{d}(\Delta \lambda )|_{\Delta \lambda =0}$. After this approximation, $\Delta \lambda$ can be eliminated, and the two functions in Eq. (34) can be recast into a single function of  $\vartheta$:

$$\begin{aligned} q_\vartheta (\vartheta )&= (2h n_2 \sigma _\mathrm{y}^n - 3s_2^*)(2h n_1 H + 6G M_1) \nonumber \\&- (2h n_1 \sigma _\mathrm{y}^n - 3s_1^*)(2h n_2 H + 6G M_2) = 0. \end{aligned}$$

(51)

Equation (51) is evaluated for discrete values of $\vartheta$ in the interval $[0,\pi /3]$. Somewhere in the interval $[0,\pi /3]$ the function $q_\vartheta (\vartheta )$ changes sign, and two bounds, $\vartheta _\mathrm{min}$ and $\vartheta _\mathrm{max}$, may therefore be established, between which the solution $\vartheta ^*$, that fulfills Eq. (51), is to be found. The value $\vartheta ^*$ is bracketed until $\vartheta ^*$ has been determined with an uncertainty of $0.01$ rad. (This bracketing implies that $q_\vartheta (\vartheta )$ is evaluated for a value $\vartheta _\mathrm{av}$, located between $\vartheta _\mathrm{min}$ and $\vartheta _\mathrm{max}$. The bounds are then updated such that $\vartheta _\mathrm{min}\leftarrow \vartheta _\mathrm{av}$ or $\vartheta _\mathrm{max}\leftarrow \vartheta _\mathrm{av}$, depending on the sign of $q_\vartheta (\vartheta _\mathrm{av})$. For a more comprehensive description of such bracketing methods, see e.g. Press et al. [39].) This preliminary estimate $\vartheta ^*$ is inserted into Eq. (34), and an error function is defined as

$$\begin{aligned} q_\lambda (\Delta \lambda ) = \sqrt{q_1^2(\vartheta =\vartheta ^*,\Delta \lambda )+q_2^2(\vartheta =\vartheta ^*,\Delta \lambda )}. \end{aligned}$$

(52)

Equation (52) is minimised with respect to $\Delta \lambda$, again using a simple bracketing technique. The value $\Delta \lambda ^*$ that minimises Eq. (52) is bracketed until the uncertainty in $\Delta \lambda ^*$ is 0.0001. The preliminary estimates $\{\vartheta ^*,\Delta \lambda ^*\}$ are, in general, close to the true solution. These estimates are therefore used as the initial guess in a standard Newton-Raphson algorithm, and Eq. (34) may then be solved for $\vartheta$ and $\Delta \lambda$ with the desired degree of accuracy.

The computational scheme used for updating stresses is summarised in Table 1.

Table 1 Computational scheme for integration of stresses

The stress components are stored on vector form such that $\overline{\varvec{{\sigma }}}^{n+1}=[\sigma _{11} \; \sigma _{22} \; \sigma _{33} \; \sigma _{12} \; \sigma _{13} \; \sigma _{23}]^\mathrm{T}$. In a similar way, the strain vector is defined as

$$\begin{aligned} \overline{{\varvec{\epsilon }}}^{n+1}=[\epsilon _{11} \; \epsilon _{22} \; \epsilon _{33} \; 2\epsilon _{12} \; 2\epsilon _{13} \; 2\epsilon _{23}]^\mathrm{T}. \end{aligned}$$

An efficient numerical implementation of the material model also requires that the algorithmic stiffness matrix, $\overline{\mathbf{D}}_\mathrm{alg}^{n+1}=\partial \overline{\varvec{{\sigma }}}^{n+1}/\partial \overline{{\varvec{\epsilon }}}^{n+1}$, is established. The expressions for computing the algorithmic stiffness tensor $D_{ijkl}^\mathrm{alg}$ were derived in the previous subsection. The tensors $B_{ij}$, $P_{ijkl}$, $R^*_{ijkl}$, $Q^*_{ijkl}$, $\varLambda _{ijkl}$, $S_{ijkl}$, $W_{ijkl}$, $U_{ijkl}$, $X_{ijkl}$ are straight-forward to compute. The evaluation of $B_{ij}$ requires some special attention, though. As $\vartheta$ approaches multiples of $\pi /3$, $h^{\prime \prime }$ goes towards infinity, whereas $m_{ij}$ goes towards zero. The product, $h^{\prime \prime } m_{ij}$, however, approaches zero. Consequently, this computational step needs special treatment in the implementation.

The computation of the tensors $R_{ijkl}$ and $Q_{ijkl}$ requires the inversion of the tensor $\varLambda _{ijkl}$. For this reason, the tensor components (that include several doublets due to symmetry) of a tensor $L_{ijkl}$ are stored in a $6\times 6$ matrix $\overline{\mathbf{L}}$ according to

$$\begin{aligned} \overline{\mathbf{L}} = \left[ \begin{array}{cccccc} L_{1111} &{} L_{1122} &{} L_{1133} &{} \beta L_{1112} &{} \beta L_{1113} &{} \beta L_{1123} \\ L_{2211} &{} L_{2222} &{} L_{2233} &{} \beta L_{2212} &{} \beta L_{2213} &{} \beta L_{2223} \\ L_{3311} &{} L_{3322} &{} L_{3333} &{} \beta L_{3312} &{} \beta L_{3313} &{} \beta L_{3323} \\ L_{1211} &{} L_{1222} &{} L_{1233} &{} \beta L_{1212} &{} \beta L_{1213} &{} \beta L_{1223} \\ L_{1311} &{} L_{1322} &{} L_{1333} &{} \beta L_{1312} &{} \beta L_{1313} &{} \beta L_{1323} \\ L_{2311} &{} L_{2322} &{} L_{2333} &{} \beta L_{2312} &{} \beta L_{2313} &{} \beta L_{2323} \end{array} \right] , \end{aligned}$$

(53)

where the factor $\beta$ takes on the value 1 if the matrix $\overline{\mathbf{L}}$ is associated with the strain differential $\mathrm{d}\overline{{\varvec{\epsilon }}}^{n+1}$ and 2 otherwise. Hence, matrices $\overline{{\varvec{{\varLambda }}}}$, $\overline{\mathbf{R}}^*$, and $\overline{\mathbf{Q}}^*$ are constructed from the components of tensors $\varLambda _{ijkl}$, $R^*_{ijkl}$, and $Q^*_{ijkl}$, respectively. The $6\times 6$ matrix $\overline{{\varvec{{\varLambda }}}}$ is straight-forward to invert, and the matrices $\overline{\mathbf{R}}=\overline{{\varvec{{\varLambda }}}}^{-1}\overline{\mathbf{R}}^*$ and $\overline{\mathbf{Q}}=\overline{{\varvec{{\varLambda }}}}^{-1}\overline{\mathbf{R}}^*$ may therefore be computed. From the matrices $\overline{\mathbf{R}}$ and $\overline{\mathbf{Q}}$, the tensors $R_{ijkl}$ and $Q_{ijkl}$ may then be constructed by reversing the process illustrated in Eq. (53).

Once $R_{ijkl}$ and $Q_{ijkl}$ have been established, it is again straight-forward to compute the remaining tensors $T_{ijkl}$, $A_{ijkl}$, $Y_{ij}$, $V_{ij}$, $F_{ijkl}$, and $Z_{ijkl}$. The components of the tensors $F_{ijkl}$ and $Z_{ijkl}$ are stored in the matrices $\overline{\mathbf{F}}$ and $\overline{\mathbf{Z}}$, respectively, in accordance with Eq. (53), and the algorithmic stiffness matrix is then computed as $\overline{\mathbf{D}}_\mathrm{alg}^{n+1}=\partial \overline{\varvec{{\sigma }}}^{n+1}/\partial \overline{{\varvec{\epsilon }}}^{n+1}=\overline{\mathbf{F}}^{-1}\overline{\mathbf{Z}}$.

4 Numerical examples

4.1 Prerequisites

The plasticity model described in the previous sections was implemented in the commercial finite element code Abaqus. In Abaqus, an updated Lagrangian framework is used to solve finite strain plasticity problems. This framework employs a co-rotational formulation for the rate constitutive hypoelastic-plastic equations to account for rotation of principal axes of deformation. For details about the precise implementation, the reader is referred to the Abaqus manual [40]. Hence, even though the present model is formulated for the infinitesimal strains, when implemented in Abaqus, full account of finite strains is taken. At this junction, we would also like to point out that the current small strain formulation can be extended to finite strain by use of a multiplicative split of the deformation gradient into a plastic and elastic part assuming a hyperelasto-plastic material response as outlined in [41]. Moreover, an interesting discussion on finite element formulations for finite strains is given in [42].

In the present section, two numerical examples are provided to assess the influence of the invariant $J_3$ on the plastic yield behaviour under different loading conditions. The two geometries analysed are two types of test specimens.

The material analysed is a cold-rolled dual-phase steel (Docol 600DL) that has been tested experimentally by, for example Gruben et al. [43, 44] and also in the laboratory at the department of the present authors (unpublished data). The plastic response of this material in uniaxial tension can be modelled by the hardening function

$$\begin{aligned} \sigma _\mathrm{y} = \sigma _0\left[ \frac{\sigma _\mathrm{s}}{\sigma _0} \!-\! \left( \frac{\sigma _\mathrm{s}}{\sigma _0} \!-\! 1\right) \exp \left( -\frac{\epsilon _\mathrm{e}^\mathrm{p}}{\epsilon _\mathrm{s}}\right) \right] \left( 1\!+\!\frac{\epsilon _\mathrm{e}^\mathrm{p}}{\epsilon _\mathrm{0}}\right) ^N, \end{aligned}$$

(54)

where the material parameters take on the values $\sigma _0=380$ MPa, $\sigma _\mathrm{s}/\sigma _0=1.21$, $N=0.117$, and $\epsilon _\mathrm{s}=0.0206$. The elastic response is given by Young’s modulus $E=200$ GPa and Poisson’s ratio $\nu =0.3$, and $\epsilon _0=\sigma _0/E=0.0019$. The hardening function is illustrated in Fig. 5.

Fig. 5

Hardening function representative of the cold-rolled dual-phase steel Docol 600DL ($\sigma _0=380$ MPa, $\sigma _\mathrm{s}/\sigma _0=1.21$, $N=0.117$, $\epsilon _0=0.0019$, $\epsilon _\mathrm{s}=0.0206$)

The parameters in the $h$-function are set to $p=4$ and $\omega _0=0.18$, which appears to be a versatile choice. Furthermore, we make use of results obtained by Hosford [32], who analysed the yield behaviour in fcc and bcc polycrystalline metals by use of a self consistent model for crystal slip. Hosford found that an exponent in the range 6 to 10 (depending on lattice and hardening) in the yield criterion given by Eq. (2) captures the behaviour in these polycrystals fairly well. This translates to a $\mu$ value in the range 0.03 to 0.07. Here, $\mu =0.06$ is taken as a representative value, which together with the limit values 0 and 0.12345 will be used in the numerical examples.

4.2 Plane strain tension specimen

The first load case to be simulated is the stretching of a plane strain tension specimen, the geometry of which is shown in Fig. 6. The specimen is loaded by a prescribed displacement $\Delta$, causing a tensile force $P$, as indicated in Fig. 6.

Fig. 6

Geometry of plane strain tension specimen (thickness: 2 mm)

Due to symmetry, an eighth of the specimen was discretised using 4800 quadratic hexahedral hybrid elements, and the stretching was analysed in Abaqus. The resulting load-displacement curves were extracted and are displayed in Fig. 7.

Fig. 7

Predicted load-displacement curves for a plane strain tension specimen for $\mu =0$ (blue), 0.06 (green), and 0.12345 (red). (Color figure online)

As can be seen from Fig. 7, the three curves are identical in the initial elastic regime. Then as the specimens start to deform plastically, the force response of the specimens decrease with increasing $\mu$.

In Fig. 8, the distributions of the invariants $\xi$ and $T=\sigma _\mathrm{h}/\sigma _\mathrm{e}$ (stress triaxiality) at the peak load are displayed. It is clear from Fig. 8a, that this specimen is not able to produce a strict plain strain state at the centre of the specimen, i.e. a state with $\xi =0$ and $T=1/\sqrt{3}\approx 0.577$. For the von Mises material ($\mu =0$), there is a minor part of the cross-sectional area where $\xi$ approaches 0.5, but most of the cross-section is still in a state of uniaxial tension. For the Tresca case ($\mu =0.12345$), the whole cross-section is virtually in a state of uniaxial tension, i.e. $\xi$ is about 1. It may be noted, however, that a small distance from the central cross-section there is a strip of material that appears to be more or less in a state of plain strain, i.e. $\xi \approx 0$. In Fig. 8b, it may be noted that there is a significant gradient in the stress triaxiality. It is clear, that as the material approaches a Tresca material (i.e. $\mu$ increases), the gradient is weakened, and the triaxiality peak at the centre of the specimen decreases.

Fig. 8

Distribution of stress fields in the PST specimen at maximum force level in tensile test: a $\xi$ and b $T=\sigma _\mathrm{h}/\sigma _\mathrm{e}$

The constraint imposed by the geometry on the normal plastic strain component in the $X_2$-direction would promote a state of plane strain. However, for a near Tresca material with an associated flow rule subjected to an overall state of uniaxial tension, a very small deviation from the prevailing axisymmetric stress state is needed in order to satisfy a plane strain constraint.

4.3 Plane strain specimen

The second geometry to be considered is a plane strain specimen, illustrated in Fig. 9. The specimen is again loaded by a prescribed displacement $\Delta$, causing a tensile force $P$, as indicated in Fig. 9. Again an eighth of the specimen was modelled and discretised using 5432 quadratic hexahedral hybrid elements, and the same three values of $\mu$ were considered. The resulting load-displacement curves were extracted and are displayed in Fig. 10.

Fig. 9

Geometry of plane strain specimen

Fig. 10

Predicted load-displacement curves for a plane strain specimen for $\mu =0$ (blue), 0.06 (green), and 0.12345 (red). (Color figure online)

As can be seen from Fig. 10, the three curves are again identical in the initial elastic regime. Then as the specimens start to deform plastically, the force response of the specimens decrease with increasing $\mu$.

In Fig. 11, the distributions of the invariants $\xi$ and $T=\sigma _\mathrm{h}/\sigma _\mathrm{e}$ at the peak load are displayed. According to Fig. 11a, this specimen is actually able to produce a plain strain state fairly well at the centre of the specimen. For the von Mises material ($\mu =0$), about half of the cross-sectional area is in a state of plain strain, and as the edge is approached, the cross-section approaches a state of uniaxial tension. Even for the intermediate case ($\mu =0.06$), the plain strain state is accomplished fairly well, whereas for the Tresca case ($\mu =0.12345$), the whole cross-section is again in a state that is close to uniaxial tension. When it comes to the stress triaxiality in Fig. 11b, there is again a significant gradient in the stress triaxiality, which decreases as the material approaches a Tresca material (i.e. $\mu$ increases).

Fig. 11

Distribution of stress fields in the PS specimen at maximum force level in tensile test: (a) $\xi$ and (b) $T=\sigma _\mathrm{h}/\sigma _\mathrm{e}$

5 Discussion

It has long been recognised, that the yield behaviour of some ductile metals show a dependence on the third stress invariant $J_3$ [17–24], and several yield functions have been proposed to account for this behaviour (e.g., [26–28, 30–37]). In the present work, we propose a new $J_2$- and $J_3$-dependent yield function that we also believe is suitable for numerical implementation into a finite element framework. The proposed yield function deviates from the non-quadratic function by Hershey–Hosford in Eq. (2) in some decisive ways. Using a quadratic yield function (von Mises) with a constant curvature as a reference, strong deviations in curvature of the proposed yield function first occur at the axisymmetric stress states. By contrast, in the Hershey-Hosford yield function, strong curvature deviations first arise at the shearing stress states. This difference will affect the possibility for localization of plastic flow as that is sensitive to the curvature of the yield surface.

Implementation of standard $J_2$-plasticity is relatively straight-forward (see e.g. Simo and Hughes [45]). However, the inclusion of a dependence on $J_3$ in the yield criterion and the use of an associated flow rule lead to some challenges when it comes to the numerical implementation. When applying Tresca-like yield criteria, the corners that appear in the yield surface must be dealt with. Such non-smooth yield functions can be treated numerically (Koiter [46] and Mandel [47, 48]), but smooth functions are preferable. The present model is able to account for a Tresca-like behaviour, while still retaining rounded corners that do not cause any significant numerical problems. A second challenge is that in the expressions for the stress updating, a term $\mathbf{s}\cdot \mathbf{s}$ appears together with $\mathbf{s}$-dependent terms, implying that the evolution law for the stress components are not independent. Hence, in general a non-linear equation system, i.e. Eq. (31), with five unknowns needs to be solved. (In general, symmetric tensors have six independent components, but since the trace of the stress deviator is zero, this tensor only has five independent components). In principle, this can be done (this is the path taken by Gao et al. [37]), but this is a relatively unstable and time-consuming way. Hence, in the present formulation, we make use of the fact that the system in Eq. (31) may be reduced to an equation system for the eigenvalues of the stress deviator, which eventually leads to an equation system with only two unknowns, i.e. $\vartheta$ (the Haigh-Westergaard angular coordinate) and $\Delta \lambda$ (the increment in equivalent plastic strain). This reduced non-linear equation system is solved using an iterative procedure, and the numerical scheme adopted appears to be very stable from a numerical point of view.

The plastic hardening function $\sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p})$ is defined as a function of the equivalent plastic strain, $\epsilon _\mathrm{e}^\mathrm{p}$. The relation between the increment in equivalent plastic strain and the increments of the components of the plastic strain tensor in the present work differs somewhat from what is common in standard $J_2$-plasticity, see Eq. (19). The difference stems from the fact that in the present theory, the stress deviator, $\mathbf{s}$, and the plastic strain increments, $\dot{{\varvec{\epsilon }}}^\mathrm{p}$, are not co-axial (as in standard $J_2$-theory). Hence, not all plastic strains will produce plastic work. (The tensor $\mathbf{m}$ is orthogonal to $\mathbf{s}$, and therefore the part of the plastic strain increments associated with $\mathbf{m}$ does not contribute to the plastic work.) One way to proceed would be to retain the standard definition of the equivalent plastic strain – i.e. allow all plastic strains to contribute to strain hardening – and accept that $\dot{\epsilon }_\mathrm{e}^\mathrm{p}$ would not (in general) be the work conjugate of $\sigma _\mathrm{e}$ (i.e. $\dot{\epsilon }_\mathrm{e}^\mathrm{p}$ would differ from $\dot{\lambda }$). The approach opted for here, however, is to assume that strain hardening only is produced by that fraction of the plastic strains that produces plastic work. In this case, $\dot{\epsilon }_\mathrm{e}^\mathrm{p}$ is still the work conjugate of $\sigma _\mathrm{e}$, and $\dot{\epsilon }_\mathrm{e}^\mathrm{p}$ is defined according to Eq. (19). Note, however, that in all the three special cases of uniaxial tension, biaxial tension, and pure shear, the equivalent plastic strain increment in the present theory coincides with the increment in standard $J_2$-theory, since in all of these three cases, either $\gamma$ or $\omega$ vanishes, see Eq. (19). Furthermore, if the plastic potential had been chosen as $g=\sigma _\mathrm{e}$, as in standard $J_2$-theory, the plastic strain increments would be co-axial with the stress deviator, but the flow rule would have been non-associative. Here, however, we choose to formulate the flow rule in accordance with the principle of maximum plastic work [49–51], which requires an associative flow rule.

From a material testing perspective, the primary new material parameter to determine is $\mu$. A standard uniaxial test on a (axisymmetric) tensile specimen enables the determination of the hardening function $\sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p})$, i.e. $\sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p})=\sigma (\epsilon ^\mathrm{p})$, where $\sigma (\epsilon ^\mathrm{p})$ denotes the stress vs. plastic strain data from the uniaxial test. In addition to this, a test in pure shear on a thin-walled tube specimen [37, 52] would be a sensible choice, in which case a relation $(1-\mu )\sigma _\mathrm{y}(\epsilon _\mathrm{e}^\mathrm{p})=\sqrt{3}\tau (\gamma ^\mathrm{p})$ is expected, where $\tau (\gamma ^\mathrm{p})$ denotes the shear stress vs. plastic shear data from the shear test. (In a pure shear test, the relation $\epsilon _\mathrm{e}^\mathrm{p}=\gamma ^\mathrm{p}/\sqrt{3}$ holds.) The parameter $\mu$ could then be determined by direct comparison of test results from the two different types of specimen.

For sheet metals, however, only planar types of specimen are, in practice, available. For this reason, different types of plane strain test geometries were investigated in the numerical examples. It is of special interest to see if their load responses can be used to determine the material parameter $\mu$ in a simple manner. Thus, the proposed plasticity model was implemented in Abaqus and applied in simulations of two test specimens. It is clear from the load-displacement curves (see Figs. 7, 10) that a $J_3$-dependence in the yield function has a significant impact on the predicted load levels. The relative difference in predicted load for the two specimens is displayed in Fig. 12. The $\mu$ levels applied (0.06 and 0.12345) are indicated in Fig. 12 as horizontal dashed lines. It can be observed, that the impact of $\mu$ on the predicted load is strongest for the plane strain (PS) specimen and weaker for the plane strain tension (PST) specimen. It should be noted, though, that the extent of the curves along the abscissa depends on specimen dimension, and therefore the curves are not fully comparable. The marked increase in relative difference seen at the end of each curve is associated with the diffuse necking modes that start to develop in the post peak force regime, see Figs. 7 and 10. This indicates that an increase in the material parameter $\mu$, promotes an earlier onset of localization in plastic deformation. It has been recognized for some time, that ductile failure in some materials not only depends strongly on stress triaxiality, but also on the deviatoric stress state, e.g. quantified in terms of $L$ (the Lode parameter), $\xi$ or $\omega$  [38, 53–56]. Localization of plastic flow often acts as a precursor of ductile failure. Therefore, for materials with a yield behaviour in between the von Mises and Tresca surfaces, we surmise that it may be of importance to correctly account for the plastic flow behaviour if ductile failure is to be modelled accurately.

Fig. 12

Relative difference in predicted load during testing for plane strain tension (PST) and plane strain (PS) specimens; results for $\mu =0.06$ (green lines) and $\mu =0.12345$ (red lines). The symbols ‘$\odot$’ indicate the point where the maximum load appears in each simulation. (Color figure online)