Known approaches to the analysis of the deformation properties of polymer textile threads are based on the description of generalized experimental relaxation and creep curves using normalized relaxation and delay functions, for which the integral curve of the normal distribution over logarithmic scale of the reduced time is most often selected [1].

Due to the different complex composition and macrostructure of polymer textile threads, the study of the mechanical properties of some of them, especially multicomponent threads, can be difficult because they have more complex relaxation and delay times spectra due to the superposition of elementary spectra corresponding to components that make up the thread [2].

This circumstance stimulated the search for mathematical models of deformation properties based on new relaxation and delay functions corresponding to more complex spectra [3].

When constructing a mathematical model of viscoelasticity, both the requirement for the minimum number of parameters of the mathematical model and their physical validity were taken into account.

The simplification of the mathematical model of viscoelasticity is achieved by taking into account the nonlinearity in the integral relaxation and delay kernels by setting functions of average statistical relaxation and delay times [4].

One of the considered versions of mathematical simulation of the viscoelastic properties of the polymer textile threads is based on the Cauchy probability distribution of relaxing and delaying particles [5]:

$$ {E}_{\upvarepsilon t}={E}_0-\left({E}_0-{E}_{\infty}\right){\upvarphi}_{\upvarepsilon t}, $$
(1)
$$ {D}_{\upsigma t}={D}_0+\left({D}_{\infty }-{D}_0\right){\upvarphi}_{\upsigma t}, $$
(2)
$$ {\upvarphi}_{\upvarepsilon t}=\frac{1}{2}+\frac{1}{\uppi}\arctan \left(\frac{1}{b_{n\upvarepsilon}}\cdot \ln \frac{t}{\uptau_{\upvarepsilon}}\right), $$
(3)
$$ {\upvarphi}_{\upsigma t}=\frac{1}{2}+\frac{1}{\uppi}\arctan \left(\frac{1}{b_{n\upsigma}}\cdot \ln \frac{t}{\uptau_{\upsigma}}\right), $$
(4)

where Eεt is the relaxation modulus; Dσt is the compliance; t is the time; 1/bnε is the intensity parameter of the relaxation process; 1/bnσ is the intensity parameter of the creep process; τε is the relaxation time (the time during which half of the relaxation process passes at the specified deformation value); τσ is the delay time (the time during which half of the creep process passes at the specified stress value); Eεt = σ/ε is the relaxation modulus; E0 is the elasticity modulus; E∞ is the viscoelasticity modulus; Dσt = ε/σ is the compliance; D0 is the initial compliance; D∞ is the ultimate equilibrium compliance; ε is the deformation; σ is the stress; φεt is the relaxation function; φσt is the creep function, set in the form of a normalized arctangent of the logarithm of the reduced time (NAL).

The proposed version is most suitable for predicting the deformation processes of polymer textile threads of complex macrostructure, since it is known that the sum of random variables distributed according to the normalized Cauchy law is also distributed according to the same law. It means that, if one assumes that the relaxing and delaying particles of the fibres that make up the thread are distributed over the internal relaxation and delay times according to the Cauchy law, then one can assume that both macrorelaxing and macrodelaying particles are distributed according to this law [6].

The undoubted advantage of the mathematical model of Eqs. (1)-(4) is that it contains the minimum number of parameters that have a clear physical meaning [7]: \( {E}_0=\underset{t\to 0}{\lim }{E}_{\upvarepsilon t} \), \( {E}_{\infty }=\underset{t\to \infty }{\lim }{E}_{\upvarepsilon t} \), \( {D}_0=\underset{t\to 0}{\lim }{E}_{\upsigma t} \), \( {D}_{\infty }=\underset{t\to \infty }{\lim }{E}_{\upsigma t} \), are the asymptotic values of the relaxation and compliance moduli;

- structural parameters bnε and bnσ characterize the rate of relaxation and creep processes: these parameters correspond to the logarithm of the reduced time of “half-relaxation” (half of the relaxation process at the deformation ε occurs in the time interval t ∈ [t′, t′′], where ln(t′/τε)=bnε, ln(t′′/τε)=bnε) and “half-delay” (half of the creep process at the stress σ occurs in the time interval t ∈ [t′, t′′] , where ln(t′/τσ)=bnσ, ln(t′′/τσ)=bnσ);

- functions of relaxation \( {f}_{\upvarepsilon_1\upvarepsilon} \) = ln(t1/τε) and delay \( {f}_{\upsigma_1\upsigma} \) = ln(t1/τσ) times characterizing the shifts of the curves of relaxation and creep “families” along the logarithmic-time scale are contained, respectively, in the structuredeformation-time argument-functional

$$ {W}_{\upvarepsilon t}=\frac{1}{b_{n\upvarepsilon}}\ln \frac{t}{\uptau_{\upvarepsilon}}=\frac{1}{b_{n\upvarepsilon}}\left(\ln \frac{1}{t_1}+\ln \frac{t_1}{\uptau_{\upvarepsilon}}\right) $$
(5)

and n the structure-force-time argument-functional

$$ {W}_{\upsigma t}=\frac{1}{b_{n\upsigma}}\ln \frac{t}{\uptau_{\upsigma}}=\frac{1}{b_{n\upsigma}}\left(\ln \frac{1}{t_1}+\ln \frac{t_1}{\uptau_{\upsigma}}\right) $$
(6)

The relatively slow convergence of the NAL function (for example, compared to the probability integral) to its asymptotic values allows interpolating the relaxation modulus Eεt and compliance Dσt in a fairly wide time interval, which allows predicting both fast-going and long-term deformation processes.

It should be noted that the choice of a normalized function for the mathematical model of the viscoelastic properties of polymer materials is complicated by the fact that it is impossible to give preference to any of them a priori. Experiment is the main criterion for selection. The presence of several normalized functions for simulation allows making a more correct choice and thereby increasing the prediction reliability [8].

The study of viscoelastic characteristics of polymer textile threads based on the mathematical model of Eqs. (1)-(4) has shown that the calculated value of the elastic modulus E0 is higher than that calculated using mathematical models based on other normalized functions, and is close to the acoustic value Eak, which is also physically justified, since the propagation velocity of elastic interactions in polymer textile threads is close to sonic. The value of the viscoelastic modulus E∞, which characterizes the lower asymptote of the relaxation modulus in long-term processes, has also decreased, which, in fact, expands the relaxation range. A similar conclusion can be drawn about the creep process. This circumstance favourably distinguishes the NAL function from the previously used normalized relaxation and delay functions (for example, the probability integral, the Kohlrausch function, the hyperbolic tangent, etc.).

Thus, the use of the normalized NAL function as the basis of the mathematical model of viscoelasticity allows simulating the deformation properties of polymer textile threads with a sufficient degree of accuracy. The indicated simulation expands the deformation-time and force-time boundaries of predicting deformation processes. The analytical setting of the NAL function and its belonging to the class of elementary functions simplifies differential-integral transformations within the framework of the considered mathematical model and facilitates the process of finding viscoelastic characteristics.

Prediction of deformation processes of polymer textile threads is traditionally carried out on the basis of the known integral Boltzmann-Volterra relations: Eq. (8) for the process of nonlinear hereditary relaxation and Eq. (9) for the process of nonlinear hereditary creep [9]:

$$ {\upsigma}_t={E}_0{\upvarepsilon}_t-\left({E}_0-{E}_{\infty}\right)\cdot \int_0^t{\upvarepsilon}_{\uptheta}\cdot {\upvarphi}_{\upvarepsilon, t-\uptheta}^{\prime }d\uptheta, $$
(7)
$$ {\upvarepsilon}_t={D}_0{\upsigma}_t-\left({D}_{\infty }-{D}_0\right)\cdot \int_0^t{\upsigma}_{\uptheta}\cdot {\upvarphi}_{\upsigma, t-\uptheta}^{\prime }d\uptheta $$
(8)

with integral relaxation and delay kernels corresponding to the mathematical model of Eqs. (1)-(6):

$$ {\upvarphi}_{\upvarepsilon t}^{\prime }=\frac{\partial {\upvarphi}_{\upvarepsilon t}}{\partial t}=\frac{1}{\uppi}\cdot \frac{1}{b_{n\upvarepsilon}}\cdot \frac{1}{1+{W}_{\upvarepsilon t}^2}\cdot \frac{1}{t}, $$
(9)
$$ {\upvarphi}_{\upsigma t}^{\prime }=\frac{\partial {\upvarphi}_{\upsigma t}}{\partial t}=\frac{1}{\uppi}\cdot \frac{1}{b_{n\upsigma}}\cdot \frac{1}{1+{W}_{\upsigma t}^2}\cdot \frac{1}{t}. $$
(10)

The advantage of using the integral kernels of Eqs. (9) and (10) for simulating deformation processes, as a consequence of the mathematical model of Eqs. (1)-(6), is the possibility of expanding the confidential prediction area towards “long” (long-term processes) and “short” times (short-term processes) with a decrease in the prediction error due to reducing the influence of the quasi-instantaneous deformation factor at the beginning of the process.

In addition, the prediction accuracy improving is based on methods for calculating improper non-linear hereditary integrals of Eqs. (7), (8), constructed on a non-uniform division of the time scale, taking into account the specifics of the process under consideration.

For example, when predicting active (fast-going) processes characterized by an increase in the deformation rate, it is advisable to divide the time scale according to an increasing geometric progression in order to best take into account the influence of the quasi-instantaneous deformation factor at the beginning of the process. When predicting long-term processes characterized by a decrease in the deformation rate, it is advisable to divide the time scale according to a decreasing geometric progression in order to best take into account the long-term deformation effects.

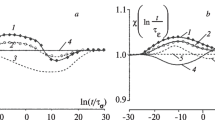
The developed methods for calculating the integrals of nonlinear hereditary viscoelasticity of Eqs. (7), (8) on the basis of the mathematical model with the NAL function were tested on various deformation processes. An example of calculating the relaxation (Fig. 1) and creep (Fig. 2) processes of a polyester thread shows the similarity of the calculated points to the values obtained from the experiment.

Fig. 1.
figure 1

“Family” of polyester thread relaxation curves at different deformation values (ε, %):1) 1; 2) 2; 3) 3; 4) 4; 5) 5; ○ are the points calculated without correction for the plastic component of deformation; ✳ are the points calculated taking into account the correction for the plastic component.

Full size image
Fig. 2.
figure 2

“Family” of polyester thread creep curves at different stress values (σ, MPa): 1) 6.6; 2) 13.2; 3) 19.8; 4) 26.4; 5) 33.0; ○ are the points calculated without correction for the plastic component of deformation; ✳ are the points calculated taking into account the correction for the plastic component.

Full size image

The method of introducing a correction for the accumulation of the plastic component of deformation, which does not depend on the deformation process type, allows improving the accuracy of predicting deformation processes. Thus, for example, the relaxation process calculated by the formula

$$ {\upsigma}_{t\ \textrm{calc}}=\upeta {\sigma}_t+\left(1\ \upeta \right){E}_0{\upvarepsilon}_t, $$
(11)

where σt is the stress value calculated by Eq. (7), gives more accurate results (Fig. 1) when

$$ \upeta =\left({\upvarepsilon}_{\ast }-{\upvarepsilon}_{\textrm{res}}\right)/{\upvarepsilon}_{\ast }, $$
(12)

where η is the coefficient of deformation reversibility, calculated experimentally; ε* is the deformation before the load is removed; εres is the residual deformation after the load is removed.

Similarly, it is possible to calculate the total accumulated deformation εt calc by the formula

$$ {\upvarepsilon}_{t\ \textrm{calc}}={\upvarepsilon}_{\textrm{res}.}+\frac{1}{\upeta}{\upvarepsilon}_e, $$
(13)

where εt is the deformation calculated by Eq. (8) (Fig. 2). Here, one can also see an improvement of the prediction accuracy [13].

Consequently, introduction of a correction for the deformation irreversibility allows improving the accuracy of predicting viscoelastic processes.