Prediction of Creep of Synthetic Protective Clothing Materials

Methods for predicting creep processes of synthetic sewing materials used for devices of personal protection from mechanical impacts are reviewed.

An example of use of synthetic clothing materials in devices of individual protection is their use as inner linings of protective helmets for guarding the head of the person from injury, for example, during construction works.

Clothing materials and structures therefrom must have specific elastic and viscoelastic properties. In view of this, a pressing task is to predict the creep of synthetic clothing materials or structures therefrom under various conditions of force action.

Examples of such conditions could be various types of deformation-recovery processes under both full and partial loads. The simplest loading condition is the deformation process with a constant rate of deformation [1].

This process is described experimentally using tensile-test diagram, which could serve as a means of control of accuracy of prediction of elastic and more intricate conditions of deformation.

The methods of determination of creep characteristics of synthetic clothing materials are based on use of mathematical models that approximate experimental “families” of creep curves via normalized functions. Let us analyze one of the variants of such method [2].

The stress-strain state of synthetic clothing material in the domain of nondestructive loads is described by Boltzmann-Volterra integral equation for creep process

$$ {\upvarepsilon}_t={D}_0{\upsigma}_t+\underset{0}{\overset{t}{\int }}{\upsigma}_{t-s}{D}_{\upsigma s}^{\prime } ds $$

(1)

where ${D}_{\upsigma s}^{\prime }=\partial {D}_{\upsigma s}/\partial s$ is the creep kernel expressing force-time analogy, σ_t is the stress, ε_t is the strain (deformation), D₀ is the initial compliance, D_∞ is the ultimate equilibrium compliance, and t is the time.

Let us approximate compliance D_σt by the normalized function φ_σt [3]; D_σt = D₀ + (D_∞ − D₀)φ_σt, which we will put as

$$ {\upvarphi}_{\upsigma t}=\frac{1}{2}+\frac{1}{\uppi}\mathrm{arctg}\left({W}_{\upsigma t}\right)=\upvarphi \left({W}_{\upsigma t}\right) $$

(2)

Where

$$ {W}_{\upsigma t}=\frac{1}{b_{p\upsigma}}\ln \frac{t}{\uptau_{\upsigma}}=\frac{1}{b_{p\upsigma}}\left[\ln \left(\frac{t}{t_1}\right)+\ln \left(\frac{t_1}{\uptau_{\upvarepsilon}}\right)\right] $$

(3)

is the structural-force-time argument-functional, t₁ is the fixed base time, τ_σ is the delay time, and b_pσ is the structure coefficient.

The normalized logarithmic creep kernel has the form [4]

$$ {\overline{r}}_{\upsigma t}=\frac{\partial {\upvarphi}_{\upsigma t}}{\partial \ln t}=\frac{1}{b_{p\upsigma}}\cdot \frac{1}{\uppi}\cdot \frac{1}{1+{W}_{\upsigma t}^2} $$

(4)

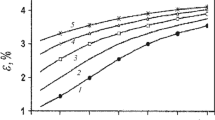
Let us analyze the method of processing of the “family” of creep curves (Fig. 1) using the example of cloak fabric used in impact-protective helmets with a breaking deformation value of 45%.

Fig. 1.

Experimental family of creep curves for cloak fabric at various magnitudes of forces (P, g): 1 − 500, 2 − 750, 3 − 1000, 4 − 1250, 5 − 1500.

Instead of the stress σ = const, let us consider the force magnitudes P = σF, where F = const is the area of the fabric sample cross-section calculated with due regard for the density of interweaving of yarns [5].

The kernel r_σt attains its extreme value ${\overline{r}}_{\upsigma t}=\left(1/{b}_{n\upsigma}\right)\cdot \left(1/\uppi \right)$ at t = τ_σ, which corresponds to W_τ = 0, φ_τ = 0.5, D_τ = 0.5(D₀ + D_∞).

This fact enables us to determine the creep process intensity parameter [6]

$$ \frac{1}{b_{p\upsigma}}=\frac{\uppi}{2}\cdot \frac{D_{\uptau}^{\prime }}{\Delta {D}_{\uptau}} $$

(5)

the force-time function [7]

$$ {f}_{\upsigma}=\ln \left(\frac{t_1}{\uptau_{\upsigma}}\right)={b}_{p\upsigma}\cdot {W}_{\upsigma {t}_1} $$

(6)

and the asymptotic values of D₀ and D_∞.

In our case, the calculated value of the creep process intensity was 1/b_pσ = 0.216 and the asymptotic compliance values were D₀/F = 37.531/kg and D_∞/F = 20.469/kg. The curve of force-time function [7] is shown in Fig. 2.

Fig. 2.

Force-time function f_σ of cloak fabric.

Thus, by calculating the creep parameter using the described method we can predict the desired deformation conditions on the basis of integral equation (1) [8].

The process of deformation of cloak fabric with a constant deformation rate ε = 0.00083/sec is illustrated in Fig. 3, where experimental and calculated tensile-test diagrams are shown. As evident from their comparison, the extension process is calculated with a relative error of not more than 10 %, which is technically admissible [9].