Distribution of Two-Dimensional Unsteady Sediment Concentration in an Open Channel Flow

Abstract

An unsteady two-dimensional transport equation is considered to investigate the distribution of suspended sediment in an open channel turbulent flow, where the mechanism of hindered settling is also taken into account. Due to the consideration of concentration-dependent settling velocity on sediment transportation, the transport equation is a partial differential equation with a highly nonlinear term, which has been solved numerically by using the alternating direction implicit (ADI) finite-difference method. It is found that the sediment concentration increases along the vertical direction due to the inclusion of hindered settling effect.

1 Introduction

In an open channel turbulent flow, the study of sediment transport is a challenging task due to the irregular behavior of the turbulence. Sediment transport is mainly classified into two categories: suspended sediment transport and bed-load transport. The transportation of non-equilibrium suspended sediment is one of the important problems in the area of sediment transport.

Hjelmfelt and Lenau [1], Liu and Nayamatullah [2], Liu [3] and Jing et. al. [4] worked on the transportation of non-equilibrium suspended sediments. Hjelmfelt and Lenau [1] and Liu [3] studied the steady two-dimensional suspended sediment transport problem, and Liu and Nayamatullah [2] solved the one-dimensional unsteady non-equilibrium suspended sediment transport problem by GITT technique. The problems of non-equilibrium sediment transport are generally governed by partial differential equations. It is observed by researchers that in high concentrated flows, the settling velocity of the suspended sediment particles decreases in comparison with that in clear fluid. This physical phenomenon is commonly known as the hindered settling effect. Inclusion of this phenomenon makes the governing equation nonlinear in nature, and hence, the problem becomes more challenging.

In this model, we consider the unsteady two-dimensional non-equilibrium transport problem considering the hindered settling effect and solve the problem by alternating direction implicit (ADI) finite-difference scheme. The obtained results are discussed with figures and based on that important conclusions are drawn.

2 Mathematical Modeling

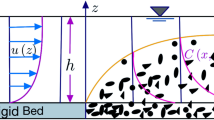
We consider an unsteady two-dimensional transport equation to describe the distribution of suspended sediment in an open channel (separation width h) turbulent flow. The flow in the axial (stream-wise) and vertical directions is represented by a Cartesian coordinate system, say, x and y. We assume that the flow is uniform in the axial direction and also independent of time; thus, the velocity varies only in the vertical direction. In the following subsections, the problem has been mathematically formulated.

2.1 Governing Equation

The governing equation for the unsteady two-dimensional suspended sediment concentration distribution in a wide open channel flow is given as follows:

$$\begin{aligned} \frac{\partial c}{\partial t}+u\frac{\partial c}{\partial x}-\frac{\partial }{\partial y}\big (\omega _{\text {s}}c\big )=\frac{\partial }{\partial y}\Big (\epsilon _{\text {s}}\frac{\partial c}{\partial y}\Big ), \end{aligned}$$

(1)

where c is the volumetric sediment concentration, t denotes time. u is the flow velocity in stream-wise direction, $\epsilon _{\text {s}}$ is the sediment diffusivity in the vertical direction, and $\omega _{\text {s}}$ is the settling velocity of the sediment particles which is treated as a function of concentration c. In high concentrated flow, the magnitude of $\omega _{\text {s}}$ is less than that of $\omega _{0}$ and the relationship between them is provided by Richarson and Zaki [5] as

$$\begin{aligned} \omega _{\text {s}}=\omega _{0}(1-c)^{{n_{\text {H}}}}, \end{aligned}$$

(2)

where $\omega _{0}$ is the settling velocity of the particles in clear fluid and $n_{\text {H}}$ is the exponent of reduction whose value depends on the particle Reynolds number. In the present work, taking the average value of $n_{\text {H}}$ as 4, the governing equation (1) becomes:

$$\begin{aligned} \frac{\partial c}{\partial t}+u\frac{\partial c}{\partial x}-\omega _{0}\frac{\partial }{\partial y}\Big [c(1-c)^{4}\Big ]=\frac{\partial }{\partial y}\Big (\epsilon _{\text {s}}\frac{\partial c}{\partial y}\Big ). \end{aligned}$$

(3)

2.2 Initial and Boundary Conditions

The boundary conditions at top and bottom surface are considered according to Hjelmfelt and Leanu [1] as follows

$$\begin{aligned} c=0 ~ ~\text{ at }~~ y=h, \end{aligned}$$

(4)

and

$$\begin{aligned} c=c_{a} ~ ~\text{ at }~~ y=a, \end{aligned}$$

(5)

respectively, where $c_{a}$ is the reference concentration at the reference level $y=a$. At the inlet, we consider that there is uniform sediment concentration, i.e.,

$$\begin{aligned} c=1 ~ ~\text{ at }~~ x=0, \end{aligned}$$

(6)

and at initial time

$$\begin{aligned} c=1 ~ ~\text{ at }~~ t=0. \end{aligned}$$

(7)

2.3 Dimensionless Form of Governing Equation Together with Initial and Boundary Conditions

The governing equation (3) and the boundary conditions (4–7) are non-dimensionalized as per the following scales:

$$\begin{aligned} C=\frac{c}{c_{a}}, ~~~ ~~~ Y=\frac{y}{h},~~~ X=\frac{x}{h}, ~~~ T=\frac{tu_{*}}{h}, \end{aligned}$$

$$\begin{aligned} A=\frac{a}{h} ,~~~ K(Y)=\frac{\epsilon _{t}}{\beta u_{*}h} , ~~~ U(Y)=\frac{u}{u_{*}} ,~~~ V_{0}=\frac{\omega _{0}}{u_{*}}, \end{aligned}$$

where $u_{*}$ is the shear velocity and $\beta$ is the ratio of turbulent diffusivity $\epsilon {_t}$ to sediment diffusivity $\epsilon _{\text {s}}$. Accordingly, the dimensionless form of Eq. (3) and boundary conditions (4–7) becomes:

$$\begin{aligned} \frac{\partial C}{\partial T}+U(Y)\frac{\partial C}{\partial X}-V_{0}\frac{\partial }{\partial Y}\big [C(1-c_{a}C)^{4}\big ]=\frac{\partial }{\partial Y}\Big (K(Y)\frac{\partial C}{\partial Y}\Big ), \end{aligned}$$

(8)

$$\begin{aligned} C(T,X,Y)=0 ~ ~\text{ at }~~ Y=1, \end{aligned}$$

(9)

$$\begin{aligned} C(T,X,Y)=1 ~ ~\text{ at }~~ Y=A, \end{aligned}$$

(10)

$$\begin{aligned} C(T,X=0,Y)=1, \end{aligned}$$

(11)

and

$$\begin{aligned} C(T=0,X,Y)=1, \end{aligned}$$

(12)

So, finally, we have a PDE with nonlinear term $(1-c_a C)^4$ given by Eq. (8) together with the boundary conditions (Eqs. 9 and 10) and the initial conditions (Eqs. 11 and 12) which we will solve numerically.

3 Numerical Solution

In the present problem, the concentration distribution of suspended sediment in an open channel flow is described by the two-dimensional unsteady convection-diffusion Eq. (8). Due to the complexity in Eq. (8), we have adopted an alternating direction implicit (ADI) finite-difference scheme [6] to solve Eq. (8) together with initial and boundary conditions (9)–(12). In ADI method, the finite-difference equation can be factored into a multistage process to step ahead one-time increment in such a way that the solution of the nonlinear equations emerging at each time level is very easy to handle computationally.

The whole width of the channel is divided into ($M-1$) equal parts, having length $\Delta X$ in the axial direction and $\Delta Y$ in the vertical direction. The time increment is denoted by $\Delta T$. The lengths in the vertical and axial directions are represented by the grid point j and k, whereas time is represented by the grid point i. So the general formulae are: $Y_j=A+(j-1)^* \Delta Y$, $X_k= (k-1)\times \Delta X$ and $T_i= (i-1)\times \Delta T$, respectively.

Utilizing Douglas–Rachford [7] procedure on the convection diffusion equation (8), the finite difference equation splits into two implicit equations, as

$$\begin{aligned}&\left[ 1- \Delta T \left\{ \frac{\partial K}{\partial Y}+V_0 (c_a C(i,j)-1)^3 (5c_a C(i,j)-1) \right\} S_{Y}-K \Delta T S_{YY} \right] C^*(i+1)\nonumber \\&\quad =(1- U(Y) \Delta T S_{X})C(i), \end{aligned}$$

(13a)

$$\begin{aligned} (1+ U(Y) \Delta T S_{X})C(i+1)=C^*(i+1,j)+U(Y) \Delta T S_{X} C(i), \end{aligned}$$

(13b)

where $S_{Y}C^*= \frac{C^*(j+1,k)-C^*(j-1,k)}{2\Delta Y}, \;S_{YY}C^*= \frac{C^*(j+1,k)-2C^*(j,k)+C^*(j-1,k)}{\Delta Y^2}$ and $S_{X}C= \frac{C(j,k+1)-C(j,k-1)}{2\Delta X}$ are the discretized operators.

Clearly, the process needs two steps: In the first step, we solve $C^*$ from Eq. (13a), and in the next step, we solve C from Eq. (13b) by using the values of $C^*$. To find the solution, we have considered a mesh size: $\Delta T =0.00001$, $\Delta Y=(1-A)/(M-1)$ and $\Delta X=1/(M-1)$ for the present problem, where $M = 500$. Different cases have been considered to investigate the hindered settling effect on the distribution of sediment concentration. In all the cases, we have assumed fixed value of $V_0=0.2$, $Y_0=0.001$, and $A=0.05$, respectively. The considered spatial and temporal discretization parameters ensure a precision of $10^{-6}$ in the results.

4 Results and Discussion

4.1 Input Functions

It is clear from Eq. (8) that to assess the solution, known expression for the functions K(Y) and U(Y) are needed. So, in the present problem we consider the following expressions (Liu [3]):

$$\begin{aligned} K(Y)=\kappa Y(1-Y), \end{aligned}$$

(14)

and

$$\begin{aligned} U(Y)=\frac{1-Y_{0}}{Y_{0}-\ln Y_{0}-1}\ln {\frac{Y}{Y_{0}}}~~\text{ for }~~Y_{0}\le Y\le 1, \end{aligned}$$

(15)

where $\kappa$ is the universal von Karman constant $(=0.41)$ and $Y_{0}=0.001$.

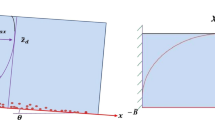
4.2 Validation of the Solution

In this section, we validate our obtained solution with the existing models. In Fig. 1a, the concentration profile is the same as the well-known Rouse profile [8], who found the analytical solution for steady transport equation and Fig. 1b agrees with the work of Liu [3] for two-dimensional steady non-equilibrium sediment transport. It is clear from the figure that as one tends toward the surface of the channel from the bottom, concentration profiles decrease and tend to zero which is usual characteristics of sediment concentration profile. It happens because at the surface suspended sediment particles are negligible.

Fig. 1

Vertical distribution of sediment concentration when $c_a=0.02$, $V_0=0.2$, $Y_0=0.001$ and $A=0.05$. a For $T \rightarrow \infty$, $X \rightarrow \infty$; b for $T \rightarrow \infty$, $X=2$

Fig. 2

Concentration contours at time $T=5$ (1st row) and $T=10$ (2nd row), when $V_0=0.2$, $Y_0=0.001$ and $A=0.05$. a, c For $c_a=0.005$; b, d for $c_a=0.02$

4.3 Contour Plot of Concentration Profiles

Figure 2 shows the variation of suspended sediment concentration in the stream-wise and vertical directions simultaneously. Figures 2a, b is plotted at a fixed time $T=5$ with different reference concentration and Figs. 2c, d is plotted for the same but at a fixed time $T=10$. From Figs. 2a, b it is clear that the area of concentration distribution is higher in Fig. 2b than Fig. 2a because of higher value of reference concentration. A similar kind of behavior can be seen in Fig. 2c, d for large time $T=10$.

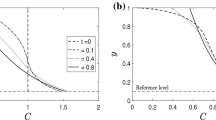
4.4 Impact of Hindered Settling Mechanism on Concentration Profile

The effect of hindered settling mechanism is shown in Fig. 3 where the vertical distribution of sediment concentration is plotted at different time. In Fig. 3a, b, reference concentration is taken as $c_{a}=0.005$ and $c_{a}=0.02$, respectively, and it can be seen from the figures that the effect is more in Fig. 3b comparison with Fig. 3a. It happens because the hindered settling effect is more effective in high concentrated flow due to the presence of surrounding particles.

Fig. 3

Vertical distribution of sediment concentration under the effect of settling velocity of particles, when $V_0=0.2$, $Y_0=0.001$, $A=0.05$ and $X=3$. a For $c_a=0.005$, $n_{\text {H}}=0$ (solid line), $n_{\text {H}}=4$ (dashed line); b For $c_a=0.02$, $n_{\text {H}}=0$ (solid line), $n_{\text {H}}=4$ (dashed line)

5 Conclusions

Distribution of suspended sediment is studied in the present work for an unsteady two-dimensional turbulent flow through an open channel. The presence of sediment affect the settling velocity of a particle which is commonly known as the hindered settling effect, and accordingly, the concentration profile is also changed. This phenomenon is taken into account in the governing partial differential equation, and ADI method is adopted to solve the equation numerically. At large time and far from the downstream, the concentration shows similarity with Rouse [8] profile of concentration. Contour plots of concentration at different times are plotted to see the variation of concentration along vertical and axial direction. Also that, at a fixed time and axial direction, concentration is plotted with and without hindered settling effect and it is found that higher the concentration, more is the change in concentration due to inclusion of hindered settling effect.