1 Introduction

Since Russell observed the solitary wave in 1834, it has attracted the attention of researchers from many different areas, such as fluid mechanics, coastal engineering, applied mathematics, quantum mechanics, solid mechanics and the study of sand dunes [1,2,3,4,5,6,7,8]. Because of the importance of the solitary wave, there have been many mathematical models developed for it, such as the Boussinesq equation, the KdV equation and the Green Naghdi equation [3, 9,10,11,12,13]. However, most existing mathematical models developed for the shallow water solitary wave are based on the Eulerian method. Solving the Eulerian equation can usually yield the flow field. But it is very difficult to calculate the particle motion in terms of the flow field, because the relation between these two variables is quite complex. Even for the line periodic gravity water wave with a line periodic flow field, there are no closed particle orbits [14, 15]. It has also been proved that there are no closed particle paths in Stokes waves with moderate and large amplitude [16, 17]. Hence, it is inconvenient for the Eulerian equation to copy with the problems with moving boundaries, such as the free surface and moving coastline.

It is known that an alternative approach for the fluid is the Lagrangian method, which describe the fluid motion by tracing particle trajectories. Compared with the Eulerian method, the Lagrangian method is more appropriate for the problems with moving boundaries [18, 19]. From the Lagrangian perspective, the water is seen as a dynamical system with infinite moving particles. The kinetic and potential energies of this system can be formulated easily. If the water is inviscid, it is quite natural using the Hamilton variational principle in the analytical mechanics to derive the Lagrangian water equation [20]. Actually, the Hamilton variational principle can provide a unifying framework for formulating the governing equations [21,22,23,24] or numerical schemes [25,26,27,28,29] of different water problems. In Ref. [21], Zhong and Yao firstly applied the Lagrangian method to address the shallow water solitary wave. They used the horizontal displacement to describe the evolution of water wave and assumed that the horizontal displacement is independent of the vertical coordinate, which is a displacement version of shallow water approximation. By using the Hamilton variational principle, they derived the follow displacement shallow water equation (DSWE)

$$\ddot{u} - \frac{{h^{2} }}{3}\ddot{u}_{xx} - gh\left( {u_{xx} - 3u_{x} u_{xx} } \right) = 0,$$
(1)

where \(u\left( {x,t} \right)\) is the horizontal displacement of the water particle, \(g\) is the gravity acceleration, and \(h\) is the water depth. Subsequently, Liu and Lou extended Zhong’s DSWE to the two-dimensional solitary wave problem in Ref. [22], where a (2 + 1)-dimensional displacement shallow water wave equation (2DDSWWE) was developed. In Refs. [30, 31], the 2DDSWWE was modified by adding the effect of the fluid viscidity. The two-dimensional displacement solitary wave solutions were discussed in Refs. [22, 23]. Some numerical algorithms for the DSWE were proposed in Refs. [25,26,27], and it is found that the DSWE performs excellent with respect to the simulation for shallow water with the sloping water bottom and wet–dry interface.

It should be noted that in all the motioned works about the DSWE, the vertical displacement is expressed as a Taylor series, and only the first three terms are retained. If more higher nonlinear terms are considered in the DSWE, more accurate solutions will be obtained. Hence it is worth improving the DSWE by keeping more higher nonlinear terms, which will be addressed in Sect. 2. Two improved displacement shallow water equations are developed. In Sect. 3, the solitary wave solutions of the proposed equations are given by using the gauge transformation and the exp-function method. Finally, some conclusions are presented.

2 Displacement shallow water equation

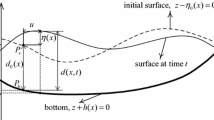
In this section, we formulate the governing equations for the shallow water gravity waves. The water is assumed to be an incompressible and inviscid fluid of constant density which is boxed in a rectangular box, shown by Fig. 1 and posses a free surfaces. The bottom plane is defined by \(z = - h\). The surface-energy effects are negligible.

Fig. 1
figure 1

Shallow water system

Full size image

Let \(\left( {x,z} \right)\) represents the location of certain particle in water at initial time \(t_{0}\), and \(\left( {X,\;Z} \right)\) the location of this particle at time \(t\). Let \(u \equiv u\left( {x,z,t} \right)\) and \(w \equiv w\left( {x,z,t} \right)\) represent water displacements in \(x\) and \(z\) directions, respectively. Obviously, we have

$$\begin{aligned} X\left( {x,z,t} \right) = x + u\left( {x,z,t} \right), \hfill \\ Z\left( {x,z,t} \right) = z + w\left( {x,z,t} \right). \hfill \\ \end{aligned}$$
(2)

Based on the continuum mechanics [32], the continuity equation for the incompressible water is

$$J = \left| {\begin{array}{*{20}c} {\frac{\partial X}{\partial x}} & {\frac{\partial X}{\partial z}} \\ {\frac{\partial Z}{\partial x}} & {\frac{\partial Z}{\partial z}} \\ \end{array} } \right| = \left( {1 + u_{x} } \right)\left( {1 + w_{z} } \right) - u_{z} w_{x} = 1.$$
(3)

The kinetic energy of the water system, denoted by \(T\), reads

$$T = \int_{ - L}^{L} {\int_{ - h}^{0} {\frac{1}{2}\rho u_{t}^{2} } } {\text{d}}x{\text{d}}z + \int_{ - L}^{L} {\int_{ - h}^{0} {\frac{1}{2}\rho w_{t}^{2} } } {\text{d}}x{\text{d}}z,$$
(4)

where \(\rho\) is the mass density, \(u_{t}\) and \(w_{t}\) are the horizontal and vertical velocities, respectively.

The potential energy of the water system, denoted by \(U\), reads

$$U = \int_{ - L}^{L} {\int_{ - h}^{0} {\rho g\left( {z + w} \right)} } {\text{d}}z{\text{d}}x.$$
(5)

According to the displacement shallow water approximation [21], i.e., the horizontal displacements is assumed to be independent of the vertical coordinate \(z\), we have \(u_{z} = 0\). So Eq. (3) can be rewritten as

$$w_{z} = \frac{{ - u_{x} }}{{1 + u_{x} }},$$
(6)

which shows that the vertical displacement distributes linearly along the vertical coordinate \(z\). Integrating Eq. (6) with respect to \(z\) and noting that the vertical displacement at the water bottom \(z = - h\) is zero, i.e., \(w\left( {x, - h,t} \right) = 0\), we obtain

$$w\left( {x,z,t} \right) = - \frac{{u_{x} \left( {z + h} \right)}}{{1 + u_{x} }}.$$
(7)

In terms of Eq. (7), the vertical velocity is

$$w_{t} = - \left( {z + h} \right)\frac{{u_{xt} }}{{\left( {1 + u_{x} } \right)^{2} }},$$
(8)

The free water surface profile can be expressed by using the positions of the particles on the water surface, i.e., \(\left( {x + u\left( {x,0,t} \right),\;\;\eta \left( {x,\;t} \right)} \right)\), where

$$\eta \left( {x,t} \right) = w\left( {x,0,t} \right) = - \frac{{u_{x} h}}{{1 + u_{x} }}.$$
(9)

Combing Eqs. (7) with (9) yields

$$w\left( {x,z,t} \right) = \eta \left( {x,t} \right)\left( {\frac{z + h}{h}} \right).$$
(10)

Substituting Eqs. (8) and (10) into Eqs. (4) and (5), respectively, yields

$$T = \int_{ - L}^{L} {\frac{1}{2}\rho hu_{t}^{2} } {\text{d}}x + \int_{ - L}^{L} {\frac{{h^{3} }}{6}\rho \left[ {\frac{{u_{xt} }}{{\left( {1 + u_{x} } \right)^{2} }}} \right]^{2} } {\text{d}}x$$
(11)

and

$$U = \int_{ - L}^{L} {\frac{h}{2}\rho g\eta } {\text{d}}x + C,\;\;\;C = \int_{ - L}^{L} {\int_{ - h}^{0} {\rho gz} } {\text{d}}z{\text{d}}x.$$
(12)

The action integral of the water system reads

$$S = \int_{{t_{0} }}^{t} {\left( {T - U} \right)} {\text{d}}s.$$
(13)

where \(s\) is a variable of integration in the inteval \(\left[ {t_{0} ,\;t} \right]\). Substituting Eqs. (11) and (12) into the action integral (13) and using the Hamilton variational principle, we have

$$\ddot{u} - \frac{{h^{2} }}{3}\left( {\frac{{u_{xxtt} }}{{\left( {1 + u_{x} } \right)^{4} }} - \frac{{4u_{xx} u_{xtt} + 4u_{xt} u_{xxt} }}{{\left( {1 + u_{x} } \right)^{5} }} + \frac{{10u_{xx} u_{xt}^{2} }}{{\left( {1 + u_{x} } \right)^{6} }}} \right) - gh\frac{{u_{xx} }}{{\left( {1 + u_{x} } \right)^{3} }} = 0.$$
(14)

Equation (14) is called the fully nonlinear DSWE (FNDSWE), because there is no approximation for it, except the shallow water approximation. Once the horizontal displacement \(u\) is obtained by solving Eq. (14), the vertical displacement can be obtained with the aid of Eq. (7).

It is clear that the FNDSWE (14) is much more complex than the DSWE (1). Noting that the vertical velocity is much smaller than the horizontal velocity for the shallow water wave problem [21, 25, 33], the vertical velocity can be approximated as

$$w_{t} = - \left( {z + h} \right)u_{xt} .$$
(15)

Substituting Eq. (15) into Eq. (4) yields the following approximated kinetic energy

$$T \approx T_{\text{Zhong}} = \int_{ - L}^{L} {\frac{1}{2}\rho hu_{t}^{2} } {\text{d}}x + \int_{ - L}^{L} {\frac{{h^{3} }}{6}\rho u_{xt}^{2} } {\text{d}}x.$$
(16)

The vertical displacement (7) can be represented as a Taylor series in \(u_{x}\). Keeping only the first three terms, Eq. (9) is approximated as

$$\eta \left( {x,t} \right) \approx \eta_{\text{Zhong}} = - u_{x} h\left( {1 - u_{x} + u_{x}^{2} } \right).$$
(17)

Substituting Eq. (17) into Eq. (12), the potential energy is approximated as

$$\begin{aligned} U \approx U_{\text{Zhong}} &= \int_{ - L}^{L} {\frac{h}{2}\rho g\eta_{\text{Zhong}} } {\text{d}}x + C \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; & = - \int_{ - L}^{L} {\frac{{h^{2} }}{2}\rho gu_{x} } {\text{d}}x + \int_{ - L}^{L} {\frac{{h^{2} }}{2}\rho g\left( {u_{x}^{2} - u_{x}^{3} } \right)} {\text{d}}x + C \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;& = \int_{ - L}^{L} {\frac{{h^{2} }}{2}\rho g\left( {u_{x}^{2} - u_{x}^{3} } \right)} {\text{d}}x + C, \hfill \\ \end{aligned}$$
(18)

in which the boundary condition \(u\left( { - L,t} \right) = u\left( {L,t} \right) = 0\) is used. Expressions (16) and (18) were firstly presented by Zhong, et al. [21]. Substituting Eqs. (16) and (18) into the action integral Eq. (13) and using the Hamilton variational principle yields the DSWE (1). It is obvious that DSWE (1) is based on the approximation (17), which keeps only the first three terms. If we keep the first four terms, i.e.,

$$\eta \left( {x,t} \right) \approx \eta_{\text{e}} = - u_{x} h\left( {1 - u_{x} + u_{x}^{2} - u_{x}^{3} } \right),$$
(19)

the potential energy can be approximated as

$$U \approx U_{\text{e}} = \int_{ - L}^{L} {\frac{{h^{2} }}{2}\rho g\left( {u_{x}^{2} - u_{x}^{3} + u_{x}^{4} } \right)} {\text{d}}x + C.$$
(20)

Substituting Eq. (16) and (20) into the action integral Eq. (13) and using the Hamilton variational principle yields

$$\ddot{u} - \frac{{h^{2} }}{3}\ddot{u}_{xx} - ghu_{xx} \left( {1 - 3u_{x} + 6u_{x}^{2} } \right) = 0,$$
(21)

which contains a higher nonlinear term, \(6u_{x}^{2} u_{xx}\), compared with the DSWE (1), and is called the extended DSWE (EDSWE).

In the next section, the exact solitary wave solutions of the EDSWE and FNDSWE are derived by using different methods.

3 The solitary wave solutions

3.1 The solitary wave solution of EDSWE

We firstly look for the solitary wave solution of the EDSWE (21) by using the gauge transformation:

$$u\left( {x,t} \right) = u\left( \xi \right),\;\;\;\xi = x - ct,$$
(22)

where \(c\) is the velocity of the solitary wave. Substituting Eq. (22) into Eq. (21) yields a nonlinear ordinary differential equation

$$c^{2} u^{\prime\prime} - c^{2} \frac{{h^{2} }}{3}u'''' - gh\left[ {u^{\prime\prime} - 3u^{\prime}u^{\prime\prime} + 6\left( {u^{\prime}} \right)^{2} u^{\prime\prime}} \right] = 0,$$
(23)

where

$$u^{\prime} = \frac{{{\text{d}}u\left( \xi \right)}}{{{\text{d}}\xi }},\;\;u^{\prime\prime} = \frac{{{\text{d}}^{2} u\left( \xi \right)}}{{{\text{d}}\xi^{2} }},\;\;\;u'''' = \frac{{{\text{d}}^{4} u\left( \xi \right)}}{{{\text{d}}\xi^{4} }}.$$
(24)

Integrating Eq. (23) once over \(\xi\) and letting the integration constant to be zero, we can obtain

$$c^{2} u^{\prime} - c^{2} \frac{{h^{2} }}{3}u^{\prime\prime\prime} - gh\left[ {u^{\prime} - \frac{3}{2}\left( {u^{\prime}} \right)^{2} + 2\left( {u^{\prime}} \right)^{3} } \right] = 0.$$
(25)

Setting

$$f = \frac{{{\text{d}}u\left( \xi \right)}}{{{\text{d}}\xi }},$$
(26)

Equation (25) can be rewritten as

$$c^{2} f - c^{2} \frac{{h^{2} }}{3}f^{\prime\prime} - gh\left[ {f - \frac{3}{2}f^{2} + \frac{6}{3}f^{3} } \right] = 0.$$
(27)

Next, we use the exp-function method [34] to solve Eq. (27). The exp-function method is based on the assumption that the solution can be expressed in the following form:

$$f = \frac{{a_{c} { \exp }\left( {ek\xi } \right) + \cdots + a_{ - d} { \exp }\left( { - dk\xi } \right)}}{{a_{p} { \exp }\left( {pk\xi } \right) + \cdots + a_{ - q} { \exp }\left( { - qk\xi } \right)}},$$
(28)

where \(e\), \(d\), \(p\) and \(q\) are positive integers which are unknown to be further determined, \(a_{n}\) and \(k\) are unknown constants.

By simple calculation, we have

$$f^{3} = \frac{{b_{3} { \exp }\left( {3ek\xi } \right) + \cdots + b_{4} { \exp }\left( { - 3dk\xi } \right)}}{{b_{1} { \exp }\left( {3pk\xi } \right) + \cdots + b_{2} { \exp }\left( { - 3qk\xi } \right)}}$$
(29)

and

$$f^{\prime\prime} = \frac{{d_{3} { \exp }\left( {\left( {e + 2p} \right)k\xi } \right) + \cdots + d_{4} { \exp }\left( { - \left( {d + 2q} \right)k\xi } \right)}}{{d_{1} { \exp }\left( {3pk\xi } \right) + \cdots + d_{2} { \exp }\left( { - 3qk\xi } \right)}},$$
(30)

where \(b_{i}\) and \(d_{i}\) are unknown constants. By balancing the highest order term in Eq. (29) with the highest order term in Eq. (30), we have \(2e + p = e + 2p\), i.e., \(p = e\). Balancing the lowest order term in Eq. (29) with the lowest order term in Eq. (30) yields \(d = q\).

For simplicity, we set \(p = e = 1\) and \(q = d = 1\), so Eq. (28) reduces to

$$f = \frac{{a_{0} { \exp }\left( {k\xi } \right) + a_{1} + a_{2} { \exp }\left( { - k\xi } \right)}}{{b_{0} { \exp }\left( {k\xi } \right) + b_{1} + b_{2} { \exp }\left( { - k\xi } \right)}}.$$
(31)

Substituting Eq. (31) into Eq. (27) and equating the coefficients of \({ \exp }\left( {nk\xi } \right)\) to be zeros, we have

$$a_{0} = a_{2} = 0,\;\;k^{2} = \frac{{3\left( {\alpha - 1} \right)}}{{\alpha h^{2} }},\;\;a_{1} = - 2b_{1} \left( {\alpha - 1} \right),\;\;\;b_{1} = \pm \frac{{2\,\sqrt {b_{0} b_{2} \,\left( {4\alpha - 3} \right)} }}{3\, - 4\,\alpha },$$
(32)

where \(\alpha = {{c^{2} } \mathord{\left/ {\vphantom {{c^{2} } {gh}}} \right. \kern-0pt} {gh}}\). Combining Eqs. (19) with (31) yields

$$\eta \left( {x,t} \right) = - fh\left( {1 - f + f^{2} - f^{3} } \right).$$
(33)

Once \(\eta\) is obtained, the vertical displacement can be given by substituting Eq. (33) into Eq. (10). According to Eq. (26), the horizontal displacement \(u\left( \xi \right)\) can be written as

$$u\left( \xi \right) = u_{0} + \int_{0}^{\xi } {f\left( x \right)} {\text{d}}x = u_{0} + \frac{{2a_{1} {\text{atan}}\left( {\frac{{b_{1} + 2b_{0} e^{k\xi } }}{{\sqrt {4b_{0} b_{2} - b_{1}^{2} } }}} \right)}}{{k\sqrt {4b_{0} b_{2} - b_{1}^{2} } }} - \frac{{2a_{1} {\text{atan}}\left( {\frac{{b_{1} + 2b_{0} }}{{\sqrt {4b_{0} b_{2} - b_{1}^{2} } }}} \right)}}{{k\sqrt {4b_{0} b_{2} - b_{1}^{2} } }},$$
(34)

where \(u_{0} = u\left( 0 \right)\).

The free water surface profile can be expressed by using the positions of the particles on the water surface, i.e., \(\left( {X\left( {x,\;0,\;t} \right),\;\;Z\left( {x,\;0,\;t} \right)} \right)\), in which

$$X\left( {x,\;0,\;t} \right) = x + u\left( \xi \right),\;\;Z\left( {x,\;0,\;t} \right) = \eta \left( {\xi ,z} \right).$$
(35)

It can be seen from Eqs. (33)–(35) that the wave profile is dependent on the unknown constants \(b_{i}\) and \(\alpha\). The wave shape is not changed in the case that \(b_{0} = b_{2} \ge 0\), which means \(f^{\prime}\left( 0 \right) = 0\) and \(\eta^{\prime}\left( 0 \right) = 0\). Hence, \(b_{1}\) and \(\alpha\) are the key parameters which affect the wave shape. We will discuss different types of waves by using different values of \(b_{1}\) and \(\alpha\) as follow.

Case 1

We firstly set \(\alpha \ge 1\) and \(b_{1} > 0\), which means

$$a_{1} = \frac{{ - 4b_{0} \left( {\alpha - 1} \right)}}{{\sqrt {\,4\alpha - 3} }},\;\;\;b_{1} = \frac{{2b_{0} }}{{\sqrt {\,4\alpha - 3} }},\;\;\;k = \sqrt {\frac{{3\left( {\alpha - 1} \right)}}{{\alpha h^{2} }}} .$$
(36)

Substituting Eq. (36) into Eqs. (31) and (34) yields

$$f = \frac{{ - 2\left( {\alpha - 1} \right)}}{{\sqrt {\,4\alpha - 3} \cosh \left( {k\xi } \right) + 1}}$$
(37)

and

$$u\left( \xi \right) = u_{0} + \sqrt {\frac{{4\alpha h^{2} }}{3}} \left[ {{\text{atan}}\left( {\frac{{1 + \sqrt {4\alpha - 3} }}{{2\sqrt {\alpha - 1} }}} \right) - {\text{atan}}\left( {\frac{{1 + e^{k\xi } \sqrt {4\alpha - 3} }}{{2\sqrt {\alpha - 1} }}} \right)} \right],$$
(38)

which shows that the horizontal displacement is a kink solitary wave. Substituting Eq. (37) into Eq. (33) will give \(\eta\). In terms of Eqs. (10) and (33), the vertical displacement can be written as

$$w = - f\left( {1 - f + f^{2} - f^{3} } \right)\left( {z + h} \right).$$
(39)

Letting \(\eta \left( 0 \right) = \eta_{0}\) be the amplitude of the solitary wave, we have

$$e = - f_{0} \left( {1 - f_{0} + f_{0}^{2} - f_{0}^{3} } \right),\;\;\;e = {{\eta_{0} } \mathord{\left/ {\vphantom {{\eta_{0} } h}} \right. \kern-0pt} h},$$
(40)

and

$$f_{0} = f\left( 0 \right) = \frac{{ - 2\left( {\alpha - 1} \right)}}{{\sqrt {\,4\alpha - 3} + 1}}.$$
(41)

Solving Eq. (40) gives \(\alpha\). Once \(\alpha\) is obtained, the velocity of the solitary wave can be determined in terms of \(c = \sqrt {gh\alpha }\). It can be seen from Eq. (37) that \(f < 0\). Noting that \(- f = - {{{\text{d}}u} \mathord{\left/ {\vphantom {{{\text{d}}u} {{\text{d}}\xi }}} \right. \kern-0pt} {{\text{d}}\xi }} = {{u_{t} } \mathord{\left/ {\vphantom {{u_{t} } c}} \right. \kern-0pt} c}\) represents the ratio of the particle horizontal velocity to the solitary wave velocity, \(f < 0\) means all the particles move in the direction of wave propagation at a positive speed. This deduction is same as that provided by Constantin et al. in Ref. [35].

Moreover, it is worth noting in terms of Eqs. (36)–(41) that for case 1, the water wave have the following three different shapes, which is dependent on the parameter \(\alpha\).

Case 1.1

When \(\alpha < 3\), \(- f < 1\), which means the horizontal velocity of each particle is smaller than the solitary wave velocity. For this case, the water surface is a common solitary wave with peak form, as shown in Fig. 2a.

Fig. 2
figure 2

The profiles of the different solitary waves, \(h = 0.1\;{\text{m}}\), \(g = 10\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {{\text{s}}^{ 2} }}} \right. \kern-0pt} {{\text{s}}^{ 2} }}\)

Full size image

Case 1.2

When \(\alpha = 3\), \(- f\left( 0 \right) = 1\). For this case, the gradient of the water surface at \(\xi = 0\) is infinite, and there is a sharp peak on the solitary wave crest, as shown in Fig. 2b.

Case 1.3

When \(\alpha > 3\), there exist some particles with horizontal velocities larger than the solitary wave velocity. For this case, the water surface is a loop solitary wave, as shown in Fig. 2c.

Case 2

We next set \(\alpha \ge 1\) and \(b_{1} < 0\), which yields

$$a_{1} = \frac{{4b_{0} \left( {\alpha - 1} \right)}}{{\sqrt {\,4\alpha - 3} }},\;\;\;b_{1} = - \frac{{2b_{0} }}{{\sqrt {\,4\alpha - 3} }},$$
(42)
$$f = \frac{{2\left( {\alpha - 1} \right)}}{{\sqrt {\,4\alpha - 3} \cosh \left( {k\xi } \right) - 1}},$$
(43)

and

$$u\left( \xi \right) = u_{0} + \sqrt {\frac{{4\alpha h^{2} }}{3}} \left[ {{\text{atan}}\left( {\frac{{e^{k\xi } \sqrt {4\alpha - 3} - 1}}{{2\sqrt {\alpha - 1} }}} \right) - {\text{atan}}\left( {\frac{{\sqrt {4\alpha - 3} - 1}}{{2\sqrt {\alpha - 1} }}} \right)} \right].$$
(44)

In this case, substituting Eq. (43) into Eq. (33) could yield a type of solitary wave with more loops, as shown in Fig. 2d, e.

Case 3

At last, we set \(\frac{3}{4} < \alpha < 1\), which means that \(k = {\text{i}}K\) is an imaginary number and

$$K = \sqrt {\frac{{3\left( {1 - \alpha } \right)}}{{\alpha h^{2} }}} ,\;\;a_{1} = - \frac{{4b_{0} \left( {1 - \alpha } \right)}}{{\sqrt {4\alpha - 3} }},\;\;\;b_{1} = - \frac{{2b_{0} }}{{\sqrt {4\alpha - 3} }}.$$
(45)

Substituting Eq. (36) into Eq. (31) yields a periodic solution as follow

$$f = \frac{{ - 2\left( {1 - \alpha } \right)}}{{\sqrt {4\alpha - 3} \cos \left( {K\xi } \right) - 1}}.$$
(46)

Integrating Eq. (46) once over \(\xi\) yields the horizontal displacement as follow

$$u = \frac{{2{\text{atan}}\left( {{ \tan }\left( {\frac{K\xi }{2}} \right)\frac{{\sqrt {C + 2} }}{\sqrt C }} \right) - 2{\text{atan}}\left( {{ \tan }\left( {\frac{K\xi }{2}} \right)} \right) + K\xi }}{{\sqrt C K\sqrt {C + 2} }},\quad C = \frac{1}{{\sqrt {4\alpha - 3} }} - 1.$$
(47)

Figure 2f displays the periodic wave in the case of \(\alpha = 0.8\).

3.2 The solitary wave solution of FNDSWE

Similar on the previous section, we substitute the gauge transformation (22) into the FNDSWE (14) to obtain the following nonlinear ordinary differential equation

$$c^{2} u^{{\prime \prime }} - \frac{{h^{2} }}{3}c^{2} \left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}\xi^{2} }}\frac{{u^{{\prime \prime }} }}{{\left( {1 + u^{{\prime }} } \right)^{4} }} + \frac{\text{d}}{{{\text{d}}\xi }}\frac{{2\left( {u^{{\prime \prime }} } \right)^{2} }}{{\left( {1 + u^{{\prime }} } \right)^{5} }}} \right] + \frac{gh}{2}\frac{\text{d}}{{{\text{d}}\xi }}\frac{1}{{\left( {1 + u^{{\prime }} } \right)^{2} }} = 0.$$
(48)

Integrating Eq. (48) with respect to \(\xi\) yields

$$c^{2} u^{{\prime }} - \frac{{h^{2} }}{3}c^{2} \left[ {\frac{\text{d}}{{{\text{d}}\xi }}\frac{{u^{{\prime \prime }} }}{{\left( {1 + u^{{\prime }} } \right)^{4} }} + \frac{{2\left( {u^{{\prime \prime }} } \right)^{2} }}{{\left( {1 + u^{{\prime }} } \right)^{5} }}} \right] + \frac{gh}{2}\frac{1}{{\left( {1 + u^{{\prime }} } \right)^{2} }} = C_{1} ,$$
(49)

where \(C_{1}\) is unknown constant. Letting \(f = {{{\text{d}}u} \mathord{\left/ {\vphantom {{{\text{d}}u} {{\text{d}}\xi }}} \right. \kern-0pt} {{\text{d}}\xi }}\), Eq. (49) can be rewritten as

$$c^{2} f - \frac{{h^{2} }}{3}c^{2} \left[ {\frac{{f^{{\prime \prime }} }}{{\left( {1 + f} \right)^{4} }} - \frac{{2\left( {f^{{\prime }} } \right)^{2} }}{{\left( {1 + f} \right)^{5} }}} \right] + \frac{gh}{2}\frac{1}{{\left( {1 + f} \right)^{2} }} = C_{1} .$$
(50)

For the solitary wave solution, \(\mathop {\lim }\limits_{\xi \to \infty } f\left( \xi \right) = 0\), hence we have \(C_{1} = {{gh} \mathord{\left/ {\vphantom {{gh} 2}} \right. \kern-0pt} 2}\). Multiplying Eq. (50) by \(f^{{\prime }} = {{{\text{d}}f} \mathord{\left/ {\vphantom {{{\text{d}}f} {{\text{d}}\xi }}} \right. \kern-0pt} {{\text{d}}\xi }}\) yields

$$c^{2} \frac{1}{2}\frac{{{\text{d}}f^{2} }}{{{\text{d}}\xi }} - \frac{{h^{2} }}{6}c^{2} \frac{\text{d}}{{{\text{d}}\xi }}\frac{{\left( {f^{{\prime }} } \right)^{2} }}{{\left( {1 + f} \right)^{4} }} + \frac{gh}{2}\frac{\text{d}}{{{\text{d}}\xi }}\frac{f}{{\left( {1 + f} \right)}} = \frac{gh}{2}\frac{{{\text{d}}f}}{{{\text{d}}\xi }}.$$
(51)

Integrating Eq. (51) with respect to \(\xi\) and letting the integration constant be zero, we have

$$c^{2} f^{2} - \frac{{h^{2} }}{3}c^{2} \frac{{\left( {f^{{\prime }} } \right)^{2} }}{{\left( {1 + f} \right)^{4} }} + gh\frac{f}{{\left( {1 + f} \right)}} = ghf.$$
(52)

Substituting \(f = \frac{ - \eta }{h + \eta }\) into Eq. (52), we have

$$\left( {\eta^{\prime}} \right)^{2} = \frac{{3\eta^{2} \left( {c^{2} - gh - g\eta } \right)}}{{c^{2} \left( {h + \eta } \right)^{2} }}.$$
(53)

Letting \(\xi = 0\) and noting that \(\eta \left( 0 \right) = \eta_{0}\) and \(\eta^{\prime}\left( 0 \right) = 0\), the velocity of the solitary wave can be written as

$$c^{2} = g\left( {h + \eta_{0} } \right).$$
(54)

In case of \(\xi \ge 0\), Eq. (53) can be rewritten as

$$\eta^{{\prime }} = - \sqrt {\frac{{3\eta^{2} \left( {c^{2} - gh - g\eta } \right)}}{{c^{2} \left( {h + \eta } \right)^{2} }}} .$$
(55)

It is easily observed from Eq. (55) that

$$\begin{aligned} \xi & = \int_{\eta }^{{\eta_{0} }} {\frac{{c\left( {h + x} \right)}}{{x\sqrt {3\left( {c^{2} - gh - gx} \right)} }}} {\text{d}}x \\ & = \int_{\eta }^{{\eta_{0} }} {\frac{ch}{{x\sqrt {3\left( {c^{2} - gh - gx} \right)} }}} {\text{d}}x + \int_{\eta }^{{\eta_{0} }} {\frac{c}{{\sqrt {3\left( {c^{2} - gh - gx} \right)} }}} {\text{d}}x \\ & = \frac{c}{{\sqrt {3g} }}\left[ {2\sqrt {\eta_{0} - \eta } - \frac{h}{{\sqrt {\eta_{0} } }}\ln \left( {\frac{{\sqrt {\eta_{0} } - \sqrt {\eta_{0} - \eta } }}{{\sqrt {\eta_{0} } + \sqrt {\eta_{0} - \eta } }}} \right)} \right]. \\ \end{aligned}$$
(56)

For the case \(\xi < 0\), we have

$$\xi = \frac{c}{{\sqrt {3g} }}\left[ {\frac{h}{{\sqrt {\eta_{0} } }}\ln \left( {\frac{{\sqrt {\eta_{0} } - \sqrt {\eta_{0} - \eta } }}{{\sqrt {\eta_{0} } + \sqrt {\eta_{0} - \eta } }}} \right) - 2\sqrt {\eta_{0} - \eta } } \right].$$
(57)

Equation (57) describes the relation between \(\xi\) and \(\eta\). The horizontal displacement \(u\left( \xi \right)\) can be obtained by using

$$u\left( \xi \right) - u_{0} = \int_{0}^{\xi } {f\left( x \right)} {\text{d}}x = f\left( \xi \right)\xi - \int_{0}^{\xi } x {\text{d}}f\left( x \right),$$
(58)

in which \(\xi \ge 0\) and \(u_{0} = u\left( 0 \right)\). Using \(\eta = \frac{ - fh}{f + 1}\), Eq. (56) can be rewritten as

$$\xi = \frac{c}{{\sqrt {3g} }}\left[ {2\sqrt {\eta_{0} } \sqrt {\frac{fa + 1}{f + 1}} - \frac{h}{{\sqrt {\eta_{0} } }}\ln \left( {\frac{{\sqrt {f + 1} - \sqrt {fa + 1} }}{{\sqrt {f + 1} + \sqrt {fa + 1} }}} \right)} \right],\;\;\;a = \frac{{\eta_{0} + h}}{{\eta_{0} }}.$$
(59)

For \(\xi = 0\), \(f\left( 0 \right) = - a^{ - 1}\). Substituting Eq. (59) into Eq. (58) yields

$$u\left( \xi \right) - u_{0} = f\left( \xi \right)\xi - \int_{f\left( 0 \right)}^{f\left( \xi \right)} {\frac{c}{{\sqrt {3g} }}\left[ {2\sqrt {\eta_{0} } \sqrt {\frac{fa + 1}{f + 1}} - \frac{h}{{\sqrt {\eta_{0} } }}\ln \left( {\frac{{\sqrt {f + 1} - \sqrt {fa + 1} }}{{\sqrt {f + 1} + \sqrt {fa + 1} }}} \right)} \right]} {\text{d}}f.$$
(60)

With the aid of Maple, we obtain

$$\begin{aligned} & \int_{f\left( 0 \right)}^{f\left( \xi \right)} {\ln \left( {\frac{{\sqrt {f + 1} - \sqrt {fa + 1} }}{{\sqrt {f + 1} + \sqrt {fa + 1} }}} \right)} {\text{d}}f \\ & \quad = f\ln \left( {\frac{{\sqrt {f + 1} - \sqrt {fa + 1} }}{{\sqrt {f + 1} + \sqrt {fa + 1} }}} \right) - \frac{{\ln \left[ {2af + 2\sqrt a \sqrt {f + 1} \sqrt {af + 1} + a + 1} \right]}}{\sqrt a } + \frac{{\ln \left( {a - 1} \right)}}{\sqrt a }, \\ \end{aligned}$$
(61)

and

$$\int_{f\left( 0 \right)}^{f\left( \xi \right)} {\sqrt {\frac{fa + 1}{f + 1}} {\text{d}}f} = \frac{{\sqrt a \sqrt {f + 1} \sqrt {af + 1} - \left( {a - 1} \right)\ln \left( {a\sqrt {f + 1} + \sqrt a \sqrt {af + 1} } \right)}}{\sqrt a } + \frac{{\left( {a - 1} \right)\ln \left( {\sqrt a \sqrt {a - 1} } \right)}}{\sqrt a }.$$
(62)

Combining Eqs. (56), (61) and (62) with Eq. (60) yields

$$u\left( \xi \right) = u_{0} - \frac{{2\sqrt {\eta_{0} } c}}{{\sqrt {3g} }}\sqrt {\frac{af + 1}{f + 1}} = u_{0} - \frac{{2\sqrt {\eta_{0} } c}}{{\sqrt {3g} }}\sqrt {\frac{{\eta_{0} - \eta }}{{\eta_{0} }}} = u_{0} - \frac{2c}{{\sqrt {3g} }}\sqrt {\eta_{0} - \eta } ,$$
(63)

which gives the relation between the horizontal and vertical displacements.

It can be seen from Eqs. (56) and (63) that

$$\xi = - u\left( \xi \right) + u_{0} - \frac{c}{{\sqrt {3g} }}\frac{h}{{\sqrt {\eta_{0} } }}\ln \left( {\frac{{\sqrt {\eta_{0} } - \sqrt {\eta_{0} - \eta } }}{{\sqrt {\eta_{0} } + \sqrt {\eta_{0} - \eta } }}} \right),$$
(64)

which can also be rewritten as

$$\eta \left( \xi \right) = \eta_{0} {\text{sech}}^{2} \left( {\frac{{\sqrt {3g\eta_{0} } }}{2ch}\left( {\xi + u - u_{0} } \right)} \right).$$
(65)

Substituting Eq. (65) into Eq. (10) yields

$$w = \eta_{0} {\text{sech}}^{2} \left( {\frac{{\sqrt {3g\eta_{0} } }}{2ch}\left( {\xi + u - u_{0} } \right)} \right)\left( {\frac{z + h}{h}} \right).$$
(66)

Corollary

Under the assumption that the horizontal displacement is independent of the vertical coordinate\(z\), the particle trajectory is a parabolic curve.

Proof

For a particle localized initially at \(\left( {0,\;z} \right)\), the position of the particle at time \(t\) is \(\left( {X\left( {0,\;z,\;t} \right),\;\;Z\left( {0,\;z,\;t} \right)} \right)\), in which

$$X\left( {0,\;z,\;t} \right) = u\left( \xi \right),\;\;Z\left( {0,\;z,\;t} \right) = z + w\left( {\xi ,z} \right),\;\;\xi = - ct.$$
(67)

In terms of Eqs. (10) and (63), we have

$$Z\left( {0,z,t} \right) = z + \frac{z + h}{h}\left[ {\eta_{0} - \frac{3}{{4\left( {h + \eta_{0} } \right)}}X^{2} \left( {0,z,t} \right)} \right],\;\;\; - 2c\sqrt {\frac{{\eta_{0} }}{3g}} \le X\left( {0,z,t} \right) \le 2c\sqrt {\frac{{\eta_{0} }}{3g}} ,$$
(68)

which defines the particle trajectory. Equation (68) shows that the particle trajectory is a parabolic curve, under the assumption that the horizontal displacement is independent of the vertical coordinate \(z\). □

4 Conclusions

In this paper, the displacement are used to describe the shallow water system. Two shallow water equations are derived based on the Hamilton variational principle. The first equation is the extended displacement shallow water equation (EDSWE). The EDSWE contains a higher order nonlinear term which is omitted in the original displacement shallow water equation developed by Zhong et al. By using the exp-function method, we analytically solve the EDSWE and obtain different types of waves, including the regular solitary wave, the loop solitary wave, the solitary wave with a sharp peak, and a periodic wave. The second equation is the fully nonlinear displacement shallow water equation (FNDSWE). In FNDSWE, all the nonlinear terms are considered, and the only assumption is the horizontal displacement is independent of the vertical coordinate \(z\). The solitary wave solution of the FNDSWE is obtained. It is found that under the shallow water approximation, the particle trajectory of the solitary wave is a parabolic curve.