Solitary wave solutions of three special types of Boussinesq equations

Abstract

In this paper, the $(G'/G)$-expansion method is employed to construct more general solitary wave solutions of three special types of Boussinesq equation, namely Boussinesq equation, improved Boussinesq equation and variant Boussinesq equation, where the French scientist Joseph Valentin Boussinesq (1842–1929) described in the 1870s model equations for the propagation of long waves on the surface of water with a small amplitude. Our work is motivated by the fact that the $(G'/G)$-expansion method provides not only more general forms of solutions but also periodic, solitary waves and rational solutions. The method appears to be easier and faster by means of a symbolic computation.

1 Introduction

In the recent decades, a new direction related to the investigation of nonlinear evolution equations (NLEEs) and processes has been actively developing in various areas of sciences. Nonlinear evolution equations have been the important subject of study in various branches of sciences such as physics, fluid mechanics and chemistry. The analytical solutions of NLEEs are of fundamental importance, since many of mathematical–physical models are described by NLEEs. Among the possible solutions to NLEEs, certain special form of solutions may depend only on a single combination of variables such as solitons. In mathematics and physics, a soliton is a self-reinforcing solitary wave, a wave packet or pulse, that maintains its shape while it travels at constant speed. Solitons are caused by a cancelation of nonlinear and dispersive effects in the medium. The term “dispersive effects” refers to a property of certain systems where the speed of the waves varies according to frequency. Solitons arise as the solutions of a widespread class of weakly nonlinear dispersive partial differential equations describing physical systems. The soliton phenomenon was first described by John Scott Russell (1808–1882) who observed a solitary wave in the Union Canal in Scotland. He reproduced the phenomenon in a wave tank and named it the “Wave of Translation” (also known as solitary wave or soliton) [1]. The soliton solutions are typically obtained by means of the inverse scattering transform [2] and be in dept their stability to the integrability of the field equations.

In fluid mechanics, the Boussinesq approximation for water waves is a valid approximation for weakly nonlinear and fairly long waves. The approximation is named after Joseph Valentin Boussinesq (1842–1929), who first derived them in response to the observation by John Scott Russell of the wave of translation [3, 4]. According to paper of Boussinesq published in the year 1872 (see reference [4]), for water waves on an incompressible fluid and irrotational flow in the (x, z) plane, the boundary conditions at the free surface elevation $z = \eta (x,t)$ are:

$$\begin{aligned} \begin{aligned}&\frac{\partial \eta }{\partial t}+\mathbf{v }\frac{\partial \eta }{\partial x}-\mathbf{w }=0,\\&\frac{\partial \varphi }{\partial t}+\frac{1}{2}(\mathbf{v }^2+\mathbf{w }^2)+g\eta =0, \end{aligned} \end{aligned}$$

(1)

where $\mathbf{v }= \tfrac{\partial \varphi }{\partial x}$ is the horizontal flow velocity component, $\mathbf{w }= \tfrac{\partial \varphi }{\partial z}$ is the vertical flow velocity component, and g is the acceleration by gravity. Now, the Boussinesq approximation for the velocity potential $\varphi$, as given above, is applied in these boundary conditions. Further, in the resulting equations only the linear and quadratic terms with respect to $\eta$ and $\mathbf{v }_b$ are retained (with $\mathbf{v }_\mathrm{b} = \partial \varphi _b/\partial x$ the horizontal velocity at the bed $z = -h$). The cubic and higher-order terms are assumed to be negligible. Then, the following partial differential equations are obtained:

$$\begin{aligned} \begin{aligned}&\frac{\partial \eta }{\partial t}+\frac{\partial }{\partial x}\Big (\big (h+\eta \big )\mathbf{v }_\mathrm{b}\Big )=\frac{1}{6}h^3\frac{\partial ^3 \mathbf{v }_\mathrm{b}}{\partial x^3},\\&\frac{\partial \mathbf{v }_\mathrm{b}}{\partial t}+\mathbf{v }_\mathrm{b}\frac{\partial \mathbf{v }_\mathrm{b}}{\partial x}+g\frac{\partial \eta }{\partial x}=\frac{1}{2}h^2\frac{\partial ^3 \mathbf{v }_\mathrm{b}}{\partial t\partial x^2}, \end{aligned} \end{aligned}$$

(2)

This set of equations has been derived for a flat horizontal bed, i.e., the mean depth h is a constant independent of position x. When the right-hand sides of the above equations are set to zero, they reduce to the shallow water equations. Under some additional approximations, but at the same order of accuracy, Eq. (2) can be reduced to a single partial differential equation for the free surface elevation $\eta (x,t)$:

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 \eta }{\partial t^2}-gh\frac{\partial ^2 \eta }{\partial x^2}-gh\frac{\partial ^2}{\partial x^2}\Big (\frac{3}{2}\frac{\eta ^2}{h}+\frac{1}{3}h^2\frac{\partial ^2 \eta }{\partial x^2} \Big )=0, \end{aligned} \end{aligned}$$

(3)

In dimensionless quantities, by using the water depth h and gravitational acceleration g for non-dimensionalization, Eq. (3) after normalization leads:

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 \psi }{\partial \tau ^2}-\frac{\partial ^2 \psi }{\partial \chi ^2}-\frac{\partial ^2}{\partial \chi ^2}\Big (\frac{1}{2}\psi ^2+\frac{\partial ^2 \psi }{\partial \chi ^2} \Big )=0, \end{aligned} \end{aligned}$$

(4)

where $\psi =3\frac{\eta }{h},\,\tau =\sqrt{3\frac{g}{h}}\,t,$ and $\chi =\sqrt{3}\frac{x}{h}.$ Equation  (4) can be written as follows [5]

$$\begin{aligned} \begin{aligned} u_{\mathrm{tt}}-u_{\mathrm{xx}}-\left( \frac{1}{2}u^2+qu_{\mathrm{xx}}\right) _{\mathrm{xx}}=0, \end{aligned} \end{aligned}$$

(5)

where $|q|=1$ is a real parameter. Setting $q =-1$ gives the good Boussinesq equation (GB) or well-posed Boussinesq equation, while setting $q = 1$ we get the bad Boussinesq equation (BB) or ill-posed classical Boussinesq equation. Following Bogolubsky’s modification [6] in Eq. (5) when the term $qu_{\mathrm{xx}}$ is replaced with $qu_{\mathrm{tt}}$, it gives the so-called improved Boussinesq equation (IBq):

$$\begin{aligned} u_{\mathrm{tt}}-u_{\mathrm{xx}}-\left( \frac{1}{2}u^2+qu_{\mathrm{tt}}\right) _{\mathrm{xx}}=0, \end{aligned}$$

(6)

Similarly, using an analogous characterization used for Boussinesq Eq. (5), the IBq equation for $q =-1$ will give the good or well-posed (GIBq), while for $q = 1$ the bad or ill-posed (BIBq) equation. The IBq equation appears in studying the transverse motion and nonlinearity in acoustic waves on elastic rods with circular cross section. In particular, the BIBq is used to discuss the wave propagation at right angles to the magnetic field and also to approach the bad BS equation (see Makhankov [7]) or to study ion-sound(s) waves (see Bogolubsky [6]).

There are some review articles and works that have been focused on studying the classical Boussinesq equation from various points of view. The initial boundary value and the Cauchy problem of (5) have been described in [8,9,10,11]. Yazhima [12] studied the nonlinear evolution of a linearly stable solution, while the exponentially decaying solution of the spherical Boussinesq equation was obtained by Nakamura [14]. A general approach to construct exact solution to (5) is given by Clarkson [9], and Hirota [10] has deduced conservation laws and has examined N-soliton interaction. Bona and Sachs, in [8], have discussed that the special solitary wave solutions for Eq. (5), when nonlinear term is $u^2$, are nonlinearly stable for a range of their wave speeds. The global existence of the strong solution and small amplitude solution for the Cauchy problem of the multi-dimensional Eq. (5) is proved in [13].

And finally, the following variant of Boussinesq equation

$$\begin{aligned} \begin{aligned}&u_{t}+uu_x+v_x+qu_{\mathrm{xx}}=0,\\&v_t+(uv)_x+pu_{\mathrm{xxx}}-qv_{\mathrm{xx}}=0, \end{aligned}\qquad p,q\in {\mathbb {R}} \end{aligned}$$

(7)

was studied by Sachs [15] for Painleve property and rational solutions. Yao and Li [16] applied a direct algebraic method to construct some interesting closed-form traveling wave solutions for Eq. (7). In Eq. (7), p, q are real constants that represent different dispersive powers. If $p = 0, q \ne 0,$ Eq. (7) leads to approximate equations for the long-wave equation. While if $p = 1, q = 0$, Eq. (7) becomes to a simple variant of Boussinesq equation where discussed by Fu et al. in their paper [17], and same variant has been the subject of study by Zhang [18], wherein the author has applied the homogeneous balance method to construct the multi-solitary wave solutions. Recently, in [19], Singh and Gupta used the symmetry method based on the Fréchet derivative of the differential operators to variational coefficient of (7), and Wu and He in [20] applied the Exp-function method in Eq. (7).

On the other hand, recently, the $(G'/G)$-expansion method, firstly introduced by Wang et al. [21], has become widely used to search for various exact solutions of NLEEs [21,22,23,24,25,26,27,28,29]. The value of the $(G'/G)$-expansion method is that one treats nonlinear problems by essentially linear methods. The method is based on the explicit linearization of NLEEs for traveling waves with a certain substitution, which leads to a second-order differential equation with constant coefficients. Moreover, it transforms a nonlinear equation to a simple algebraic computation. Although many efforts have been devoted to find various methods to solve (integrable or non-integrable) NLEEs, there is no unified method. The main merits of the $(G'/G)$-expansion method over the other methods are that it gives more general solutions with some free parameters which, by suitable choice of the parameters, turn out to be some known solutions gained by the existing methods.

Our first interest in the present work is in implementing the $(G'/G)$-expansion method to show its power in handling nonlinear partial differential equations (PDEs), so that one can apply it to other models of various types of nonlinearity. The next interest is in the determination of exact traveling wave solutions for generalized Eqs.  (5, 6, 7).

2 Description of the $(G'/G)$-expansion method

The objective of this section is to outline the use of the $(G'/G)$-expansion method for solving certain nonlinear PDEs. Suppose we have a nonlinear PDE for u(x, t),  in the form

$$\begin{aligned} P(u,u_x,u_t,u_{\mathrm{xx}},u_{\mathrm{xt}},u_{\mathrm{tt}},\ldots )=0, \end{aligned}$$

(8)

where P is a polynomial in its arguments, which includes nonlinear terms and the highest order derivatives. The transformation $u(x,t)=U(\xi ),\ \xi =x-\omega t,$ reduces Eq. (8) to the ordinary differential equation (ODE)

$$\begin{aligned} P(U,U',-\omega U',U'',-\omega U'',\omega ^2U'',\ldots )=0, \end{aligned}$$

(9)

where $U=U(\xi ), \omega$ is constant and prime denotes derivative with respect to $\xi$. We assume that the solution of Eq. (9) can be expressed by a polynomial in $(G'/G)$ as follows:

$$\begin{aligned} U(\xi )=\sum _{i=1}^m\alpha _i \Big (\frac{G'}{G}\Big )^i+\alpha _0,\quad \alpha _m\ne 0. \end{aligned}$$

(10)

where $\alpha _0,$ and $\alpha _i,$ for $i=1,2,\ldots ,m$, are constants to be determined later, $G(\xi )$ satisfies a second-order linear ordinary differential equation (LODE):

$$\begin{aligned} \frac{\mathrm{d}^2G(\xi )}{\mathrm{d}\xi ^2}+\lambda \frac{\mathrm{d}G(\xi )}{\mathrm{d}\xi }+\mu G(\xi )=0. \end{aligned}$$

(11)

where $\lambda$ and $\mu$ are arbitrary constants. Using the general solutions of Eq. (11), we have

$$\begin{aligned} \frac{G'(\xi )}{G(\xi )}=\left\{ \begin{array}{l} \frac{\sqrt{\lambda ^2-4\mu }}{2}\Bigg (\frac{C_1\sinh (\frac{\sqrt{\lambda ^2-4\mu }}{2}\xi )\, +\,C_2\cosh (\frac{\sqrt{\lambda ^2-4\mu }}{2}\xi )}{C_1\cosh (\frac{\sqrt{\lambda ^2-4\mu }}{2}\xi )+C_2\sinh (\frac{\sqrt{\lambda ^2-4\mu }}{2}\xi )}\Bigg ) -\frac{\lambda }{2},\\ \quad \text {for } \lambda ^2-4\mu >0,\\ \frac{\sqrt{4\mu -\lambda ^2}}{2}\Bigg (\frac{-C_1\sin (\frac{\sqrt{4\mu -\lambda ^2}}{2}\xi ) +C_2\cos (\frac{\sqrt{4\mu -\lambda ^2}}{2}\xi )}{C_1\cos (\frac{\sqrt{4\mu -\lambda ^2}}{2}\xi )+C_2\sin (\frac{\sqrt{4\mu -\lambda ^2}}{2}\xi )}\Bigg ) - \frac{\lambda }{2},\\ \quad \text {for } \lambda ^2-4\mu <0, \end{array}\right. \nonumber \\ \end{aligned}$$

(12)

and it follows from (10) and (11) that

$$\begin{aligned} \begin{aligned} U'&=-\sum _{\ell =1}^m\ell \ \alpha _\ell \Big (\left( \frac{G'}{G}\right) ^{\ell +1}+\lambda \left( \frac{G'}{G}\right) ^\ell +\mu \left( \frac{G'}{G}\right) ^{\ell -1}\Big ),\\ U''&=\sum _{\ell =1}^m\ell \ \alpha _\ell \Big ((\ell +1)\left( \frac{G'}{G}\right) ^{\ell +2}\\&\quad +(2\ell +1)\lambda \left( \frac{G'}{G}\right) ^{\ell +1} +\ell \left( \lambda ^2+2\mu \right) \left( \frac{G'}{G}\right) ^{\ell }\\&\quad +(2\ell -1)\lambda \mu \left( \frac{G'}{G}\right) ^{\ell -1} +(\ell -1)\mu ^2\left( \frac{G'}{G}\right) ^{\ell -2}\Big ), \end{aligned} \end{aligned}$$

(13)

and so on, here the prime denotes the derivative with respective to $\xi$. To determine u explicitly, we take the following four steps:

Step 1 Determine the integer m by substituting Eq. (10) along with Eq. (11) into Eq. (9) and balancing the highest order nonlinear term(s) and the highest order partial derivative.

Step 2 Substitute Eq. (10) gives the value of m determined in Step 1, along with Eq. (11) into Eq. (9) and collect all terms with the same order of $(G'/G)$ together; the left-hand side of Eq. (9) is converted into a polynomial in $(G'/G)$. Then set each coefficient of this polynomial to zero to derive a set of algebraic equations for $k, \omega , \lambda , \mu , \alpha _0$ and $\alpha _i,$ for $i=1,2,\ldots ,m$.

Step 3 Solve the system of algebraic equations obtained in Step 2, for $k, \omega , \lambda , \mu , \alpha _0$ and $\alpha _i,$ for $i=1,2,\ldots ,m$, by use of Maple.

Step 4 Use the results obtained in above steps to derive a series of fundamental solutions $u(\xi )$ of Eq. (9) depending on $(G'/G)$, since the solutions of Eq. (11) have been well known for us, and then, we can obtain exact solutions of Eq. (8).

3 Application

In this section, we will demonstrate the $(G'/G)$-expansion method on three of the well-known Boussinesq-type Eqs. (5, 6, 7).

3.1 Boussinesq equation

To look for the traveling wave solution of Boussinesq equation (5), we use the gauge transformation:

$$\begin{aligned} u(x,t)=U(\xi ), \end{aligned}$$

(14)

where $\xi =kx+\omega t,$ and $\omega$ is constant. We substitute Eq. (14) into Eq. (5) to obtain nonlinear ordinary differential equation

$$\begin{aligned} \left( \omega ^2-k^2\right) U-k^2\big (\frac{1}{2}U^2+q U''\big )=R_0, \end{aligned}$$

(15)

where $R_0$ is a integration constant. According to Step 1, we get $m+ 2 = 2m$, and hence, $m = 2.$ We then suppose that Eq. (15) has the following formal solutions:

$$\begin{aligned} U=\alpha _2\left( \frac{G'}{G}\right) ^2+\alpha _1\left( \frac{G'}{G}\right) +\alpha _0,\qquad \alpha _2\ne 0, \end{aligned}$$

(16)

where $\alpha _2, \alpha _1,$ and $\alpha _0,$ are constants which are unknown to be determined later. Substituting Eq. (16) along with Eq. (11) into Eq. (15) and collecting all terms with the same order of $(G'/G)$ together, the left-hand sides of Eq. (15) are converted into a polynomial in $(G'/G)$. Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for $\omega , \lambda , \mu , \alpha _0, \alpha _1,$ and $\alpha _2.$ as follows:

$$\begin{aligned} \begin{aligned}&\left( \frac{G'}{G}\right) ^0:\ \left( {\omega }^{2}-k^2\right) \alpha _{{0}}-\frac{1}{2}k^2{\alpha _{{0}}}^{2} -k^4q\lambda \mu \alpha _ {{1}}\\&\qquad \qquad -2k^4q{\mu }^{2}\alpha _{{2}}-R_{{0}} =0,\\&\left( \frac{G'}{G}\right) ^1:\ \left( {\omega }^{2}-k^2\right) \alpha _{{1}}-k^2\alpha _{0}\alpha _{1} -6k^2q\lambda \mu \alpha _{2}\\&\qquad \qquad -k^4q({\lambda }^{2 }+2\mu )\alpha _{1} =0 ,\\&\left( \frac{G'}{G}\right) ^2:\ \big (\omega ^2-k^2-4k^4q(\lambda ^2+2\mu ) \big )\alpha _2-k^2\alpha _0\alpha _2 \\&\qquad \qquad -3k^4q\lambda \alpha _1-\frac{1}{2}k^2\alpha _1^2 =0,\\&\left( \frac{G'}{G}\right) ^3:\ 10k^4q\lambda \alpha _{2}+k^2\alpha _{1}\alpha _{2}+2k^4q\alpha _{1}=0,\\&\left( \frac{G'}{G}\right) ^4:\ \frac{1}{2}k^2{\alpha _{2}}^{2}+6k^4q\alpha _{2}=0, \end{aligned}\nonumber \\ \end{aligned}$$

(17)

Solving the obtained algebraic equations by use of Maple, we get the following results:

$$\begin{aligned} \begin{aligned} \alpha _0&=\tfrac{1}{k^2}(\omega ^2-k^2)-12k^2q\mu \\&\quad \mp \tfrac{1}{k^2}\sqrt{(\omega ^2-k^2)^2-2k^2R_0},\\ \alpha _1&=\mp 12\sqrt{\mp q(4k^4q\mu +\sqrt{(\omega ^2-k^2)^2-2k^2R_0})},\\ \alpha _2&=-12qk^2,\\ \lambda&=\pm \frac{1}{qk^2}\sqrt{\pm q(4k^4q\mu +\sqrt{(\omega ^2-k^2)^2-2k^2R_0})}, \end{aligned} \end{aligned}$$

(18)

and $k,\omega$ and $\mu$ are arbitrary constants. Therefore, substituting the above case in (16), we get

$$\begin{aligned} U_{\pm }= & {} -12qk^2\ \left( \frac{G'}{G}\right) _{\pm }^2\nonumber \\&\mp 12\sqrt{\mp q\left( 4qk^4\mu +\sqrt{\left( \omega ^2-k^2\right) ^2-2k^2R_0}\right) } \left( \frac{G'}{G}\right) _{\pm }\nonumber \\&+\tfrac{1}{k^2}(\omega ^2-k^2)-\,12qk^2\mu \mp \tfrac{1}{k^2}\sqrt{\left( \omega ^2-k^2\right) ^2-2k^2R_0},\nonumber \\ \end{aligned}$$

(19)

Substituting the general solutions (12) into Eq. (19), we obtain three types of traveling wave solutions of Boussinesq Eq. (5) in view of the positive, negative or zero of $\lambda ^2-4\mu$.

When $\varvec{\mathcal {D}}=\lambda ^2-4\mu =\pm \frac{1}{qk^4}\sqrt{(\omega ^2-k^2)^2-2k^2R_0}>0,$ we obtain hyperbolic function solution $U_{\varvec{\mathcal {H}}},$ of Boussinesq Eq. (5) as follows:

$$\begin{aligned} \begin{aligned} U_{\varvec{\mathcal {H}}}(\xi )_{\pm }&=-12qk^2\ \left( \frac{G'}{G}\right) _{\pm }^2\\&\quad \mp 12\sqrt{\mp q\left( 4qk^4\mu +\sqrt{\left( \omega ^2-k^2\right) ^2-2k^2R_0}\right) } \left( \frac{G'}{G}\right) _{\pm }\\&\quad +\tfrac{1}{k^2}\left( \omega ^2-k^2\right) -12qk^2\mu \mp \tfrac{1}{k^2}\sqrt{\left( \omega ^2-k^2\right) ^2-2k^2R_0}, \end{aligned}\nonumber \\ \end{aligned}$$

(20)

where $(\frac{G'}{G})_{\pm }= \frac{\sqrt{\varvec{\mathcal {D}}}}{2}\Bigg (\frac{C_1\sinh (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi ) +C_2\cosh (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi )}{C_1\cosh (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi )+C_2\sinh (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi )}\Bigg ) -\frac{\lambda }{2}$, $\xi =kx+\omega t,$ and $C_1,C_2,$ are arbitrary constants. It is easy to see that the hyperbolic solution (20) can be rewritten at $C_1^2>C_2^2,$ as follows

$$\begin{aligned} u_{\varvec{\mathcal {H}}}(x, t)= & {} -3k^2q\varvec{\mathcal {D}}\tanh ^2\Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big )\nonumber \\&-\frac{-2qk^4\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(21a)

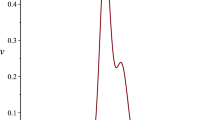
(see Fig. 1) while at $C_1^2<C_2^2,$ one can obtain

$$\begin{aligned} u_{\varvec{\mathcal {H}}}(x, t)= & {} -3k^2q\varvec{\mathcal {D}}\coth ^2\Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big )\nonumber \\&-\frac{-2qk^4\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(21b)

where $\xi =kx+\omega t,\ \eta _{_{\varvec{\mathcal {H}}}}=\tanh ^{-1}\Big (\frac{C_1}{C_2}\Big ),$ and $k, \omega$ and $\mu$ are arbitrary constants. Now when $\varvec{\mathcal {D}}=\lambda ^2-4\mu =\pm \frac{1}{qk^4}\sqrt{(\omega ^2-k^2)^2-2k^2R_0}< 0,$ the trigonometric function solutions $U_{\varvec{\mathcal {T}}}$ of Boussinesq Eq. (5) will be:

$$\begin{aligned} \begin{aligned} U_{\varvec{\mathcal {T}}}(\xi )_{\pm }&=-12qk^2\ \left( \frac{G'}{G}\right) _{\pm }^2\\&\quad \mp 12\sqrt{\mp q\left( 4qk^4\mu +\sqrt{\left( \omega ^2-k^2\right) ^2-2k^2R_0}\right) } \left( \frac{G'}{G}x\right) _{\pm }\\&\quad +\tfrac{1}{k^2}\left( \omega ^2-k^2\right) -12qk^2\mu \mp \tfrac{1}{k^2}\sqrt{\left( \omega ^2-k^2\right) ^2-2k^2R_0}, \end{aligned}\nonumber \\ \end{aligned}$$

(22)

where $(\frac{G'}{G})_{\pm }=\frac{\sqrt{-\varvec{\mathcal {D}}_{\pm }}}{2}\Bigg (\frac{-C_1\sin (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}_{\pm }}\ \xi ) +C_2\cos (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}_{\pm }}\ \xi )}{C_1\cos (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}_{\pm }}\ \xi )+C_2\sin (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}_{\pm }}\ \xi )}\Bigg ) -\frac{\lambda }{2}$, $\xi =kx+\omega t,$ and $C_1,C_2,$ are arbitrary constants. Similarly, the trigonometric solutions (22) can be rewritten at $C_1^2>C_2^2,$ and $C_1^2<C_2^2,$ as follows, respectively,

$$\begin{aligned} u_{\varvec{\mathcal {T}}}(x, t)= & {} 3k^2q\varvec{\mathcal {D}}\tan ^2\Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big )\nonumber \\&-\frac{-2qk^4\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(23a)

$$\begin{aligned} u_{\varvec{\mathcal {T}}}(x, t)= & {} 3k^2q\varvec{\mathcal {D}}\cot ^2\Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big )\nonumber \\&-\frac{-2qk^4\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(23b)

where $\xi =kx+\omega t,\ \eta _{_{\varvec{\mathcal {T}}}}=\tan ^{-1}\Big (\frac{C_1}{C_2}\Big ),$ and $k, \omega$ and $\mu$ are arbitrary constants. Finally, when $\lambda ^2-4\mu =0,$ then, the rational function solutions to Eq. (5) will be:

$$\begin{aligned} u_{\mathrm{rat}}(x,t)=-\frac{12k^2qC_2^2}{\big (C_1+C_2(kx+\omega t)\big )^2}+\frac{\omega ^2}{k^2}-1. \end{aligned}$$

(24)

where $C_1,C_2,k,$ and $\omega$ are arbitrary constants.

Fig. 1

Hyperbolic solution [Eq. (21a)] of Boussinesq Eq.  (5), for $k=1, \omega =\frac{5}{2}, R_0=0, q=-1$ and $\eta _{_{\varvec{\mathcal {H}}}}=0$

3.2 Improved Boussinesq equation

Similar on previous section, to obtain the traveling wave solution of improved Boussinesq Eq. (6), we substitute the gauge transformation (14) into Eq. (6) to obtain nonlinear ordinary differential equation

$$\begin{aligned} (\omega ^2-k^2)U''-k^2\Big (\frac{1}{2}U^2+q\omega ^2U''\Big )''=0, \end{aligned}$$

(25)

According to Step 1, we get $m+ 4 = 2m+2$, and hence, $m = 2.$ Then similar on previous section, we suppose that Eq. (25) has the same formal solutions (16). Substituting Eq. (16) along with Eq. (11) into Eq. (25) and collecting all terms with the same order of $(G'/G)$ together, the left-hand sides of Eq. (25) are converted into a polynomial in $(G'/G)$. Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for $k, \omega , \lambda , \mu , \alpha _0, \alpha _1,$ and $\alpha _2,$ as follows:

$$\begin{aligned} { \begin{aligned}&\left( \frac{G'}{G}\right) ^0:\ \bigg (\Big (-\mu {\omega }^{2}\lambda \left( {\lambda }^{2}+8 \mu \right) \alpha _{{1}}\\&\quad -2{\mu }^{2}{\omega }^{2}\alpha _{{2}}\left( 8 \mu +7{\lambda }^{2}\right) \Big )q-2{\alpha _{{1}}}^{2}{\mu }^{ 2}\\&\quad -\lambda \mu \left( 1+2\alpha _{{0}}\right) \alpha _{{1}}-2{ \mu }^{2}\alpha _{{2}}\left( 1+2\alpha _{{0}}\right) \bigg ){k}^{2} \\&\quad +2{\omega }^{2}\alpha _{{2}}{\mu }^{2}+{\omega }^{2}\alpha _{{1}}\lambda \mu =0,\\&\left( \frac{G'}{G}\right) ^1:\ \bigg (\Big (-{\omega }^{2}\left( 22{\lambda }^{2}\mu +16{\mu }^{2 }+{\lambda }^{4}\right) \alpha _{{1}}\\&\quad -30\mu {\omega }^{2}\alpha _{{2}} \lambda \left( {\lambda }^{2}+4\mu \right) \Big )q-6{\alpha _{{ 1}}}^{2}\lambda \mu \\&\quad +\left( -2\mu -{\lambda }^{2}-12\alpha _{{2}}{ \mu }^{2}-4\alpha _{{0}}\mu \right. \\&\quad \left. -2\alpha _{{0}}{\lambda }^{2}\right) \alpha _{{1}}-6\lambda \mu \alpha _{{2}}\left( 1+2\alpha _{{0}} \right) \bigg ){k}^{2}\\&\quad +{\omega }^{2}\left( 2\mu +{\lambda }^{2} \right) \alpha _{{1}}+6{\omega }^{2}\alpha _{{2}}\lambda \mu =0,\\&\left( \frac{G'}{G}\right) ^2:\ \bigg (\Big (-15\,{\omega }^{2}\lambda \left( {\lambda }^{2}+4\,\mu \right) \alpha _{{1}}\\&\quad -8\,{\omega }^{2}\alpha _{{2}}\left( 29\,{\lambda } ^{2}\mu +2\,{\lambda }^{4}+17\,{\mu }^{2}\right) \Big )q\\&\quad +\left( -4 {\lambda }^{2}-8\mu \right) {\alpha _{{1}}}^{2}-3\lambda \left( 1+ 2\alpha _{{0}}+10\alpha _{{2}}\mu \right) \alpha _{{1}}\\&\quad -4\alpha _{{2 }}\big (3\alpha _{{2}}{\mu }^{2}+2\mu \\&\quad +{\lambda }^{2}+4\alpha _{{0} }\mu +2\alpha _{{0}}{\lambda }^{2}\big )\bigg ){k}^{2}\\&\quad +3{\omega } ^{2}\alpha _{{1}}\lambda +4{\omega }^{2}\alpha _{{2}}\left( 2\mu +{ \lambda }^{2}\right) =0,\\&\left( \frac{G'}{G}\right) ^3:\ \bigg (\Big (-10{\omega }^{2}\left( 4\mu +5{\lambda }^{2} \right) \alpha _{{1}}\\&\quad -10{\omega }^{2}\alpha _{{2}}\lambda \left( 13 {\lambda }^{2}+44\mu \right) \Big )q-10{\alpha _{{1}}}^{2} \lambda \\&\quad +\left( -4\alpha _{{0}}-2-36\alpha _{{2}}\mu -18\alpha _{{2} }{\lambda }^{2}\right) \alpha _{{1}}\\&\quad -2\alpha _{{2}}\lambda \left( 14 \alpha _{{2}}\mu +10\alpha _{{0}}+5\right) \bigg ){k}^{2}\\&\quad +10{ \omega }^{2}\alpha _{{2}}\lambda +2{\omega }^{2}\alpha _{{1}} =0,\\&\left( \frac{G'}{G}\right) ^4:\ \bigg (\Big (-60{\omega }^{2}\alpha _{{1}}\lambda -30{\omega }^{2} \alpha _{{2}}\left( 11{\lambda }^{2} +8\mu \right) \Big )q\\&\quad -6{ \alpha _{{1}}}^{2}-42\alpha _{{2}}\alpha _{{1}}\lambda \\&\quad -2\alpha _{{2}} \left( 16\alpha _{{2}}\mu +8\alpha _{{2}}{\lambda }^{2}+3+6\alpha _{ {0}}\right) \bigg ){k}^{2}+6{\omega }^{2}\alpha _{{2}} =0,\\&\left( \frac{G'}{G}\right) ^5:\ \Big (\left( -24{\omega }^{2}\alpha _{{1}}-336{\omega }^{2}\alpha _ {{2}}\lambda \right) q\\&\quad -36{\alpha _{{2}}}^{2}\lambda -24\alpha _{{2}} \alpha _{{1}}\Big ){k}^{2} =0,\\&\left( \frac{G'}{G}\right) ^6:\ \left( -10\,{\alpha _{{2}}}^{2}-120\,q{\omega }^{2}\alpha _{{2}} \right) {k}^{2} =0, \end{aligned}} \end{aligned}$$

(26)

and solving by use of Maple, we get the following results:

$$\begin{aligned}&\Bigg \{\alpha _0=-{\frac{8\,q{k}^{2}\omega ^2\mu +q{k}^{2}\omega ^2{\lambda }^{2}+k^2-{\omega }^{2}}{{k}^{2}}}\nonumber \\&\quad \alpha _1=-12\,\omega ^2q\lambda ,\, \alpha _2=-12\,\omega ^2q\Bigg \}, \end{aligned}$$

(27)

and $k,\omega ,\lambda$ and $\mu$ are arbitrary constants. Therefore, the solution (16) leads to

$$\begin{aligned} U= & {} -12\,\omega ^2q\ \left( \frac{G'}{G}\right) ^2-12\,\omega ^2q\lambda \left( \frac{G'}{G}\right) \nonumber \\&-{\frac{8\,q{k}^{2}\omega ^2\mu +q{k}^{2}\omega ^2{\lambda }^{2}+k^2-{\omega }^{2}}{{k}^{2}}}, \end{aligned}$$

(28)

Now, for $\varvec{\mathcal {D}}=\lambda ^2-4\mu >0,$ and $\varvec{\mathcal {D}}=\lambda ^2-4\mu <0,$ the hyperbolic function solution $U_{\varvec{\mathcal {H}}}$ and trigonometric function solution $U_{\varvec{\mathcal {T}}}$ of improved Boussinesq Eq. (6) are obtained as follows, respectively:

$$\begin{aligned}&U_{\varvec{\mathcal {H}}}(\xi )\nonumber \\&\quad =-3\omega ^2q\bigg ( \frac{\sqrt{\varvec{\mathcal {D}}}\big [C_1\sinh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )+C_2\cosh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )\big ]}{C_2\sinh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )+C_1\cosh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )}-\lambda \bigg )^2\nonumber \\&\qquad -\,6\omega ^2q\lambda \bigg ( \frac{\sqrt{\varvec{\mathcal {D}}}\big [C_1\sinh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )+C_2\cosh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )\big ]}{C_2\sinh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )+C_1\cosh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )}-\lambda \bigg )\nonumber \\&\qquad -\,{\frac{8\,q{k}^{2}\omega ^2\mu +q{k}^{2}\omega ^2{\lambda }^{2}+k^2-{\omega }^{2}}{{k}^{2}}}, \end{aligned}$$

(29)

$$\begin{aligned}&U_{\varvec{\mathcal {T}}}(\xi )\nonumber \\&\quad =-3\omega ^2q\bigg ( \frac{\sqrt{-\varvec{\mathcal {D}}}\big [-C_1\sin \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )+C_2\cos \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )\big ]}{C_2\sin \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )+C_1\cos \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )}-\lambda \bigg )^2\nonumber \\&\qquad -\,6\omega ^2q\lambda \bigg ( \frac{\sqrt{-\varvec{\mathcal {D}}}\big [-C_1\sin \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )+C_2\cos \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )\big ]}{C_2\sin \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )+C_1\cos \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )}-\lambda \bigg )\nonumber \\&\qquad -{\frac{8\,q{k}^{2}\omega ^2\mu +q{k}^{2}\omega ^2{\lambda }^{2}+k^2-{\omega }^{2}}{{k}^{2}}}, \end{aligned}$$

(30)

where $\xi =kx+\omega t,$ and $C_1,C_2,$ are arbitrary constants. It is easy to see that the hyperbolic solution (34) and trigonometric solution (36) can be rewritten at $C_1^2>C_2^2$ as follows

$$\begin{aligned} u_{\varvec{\mathcal {H}}}(x, t)= & {} -3\omega ^2q\varvec{\mathcal {D}}\tanh ^2\Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big ) \nonumber \\&-\frac{-2qk^2\omega ^2\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(31a)

$$\begin{aligned} u_{\varvec{\mathcal {T}}}(x, t)= & {} 3\omega ^2q\varvec{\mathcal {D}}\tan ^2\Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big )\nonumber \\&-\frac{-2qk^2\omega ^2\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(31b)

while at $C_1^2<C_2^2,$ one can obtain

$$\begin{aligned} u_{\varvec{\mathcal {H}}}(x, t)= & {} -3\omega ^2q\varvec{\mathcal {D}}\coth ^2\Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big )\nonumber \\&-\frac{-2qk^2\omega ^2\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(32a)

$$\begin{aligned} u_{\varvec{\mathcal {T}}}(x, t)= & {} 3\omega ^2q\varvec{\mathcal {D}}\cot ^2\Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big )\nonumber \\&-\frac{-2qk^2\omega ^2\varvec{\mathcal {D}}-\omega ^2+k^2}{k^2}, \end{aligned}$$

(32b)

where $\xi =kx+\omega t,\ \eta _{_{\varvec{\mathcal {H}}}}=\tanh ^{-1}\Big (\frac{C_1}{C_2}\Big ),\,\eta _{_{\varvec{\mathcal {T}}}}=\tan ^{-1}\Big (\frac{C_1}{C_2}\Big ),$ and $k, \omega , \lambda ,$ and $\mu$ are arbitrary constants. The graph of hyperbolic function solution (31a) is shown in the Fig. 2.

Finally, when $\lambda ^2-4\mu =0,$ then the rational function solutions of improved Boussinesq Eq. (6) will be:

$$\begin{aligned} u_{\mathrm{rat}}(x,t)=-\frac{12\omega ^2qC_2^2}{\big (C_1+C_2(kx+\omega t)\big )^2}+\frac{\omega ^2}{k^2}-1, \end{aligned}$$

(33)

where and $C_1,C_2,k,$ and $\omega$ are arbitrary constants.

Fig. 2

Hyperbolic solution [Eq. (31a)] of improved Boussinesq Eq. (6), for $k=1, \omega =2, q=-1, \lambda =2, \mu =\frac{1}{4}$ and $\eta _{_{\varvec{\mathcal {H}}}}=0$

3.3 Variant Boussinesq equation

Finally, consider the nonlinear Variant Boussinesq Eq. (7). By using the transformation $u(x,t)=U(\xi ), v(x,t)=V(\xi ),$ where $\xi =kx+\omega t,$ and once integrating respect to $\xi$, Eq. (7) becomes an following ordinary differential equation,

$$\begin{aligned}&\omega U+\frac{k}{2}U^2+kV+qk^2 U'=\varvec{\mathcal {R}}_1, \end{aligned}$$

(34)

$$\begin{aligned}&\omega V+kUV+pk^3U''-qk^2V'=\varvec{\mathcal {R}}_2, \end{aligned}$$

(35)

where $\varvec{\mathcal {R}}_1$ and $\varvec{\mathcal {R}}_2$ are the integration constants of first and second equation of system (7), respectively. From Eq. (34), we get

$$\begin{aligned} V=\frac{1}{k}\big (\varvec{\mathcal {R}}_1-\omega U-\frac{k}{2}U^2-qk^2 U'\big ), \end{aligned}$$

(36)

By substituting Eq. (36) into Eq. (35), and for simplifying we set $\varvec{\mathcal {R}}_2=0,$ we get the following covering equation

$$\begin{aligned}&\left( \varvec{\mathcal {R}}_1-\frac{\omega ^2}{k}\right) U-\frac{3}{2}\omega U^2-\frac{k}{2}U^3\nonumber \\&\quad +\,k^3\left( p+q^2\right) U'' +\frac{\omega }{k}\varvec{\mathcal {R}}_1=0, \end{aligned}$$

(37)

According to Step 1, we get $m+ 2 = 3m$, and hence, $m = 1.$ We then suppose that Eq. (37) has the following formal solution:

$$\begin{aligned} U=\alpha _1\left( \frac{G'}{G}\right) +\alpha _0,\qquad \alpha _1\ne 0, \end{aligned}$$

(38)

where $\alpha _1,$ and $\alpha _0,$ are constants, which are unknown to be determined later. In a similar manner, substituting Eq. (38) into Eq. (37) and collecting all terms with the same order of $(G'/G)$ and setting each coefficient of each polynomial to zero, we derive the following set of algebraic equations for $k, \omega , \lambda , \mu ,\alpha _0,$ and $\alpha _1$:

$$\begin{aligned}{ \begin{aligned}&\left( \frac{G'}{G}\right) ^0:\ k^3\alpha _1\mu (p+q^2)\lambda -\frac{1}{2}\alpha _0^3k + \varvec{\mathcal {R}}_1\alpha _0-\varvec{\mathcal {R}}_2\\ {}&\quad -\frac{3}{2}\omega \alpha _0^2 - \frac{\omega }{k}(\alpha _0\omega -\varvec{\mathcal {R}}_1)=0,\\&\left( \frac{G'}{G}\right) ^1:\ (p+q^2)(2\mu +\lambda ^2)\alpha _1k^3\\&\quad -\frac{3}{2}\alpha _1\alpha _0^2k +\left( \varvec{\mathcal {R}}_1-3\omega \alpha _0\right) \alpha _1 -\,\frac{\omega ^2}{k}\alpha _1=0 ,\\&\left( \frac{G'}{G}\right) ^2:\ 3\lambda (p+q^2)\alpha _1k^3-\frac{3}{2}\alpha _1^2\alpha _0k -\,\frac{3}{2}\omega \alpha _1^2=0 ,\\&\left( \frac{G'}{G}\right) ^3:\ (2p+2q^2)\alpha _1k^3-\frac{1}{2}\alpha _1^3k=0 , \end{aligned}} \end{aligned}$$

Solving the above set of algebraic equations by use of Maple, we get the following results:

$$\begin{aligned} \begin{aligned}&\Big \{\alpha _0=\pm \lambda k\sqrt{p+q^2}-\frac{\omega }{k},\ \alpha _1=\pm 2k\sqrt{p+q^2},\ \mu \\&\quad =\lambda ^2-\frac{1}{4}\ \frac{2\varvec{\mathcal {R}}_1k+\omega ^2}{k^4(p+q^2)}\Big \}, \end{aligned} \end{aligned}$$

(39)

and $k,\omega ,\lambda$ are arbitrary constants, and therefore, substituting the above case in (38), we get

$$\begin{aligned} U=\pm 2k\sqrt{p+q^2}\ \left( \frac{G'}{G}\right) \pm \lambda k\sqrt{p+q^2}-\frac{\omega }{k}, \end{aligned}$$

(40)

Therefore, for $\varvec{\mathcal {D}}=\lambda ^2-4\mu =\frac{2\varvec{\mathcal {R}}_1k+\omega ^2}{k^4(p+q^2)} > 0,$ and $\varvec{\mathcal {D}}=\lambda ^2-4\mu =\frac{2\varvec{\mathcal {R}}_1k+\omega ^2}{k^4(p+q^2)} < 0,$ the hyperbolic function solution $U_{\varvec{\mathcal {H}}}$ and trigonometric function solution $U_{\varvec{\mathcal {T}}}$ of variant Boussinesq Eq. (7) are obtained, respectively, as follows:

$$\begin{aligned}&U_{\pm \varvec{\mathcal {H}}}(\xi )=\pm \, k\sqrt{p+q^2}\nonumber \\&\quad \times \bigg ( \frac{\sqrt{\varvec{\mathcal {D}}}\big [C_1\sinh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )+C_2\cosh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )\big ]}{C_2\sinh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )+C_1\cosh \big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \big )}-\lambda \bigg )\nonumber \\&\quad \pm \, \lambda k\sqrt{p+q^2}-\frac{\omega }{k}, \end{aligned}$$

(41)

$$\begin{aligned}&U_{\pm \varvec{\mathcal {T}}}(\xi )=\mp k\sqrt{p+q^2}\nonumber \\&\quad \times \bigg ( \frac{\sqrt{-\varvec{\mathcal {D}}}\big [C_2\cos \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )-C_1\sin \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )\big ]}{C_2\sin \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )+C_1\cos \big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \big )}+\lambda \bigg )\nonumber \\&\quad \pm \,\lambda k\sqrt{p+q^2}-\frac{\omega }{k}, \end{aligned}$$

(42)

and from (36), the $V_{\varvec{\mathcal {H}}}(\xi )$ and $V_{\varvec{\mathcal {T}}}(\xi )$ is obtained as follows:

$$\begin{aligned}&V_{\pm \varvec{\mathcal {H}}}(\xi )\nonumber \\&\quad = \frac{(2\varvec{\mathcal {R}}_1k+\omega ^2)(\sqrt{p+q^2}\mp q)(C_1^2+C_2^2)}{2k^2\sqrt{p+q^2}\Big [C_2\sinh \Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \Big )+C_1\cosh \Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi \Big )\Big ]^2}, \end{aligned}$$

(43)

$$\begin{aligned}&V_{\pm \varvec{\mathcal {T}}}(\xi )\nonumber \\&\quad = \frac{(2\varvec{\mathcal {R}}_1k+\omega ^2)(\sqrt{p+q^2}\mp q)(C_1^2+C_2^2)}{2k^2\sqrt{p+q^2}\Big [C_2\sin \Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \Big )+ C_1\cos \Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi \Big )\Big ]^2},\nonumber \\ \end{aligned}$$

(44)

where $\xi =kx+\omega t,$ and $C_1,C_2,$ are arbitrary constants. It is easy to see that the hyperbolic and trigonometric solutions (41, 42, 43, 44) can be rewritten at $C_1^2>C_2^2$ as follows

$$\begin{aligned} u_{\pm \varvec{\mathcal {H}}}(x, t)= & {} \pm \, k\sqrt{p+q^2}\sqrt{\varvec{\mathcal {D}}}\tanh \Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big ) -\frac{\omega }{k},\nonumber \\ \end{aligned}$$

(45a)

$$\begin{aligned} u_{\pm \varvec{\mathcal {T}}}(x, t)= & {} \pm \, k\sqrt{p+q^2}\sqrt{-\varvec{\mathcal {D}}}\tan \Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big )\,-\,\frac{\omega }{k}, \nonumber \\ \end{aligned}$$

(45b)

$$\begin{aligned} v_{\pm \varvec{\mathcal {H}}}(x, t)= & {} \frac{1}{2}\ \frac{(2\varvec{\mathcal {R}}_1 k+\omega ^2)(\sqrt{p+q^2}\mp q)}{k^2\sqrt{p+q^2}}\ \nonumber \\&\times \text {sech}^2\Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big ), \end{aligned}$$

(45c)

$$\begin{aligned} v_{\pm \varvec{\mathcal {T}}}(x, t)= & {} \frac{1}{2}\ \frac{(2\varvec{\mathcal {R}}_1 k+\omega ^2)(\sqrt{p+q^2}\pm q)}{k^2\sqrt{p+q^2}}\ \nonumber \\&\times \sec ^2\Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big ), \end{aligned}$$

(45d)

while at $C_1^2<C_2^2,$ one can obtain

Fig. 3

Hyperbolic solution [Eq. (45a)] of variant Boussinesq Eq. (7), for $k=\frac{2}{3}, \omega =-\frac{1}{2}, \varvec{\mathcal {R}}_1=0, p=1$ and $q=-1$

Fig. 4

Hyperbolic solution [Eq. (45c)] of improved Boussinesq Eq. (7), $k=\frac{2}{3}, \omega =-\frac{1}{2}, \varvec{\mathcal {R}}_1=0, p=1, q=-1$ and $\eta _{_{\varvec{\mathcal {H}}}}=0$

$$\begin{aligned} u_{\pm \varvec{\mathcal {H}}}(x, t)= & {} \pm k\sqrt{p+q^2}\sqrt{\varvec{\mathcal {D}}}\coth \Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big )-\,\frac{\omega }{k},\nonumber \\ \end{aligned}$$

(45e)

$$\begin{aligned} u_{\pm \varvec{\mathcal {T}}}(x, t)= & {} \pm k\sqrt{p+q^2}\sqrt{-\varvec{\mathcal {D}}}\cot \Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big )-\frac{\omega }{k},\nonumber \\ \end{aligned}$$

(45f)

$$\begin{aligned} v_{\pm \varvec{\mathcal {H}}}(x, t)= & {} -\frac{1}{2}\ \frac{(2\varvec{\mathcal {R}}_1 k+\omega ^2)(\sqrt{p+q^2}\mp q)}{k^2\sqrt{p+q^2}}\ \nonumber \\&\times \text {csch}^2\Big (\frac{1}{2}\sqrt{\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {H}}}}\Big ), \end{aligned}$$

(45g)

$$\begin{aligned} v_{\pm \varvec{\mathcal {T}}}(x, t)= & {} \frac{1}{2}\ \frac{(2\varvec{\mathcal {R}}_1 k+\omega ^2)(\sqrt{p+q^2}\mp q)}{k^2\sqrt{p+q^2}}\ \nonumber \\&\times \csc ^2\Big (\frac{1}{2}\sqrt{-\varvec{\mathcal {D}}}\ \xi +\eta _{_{\varvec{\mathcal {T}}}}\Big ), \end{aligned}$$

(45h)

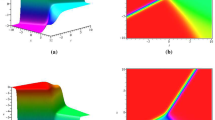
where $\xi =kx+\omega t,\ \eta _{_{\varvec{\mathcal {H}}}}=\tanh ^{-1}\Big (\frac{C_1}{C_2}\Big ),\,\eta _{_{\varvec{\mathcal {T}}}}=\tan ^{-1}\Big (\frac{C_1}{C_2}\Big )$ and $k, \omega ,$ are arbitrary constants. Figures 3 and 4 show the graphs of hyperbolic function solutions (45a) and (45c), respectively. Finally, when $\lambda ^2-4\mu =0,$ then $k=-\frac{1}{2}\frac{\omega ^2}{\varvec{\mathcal {R}}_1},$ and therefore, the rational function solutions to Eq. (39) will be:

$$\begin{aligned} u_{{\mathrm{rat}\pm }}(x,t)= & {} \frac{\mp \omega ^2 C_2+2\varvec{\mathcal {R}}_1^2C_2\ \xi +2\varvec{\mathcal {R}}_1^2C_1}{\varvec{\mathcal {R}}_1\omega \big (C_2\ \xi + C_1\big )}, \end{aligned}$$

(46a)

$$\begin{aligned} v_{{\mathrm{rat}\pm }}(x,t)= & {} -\frac{1}{2}\frac{\omega ^4 C_2}{\varvec{\mathcal {R}}_1^2\big (C_2\ \xi + C_1\big )^2}, \end{aligned}$$

(46b)

where $\xi =-\frac{1}{2}\frac{\omega ^2}{\varvec{\mathcal {R}}_1}x+\omega t,$ and $C_1,C_2,\omega$ and $\varvec{\mathcal {R}}_1\ne 0$ are arbitrary constants.

4 Conclusions

This study shows that the $(G'/G)$-expansion method is quite efficient and practically well suited for use in finding exact solutions for the three types of Boussinesq equation, namely the Boussinesq equation, improved Boussinesq equations and variant Boussinesq equation. The reliability of the method and the reduction in the size of computational domain give this method a wider applicability. Though the obtained solutions represent only a small part of the large variety of possible solutions for the equations considered, they might serve as seeding solutions for a class of localized structures existing in the physical systems. Furthermore, our solutions are in more general forms, and many known solutions to these equations are only special cases of them. With the aid of Maple, we have assured the correctness of the obtained solutions by putting them back into the original equation.