1 Introduction

The overall aim of our study is to learn more about how concepts relevant for understanding functions develop for learners across the years of secondary/high school. We created an opportunity setting to produce data from two different curricula systems from two different countries. This enabled us to examine the conceptual development of function knowledge in different schooling situations, using classes taught by teachers interested in learning about this. We build on the strong body of research about dimensions and difficulties in learning functions to develop a survey instrument that could be accessed by the youngest secondary students but also addresses and examines progression to the oldest students. Our task selection and design enable students to reveal, and teachers to observe, relevant understandings. The data arising from the use of the instrument led us to realisations about students’ learning towards functions and suggested differences and similarities between the countries that indicate the influence of teaching and curriculum. The instrument is itself a contribution to exploratory research.

We compare some students from England and Israel because the focus on functions in Israel’s national curriculum is formal from age 12, i.e., presented sequentially using conventional symbolisation, language, and methods, whereas it is less formal in England. We know background differences because of our intimate knowledge of the educational systems. Pedagogy varies among teachers, but teachers in both countries remain close to their national sanctioned curriculum in what they teach. Knowledge of the curriculum and of teachers’ expectations gives adequate information about enactment for us to conjecture plausible reasons to explain differences that show up in students’ performance. We also matched, as far as possible, variables such as social class, prior attainment, and expected performance. Socio-economic backgrounds of the schools in our study were similar relative to their national norms, being comprehensive in intake.

Comparison has thrown up issues for each country individually that might not have arisen without the comparison. We have published several papers already about some of these. The study has raised issues of curriculum order, such as when and how formal treatment of functions begins, and the effects of that on students’ reactions to the word “function” (Ayalon, Watson, & Lerman, 2017), similarities and differences in students’ responses to tasks when they have acquired formal approaches to functions or have facility with informal approaches (Ayalon, Watson, & Lerman, 2016b), and the effects of detail in the design of tasks, particularly generalisation of linear functions from data (Ayalon, Watson, & Lerman, 2015). We now compare progression in the two countries. This is not done to produce national comparative data, but to highlight differences in learning where curriculum expectations at different ages are very different. This places students’ progression in sociocultural contexts, rather than only in the cognitive development of individuals, and hence has implications for curriculum and teaching since these are ways in which different cultural expectations are mediated in schooling. We present a summary of findings and pose the question:

  • What possible explanations can be provided for similarities and differences in students’ performances in the two countries?

We revisit this question in the final discussion, following the design and results sections.

The breadth of this overview necessitates brevity; elaborations are available in our previous papers, to which we refer.

First, we review a selection of related literature. We then describe the curriculum contexts, followed by our task design intentions and methods of analysis. Subsequently, we analyse the students’ responses to the tasks and compare categorizations between countries. The analysis is based on our empirical data and interaction with the literature. Our comparisons lead to conjectures about relationships among curriculum, teaching, design and students’ responses, offering areas for future research. In this paper, these conjectured relationships, and the survey itself, are our contributions to knowledge.

2 Theoretical background

Drawing on sociocultural theory, our perspective is that teaching and curriculum are critical in learning; hence, differences in these will determine, or affect significantly, what students learn; in turn, students’ knowledge gives insights into teaching and enactment of curriculum (e.g., Daniels, 1993; Lerman, 2001).

End-of-school and undergraduate understandings of function have been described by many researchers (e.g., Dubinsky & Harel, 1992; Sfard, 1991, 1992; Sierpinska, 1992; Slavit, 1997; Vinner & Dreyfus, 1989). Tall (1992) writes about how students move from a view of functions as instructions to move between two sets of numbers, to correspondences between elements of the sets, to relations between variations, and finally to functions as objects. This progression is broadly common throughout the literature and includes views of functions as (a) ordered pairs or (b) correlations between changes in variables. These two views appear as “correspondence” and “covariation” in research about generalising functions (e.g., Confrey & Smith, 1994, 1995; Leinhardt, Zaslavsky, & Stein, 1990). Correspondence might relate to mapping and input-output images of functions. Covariation might relate to graphing representations, dynamic phenomena, to each variable being seen as a parametric function of time (Confrey & Smith, 1995; Saldanha & Thompson, 1998), and to comparing changes in dependent variables to changes in independent variables (Carlson & Oehrtman, 2005; Thompson & Carlson, 2017). For school-level research, we see “rate of change” as the formal or numerical expression of changes in one variable in terms of another and observe that:

In situations where rate of change can be calculated, it might be correctly deduced through a procedural approach… without any awareness of what it means in terms of covariation; alternatively, a student might express a situation qualitatively as covariation but be unable to operationalise this idea as a rate of change. (Ayalon, Watson, & Lerman, 2016a, p. 1156)

In school, functions are almost always continuous so covariation has the same meaning as rate of change. Gradient is closely related to covariation and rate, and in school, this usually relates to slopes of graphs. Connecting gradient to overall or instantaneous rate of change depends on seeing the graph as representing a dynamic situation (Gravemeijer & Doorman, 1999). For linear functions, instantaneous rate of change is indistinguishable from change on an interval and hence gradient, whereas for non-linear functions, a formal understanding of gradient requires instantaneous rate of change.

In generalising functions from sequential data, a term-to-term approach is often observed to dominate students’ approaches (e.g., Radford, 2008; Stacey, 1989; Steele, 2008), and whereas the changes in the dependent variable are important for understanding covariation, the move from discrete change to a covariational understanding is not straightforward (e.g., Blanton & Kaput, 2011; see also Ayalon et al., 2016a, p. 1156). Misapplication of proportional reasoning in sequential contexts is also common among students (Stacey, 1989; Van Dooren, De Bock, Hessels, Janssens, & Verschaffel, 2005).

In school, variables are either symbols in algebraic representations or visible in situations and can be counted or measured. Young children are capable of adopting a modelling perspective, i.e., identifying the behaviour of variables, given a suitable experiment (e.g., Ainley & Pratt, 2005; Dreyfus & Eisenberg, 1983; Karplus, 1978). They can connect situations to graphical representations such as saying where and why “it goes up” or “down”, sketching a likely graph, or describing the effects of varying parameters. Less is known about how students understand the use of variables in algebra, or “compound” variables that are implicit, such as density and speed.

Several difficulties in connecting graphs to situations have been found in research. The most frequently cited is interpreting a graph as a picture (e.g., Clement, 1985; Janvier, 1981). Students deal more competently with graphs of functions when one of the variables is time or time-dependent (Janvier, 1981; Thompson, 1994) but time may not be understood as a variable if graphs are always read chronologically from left to right (Monk, 1994).

Progression in conceptual understanding depends on curriculum order and enactment (e.g., Roth & Radford, 2011) as well as students’ learning capabilities and experience. In our knowledge of students learning about functions, there seemed to us to be no accounts of how, over time, learning relates to curriculum order and teaching focus.

3 Israeli and English curricula and teacher expectations

The Israeli curriculum is regulated by the Ministry of Education and textbooks are officially approved. The national mathematics curriculum (Ministry of Education, 2009) provides detailed recommendations for teaching functions, which are named as such. In grade 7 (ages 12–13), function is a relationship between an independent and a dependent quantity using verbal, graphical, tabular, and algebraic representations. Formal notation is introduced in grade 7 using y or f(x) and function is defined as matching a particular number to a number chosen from a domain. “Rate” is taught in grade 7 including varying rates, and there is a focus on changes in the function value when x changes. Students have earlier experience with patterns and sequences. The main focus in grade 8 is linear functions, emphasising constant rate of change, straight line graphs, and the form y = mx + b. The focus in grade 9 is on characteristics and transformations of quadratic functions. In grades 10–12, formal calculus is introduced.

The statutory national curriculum in England at the time of the study did not require a formal treatment of functions until years 11/12 (equivalent to grades 10/11) for those who opt to continue to study mathematics (QCA, 2007). Introduction to functions is through generalising sequences and mappings that connect domain values to range values. Data tables are used to plot graphs whose properties are then studied in their own right. Most textbooks provide input-output “machines” to develop algebraic expressions which are variously called rules, equations, or graphs rather than “functions”. Rate of change arises implicitly as the gradient of linear functions, and this idea extends to varying rates of change through quadratic functions, or through modelling motion, with older students as a starting point for calculus through qualitative and quantitative study of increasing and decreasing functions. The ideas of rate and rate of change were not salient in the English curriculum at the time of our study before early calculus.Footnote 1 Most English students will therefore not know much about the word function until about 15 years of age but will have some experience of linear graphs connected to sequences, and quadratic graphs (which may or may not have been called functions), or input-output mappings, and may have heard “function machine” in relation to these. They will have met the y = notation. After 16, mathematics is only studied by specialist students.

Students in both countries will also have met various graphs of realistic and statistical data, not described as functions. The only non-smooth, non-continuous, and non-calculable graphs they will definitely have met would be journey graphs, but they may have met others through investigating other realistic phenomena. Graphs will have been constructed from graph-plotting software, from calculating points and plotting, from function sketching, and from realistic data or presented for interpretation.

All teachers contributing to this study were knowledgeable about functions to at least first university degree level and hence could enrich students’ experience beyond the curriculum and textbook expectations if they chose to. There were two pairs in each country: four teachers teaching in two schools. The teachers taught the full age range of our study; the classes we surveyed were their own classes, and one or other of them taught the highest achieving group in each year. An exception is that the grade 12 class in Israel was from a different school for practical reasons.

The expectations of the participating teachers suggest what they emphasise in their teaching. Israeli teachers confirmed that their teaching from grade 7 includes explicit reference to functions and rates of change as foundational ideas. Input-output and mapping ideas were not taught. The teachers from England said that students would meet input-output models in year 7 (grade 6) or before, and some teachers use the word function in the context of input-output machines. Explicit use of the word and notation is in year 11 (grade 10) when students meet transformations of linear and quadratic functions. Mapping between sets is developed in year 12 (grade 11) as an introduction to a formal treatment of functions in year 13 (grade 12). Rate of change would first be discussed by these older students in the context of finding derivatives from the first principles.

These generalisations are the background for analysing differences in Israeli and English students’ responses in our study.

4 Design of survey tasks and methods

We started with a draft conceptual map of functions seen from both pure mathematical and modelling perspectives based on our own experience and knowledge about functions. It had over 50 components and plotted hypothetical connections between the components of a conventional understanding of functions. This produced a school-orientated version of the seminal analysis provided by Sierpinska (1992) in which she identifies 19 components and a similar number of possible obstacles to learning. This “top-down” map was then compared to the curricula of the two countries, and to empirical studies, and to teachers’ expectations. From this conceptual investigation and the literature, we identified understanding relationships between variables as a key idea in progression towards function understanding, connecting formal and modelling developmental pathways (Ayalon et al., 2016a, b). The components we identified included selection and recognition of variables of various kinds; expression of relations between variables (correspondence, covariation, rates of change, gradient); and interpretation of relations presented as graphs, equations, formulae, and situations. In school, these typically arise through students’ learning in the areas of graphing and interpreting, generalising from sequential data, relating variables in data and in phenomena, conceptualising rate of change, understanding linear and other relationships, and using formal, informal, abstract, and realistic contexts. Our survey design started from these ideas and used tasks which could reveal students’ understanding of some of these ideas, as well as their end-of-school concept image of functions which we have reported elsewhere (Ayalon et al., 2017).

We developed an instrument over several design cycles working closely with our eight teachers, four in each country, to ensure breadth of curriculum perspectives and accessibility for their students. These cycles included initial discussions; redesign based on teacher comments about curriculum relevance; small trials in schools; and further redesign based on students’ written responses and discussion with teachers about possible misunderstandings of the tasks, time taken to do the whole survey, content coverage and duplication, and willingness to administer the survey as a useful component of their teaching. The purpose of the instrument was to study some components of function understanding across all secondary age students, not at the level of individuals, but to give an overall picture. We had to make it manageable for teachers, i.e., short and student-friendly, while being informative for them and us.

We used tasks from Wilmot, Schoenfeld, Wilson, Champney, and Zahner (2011) and Swan (1980) as starting points for our design as these are based on considerations from the literature, checking that these would be accessible for students and had enough relevant familiarity. The instrument used by Wilmot et al. was to test for “college readiness” and Swan’s tasks were designed for teaching, focusing on graphing and the meaning of symbolic representations, so we had to select, adapt, and create to devise a succinct collection of tasks that would span progress towards understanding functions.

As well as helping to design the instrument, the same teachers administered it in their classes, providing an opportunistic population from which we could learn about similarities and differences.

Language was agreed with the teachers, and two of the authors being bilingual in Hebrew and English meant that language differences were understood. Students’ responses were written in booklets containing the tasks. The survey was then trialled. Outcomes and difficulties were discussed with teachers and further adaptations made. Our aim was to find out what students do, and see if, how and when they surmounted common difficulties identified in the literature. The final design and our analysis of the final data therefore drew on teachers’ knowledge and their expectations of students’ responses, teachers’ reports of the order and content of their teaching, knowledge of curriculum, knowledge of tasks familiar in textbooks and tests, and knowledge from research as described above. The five tasks we discuss in this paper could all be accessed via the curriculum in both countries. A sixth task depended on interpreting formal definitions of the word function and detailed analysis is reported elsewhere (Ayalon et al., 2017). The tasks appear in the “Results” section below so that students’ responses can be directly compared to the task presentations.

4.1 Sample

Here, we focus on data from higher achieving classes only, to focus on those whose knowledge of functions should provide a foundation for further study. In both countries, these classes were between 30 and 50% of the age cohort, varying a little across years, except in the case of England years 12 and 13 for which the students we used were the only ones studying mathematics. The sample is large enough to encompass a range of possible responses while being small enough to analyse individual responses in detail. From each class, teachers sampled 10 scripts from the alphabetised class listFootnote 2 and anonymised them. In this way, we received, from such classes, 70 scripts from English years 7 to 13 inclusive and 60 scripts from Israel years 7 to 12. From here on, we use grade equivalents for both countries to ensure we are comparing similar ages and omit England grade 6 since we have no comparative scripts from Israel. To avoid applying a heavy workload on teachers, each school provided data from alternate years, so one school provided grades 7, 9, and 11 and the other grades 8, 10, and 12. Ethical permissions and protocols were pursued; in Israel, this was treated as an outside intervention test and in England as a diagnostic process undertaken by teachers in the normal course of their work.

4.2 Data analysis

The analysis is the comparison of task responses from two small opportunistic samples, used to gain insight into the similarities and differences in students’ ways of thinking that arise in different curriculum systems. For each task, we categorised all the different approaches students had taken, whether successful or not, from all the data, thus reducing the data to a few general approaches. We started by openly coding responses and then looked for similarities across the data as categories. In addition, the identification of mathematical reasoning in students’ responses allowed us to make inferences about their understanding, and where there is existing relevant research about students’ thinking, we tested existing categorisations to see if they could also be applied. Decisions about interpretation were made collaboratively among the research team by discussion and consensus. Categorisations were constantly checked against the whole data set, and between ourselves, testing distinctions to see if all responses fitted into one, and only one category. This process required several passes through the whole data, often going back to both the literature and individual scripts to gain further insights. For each task, the categories of responses are task-specific and include all the approaches we could identify. This is to generate as full a picture as possible of what students actually do in function-related tasks. Categories are presented below relating to each task. Once the data had been reduced, we collected raw frequencies and used these to compare across years and across countries. However, this is primarily a qualitative study, with data directing us towards possible issues of interest. Since we had small samples, it was then possible to look again at particular examples to make sense of differences. Similarities and differences were therefore identified empirically, using the emergent categories. We looked for qualitative similarities and differences in the responses and also identified differences where quantitative data showed different trends across years, or proportional differences of more than 25%.

5 Results

For each task, we introduce the task, its foci, and the teachers’ expectations. We then provide the analytical categories with some examples (quotations given in italics) and frequencies representing the distribution of the categories across years within the English and the Israeli classes. Note that we have only recorded responses, not non-responses, so totals will not always be 10 for each country and grade. We draw attention to similarities or differences and conjecture about reasons.

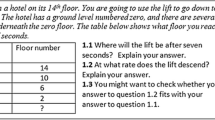
5.1 Task 1

Task 1 (Fig. 1) focuses on rate of change, implicitly and explicitly, when an elevator descends. The term-to-term pattern of the table vertically requires some thought as there is a “break” in the time sequence. Question 1.2 asks explicitly for rate, which is not defined, so the data needs transformation into “floors per second”. The last part of the task suggests revisiting the data where students may have ignored the independent variable.

Fig. 1
figure 1

Task 1

Full size image

Israeli teachers believed students would be able to answer these questions. Rate of change is formally met at the end of grade 7. English teachers anticipated that students of all ages would spot the correct missing value in 1.1, but they expected students to have some problems with 1.2 since rate as a taught idea first appears in the curriculum in grade 12. All teachers and students assumed constant speed. Three categories of expressions of rate of change emerged, as presented in Table 1.

Table 1 Categories of response for task 1
Full size table

Table 2 presents the distribution of the categories of expressions of rate of change.

Table 2 Distribution of task 1 categories in English and Israeli classes
Full size table

By the end of school, students in both countries show similar covariational approaches, but throughout this study, it must be remembered that the English students in grades 11 and 12 are following a self-selected specialist course where the Israelis are higher performing but not necessarily seeing themselves as specialists. Almost all students, from both countries, provided formal expressions of rate of change as floors per second for question 1.2, but several chose − 2 when asked to find where the lift will be after 7 s (question 1.1), explaining that the lift is going down 4 every second, thus focusing only on the dependent variable. However, when asked to find the rate at which the lift descends, they used both variables to get the correct answer. English students made many more errors in 1.1 (30 vs. 12% of all students) but these decreased with age and older students performed similarly to Israeli students. In Israel, more students used covariation throughout the age range. The younger English students were more likely to make the typical error of treating the dependent variable as a sequence but were also more competent with rate than their teachers expected. Israeli students seemed better prepared for this question and more likely to compare changes in both variables.

5.2 Task 2

Task 2 (Fig. 2) asks students to interpret a pattern sequence for the perimeter of a chain of hexagons. The general expression could be developed in a number of ways, such as using correspondence or covariation, and is a familiar task for students, although data are presented in an unfamiliar way. We presented data non-sequentially to deter term-to-term assumptions. Question 2.2 asks for a general method to compute the perimeter. The relationship has to be inferred by transforming the data and comparing it to the diagram. Question 2.3 asks for an algebraic expression, an explicit request for a new representation. The previous questions are intended to direct students towards the relations and structure they need to express. Question 2.4 asks for an explanation in words.

Fig. 2
figure 2

Task 2

Full size image

All teachers expected that students would use input-output and correspondence reasoning using step size as the multiplier. Four categories emerged in students’ attempts to find and express relations in the data, as presented in Table 3, and their distribution is shown in Table 4.

Table 3 Categories for task 2
Full size table
Table 4 Distribution of categories of task 2
Full size table

We also returned to the scripts to see how successful these approaches were. Students overwhelmingly used a correspondence approach to suggest a general rule for the relation between the number of hexagons and the perimeter. Of the Israeli students choosing this approach, 41/43 presented a correct formula, mainly referring to the structure of the shapes to explain it, but the English proportion was only 20/40 (categories 2 and 4). Half of the English students made errors, mainly assuming proportionality, and their correspondence reasoning did not take the structure into account (Rivera & Becker, 2008). None of the Israeli responses made the proportional error; the three incorrect responses seemed to be due to an inability to complete a deconstructive approach correctly. More English than Israeli students used arguments arising from differences in the data sequence, and these approaches were more successful for them, proportionally, than those who tried to use correspondence.

5.3 Task 3

Task 3 (Fig. 3) requires students to read the gradient in two representations. All teachers reported teaching this in grade 8. The use of the description “straight line” was to give a clue to younger students about our use of “parallel”.

Fig. 3
figure 3

Task 3

Full size image

Four categories of expression of gradient emerged, see Table 5.

Table 5 Categories for task 3
Full size table

Table 6 presents the distribution of categories of expression of gradient in the English and the Israeli classes, respectively.

Table 6 Distribution of categories of task 3
Full size table

English students were less successful in general; about a half of the students overall (the proportion decreases with age) showed no evidence of using gradient, including some older specialist students. Partial use is shown mostly in the middle age bands (grs 8 to 10), when according to the teachers, we would expect a stronger understanding. Formal treatment of gradient appears only in older students. In Israel, success was evident from gr8 with a reduction in gr10, increasing again for older students.

5.4 Task 4

Task 4 (Fig. 4) exposes what students think the important features of quadratic graphs might be, indicating a shift towards functions being objects in their own right. By asking students to compare and classify features, we made the task accessible to all students, whether or not they had studied quadratic functions, and also gave them the responsibility for finding characteristics. Teachers of both countries reported that students learn to plot quadratic functions from gr8 onwards and might highlight important analytical features, by which we mean features that relate to mathematical rather than pictorial analysis.

Fig. 4
figure 4

Task 4

Full size image

Four categories of response emerged:

  1. 1.

    No reference to features at all

  2. 2.

    Reference only to visual features (e.g., thin, high, low) that do not express reasoning about variables or functions

  3. 3.

    Reference also to (at least one) analytical features (e.g., orientation, transformation, turning point, zeroes) informally

  4. 4.

    Reference to (at least one) analytical features using formal language

Table 7 shows examples of some of the features used by students and how they were expressed, informally or formally.

Table 7 Examples of features in task 4
Full size table

Table 8 presents the distribution of categories related to levels of interpreting graphs of quadratic functions.

Table 8 Distribution of categories of task 4
Full size table

Overall, a similar proportion of students identified appropriate features in both countries, 82% in England and 77% in Israel. Choice of features was similar in both countries, with orientation and zeroes being the most frequent, followed by turning point (for reasons of space, we cannot show this data). Progression in both countries was as expected, but with the additional finding that several students chose features that showed an analytical understanding of the important features of graphs before formal teaching. In England, there was an overall less use of formal language and expressions for the chosen characteristics, even among students who had been formally taught (28% formal use in England and 55% in Israel).

5.5 Task 5

In task 5 (Fig. 5) (from Swan, 1980), students had to match four situations to graphs. All situations focus on identifying variables, forming relations between them (in particular covariation), and noticing contextual features and were selected according to an expected increase of difficulty: (i) straightforward identification of unidimensional variables; (ii) choice of possible variables; (iii) the use of compound variables; and (iv) compound variables and an inverse relationship. Each choice had to be explained.

Fig. 5
figure 5

Task 5

Full size image

Teachers reported that students from gr7 onwards meet real-life graphs of different descriptions (e.g., conversion graphs, distance-time graphs, volume-time graphs). However, whereas the English teachers expected that there would not be much variation in response throughout grs 8 to 12 or between situations, the Israeli teachers anticipated difficulties for all students as they are not used to constructing the variables themselves.

An iterative comparison of all responses resulted in three general codes:

  1. 1.

    No choice

  2. 2.

    Lack of full analysis

  3. 3.

    Full analysis

There were four sources of difficulty, which we exemplify in Table 9.

Table 9 Categories of difficulties in task 5
Full size table

Tables 10 presents the distribution of categories where there were responses.

Table 10 Distribution of categories of task 5
Full size table

Students in the two countries were similar in their approaches and difficulties. Progression was different, however. In England, the number of responses offering no analysis decreased from 33 to 3, and the proportion being successful increased. In Israel, there was no clear overall progression that we could discern after grade 7, the strongest success rate being in gr10. Difficulties were similar in both countries and across ages, suggesting that they relate to the task rather than curriculum and pedagogy (see Ayalon et al., 2016a). In situation 2, some students focused only on one variable; in situations 2 and 4, some students chose irrelevant variables; in situation 3, some chose an upside down graph; in situations 3 and 4, several assumed linearity. We did not find any obvious instances of confusing graphs with pictures.

6 Discussion and conjectures

In this discussion, we focus, task by task, on what differences and similarities within and between countries might plausibly be due to curriculum and what to task features.

In task 1, differences in success and approach suggest that errors arise from curriculum differences. The English curriculum emphasises generalisation of sequences and students tend to be given tables of values to generalise, which require focussing only on the dependent variable and assuming the independent variable merely runs through sequence position numbers; many therefore focused only on the dependent variable. The Israeli curriculum focuses on function more formally, expressing y in terms of x.

However, the rate of change aspect was similarly successful in both countries so we assume some fundamental capability despite curriculum difference. We conjecture that success in this part is due to the requirement to compare data from both columns explicitly—and possibly that context plays a part (Ayalon et al., 2016a).

In task 2, students have to avoid the common recursive approach to sequential data, and assumptions about proportionality, and indeed, only a few students made these errors. We conjecture that this indicates the importance of design and presentation. Differences between countries suggest that errors are linked to curriculum in this case as well. Correspondence, in the form of function machines, appears in many English textbooks but is used for solving some linear equations and deciding order of operations, and not often attached to the task of generalising sequential data, although this is an explicit curriculum aim. Moreover, in England, in their teaching on proportionality, our collaborating teachers emphasise layout of data as a tool to draw attention to relationships. We conjecture therefore that question 2.2 might have been treated by some as a “missing number” problem because that was an option offered by the layout of the data, triggering a mistaken response. Formal teaching in Israel about correspondence approaches appears to have avoided assumptions about proportionality. Observations from tasks 1 and 2 have been reported in more detail in Ayalon et al. (2015).

In task 3, informal knowledge and even a geometrical understanding of parallel are of little help because of the formality of the task presentation. Differences between countries suggest that the more formal teaching in Israel provided students with tools with which to pick the gradient from the representations; the reduction between grades 9–11 could indicate that formal ideas are forgotten if they are not used, but this could be an over-interpretation in a small data set.

In task 4, students in both countries identified the same features of function graphs, whether expressed formally or informally, even before these had been taught. In task 5, formal knowledge about functions had little part to play, and we conjecture that relating verbal and graphical descriptions of phenomena is influenced more by features of the phenomena than by formal teaching. The English curriculum includes specific attention to applications and this appears to have had a positive effect on progress.

From this summary of similarities and differences, it seems that both earlier or later, formalisation can lead to similar capabilities by the end of school, except that in England, this is only known for specialist students. We can also say that preference for a term-to-term approach and assumptions of proportionality are related to task and presentation, and students will use correspondence approaches in suitable circumstances. Direct curriculum experience of correspondence, such as linking input-output models to constructing functions from data, might make success more likely. We can also say that younger students can understand rate operationally, whether taught or not, but relating this to gradient is more likely if it is formally taught. We did not test variable rate directly, only contextually in task 5, and this was well handled even by those who had not been formally taught about it.

An overview of students’ performance across the mathematical tasks confirmed that the idea of relations between variables gave a strong connecting thread to their performance and progress (Ayalon et al., 2016a, b), and that this idea has both informal and formal impacts on students’ learning and performance on our tasks. Israeli students tended towards formal and correspondence approaches and English students seemed more likely to intuit about variability, whether correctly or not, using formal understandings later.

To return to our aim of learning more about progression towards functions, we now conjecture that rate and rate of change arise not only through formal mathematics teaching but also through other experiences, such as the elevator in task 1. We can also say that it is possible for students to recognise the important analytical features of graphs of functions, even if they have not yet been taught about those functions, and experience of graphing realistic situations might be the support for this. Formalisation gives language and other symbolic representations that provide access and precision to these ideas, e.g., the use of “gradient”, and the ideas themselves can develop in informal and formal ways. It is also possible to improve qualitative understanding of functions and avoid the picture-graph confusion. We also conjecture that a correspondence approach to functions avoids simplistic assumptions about data patterns. Experience of school tasks, and the ways in which they are presented, can have a limiting effect on whether students use covariation or correspondence reasoning (Ayalon et al., 2016b).

6.1 Reflections

We emphasise that the survey was designed with teachers from both countries, who all thought it related to their teaching and their understanding of functions. Our use of a small sample, with known teachers, has allowed us to probe deeply into the students’ responses to tasks that teachers believed to be appropriate. We also have the advantage of being embedded in the mathematical classroom cultures of both countries in our work as educators and thus have been able to ask cogent questions about expectations, curriculum order, and the focus of teaching. We also know that the teachers were all strongly guided by their sanctioned curriculum. We know that any differences in students’ performance on the task are not because of teacher knowledge expectations about students’ capacity to learn. We deduce that they are also not about any underlying cognitive capabilities, since the students had similar background achievement in relation to their own countries and cohorts. A match between different student performance and the different curriculum foci is noticeable throughout, but eventually, performance on all these tasks is similar among older students in both countries, suggesting two different but converging curriculum trajectories towards success in these five tasks, a more formal trajectory in Israel and a more informal trajectory in England. However, it does not make predictions about their preparedness for future work with functions (see Ayalon et al., 2017).

In the course of our research with this small sample, we have found small-scale contradictions to some well-reported claims, such as picture-graph confusion, an assumption of proportionality, and a tendency to term-to-term reasoning. These, therefore, are not “givens” about student cognition but constructed, or not, by curriculum and pedagogy.

Most importantly, we do not suggest that one curriculum route is “better” than another but that different curricula can shape different conceptualisation of functions. Within that overall shaping, task design matters since different tasks draw differently on mixtures of formal and informal knowledge, and pedagogic approaches matter because they generate familiarity with certain formats and task types and unfamiliarity with others.