Introduction

We focus on the function concept as an explicit and implicit foundation for advanced study involving mathematics. We take the view that function understanding combines several earlier algebraic and graphical concepts, used both formally and informally. We therefore set out to learn systematically about students’ particular ways of seeing functions at different stages of secondary school, intending that our insights could contribute to curriculum and pedagogic choices. We build on a strong body of research that reveals dimensions and difficulties in learning functions to develop a survey instrument that could be accessed by the youngest students but would also address and examine what we interpreted would reveal progression right through to the oldest students. Our aim in this paper is to report on data from Israeli students indicating progression in identifying and expressing a variety of relations between quantities. This study is of importance beyond Israel because of the formal focus on functions in their national curriculum from age 12. This small study also shows the value of longitudinal study across school years, rather than depending on separate studies of particular concepts and tasks.

Working closely with Israeli teachers, the survey was given to 20 high and average achieving students from each of years 7–11 and to 10 high achieving students from year 12, a total of 110 students. The ideas that contribute to the function concept develop throughout students’ school experience, younger students learning algebraic tools and also maybe plotting data from realistic situations and interpreting it informally. Leinhardt, Zaslavsky & Stein (1990), in their review of research into functions learning, describe different perspectives on functions: “mathematical presentation [of functions] is usually from an algebraic function rule to ordered pairs to a graph, or from a data table of ordered pairs to a graph. … [and] scientific presentation, … proceeds from observation, to data array, to ordered pairs of data, to selection of axis labels, to scale construction, to graph and (maybe) to function.” (Leinhardt et al. 1990, p. 3). For us, progression refers to these ideas and competencies developing over time. Our analytical approach is to identify qualitatively what students appear to do, and whether their solutions are complete, in a range of tasks relating to functions, and we try to account for their behaviour. Indications of progression are presented as conjectures, based in a small sample, about the role and effect of formal teaching about functions and variables, and connections between formal knowledge and informal understandings.

First, we describe the curriculum context. We then review a selection of literature about learning functions, followed by a description of our task design intentions and methods of analysis. Subsequently, we analyse the students’ responses to the tasks, categorise them and identify progression. We compare the responses to the literature and curriculum and make conjectures about the relationships between curriculum, teaching, design and progression, pointing out areas for future research.

Curriculum Context

As a country with a centralised educational system, the Israeli school curriculum is developed and regulated by the Ministry of Education, and textbooks have to be officially approved. The national mathematics curriculum in Israel for secondary schools (Ministry of Education, 2009) provides detailed recommendations related to teaching functions. In seventh grade (year 7, ages 12–13), one main aim is presenting the concept of function as a relationship between two quantities, one depending on the other. Four different representations are used: verbal, graphs, tables of values and algebraic expressions; formal notation is introduced, either using y or f(x); and a (numerical) function is defined as matching a particular number to any number (chosen from a domain). Rate is also taught in year 7, and a second aim with functions is to compare the change (including varying rates) in the value of y or f(x) when x changes using graphs and tables. Before/earlier to year seven, students work on patterns and sequences. The main focus in year 8 is the linear function, emphasising its constant rate of change, straight line graphs and the form y = mx + b.Footnote 1 The focus in year 9 is on characteristics and transformations of quadratic functions. In years 10–12, formal calculus is introduced. This curriculum information provides the background for raising conjectures.

Theoretical Background

There is a substantial body of literature about difficulties and possibilities in students’ learning of functions while understanding its foundational role in higher mathematics (e.g. Sajka, 2003; Vinner & Dreyfus, 1989). Dreyfus & Einsenberg (1982) conducted a progression study in grades 6 to 9, focusing on the formation of a functions concept rather than components of such a concept. We are more interested in the components and draw to some extent on studies of learners’ behaviour in particular conceptual contexts.

In their seminal review of research on school tasks associated with functions, graphs and graphing, Leinhardt et al. (1990) developed four overlapping constructs: the action of the student or learner, the situation, the variables and their nature and the focus. We found their framework to be useful for designing and characterising our tasks as well as in interpreting the findings. We therefore used it as an organiser for a review of relevant literature.

Action

Leinhardt et al. (1990) classify tasks into two, non-exclusive, categories of action: interpretation and construction. By ‘interpretation’, they mean the action by which a student gains meaning from a graph, equation or situation. ‘Construction’ is about generating new objects that are not given, such as building a graph or an algebraic representation. Interpretation can be local, such as determining when specific events or conditions are met, or it can be global, such as focusing on patterns or rate of change and gaining meaning about the relationship between variables, their covariation. Understanding global features of a graph is valuable for later mathematics: calculus and modeling. Goldenberg (1987) has pointed out that a qualitative approach to relationships, necessary for interpretation in realistic contexts, uses students’ common sense, intuitions and reality-checking strategies. Construction, like interpretation, can also be either local (e.g. plot points) or global (e.g. sketch a graph).

Two general approaches to interpreting and constructing functional relationships from data are often discussed in the literature arising from observations of students’ methods: correspondence and covariation (e.g. Confrey & Smith, 1994, 1995). The correspondence approach builds a rule for determining the unique y-value from any given x-value, thus building a correspondence between x and y. The correspondence approach is emphasised in the notation: y = f(x) and also some teaching methods, such as input–output models, and makes a plausible contribution towards understanding that relations between two sets of numbers might (sometimes) be expressed as general algebraic ‘rules’. The Israeli curriculum gives emphasis to a correspondence view of function by introducing f(x) notation as an option, which the teachers in our survey adopted.

A covariation approach to functions involves an understanding of the manner in which the dependent and independent variables change. It entails being able to coordinate movement from y m to y m + l with movement from x m to x m + l. With tables of values, it involves the coordination of the variation in two or more columns as one moves down (or up) the table; with a graph, it involves understanding changes in vertical value as one moves horizontally. A covariation approach is a precursor both to calculus and to modeling natural phenomena. Our perspective is that these approaches need to be connected to provide a full understanding, so we see ‘rate of change’ as an instantiation of a relationship in which changes in one variable can be expressed formally or numerically in terms of changes in another variable, where covariation more generally might not provide this precision. In situations where rate of change can be calculated, it might be correctly deduced through a procedural approach such as comparing step sizes or drawing ‘gradient’ triangles without any awareness of what it means in terms of covariation; alternatively, a student might express a situation qualitatively in terms of covariation but be unable to operationalise this idea as a rate of change. The Israeli curriculum includes varying and constant rates of change with graphs and tables and practical situations, so encourages a covariational view as well as a correspondence view.

Research about generalising from sequential data arising from spatial sequence patterns shows that students tend to reason about the differences in the dependent variable only (e.g. Stacey, 1989). Lack of attention to the independent variable means that a student could appear to be thinking of covariation by considering step change in the dependent variable, particularly where sequence patterns have been a normal classroom practice, without any sense of coordinating this with the position variable or time variable. A full covariation approach is considered by some authors to be harder to understand because the focus is on change rather than quantity (Mevarech & Kramarsky, 1997). However, children have been seen to possess intuitive ideas about covariation through observations of physical phenomena that surround them every day (Confrey & Smith, 1994), and a recursive approach to sequential data can provide a basis for covariational reasoning.

Carlson, Jacobs, Coe, Larsen & Hsu (2002) use observations of calculus students working in a dynamic function situation to propose a framework of five mental actions that describe the reasoning abilities involved: (1) coordination of variables; (2) direction of change; (3) coordination of the amount of change in the two variables; (4) average rate of change over uniform increments; and (5) instantaneous rate of change. Flexible movement between mental actions 3, 4, and 5 was difficult for precalculus students, and many only employed mental actions 1 and 2. Confrey & Smith (1994) report that young children were able to develop the idea of ‘unit per unit’ (p. 153) comparison in concrete situations, while Blanton & Kaput (2011) revealed that children at early age can demonstrate covariation when a problem is contextualised and a pattern is directly proportional to the step number—they could articulate y = mx relationships in discrete situations. So while rate of change can be understood in some circumstances, varying rate of change is a significant hurdle. Herbert & Pierce (2012) identified important aspects of rate of change that were missing or incomplete among year 10 students: awareness of relationships between two changing quantities, especially when varying, and quantification of rate of change.

Most studies about generalisation of functions presented as spatial sequences agree that young adolescents find it difficult to reach theoretical generalisations; they tend to use a term-to-term approach to the dependent variable so that later terms, beyond the given, are difficult to evaluate (e.g. Radford, 2008; Stacey, 1989). Several researchers have suggested that task presentation influences students’ approaches since presenting data as numerical sequences can encourage a term-to-term approach, which can be successful in generating subsequent terms but significantly precedes their capability to generalise a function (e.g. Orton, Orton & Roper, 1999). Where students are asked to construct generalisations from sequential spatial diagrams instead of numerical data, they might build up the shape by adding components or count sub-configurations and subtract sides that overlap. Rivera & Becker (2008) found the latter approach to be more error-prone. Misapplication of proportional reasoning in sequential contexts, and also in word problems, is common, leading students to assume, for example, that f(100) must be equal to 10f(10) (Stacey, 1989; Van Dooren, De Bock, Hessels, Janssens & Verschaffel 2005). In the study of Van Dooren, in which the situations were not presented as sequences, frequency of this error peaked in grade 5 and fell in later years.

Situation

‘Situation’ refers to two aspects: the surrounding setting of the task and the context of the problem. The setting for our survey is always the classroom and students are used to ‘taking tests’ in that place. To take account of different pathways towards functions, school mathematics often includes contextual applications, designed to deepen students’ understanding of the abstract mathematical concepts as well as to give experience of the processes of mathematical modeling. Much of the research about functions, such as covariation, involves students’ understanding physical phenomena, and children can often analyse and handle covariation using everyday knowledge before they can do so in formal settings. For example, Dreyfus & Eisenberg (1982) observed that intuitive understandings were not necessarily associated with formal understanding of functions; they also identified some progression of intuitions during grades 6 to 9.

Variables

The notion of a variable is fundamental to understanding functional relationships and graphical representations and is a prerequisite for making sense of covarying quantities. There are several meanings and aspects of variables. A variable might be seen as static or dynamic: the static interpretation emphasises a variable as a symbolic tool for generalisation or for describing patterns; the dynamic focuses on how variations in one quantity relate to variations in others (Janvier, 1981). A dynamic approach to variable can be represented in a number of ways (e.g. use of dynamic software to generate a graph as the dependent variable changes).

A variable can be contextual or abstract. Contextualised variables are most often continuous in nature, although they may not be represented as continuous. Many contextualised tasks include a time variable. Interpretation and construction of graphs in which one of the variables is time are relatively easy because the variation associated with time seems natural (Janvier, 1981). This can lead to students to ignore the meaning of the independent variable or to interpret the shape of a graph of a situation as a picture of that situation (e.g. Schultz, Clement & Mokros, 1986). The construction of axes is not straightforward (Leinhardt et al., 1990), particularly when the variables are unusual for the learner. If these are provided, students do not need to identify variables and decide how to represent them. In sequence tasks, the independent variable might not be recognised because it is the natural number sequence; in input–output tasks, the independent variable might be seen as a specific value or a placeholder. When variables are abstract, e.g. numbers, there is little research about students’ understanding. Variables can be numeric or non-numeric, discrete or continuous and might also be compound units or rates, such as speed, density and price per unit.

Focus

‘Focus’ refers to the location of the attention within a specific task. There may be several possible foci in any task. A novice may focus on axes, scales or how individual points are connected, because they are drawing or calculating or plotting these, where a task author or teacher may expect the focus to be on a particular property of a function.

The considerations described in the above sections guided the design of our survey tasks. To understand progression towards functions in school contexts, we based our design on what is already known about learning about functions and also on what is known about the curriculum that students have experienced and what teachers expect of students.

Design of Survey Tasks

First, we developed a hypothetical conceptual map of functions seen from both pure mathematical and modeling perspectives based on our own experience. We compared this map to the curriculum, and to the literature, and to teachers’ expectations. From this conceptual investigation, which cannot be reported here for reasons of space, we identified understanding relationships between variables as a key idea in all possible pathways of development towards functions understanding in school. In order to understand functions for calculus or modeling purposes, they need to understand rate of change, and for this, they have to recognise variables, identify them and understand how they relate. We developed the survey instrument over several design cycles working closely with eight teachers, four in Israel and four in England to ensure a breadth of curriculum perspectives. We used tasks from Wilmot, Schoenfeld, Wilson, Champney & Zahner (2011) and Swan (1980) as resources as these are based on the considerations above. As well as working on the instrument, the same teachers also conducted the survey and provided insights about their pedagogy.

We included task features to address the framework from Leinhardt et al. (1990) described above (see Table 1) with each individual task addressing several issues that arose in our review. The questions had to be accessible for students in years 7 to 12. Together with the teachers, we made tasks that appeared familiar so that students would be able to access them but varied the representations so that students may not respond habitually to them. The familiarity of language used was agreed with the teachers. It was then trialed and the outcomes and difficulties were discussed with teachers and further adaptations made. Our aim was to support students to find out what they can do, rather than offer questions that might encourage common errors. The final version using six tasks was approved by the teachers. The final design and our analysis therefore drew on teachers’ knowledge and expectations of students, teachers’ reports of the order and content of their teaching, knowledge of curriculum, knowledge of tasks familiar in textbooks and tests and knowledge from research literature as described above. For this paper, we focus on the three survey tasks that involve identification of variables and the relationships between quantities. Information about other tasks and performance of other students can be found elsewhere (Ayalon, Lerman & Watson, 2013, 2014a, b; Ayalon, Watson & Lerman, manuscript submitted for publication). The tasks appear in the ‘Results’ section below so that students’ responses can be directly compared to the task presentations.

Table 1 The tasks in terms of the four constructs suggested by Leinhardt et al. (1990)
Full size table

We started with tasks involving linear data for several reasons, younger students in our range would be familiar with linear sequence tasks and hence there would be access for all, and data arising from familiar phenomena are usually presented in sequential tabular form. We wanted to deter students from reasoning directly from numbers as in Orton et al. (1999). Instead, we wanted to see if they could reason about the situational variables, including the independent variable. We took this into account in our design of task A (Fig. 1 in ‘Results’ section) by not having a natural number sequence as the independent variable and in task B (Fig. 2 in ‘Results’ section) by presenting non-sequential data for a sequential growth structure, thus upsetting some of the tendencies reported in Stacey (1989) and Orton et al. (1999) but retaining spatial diagram ordering used by Radford (2008). We reasoned that this would encourage students to take the independent variable into account and hence enable them to transform recursive approaches into covariational approaches. We also chose not to present proportional situations, since Van Dooren et al. (2005) had shown these to be fairly easy for younger students, and we wanted to see if students would avoid making incorrect proportional assumptions. The tabular and non-tabular presentations provide opportunities to show correspondence or covariational reasoning to generalise the situations. We asked for verbalisation of the relationship to get extra information about students’ reasoning, and this could also provide scaffolding for some students to construct the algebraic form (Radford, 2000).

Fig. 1
figure 1

Task A

Full size image
Fig. 2
figure 2

Task B

Full size image

Task C (Fig. 3 in ‘Results’ section) involves matching four verbal descriptions of non-linear situations to sketches of graphs. Dynamic situations involving matching verbal situations and graphs support the role of functions in representing variations (e.g. Swan, 1980). Our four situations focus on identifying the variables, forming the relation between them (in particular covariation) and noticing contextual features. Rates of change vary in all the situations. We added a drawing of axes to each situation included in the original task (Swan, 1980) and asked students to label variables to help them be explicit about variables and relations; we did this because it might scaffold students’ attention to choice and behaviour of variables (Leinhardt et al., 1990). This subset of tasks from the whole survey presents varied opportunities for students to identify contextual and quasi-contextual (task B) variables and reason about behaviour and relations between independent and dependent variables in formal (algebraic) and informal (verbal) ways. Students who do well in these tasks would be prepared for applications and modeling with functions and for considering more formal approaches to varied rates of change.

Fig. 3
figure 3

Task C

Full size image

Table 1 above shows how these three tasks address the categories and considerations arising in this summary of the theoretical background.

Methods

Sample

To make conjectures about progression towards the function concept in secondary years of schooling, we needed detailed data from a suitable spread of students in terms of age and past attainment, including higher achieving students who are most likely to need functions in later study or employment. We needed a sample that is large enough to encompass a wide range of possible responses while being small enough to analyse individual responses in detail. The survey was given to two suitable Israeli classes from each of year 7 to year 11, a highest achieving class (H) and a middle achieving class (M) and to a high achieving Israeli class (H) of year 12. The reason for including high and middle achieving groups was to get a spread of possible competency with the tasks. Year 7 to 11 classes were from two schools with each school providing data from alternate years. The year 12 class was from a third school for practical reasons. Using a range of schools ensured that we were not reporting an individual school effects, that we did not overburden institutions and that teachers engaged in productive discussions when they met. The survey was done in normal lessons, and we took random anonymised samples of 10 scripts from each class (110 scripts).

Data Analysis

For each task, we used a grounded approach to categorising all the different approaches students had taken. The responses were coded and organised according to the reasoning that could be inferred from answers. Decisions about interpretation were made collaboratively among the research team by discussion and consensus. We constantly checked categorisations against the whole data set, and between ourselves, testing distinctions to see if all responses fitted into one and only one category. This process required several passes through the whole data. The analytical process was thus iterative and comparative. For each task, the categories of responses are task-specific and include all approaches, whether successful or not. This is to generate as full a picture as possible of what students do in functions-related tasks. Detailed categories are presented below relating to each task.

Results

For each task, we introduce the task, the teachers’ expectations, the analytical categories (with examples) and quantitative results representing the distribution of the categories across years within the H and M groups. We report these cohorts separately so that the performance of the highest achieving students can be seen, and we draw attention to significant similarities or differences between the H and M cohorts in case there are some. We focus our remarks on identification of variables and relating variables.

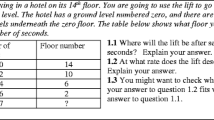
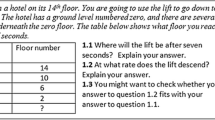
Task A (Fig. 1) focuses on rate of change, implicitly and explicitly, when an elevator descends. Constant speed is implied and was assumed by all teachers and students. The 2-s gaps followed by a ‘break’ in the time sequence in the data table were designed to help students notice that the term-to-term pattern of the table vertically requires some thought; the missing value was an attempt to draw attention to the break so that students would not be controlled by a linear pattern down the table. Question 1.2 asks explicitly for rate, which is not defined but examples are given, so that the data table needs to be transformed into ‘floors per second’. The last part of the task is intended to encourage critical reflection.

Teachers anticipated that students of all ages and groups would spot the correct missing value in 1.1 and succeed in finding the correct rate in 1.2. Although the concept of rate of change is not met formally until the end of year 7, teachers expected that year 7 students would be able to answer intuitively. Three categories of expressions of rate of change emerged, as presented in Table 2.

Table 2 Categories of response for task A
Full size table

Tables 3 and 4 present the distribution of the categories of expressions of rate of change in the H and M classes, respectively. As shown in Table 3, almost all H group students provided formal expressions of rate of change as floors per seconds for question 1.2, but 10 % chose the wrong answer of −2 when asked to find where the lift will be after 7 s, explaining that the lift is going down four every second. However, when asked to find the rate at which the lift descends, they used both variables to get the correct answer. Despite the stimulus in question 1.3, there was no evidence that any rethought question 1.1. The familiarity of the tabular form had apparently led them to ignore the independent variable until they had to use it for 1.2. In the M classes, a higher proportion of students made this mistake, and nine students, mainly younger ones, made this error throughout the whole task.

Table 3 Distribution of the categories of expressions of rate of change within the H classes
Full size table
Table 4 Distribution of the categories of expressions of rate of change within the M classes
Full size table

H and M classes both show some progression towards full capability in task A, although progress in M classes is a trend rather than a smooth increase. In the H classes, there is nearly full competence by year 8, whereas in the M classes, this happens by year 10. All students appeared to assume constant speed, as had the teachers.

Task B

Task B (Fig. 2) asks students to interpret a geometric pattern sequence that represents the perimeter of a chain of hexagons. It asks for a general expression which could be developed in a number of ways, such as using correspondence or covariation, and is a familiar type of task for students, although data are presented in an unfamiliar way. Question 2.1 requires finding numerical relations between given numbers of hexagons and the corresponding perimeter according to a given pattern. To avoid sequential reasoning, we presented data non-sequentially. Question 2.2 asks for a general computation method to obtain the perimeter of a large number of hexagons. This question cannot be answered directly from the data as a relationship has to be inferred by transforming the given data and comparing it to the diagram. Question 2.3 asks for an algebraic expression to describe the perimeter of any number of hexagons. This is an explicit request for a new representation and no direct support is given, but the previous questions are intended to direct students towards understanding the relations and structure they need to express. Question 2.4 asks for an explanation, that is a transformation into words.

Teachers expected students of year 7 classes to do fairly well since such tasks are posed in that year, although M students could find generating the algebraic expression in 2.3 difficult. Such tasks are not used after year 7 so they expected difficulties in 2.3 to be repeated in year 8 and onward, including for some H class students. Teachers also reported that students would probably use correspondence approaches since such methods were familiar. They expected students to use input–output reasoning with the step size as the multiplier.

Two parallel iterative and comparative analysis processes were implemented, one to describe approaches to functional reasoning and another to classify formality of generalisation. Five categories of approaches to functional reasoning emerged in students’ attempts to find and express relations in the data, as presented in Table 5.

Table 5 Categories of functional reasoning for task B
Full size table

Success in generalising was also categorised to see which approaches were more successful: (1) no correct generalisation of any kind; (2) generalisation expressed correctly in verbal terms only; or (3) generalisation expressed correctly verbally as well as algebraically.

Tables 6 and 7 present the distribution of the approaches to functional reasoning in students’ responses in the H and M, respectively. As shown in Table 6, the most common approach to conceptualising the functional relationships within both classes was the correspondence approach with students suggesting a general rule for the relation between the number of hexagons and the perimeter. The covariation approach of coordinating the two varying quantities while attending to the ways in which they change in relation to each other was less widespread, and was rare in the M classes, possibly because it required reorganisation of the data. In the H classes, a few students assumed linearity and then used formal knowledge: coordinate geometry and arithmetic sequences.

Table 6 Distribution of the approaches to functional reasoning and representation of generalisation within the H classes
Full size table
Table 7 Distribution of the approaches to functional reasoning and representation of generalisation within the M classes
Full size table

The triples in the cells of Tables 6 and 7 show the distribution of generalisation categories as described above.

As Table 6 shows, almost all students in the H classes generated the correct generalisation verbally and succeeded in forming it algebraically. Only one student verbalised a correct calculation without generating the corresponding algebraic expression. As shown in Table 7, about half of the M class students generated the correct generalisation verbally and succeeded in forming it algebraically, with four students verbalising a correct calculation without generating the corresponding algebraic expression. We cannot assume that verbalisation preceded the construction of a symbolic representation (Radford, 2000), but success in these two tasks was closely related.

For both H and M students, those who did not succeed with the correspondence approach applied deconstructive forms of generalisation based on counting each sub-configuration and did not manage to take away sides that overlap, similar to findings of Rivera & Becker (2008) who used similar sequential spatial sequences. For example, a student wrote ‘100 × 6 − 50 = 550, because you multiply the number of hexagons by the number of sides and then subtract the common sides’. Those who did not succeed with a covariation approach failed because they did not take starting values into account.

There is progression in the H classes and nearly full competence from year 8 onwards. In the M classes, although rate of success was lower, the overall trend is towards success, achieving nearly full competence in year 10. Proportions of students using various approaches are broadly similar across ages.

Task C

In task C (Fig. 3), students had to match four situations to graphs, selected according to an expected increase of difficulty: (i) straightforward identification of unidimensional variables; (ii) choice of variables; (iii) the use of compound variables; and (iv) compound variables and an inverse relationship. All situations focus on identifying variables, forming relations between them (in particular covariation) and noticing contextual features, such as zeroes and constants. In the terms of Carlson et al. (2002), these tasks would show us whether students could coordinate variables; identify the right direction of change; and maybe coordinate the amount of change in the two variables, i.e. their levels 1, 2 and 3 of covariation, always supposing that they first identified suitable variables.

Teachers reported that students from year 7 onwards meet various real-life graphs, e.g. conversion, distance/time and volume/time graphs, but students are usually given the variables. The teachers anticipated difficulties for all students as they are not used to constructing the variables themselves. Older students would not necessarily succeed more than the younger students, they suggested, but students from groups H would succeed more than students from M groups, as H students are more used to complex and unfamiliar tasks.

An iterative comparison of all 110 × 4 responses resulted in three general codes:

  1. 1.

    No choice, often accompanied by ‘I don’t know’

  2. 2.

    Lack of full analysis

  3. 3.

    Full analysis

Full analysis, which ought to show relevant choice of variables and the Carlson et al. (2002) first three levels applied to the situation that had been described verbally, was hampered by five sources of difficulty, which we exemplify in Table 8.

Table 8 Categories of difficulties in Task C
Full size table

Tables 9 and 10 present the distribution of categories taking all four situations into account in H and M classes, respectively. Students were less competent in this task than in tasks A and B. Moreover, in both H and M groups, there is no age-related progression towards full analytical interpretation. The quadruples in the cells show the distribution between the situations i–iv, respectively.

Table 9 Distribution of level of analysis within the H classes
Full size table
Table 10 Distribution of level of analysis within the M classes
Full size table

Analysis of the sources for difficulties in category 2 revealed that categories 2a, 2b, 2c, 2d and 2e (see Table 8) constituted 1, 16, 38, 40 and 5 % of all the H classes’ responses, respectively. Similarly, these categories constituted 7, 21, 40, 25 and 7 % of all the M classes’ responses, respectively. These findings show the criticality of identifying relevant variables and interpreting covariation in the verbal statement and the graph (2b, 2c, 2d), rather than the picture/graph confusion (2a) prominent in the literature (Schultz, Clement & Mokros, 1986). 2e is not described in the literature as far as we have been able to ascertain.

There was considerable variation in the frequency of these difficulties between situations. Irrelevant choice of one variable (2b) appeared in situations ii and iv only, plotting profit against time instead of ticket price in ii and distance or the distance remaining as related to time or speed in situation iv (see second example in Table 8). Most responses associated with category 2c appeared in situation iv, making the linear assumption, and situation iii, making the linear assumption (see third example in Table 8) or choosing the wrong way up. 2d problems were most common in situation i, i.e. not noticing that there was a period when all were applauding (saturation) (see fourth example in Table 8). All the 2a and 2e problems appeared in situation ii (see first and fifth examples in Table 8). There was little variation in the frequency of these categories across years, suggesting that certain sources of difficulties may be associated with some situations and not with others, and they persist in advanced years.

Discussion

No generalisations can be assumed from our small data set; rather we generate conjectures about conceptualisation and progression towards function understanding that can contribute to future thinking, and we challenge some assumptions about learners. From this data, with these three tasks, with these students, there appears to be progression over time towards a strong understanding of functions in the areas of rate of change and building correspondence relations in discrete, sequential, linear situations. In the H classes, there is nearly full competence by year 8, in the M classes by year 10. However, there is no discernible progression over time in matching graphs to verbal descriptions of situations; these appear to be situation-specific.

Both tasks A and B were designed to disrupt naive recursive reasoning and encourage students towards thinking about the situations and structures from which the data comes, rather than just thinking about numbers. Students in H and M classes were relatively successful and made some progress in overcoming unusual features in familiar task types to construct correct rates of change in task A and generalisations in task B. In task A, students showed high levels of competence with the global task of finding rate of change but made some mistakes with local data, although these were to some extent induced by the task presentation having unfamiliar features. Older students did not make these local mistakes, perhaps because of having more experience with non-sequential data presented in tabular form. Rate of change was mainly correctly deduced.

In task B, students overwhelmingly took a constructive, correspondence approach either by making local correct assumptions about linear functions or by analysing global overall structure. It seems that their curriculum experience has allowed them to develop a robust understanding of linear correspondence relations that do not depend on sequential data, even in a sequential context—only a very few tried to resort to sequential methods. This is contrary to some research reports in similar sequence pattern contexts with the same age of students: that they tend to begin with a term-to-term/additive approach (e.g. Stacey, 1989; Orton et al., 1999). No students assumed proportionality and few used term-to-term reasoning; the majority of students opted for a correspondence approach to produce an input–output model and explain it appropriately. This is contrary to some results about improperly applied direct proportional reasoning (Stacey, 1989; Van Dooren et al., 2005) However, in the study by Van Dooren et al. (2005), no sequence diagrams were provided, just a worded situation in similar form to the text of task B. They found that students within our age range had begun to distinguish between proportional and non-proportional situations in linear contexts, like ours, and their error rate was about 20 %. We go further than van Dooren et al. to claim that task design, curriculum and teaching, as well as age, make a difference.

In task C, there was no overall progression that we could discern, for either H or M classes, although H classes did better throughout. The sources of difficulties encountered by students appeared not to change across years in both H and M groups, but they did vary between specific situations, suggesting that certain sources of difficulties may be associated with some situations and not with others. In situation i, the main difficulty was taking all features into account (i.e. considering saturation), but the variables were fairly easy to discern. In situation ii, the most common problem was identifying variables and a tendency to try and use an irrelevant variable of ‘time’—a tendency known in the literature (e.g. Janvier, 1981). In situations iii and iv, forming a relationship that related to the contextual details was the main difficulty. In these situations, compound variables—rate of price change and speed—had to be considered, known to cause difficulty (Herbert & Pierce, 2012; Orton, 1983), although, according to the curriculum and to teachers, the concept of rate is formally introduced in the curriculum in year 7 and assumed (by the teachers) to be informally understood before that. Overall, no positive curriculum effects on task C responses can be indicated, since there were no signs of progress. This is as the teachers anticipated, but this does not mean we should not be concerned, as identifying variables and relating their behaviours should be a focus in mathematics learning. Moreover, Dreyfus & Eisenberg (1982) found that intuitive approaches did show some improvement during adolescence in their study. Being able to identify variables, including continuous, non-time, simple and compound situational variables, is valuable for advanced mathematics: calculus and modeling (e.g. Goldenberg, 1987). If students are always given variables and graphs (as according to the teachers is the case), they may be able to deduce covariational relationships but only undertake a small part of the modeling process that gives broad purpose to understanding functions. If we consider modeling capability to be a valued aim, the findings of this study suggest that students need to be presented with more opportunities to identify and express variables. We would also argue that the first stage of understanding covariation of Carlson et al. (2002) (i.e. coordination of variables) depends on first understanding the nature of the variables involved.

To better understand these findings, we further ask about the effects of task design and curriculum: Was it the task design that avoided the production of common problems of incorrect proportional reasoning or over-dependence on term-to-term reasoning? Certainly, our tasks were designed to challenge these tendencies, but the use of correspondence reasoning would also be due to curriculum, and teaching and students needed to be capable of adapting methods, which they did. We could also ask if formal teaching of functions in year 7 onwards plays a part? Certainly teaching and curriculum play a part, because students were very competent in using correspondence successfully, and perhaps, the use of f(x) notation enables them to focus on functions as ‘actions on x’ rather than as sequential change. However, our initial analysis of two other tasks in the survey that relate to formal knowledge does not show formal techniques and concepts being used progressively and consistently through the curriculum, rather they peak in years where these are taught but are not sustained at the same level in subsequent years. Use of formal knowledge seemed to be dependent on recency. We conjecture that conceptual understanding of linear functions is more complex, and more robust, than formal knowledge alone but are unable to provide evidence in this paper. All we can say is that it would be premature to assume that formal teaching had allowed the correspondence approach to dominate. Our data does, however, support a concern about lack of progression in task C, which indicates difficulties with modeling realistic phenomena, particularly worrying as the Israeli curriculum introduces the idea of variable rate of change in year 7.

Conclusion

Our approach looks at progression towards the function concept through secondary years in Israel, where the curriculum takes a formal approach to functions, alongside a realistic approach, from grade 7 onwards. Some findings contradict statements about students’ difficulties reported elsewhere, so we conjecture that curriculum, pedagogy and our task design played a part in producing different results: the successful use of correspondence approaches in linear contexts. We also raise concerns about lack of progression in some aspects of modeling contexts: identification of relevant variables and understanding how they relate, despite curriculum focus in early secondary years on varied rates of change.

Our future research will consist of comparison of data from England, where the function curriculum is less formal, in order to learn more about the effects of curriculum. The survey could be applied across wider samples in individual countries, using our categorisation, to smooth out effects of different pedagogy and focus on curriculum effects.