Efficient and effective algorithms for densest subgraph discovery and maintenance

Abstract

The densest subgraph problem (DSP) is of great significance due to its wide applications in different domains. Meanwhile, diverse requirements in various applications lead to different density variants for DSP. Unfortunately, existing DSP algorithms cannot be easily extended to handle those variants efficiently and accurately. To fill this gap, we first unify different density metrics into a generalized density definition. We further propose a new model, c-core, to locate the general densest subgraph and show its advantage in accelerating the search process. Extensive experiments show that our c-core-based optimization can provide up to three orders of magnitude speedup over baselines. Methods for maintenance of c-core location are designed to accelerate updates on dynamic graphs. Moreover, we study an important variant of DSP under a size constraint, namely the densest-at-least-k-subgraph (DalkS) problem. We propose an algorithm based on graph decomposition, and it is likely to give a solution that is at least 0.8 of the optimal density in our experiments, while the state-of-the-art method can only ensure a solution with a density of at least 0.5 of the optimal density. Our experiments show that our DalkS algorithm can achieve at least 0.99 of the optimal density for over one-third of all possible size constraints. In addition, we develop an approximation algorithm for the DalkS problem that can be more efficient than the state-of-the-art algorithm while keeping the same approximation ratio of $\frac{1}{3}$.

1 Introduction

Graph data plays essential roles in modeling relationships among objects in various domains, such as social networks, transportation, and biology [39]. To name a few, the Facebook community has been studied using a graph model with a mapping between users and vertices [65]. The pages and hyperlinks in the World Wide Web can be viewed as vertices and edges in a directed graph [37]. In a graph representing proteins and their interactions, chemical molecules and covalent bonds are mapped to vertices and edges, respectively [66]. To study the alternation of patterns and functional connectivity in brains, neuroscientists examine weighted 3-D graphs transformed from brain images [2].

The densest subgraph problem (DSP) has received much attention and lies in the heart of graph mining [9] since it has applications in many fields such as anomaly detection [15], bioinformatics [26], community detection [14], and financial markets [19]. The original density definition of a graph is given by the number of edges over the number of vertices, i.e., $\frac{m}{n}$, where m and n denote the edge and vertex number, respectively.

1.1 Generalized density

However, there are many scenarios that cannot be covered by the original density, such as weighted density, denominator weighted density, and h-clique density. The relationship of different densities is depicted in Fig. 2 and will be illustrated soon. First, the edges of graphs in real applications often carry weights. For example, in the flight network [16] airports are denoted as vertices, flights are denoted as edges, and the weight of an edge represents the flight frequency between two airports. Second, Goldberg [29] proposed the denominator weighted density where the weights of vertices are on denominators, and such a weighted density is also adopted by several follow-up studies such as [13, 56]. For instance, Sawlani and Wang [56] developed a method to solve DSP on directed graphs by transforming the directed graph into a set of vertex-weighted graphs and solving the DSP upon the weighted density, where vertex weights are on denominators. Beyond the above, to extract near-clique subgraphs, Tsourakakis [62] introduced the h-clique density. This density metric was found to help identify cohesive groups in large networks.

There are ample applications for the above density metrics. Taking the weighted density where all weights are on the numerator as an example, a method to detect fraudsters in camouflage adopts the weighted density on weighted graphs and solves the corresponding DSP [33]. Goldberg’s max-flow-based algorithm [29], and Chandra’s flow-based near-optimal algorithm [13] can be modified to handle the weighted density. Charikar’s peeling algorithm [12] and Greedy++ [11], which repeats the peeling algorithm several times, can also be extended to handle some of the above density metrics.

However, the limitation of these aforementioned methods under new density metrics is that they are either not scalable to large graphs or not capable of yielding a dense graph with a near-optimal density guarantee. Meanwhile, previous work barely targets building a general framework to boost DSP algorithms over a diverse range of density metrics. To fill this gap, we propose to use a generalized supermodular density to unify different metrics and develop a framework to speed up the generalized densest subgraph problem (GDS).

1.2 DalkS

In some circumstances, users demand for finding large dense graphs. For example, an activity organizer may want to have at least k participants who are familiar with each other. Given such a kind of demand, the densest at-least-k-subgraph problem (DalkS) [3], which is an important yet well-studied variant of DSP, is proposed to ensure that the dense graph has at least k vertices. Large dense subgraphs are useful in many domains such as distributed system [55], spam detection [27] and social networks [47]. Finding the exact solution for DalkS has been proven to be NP-hard [6, 46]. Therefore, some algorithms [3, 9, 13, 36, 55] are developed to approximate the exact DalkS. However, no existing work has devised a method to generate a solution with guarantees better than $0.5 \cdot OPT$, i.e. half of the optimal density.¹ In this paper, we will propose a new algorithm based on graph decomposition, which can obtain a solution better than the $0.5 \cdot OPT$ solution with a very high likelihood.

1.3 Contributions

In this paper, one of our main goals is to devise a method to accelerate the densest subgraph discovery w.r.t. the generalized density, particularly on large graphs, so that the near-optimal densest subgraphs can be found within a short time. For dynamic graphs, we develop efficient algorithms to make the acceleration effective even when updates on graphs are very frequent. Another breakthrough we make for DalkS, an important variant of DSP, is proposing a new algorithm that is likely to obtain a solution better than the $0.5 \cdot OPT$ solution achieved by the state-of-the-art. Moreover, we devise an algorithm that has a lower time cost than the fastest existing algorithm in practice. We briefly summarize our contributions below.

• We introduce a new dense subgraph model, c-core, which is general to cover many density metrics for GDS. We propose a framework to accelerate algorithms for GDS based on the c-core location.

• Based on c-cores, we propose an exact algorithm and an approximation algorithm with advanced pruning techniques for flow-based computations and a new strategy to search for the optimal density for the algorithm proposed by Chekuri et al. [13].²

• For dynamic graphs where edges can be inserted and deleted, we develop efficient algorithms to maintain c-core locations.

• We successfully derive the upper bound for the size of the exact solution for DalkS and devise a new approximation to DalkS based on our density-friendly decomposition.

• We devise an algorithm for DalkS that can be more efficient than the fastest algorithms in the literature, while still ensuring the same approximation ratio.

• We conduct experiments on 12 real-world weighted and unweighted graphs with up to 1.8 billion edges. Our proposed algorithms are faster than existing algorithms on both static and dynamic graphs. Additionally, we empirically show that our proposed approximation algorithm for the DalkS problem can output a solution very close to the optimal solution in most scenarios.

Remark

An earlier version of this work has appeared in the SIGMOD 2023 conference [68]. Additional contributions in this work mainly include the maintenance of c-core location for dynamic graphs and fast DalkS algorithms with experiments to verify their performance.

1.4 Outline

The organization of the paper is as follows. In Sect. 2, we review the related work. In Sect. 3, we unify different density metrics and define the GDS problem. Section 4 introduces the new c-core model and builds its connection with the GDS problem. Section 5 follows with GDS algorithms based on c-core. We introduce efficient methods to maintain c-core location in Sect. 6. An approximation algorithm and a faster algorithm to DalkS will be presented in Sect. 7. Experimental results are shown in Sect. 9, and Sect. 10 concludes our work.

2 Related work

Among different types of dense subgraphs, the Densest Subgraph Problem (DSP) [23] lies at the core of large-scale data mining [9]. We focus on the densest subgraph problem and its variants in the following.

2.1 Densest subgraph problem (DSP)

A fundamental focus which lies in the heart of graph mining is to find dense subgraphs [28]. The commonly used edge-density of an undirected unweighted graph G(V, E) is $\frac{m}{n}$ with $n = |V|$ and $m = |E|$ [29]. Works on weighted graphs mainly use two density metrics: one places all the weights on the numerator [29, 33], and the other places the weights of vertices on the denominator [29, 56]. We will give a generalized density definition to cover both cases and more variants.

To solve the densest subgraph problem (DSP), Goldberg [29] devised a max-flow-based algorithm to obtain exact solutions. Despite its high accuracy, the flow-based approach fails to be scaled to very large graphs with tens of millions of edges. Later, a new concept, clique-density, was proposed and efficient exact algorithms for finding the corresponding DS were developed in [22, 63]. Saha et al. [54] then studied the most probable DS using clique-density and pattern-density in uncertain graphs. To scale up k-clique DS detection, He et al. [32] proposed SCT*-Index to compactly organize the k-cliques. Generally, the exact DSP algorithms [29, 41, 63] work well on graphs of small or moderate size, but suffer from large graphs.

To further boost efficiency, several approximation algorithms have been developed. Charikar [12] proposed a $\frac{1}{2}$-approximation method³ for unweighted graphs by repeatedly peeling the vertex with the smallest degree. Bahmani et al. [9] introduced a new algorithm over streaming models running in $O(m \cdot \frac{\log {n}}{\epsilon })$ to guarantee a $\frac{1}{2+2\epsilon }$-approximation. Feng et al. [25] used spectral theory to develop an algorithm faster than Charikar’s peeling to yield a solution with comparable accuracy. In order to avoid calling maximum flow, Boob et al. [11] designed an empirically efficient method called Greedy++ by repeating the peeling process multiple times. Chandra et al. [13] gave a flow-based $(1-\epsilon )$-approximation algorithm by performing a limited number of blocking flows on the flow network.

Despite the focus on DSP, little can find an approximation close to the exact solution while maintaining efficiency, especially for the generalized density definition. This bottleneck becomes even trickier when large-scale graphs of up to billions of edges are considered. Therefore, some applications involving DSP on large graphs only utilize naive peeling to make the approximation. For instance, Hooi et al. [33] used a $\frac{1}{2}$-approximation DSP algorithm on weighted graphs to find the fraudsters as the alternative to the exact solution.

2.2 Variants of DSP

DSP has also been studied on other graphs, e.g., directed graphs [12, 36, 42, 43, 45], dynamic graphs [21, 35], and hypergraphs [10, 34]. Tatti et al. [61] and Danisch et al. [17] studied the density-friendly decomposition problem to decompose the graph into a chain of subgraphs, where each inner subgraph is denser than the outer ones. Qin et al. [52] and Ma et al. [44] studied the locally densest subgraphs problem to find multiple locally dense regions from the graph.

When size-bound restrictions are imposed, the densest subgraph problem becomes NP-hard [6, 8, 24, 46]. Specifically, Andersen and Chellapilla [3] utilized Charikar’s peeling algorithm to always yield a $\frac{1}{3} \cdot OPT$ solution to the densest at-least-k-subgraph problem (DalkS), where an at-least-k-subgraph means a subgraph with at least k vertices. Chekuri et al. [13] then extended the $\frac{1}{3}$-approximation method to the densest at-least-k supermodular subset problem. To achieve better solutions, Khuller and Saha [36] provided a combinatorial algorithm and a linear-programming-based algorithm to output a $\frac{1}{2} \cdot OPT$ solution. However, the existing DalkS solution cannot obtain a better guarantee than a solution with density of at least 0.5 of the optimal density.

2.3 Comparison

Since some parts of our work are based on [13], we identify our related contributions compared to it: First, Chekuri et al. [13] devised a flow network and a brief idea for finding DSP with this flow network. Based on the flow network, we complete the implementation detail of how to search for subgraphs with guessed densities and developed the algorithm FlowApp. We observe that FlowApp is not efficient enough and propose a faster algorithm FlowApp* to achieve acceleration (Sect. 5). Second, Chekuri et al. [13] directly investigated the generalized supermodular density, while we manage to show that multiple density metrics are special cases of the generalized supermodular density (Sect. 3). To the best of our knowledge, we propose to unify weighted density (Definition 3.4), denominator weighted density (Definition 3.5) and h-clique density (Definition 3.6) by the generalized supermodular density (Definition 3.3) for the first time.

3 Problem definition

In this section, we first review the concept of generalized supermodular density and the generalized densest subgraph based on this density. We then show that several existing DSP variants can be viewed as special cases of the generalized densest subgraph.

Definition 3.1

(Doubly Weighted Graph [67]) A doubly weighted graph is a 4-tuple $G(V, E, W_V, W_E)$, where V and E denote the sets of vertices and edges, respectively, $W_{V}=\{w_{v}|v\in V\}$ contains vertex weights, and $W_{E}=\{w_{e}|e\in E\}$ contains edge weights.

Fig. 1

Doubly weighted graph and c-core

We denote the subgraph induced by $S \subseteq V$ as G[S], and the edge set in G[S] as E(S).

Example 3.1

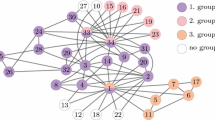
Fig. 1 presents an instance of doubly weighted graph. The numbers on vertices and edges are their weights, respectively. For instance, node c has weight 4 and edge (c, e) has weight 3.

The doubly weighted graph is general and it covers the concept of the weighted graph. Many density metrics can be defined on the doubly weighted graph such as weighted density and clique density. We propose to unify these density metrics by a generalized supermodular density. Before introducing the generalized supermodular density definition, we first review the concepts of supermodular and submodular as its foundation.

Definition 3.2

(Supermodular & Submodular [13]) Given a space $2^V$, a real-valued set function $f: 2^V \rightarrow \mathbb {R}$ is supermodular if and only if $f(W) + f(U) \le f(W \cup U) + f(W \cap U)$, where W and U are any two subsets of V. A set function $g: 2^V \rightarrow \mathbb {R}$ is submodular if and only if $-g$ is supermodular.

Definition 3.3

(Generalized Supermodular Density [13]) Given a doubly weighted graph $G(V, E, W_{V}, W_{E})$ and $S \subseteq V$, the generalized supermodular density of S can be described as

$$\begin{aligned} \rho (S) = \frac{f(S)}{g(S)} \end{aligned}$$

(3.1)

where $f: 2^{V} \rightarrow \mathbb {R}^{+}$ is a nonnegative supermodular function and $g: 2^{V} \rightarrow \mathbb {R}^{+}$ is a nonnegative submodular function.

Next, we show that several well-known density variants can be regarded as special cases of the generalized supermodular density.

Definition 3.4

(Weighted Density [29, 33]) Given a weighted graph $G(V, E, W_V, W_E)$ and $S \subseteq V$, the weighted density of S is given by

$$\begin{aligned} \rho _{W}(S) = \frac{\sum _{e \in E(S)} w_e + \sum _{v \in S} w_v}{|S|} \end{aligned}$$

(3.2)

Proposition 3.1

The weighted density (Definition 3.4) is a special case of the generalized supermodular density (Definition 3.3) with $g(S)=|S|$ and $f(S)=\sum _{e \in E(S)} w_e + \sum _{v \in S} w_v$.

Proof

g(S), the denominator, is both supermodular and submodular. For f(S), given any two subsets $U, W \subseteq V$, we have $f(W \cup U) + f(W \cap U) \ge f(W) + f(U)$, as the left hand side contains extra edge weights for all $e=(u,v)$ where $u\in W\setminus U$ and $v \in U \setminus W$. $\square$

Definition 3.5

(Denominator weighted density [29]) Given a weighted graph $G(V, E, W_V, W_E)$ and $S \subseteq V$, the denominator weighted density of S is given by

$$\begin{aligned} \rho _{DW}(S) = \frac{\sum _{e \in E(S)} w_e}{\sum _{v \in S} w_v} \end{aligned}$$

(3.3)

Proposition 3.2

The denominator weighted density is a special case of the generalized supermodular density (Definition 3.3).

Definition 3.6

(h-clique density [41, 64]) Given a graph G, for any $S\subseteq V$ its h-clique density can be defined as

$$\begin{aligned} \rho _{h}(S)=\frac{c_{h}(S)}{|S|}, \end{aligned}$$

where $c_{h}(S)$ is the number of h-cliques induced by S.

Proposition 3.3

The h-clique density is a special case of the generalized supermodular density (Definition 3.3).

Proposition 3.2 and Proposition 3.3 can be proved similarly as Proposition 3.1. The relationship of different density definitions is also illustrated in Fig. 2.

Figure 2 depicts the relationships among different density metrics. As can be seen, the generalized supermodular density covers the original density, the weighted density, the denominator density and the h-clique density. The original density is a special case of all of the other density metrics.

Fig. 2

Relationship of different densities

Based on the generalized supermodular density definition, we can define the generalized densest subgraph problem.

Problem 3.1

(Generalized Densest Subgraph (GDS) Problem [13]) Given a doubly weighted graph G and a generalized supermodular density metric $\rho (S) = \frac{f(S)}{g(S)}$, the GDS problem aims to find the generalized densest subgraph, i.e., $G[S^{*}]$ where $S^{*}= \arg \max _{S \subseteq V} \rho (S)$.

Example 3.2

Taking the graph on Fig. 1 as an example, if the generalized supermodular density $\rho (S)=\rho _{W}(S)$, i.e., the weighted density (Definition 3.4), then the GDS will be a subgraph induced by $\{c, g, e\}$ with the density of $\frac{17}{3}$. Similarly, if $\rho (S)=\rho _{DW}(S)$, then the GDS will be $G[\{e, f, d\}]$ with a density of 1.5; if $\rho (S)=\rho _{h}(S)$ with $h=3$, then the GDS will be $G[\{c, d, e, f, g\}]$ with a density of $\frac{3}{5}$.

In some applications, the densest subgraph with a size constraint is desired. For example, when organizing conferences, the organizer may want to have at least k participants. Hence, the densest at least k subgraph problem (DalkS) is one kind of DSP with size constraint.

Problem 3.2

(Densest at-least-k-subgraph (DalkS) problem [3]) Given a doubly weighted graph G, a corresponding density metric $\rho (S)$ and a size lower bound k, DalkS aims to find the densest at-least-k-subgraph $G[K^{*}]$, where $K^{*} = \arg \max _{K \subseteq V \wedge |K| \ge k} \rho (K)$.

In this paper, we mainly consider the weighted density (Definition 3.4) for the DalkS problem. Example 3.3 can show what are the exact solutions for DalkS for different size constraints k.

Example 3.3

If $\rho (S)=\rho _{W}(S)$ is adopted for DalkS on the graph shown in Fig. 3, the DalkS is just the GDS when $k \le 3$. When $k = 4$, the DalkS is induced by $\{c, d, e, g\}$ with a density $\frac{11}{2}$; when $k=5$, the DalkS is induced by $\{c, d, e, f, g\}$ with a density $\frac{27}{5}$; when $k=6$, the DalkS is induced by $\{a, c, d, e, f, g\}$ with a density $\frac{31}{6}$; when $k=7$, the whole graph serves as the DalkS.

4 c-core and GDS

In this section, we introduce a new core model inspired by k-core [57] on unweighted graphs. Next, we present an algorithmic framework that leverages the connection between the cores and the GDS to speed up the GDS searching process.

4.1 Contribution and c-core

The new core model is based on a novel concept, namely contribution.

Definition 4.1

(Contribution) Given a doubly weighted graph $G(V, E, W_V, W_E)$, a generalized supermodular density $\rho (S)=\frac{f(S)}{g(S)}$, and a subset $S \subseteq V$, where f and g are defined on space $2^V$. The contribution of a vertex $v \in S$ is

$$\begin{aligned} c_S(v) = \frac{f(S) - f(S \backslash v)}{g(S) - g(S \backslash v)} \end{aligned}$$

(4.1)

The subscript of contribution notation means the contribution of the node is calculated with respect to a specific subset $S \subseteq V$.

Definition 4.2

(c-core) Given a weighted graph $G(V, E, W_V, W_E)$, a positive real value c, and a generalized supermodular density $\rho (S)=\frac{f(S)}{g(S)}$, where $S\subseteq V$, a subgraph G[S] is a c-core w.r.t. G if it satisfies

• 1. $\forall v \in S$, $c_S(v) \ge c$;

• 2. $\not \exists S' \subseteq V$, s.t. $S \subset S'$ and $S'$ satisfies (1).

Next, we use an example to illustrate c-cores on a weighted graph when the generalized supermodular density $\rho (S)=\rho _{DW}(S)$ (Definition 3.5). Specifically, we have $\rho (S)=\frac{f(S)}{g(S)}=\frac{\sum _{e \in E(S)} w_e}{\sum _{v \in S} w_v}$.

Example 4.1

Reconsider the graph in Fig. 1. According to Definition 4.1, the contribution of a vertex u w.r.t. a subset $S\subseteq V$ is $c_{S}(u) = \frac{\sum _{e: v \in e \wedge e\in E(S)} w_e}{w_u}$. Based on the contribution formula, the whole graph G[V] is a 0.25-core, as $c_{V}(a)=0.25$ is the smallest contribution value among all vertices. If we remove the vertices whose contribution values are not larger than 0.25, we will obtain a subset $S_{1}=\{c, d, e, f, g\}$, i.e., a and b are removed. $G[S_{1}]$ is a 1-core, as $c_{S_{1}}(c)=1$ is the smallest among $S_{1}$. Peeling vertex with a contribution not larger than one will give us a new subset $S_{2}=\{d, e, f, g\}$, where $G[S_{2}]$ is a 2-core. Similarly, we can also obtain the 2.5-core, $G[S_{3}]$, where $S_{3}=\{e,f,d\}$ by peeling vertices with a contribution not larger than two.

The above example shows that a series of c-cores with increasing coreness of a graph can be obtained by keeping peeling vertices. Similar to the generalized supermodular density covering several density variants, the c-core model can also cover several well-known core models. s-core [20], related to the weighted density (Definition 3.4), is one of such core models.

Definition 4.3

(Strength [20]) Given a doubly weighted graph $G(V, E, W_{V}, W_{E})$ and a vertex $v \in V$. The strength of the node w.r.t. a subset S is defined as

$$\begin{aligned} s_{S}(v) = w_v + \sum _{e: u\in e \wedge e \in E(S) } w_e \end{aligned}$$

(4.2)

Definition 4.4

(s-core [20]) Given a doubly weighted graph $G(V, E, W_V, W_E)$ and a vertex set $S\in V$. A subgraph G[S] is a s-core w.r.t G if it satisfies

• 1. $\forall v \in S$, $s_S(v) \ge s$;

• 2. $\not \exists S' \subseteq V$, s.t. $S \subset S'$ and $S'$ satisfies (1).

Proposition 4.1

Strength (Definition 4.3) is a special case of contribution (Definition 4.1) and thus s-core is a special case of c-core.

Proof

Let $g(S) = |S|$ and $f(S) = \sum _{v \in S} w_v + \sum _{e \in E(S)} w_e$ in the generalized supermodular density. Observe that g is submodular and f is supermodular. We specialize contribution to strength by definition, i.e. $c_S(v) = s_S(v)$. $\square$

Definition 4.5

(h-clique degree [41]) Given a graph G(V, E) and a vertex $v \in V$. The h-clique degree of the node v w.r.t. a subset S is defined as

$$\begin{aligned} deg_{S}(v, h) = |\{\psi | \psi \in G[S], v \in \psi \}|, \end{aligned}$$

(4.3)

where $\psi$ is an instance of h-clique.

Definition 4.6

(h-clique-core [41]) Given a graph G(V, E) and a vertex set $S\in V$, a subgraph G[S] is a h-core w.r.t. G if it satisfies

• 1. $\forall v \in S$, $deg_S(v, h) \ge h$;

• 2. $\not \exists S' \subseteq V$, s.t. $S \subset S'$ and $S'$ satisfies (1).

Proposition 4.2

h-clique degree (Definition 4.5) is a special case of contribution (Definition 4.1) and thus h-clique-core is a special case of c-core.

Proof

Let $g(S) = |S|$ and $f(S) = |\{\psi |\psi \in G[S]\}|$ in the generalized supermodular density. Observe that g is submodular and f is supermodular. We specialize contribution to h-clique-degree by definition, i.e. $c_S(v) = deg_S(v, h)$. $\square$

Based on the above discussions, we can find that c-core is efficient to compute via peeling and general to cover different core models. Next, we will show that c-core can also be used to locate the GDS in a small subgraph to speed up the GDS searching.

4.2 Locating GDS in c-cores

We derive some useful properties of c-core and show that these properties are powerful to locate the GDS in some cores. Lemma 4.1 reveals that the contribution (Definition 4.1) of any vertex in the GDS is at least the density of the GDS.

Lemma 4.1

Given a doubly weighted graph G and a generalized supermodular density $\rho (S) = \frac{f(S)}{g(S)}$, suppose $G[S^{*}]$ is the GDS w.r.t. $\rho$. For any $U \subseteq S^{*}$, we have $\frac{f(S^{*}) - f(S^{*} {\setminus } U)}{g(S^{*}) - g(S^{*} {\setminus } U)} \ge \rho (S^{*})$.

Proof

We prove the lemma by contradiction. Suppose we have $\frac{f(S^{*})-f(S^{*} \backslash U)}{g(S^{*})-g(S^{*} \backslash U)} < \rho (S^{*})$.

$$\begin{aligned}&\rho (S^{*}) \cdot (g(S^{*}) - g(S^{*} \backslash U))> f(S^{*}) - f(S^{*} \backslash U)\nonumber \\&\quad \Longrightarrow f(S^{*} \backslash U)> \rho (S^{*}) \cdot g(S^{*} \backslash U)\nonumber \\&\quad \Longrightarrow \rho (S^{*} \backslash U) = \frac{f(S^{*} \backslash U)}{g(S^{*} \backslash U)} > \rho (S^{*}) \end{aligned}$$

(4.4)

$\square$

To locate the GDS in c-cores, we first introduce an important property of vertex contribution.

Lemma 4.2

Suppose there are two vertex subsets $S_{1}$ and $S_{2}$ satisfying $S_{1}\subseteq S_{2} \subseteq V$. We have $\forall v \in S_{1}$, $c_{S_{1}}(v) \le c_{S_{2}}(v)$.

Proof

$c_{S_{2}}(v) = \frac{f(S_{2})-f(S_{2}{\setminus } v)}{g(S_{2})-g(S_{2}{\setminus } v)} \ge \frac{f(S_{1})-f(S_{1}{\setminus } v)}{g(S_{1})-g(S_{1}{\setminus } v)} = c_{S_{1}}(v)$. The inequality holds because f(S) is supermodular and g(S) is submodular. $\square$

Based on Lemmas 4.1 and 4.2, we can derive the theorem to locate the GDS in some c-cores. Let the GDS be $G[S^{*}]$ and its density be $\rho (S^{*})$ which is the optimal density. Theorem 4.1 indicates that the GDS $G[S^{*}]$ is a subgraph of the c-core with c equal to the optimal density.

Theorem 4.1

Given a doubly weighted graph $G(V, E, W_V, W_E)$, suppose $G[S^{*}]$ is the GDS. Denote the $\rho (S^{*})$-core as G[C]. Then, $S^{*} \subseteq C$.

Proof

We prove the theorem by contradiction. Suppose $U=S^{*} {\setminus } C \ne \emptyset$. By Lemma 4.1, for any $u \in U \subseteq S^{*}$, we have $c_{S^{*}}(u) \ge \rho (S^{*})$. By Lemma 4.2, $\forall u \in U$, $\rho (S^{*}) \le c_{S^{*}}(u) \le c_{S^{*} \cup C}(u)$. Hence, $G[S^{*} \cup C]$ is a larger $\rho (S^{*})$-core than G[C], which contradicts the definition of c-core. $\square$

4.3 c-core-based algorithmic framework

Based on Theorem 4.1, we know that the GDS can be located in the $\rho (S^{*})$-core. However, we do not know the exact value $\rho (S^{*})$ as a priori before the GDS is found. Fortunately, the density of the densest c-core via peeling can serve as a lower bound of $\rho (S^{*})$. In practice, utilizing the density of the densest c-core can help reduce the graph size.

We present an algorithmic framework to accelerate the GDS searching in Algorithm 1. Let $G[\tilde{S}]$ be the densest c-core obtained by peeling on G. In the framework for acceleration, we first find the $G[\tilde{S}]$ via peeling (line 1), use the density of the $G[\tilde{S}]$ as the lower bound $\hat{\rho }$ of $\rho (S^{*})$ (line 2) and find the $\hat{\rho }$-core, $G'$ (line 3). Note that $G[S^{*}] \subseteq \rho (S^{*})$-core $\subseteq \hat{\rho }$-core $= G^{'}$. Next, we can run any GDS algorithm GDSalg on $G'$ to find the (approximate) GDS (line 4). We can observe that this framework can locate the GDS in a small subgraph. Hence, the invoked GDS algorithm will be boosted as it only needs to process a small subgraph.

Algorithm 1

cCoreGDS

Example 4.2

This example shows the process of Algorithm 1 cCoreGDS on the graph in Fig. 1 with denominator weighted density (Definition 3.5). Following Example 4.1, we obtain a series of c-cores, $S_1 = \{c, d, e, f, g\}$, $S_2 = \{d, e, f, g\}$ and $S_3 = \{d, e, f\}$ with density 1, $\frac{16}{11}$, $\frac{12}{7}$ and $\frac{3}{2}$ respectively. Observe that in this case, the densest c-core is the subgraph induced by $S_2$, which is not the c-core with the largest coreness. Then we let $\tilde{S}$ in Algorithm 1 be $S_2$ and $\hat{\rho } = \rho (S_2) = \frac{12}{7}$. Starting from the whole graph, we peel all vertices with their contribution less than the coreness $\hat{\rho }$. Vertices a, b, c are peeled sequentially and the remaining vertices all have at least $\hat{\rho }$ contributions. The subgraph induced by $\{d, e, f, g\}$ is a $\hat{\rho }$-core by definition and it is the $G^{'}$ in Algorithm 1. Finally, we run the GDS algorithm on the graph $G^{'}$.

5 GDS Algorithms

In this section, we first review existing DSP algorithms on unweighted graphs and discuss how they can be adapted to the GDS problem and fitted into our algorithmic framework. Next, we propose new acceleration techniques for flow-based algorithms to improve their efficiency.

5.1 Existing algorithms

The flow-based exact algorithm [29] The main idea of Goldberg’s flow-based approach [29] is to compare the density of the densest subgraph with a guess value g via max-flow computation and do the binary search to narrow the guess range. Although it can provide accurate results, the max-flow computation is very time costly, especially on large-scale graphs.

Algorithm 2 gives the pseudo-code of Goldberg’s FlowExact [29]. First, the guess range of the density is initialized as $l=0$ and $r=\max _{v\in V}{c_{V}(v)}$, the maximum contribution (Definition 4.1) among all vertices (line 1). Next, the while loop repeats the binary search to shrink the guess range until the range is smaller than a given coreness (lines 2–8). For each guessed g, the algorithm constructs a flow network (line 4), computes the minimum st-cut (line 5), and updates the range as well as $S^{*}$ based on st-cut (lines 6–7). FlowExact can be extended to handle the weighted density (Definition 3.4). When the weights on edges and vertices are integers, we can guarantee an exact solution by requiring $\delta < \frac{1}{|V| \cdot (|V| - 1)}$ [29].

Algorithm 2

FlowExact [29]

The flow-based approximation algorithm [13] The flow-based approximation algorithm FlowApp is proposed by Chekuri et al. [13] to solve DSP. Compared to Goldberg’s FlowExact, FlowApp does not need to run the full maximum flow algorithm. In other words, it can terminate in advance for a given error tolerance $\epsilon$. But it also suffers from the huge cost of performing flow computations on large-scale graphs.

Fig. 3

Flow network constructed from the 2.5-core

Both FlowExact and FlowApp can be applied to doubly weighted graphs. For example, if the weighted density (Definition 3.4) is adopted as the generalized supermodular density, the flow network can be constructed as shown in Fig. 3 for the 2.5-core in Fig. 1. Besides, [13, 29] provide the flow network for GDS on denominator weighted density (Definition 3.5).

Example 5.1

Figure 3 shows the flow network built upon the 2.5-core in Fig. 1 to solve GDS based on Definition 3.4. Each element in the vertex set $\{e, f, d\}$ and the edge set $\{(e, f), (f, d), (e, d)\}$ is treated as a node in the constructed flow network. A source node s is linked to vertex nodes and edge nodes by arcs. The capacity of arcs from s to vertex nodes are weights on the vertices, while the capacity of arcs from s to edge nodes are weights on the edges. Each vertex node is connected to its incident edge nodes by arcs having infinite capacity. Finally, arcs with the capacity of guessed value g will be built between each edge node and the sink node t.

Apart from the above two flow-based algorithms, Greedy++ [11] and the Frank-Wolfe-based algorithm [17] can also be adapted to doubly weighted graphs, and fitted into the cCoreGDS framework by replacing GDSalg in line 4 of Algorithm 1 with the corresponding algorithm. Fang et al. [22] devised methods to accelerate DS algorithms with h-clique density. However, they did not study the generalized super-modular density. Our cCoreGDS framework encompasses their approach as a specialized instance. By wrapping the algorithms into the cCoreGDS framework, we can perform the GDS searching on smaller subgraphs instead of the whole large graph.

5.2 Boosting flow-based algorithms via cores

Taking a closer look at the flow-based algorithms, we can find that the searching range of the optimal density is shrinking along with the binary search. Hence, the lower bound of the density is monotonically increasing during the binary search. In this case, when the lower bound l in Algorithm 2 increases, we can locate the GDS in a c-core with a higher coreness and smaller size. Replacing the if statement (lines 6–7) in Algorithm 2 with the following lines (Algorithm 3), FlowExact may be possibly boosted by c-cores with smaller sizes during the binary search.⁴ Similar code with minor changes can also be added to FlowApp.

Algorithm 3

c-core-based pruning in flow-based algos

5.3 New density search strategy for FlowApp

FlowApp [13] as a flow-based approximation can enrich the library of DS algorithms with interpretation related to linear programming [11]. However, it needs a strategy to search for the optimal density value, because only a brief idea about it was given (see Corollary 2.1 in [13]). That is one can initialize the error tolerance as $\tilde{\epsilon } = 0.5$ and then decrease it by half once the (1-$\tilde{\epsilon }$)-approximation of the subgraph with the new guessed density is found. However, they did not elaborate on how to find the (1-$\tilde{\epsilon }$)-approximation. We give the details and present the strategy in Algorithm 4. Next, to further reduce the searching cost, we develop an advanced searching strategy, which will be given in Algorithm 5.

Similar to the binary search in FlowExact, the searching strategy in FlowApp [13] also needs to guess the density g within a range (l, r) with some error tolerance $\epsilon _{0}$. For the guessed g, FlowApp will perform a fixed number of blocking flows [1, 4, 30, 58, 60] on the constructed flow network such as the one in Fig. 3. On the residual network after blocking flows, either there exists an easy-to-get subgraph with a density of at least $(1-\tilde{\epsilon }) \cdot g$, or there exists no subgraph of density larger than g. The searching range (l, r) will be shrunk accordingly based on one of the two possible outcomes until the error tolerance given by the user is fulfilled.

Algorithm 4

FlowApp [13]

Algorithm 4 gives the pseudo-code of FlowApp. FlowApp first initializes the error bound $\tilde{\epsilon }$ to $\frac{1}{2}$, and the density range (l, r) to $(0, \max _{v\in V}{c_{V}(v)})$ (line 1). Then, we have a while loop to keep guessing the density g and shrink the density range (l, r) based on the result of blocking flows (lines 2–12). In each iteration, the algorithm guesses g, constructs the flow network F, and performs a fixed number of blocking flows (lines 3–6). If there exists an augmenting path in F after blocking flows, this means that there exists a subgraph with the density of at least $(1-\tilde{\epsilon }) \cdot g$ (lines 7–9). If $(1-\tilde{\epsilon }) \cdot g \le l$, FlowApp reduces the error guarantee $\tilde{\epsilon }$ by half, as shown in Case 2 in Fig. 4a; otherwise l will be updated to $(1-\tilde{\epsilon }) \cdot g$, as shown in Case 1 in Fig. 4a and FlowApp saves the residual graph of F to $R_{l}$ (lines 8–9). If no augmenting path exists, FlowApp updates r to g (line 11), and halves the error bound $\tilde{\epsilon }$. FlowApp terminates the loop until the error bound $\tilde{\epsilon }$ satisfies the requirement $\epsilon$ (line 2). Finally, it extracts the $(1-\epsilon )$-approximation GDS $G[\tilde{S}^{*}]$ from the residual graph $R_{l}$ and returns it as the output (lines 13–14).

Reviewing the above process, we can find that when the while loop is terminated, we have the possible density range (l, r) satisfying $\frac{l}{r}>(1-\epsilon )$. Hence, we can extract a $(1-\epsilon )$-approximate GDS from the residual graph $R_{l}$ by Theorem 2.1 in [13].

Fig. 4

Illustration of density searching strategies

Observations. In practice, we find the strategy to update $\tilde{\epsilon }$ in FlowApp [13], which initializes $\tilde{\epsilon }=\frac{1}{2}$ and decreases it by half when appropriate, is sometimes not efficient. The reason lies in the case where there exists a subgraph with density at least $(1-\tilde{\epsilon }) \cdot g$, as shown in Fig. 4a. The narrowing of the density range is slow when $(1 - \tilde{\epsilon }) \cdot g$ is only slightly greater than l in Case 1 or even unchanged in Case 2. Meanwhile, the error bound $\tilde{\epsilon }$ is halved only in Case 2 and can stay the same for several iterations. Hence, the error bound $\tilde{\epsilon }$ cannot fall below $\frac{\epsilon }{2}$ quickly to fulfill the requirement.

To overcome the inefficiency caused by the above intricate strategy, we propose a novel and simple strategy, where the error bound $\tilde{\epsilon }$ is decided adaptively based on the density range (l, r). The advantage of our strategy is that the density range

• 1. reduces by $\frac{1}{4}$ steadily, when there exists a subgraph with density at least $(1-\tilde{\epsilon }) \cdot g$, as shown in Fig. 4b, where l is set as $(1-\tilde{\epsilon })g = \frac{l+g}{2}$ in the next iteration;

• 2. reduces by half, when there exists no such subgraph.

Based on this novel strategy, we design a new $(1-\epsilon )$-approximation algorithm, FlowApp*, in Algorithm 5. The steps of FlowApp* are similar to FlowApp. The differences are mainly related to the density searching strategy, as listed below:

• 1. the error bound $\tilde{\epsilon }$ is given by $\frac{g-l}{2\,g}$, where $g=\frac{r+l}{2}$ is the guessed density, and does not follow a fixed decreasing strategy like that in FlowApp (line 3);

• 2. if there exists a augmenting path in F, l can be safely updated to $(1-\tilde{\epsilon })\cdot g = \frac{g+l}{2}$ (lines 7–8);

• 3. the while loop will be terminated when $\tilde{\epsilon } < \frac{\epsilon }{3 - 2\epsilon }$ (line 2).

Algorithm 5

FlowApp*

With the new density searching strategy, our FlowApp* can still output a $(1-\epsilon )$-approximation result.

Proposition 5.1

Algorithm 5 can output a $(1-\epsilon )$-approximation.

Proof

Consider the last iteration of the while loop. If there exists a subgraph with a density of at least $(1 - \tilde{\epsilon })g$, we have $(1 - \tilde{\epsilon })g < \rho (S^{*}) \le (1 + 2\tilde{\epsilon })g$. The second ineuqality can be obtained from $(1+2\tilde{\epsilon })g = (1+\frac{g-l}{g})g = 2\,g - l = r \ge \rho (S^{*})$. The condition $max_{\rho (S^{*})} (1 - \frac{l}{\rho (S^{*})}) < \epsilon$ can guarantee that we have a $(1-\epsilon )$-approximation. Then we get $1 - \frac{(1-\tilde{\epsilon })g}{(1+2\tilde{\epsilon })g} < \epsilon$ which is equivalent to $\tilde{\epsilon } < \frac{\epsilon }{3 - 2\epsilon }$. Otherwise, we do not have a subgraph with density larger than g, $l < \rho (S^{*}) \le g$ and $\text {max}_{\rho (S^{*})}(1 - \frac{l}{\rho (S^{*})}) = 1 - \frac{l}{g} = 2(\frac{1}{2} - \frac{l}{2\,g}) = 2 \frac{g-l}{2\,g} = 2 \tilde{\epsilon } < \epsilon$ can imply $\tilde{\epsilon } < \frac{\epsilon }{2}$. But this condition is satisfied automatically when we require $\tilde{\epsilon } < \frac{\epsilon }{3 - 2\epsilon }$ when $\epsilon < \frac{1}{2}$. $\square$

We further analyze why FlowApp* (Algorithm 5) is faster than FlowApp (Algorithm 4). Comparing (a) and (b) in Fig. 4, we observe that FlowApp cannot guarantee how much the searching range is decreased, while FlowApp* ensures that it can reduce the searching range by at least $\frac{1}{4}$. From the perspective of the termination condition, the faster the decrease of $\tilde{\epsilon }$, the faster the speed of the whole algorithm. In FlowApp, $\tilde{\epsilon }$ cannot decrease (Case 1 in Fig. 4a). In FlowApp*, we notice that $\tilde{\epsilon }$ always decreases during the while loop, shown in the following proposition.

Proposition 5.2

In Algorithm 5, $\tilde{\epsilon }$ strictly decreases. $\tilde{\epsilon }$ in the $(i+1)$-iteration is smaller than the value in the i-th iteration, i.e., $\tilde{\epsilon }_{i+1} < \tilde{\epsilon }_i$.

Proof

Suppose in the i-th loop, there is an augmenting path in F. Then $\frac{\tilde{\epsilon }_{i+1}}{\tilde{\epsilon }_{i}} = \frac{\frac{g_{i+1} - l_{i+1}}{2 g_{i+1}}}{\frac{g_i - l_i}{2 g_i}} = \frac{g_i}{g_{i+1}} \cdot \frac{g_{i+1} - l_{i+1}}{g_i - l_i}$, where the subscripts (i or $i+1$) denote the values in the corresponding iteration of the while loop. Observe that $\frac{g_i}{g_{i+1}} < 1$ and $\frac{g_{i+1} - l_{i+1}}{g_i - l_i} = \frac{3}{4}$. Consequently $\frac{\tilde{\epsilon }_{i+1}}{\tilde{\epsilon }_{i}} < \frac{3}{4}$. On the other hand, if there is no augmenting path, we have $\frac{\tilde{\epsilon }_{i+1}}{\tilde{\epsilon }_{i}} < 1$ since $\tilde{\epsilon }_{i+1} = \frac{\frac{g_i + l_i}{2} - l_i}{2 \cdot \frac{g_i + l_i}{2}} = \frac{g_i - l_i}{2g_i + 2l_i} < \frac{g_i - l_i}{2g_i} = \tilde{\epsilon }_{i}$. $\square$

6 GDS maintenance for dynamic graphs

Dynamic graphs involving frequent updates have a wide range of applications in the real world, such as social network analysis and human epidemiology [59]. The DSP in dynamic graphs refers to maintaining the densest subgraph with respect to the updates [48]. In Sect. 5, we have devised efficient algorithms to find GDS based on c-cores over static graphs. In this section, we study how to maintain a small dense c-core G[C] that contains the densest subgraph in dynamic graphs. We can effectively apply our c-core-based acceleration technique in dynamic graphs when fast updates and queries are required. Since maintenance with different density metrics is similar, we focus on weighted density (Definition 3.4) for doubly weighted graphs. Without loss of generality, two types of updates are considered: insertion and deletion of edges. The vertex updates can be regarded as a series of edge updates.⁵ The increase and decrease of weights resemble the insertion and deletion respectively when designing efficient maintenance algorithms. We aim to efficiently maintain a dense c-core as the approximate GDS whenever a graph update is made.

Many efficient methods for the maintenance of k-core have been proposed [5, 40, 69]. However, they cannot be directly applied to maintain G[C] because k-core maintenance concerns the coreness⁶ for each vertex while our goal is to keep a small GDS approximate containing the GDS. Besides, the k-core maintenance only considers unweighted graphs, while we study doubly weighted graphs.

A straightforward way to maintain the dense c-core containing the GDS is to perform a peeling from scratch each time an edge is inserted or deleted. The pseudocode is presented in Algorithm 6 cCoreRecomp. In cCoreRecomp, we define $G[V_o]$, $G[\tilde{S}_o]$, and $G[C_o]$ as subgraphs and $\hat{\rho }_o$ as densities of $G[\tilde{S}_o]$ before the current update (insertion/deletion). The elements marked with a subscript ± represent the outcomes following the current update. The algorithm first finds the densest c-core $G[\tilde{S}_{\pm }]$ via peeling and the corresponding density $\hat{\rho }_{\pm }$ (lines 1-2). Next, it peels the graph again to obtain the $\hat{\rho }_{\pm }$-core (lines 3-4).

Algorithm 6

cCoreRecomp

We will shortly show that $G[C_{\pm }]$ maintained in this algorithm is an approximation to the GDS in $G[V_{\pm }]$ by Theorem 6.1. Before formally introducing Theorem 6.1, we first give Lemma 6.1.

Lemma 6.1

Given a weighted graph $G(V, E, W_V, W_E)$, suppose R is the vertex set that induces the c-core with threshold c, then $\frac{c}{2} \le \rho (R) \le c_{max}$, where $c_{max}$ is the maximum contribution among V.

Proof

Let $W_{V_R}$ and $W_{E_R}$ be the sum of weights of all vertices and edges within G[R]. Suppose r is the number of vertices in R. We have

$$\begin{aligned}&r \times c \le W_{V_R} + 2W_{E_R}\nonumber \\&\frac{r \times c}{2} \le \frac{W_{V_R}}{2} + W_{E_R}\nonumber \\&\frac{c}{2} \le \frac{\frac{W_{V_R}}{2} + W_{E_R}}{r} \le \frac{W_{V_R} + W_{E_R}}{r} = \rho (R) \end{aligned}$$

(6.1)

For the upper bound, we have

$$\begin{aligned}&W_{E_R} + W_{V_R} \le 2W_{E_R} + W_{V_R}\le r \cdot c_{max} \nonumber \\&\rho (R) = \frac{W_{E_R} + W_{V_R}}{r} \le c_{max} \end{aligned}$$

(6.2)

$\square$

Theorem 6.1

$G[\tilde{S}_{\pm }]$ and $G[C_{\pm }]$ in cCoreRecomp are $\frac{1}{3} \cdot OPT$ and $\frac{1}{6} \cdot OPT$ solutions to the DS, respectively, in a doubly weighted graph $G[V_{\pm }]$ with weighted density (Definition 3.4). Besides, the approximation ratios for $G[\tilde{S}_{\pm }]$ and $G[C_{\pm }]$ will be improved to $\frac{1}{2} \cdot \text {OPT}$ and $\frac{1}{4} \cdot \text {OPT}$, respectively, in unweighted graphs with original edge density.

Proof

$G[C_{\pm }]$ is a $\hat{\rho }$-core. Thus, it has a density at least $\frac{1}{2} \hat{\rho }_{\pm }$ by Lemma 6.1. We have inequalities $\hat{\rho }_{\pm } \ge \frac{1}{3} OPT$ [3] and $\hat{\rho }_{\pm } \ge \frac{1}{2} OPT$ [12] for weighted density and original edge density. $\square$

Remark

$G[\tilde{S}_{\pm }]$ has a higher density than $G[C_{\pm }]$. It is guaranteed that $G[C_{\pm }]$ contains the GDS, while the GDS may not be contained in $G[\tilde{S}_{\pm }]$.

Repeated peeling is time costly when updates become very frequent. Following the intuition that inserting or deleting a single edge will not impose a great impact on the c-core location, we develop efficient algorithms that focus on maintaining $G[C_{\pm }]$ for edge insertion and edge deletion in Sects. 6.1 and 6.2, respectively.

In the following, we denote $G[V_{+}]$ and $G[V_{-}]$ as the updates from $G[V_o]$ due to insertion and deletion, respectively, $G[\tilde{S}_{+}]$ and $G[\tilde{S}_{-}]$ as updates from $G[\tilde{S}_o]$, $\hat{\rho }_{+}$ and $\hat{\rho }_{-}$ as densities of $G[\tilde{S}_{+}]$ and $G[\tilde{S}_{-}]$, and $G[C_{+}]$ and $G[C_{-}]$ as the $\hat{\rho }_{+}$-core and $\hat{\rho }_{-}$-core that contains the GDS after the edge insertion and edge deletion, respectively.

6.1 Edge insertion

To avoid the aforementioned recomputation from scratch for each edge insertion, we develop Algorithm 7 cCoreIns for efficient incremental maintenance. The algorithm is composed of the computation of $\hat{\rho }_{+}$ and the maintenance of $G[C_{+}]$.

6.1.1 Computing $\varvec{\hat{\rho }_{+}}$

The first step is the computation of the new estimate $\hat{\rho }_{+}$. For insertion, the optimal density cannot decrease. Therefore, $\hat{\rho }_{+}$ is expected to be larger than or equal to $\hat{\rho }_o$.

• If $(u, v) \in G[\tilde{S}_o]$, a c-core potentially denser than $G[\tilde{S}_o]$ may be contained in $G[\tilde{S}_o]$. Peeling on $G[\tilde{S}_o]$ suffices to find any larger estimate and $G[\tilde{S}_{+}]$ (lines 5–6).

• If $(u, v) \not \in G[\tilde{S}_o]$, a c-core denser than $\hat{\rho }_o$ is less likely since the edge does not exist in the dense $G[\tilde{S}_o]$. In this case, we simply retain $G[\tilde{S}_o]$ and $\hat{\rho }_o$ (line 8). Note $\hat{\rho }{+}$ from cCoreIns should not greatly differ in the long term from cCoreRecomp, as cCoreRecomp will recompute $\hat{\rho }{+}$ via peeling $G[V_{+}]$ occasionally (line 18).

6.1.2 Maintaining $G[C_{+}]$

After computing $\hat{\rho }_{+}$, we need to maintain the $\hat{\rho }_{+}$-core $G[C_{+}]$ in $G[V_{+}]$. We utilize Theorem 6.2 and Theorem 6.3 to illustrate the procedure, analyzing two cases:

• If both endpoints of the inserted edge are in $C_o$, then $G[C_{+}]$ is contained in $G[C_o]$. We peel $G[C_o]$ to obtain $G[C_{+}]$ (line 10).

• If one endpoint is not in $C_o$, we check whether $C_o$ is a proper subset of $C_{+}$.

  • If $s_u < \hat{\rho }_{+}$ or $s_v < \hat{\rho }_{+}$, we have that $(u, v) \not \in G[C_{+}]$ by Theorem 6.2. By Theorem 6.3, this means $C_o \not \subset C_{+}$, so $C_{+} \subseteq C_o$. We peel $G[C_o]$ to get $G[C_{+}]$ (lines 20-21, 23-24).

  • If $s_u \ge \hat{\rho }_{+}$ and $s_v \ge \hat{\rho }_{+}$, whether $(u, v) \in G[C_{+}]$ cannot be determined. We call cCoreRecomp to get $G[C_{+}]$ (line 17 – 18).

Our experiments show that the $G[C_{+}]$ output in cCoreIns is the same as that in cCoreRecomp after each insertion across all datasets. $G[C_{\pm }]$ ouput by cCoreRecomp must be a subgraph of $G[C_{+}]$ output by cCoreIns, since $G[C_{+}]$ is the c-core with lower threshold. Thus, $G[C_{+}]$ is guaranteed to contain the GDS and algorithms using c-location to find GDS in $G[C_{+}]$ remain accurate. Additionally, $|C_{+}| \le |C_o|$ unless cCoreRecomp is called, making the c-core-location still effective in reducing time cost. The reason is that cCoreRecomp is invoked only if there’s a possibility that $(u, v) \in G[C_{+}]$, while it is ensured by Theorem 6.3 that $C_{+} \subseteq C_{o}$ when $(u, v) \not \in G[C_{+}]$.

Theorem 6.2

Given the inserted edge $e = (u, v)$, denote $\sum _{r \in N_{>}(u)} w(u, r)$ as $s_u$, where $N_{>}(u)$ is the vertex set $\{r| (u, r) \in G[V_{+}], c_{V_{+}}(r) \ge \hat{\rho }_{+}\}$. $s_{v}$ is defined similarly. If $s_u < \hat{\rho }_{+}$ or $s_v < \hat{\rho }_{+}$, $(u, v) \not \in G[C_{+}]$.

Proof

We prove this by contradiction. Suppose $(u, v) \in G[C_{+}]$.

Denote the vertex set $\{r| (u, r) \in G[C_{+}], c_{C_{+}}(r) \ge \hat{\rho }_{+}\}$ as $N_{\gg }(u)$ and $\sum _{r \in N_{\gg }(u)} s(u, r)$ as $\tilde{s}_u$. $N_{\gg }(u)$ is the set of all neighbors of u in $G[C_{+}]$ and $\tilde{s}_u$ is the sum of weights of u’s adjacent edges in $G[C_{+}]$. Since $u \in C_{+}$ and $G[C_{+}]$ is the $\hat{\rho }_{+}$-core, $\tilde{s}_u \ge \hat{\rho }_{+}$. $C_{+} \subset V_{+}$ implies $s_u \ge \tilde{s}_u$. Thus $s_u \ge \hat{\rho }_{+}$. By the same derivation, $s_v \ge \hat{\rho }_{+}$. This contradicts our assumption. $\square$

Theorem 6.3

Let $e = (u, v)$ be the inserted edge. If $(u, v) \not \in G[C_{+}]$, then $C_{+} \subseteq C_o$.

Proof

We first prove that $C_o \not \subset C_{+}$. Suppose $C_o \subset C_{+}$. Because of insertion, $\hat{\rho }_{+} \ge \hat{\rho }$. Without loss of generality, suppose $u \not \in C_{+}$. Deletion of e from $G[V_{+}]$ does not influence $G[C_{+}]$. Now $G[C_{+}]$ is the $\hat{\rho }$-core in $G[V_o]$ instead of $G[C_o]$, which is a contradiction. Given that $C_o \not \subset C_{+}$, we have $C_{+}\subseteq C_o$ or $C_{+} \setminus C_o \ne \emptyset$. However, the facts that $(u, v) \not \in G[C_{+}]$ and $\hat{\rho }_{+} \ge \hat{\rho }$ imply that $C_{+} {\setminus } C_o \ne \emptyset$ is not possible. $\square$

Algorithm 7

cCoreIns

6.2 Edge deletion

To avoid redundant computation when deleting edges, we propose Algorithm 8 cCoreDel to efficiently delete an edge and maintain $G[C_{-}]$. Similar to cCoreIns, cCoreDel involves computing $\hat{\rho }_{-}$ and maintaining $G[C_{-}]$.

Algorithm 8

cCoreDel

$\varvec{\hat{\rho }_{-}}$ and $\varvec{G[C_o]}$. We investigate three cases in cCoreDel. Note that $G[C_{-}]$ output by cCoreDel is guaranteed to be the same as G[C] output by cCoreRecomp.

• If either u or v is not in $C_o \cup \tilde{S}_o$, then $G[\tilde{S}_o]$ remains the densest c-core in $G[V_{-}]$. Thus, $\hat{\rho }_{-} = \hat{\rho }_o$ and we set $G[C_{-}] = G[C_o]$ (lines 4-6).

• If one endpoint is in $C_o \setminus \tilde{S}_o$ and both are in $\tilde{S}_o \cup C_o$, then $\hat{\rho }_{-} = \hat{\rho }_o$. However, the $\hat{\rho }_{-}$-core $G[C_{-}]$ in $G[V_{-}]$ may differ from $G[C_o]$ in $G[V_o]$. We peel $G[C_o]$ to obtain $G[C_{-}]$ (lines 10-11), since vertices outside $C_o$ cannot be in the $\hat{\rho }_{-}$-core.

• In the worst case, both u and v are in $\tilde{S}_o$, possibly making $\hat{\rho }_{-} < \hat{\rho }_o$. Then, we must invoke cCoreRecomp to find the $\hat{\rho }_{-}$-core.

7 Our DalkS approximation algorithms

7.1 Decomposition-based DalkS algorithm

The densest at-least-k-subgraph (DalkS) problem is one kind of DSP with a size constraint, which has been proven to be NP-hard [6,7,8, 24, 46]. Although the peeling-based DalkS algorithm [3] is fast, it can only output a $\frac{1}{3} \cdot OPT$ solution result, which is far from optimal. To the best of our knowledge, the state-of-the-art approach based on linear programming proposed by Khuller and Saha [36] can output a $0.5 \cdot OPT$ solution, which is still not satisfactory. In this section, we propose a new algorithm based on our theory (Theorem 7.2) bridging decomposed graphs and DalkS to extract subgraphs close to the optimal solution of DalkS from the density-friendly graph decomposition [36, 61]. We show that although DalkS is NP-hard for general k’s, finding exact solutions within polynomial time for k’s that are corresponding to the size of subgraphs returned by density-friendly decomposition is possible (Theorem 7.4). In Sect. 9, we verify that our solution is usually better than a $0.5 \cdot OPT$ solution in terms of approximation ratio guarantee. Our decomposition-based DalkS algorithm is particularly useful for users requiring a high approximation ratio guarantee when the ground-truth DalkS is unknown.

A key finding inspires our DalkS algorithm DecomDalkS that the GDS $G[S^{*}]$ must be contained in the DalkS $G[K^{*}]$ if $|S^{*}| \le k$, as shown in Theorem 7.1. In this paper, we focus on the weighted density (Definition 3.4) for DalkS. The reason for choosing the weighted density is that it is more general than the original density. Existing works on DalkS only consider the original density. Thus, our algorithm is more general than existing ones in the literature.

Theorem 7.1

Given a doubly weighted graph G and size constraint k, let $G[S^{*}]$ denote the GDS and $G[K^{*}]$ denote the DalkS. If $k \ge |S^{*}|$, we have $S^{*} \subseteq K^{*}$.

Proof

Suppose for contradiction, $|S^{*} {\setminus } K^{*}| \not = \emptyset$. Adding $S^{*} {\setminus } K^{*}$ to K will result in a subgraph denser than $G[K^{*}]$ by Lemma 4.1. $\square$

Motivated by Theorem 7.1 that the GDS is contained in DalkS, can we adopt the following strategy to obtain the near-optimal DalkS?

• 1. Find the GDS from doubly weighted graph G;

• 2. Remove the GDS from G and redistribute some weights;

• 3. Repeat the above process until the size of the union of all GDS’s is larger than k, and use the union as a result.

The above strategy can give us a high-quality result, which will be proven later. Meanwhile, [61] used the above process to perform the density-friendly graph decomposition on unweighted graphs. By deriving properties of density-friendly graph decomposition, which are not shown in [61] and other decomposition work [17], we successfully extract the solution close to the exact DalkS from the decomposition for the first time.

Algorithm 9

DecomDalkS

We present our DalkS algorithm DecomDalkS for doubly weighted graphs in Algorithm 9. DecomDalkS first initializes the approximate DalkS as an empty set (line 1). Next, we repeat extractions of the GDS $G[S^{*}]$ from G (line 3), redistribute weights of edges between vertices inside and outside $S^{*}$ to corresponding vertices outside $S^{*}$ (lines 4–5), remove $S^{*}$ and its adjacent edges from G (line 6), and merge $S^{*}$ to $\tilde{K}^{*}$ (line 7), until $\tilde{K}^{*}$ contains at least k vertices (line 2). We return $G[\tilde{K}^{*}]$ as the approximate DalkS (line 8).

Example 7.1

Take the graph in Fig. 1 as an example to demonstrate steps in DecomDalkS with different required k. For clarity, we first list the result of decomposition beforehand. It is easy to obtain $S^{*}_1 = \{c, g, e\}$, $S^{*}_2 = \{f, d\}$, $S^{*}_3 = \{a\}$ and $S^{*}_4 = \{b\}$. If $k \le 3$, the output is exactly the GDS induced by $S^{*}_1$; if $k = 4$, the output is the subgraph induced by $S^{*}_1 \cup S^{*}_2$, which is a $0.8 \cdot OPT$ solution; if $k = 5$, the output is the same with the case when $k=4$, but this time it is an exact solution; similarly when $k=6$ or $k=7$, DecomDalkS is able to return an exact solution.

By the following theorem, our algorithm DecomDalkS is likely to give a solution with density larger than $0.5 \cdot OPT$, which is the density of the solution given by the state-of-the-art approximation.

Theorem 7.2

$G[\tilde{K}^{*}]$ output by DecomDalkS (Algorithm 9) is a $\frac{k}{|\tilde{K}^{*}|}$-approximation to the DalkS, $G[K^{*}]$, with size lower bound k.

According to our experimental results, the approximation ratio guarantee given by DecomDalkS, $\frac{k}{|\tilde{K}^{*}|}$ is at least 0.8 in most cases. Before delving into the details of Theorem 7.2, we use a real data case study in Example 7.2 to illustrate the practical usefulness of DecomDalkS, particularly when a high approximation ratio guarantee is required.

Example 7.2

Suppose one wants to find an approximation to DalkS with k around 50, 000 from the LiveJournal graph that has close to 4, 000, 000 vertices in total. Without our method, the best approximation ratio one can expect to guarantee is 0.5 within polynomial time. However, on the other hand, one can first do density-friendly decomposition over the LiveJournal. Having vertex size close to k, some subgraphs $G[S_1], G[S_2], G[S_3]$ with $|S_1| = 49,992, |S_2| = 50,006, |S_3| = 50,021$ can be found in the return of the decomposition. In DecomDal k S, the $G[S_2]$ will be output as the approximate solution with the guaranteed ratio $\frac{k}{|\tilde{K}^*|} = \frac{k}{|S_1|} = \frac{50000}{50006} = 0.99988 > 0.5$ when $k = 50,000$. Though one does not know the exact DalkS, he is likely to be satisfied with a solution that is guaranteed to have a density larger or equal to 0.99988 of the optimal density. Further, one can obtain the exact DalkS solution if the query k is adjusted to be 49, 992, 50, 006, or 50, 021. Since DecomDal k S has the nice $\frac{k}{|\tilde{K}^*|}$ theoretical ratio lower bound, one can possibly obtain better approximation guarantee of solutions output by other methods when $\frac{k}{|\tilde{K}^*|} > \frac{1}{2}$ from DecomDal k S and those solutions from other methods have larger empirical density than the $G[\tilde{K}^*]$ output by DecomDal k S.

In the followings, we present our theoretical findings. As DecomDalkS keeps updating G at each iteration, we use Table 1 to denote the related variables in i-th iteration of the while loop to facilitate the explanation of the procedure and relevant derivation.

Table 1 Notations in the while loop of DecomDalkS

To prepare for the proof of Theorem 7.2, we define the so-called marginal weights as the extension of marginal edge number in [61].

Definition 7.1

(Marginal weight) Suppose we have two disjoint vertex subsets $X \subseteq V$ and $Y \subseteq V$. Denote the edge set to connect X and Y as $E(X,Y) = \{e=(u,v) \in E|u \in X, v \in Y\}$. The marginal weight of X w.r.t Y is $W_{\Delta }(X, Y):= \sum _{e \in E(X)} w_e + \sum _{v \in X} w_v + \sum _{e \in E(X,Y)} w_e$.

We denote the weight of X as $W(X) = \sum _{e \in E(X)} w_e + \sum _{v \in X} w_v$. Hence, the marginal weight of X w.r.t. Y contains more weights of edges connecting X and Y compared to W(X).

Next, we introduce some useful lemmas related to marginal weights.

Lemma 7.1

Let $G[S^{*}]$ be the GDS in G. Then we have $\forall X \subseteq V {\setminus } S^{*}$, $\frac{W(S^{*})}{|S^{*}|} > \frac{W_{\Delta }(X, S^{*})}{|X|}$.

Proof

Because $G[S^{*}]$ is the GDS of G, the following inequality holds

$$\begin{aligned} \rho (S^{*}\cup X) = \frac{W(S^{*}) + W_{\Delta }(X, S^{*})}{|S^{*}| +|X|} < \frac{W(S^{*})}{|S^{*}|} = \rho (S^{*}). \end{aligned}$$

Then the result will be straightforward to see. $\square$

Lemma 7.2

Suppose we have vertex subsets D, A, and B, where D is disjoint from both A and B and nonempty. If $0< |A| < |B|$ and $\frac{W(D)}{|D|}> \frac{W_{\Delta }(A, D)}{|A|} > \frac{W_{\Delta }(B, D)}{|B|}$, we have $\rho (A\cup D) = \frac{W(D) + W_{\Delta }(A, D)}{|D| + |A|} > \frac{W(D) + W_{\Delta }(B, D)}{|D| + |B|}=\rho (B\cup D)$.

Proof

Firstly we let

$$\begin{aligned} W_1&= \left( \frac{W(D)}{|D|} - \frac{W_{\Delta }(A, D)}{|A|}\right) \cdot (|B| - |A|) \cdot |D|\nonumber \\ W_2&= \left( \frac{W_{\Delta }(A, D)}{|A|} - \frac{W_{\Delta } (B, D)}{|B|}\right) \cdot |B| \cdot (|D| + |A|) \end{aligned}$$

(7.1)

Taking the difference between $\frac{W(D) + W_{\Delta }(A, D)}{|D| +|A|}$ and $\frac{W(D) + W_{\Delta }(B, D)}{|D| + |B|}$ yields

$$\begin{aligned}&\frac{W(D) + W_{\Delta }(A, D)}{|D| + |A|} - \frac{W(D) +W_{\Delta }(B, D)}{|D| + |B|}\nonumber \\&\quad = \frac{W_1 + W_2}{(|D| + |B|) \cdot (|D| + |A|)} > 0 \end{aligned}$$

(7.2)

$\square$

Fig. 5

Relationship among subgraphs

In the following, we refer readers to Fig. 5a for visualizing Lemma 7.3 and Theorem 7.3; and Fig. 5b for visualizing Theorem 7.4.

Lemma 7.3

For any iteration in the while loop, we have $\forall i$, $|H_{i}| \le |S^{*}_{i}| + |H_{i+1}|$.

Proof

Firstly, $S^{*}_i \subseteq H_i$ by Theorem 7.1. Let $H_i = B_i \cup S^{*}_i$, where $B_i$ is disjoint from $S^{*}_i$. We claim that $|B_i| \le |H_{i+1}|$. Otherwise suppose that $|B_i| > |H_{i+1}|$. By the definition of $S^{*}_i$ and Lemma 7.1, we have $\frac{W(S^{*}_{i})}{|S^{*}_{i}|}> \frac{W_{\Delta }(H_{i+1}, S^{*}_{i})}{|H_{i+1}|} > \frac{W_{\Delta }(B_i, S^{*}_i)}{|B_i|}$ w.r.t. $G_{i}$. We use Lemma 7.2 and conclude that

$$\begin{aligned} \frac{W(H_{i})}{|H_{i}|}&= \frac{W(S^{*}_{i}) + W_{\Delta } (B_i, S^{*}_i)}{|S^{*}_i| + |B_i|}\nonumber \\&\le \frac{W(S^{*}_{i}) + W_{\Delta }(H_{i+1}, S^{*}_i)}{|H_{i+1}| + |B_i|} = \frac{W(S^{*}_{i} \cup H_{i+1})}{|S^{*}_i| + |H_{i+1}|} \end{aligned}$$

(7.3)

Observe that the graph induced by $S^{*}_{i} \cup H_{i+1}$ is now a denser subgraph than $H_{i}$ with at least $k - |\bigcup _{j=1}^{i-1} S^{*}_j|$ vertices on $G_{i}$. It contradicts with the fact that $H_i$ is the densest subgraph with at least $k - |\bigcup _{j=1}^{i-1} S^{*}_j|$ vertices. Because $|B_i| \le |H_{i+1}|$, we have $|H_i| = |S^{*}_i| + |B_i| \le |S^{*}_i| + |H_{i+1}|$. $\square$

Theorem 7.3

Suppose the exact solution for DalkS is $G[K^{*}]$. Then we have $|K^{*}| \le |\tilde{K}^{*}|$, where $\tilde{K}^{*}$ is the vertex set of the final output in Algorithm 9.

Proof

Because $S^{*}_i$’s are disjoint, we have

$$\begin{aligned} \left| \bigcup _{j=1}^{i} S^{*}_j \cup H_{i+1}\right| = \sum _{j=1}^{i}|S^{*}_j| + |H_{i+1}| \end{aligned}$$

(7.4)

Suppose the while loop is executed for p iterations. Based on Lemma 7.3, the following inequality holds $\forall 0 \le i \le p-2$

$$\begin{aligned} \sum _{j=1}^{i}|S^{*}_j| + |H_{i+1}| \le \sum _{j=1}^{i+1}|S^{*}_j| + |H_{i+2}| \end{aligned}$$

(7.5)

Then, combining the above two, we have the sequence of inequalities, where let $S^{*}_{[1,p]}=\bigcup _{j=1}^{p} S^{*}_j$

$$\begin{aligned} |K^{*}|&= |H_1| \le |S^{*}_1 \cup H_2| \le |S^{*}_1 \cup S^{*}_2 \cup H_3| \le \cdots \nonumber \\&\le |S^{*}_{[1, p-1]} \cup H_{p}| = |S^{*}_{[1, p]}| = |\tilde{K}^{*}| \end{aligned}$$

(7.6)

We can see that $H_{p} = S^{*}_p$, so $|H_p| = |S^{*}_p|$. $\square$

Theorem 7.4

$G[\tilde{K}^{*}]$ is the DalkS with at least $|\tilde{K}^{*}|$ vertices.

Proof

Suppose G[J] is any subgraph of the original whole graph G[V], where $|J| = |\tilde{K}^{*}|$. Let $I = J \cap \tilde{K}^{*}$, $B = J {\setminus } I$ and $S_{i}^{'} = S^{*}_i \cap (V {\setminus } I), \forall 1 \le i \le p$, where p is the number of iterations executed in the while loop. By Lemma 7.1, we have a sequence of inequalities

$$\begin{aligned} \frac{W_{\Delta }(B, I)}{|B|}< & {} \frac{W_{\Delta }(S^{*}_p, S^{*}_{[1, p-1]})}{|S^{*}_p|}< \cdots \nonumber \\< & {} \frac{W_{\Delta }(S^{*}_2, S^{*}_{[1,1]})}{|S^{*}_2|}) < \frac{W(S^{*}_1)}{|S^{*}_1|} \end{aligned}$$

(7.7)

Taking a closer look at the weights that $\tilde{K}^{*} \setminus I$ and B bring to I, one can verify the following results with the aid of Lemma 4.1. Note that in the i-th iteration, we transform the problem of density-friendly decomposition to solving GDS on the doubly weighted graph $G_{i}$.

$$\begin{aligned} W_{\Delta }(\tilde{K}^{*} \backslash I, I)&=\sum _{i=1}^{p} W_{\Delta }(S_i^{'}, S^{*}_{[1,i-1]}) \nonumber \\&\ge \sum _{i=1}^{p} |S_i^{'}| \cdot \frac{W_{\Delta }(S_i, S^{*}_{[1, i-1]})}{|S_i|}\nonumber \\&> \frac{W_{\Delta }(B, I)}{|B|} \cdot \sum _{i=1}^{p} |S_i^{'}|\nonumber \\&=\frac{W_{\Delta }(B, I)}{|B|} \cdot |B| = W_{\Delta }(B, I) \end{aligned}$$

(7.8)

Adding both sides by W(I) and dividing by $|\tilde{K}^{*}|$ yields

$$\begin{aligned} \frac{W(\tilde{K}^{*})}{|\tilde{K}^{*}|}&= \frac{W(I) +W_{\Delta }(\tilde{K}^{*} \setminus I, I)}{|\tilde{K}^{*}|}\nonumber \\&>\frac{W(I) + W_{\Delta }(B, I)}{|\tilde{K}^{*}|} = \frac{W(J)}{|J|} \end{aligned}$$

(7.9)

$\square$

Based on the above theorems and lemma, we can prove Theorem 7.2 now.

Proof of Theorem 7.2

From Theorem 7.3, we know that $|K^{*}| \le |\tilde{K}^{*}|$. Therefore, $W(K^{*}) \le W(\tilde{K}^{*})$ because $G(\tilde{K}^{*})$ is the densest subgraph with $|\tilde{K}^{*}|$ vertices. Then the result follows naturally

$$\begin{aligned} \frac{W(\tilde{K}^{*})}{|\tilde{K}^{*}|}/\frac{W(K^{*})}{|K^{*}|} =\frac{|K^{*}|}{|\tilde{K}^{*}|} \cdot \frac{W(\tilde{K}^{*})}{W(K^{*})} \ge \frac{k}{|\tilde{K}^{*}|} \end{aligned}$$

(7.10)

$\square$

When $|\tilde{K}^{*}|$ is close to k, our approximation will be a good solution. In particular, we have the exact solution if $|\tilde{K}^{*}| = k$. In Sect. 9.5, we will show that our approximate DalkS’s have guaranteed ratio close to 1 in most cases.

We remark that when $|\tilde{K}^{*}| > 2k$, one can use the combinatorial algorithm [13] (Combinatorial-DalkSS) to generate a $\frac{1}{2}$-approximation naturally. In other words, if $|\tilde{K}^{*}| = |S^{*}_{[1,p]}| > 2k$, one can extract $S^{*}_{[1, i]}, \forall 1 \le i \le p$ and randomly add $\max (k-|S^{*}_{[1, i]}|, 0)$ vertices to each $S^{*}_{[1,i]}$, and choose the densest induced subgraph among them, which will yield a $0.5 \cdot OPT$ solution.

7.2 A faster $\frac{1}{3}$-approximation algorithm to DalkS

DecomDalkS based on decomposition delivers powerful accuracy improvements over existing work for the DalkS problem. A natural question arises – can the fastest algorithm, GreedyDalkS, be further accelerated?

GreedyDalkS, proposed by Andersen and Chellapilla [3], uses a greedy peeling to guarantee $\frac{1}{3} \cdot OPT$ solutions. To our best knowledge, it is the fastest algorithm with a theoretical guarantee. Notably, the spectral approach proposed by Feng et al. [25] is comparably fast but it lacks density guarantees.

We propose FastDalkS, the first algorithm that can be faster than the greedy peeling and meanwhile hold matching density guarantees. For a small k, it returns $\frac{1}{3} \cdot OPT$ densities more efficiently. Empirically, FastDalkS consistently meets or exceeds the densities returned by GreedyDalkS.

The bottleneck for GreedyDalkS lies in maintaining a min-heap of all vertices during peeling. FastDalkS instead first estimates the optimal density $\hat{\rho }$ on a small graph. With $\hat{\rho }$ and the relationship between the $\frac{1}{3} \cdot OPT$ solution and certain c-cores, it performs peeling on a smaller graph to achieve the approximation.

Details of FastDalkS are shown in Algorithm 10. Firstly, we collect $2^{j} \cdot k$ vertices with top contribution in V (Definition 4.1) to form W, where j is a hyperparameter. For small k, |W| is also small. Peeling G[W] gives a good estimate $\hat{\rho }$ (lines 2-4). To guarantee $\frac{1}{3} \cdot OPT$ solutions, vertices with contribution at least $\frac{2}{3}\hat{\rho }$ are added to C forming $W'$ (line 5). This aligns with the intuition that only vertices with contribution $\ge \hat{\rho }$ can potentially increase the density. Finally, peeling $G[W']$ yields the solution (lines 6-7). We verify the $\frac{1}{3} \cdot OPT$ guarantee for FastDal k S in Theorem 7.5.

Algorithm 10

FastDal k S

Theorem 7.5

$G[C^{'}]$ output by FastDalkS is a $\frac{1}{3} \cdot OPT$ solution to DalkS in G[V].

Proof

Denote DalkS as $G[K^{*}]$ and its density as $\rho ^{*}$. Let $\frac{2}{3} \rho ^{*}$-core of G[V] be G[H]. By Lemma 6.1, $\rho (H) \ge \frac{1}{3} \rho ^{*}$. Because $W^{'}$ is the union of C and $\{v | c_V(v) \ge \frac{2}{3} \hat{\rho }\}$, $W^{'}$ contains the $\frac{2}{3} \hat{\rho }$-core of G[V]. Then $W^{'}$ also contains H by the fact that $\rho ^{*} \ge \hat{\rho }$.

• 1. If $|H| \ge k$, $\rho (C^{'}) \ge \rho (H)$, i.e. $\frac{1}{3} \rho ^{*}$, since H must be one of vertex sets in $\{C^{'}_k, C^{'}_{k+1}, \cdots , C^{'}_{|W^{'}|}\}$.

• 2. Otherwise suppose the $|H| < k$. In the followings, We prove that $\rho (C^{'}_{k}) \ge \frac{1}{3} \rho ^{*}$. The optimal density can be calculated as $\rho ^{*} = \frac{W(K^{*})}{|K^{*}|}$. We have

  $$\begin{aligned} \rho (C^{'}_{k}) = \frac{W(C^{'}_{k})}{|C^{'}_{k}|} =\frac{W(C^{'}_{k})}{k} \ge \frac{1}{3}\frac{W(K^{*})}{k} \ge \frac{1}{3}\frac{W(K^{*})}{|K^{*}|}, \end{aligned}$$

  (7.11)

  where the $W(C'_{k}) \ge \frac{W(K^*)}{3}$ comes from Lemma 2 in section 3 of [3] that the $\frac{2}{3} \rho ^{*}$-core of G[V] has total weights at least $\frac{1}{3} W(K^{*})$, where $W(K^{*})$ is the total weights of $G[K^{*}]$ by extending the lemma to doubly weighted graphs.

Since $C^{'}$ induces the densest graph during peeling $W^{'}$, $\rho (C^{'}) \ge \rho (C^{'}_k) \ge \frac{1}{3} \rho ^{*}$. Thus $G[C^{'}]$ is a $\frac{1}{3} \cdot OPT$ solution to $G[K^{*}]$. $\square$

Although designed for DalkS, setting the least vertex number equal to 0 in FastDalkS gives an algorithm for the DSP problem, which we call as FastDS. Its processing pipeline is shown in Algorithm 11. FastDS collects the top $1\%$ contributing vertices into W for estimating the optimal density. For DSP with original edge densities, Theorem 4.1 guarantees that fewer vertices need to be added to $W'$ (line 5). We verify in Theorem 7.6 that FastDS guarantees a $\frac{1}{2} \cdot OPT$ solution for solving DSP.

Algorithm 11

FastDS

Theorem 7.6

$G[C^{'}]$ output by FastDS in Algorithm 11 is a $\frac{1}{2} \cdot OPT$ solution to DS in G[V].

Proof

Denote DS as $G[S^{*}]$ and its density as $\rho ^{*}$. $S^{*}$ is contained in $\rho ^{*}$-core, so it is also contained in $\hat{\rho }$-core. Given that $W^{'}$ is the union of C and $\{v | c_V(v) \ge \hat{\rho }\}$, $W^{'}$ contains $\hat{\rho }$-core and thus contains $S^{*}$. Therefore, $G[C^{'}]$ yielded by peeling is $\frac{1}{2}$-approximation to $G[S^{*}]$ [12]. $\square$

Fig. 6

FastDalkS reduces time complexity

FastDalkS is the most effective when the constraint k is relatively small compared to |V| for two reasons:

• 1. The expected size of W, i.e. $2^{j} \cdot k$, does not exceed |V|, so we do not bother to adjust the value of j to make sure that $2^{j} \cdot k < |V|$.

• 2. W remains small, so computing $\hat{\rho }$ is fast. Even if no vertices are ruled out for $W'$, FastDalkS has comparable speed to GreedyDalkS.

We further use Example 7.3 to compare GreedyDalkS and FastDalkS.

Example 7.3

We use the unweighted graph in Fig. 6 to illustrate why FastDalkS is faster than GreedyDalkS usually. The whole graph is composed of 26 subgraphs G[A], G[B], G[C], $\cdots$, G[X], G[Y], G[Z]. G[A] is a $d^{*}$-clique, that is $|A| = d^{*}$ and all vertices in A are adjacent. The other 25 subgraphs are identical d-cliques. Let $d^{*} = 6d + 1$ and d be a large integer. Note that $\rho (A) = \frac{(d^{*} - 1) \cdot d^{*}}{2 d^{*}} = \frac{d^{*}-1}{2} = \frac{6d+1-1}{2} = 3d$, while $\rho (B) = \rho (C) = \cdots = \rho (Y) = \rho (Z) = \frac{d-1}{2}$. Suppose we are required to find the $\frac{1}{3}$-approximation to DalkS in this graph when $k = \lceil \frac{d^{*}}{12} \rceil$. By observation, we know that the exact DalkS is G[A] and the optimal density is 3d.

Consider running GreedyDal k S on the graph. All d-cliques will be successfully peeled before vertices in A are peeled. When a vertex is peeled, we need to maintain the min-heap. Specifically, we place the last vertex in the heap at the first position and then heapify it. Besides, we have to update the strength of the peeled vertex’s neighbors. We also heapify those neighbor vertices. Therefore, it is time costly for GreedyDalkS to maintain the min-heap for all vertices, i.e. $A \cup B \cup \cdots \cup Y \cup Z$, in the peeling process.

Consider running FastDalkS on the graph. Suppose we choose $j = 3$. Approximately, $|W| = 2^3 \cdot \frac{d^{*}}{12} = \frac{2}{3} d^{*}= 4d$. We will arbitrarily choose 4d vertices in A to form W. Note that G[W] is a 4d-clique, so $\hat{\rho } = \rho (W) = \frac{4d - 1}{2}$. The threshold $\frac{2}{3} \hat{\rho }$ is approximately $\frac{4}{3} d$ and thus all the vertices in d-cliques will not be included in $W^{'}$. In this case, we avoid a min-heap containing all vertices. Instead, we focus on a much smaller set $W^{'} = K^{*}$ to perform peeling.

8 Complexity analysis

In this section, we analyze both the time and the space complexity for our proposed algorithms cCoreExact, cCoreApp*, cCoreIns, cCoreDel, DecomDalkS and FastDalkS with the original density metric. The complexity with other density metrics are similar. First, let the input graph be G(V, E) and the c-core to locate GDS be $G^{'}(V^{'}, E^{'})$.

The space complexity for all algorithms is $O(|V| + |E|)$ since storing information for vertices and edges dominates the complexity. We provide the time complexity in the following, along with sketches of the proof.

Proposition 8.1

The time complexity of cCoreExact is $O(|E| + |V| \cdot \log (|V|) + |V^{'}|^2 \cdot |E^{'}| \cdot \log (|V^{'}|))$.

Proof

Otaining $G^{'}$ takes $O(|E| + |V| \cdot \log (|V|))$ time. The Dinic’s algorithm [18] is to run $\log (|V^{'}|)$ times blocking flows on the c-core. Every time it costs $O(|V^{'}|^2 \cdot |E^{'}|)$ time to compute the blocking flow, so the total time cost is $O(|E| + |V| \cdot \log (|V|)) + O(|V^{'}|^2 \cdot |E^{'}| \cdot log(|V^{'}|))$ and the proposition is proved. $\square$

Proposition 8.2

The time complexity of cCoreApp* is $O(|E| + |V| \cdot \log (|V|) + |E^{'}| \cdot \log (|V^{'}|) \cdot log(|E^{'}|) \cdot \log (\frac{(|V^{'}| + |E^{'}|)^2}{|E^{'}|})/\epsilon )$.

Proof

In FlowApp* (Algorithm 5), the number of blocking flow is set to be $h = 2 \lceil \log (2|E|) \rceil + 2$ [13]. When the GDS is located in $G^{'}$, we have h blocking flows for every search for new densities and each of them takes $O(2|E^{'}|\cdot \log (|E^{'}|) \cdot \log (\frac{(|V^{'}| + |E^{'}|)^2}{|E^{'}|})/\epsilon )$ [31]. Using the strategy we propose to search for new densities, we perform the search for $\log _{\frac{4}{3}}(|V^{'}|)$ times. Therefore, the total time cost for running blocking flow is $O(|E^{'}| \cdot \log (|V^{'}|) \cdot \log (|E^{'}|) \cdot \log (\frac{(|V^{'}| + |E^{'}|)^2}{|E^{'}|}))/\epsilon )$. By adding the complexity of obtaining $G^{'}$, the result follows.⁷$\square$

Proposition 8.3

The time complexity of cCoreIns and cCoreDel are $O(|E_{\tilde{S}}| \cdot log(|\tilde{S}|) + |E_{C}| \cdot log(|C|))$ when there is a hit, where $G(\tilde{S}, E_{\tilde{S}})$ is the dense subgraph and $G(C, E_C)$ is the $\hat{\rho }$-core.

8.1 Efficiency of cCoreIns

Although cCoreIns and cCoreRecomp have the same worst-case time complexity, cCoreIns is much faster in practice. The size of $\tilde{S}_o$ is small, so computing $\hat{\rho }{+}$ is negligible. The bottleneck lies in the maintenance of $G[C_{+}]$. We call the cases that perform peeling on $G[C_o]$ only, to get $G[C_{+}]$ (lines 10, 21, 24 in Algorithm 7) hits, hence greatly reducing the time cost versus calling cCoreRecomp (line 18). The possibility of a hit is high since $\hat{\rho }_{+}$ is large while $s_u$ or $s_v$ is small if one of them is not in the dense region. Experiments in Sect. 9 will verify the efficiency.

8.2 Efficiency of cCoreDel

In the worst case, cCoreDel has the same time complexity as cCoreRecomp. Similar to insertion, we call those cases that avoid calling cCoreRecomp the hits (lines 6, 11 in Algorithm 8). The probability of a hit is high since $\tilde{S}_o$ is usually small and $C_o$ is only slightly larger.

Proposition 8.4

In the worst case, the time complexity of the algorithm DecomDalkS is $O(k \cdot |V|^2 \cdot |E| \cdot \log (|V|))$.

Proof

In the worst case, the time cost of cCoreExact becomes $O(|V|^2 \cdot |E| \cdot \log (|V|))$. At most k times of decomposition is needed. $\square$

Proposition 8.5

Let the graphs induced by W and $W^{'}$ be $G(W, E_W)$ and $G(W^{'}, E_{W^{'}})$, respectively. The time complexity of FastDal k S is $O((|V| + |E_W|) \cdot log(|W|) + |E_{W^{'}}| \cdot log(|W^{'}|))$.

Proof

To find W, we first use a min-heap to store $|W| = 2^j \cdot k$ vertices with top strength. The initialization of the min heap takes $O(\frac{|W|}{2} \cdot log(|W|))$. Comparing the strength to maintain |W| vertices with top strength takes $O((|V| - |W|) \cdot log(|W|))$. Peeling G[W] and $G[W^{'}]$ to obtain C and $C^{'}$ has complexity $O(|E_W| \cdot log(|W|))$ and $O(|E_{W^{'}}| \cdot log(|W^{'}|))$ respectively. Union of C and $\{v | s_V(v) \ge \frac{2}{3} \hat{\rho }\}$ has complexity O(|V|). Finally, we sum all and obtain the result $O(\frac{|W|}{2} \cdot log(|W|) + (|V| - |W|) \cdot log(|W|) + |E_W| \cdot log(|W|) + |E_{W^{'}}| \cdot log(|W^{'}|) + |V|) = O((|V| + |E_W|) \cdot log(|W|) + |E_{W^{'}}| \cdot log(|W^{'}|))$. $\square$

9 Experiment

9.1 Setup

9.1.1 Datasets

We mainly use twelve real-world graphs to perform our experiments. Half of them are unweighted graphs shown in Table 2, while the other half are weighted graphs shown in Table 3. The second column on both tables gives short names for the datasets. The edge number varies from around thirty thousand up to two billion. Besides, datasets in Table 6 are presented separately to verify the generality of our c-core-based acceleration. Since the graphs in Tables 2 and 3 are undirected, they are not applicable for assessing the efficiency of c-core-based acceleration regarding denominator-weighted density.

Table 2 Unweighted graphs

Table 3 Weighted graphs

We briefly introduce our weighted graphs in Table 3. Libimseti [53] is a weighted graph where vertices represent users, and the weights on edges are ratings given by a user to another one. FacebookForum [51] is a social network where vertices are users, and the weight on each edge is the number of messages. Newman [49] is a scientific collaboration network where a vertex represents an author, and the weight on the edge means the number of joint papers between two authors. OpenFlights [50] contains airports as vertices, and the weight refers to the number of routes between two airports.

An unweighted graph can be viewed as a weighted graph where each edge has a weight value of one. Depending on the application, e.g., fraud detection [33], some methods for weighing unweighted graphs have also been invented, and we use the method proposed by Hooi et al. [33]. Suppose we have vertices u and v in G with an edge e to connect them. We assign weight $w_e =[\log (\frac{10}{deg_G(u)+5})]+[\log (\frac{10}{deg_G(v)+5})]$ to the edge, where $deg_{G}(u)$ denotes the degree of u in G. The weighing method is applied to unweighted graphs, LiveJournal [38] and YouTube [38].

9.1.2 Algorithm

In our experiments, several algorithms are involved, and their performance provides evidence for our theoretical results. We list them and do a short review.

• FlowExact [29] is the exact GDS algorithm based on the flow network. Its details can be found in [29].

• cCoreExact is our exact GDS algorithm which is based on flow network [29] and c-core acceleration (Sects. 4.3 and 5.2) on FlowExact.

• FlowApp [13] is the $(1-\epsilon )$-approximation algorithm based on max-flow computation. It differs from FlowExact, as it does not require finding the exact maximum flow.

• FlowApp* is our $(1-\epsilon )$-approximation algorithm with better density searching strategy. (Sect. 5.3)

• cCoreApp* is our $(1-\epsilon )$-approximation algorithm FlowApp* with c-core-based acceleration. (Sects. 4.3 and 5.2)

• Greedy++ is an approximate algorithm to find GDS (especially for Definition 3.4). Each time, it will use the information obtained in previous times. The detail of it can be found in [11].

• cCoreG++ is our accelerated Greedy++ based on c-core.

• cCoreRecomp is the algorithm leveraging peeling on the whole graph to maintain the approximate GDS when an edge is inserted or deleted.

• cCoreIns and cCoreDel are our efficient algorithms to maintain the approximate GDS via incrementally updating c-core.

• DecomDalkS is our decomposition-based near-optimal DalkS algorithm. (Sect. 7.1)

• FastDal k S is our faster $\frac{1}{3}$-approximation algorithm to DalkS. (Sect. 7.2)

All algorithms are implemented in C++.⁸ We perform experiments on a Linux machine equipped with two Intel(R) Xeon(R) Silver 4210R CPU @ 2.40GHz processors with 10 cores and O2 optimization. In our experiments, Dinic’s algorithm [18] is used to find blocking flows or attain maximum flow for all flow-based methods. For other alternative blocking flow algorithms including parallelizable ones, we refer readers to [1, 4, 30, 58, 60].

9.2 Evaluation of c-core-based acceleration

Table 4 Running time of different GDS algorithms

9.2.1 Running time

To evaluate our c-core-based acceleration techniques, we compare the running time of two core-based algorithms, cCoreExact and cCoreApp*, with their corresponding baseline methods, FlowExact and FlowApp*, respectively. To show how powerful the acceleration based on c-core is, we further perform a comparison between the c-core-based approaches and Greedy++ [11]. For FlowExact and cCoreExact, we can obtain the exact GDS. For FlowApp, FlowApp*, cCoreApp, and cCoreApp*, we require them to give $0.999 \cdot OPT$ solution results. For Greedy++ and cCoreG++, we run 100 iterations to obtain a $0.909 \cdot OPT$ solution⁹ based on the conjecture that Greedy++ can obtain a $(1+\frac{1}{\sqrt{T}})$ factor approximation after T iterations.

We present the running time of the five algorithms in Table 4. The second to fifth columns represent the time cost of the corresponding algorithm. The last three columns show the corresponding time–cost ratios. The original and weighted density are used for unweighted and weighted graphs respectively in Table 4.

From Table 4, we make the following observations:

• cCoreExact is up to three orders of magnitude faster than Flow Exact, especially on large scale-graphs. For example, FlowExact can provide more than 6000 times speedup on LiveJournal and YouTube. The speedup of cCoreApp* over FlowApp* is similar. The c-core-based acceleration is also effective in Greedy++. For example, cCoreG++ has 137.85, 32.55 and 76.95 speedup over Greedy++ on YouTube, Friendster and Orkut, respectively.

• Acceleration using c-core makes the flow-based approaches for GDS searching scalable to very large graphs. On very large graphs such as Friendster, Orkut, LiveJournal, and MovieLens, FlowExact and FlowApp* cannot give a satisfactory answer within a reasonable running time. In contrast, cCoreExact and cCoreApp* make it possible to find the exact or near-optimal solution within 50 min for all graphs.

• Compared with Greedy++, cCoreExact can find a better GDS with less time cost. All ratios in the last column of Table 4 are greater than one. We observe that on nine out of twelve datasets, cCoreExact is over ten times faster than Greedy++. The densities of the subgraphs found by cCoreExact and Greedy++ are shown in Table 5. On four datasets, i.e., Friendster, LiveJournal, MovieLens, and OpenFlights, Greedy++ cannot attain the optimal density achieved by cCoreExact. This result is consistent with the iteration number chosen as $T = 100$ for Greedy++. If a 0.999-approximation is required for Greedy++, the iteration should be set as $T = 1,000,000$ according to the convergence conjecture provided by [11]. However, the time cost of Greedy++ with $T = 1,000,000$ is much larger than that of cCoreExact (one can multiply the ratio of the last column by 10, 000 to estimate).

Table 5 Best density by cCoreExact and Greedy++

9.2.2 Memory usage

We evaluate the memory usage of cCoreExact and FlowExact over seven datasets. For other datasets, FlowExact cannot finish reasonably within 72 h. The memory evaluation results are reported in Fig. 7. We can find that the memory cost of cCoreExact is less than FlowExact on all seven datasets. Besides, the memory cost of cCoreExact is smaller than FlowApp and FlowApp*, while the cost of the latter two is comparable.

Fig. 7

Memory cost of cCoreExact and FlowExact

9.2.3 Core size

To explain the improvement of c-core-based acceleration over running time and memory usage, we examine the sizes of $\hat{\rho }$-core in cCoreGDS (Algorithm 1) and the whole graph for different datasets. Given that the $\hat{\rho }$-core is a much smaller subgraph by several orders of magnitude, which is shown in Fig. 8,¹⁰ the faster running time and the less memory usage are not surprising.

Fig. 8

Number of vertices in the whole graph and $\hat{\rho }$-core

9.2.4 Generality

We conduct additional experiments on other density metrics to empirically show the generality of c-core acceleration. We choose three directed graphs with different sizes and transform them into bipartite vertex and edge-weighted graphs¹¹ as described in [56] to facilitate the directed densest subgraph finding. The GDS is found based on the denominator weighted density metric (Definition 3.5), where the vertex weight is placed on the denominator. The statistics of the three directed graphs, as well as the time cost of FlowExact and cCoreExact over those graphs, are presented in Table 6. We can find that the c-core-based acceleration can also provide up to 100 times speedup over the baseline method with Definition 3.5.

Table 6 Performance of GDS algorithms with Definition 3.5

9.3 Evaluation of approximation algorithms

Here, we further evaluate the approximation algorithms.

9.3.1 Density searching strategies in flow-based approximation algorithms

In Sect. 5.3, we design a new strategy to search the optimal density for the flow-based approximation algorithm and propose FlowApp* based on this new strategy. Here, we perform an ablation study over the strategy to evaluate the speedup provided by FlowApp* over FlowApp. Figure 9 shows the ratio of time cost by FlowApp over that by FlowApp*, i.e. $\frac{time(FlowApp)}{time(FlowApp*)}$. It is easy to see that FlowApp* is faster than FlowApp on eleven out of twelve datasets. On Orkut, the ratio is 0.98, just slightly less than 1. The average speedup for the other eleven datasets is 3.07, and the greatest speedup is 7.88.

9.3.2 Time cost vs. accuracy

We further test the tradeoff between efficiency and accuracy for three $(1-\epsilon )$-approximation algorithms, cCoreApp* based on flow and Greedy++, cCoreG++ based on iterative peeling. We display the time cost w.r.t accuracy in Fig. 10. The time cost for Greedy++ and cCoreG++ are calculated under the unproven conjecture of approximation ratio in [11]. From the result, we can find that cCoreApp* can achieve high accuracy in a much shorter running time compared to Greedy++. Though the curve of cCoreApp* is above that of cCoreG++, it can be more naturally extended to hyper-graph for its flow-based nature.

9.4 Performance of cCoreIns and cCoreDel

We evaluate cCoreIns and cCoreDel on three unweighted graphs (DP, LJ, YT) and two weighted graphs (LB, NM). For insertion, we randomly add 1,000 edges, with weights of 1-10 for weighted graphs. For deletion, we randomly remove 1,000 edges.

Fig. 9

Speedup of FlowApp* over FlowApp

Fig. 10

Time cost vs. accuracy of approximation algorithms

Table 7 Speedup of maintenance

The running time and the speedups over cCoreRecomp are displayed in Table 7. Average speedups are $73.95 \times$ for edge insertion and $163.45 \times$ for edge deletion, with max speedups of $172.67 \times$ on LJ and $325.98 \times$ on LJ. After each operation, cCoreIns/cCoreDel output the same G[C] as cCoreRecomp, effectively maintaining the approximate GDS during updates.

As mentioned in Sect. 6, a hit reduces the time cost by avoiding the invocation of cCoreRecomp. We record hit times in Table 8. cCoreIns has >990 hits for all graphs, while cCoreDel has $\ge$945.

Table 8 Hit rate for cCoreIns and cCoreDel

In Fig. 11, we plot ratios $\frac{\tilde{S}}{|V|}$ and $\frac{|C|}{|V|}$ over updates. The ratios do not vary much during 1000 times updates. Observe that $|\tilde{S}|$ and |C| are much smaller than |V|. The largest ratio is $\frac{|C|}{|V|} = 1.98 \%$ on LB, while the smallest one is $\frac{|\tilde{S}|}{|V|} = 0.0096 \%$ on LJ. We also observe that sizes of C are larger than $\tilde{S}$. These facts can help explain why the likelihood of a hit is high following the argument of efficiency in Sect. 6.

Table 9 Time cost of FastDal k S and GreedyDal k S

9.5 Evaluation of DecomDalkS

In Sect. 7, we have shown that DecomDalkS can output a $\frac{k}{|\tilde{K}^{*}|} \cdot OPT$ solution,¹², but have not yet shown the practical usefulness of the algorithm since $|\tilde{K}^{*}|$ is unknown until we obtain the result $\tilde{K}^{*}$. We execute DecomDalkS on four graphs and calculate the factor $\frac{k}{|\tilde{K}^{*}|}$ for any positive integer parameter k, which is no larger than the total number of vertices in the whole graph. Figure 12 reports the proportion of the factor range for $\frac{k}{|\tilde{K}^{*}|}$, i.e., $0 \sim 0.8$, $0.8 \sim 0.95$, $0.95 \sim 0.99$ and $0.99 \sim 1$, over four datasets¹³ We observe that on all four datasets, the fraction of k values where DecomDalkS cannot guarantee a solution with density at least 0.8 of the optimum is less than $1\%$. We also note that the factor is larger than 0.5 for any possible k on LiveJournal, Amazon, and DBLP. Interestingly, it is found that on all four graphs, our algorithm can output a subgraph better than $0.99 \cdot OPT$ solution for over one-third of possible k values. Therefore, our algorithm can usually return a solution close to the exact DalkS, while the state-of-the-art approach based on linear programming offers $0.5 \cdot OPT$ solution guarantees. The time cost of DecomDalkS on LiveJournal, Amazon, DBLP, and Newman is 22 m 16 s, 1 m 53 s, 54 s, and 2 s, respectively. We remark that DecomDalkS can be compared with the algorithm based on linear programming ensuring $0.5 \cdot OPT$ solutions because both of them focus on the theoretical guarantee rather than empirical density. This means their objective is to quantify the gap between the output’s density and the density of the unknown exact DalkS. The limitation of DecomDalkS is that the accurate quantified gap can be obtained only after the density-friendly decomposition is performed, while the linear programming approach can quantify the gap before running the algorithm.

Fig. 11

The size of $\tilde{S}$ and C over V

Fig. 12

Approx. ratios guaranteed by DecomDalkS

Table 10 Speedup of FastDalkS over GreedyDalkS

Table 11 Cases when the density ouput by FastDalk S different from GreedyDalkS

9.6 Evaluation of FastDalkS

Table 9 reports the running time cost of FastDal k S and GreedyDal k S on four graphs, where $\frac{k}{|V|}$ are $0.01 \%$, $0.05 \%$, $0.10 \%$, $0.50 \%$ and $1.0 \%$. The hyper-parameter is set as $j = 3$. Our FastDal k S algorithm provides significant savings. For instance, it costs 5m44s on FT when $\frac{k}{|V|}$ is $0.10 \%$ and saves 7m4s. The speedup that FastDal k S provides can be verified in Table 10, which ranges from 1.50$\times$ to 5.29$\times$, with an average of 3.38$\times$. The densities output by FastDal k S and GreedyDal k S are almost the same. Those cases when the two algorithms output different densities are listed in Table 11. Surprisingly, all densities returned by FastDal k S are greater than the ones returned by GreedyDal k S in these cases. FastDal k S is the first $\frac{1}{3}$-approximation for DalkS faster than GreedyDal k S. Theoretically, FastDS has the same complexity as FastDal k S for $k/|V|=1.0\%$. The time complexity of greedy peeling for DSP is the same as that of GreedyDal k S. Therefore, we do not list the statistics of FastDS separately.

10 Conclusion

This paper investigates the densest subgraph discovery problem with generalized supermodular density and size constraints. We first review and discuss the limitations of existing methods. Next, we show the generalized supermodular density can cover several well-known density variants and devise general acceleration strategies and efficient algorithms to find GDS. In detail, we propose a new concept called c-core and show its applications to find the densest subgraph with generalized supermodular density. Based on c-cores, we devise efficient algorithms cCoreExact and cCoreApp* to find the GDS. Efficient methods cCoreIns and cCoreDel to maintain the approximate GDS are studied for dynamic graphs. For DalkS, we propose DecomDalkS based on graph decomposition to guarantee high accuracy and FastDal k S to achieve fast speed. We perform extensive experiments for proposed algorithms on twelve real-world graphs and show that they are efficient (by running up to three orders of magnitude faster) and accurate (by providing exact or near-optimal solutions).