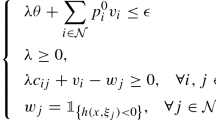Abstract
This paper investigates the computational aspects of distributionally robust chance constrained optimization problems. In contrast to previous research that mainly focused on the linear case (with a few exceptions discussed in detail below), we consider the case where the constraints can be non-linear to the decision variable, and in particular to the uncertain parameters. This formulation is of great interest as it can model non-linear uncertainties that are ubiquitous in applications. Our main result shows that distributionally robust chance constrained optimization is tractable, provided that the uncertainty is characterized by its mean and variance, and the constraint function is concave in the decision variables, and quasi-convex in the uncertain parameters. En route, we establish an equivalence relationship between distributionally robust chance constraint and the robust optimization framework that models uncertainty in a deterministic manner. This links two broadly applied paradigms in decision making under uncertainty and extends previous results of the same spirit in the linear case to more general cases. We then consider probabilistic envelope constraints, a generalization of distributionally robust chance constraints first proposed in Xu et al. (Oper Res 60:682–700, 2012) for the linear case. We extend this framework to the non-linear case, and derive sufficient conditions that guarantee its tractability. Finally, we investigate tractable approximations of joint probabilistic envelope constraints, and provide the conditions when these approximation formulations are tractable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many optimization and decision making problems, when facing stochastic parameter uncertainty, can be tackled via the celebrated chance constraint paradigm. Here, a deterministic constraint is relaxed, and instead is required to hold with a certain probability (w.r.t. the uncertain parameter). That is, given a constraint \(f({\mathbf {x}},\varvec{\delta }) \ge \alpha \) where \({\mathbf {x}}\) denotes the decision variable, \(\alpha \in {\mathbb {R}}\) denotes the target value, and \(\varvec{\delta }\), the uncertain parameter, follows a distribution \(\mu \), one solves:
for some value \(p \in (0,1)\). Chance constraints were first proposed by Charnes and Cooper [11], and since then there has been considerable work, e.g., Miller and Wagner [31], Prékopa [34], Delage and Mannor [16], and many others; we refer the reader to the textbook by Prékopa [35] and references therein for a thorough review.
While the chance constraint formulation is conceptually intuitive, it has two disadvantages that limit its practical applications. First, it is usually difficult to obtain enough samples to accurately estimate the distribution \(\mu \). Second, optimization problems involving chance constraints are notoriously hard to solve, even when \(f(\cdot , \cdot )\) is bilinear (i.e., linear in either argument) and \(\mu \) is a uniform distribution (Nemirovski and Shapiro [32]). Indeed, the only known tractable case of the chance constraint formulation is when \(f(\cdot , \cdot )\) is bilinear and \(\mu \) follows a radial distribution (Calafiore and El Ghaoui [10]; Alizadeh and Goldfarb [1]).
A natural extension of the chance constraint paradigm that overcomes the above mentioned problems is the distributionally robust chance constrained (DRCC) approach (e.g., Calafiore and El Ghaoui [10], Erdogan and Iyengar [22], Delage and Ye [17], Zymler et al. [41]). In this paradigm, the distribution of the uncertain parameter is not precisely known, but instead, it is assumed to belong to a given set \({\mathfrak {P}}\). Constraint (1) is then replaced with the following constraint
In words, (2) requires that for all possible probability distributions of the stochastic uncertainty, the chance constraint must hold. Typically, \(\mathfrak {P}\) is characterized by the mean, the covariance, and sometimes the support of the distribution as well, all of which can be readily estimated from finite samples. The DRCC approach also brings in computational advantages, e.g., Cheung et al. [14] developed safe tractable approximations of chance constrained affinely perturbed linear matrix inequalities. A celebrated result by Calafiore and El Ghaoui [10] shows that when \(f(\cdot , \cdot )\) is bilinear and \(\mathfrak {P}\) is characterized by the mean and the variance, DRCC (2) can be converted into a tractable second order cone constraint.
Yet, most previous results on the tractability of DRCC are restricted to the case that \(f(\cdot , \cdot )\) is bilinear, whereas not much has been discussed when \(f(\cdot , \cdot )\) is non-linear. One exception that we are aware of is Zymler et al. [41], where they showed that DRCC is tractable when \(f(\mathbf{x}, \varvec{\delta })\) is linear in the decision variable \(\mathbf{x}\) and quadratic or piecewise linear in the uncertainty \(\varvec{\delta }\). However, their method is built upon the S-lemma, and hence it is not clear how to extend the method to more general cases. Another one is Cheng et al. [13] where they studied the knapsack problem with distributionally robust chance constraints when \(f(\mathbf{x}, \varvec{\delta })\) is piecewise linear in the uncertainty \(\varvec{\delta }\) and provided its equivalent formulation when the first and second moment and the support information of \(\varvec{\delta }\) are known. To the best of our knowledge, the general non-linear case is largely untouched.
This paper is devoted to analyzing the tractability of DRCC (and its variants) under general—i.e., non-linear—\(f(\cdot , \cdot )\). This problem is of interest, because in many applications the uncertainty is inherently non-linear, and cannot be modeled using a bilinear \(f(\cdot , \cdot )\), e.g., [9, 28, 42]; see Sect. 2 for a more detailed discussion. In particular, we consider the following constraint
where \(f(\mathbf{x},\varvec{\delta })\) is concave in \(\mathbf{x}\), and quasi-convex in \(\varvec{\delta }\). Here, following the notations from Xu et al. [40], we use \((0,\varvec{\varSigma })\) to denote all distributions with mean zero and variance \(\varvec{\varSigma }\), and let \(\varvec{\delta }\sim (0,\varvec{\varSigma })\) stand for \(\varvec{\delta }\) follows some unknown distribution \(\mu \) that belongs to \((0,\varvec{\varSigma })\). Notice that DRCC is a special case of distributionally robust optimization (e.g., [17, 21, 33, 36]) by setting the utility function to the indicator function. However, because the indicator function is neither convex nor concave in either argument, previous results on the tractability of DRO do not apply in our setup.
Our first contribution, presented in Sect. 3, establishes that Constraint (3), when \(f(\cdot , \cdot )\) is concave-quasiconvex, is tractable. En route, we derive an equivalence relationship between (3) and a robust optimization formulation using a deterministic uncertainty model (e.g., Ben-Tal et al. [5–7], Bertsimas and Sim [8]). This result thus links the two arguably most widely used approaches in optimization under uncertainty, and extends previous results of the same spirit for the linear case (e.g., Delage and Mannor [16], Shivaswamy et al. [38]).
Our second result, presented in Sect. 4, establishes the tractability of the probabilistic envelope model in the non-linear case. The probabilistic envelope model is proposed in Xu et al. [40], based on the following observation: the chance constraint (1) only guarantees that the given constraint will be satisfied with probability \(p\) or violated with the remaining \((1 - p)\) probability, but no control is provided on the degree of violation. To overcome this, Xu et al. [40] proposed the probabilistic envelope constraint framework—essentially a set of infinite number of chance constraints at all levels of potential violation. That is, replace the single DRCC in (3) with the following
where \({\mathfrak {B}}(s)\) is a given non-decreasing and right-continuous function of \(s\). However, only the bilinear case has been investigated. In this paper, we extend the probabilistic envelope constraint to non-linear uncertainties. We prove that the optimization problem involving the probabilistic envelope constraint (4) is tractable when \(f(\cdot ,\cdot )\) is concave-quasiconvex and \({\mathfrak {B}}(s)\) satisfies some weak conditions. Similarly as for the (single) DRCC case, we establish a linkage between probabilistic envelope constraints and the comprehensive robust optimization framework using a deterministic uncertainty model (Ben-tal et al. [2, 3]).
It is worthwhile to note that the probabilistic envelope constraint is closely related to stochastic dominance constraints in the literature of stochastic programming (Dentcheva and Ruszczyński [18–20]); see Chapter 4 of the book by Shapiro et al. [37] for more details. A stochastic dominance constraint refers to a constraint of the form \(X \succeq _{(k)} Y\) where \(X\) and \(Y\) are random variables and \(\succeq _{(k)}\) stands for \(k\)-th order stochastic dominance. Thus, a probabilistic envelop constraint is indeed a first-order stochastic dominance constraint with the right hand side is a random variable whose cumulative distribution function is \({\mathfrak {B}}(s)\). However, most of the literature in optimization with stochastic dominance constraints does not address this specific case and instead focuses on the second (or higher) order constraints case, a case that preserves convexity and is more amenable to analysis. As we restrict our attention to this specific case, we choose to use the name “probabilistic envelop constraint”.
Finally, we extend our results in two ways, namely, more flexible uncertainty modeling and joint constraints. In Sect. 5, we provide tractability results for the case where the mean and variance themselves are unknown, and the case that the mean and the support of the distribution of the uncertain parameters are known. For more general uncertainty models where exact results appear difficult, we provide a conservative approximation scheme based on CVaR approximation of the chance constraints. In Sect. 6, we extend the probabilistic envelope constraint formulation to its joint chance constraint counterpart. This typically leads to a computationally challenging problem, and we adopt the CVaR approximation approach proposed by Zymler et al. [41], and show that the joint probabilistic envelope constraint can be approximated tractably under some technical conditions.
Notation. We use lower-case boldface letters to denote column vectors, upper-case boldface letters to denote matrices, and the transpose (superscript \(\top \)) of the column vectors to denote row vectors. The all-ones vector is denoted by \(\mathbf{1}\). The space of symmetric matrices of dimension \(n\) is denoted by \({\mathbb {S}}^n\). For any two matrices \(\mathbf{X},\mathbf{Y}\in {\mathbb {S}}^n\), \(\langle \mathbf{X},\mathbf{Y}\rangle =\mathrm {tr}(\mathbf{X}\mathbf{Y})\) denotes the trace scalar product, and the relation \(\mathbf{X}\succeq \mathbf{Y}\) (\(\mathbf{X}\succ \mathbf{Y}\)) implies that \(\mathbf{X}-\mathbf{Y}\) is positive semi-definite (positive definite). Random variables are always represented by \(\varvec{\delta }\). Finally, we call an optimization problem tractable if it can be solved in polynomial time and call a set tractable if it is convex and a polynomial-time separation oracle can be constructed.
2 Formulation and motivating examples
We first propose the distributionally robust chance constraint, the probabilistic envelope constraint and the joint probabilistic envelope constraint discussed in this paper. For clarity, we repeat some of the definitions given in the introduction. Given a random variable \(\varvec{\delta }\) and a function \(f(\mathbf{x},\varvec{\delta })\), a chance constraint places a lower-bound on the probability that the constraint reaches a certain target, which is defined as
As discussed above, the distributionally robust chance constraint provides protection against noise by bounding the probability of failing to achieve a pre-defined target \(\alpha \). It says nothing about what happens when, with probability at most \((1 - p)\), the target is not met. In particular, there is no control over the magnitude of violation of the constraint. To overcome this shortcoming, the probabilistic envelope constraint is proposed, which can enforce all levels of probabilistic guarantees. Given a non-decreasing function \({\mathfrak {B}}(s)\), the probabilistic envelope constraint can be written as
For example, if we want the probability of large constraint violation to decrease exponentially, then we can set \({\mathfrak {B}}(s)=1-\gamma \exp (-\beta s)\). Besides the individual probabilistic envelope constraint discussed above, we propose the following joint probabilistic envelope constraint (JPEC):
Computationally, the joint envelope constraint is more complicated. A common method to simplify it is to decompose it into \(m\) individual envelope constraints by applying Bonferroni’s inequality. However, since Bonferroni’s inequality is not tight, this approximation method is usually overly conservative. In this paper, we use the worst-case CVaR method proposed by Zymler et al. [41] to give a tractable and tighter approximation for this joint envelope constraint.
Although the three types of constraints (5), (6), and (7) above can be general, they may not be tractable due to the non-convex feasible sets. To ensure tractability, we focus on the “concave-quasiconvex” case, i.e., the function \(f\) is concave w.r.t. the decision variable, and quasi-convex w.r.t. the uncertain parameters, see the following for a precise description:
Assumption 1
Let \({\mathbb {X}}\) and \({\mathbb {Y}}\) be two convex sets, and let \(f\) be a function mapping from \({\mathbb {X}}\times {\mathbb {Y}}\) to \({\mathbb {R}}\),
-
1.
For each \(\mathbf{x}\in {\mathbb {X}}\), the function \(f(\mathbf{x},\cdot )\) is quasi-convex and continuous on \({\mathbb {Y}}\). For each \(\mathbf{y}\in {\mathbb {Y}}\), the function \(f(\cdot ,\mathbf{y})\) is concave on \({\mathbb {X}}\).
-
2.
The uncertainty \(\varvec{\delta }\) is modeled as a random variable whose mean and variance are known but its distribution is unknown. Without loss of generality, we assume the mean is zero.
Notice that Assumption 1 generalizes the case where \(f(\cdot , \cdot )\) is bilinear—a setup that previous literature mainly focused on—to the non-linear case. In particular, the uncertainty can be non-linear. Non-linearity of uncertainty arises naturally in a broad range of applications, as we demonstrate by the following examples.
2.1 Example 1: Portfolio optimization
Consider a stylized portfolio optimization problem, where an amount is to be allocated to \(n\) stocks and held for a time period \(T\). Denote the price of the \(i\)th stock after time \(T\) by \(S_i\), and our goal is to maximize the Value at Risk (VaR) of the total return of the portfolio, which leads to the following formulation, for a fixed \(\gamma \in (0,1)\)
where \(x_i\) is the allocation for the \(i\)th stock. It is well believed that the true drivers of the uncertainty in stock price is not the stock return \(S_i\) itself, but instead the compounded rates of return, i.e., \(S_i=\exp (\delta _i)\) where \(\delta _i\) is the random variable to model and analyze. For example, the celebrated log-normal model, pioneered by Black and Scholes [9], models \(S_i\) as \(S_i = \exp \big ((\mu _i-\sigma _i^2/2)T +\sqrt{T} \xi _i\big )\) where the vector \(\varvec{\xi }\) is Normally distributed with mean \(0\) and covariance matrix \(\mathbf{Q}\). This can be rewritten as \(S_i=\exp (\delta _i)\) where \(\varvec{\delta }\sim {\mathcal {N}}((\mu _i-\sigma _i^2/2)T, T\mathbf{Q})\).
One common criticism of the log-normal model is that it assumes \(\varvec{\xi }\) to be Gaussian, whereas empirical evidence suggests that \(\varvec{\xi }\) (and hence \(\varvec{\delta }\)) is fat-tailed (e.g., Jansen and deVries [26], Cont [15], Kawas and Thiele [27]). Since the Gaussian assumption ignores the fat tails, it essentially leads the managers to take more risk than she is willing to accept. On the other hand, it remains controversial about what is the most appropriate fat-tail distribution to use in modeling returns [15, 23, 26, 29], and “this controversy has proven hard to resolve” as Jensen and de Vries stated [26]. In light of this, one possible approach is to not commit to any distribution, but instead only require that the first two moments match. This leads to the following problem:
Observe that this formulation satisfies Assumption 1, i.e., the constraint is linear to the decision variable and non-linearly convex to the uncertain parameters, and the decision variables are non-negative.
In portfolio optimization, options are another cause of non-linearity of the uncertainty (Kawas and Thiele [28], Zymler et al. [42]). Suppose for each stock, the investor is allowed to purchase an European call option at the price of \(c_i\) per unit, which gives her the right to buy a unit of stock \(i\) at time \(T\) with the strike price \(p_i\). Thus, denote the stock return as \(S_i\), the return of this option is \(\max (S_i - p_i, 0)\), since the investor will execute the option if and only if \(S_i>p_i\). The portfolio optimization problem is thus formulated as
where \(\mathbf{y}\) is the investment of the European call options. Notice that the constraints are non-linear, yet convex to \(S_i\). Indeed, following the previous argument, we may further model \(S_i=\exp (\delta _i)\), and require that the first two moments of \(\varvec{\delta }\) are known. This makes the probabilistic constraint again satisfy Assumption 1.
2.2 Example 2: Transportation problem
Solving multi-stage optimization problems may also result in non-linearity of uncertainty and decision variables. We illustrate this using a transportation decision problem. Given a directed graph \({\mathcal {G}}=({\mathcal {V}}, {\mathcal {E}})\), and let \({\mathcal {S}}\subset {\mathcal {V}}\) be the set of source nodes, and \({\mathcal {D}}\subset {\mathcal {V}}\) be the set of destination nodes, with \({\mathcal {S}}\bigcap D =\emptyset \). One can think of each node in \(\mathcal {S}\) as a supplier, and each node in \(\mathcal {D}\) as a consumer.
The decision to make contains two stages: in the first stage, the decision maker needs to decide the required flow of each source node and each destination node, i.e, \(s(i)\) for \(i\in {\mathcal {S}}\) and \(d(j)\) for \(j\in {\mathcal {D}}\). One can think of this as deciding how much amount of good to order from each supplier, and how much to sell to each client. Certain linear constraints on the required flow are imposed: for example, the total supply equals to the total demand, and they must be larger than a minimum demand \(L\), i.e., \(\sum _{i\in {\mathcal {S}}} s(i) = \sum _{j\in {\mathcal {D}}} d(j) \ge L\).
In the second stage, after all the ordered goods are produced by the suppliers, the decision maker needs to decide how to transport these goods, i.e., the flow on the network from sources to destinations, by solving a minimum cost flow problem given \(s_i\) and \(d_j\). This can be formulated as a linear program, where the decision variable \(f(u,v)\) is the flow from node \(u\) to node \(v\):
Denote the optimal value by \(h(\mathbf{s}, \mathbf{d}, \varvec{\delta })\). Suppose \(\varvec{\delta }\) represents uncertain parameters whose values are only revealed at stage two, then to ensure that the total transportation cost is low with high probability, the first stage decision can be formulated using DRCC:
It is easy to verify that \(-h(\mathbf{s},\mathbf{d},\varvec{\delta })\) is non-linearly concave w.r.t. the decision variables \((\mathbf{s},\mathbf{d})\) and non-linearly convex w.r.t. \(\varvec{\delta }\). Thus, the above transportation problem satisfies Assumption 1.
3 The chance constraint case
This section is devoted to the (individual) distributionally robust chance constraint case (5). Our main theorem shows that when function \(f(\mathbf{x},\varvec{\delta })\) satisfies Assumption 1, then a DRCC is equivalent to a robust optimization constraint. This bridges the two main approaches in optimization under uncertainty, namely, stochastic programming, and robust optimization. We then investigate the tractability of DRCC, providing sufficient conditions for the individual DRCC (5) to be tractable.
3.1 Equivalence to robust optimization
In this subsection we show that DRCC is equivalent to robust optimization by analyzing the feasible set given by the constraint (5), which we denote by
Our main tool to analyze \(S\) is the following result from Marshall and Olkin [30].
Lemma 1
Let \(\varvec{\delta }=(\delta _1,\ldots ,\delta _k)\) be a random vector with \({\mathbb {E}}[\varvec{\delta }]=0\), \({\mathbb {E}}[\varvec{\delta }\varvec{\delta }^\top ]=\varvec{\varSigma }\), and \(T \subseteq {\mathbb {R}}^k\) be a closed convex set. Then we have
where \(\theta =\inf _{\mathbf{y}\in T}\sqrt{\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}}\), and the equality can always be attained.
Notice that one technical difficulty that we face to apply Lemma 1 is that the set \(\{\varvec{\delta }| f(\mathbf{x},\varvec{\delta }) <\alpha \}\) may not be closed. Hence we extend Lemma 1 to the case where \(T\) is not necessarily closed:
Lemma 2
Let \(T \subseteq {\mathbb {R}}^k\) be a convex set. Denote \(\theta =\inf _{\mathbf{y}\in T}\sqrt{\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}}\). Then we have
Proof
When \(T\) is empty, we have \(\sup _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })}{\mathbb {P}}[\varvec{\delta }\in T]=0\). On the other hand, \(\theta =\inf _{\mathbf{y}\in T}\sqrt{\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}}\!=\!+\infty \) which implies \(1/(1\!+\!\theta ^2)\!=\!0\). Hence the lemma holds.
When \(T\) is non-empty, \(T\) has a non-empty relative interior. Let \(\mathbf{x}_0\) be a point in the relative interior of \(T\). Let \(\overline{T}\) be the closure of \(T\), and for \(0\le \lambda < 1\) define \(\underline{T}(\lambda )\) by
Thus, we have \(\underline{T}(\lambda )\) is closed, convex, and \(\underline{T}(\lambda ) \subseteq T\). Define
and hence \(\underline{\theta }(\lambda ) \ge \theta \ge \overline{\theta }\). On the other hand, for any \(\mathbf{x}\in \overline{T}\), one can construct a sequence \(\mathbf{x}_i \rightarrow \mathbf{x}\) such that \(\mathbf{x}_i \in \underline{\theta }(\lambda _i)\) for some \(\{\lambda _i\}_{i=1}^{\infty }\), by the definition of \(\underline{T}(\lambda )\). Thus, since \(\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\) is a continuous function of \(\mathbf{y}\), we have \(\inf _{\lambda \in [0,1)}\underline{\theta }(\lambda ) \le \overline{\theta }\), which implies \(\inf _{\lambda \in [0,1)}\underline{\theta }(\lambda ) = \overline{\theta }.\) By Lemma 1, the following inequalities hold for \(0\le \lambda <1\) since \(\underline{T}(\lambda )\) and \(\overline{T}\) are both closed convex sets:
Since \(\sup _{\lambda \in [0,1)}\frac{1}{1+\underline{\theta }(\lambda )^2} = \frac{1}{1+\overline{\theta }^2}\), we have
which establishes the lemma.\(\square \)
Now we are ready to present the main result of this subsection.
Theorem 1
Suppose \(f({\mathbf {x}}, \cdot )\) is quasi-convex for every \(\mathbf{x}\in {\mathbb {X}}\) and \(f(\cdot ,\mathbf{y})\) is concave for every \(\mathbf{y}\in {\mathbb {Y}}\), and let \(p\in (0,1)\) and set \(r=p/(1-p)\), then the feasible set \(S\) of the DRCC (5) is convex and admits
If \(f({\mathbf {x}}, \cdot )\) is further assumed to be continuous for every \(\mathbf{x}\in {\mathbb {X}}\), then the distributionally robust chance constraint \(\inf _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })}{\mathbb {P}}[f(\mathbf{x},\varvec{\delta }) \ge \alpha ] \ge p\) is equivalent to
Proof
Since \(f(\mathbf{x},\cdot )\) is quasi-convex for each \(\mathbf{x}\in {\mathbb {X}}\), the set \(T_{\mathbf{x}}\,\triangleq \,\{\mathbf{y}|f(\mathbf{x},\mathbf{y}) < \alpha \}\) is convex for fixed \(\mathbf{x}\). Then from Lemma 2, the feasible set of the constraint (5) satisfies
where (a) holds by Lemma 2. Since \(f(\cdot ,\mathbf{y})\) is concave for every \(\mathbf{y}\), we know that \(S\) is convex, as the property is preserved under arbitrary intersection. Hence we proved the first part: \(S = \{\mathbf{x}|\forall \mathbf{y}\text { such that } \mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}<r \Rightarrow f(\mathbf{x},\mathbf{y}) \ge \alpha \}\).
To show the second part, further notice that \(p\in (0, 1)\) implies \(r>0\). Thus we have
where the equality holds because for each \(\mathbf{x}\in {\mathbb {X}}\), \(f(\mathbf{x},\mathbf{y})\) and \(\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\) are both continuous in \(\mathbf{y}\) so that we can replace “\(<\)” by “\(\le \)” without effect on \(S\). \(\square \)
Thus the probabilistic uncertainty model is linked to the deterministic set based uncertainty model of robust optimization (e.g., Ben-Tal and Nemirovski [6, 7], Bertsimas and Sim [8]). This result is in the spirit of past work that has linked chance constraints to robust optimization in the linear case (e.g., Delage and Mannor [16], Shivaswamy et al. [38]).
Interestingly, based on the above theorem, we can establish an equivalence relationship between the distributionally robust chance constraint and the Worst Case Conditional Value at Risk (WCCVaR) in the convex case, which recovers a result first shown in [41] using a different proof.
Corollary 1
Suppose \(f({\mathbf {x}}, \cdot )\) is convex and continuous for every \(\mathbf{x}\in {\mathbb {X}}\), then for \(p \in (0,1)\),
Proof
See Appendix 9.1. \(\square \)
In the most general case, i.e., \(f(\mathbf{x},\varvec{\delta })\) is quasi-convex, the equivalence shown in Corollary 1 does not hold. Consider a constraint with a random variable \(\delta \):
We now construct a function \(f(\mathbf{x},\delta )\) that is quasi-convex but not convex w.r.t. \(\delta \). In particular, we construct \(f(\mathbf{x},\delta )\) that is decreasing (hence quasi-convex) and concave w.r.t. \(\delta \), such that the DRCC above holds but the constraint on the worse-case CVaR does not hold. For simplicity, denote \(-f(\mathbf{x},\cdot )\) by \(L(\cdot )\) and let \(\alpha = -\sigma \). Define \(L(\cdot )\) as follows:
It can be easily shown that the constraint \(\inf _{\delta \sim (0,\sigma )}{\mathbb {P}}[L(\delta ) \le \sigma ] \ge 0.5\) holds. Consider an uniform distribution over the interval \([-\sqrt{3\sigma },\sqrt{3\sigma }]\) which has mean \(0\) and variance \(\sigma \). By simple computation, we can see that \(\text {CVaR}_{0.5}(L(\delta )) > \sigma \) w.r.t. this uniform distribution when \(\sigma = 1\).
3.2 Tractability of individual DRCC
In this subsection we investigate the tractability of DRCC. We first provide sufficient conditions for optimization problems involving chance constraint (5) with function \(f(\mathbf{x},\varvec{\delta })\) being tractable. We then show that for the special case where \(f(\mathbf{x},\varvec{\delta })=g(\varvec{\delta })^\top \mathbf{x}\) and \(g(\varvec{\delta })\) is linear or convex quadratic, we can convert (5) to an equivalent semi-definite constraint.
Theorem 2
If function \(f(\mathbf{x},\varvec{\delta })\) satisfies Assumption 1, set \(\varvec{\Psi } \subseteq {\mathbb {X}}\) is tractable and \(p\in (0,1)\), then the following optimization problem
can be solved in polynomial time, if (1) for any fixed \(\varvec{\delta }\) the super-gradient of \(f(\cdot ,\varvec{\delta })\) can be evaluated in polynomial time; and (2) for any fixed \(\mathbf{x}\in \varvec{\Psi }\) the following optimization problems on \(\mathbf{y}\) can be solved in polynomial time,
Proof
By Theorem 1, the feasible set \(S\) of the constraint (5) is given by
To establish the theorem, it suffices to construct a polynomial-time separation oracle for \(S\) (Grötschel et al. [25]). A “separation oracle” is a routine such that for \(\mathbf{x}^*\), it can be verified in polynomial time that (a) whether \(\mathbf{x}^* \in S\) or not; and (b) if \(\mathbf{x}^*\not \in S\), a hyperplane that separates \(\mathbf{x}\) with \(S\).
We now construct such a separation oracle. To verify the feasibility of \(\mathbf{x}^*\), notice that \(\mathbf{x}^*\in S\) if and only if the optimal value of the optimization problem (10) is greater than or equal to \(\alpha \), which can be verified by solving Problem (10) directly. By assumption, this can be done in polynomial time.
If \(\mathbf{x}^*\not \in S\), then by solving Problem (10), we can find in polynomial time \(\mathbf{y}^*\) such that \(f(\mathbf{x}^*,\mathbf{y}^*)<\alpha \). Because \(f(\mathbf{x},\mathbf{y})\) is concave in \(\mathbf{x}\) for each \(\mathbf{y}\in {\mathbb {Y}}\), for any \(\mathbf{x}\in S\), the following holds
Thus, the hyperplane separating \(\mathbf{x}^*\) from the feasible set \(S\) is the following
which can be generated in polynomial time since the super-gradient of \(\mathbf{x}\) can be obtained in polynomial time. \(\square \)
We now consider the special case that \(f(\mathbf{x},\varvec{\delta })=g(\varvec{\delta })^\top \mathbf{x}\) and each component \(g_i(\varvec{\delta })\) of \(g(\varvec{\delta })\) is either quadratic convex or linear.
Corollary 2
If \(f(\mathbf{x},\varvec{\delta })=g(\varvec{\delta })^\top \mathbf{x}\) and satisfies Assumption 1 and each component of \(g(\varvec{\delta })\) is a convex quadratic or linear function, i.e., it has the form \(g_i(\varvec{\delta })=\varvec{\delta }^\top \mathbf{G}_i\varvec{\delta }+\mathbf{p}_i^\top \varvec{\delta }+q_i\), where \(\mathbf{p}_i \in {\mathbb {R}}^n\), \(q_i \in {\mathbb {R}}\) and \(\mathbf{G}_i \in {\mathbb {S}}^n\) is a symmetric semi-definite matrix (\(G_i\) is zero if \(g_i(\varvec{\delta })\) is linear), then the following optimization problem
where \(p \in (0,1)\), is equivalent to
where \(G(\mathbf{x})\,\triangleq \, \sum _{i=1}^{n}{x_i\mathbf{G}_i}\), \(P(\mathbf{x})\triangleq \sum _{i=1}^n{x_i\mathbf{p}_i}\), and \(Q(\mathbf{x}) \triangleq \sum _{i=1}^n{x_iq_i}-\alpha \).
Proof
See Appendix 9.2. \(\square \)
Notice that \(G(\mathbf{x})\), \(P(\mathbf{x})\) and \(Q(\mathbf{x})\) are all linear functions of \(\mathbf{x}\), and hence the semi-definite constraint in Problem (12) is a linear matrix inequality. Compare to the result by Calafiore and El Ghaoui [10] which only considers the case where \(f(\cdot ,\cdot )\) is bilinear, the result above holds when \(f(\mathbf{x},\cdot )\) is convex quadratic. Zymler et al. [41] showed that DRCC is tractable when \(f(\mathbf{x}, \varvec{\delta })\) is linear in \(\mathbf{x}\) and quadratic in \(\varvec{\delta }\). However, their method is built upon S-lemma, and hence it is not clear how to extend the method to more general cases. Our formulation needs stronger conditions—\(f(\mathbf{x},\cdot )\) is convex quadratic—than [41], but the equivalent formulation is simpler than [41].
4 Probabilistic envelope constraint
Recall that the probabilistic envelope constraint refers to the following:
Here, \(s\) represents allowed magnitude of constraint violation, and \({\mathfrak {B}}(s)\) is the probabilistic guarantee associated with a constraint violation no more than \(s\). Hence, \({\mathcal {B}}(s) \in (0,1)\) for all \(s\ge 0\), and is assumed to be non-decreasing without loss of generality.
When \(f(\mathbf{x},\varvec{\delta })\) is bilinear, the envelope constraint (13) is shown to be equivalent to a comprehensive robust constraint, and proved to be tractable under mild technical conditions in Xu et al. [40]. We consider in this section the tractability of (13) where \(f(\mathbf{x},\varvec{\delta })\) satisfies Assumption 1. For convenience of exposition, we rewrite (13) to an equivalent formulation as shown in the following lemma.
Lemma 3
If \({\mathfrak {B}}(s):{\mathbb {R}}^+ \mapsto (0,1)\) is a non-decreasing function that is continuous from the right, then the probabilistic envelope constraint (13) is equivalent to
Here \(t(r)\,\triangleq \, {\mathfrak {B}}^{-1}(\frac{r}{1+r})\) and \({\mathfrak {B}}^{-1}(x)\) is defined as
Furthermore, \(t(\cdot )\) is non-decreasing, \(t(0)=0\), \(\lim _{r\uparrow +\infty } t(r)=+\infty \), and \(t(\cdot )\) is continuous at the neighborhood of \(0\).
Proof
See Appendix 9.3. \(\square \)
Hence in the sequel, we analyze the probabilistic envelope constraint (14) instead of (13). The following theorem shows that a probabilistic envelope constraint is equivalent to a comprehensive robust constraint proposed in Ben-Tal et al. [2–4]. This thus extends previous results for affine cases in Xu et al. [40] to general \(f(\cdot , \cdot )\) satisfying Assumption 1.
Theorem 3
Suppose \(t:{\mathbb {R}}^+ \mapsto [0,+\infty )\) is non-decreasing, \(t(0)\!=0\), \(\lim _{r\uparrow +\infty }t(r)\!=+\infty \) and continuous at the neighborhood of \(0\). Then if function \(f(\mathbf{x},\varvec{\delta })\) satisfies Assumption 1, the probabilistic envelope constraint
is equivalent to the comprehensive robust constraint
Proof
Define the feasible set of (15) as \(S\). For any fixed \(r \ge 0\), we have
by Lemma 3 and Theorem 1. Thus, we have
Notice that without loss of generality, we can neglect the case \(r=0\) in the right hand side, as \(\{\mathbf{y}|\mathbf{y}^\top \varvec{\varSigma }^{-1} \mathbf{y}<0\} =\emptyset \). Thus we have
where in the last equality we use the fact that \(\forall \mathbf{x}\in {\mathbb {X}}\), \(f(\mathbf{x},\mathbf{y})\) and \(\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\) are both continuous in \(\mathbf{y}\), we can replace “\(<\)” by “\(\le \)” without effect on \(S\) as long as \(\{ \mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}< r \}\) is non-empty. By continuity of \(t(r)\) at \(r=0\), we further have
The second equality holds because there exists no \(\mathbf{y}\) such that \(\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\le r\) when \(r < 0\) so that the constraint \(r \ge 0\) can be removed. Hence the probabilistic envelope constraint is equivalent to
Notice that (17) is equivalent to constraint (16) by monotonicity of \(t(\cdot )\). \(\square \)
It is known that comprehensive robust optimization generalizes robust optimization (e.g., Ben-Tal et al. [2–4]). Indeed, if \(t(\cdot )\) is taken to be an indicator function, i.e., \(t(r)\,{=}\,0\) for \(r{\in } [0, c]\) and \(+\infty \) for \(r{>}c\), the formulation (16) recovers the standard robust optimization formulation with the ellipsoidal uncertainty set \(\varvec{\Omega } =\{\mathbf{y}|\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\le c\}\). On the other hand, while robust optimization guarantees that the constraint is not violated for any realization of the uncertain parameters in the set \(\varvec{\Omega }\), it makes no guarantees for realizations outside that set. In contrast, the comprehensive robust optimization formulation allows us to choose different functions \(t(\cdot )\), in order to provide different levels of protection for different parameter realizations, as opposed to the “all-or-nothing” view of standard robust optimization.
We now investigate the tractability of probabilistic envelope chance constraints. We first consider the general case where \(f(\mathbf{x},\varvec{\delta })\) is an arbitrary “concave-quasiconvex” function. The following theorem is essentially an envelope constraint counterpart of Theorem 2.
Theorem 4
If \(t(\cdot )\) satisfies the conditions in Theorem 3, \(f(\mathbf{x},\varvec{\delta })\) satisfies Assumption 1 and set \(\varvec{\Psi } \subseteq {\mathbb {X}}\) is tractable, then the optimization problem with a linear objective function and the probabilistic envelope constraint (13):
can be solved in polynomial time if (1) one can provide the super-gradient of \(f(\mathbf{x},\varvec{\delta })\) at \(\mathbf{x}\) for fixed \(\varvec{\delta }\) in polynomial time, and (2) for any fixed \(\mathbf{x}\) the following optimization problems can be solved in polynomial time:
Proof
By Theorem 3, the feasible set \(S\) can be rewritten as
Similar to the proof of Theorem 2, we construct a separation oracle to prove tractability. In order to verify the feasibility of a given \(\mathbf{x}^*\), notice that \(\mathbf{x}^* \in S\) if and only if the optimal objective value of the optimization problem (19) is greater than or equal to \(\alpha \), which can be verified by directly solving Problem (19). By assumption, this can be done in polynomial time.
If \(\mathbf{x}^* \not \in S\), then by solving Problem (19), we can find in polynomial time \((\mathbf{y}^*,r^*)\) such that \(f(\mathbf{x}^*,\mathbf{y}^*)+t(r^*) < \alpha \). Because \(f(\mathbf{x},\mathbf{y})\) is concave in \(\mathbf{x}\) for each \(\mathbf{y}\in {\mathbb {Y}}\), for any \(\mathbf{x}\in S\), we have
Hence the hyperplane separating \(\mathbf{x}^*\) from the feasible set \(S\) is the following:
which can be generated in polynomial time since the super-gradient of \(\mathbf{x}\) can be obtained in polynomial time. This completes the proof.\(\square \)
Our next result states that when \(f(\mathbf{x},\varvec{\delta })=g(\varvec{\delta })^\top \mathbf{x}\) and \(g_i(\varvec{\delta })\) is quadratic, (14) can be converted to a semi-definite constraint.
Corollary 3
Suppose \(t(\cdot )\) satisfies the conditions in Theorem 3 and is convex, \(f(\mathbf{x},\varvec{\delta })=g(\varvec{\delta })^\top \mathbf{x}\) satisfies Assumption 1 and \(\varvec{\Psi } \subseteq {\mathbb {X}}\) is tractable, then if each component \(g_i(\varvec{\delta })\) of \(g(\varvec{\delta })\) is linear or convex quadratic as in Corollary 2, the optimization problem (18) is equivalent to
where \(t^*(\beta )\) is the conjugate function of \(t(r)\), i.e., \(t^*(\beta )\,\triangleq \, \sup _{r \ge 0}{(\beta r-t(r))}\); and \(P(\cdot ), G(\cdot ), Q(\cdot )\) are defined as in Corollary 2. Furthermore, the optimization problem (18) with a linear objective function and the probabilistic envelope constraint can be solved in polynomial time if for any \(\beta \ge 0\) the following optimization problem on \(r\) can be solved in polynomial time:
Proof
See Appendix 9.3. \(\square \)
In particular, when \(t(r)\) is a convex function, the optimization problems (19) and (22) are both convex and can be solved efficiently.
5 Chance constraints: beyond mean and variance
Thus far we have studied the setup that models unknown parameters as following an ambiguous distribution with known mean and covariance. In this section we extend our results to some other models of uncertain parameters—this includes the case where the mean and the covariance themselves are unknown and can only be estimated from data; and the case where other information of the uncertain parameter (e.g., the support) may be available. Specifically, we first show that the chance constraint (5) and the probabilistic envelope constraint (6) with uncertain mean and covariance are still tractable. Then we deal with the case where the mean and support of the uncertain parameter are known. Finally, we apply distributionally robust optimization to make a conservative approximation for constraints (5) and (6) when additional information on the uncertain parameter is available.
5.1 Uncertain mean and covariance
We first study the uncertain mean and covariance case. This model of ambiguity was first proposed and studied in [17] for distributionally robust optimization, and was also investigated for linear chance constraints in [40]. We formulate the robust counterparts of the distributionally robust chance constraint (5) and the probabilistic envelope constraint (6) where the mean and covariance themselves are uncertain, and then show that optimization problems with these constraints are tractable under mild conditions. Based on Theorem 1 and Theorem 3, we can easily obtain the following corollaries. Corollary 4 and Corollary 5 show that the DRCC and the probabilistic envelope constraint with unknown mean and covariance is equivalent to a set of (infinitely many) deterministic constraints. Note that the uncertainty sets \({\mathcal {U}}\) and \({\mathcal {S}}\) can be arbitrary. Corollary 6 shows the tractability of probabilistic envelope constraints.
Corollary 4
If function \(f(\mathbf{x},\varvec{\delta })\) satisfies Assumption 1, then for \(p \in (0,1)\) the chance constraint
is equivalent to the constraint \( f(\mathbf{x},\mathbf{y}+\varvec{\mu }) \ge \alpha ,\ \forall \mathbf{y}\in {\mathbb {R}}^n,\varvec{\mu }\in {\mathcal {U}} \text { and } \varvec{\varSigma }\in {\mathcal {S}} \text { such that } \left( \begin{array}{cc} \varvec{\varSigma }&{} \mathbf{y}\\ \mathbf{y}^\top &{} \frac{p}{1-p} \\ \end{array} \right) \succeq 0, \) where \({\mathcal {U}}\) and \({\mathcal {S}}\) are the uncertainty sets of mean \(\varvec{\mu }\) and covariance \(\varvec{\varSigma }\), respectively.
Corollary 5
Suppose \(t:{\mathbb {R}}^+ \mapsto [0,+\infty )\) is non-decreasing, \(t(0)=0\), \(\lim _{r\uparrow +\infty }t(r)=+\infty \) and is continuous at the neighborhood of zero. Then if function \(f(\mathbf{x},\varvec{\delta })\) satisfies Assumption 1, the probabilistic envelope constraint
is equivalent to the constraint
where \({\mathcal {U}}\) and \({\mathcal {S}}\) are the uncertainty sets of mean \(\varvec{\mu }\) and covariance \(\varvec{\varSigma }\), respectively.
Corollary 6
Under the conditions of Corollary 5, an optimization problem with a linear objective function and the probabilistic envelope constraint (24) can be solved in polynomial time if one can provide the super-gradient of \(f(\mathbf{x},\varvec{\delta })\) at \(\mathbf{x}\) for fixed \(\varvec{\delta }\) in polynomial time, and for any fixed \(\mathbf{x}\) the following optimization problem can be solved in polynomial time:
Proof
See Appendix 9.5. \(\square \)
From Corollary 6 we see that if \(t(\cdot )\) is convex, and \({\mathcal {U}} \subseteq {\mathbb {R}}^n\) and \({\mathcal {S}} \in {\mathbb {S}}_+^{n \times n}\) are both convex sets, then the optimization problem (26) is a SDP problem which can be solved efficiently. The tractability result of the chance constraint (23) is a special case of Corollary 6, namely, \(t(r)=0\) and \(r = \frac{p}{1-p}\).
5.2 Known mean and support
We now investigate the case where the mean and the support of the uncertain parameter \(\varvec{\delta }\) are known. We show that the corresponding robust chance constraint can be reformulated as a set of infinitely many deterministic constraints, and is tractable under mild technical conditions. Unfortunately, it seems that these results can not be easily extended to the probabilistic envelope constraint case, which is hence left for future research.
Theorem 5
Suppose the mean \(\varvec{\mu }\) and support \({\mathcal {S}}\) of the uncertain parameter \(\varvec{\delta }\) are known and \({\mathcal {S}}\) is a closed convex set. If \(f(\mathbf{x}, \cdot )\) is continuous and quasi-convex for every \(\mathbf{x}\in {\mathbb {X}}\), then for \(p\in (0,1]\), the chance constraint
is equivalent to
Proof
See Appendix 9.5. \(\square \)
Theorem 6
If \(f(\mathbf{x}, \cdot )\) is quasi-convex and continuous for every \(\mathbf{x}\in {\mathbb {X}}\) and \(f(\cdot ,\mathbf{y})\) is concave for every \(\mathbf{y}\in {\mathbb {Y}}\), the mean \(\varvec{\mu }\) and support \({\mathcal {S}}\) of the uncertain parameter \(\varvec{\delta }\) are known, and \({\mathcal {S}}\) is a closed convex set, then for \(0 < p \le 1\), the optimization problem with a linear objective function and a chance constraint (27):
can be solved in polynomial time if (1) one can provide the super-gradient of \(f(\mathbf{x},\mathbf{y})\) at \(\mathbf{x}\) for fixed \(\mathbf{y}\) in polynomial time, and (2) for any fixed \(\mathbf{x}\) the following optimization problems can be solved in polynomial time:
Proof
From Theorem 5 we know that the chance constraint is satisfied if and only if the optimal value of (30) is greater than or equal to \(\alpha \). Thus, the theorem can be proved following a similar argument as the proof of Corollary 6.\(\square \)
5.3 Conservative approximation
For general sets of ambiguous distributions, optimization problems involving chance constraints are notoriously hard to solve. Recall that CVaR provides a conservative approximation of chance constraints (Nemirovski et al. [32]) , which allows us to apply DRO to approximately solve such problems. For completeness, we give the following lemma which is an extension of Nemirovski et al. [32]:
Lemma 4
Suppose that \({\mathcal {D}}\) is the ambiguity set of distributions of the uncertain parameter \(\varvec{\delta }\), then the chance constraint
can be conservatively approximated by
where \(0 \le p \le 1\), \(t \in {\mathbb {R}}\) and \(\gamma \in {\mathbb {R}}\) are decision variables, and \([x]_+=\max \{x,0\}\). Here, by “conservative approximation” we mean that any solution that satisfies (32) also satisfies (31).
Wiesemann et al. [39] proposed a unified framework for modeling and solving distributionally robust optimization problems by introducing standardized ambiguity sets
where \({\mathbb {P}}\) represents a joint probability distribution of the random vector \(\varvec{\delta }\in {\mathbb {R}}^m\) appearing in the constraint function \(f(\mathbf{x},\varvec{\delta })\) and some auxiliary random vector \(\varvec{\mu }\in {\mathbb {R}}^n\), with \(\mathbf{A}\in {\mathbb {R}}^{k \times m}\), \(\mathbf{B}\in {\mathbb {R}}^{k \times n}\), \(\mathbf{b}\in {\mathbb {R}}^{k}\), \({\mathcal {I}}=\{1,\ldots ,I\}\), \(\underline{p_i},\overline{p_i} \in [0,1]\) and \({\mathcal {C}}_i\) are the confidence sets.
Applying Theorem 1 and 5 in [39], the constraint \(\sup _{{\mathbb {P}} \in {\mathcal {D}}} {\mathbb {E}}_{\mathbb {P}}[[f(\mathbf{x},\varvec{\delta })+t]_+] \le \gamma \) can be reformulated as a semi-infinite constraint system. For succinctness, we only present the conservative approximation of the chance constraints when \(\underline{p_i}=\overline{p_i}=1\) and \(|{\mathcal {I}}|=1\) to illustrate our approach.
Theorem 7
If the ambiguity set \({\mathcal {P}}\) can be converted into
by the lifting theorem (Theorem 5 in [39]) where \(g(\cdot )\) is a convex function, then the chance constraint \(\inf _{{\mathbb {P}} \in {\mathcal {P}}} {\mathbb {P}} [f(\mathbf{x},\varvec{\delta }) \ge \alpha ] \ge p\) with \(p \in (0,1)\) can be conservatively approximated by
where \(\beta ,\lambda ,\mathbf{x}\) are decision variables. Furthermore, the optimization problem with a linear objective function and the constraint (34) can be solved in polynomial time if (1) one can provide the super-gradient of \(f(\mathbf{x},\mathbf{y})\) at \(\mathbf{x}\) for fixed \(\mathbf{y}\) in polynomial time, and (2) for any fixed \((\mathbf{x},\varvec{\beta },\lambda )\) the following optimization problems
and
can be solved in polynomial time.
Proof
From Theorem 1 in [39] and Lemma 4, the conservative approximation formulation can be easily obtained. The proof of the tractability result is similar to that of Corollary 6, and hence omitted.\(\square \)
We now extend this result to the probabilistic envelope constraint case.
Theorem 8
Suppose \(t:{\mathbb {R}}^+ \mapsto [0,+\infty )\) is convex, non-decreasing and continuous at the neighborhood of zero, and \(t(0)=0\), \(\lim _{r\uparrow +\infty }t(r)=+\infty \). If the ambiguity set \({\mathcal {D}}\) satisfies the condition in Theorem 7, the probabilistic envelope constraint \(\inf _{{\mathbb {P}} \in {\mathcal {D}}} {\mathbb {P}} [f(\mathbf{x},\varvec{\delta }) \ge \alpha -t(r)] \ge r/(1+r),\ \forall r \ge 0\) can be conservatively approximated by
Furthermore, the optimization problem with a linear objective function and this probabilistic envelope constraint can be solved in polynomial time if one can provide the super-gradient of \(f(\mathbf{x},\mathbf{y})\) at \(\mathbf{x}\) for fixed \(\mathbf{y}\) in polynomial time, and for any fixed \((\mathbf{x},\varvec{\beta },\lambda )\) the following optimization problems:
and
can be solved in polynomial time.
Proof
From Theorem 7, the probabilistic envelope constraint can be conservatively approximated by
Furthermore, by switching “min” and “max”, this can be conservatively approximated by (37). Then following a similar proof as that of Corollary 6, we obtain the tractability result to complete the proof.\(\square \)
6 Joint chance constraint
In this section we investigate the case of JPEC (7) which can be reformulated as (from Lemma 3)
where \(t(r)={\mathfrak {B}}^{-1}(r/(1+r))\). The optimization problem with the constraint (41) is usually intractable (e.g., Nemirovski and Shapiro [32]; Zymler et al. [41]), even when \(f(\mathbf{x},\varvec{\delta })\) is a bi-linear function, and approximation schemes are often used to tackle them. The most straightforward method to approximate the constraints (41) is to decompose them into several individual probabilistic envelope constraints using Bonferroni’s inequality (see below for details). A notable advantage of the Bonferroni approximation is that it is easy to implement and requires no assumptions on the function \(f_i(\mathbf{x},\varvec{\delta })\).
However, the Bonferroni approximation can be overly conservative. Zymler et al. [41] proposed a tighter approximation method called worst-case CVaR approximation that outperforms other methods including the Bonferroni approximation (e.g. Nemirovski and Shapiro [32] and Chen et al. [12]). In the rest of the section, we extend both the Bonferroni approximation and worst-case CVaR methods to JPEC. We also investigate the tractability of the two approximation schemes for \(f_i(\mathbf{x},\varvec{\delta })\) satisfying Assumption 1.
6.1 The Bonferroni approximation
The Bonferroni approximation for the JPEC (41) can be easily derived from Bonferroni’s inequality. From Theorems 2 and 4, we know that the optimization problem with a set of probabilistic envelope constraints generated by the Bonferroni approximation method is tractable, under mild technical conditions. More specifically we have the following theorem:
Theorem 9
Let \(t:{\mathbb {R}}^+ \mapsto [0,+\infty )\) be a non-decreasing function such that \(t(0)=0\) and \(\lim _{r\uparrow +\infty }t(r)=+\infty \), and \(\varvec{\epsilon }\) be a constant vector such that \(\sum _{i=1}^m{\epsilon _i}=1\) and \(\varvec{\epsilon }\ge 0\). The Bonferroni approximation of the JPEC (41) which has the form
is tractable if for each \(i\), (1) one can provide the super-gradient of \(f_i(\mathbf{x},\varvec{\delta })\) at \(\mathbf{x}\) for fixed \(\varvec{\delta }\) in polynomial time, and (2) for any fixed \(\mathbf{x}\) the following optimization problem can be solved in polynomial time:
Proof
Let \(r'=(1+r)/\epsilon _i -1\), then we have \(r'/(1+r') = 1-\epsilon _i/(1+r)\). Let \(t'(r')\,\triangleq \, t(r)\), then we apply Theorem 4 to complete the proof. \(\square \)
6.2 The worst-case CVaR approximation
Zymler et al. [41] developed a new approximation scheme for robust joint chance constraints termed Worst-case CVaR approximation. In this subsection we extend the worst-case CVaR approximation to JPEC (41). In contrast to the rest of the paper, we focus on the linear-quadratic uncertainty case, namely, \(f(\mathbf{x},\varvec{\delta })\) is linear in \(\mathbf{x}\) for any fixed \(\varvec{\delta }\) and quadratic (possibly non-convex) in \(\varvec{\delta }\) for each \(\mathbf{x}\in {\mathbb {X}}\). Then (41) can be rewritten respectively as:
where \(Q_i(\mathbf{x})\), \(y_i^0(\mathbf{x})\) and \(y_i(\mathbf{x})\) are all linear functions for \(i=1,\ldots ,m\). Zymler et al. [41] provided the Worst-case CVaR approximation for the following robust joint chance constraint
Theorem 10
[41] Let \({\mathcal {A}}\,\triangleq \, \{\varvec{\alpha } \in {\mathbb {R}}^m | \varvec{\alpha } > 0\}\). For any fixed \(\mathbf{x}\) and \(\varvec{\alpha } \in {\mathcal {A}}\), the feasible set of the worst-case CVaR approximation for the constraint (45) is
where \(\varvec{\Omega }=\text {diag}(\varvec{\varSigma },1)\).
Indeed, Zymler et al. [41] showed that the approximation quality of the worst-case CVaR is controlled by the parameter \(\varvec{\alpha }\) and that the approximation becomes exact if \(\varvec{\alpha }\) is chosen optimally. Notice that \( Z^{JCC}({\varvec{\alpha }})\) contains semi-definite constraints, and hence provides a tractable approximation to robust joint chance constraint. We now extend this methodology to the joint probabilistic envelope constraints (44). From Theorem 10, the feasible set of the constraint (44) can be approximated as
Notice that in contrast to (46), (47) is defined through uncountably many sets of constraints, and hence we need the following theorem to establish the tractability of the set \(Z^P\).
Theorem 11
Fix \(\varvec{\alpha }\in \mathcal {A}\). The optimization problem with a linear objective function and the feasible set \( Z^P(\varvec{\alpha })\) in (47) can be solved in polynomial time if for any fixed \(\mathbf{x}\), the following optimization problem can be solved in polynomial time:
where \( \mathbf{B}_i= \left( \begin{array}{cc} Q_i(\mathbf{x}) &{} \frac{1}{2} y_i(\mathbf{x}) \\ \frac{1}{2} y_i(\mathbf{x})^\top &{} y_i^0(\mathbf{x}) \\ \end{array} \right) \text{ and } \mathbf{E}= \left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 1 \\ \end{array} \right) . \)
Proof
See Appendix 9.7. \(\square \)
Interestingly, Theorem 11 provides a tractability result for individual probabilistic envelope constraint.
Corollary 7
If each component \(f_i(\cdot )\) of \(f(\cdot )\) is quadratic (and possibly non-convex), the optimization problem with a linear objective function and the probabilistic envelope constraint (6) can be solved in polynomial time if for any fixed \(\mathbf{x}\), the following optimization problem can be solved in polynomial time:
where \( \mathbf{B}= \left( \begin{array}{cc} Q(\mathbf{x}) &{} \frac{1}{2} y(\mathbf{x}) \\ \frac{1}{2} y(\mathbf{x})^\top &{} y^0(\mathbf{x}) \\ \end{array} \right) \text { and } \mathbf{E}= \left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} 1 \\ \end{array} \right) . \)
Proof
When \(m=1\), \(\alpha \) can be chosen as \(\alpha =1\) without effect on the optimal solution of (48). Then (48) can be simplified as (49). \(\square \)
Notice that Corollary 7 does not require that \(f_i(\cdot )\) is a convex quadratic function, and hence, subject to the price of a more complex formulation, is more general than Corollary 3 that investigates the probabilistic envelope constraint under convex quadratic uncertainty.
7 Simulations
In this section we illustrate two proposed approaches—chance constraint (5) and probabilistic envelope constraint (6) using the synthetic transportation problem discussed in Sect. 2.
We consider the transportation problem where the graph \(\mathcal {G}\) is a bi-parti graph between sources and destinations, i.e., \(\mathcal {V}=\mathcal {S}\bigcup \mathcal {D}\) and \(\mathcal {E}=\{(s\rightarrow d)|s\in \mathcal {S}, d\in \mathcal {D}\}\). Let \(m=|\mathcal {S}|\) and \(n=|\mathcal {D}|\), then the unit cost \(\varvec{\delta }\) is an \(m\times n\) matrix, and the transportation problem can be rewritten as
where \(\varvec{\delta }\in \mathbb {R}^{m \times n}\), \(\mathbf{1}_m\) and \(\mathbf{1}_n\) are the all-one vectors with dimension \(m\) and \(n\) respectively. The function \(h(\mathbf{s},\mathbf{d},\varvec{\delta })\) is defined by
By Theorem 2, one can solve this transportation problem by MATLAB and CVX [24]. We consider the case where there are \(10\) suppliers and \(3\) consumers, and the least demand \(L=80\). The mean \(M_{ij}\) and the variance \(\Sigma _{ij}\) of the transportation cost \(\delta _{ij}\) are set to \(100+0.1\sqrt{3(i - 1) + j}\) and \(5 / \sqrt{3(i - 1) + j}\), respectively. Then the transportation costs related to suppliers and consumers with lower serial numbers have smaller means but larger variances, i.e., lower mean cost but more risky.
Our first goal is to minimize the total cost to some fixed confidence parameter \(\gamma \). Figure 1 shows the resulting allocations for different \(\gamma \).
As expected, small \(\gamma \) leads to more conservative allocations which tend to select supplies with higher mean costs and smaller variances, while large \(\gamma \) leads to less conservative allocations which select suppliers with lower mean costs and larger variances.
In this example, the algorithm takes about 40 s on a desktop PC with Intel i7 3.4GHz CPU and 8G memory. The computational time for solving the transportation problems of different numbers of suppliers is reported in Table 1. For a large-scale problem, i.e. the number of suppliers is 1,000, our algorithm finds the result in about 30 min. From the table, it appears that the computation time scales roughly linearly with respect to the number of suppliers. Note that one can use commercial solvers such as CPLEX instead of CVX to implement this algorithm, which is typically more computationally efficient.
Using the same notations, the transportation problem with probabilistic envelope constraints can be formulated as
Our second goal is to minimize the total cost subject to a decaying probabilistic envelope \(\mathfrak {B}(s)=1-1/(1+b\sqrt{s+a/b^2})\) which implies \(t(r)=\max \{(r^2-a)/b^2,0\}\) by Lemma 3. We choose \(a=1\) and \(b=0.1,1.0,10.0\), giving different rates of decay for the probability the constraint is violated at level \(s\) for each \(s\). Based on Theorem 4, we can easily solve this problem. Figure 2 shows the resulting allocations.
Clearly, larger b corresponds to a more risk averse attitude towards large constraint violation so that the resulting allocation is more conservative and tends to choose suppliers with larger mean costs and smaller variances.
8 Conclusion
The distributionally robust chance constraint formulation has been extensively studied. Yet, most previous work focused on the linear constraint function case. In this paper, motivated by applications where uncertainty is inherently non-linear, we investigate the computational aspects of DRCC optimization problems for the general function case. We show that the DRCC optimization is tractable, provided that the uncertainty is characterized by its mean and variance, and the constraint function is concave-quasiconvex. This significantly expands the range of decision problems that can be modeled and solved efficiently via the DRCC framework. Along the way, we establish a relationship between the DRCC framework and robust optimization model, which links the stochastic model and the deterministic model of uncertainty. We then consider probabilistic envelope constraints, a generalization of distributionally robust chance constraint first proposed in Xu et al. [40], and extend this framework to the non-linear case, and obtain conditions that guarantee its tractability. Finally, we discuss two extensions of our approach, provide approximation schemes for JPEC, and establish conditions to ensure these approximation formulations are tractable.
References
Alizadeh, F., Goldfarb, D.: Second-order cone programming. Math. Program. 95(1), 3–51 (2003)
Ben-Tal, A., Bertsimas, D., Brown, D.: A soft robust model for optimization under ambiguity. Oper. Res. 58, 1220–1234 (2010)
Ben-Tal, A., Boyd, S., Nemirovski, A.: Extending scope of robust optimization: comprehensive robust counterparts of uncertain problems. Math. Program. Ser. B 107, 63–89 (2006)
Ben-Tal, A., El Ghaoui, L., Nemirovski, A.: Robust Optimization. Princeton University Press, Princeton (2009)
Ben-Tal, A., den Hertog, D., Vial, J.P.: Deriving Robust Counterparts of Nonlinear Uncertain Inequalities. CentER Discussion Paper Series No. 2012–053 (2012)
Ben-Tal, A., Nemirovski, A.: Robust convex optimization. Math. Oper. Res. 23, 769–805 (1998)
Ben-Tal, A., Nemirovski, A.: Robust solutions of uncertain linear programs. Oper. Res. Lett. 25(1), 1–13 (1999)
Bertsimas, D., Sim, M.: The price of robustness. Oper. Res. 52(1), 35–53 (2004)
Black, F., Scholes, M.: The pricing of options and corporate liabilities. J. Polit. Econ. 81, 637–659 (1973)
Calafiore, G., El Ghaoui, L.: Distributionally robust chance constrained linear programs with applications. J. Optim. Theory Appl. 130(1), 1–22 (2006)
Charnes, A., Cooper, W.W.: Chance constrained programming. Manag. Sci. 6, 73–79 (1959)
Chen, W., Sim, M., Sun, J., Teo, C.: From CVaR to uncertainty set: implications in joint chance constrained optimization. Oper. Res. 58(2), 470–485 (2010)
Cheng, J., Delage, E., Lisser, A.: Distributionally Robust Stochastic Knapsack Problem. working draft (2013)
Cheung, S.S., So, A.M., Wang, K.: Linear matrix inequalities with stochastically dependent perturbations and applications to chance-constrained semidefinite optimization. SIAM J. Optim. 22(4), 1394–1430 (2012)
Cont, R.: Empirical propertis of asset returns: stylized facts and statistical issues. Quant. Financ. 1(2), 223–236 (2001)
Delage, E., Mannor, S.: Percentile optimization for Markov decision processes with parameter uncertainty. Oper. Res. 58(1), 203–213 (2010)
Delage, E., Ye, Y.: Distributionally robust optimization under moment uncertainty with applications to data-driven problems. Oper. Res. 58(1), 595–612 (2010)
Dentcheva, D., Ruszczyński, A.: Optimization with stochastic dominance constraints. SIAM J. Optim. 14(2), 548–566 (2003)
Dentcheva, D., Ruszczyński, A.: Optimality and duality theory for stochastic optimization problems with nonlinear dominance constraints. Math. Program. Ser. A 99(2), 329–350 (2004)
Dentcheva, D., Ruszczyński, A.: Semi-infinite probabilistic optimization: first order stochastic dominance constraints. Optimization 53(5–6), 433–451 (2004)
Dupacová, J.: The minimax approach to stochastic programming and an illustrative application. Stochastics 20, 73–88 (1987)
Erdoǧan, E., Iyengar, G.: Ambiguous chance constrained problems and robust optimization. Math. Program. Ser. B 107, 37–61 (2006)
Fama, E.: The behavior of stock prices. J. Bus. 38, 34–105 (1965)
Grant, M., Boyd, S.: CVX: Matlab Software for Disciplined Convex Programming, Version 1.21. http://cvxr.com/cvx (2011)
Grötschel, M., Lovász, L., Schrijver, A.: Geometric Algorithms and Combinatorial Optimization, vol. 2. Springer, Berlin (1988)
Jansen, D., deVries, C.: On the frequency of large stock returns: putting booms and busts into perspective. Rev. Econ. Stat. 73(1), 18–24 (1991)
Kawas, B., Thiele, A.: A log-robust optimization approach to portfolio management. OR Spectr. 33, 207–233 (2011)
Kawas, B., Thiele, A.: Short sales in log-robust portfolio management. Eur. J. Oper. Res. 215, 651–661 (2011)
Kon, S.: Models of stock returns: a comparison. J. Financ. 39, 147–165 (1984)
Marshall, A.W., Olkin, I.: Multivariate Chebyshev inequalities. Ann. Math. Stat. 31(4), 1001–1014 (1960)
Miller, B., Wagner, H.: Chance-constrained programming with joint constraints. Oper. Res. 13, 930–945 (1965)
Nemirovski, A., Shapiro, A.: Convex approximations of chance constrained programs. SIAM J. Optim. 17(4), 969–996 (2006)
Popescu, I.: Robust mean–covariance solutions for stochastic optimization. Oper. Res. 55(1), 98–112 (2007)
Prékopa, A.: On Probabilistic Constrained Programming. In: Proceedings of the Princeton Symposium on Mathematical Programming, pp. 113–138 (1970)
Prékopa, A.: Stochastic Programming. Kluwer, Dordrecht (1995)
Scarf, H.: A min–max solution of an inventory problem. In: Arrow, K.J., Karlin, S., Scarf, H.E. (eds.) Studies in Mathematical Theory of Inventory and Production, pp. 201–209. Stanford University Press (1958)
Shapiro, A., Dentcheva, D., Ruszczyński, A.: Lectures on Stochastic Programming: Modeling and Theory. SIAM, Philadelphia (2009)
Shivaswamy, P., Bhattacharyya, C., Smola, A.: Second order cone programming approaches for handling missing and uncertain data. J. Mach. Learn. Res. 7, 1283–1314 (2006)
Wiesemann, W., Kuhn, D., Sim, M.: Distributionally Robust Convex Optimization (2013)
Xu, H., Caramanis, C., Mannor, S.: Optimization under probabilstic envelope constraints. Oper. Res. 60, 682–700 (2012)
Zymler S., Kuhn D., Rustem B.: Distributionally robust joint chance constraints with second-order moment information. Math. Program. 137(1–2), 167–198 (2013)
Zymler S., Kuhn D., Rustem B.: Worst-case value-at-risk of non-linear portfolios. Manage. Sci. 59(1), 172–188 (2013)
Acknowledgments
The authors thank the associate editor and two anonymous reviewers for their constructive comments which result in significant improvement of the paper. This work is supported by the Ministry of Education of Singapore through AcRF Tier Two Grant R-265-000-443-112.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
1.1 Proof of Corollary 1
For clarity, we denote \(-f(\mathbf{x},\varvec{\delta })\) and \(-\alpha \) by \(L_{\mathbf{x}}(\varvec{\delta })\) and \(\beta \), respectively. Since \(f(\mathbf{x},\varvec{\delta })\) is convex w.r.t. \(\varvec{\delta }\) for fixed \(\mathbf{x}\), \(L_{\mathbf{x}}(\varvec{\delta })\) is a concave function. Then the equivalence to establish can be rewritten as
It is well known that \(\sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\text {CVaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) \le \beta \Rightarrow \sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\mathbb {P}[L_{\mathbf{x}}(\varvec{\delta }) > \beta ] \le 1-p. \) Besides, \(\sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\mathbb {P}[L_{\mathbf{x}}(\varvec{\delta }) > \beta ] > 1-p \Leftrightarrow \sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\text {VaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) > \beta \), hence we only need to show that \(\sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\text {CVaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) > \beta \Rightarrow \sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\text {VaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) > \beta \).
Since \(\sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\text {CVaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) > \beta \), then there exists a probability distribution \(\mathbb {P}\) with zero mean, covariance \(\varvec{\varSigma }\), and \(\text {CVaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) > \beta \) when \(\varvec{\delta }\sim \mathbb {P}\). Decompose \(\mathbb {P}=\mu _1+\mu _2\) where the measure \(\mu _1\) constitutes a probability of \(p\) and the measure \(\mu _2\) constitutes a probability of \(1-p\), and that \(L_{\mathbf{x}}(y_1)\le L_{\mathbf{x}}(y_2)\) for any \(y_1\) and \(y_2\) that belong to the support of \(\mu _1\) and \(\mu _2\) respectively. By the CVaR constraint, we have \((\int _{\varvec{\delta }} L_{\mathbf{x}}(\varvec{\delta }) d\mu _2)/(1-p)>\beta \).
We now construct a new probability \(\overline{\mathbb {P}}\) as follows: let \(\mu _2'\) be a measure that put a probability mass of \(1-p\) on \(\int _{\varvec{\delta }} \varvec{\delta }d\mu _2/(1-p)\), i.e., the conditional mean of \(\mu _2\), and let \(\overline{\mathbb {P}}=\mu _1+\mu _2'\). Observe that \(\overline{\mathbb {P}}\) is a probability measure whose mean is the same as that of \(\mathbb {P}\). Moreover, notice that \(\mu _2/(1-p)\) is a probability measure, by concavity of \(L_{\mathbf{x}}(\cdot )\) we have that
which implies that \(\text {VaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) > \beta \) for \(\varvec{\delta }\sim \bar{\mathbb {P}}\).
We now show that this also implies that \(\sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\text {VaR}_{1-p}(L_{\mathbf{x}}(\varvec{\delta })) > \beta . \) Denote the covariance w.r.t \(\bar{\mathbb {P}}\) by \(\bar{\varvec{\varSigma }}\) and recall that both \(\mathbb {P}\) and \(\bar{\mathbb {P}}\) are zero mean, then
where the third equality is due to the definition of \(\mu _2'\). Note that from the construction of \(\bar{\mathbb {P}}\), we have \(\sup _{\varvec{\delta }\sim (0,\bar{\varvec{\varSigma }})}\mathbb {P}[L_{\mathbf{x}}(\varvec{\delta }) > \beta ] > 1-p. \) Denote the set \(\{\varvec{\delta }| L_{\mathbf{x}}(\varvec{\delta }) > \beta \}\) by \(T_{\mathbf{x}}\). First, we consider the case where \(\bar{\varvec{\varSigma }}\) is full rank. From Lemma 2, we have \(\inf _{\mathbf{y}\in T_{\mathbf{x}}}\mathbf{y}^\top \bar{\varvec{\varSigma }}^{-1}\mathbf{y}< r \,\triangleq \, p/(1-p)\). Since \(\bar{\varvec{\varSigma }} \preceq \varvec{\varSigma }\) and \(\bar{\varvec{\varSigma }}\) is full rank, \(\inf _{\mathbf{y}\in T_{\mathbf{x}}}\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\le \inf _{\mathbf{y}\in T_{\mathbf{x}}}\mathbf{y}^\top \bar{\varvec{\varSigma }}^{-1}\mathbf{y}< r\), which implies that \(\sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\mathbb {P}[L_{\mathbf{x}}(\varvec{\delta }) > \beta ] > 1-p\), which establishes the theorem.
The case where \(\bar{\varvec{\varSigma }}\) is not full rank requires additional work, as Lemma 2 or Theorem 1 can not be applied directly. Consider the spectral decomposition \(\bar{\varvec{\varSigma }}=\mathbf{Q}\varvec{\Lambda }\mathbf{Q}^\top \) and denote the pseudo inverse of \(\bar{\varvec{\varSigma }}\) by \(\bar{\varvec{\varSigma }}^+\). Suppose that the top \(d\) diagonal entries of \(\varvec{\Lambda }\) are non-zero. Let \(\mathbf{Q}_d\) be the submatrix of \(\mathbf{Q}\) by selecting the first \(d\) columns of \(\mathbf{Q}\) and \(\varvec{\Lambda }_d\) be the top \(d \times d\) submatrix of \(\varvec{\Lambda }\). Denote the column space of \(\bar{\varvec{\varSigma }}\) by \(\mathcal {C}\), and let \(\mathcal {Q} \,\triangleq \, \{\mathbf{z}| \mathbf{z}=\mathbf{Q}_d^\top \varvec{\delta },\ \forall \varvec{\delta }\in T_{\mathbf{x}} \cap \mathcal {C}\}\). Since there is no uncertainty in \(\mathcal {C}^{\perp }\) w.r.t \(\bar{\mathbb {P}}\),
From Lemma 2, we have \(\inf _{\mathbf{z}\in \mathcal {Q}}\mathbf{z}^\top \varvec{\Lambda }_d^{-1}\mathbf{z}< r\). In other words, there exists \(\mathbf{z}\in \mathcal {Q}\) such that \(\mathbf{z}^\top \varvec{\Lambda }_d^{-1}\mathbf{z}< r\), which implies that \(\mathbf{y}^\top \bar{\varvec{\varSigma }}^+\mathbf{y}< r\) for \(\mathbf{y}\,\triangleq \, \mathbf{Q}_d\mathbf{z}\). From the Schur complement, since \(\varvec{\varSigma }\succeq \bar{\varvec{\varSigma }} \succeq 0\), \((\mathbf{I}-\bar{\varvec{\varSigma }}\bar{\varvec{\varSigma }}^+)\mathbf{y}=0\) and \(r - \mathbf{y}^\top \bar{\varvec{\varSigma }}^+\mathbf{y}= r - \mathbf{z}^\top \varvec{\Lambda }_d^{-1}\mathbf{z}> 0\), we have \( \left( \begin{array}{cc} \varvec{\varSigma }&{} \mathbf{y}\\ \mathbf{y}^\top &{} r \\ \end{array} \right) \succeq \left( \begin{array}{cc} \bar{\varvec{\varSigma }} &{} \mathbf{y}\\ \mathbf{y}^\top &{} r \\ \end{array} \right) \succeq 0. \) Hence \( \inf _{\mathbf{y}\in T_{\mathbf{x}}}\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}< r, \) which implies that \(\sup _{\varvec{\delta }\sim (0,\varvec{\varSigma })}\mathbb {P}[L_{\mathbf{x}}(\varvec{\delta }) > \beta ] > 1-p\). \(\square \)
1.2 Proofs of Results in Sect. 3.2
1.2.1 Proof of Corollary 2
By Theorem 1, the feasible set \(S=\{\mathbf{x}|\mathbf{x}^\top g(\mathbf{y}) \ge \alpha ,\ \forall \mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\le r\}\) where \(r=p/(1-p)\). Hence, determining whether \(\mathbf{x}\in S\) is equivalent to determining whether the inner optimization problem \(\min _{\{\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\le r\}}\mathbf{x}^\top g(\mathbf{y})-\alpha \ge 0\). Rewrite the left hand side as an optimization problem on \(\mathbf {y}\):
by substituting \(g_i(\varvec{\delta })=\varvec{\delta }^\top G_i \varvec{\delta }+\mathbf{p}_i^\top \varvec{\delta }+q_i\). To prove Corollary 2, we need the following two results.
Lemma 5
Fix \(\mathbf{x}\). The optimal value of the optimization problem (50) equals that of the following SDP:
Proof
The dual problem of (50) is: \( \max _{\beta \ge 0}\min _{\mathbf{y}} \ \mathbf{y}^\top G(\mathbf{x}) \mathbf{y}+P(x)^\top \mathbf{y}+Q(\mathbf{x})+\beta \mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}-\beta r. \) By taking minimum over \(\mathbf{y}\) and the Schur complement, this can be reformulated as the SDP (51). Notice that there exists \(\mathbf{y}\) such that \(\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}< r\) since \(r > 0\), hence Slater’s condition is satisfied for (50), and the strong duality holds. \(\square \)
Thus, \(\mathbf{x}\in S\) if and only if the optimal value of problem (50) is greater than or equal to 0. This means we can convert the constraint in \(S\) into a feasibility problem as follows:
Lemma 6
Under the conditions of Corollary 2, and let \(r=p/(1-p)\), we have the constraint
is equivalent to the following problem
Proof
-
1.
Equation (52) \(\Rightarrow \) Equation (53): When Inequality (52) holds, the optimal value \(t\) of (50) must be greater than or equal to 0. So from Equation (51), we have
$$\begin{aligned} \begin{aligned} \left( \begin{array}{cc} \beta \varvec{\varSigma }^{-1}+G(\mathbf{x}) &{} \frac{1}{2}P(\mathbf{x}) \\ \frac{1}{2}P(\mathbf{x})^T &{} Q(\mathbf{x})-\beta r \\ \end{array} \right) \succeq \&\left( \begin{array}{cc} \beta \varvec{\varSigma }^{-1}+G(\mathbf{x}) &{} \frac{1}{2}P(\mathbf{x}) \\ \frac{1}{2}P(\mathbf{x})^T &{} Q(\mathbf{x})-t-\beta r \\ \end{array} \right) \succeq 0 . \end{aligned} \end{aligned}$$(54) -
2.
Equation (53) \(\Rightarrow \) Equation (52): Since the feasibility problem is solvable, \(t=0\) must be a feasible solution of (51), which implies Inequality (52).
\(\square \)
Lemma 6 immediately implies Corollary 2.\(\square \)
1.3 Proofs of results in Sect. 4
1.3.1 Proof of Lemma 3
We now show that the constraints (13) and (14) are equivalent.
-
1.
(13) \(\Rightarrow \) (14): Since \(\lim _{y \rightarrow +\infty }\mathfrak {B}(y)\) may not converge to 1, we define \(\mathfrak {B}^{-1}(x)=+\infty \) when \(\{y \ge 0 | \mathfrak {B}(y) \ge x\}=\emptyset \). Then if \(r/(1+r)\) is not in the range of \(\mathfrak {B}(s)\), we have \(t(r)=+\infty \) so that the constraint (14) is always satisfied. Otherwise, suppose that \(y^*=t(r)=\inf \{y \ge 0 | \mathfrak {B}(y) \ge r/(1+r)\}\), then we have
$$\begin{aligned} \inf _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })}\mathbb {P}[f(\mathbf{x},\varvec{\delta }) \!\ge \! \alpha -t(r)]= \inf _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })}\mathbb {P}[f(\mathbf{x},\varvec{\delta }) \ge \alpha -y^*] \ge \mathfrak {B}(y^*) \!\ge \! \frac{r}{1+r}. \end{aligned}$$ -
2.
(14) \(\Rightarrow \) (13): Since \(\mathfrak {B}(y^*) \in [0,1)\) for any \(y^* \ge 0\), there exists \(r^*\) such that \(\mathfrak {B}(y^*)=\frac{r^*}{1+r^*}\). From the definition of \(t(r)\), we have \(y^* \ge t(r^*)=\inf \{y \ge 0 | \mathfrak {B}(y) \ge r^*/(1+r^*)\}\). Hence the following inequality holds
$$\begin{aligned} \inf _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })}\mathbb {P}[f(\mathbf{x},\varvec{\delta }) \ge \alpha -y^*] \!\ge \! \inf _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })}\mathbb {P}[f(\mathbf{x},\varvec{\delta }) \!\ge \! \alpha -t(r^*)] \!\ge \! \frac{r^*}{1+r^*} = \mathfrak {B}(y^*). \end{aligned}$$
Furthermore, \(t(\cdot )\) is non-decreasing since both \(r/(1+r)\) and \(\mathfrak {B}(\cdot )\) are non-decreasing. By definition of \(t\), \(\mathfrak {B}(0)\ge 0\) leads to \(t(0)=0\); and \(\mathfrak {B}(s) <1\) for all \(s>0\) leads to \(\mathfrak {B}^{-1}(1)=+\infty \) and hence \(\lim _{r\uparrow +\infty } t(r) =+\infty \). Also, \(\mathfrak {B}(0)>0\) implies for some \(\epsilon >0\), \(\mathfrak {B}(0) \ge \epsilon \), and hence \(t(\epsilon )=0\). Thus, \(t(\cdot )\) is continuous at a neighborhood of \(0\). \(\square \)
1.4 Proof of Corollary 3:
The feasible set \(S=\{\mathbf{x}|\inf _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })} \mathbb {P}[g(\varvec{\delta })^\top \mathbf{x}\ge \alpha -t(r)] \ge \frac{r}{1+r};\ \forall r \ge 0\}\) admits
where (a) holds by Theorem 3. As each component \(g_i(\mathbf{y})\) of \(g(\mathbf{y})\) is linear or quadratic, i.e., \(g_i(\mathbf{y})=\mathbf{y}^\top \mathbf{G}_i\mathbf{y}+\mathbf{p}_i^\top \mathbf{y}+q_i\), for fixed \(\mathbf{x}\) the inner optimization problem \(\min _{\{\mathbf{y},r|\mathbf{y}^\top \varvec{\varSigma }^{-1}\mathbf{y}\le r\}}{g(\mathbf{y})^\top \mathbf{x}+t(r)-\alpha } \) can be rewritten as:
where \(G(\mathbf{x})\,\triangleq \,\sum _{i=1}^n x_i\mathbf{G}_i\), \(P(\mathbf{x})\,\triangleq \,\sum _{i=1}^n x_i\mathbf{p}_i\), and \(Q(\mathbf{x})\,\triangleq \,\sum _{i=1}^n x_iq_i-\alpha \). Thus, in order to analyze \(S\), we need to analyze the optimization problem (55). We have the following lemma:
Lemma 7
For any fixed \(\mathbf{x}\), the optimal value of problem (55) is equivalent to that of the following:
where \(t^*(x)\) is the conjugate function of \(t(r)\) defined as \(t^*(x)=\sup _{r \ge 0}{(xr-t(r))}\).
Proof
By the Schur complement and the strong duality of problem (55) (Slater’s condition holds by picking \(r=1\) and \(\mathbf{y}=0\)), one can easily obtain this lemma. \(\square \)
From Lemma 7, the constraint \( \inf _{\varvec{\delta }{\sim }(0,\varvec{\varSigma })} \mathbb {P}[g(\varvec{\delta })^\top \mathbf{x}\ge \alpha -t(r)] \ge \frac{r}{1+r},\ \forall r \ge 0, \) is equivalent to a constraint that the optimal value of the optimization problem (56) is non-negative. Thus, \(\mathbf{x}\) belongs to the feasible set of the envelope constraint if and only if \(\alpha =0\) is a feasible solution of (56), for the same \(\mathbf{x}\). This means we can remove the \(-\alpha \) term from (56). That is, when each component \(g_i(\cdot )\) of \(g(\cdot )\) is linear or quadratic, the envelope constraint is equivalent to the following feasibility problem:
Hence the optimization problem (18) is equivalent to (21), which proves the first part of the Theorem.
To prove the second part of the Theorem, it suffices to show that Problem (21) can be solved in polynomial time. We show this by constructing a polynomial time separation oracle. For any \((\beta , \mathbf{x})\), if the optimization problem (22) can be solved in polynomial time, which implies \(t^*(\beta )\) can be computed in polynomial time, then it can be verified in polynomial time whether the constraint in (21) is satisfied or not, and hence the feasibility of \((\beta , \mathbf{x})\) can be determined in polynomial time. Moreover, if \((\beta _0, \mathbf{x}_0)\) is infeasible and let \(r_0\) be the optimal solution of the problem (22) (by assumption \(r_0\) can be found in polynomial time), then we have
and we can find in polynomial time (e.g., by SVD) a vector \((\mathbf{y}_0^\top ,1)\) such that
Notice that for any feasible solution \((\beta , \mathbf{x})\), we must have
Hence we have a separating hyperplane. \(\square \)
1.5 Proofs of results in Sect. 5
1.5.1 Proof of Corollary 6
As before, we construct a separation oracle to prove tractability. In order to verify the feasibility of a given \(\mathbf{x}^*\), from Corollary 5 we know that \(\mathbf{x}^*\) is feasible if and only if the optimal value of the optimization problem (26) is greater than or equal to \(\alpha \), which can be verified by directly solving Problem (26). By assumption, this can be done in polynomial time.
If \(\mathbf{x}^*\) is not feasible, then we can find in polynomial time \((\mathbf{y}^*,r^*,\varvec{\mu }^*,\varvec{\varSigma }^*)\) such that \(f(\mathbf{x}^*,\mathbf{y}^*+\varvec{\mu }^*)+t(r^*) < \alpha \). Because \(f(\mathbf{x},\mathbf{y}+\varvec{\mu })\) is concave in \(\mathbf{x}\) for fixed \(\mathbf{y}\) and \(\varvec{\mu }\), for any feasible \(\mathbf{x}\), we have
Hence the hyperplane separating \(\mathbf{x}^*\) from the feasible set is the following:
which can be generated in polynomial time since the super-gradient of \(\mathbf{x}\) can be obtained in polynomial time. \(\square \)
1.6 Proof of Theorem 5
If \(f(\mathbf{x},\varvec{\delta }) \ge \alpha \) for all \(\varvec{\delta }\in \mathcal {S}\), the constraints (27) and (28) are satisfied, so we only need to consider the case where there exists \(\varvec{\delta }\in \mathcal {S}\) such that \(f(\mathbf{x},\varvec{\delta }) < \alpha \). Note that (27) is equivalent to \( \sup _{\varvec{\delta }\sim (\varvec{\mu },\mathcal {S})}\mathbb {P}[f(\mathbf{x},\varvec{\delta }) < \alpha ] \le 1-p, \) then we can apply the following lemma:
Lemma 8
If the conditions in Theorem 5 hold and \(\{\varvec{\delta }: f(\mathbf{x},\varvec{\delta }) < \alpha \}\) is nonempty, then
is equivalent to
Proof
Since \(\varvec{\mu }\in \mathcal {S}\) and \(\{\varvec{\delta }: f(\mathbf{x},\varvec{\delta }) < \alpha \}\) is not empty, the optimization problem in (60) is always feasible. To show the equivalence of (59) and (60), one needs to prove that the optimal objective value \(\theta ^*\) of the optimization problem in (60) equals \(\zeta =\sup _{\varvec{\delta }\sim (\varvec{\mu },\mathcal {S})}\mathbb {P}[f(\mathbf{x},\varvec{\delta }) < \alpha ]\).
The first step is to show \(\theta ^* \le \zeta \): Since \(f(\mathbf{x},\cdot )\) is continuous for fixed \(\mathbf{x}\in \mathbb {X}\) and \(\mathcal {S}\) is a closed convex set, for any \(\epsilon > 0\) there exists a feasible solution \((\varvec{\delta }_1',\varvec{\delta }_2',\theta ')\) such that \(|\theta '-\theta ^*| < \epsilon \). Construct a probability distribution \(\mathbb {P}'(\mathbf{x})\) such that \(\varvec{\delta }=\varvec{\delta }_1'\) with probability \(\theta '\) and \(\varvec{\delta }=\varvec{\delta }_2'\) with probability \(1-\theta '\), then we have \(\mathbb {P}' \in (\varvec{\mu },\mathcal {S})\). By construction we have \(\theta '\le \mathbb {P}'[f(\mathbf{x},\varvec{\delta }) < \alpha ] \le \zeta \) where the second inequality holds from \(\mathbb {P}' \in (\varvec{\mu },\mathcal {S})\). Thus we have \(\theta ^* \le \zeta \) as \(\epsilon \) can be arbitrarily small.
The second step is to prove \(\theta ^* \ge \zeta \): Consider any probability distribution \(\mathbb {\bar{P}} \in (\varvec{\mu },\mathcal {S})\), and define \(\bar{\theta } = \mathbb {\bar{P}}[f(\mathbf{x},\varvec{\delta }) < \alpha ]\), \(\bar{\varvec{\delta }}_1 = \mathbb {E}_{\mathbb {\bar{P}}}[\varvec{\delta }|f(\mathbf{x},\varvec{\delta }) < \alpha ]\) and \(\bar{\varvec{\delta }}_2 = \mathbb {E}_{\mathbb {\bar{P}}}[\varvec{\delta }|f(\mathbf{x},\varvec{\delta }) \ge \alpha ]\). We then have \(\bar{\varvec{\delta }}_1 \bar{\theta } + \bar{\varvec{\delta }}_2 (1-\bar{\theta }) = \varvec{\mu }\), \(f(\mathbf{x},\bar{\varvec{\delta }}_1) < \alpha \) and \(\bar{\varvec{\delta }}_1,\bar{\varvec{\delta }}_2 \in \mathcal {S}\), or equivalently \((\bar{\varvec{\delta }}_1,\bar{\varvec{\delta }}_2,\bar{\theta })\) is a feasible solution of the optimization problem in (60). Thus, we must have \(\mathbb {\bar{P}}[f(\mathbf{x},\varvec{\delta }) < \alpha ] = \bar{\theta } \le \theta ^*\), which implies that \(\theta ^* \ge \zeta = \sup _{\varvec{\delta }\sim (\varvec{\mu },\mathcal {S})}\mathbb {P}[f(\mathbf{x},\varvec{\delta }) < \alpha ]\). Therefore, (59) is equivalent to (60).\(\square \)
From the equivalence shown in Lemma 8, we consider the following feasibility problem parameterized by \(\theta \in [0,1]\), denoted \(\mathcal {F}_{\theta }\):
Then we have that for any \(0\le \theta _1\le \theta _2\le 1\), \(\mathcal {F}_{\theta _2}\) being feasible implies \(\mathcal {F}_{\theta _1}\) being feasible. To see this, let \((\varvec{\delta }_1^*, \varvec{\delta }_2^*)\) be a feasible solution to \(\mathcal {F}_{\theta _2}\). Hence we have \(\theta _2 \varvec{\delta }_1^* +(1-\theta _2) \varvec{\delta }_2^* =\varvec{\mu }\). Let \(\varvec{\delta }_2'\) be such that
Since \(\theta _2\ge \theta _1\), we have that \(\varvec{\delta }_2'\) is on the line segment between \(\varvec{\mu }\) and \(\varvec{\delta }_2^*\), and hence belongs to \(\mathcal {S}\) by its convexity. Furthermore, it is easy to check that \((\varvec{\delta }_1^*,\varvec{\delta }_2')\) is feasible to \(\mathcal {F}_{\theta _1}\).
Thus, constraint (60) (and equivalently the chance constraint (27)) is equivalent to \(\mathcal {F}_{1-p+\varepsilon }\) infeasible for all \(\varepsilon >0\), i.e.,
This further implies \(\mathcal {F}_{1-p}\) is infeasible, i.e.,
To see this, we only need to show that \(\mathcal {F}_{1-p}\) being feasible implies that \(\mathcal {F}_{1-p+\varepsilon }\) is feasible for some \(\varepsilon > 0\). Suppose that there exists \(\varvec{\delta }_1^* \in \mathcal {S}\) such that \(\varvec{\delta }_2^*=-\frac{1-p}{p}(\varvec{\delta }_1^*-\varvec{\mu })+\varvec{\mu }\in \mathcal {S}\) and \(f(\mathbf{x},\varvec{\delta }_1^*)<\alpha \). By continuity of \(f(\mathbf {x}, \cdot )\), we have that for a sufficiently small \(\eta >0\), \(f(\mathbf{x}, \varvec{\delta }_1') <\alpha \) where \(\varvec{\delta }_1'\triangleq (1-\eta )\varvec{\delta }_1^*+\eta \varvec{\mu }\). Note that \(\varvec{\delta }_1'\in \mathcal {S}\) and there exists \(\varepsilon >0\) such that \(-\frac{1-p+\varepsilon }{p-\varepsilon }(\varvec{\delta }_1'-\varvec{\mu })+\varvec{\mu }\in \mathcal {S}\), which implies that \(\mathcal {F}_{1-p+\varepsilon }\) is feasible.
Finally, the constraint (61) can be rewritten as
which is equivalent to (28). Therefore, the theorem follows. \(\square \)
1.7 Proofs of results in Sect. 6
1.7.1 Proof of Theorem 11
The constraints in \(Z^P\) (47) requires that for any \(r \ge 0\), we can find \(\beta \) and \(\mathbf{M}\) to satisfy \(\beta +(r+1)\langle \varvec{\Omega },\mathbf{M}\rangle \le 0\) and the other \((m+1)\) semi-definite constraints. This is equivalent to requiring that the following optimization problem has an optimal value less than or equal to \(0\) (notice that for any \(r\ge 0\), finding \(\beta \) and \(\mathbf{M}\) to satisfy the \((m+1)\) semi-definite constraints itself is trivial):
We analyze this requirement using duality. In order to find the dual problem of (63), it is more convenient for us to analyze the following problem:
Consider the dual problem, the “max” part in (64) is equivalent to
where the function \(\lambda _{\min }(\mathbf{X})\) denotes minimum eigenvalue of matrix \(\mathbf{X}\), and \(\mathbf {S}_i \triangleq \alpha _i\mathbf{B}_i-\alpha _i t(r)\mathbf{E}\). Further note that the function \(\lambda _{\min }(\mathbf{X})\) is equivalent to the following optimization problem: \( \min _{\mathbf{Y}\succeq 0, \mathrm {tr}(\mathbf{Y})=1}\mathrm {tr}(\mathbf{Y}\mathbf{X}). \) Thus (65) is equivalent to
Notice that for any fixed \(\lambda \), the objective function is continuous, convex w.r.t. \((\mathbf{Y}_i)_{i=0}^m\) and concave w.r.t. \((\beta , \mathbf{M})\). Moreover, the feasible set of \((\mathbf{Y}_i)_{i=0}^m\) is compact and does not depend on \((\beta , \mathbf{M})\). Hence Sion’s minimax theorem applies, and we have
Taking maximum over \(\beta \) and \(M\), we have that \(L(r)\) is equivalent to the following optimization problem with variables \(\mathbf{Y}_i\) and \(\lambda _i\):
By taking minimum over \(\lambda _i\), \(\min _{r \ge 0}L(r)\) can be further reformulated as (48). Hence from the analysis above, we know that (64) is equivalent to (48). To complete the proof, we construct a separation oracle of \(Z^P\) based on (48). Given \(\mathbf{x}\), if the optimization problem (48) can be solved in polynomial time, then it can be verified whether \(\mathbf{x}\in Z^P\) or not in polynomial time since \(\mathbf{x}\) is feasible if and only if the optimal value of (48) is greater than or equal to \(0\). Furthermore, if \(\mathbf{x}\not \in Z^P\), let the optimal solution of (48) be \((r^0,\{\mathbf{Y}_i^0\})\), then we have \(-\sum _{i=1}^m{\mathrm {tr}(\alpha _i\mathbf{Y}_i^0\mathbf{B}_i)}+t(r^0)\sum _{i=1}^m{\alpha _i \mathrm {tr}(\mathbf{Y}_i^0\mathbf{E})}<0\) since \(\mathbf{x}\not \in Z^P\). On the other hand, for any \(\mathbf{x}\in Z^P\), the following inequality must be satisfied
which implies that a separating hyperplane can be generated in polynomial time. \(\square \)
Rights and permissions
About this article
Cite this article
Yang, W., Xu, H. Distributionally robust chance constraints for non-linear uncertainties. Math. Program. 155, 231–265 (2016). https://doi.org/10.1007/s10107-014-0842-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-014-0842-5