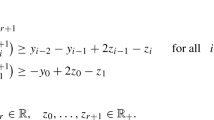Conic approximation to quadratic optimization with linear complementarity constraints

Abstract

This paper proposes a conic approximation algorithm for solving quadratic optimization problems with linear complementarity constraints.We provide a conic reformulation and its dual for the original problem such that these three problems share the same optimal objective value. Moreover, we show that the conic reformulation problem is attainable when the original problem has a nonempty and bounded feasible domain. Since the conic reformulation is in general a hard problem, some conic relaxations are further considered. We offer a condition under which both the semidefinite relaxation and its dual problem become strictly feasible for finding a lower bound in polynomial time. For more general cases, by adaptively refining the outer approximation of the feasible set, we propose a conic approximation algorithm to identify an optimal solution or an $\epsilon$-optimal solution of the original problem. A convergence proof is given under simple assumptions. Some computational results are included to illustrate the effectiveness of the proposed algorithm.

1 Introduction

Mathematical programs with linear complementarity constraints have been widely studied and applied [2, 14, 21, 23]. When there is no objective function involved, Ferris and Pang [14] provided several computational methods for finding a feasible solution. When the objective function is linear, some algorithms can be found in [18, 20, 28]. In this paper, the objective function is taken to be a general quadratic function and we consider the following quadratic program with linear complementarity constraints:

$$\begin{aligned} V_{\text {QLCP}} = \min \quad&\frac{1}{2} x^T Q x + f^T x + c\\ s.t. \quad&x \in F_{\text {LCP}}, \end{aligned}$$

(QLCP)

where Q is an $n \times n$ real symmetric matrix, $f \in {\mathbb {R}}^{n}$, $c \in R$ and

$$\begin{aligned} {F_{\text {LCP}}} = \left\{ x \in {\mathbb {R}}^n \big |x \ge 0,~Ax + b \ge 0,~ x^T (Ax + b) = 0 \right\} \end{aligned}$$

with $A \in {\mathbb {R}}^{n \times n}$ and $b \in {\mathbb {R}}^n$. Here, ${\mathbb {R}}^{n \times n}$ and ${{\mathbb {R}}}^n$ represent the $n \times n$ and n dimensional real spaces, respectively.

In this paper, convexity is not assumed for the quadratic objective function. Some commonly used notations are adopted throughout the paper. In particular, ${\mathbb {R}}^n_+$ means the first orthant of ${\mathbb {R}}^n$ and ${\mathbb {Z}}_+$ means the set of nonnegative integers; ${\mathbb {S}}^n$ denotes the set of real symmetric square matrices of order n; ${\mathbb {S}}_+^n$ is the set of all positive semidefinite matrices in ${\mathbb {S}}^n$; and ${\mathbb {S}}_{++}^n$ is the set of all positive definite matrices in ${\mathbb {S}}^n$. The vector $1_n = [1,1,\ldots ,1]_n^T$ and the matrix $I_n$ represents the identity matrix of dimension n. For a real symmetric matrix X, $X \succeq 0$ means $X \in {\mathbb {S}}_+^n$, $X \succ 0$ means $X \in {\mathbb {S}}_{++}^n$, $X \ge 0$ means every element of X is nonnegative, and $X_{ij}$ represents the element in the i-th row and the j-th column of X. For n by n real matrices $A=(A_{ij})$ and $B=(B_{ij})$, $A \cdot B =$trace$(A^T B) = \sum _{i,j=1}^n A_{ij}B_{ij}$. For a set U, $\text {int}(U)$ and $\text {ri}(U)$ denote the sets of interior points and relative interior points of U, respectively.

From the results of [19], we know problem (QLCP) is in general NP-hard, which means we cannot find a polynomial-time algorithm to solve it unless P=NP. Many papers have studied (QLCP) and its subproblems. When the quadratic objective function is convex, based on the primal-dual relationship and a logical Benders scheme, Bai et al. [2] proposed an extreme ray/point generation procedure with a two-stage approach to improve the scheme. Also, (QLCP) is a special quadratic optimization problem, thus it can be relaxed into a semidefinite programming problem [27]. For example, Engau et al. [12] introduced a technique of handling cutting planes together with the interior-point method for solving semidefinite relaxations of binary optimization problems. Besides, for mixed integer quadratically constrained quadratic programming problems, a subclass of (QLCP) problems, Saxena et al. [31] provided a convex relaxation method using the techniques of disjunctive programming and lift-and-project methodology. They also studied methods to build low-dimensional convex relaxations using projection formulations [32]. Mitchell et al. [28] further described several methods for tightening relaxations of mathematical programs with complementarity constraints. Due to the non-negativity constraint of $x \ge 0$, such problems can be equivalently reformulated as completely positive programming (CPP) problems, which were studied by Burer [8]. Bai et al. [3] exploited and generalized the results of Burer to quadratic programs over a convex cone including (QLCP) without any boundedness assumptions. However, CPP relaxation is numerically intractable since determining whether a given matrix belongs to the class of completely positive matrices is NP-complete [29]. A basic tractable relaxation is approximating the completely positive matrices by using doubly nonnegative matrices. Burer [9] proposed an efficient decomposition technique to approximately solve the doubly nonnegative program, while simultaneously producing lower bounds of the original problem. Recently, Arima et al. [1] introduced a simplified Lagrangian-CPP relaxation aiming at reducing the numbers of constraints and variables of CPP relaxation. Kim et al. [22] proposed an efficient computational method for quadratic optimization with complementarity constraints based on the Lagrangian and doubly nonnegative relaxation. Based on the convex relaxations for lower bounds, branch-and-bound is a common and effective scheme to achieve the optimal solution and optimal value [9, 16, 24].

Unlike those earlier papers, our approach is to investigate the structure of the feasible domain of problem (QLCP) and adaptively refine its outer approximation. In this way, a computable conic relaxation over the cone of nonnegative quadratic functions can be successively developed to provide a tighter lower bound for (QLCP). Then a conic approximation algorithm is presented to find either an optimal solution or an $\epsilon$-optimal solution with a convergence proof.

Conic approximation methods have recently been used in detecting copositive matrix over a p-th order cone [38] and solving box constrained quadratic programming problems [25], 0-1 quadratic knapsack problems [37], and completely positive programming problems [34]. The key idea is to provide an equivalent conic reformulation based on the concept of the cone of nonnegative quadratic functions ${D}_{F}$ and its dual cone $D_{F}^*$ over a given set F [13]. To be more precise, for a given set $F \subseteq {\mathbb {R}}^n$, we let

$$\begin{aligned} {D}_{F} =\left\{ U \in {\mathbb {S}}^{n+1} \Big | {\begin{bmatrix} 1\\x\end{bmatrix}}^T U \begin{bmatrix} 1\\ x\end{bmatrix} \ge 0 ~ \text {for~all~} x \in {F}\right\} , \end{aligned}$$

and

$$\begin{aligned} {D}_{F}^* = \text {cl~ cone}\left\{ \begin{bmatrix} 1\\x \end{bmatrix}{\begin{bmatrix} 1\\x \end{bmatrix}}^T \in {\mathbb {S}}^{n+1}~ \Big |~ x \in {F}\right\} , \end{aligned}$$

where “cl” means the closure and “cone” stands for the conic hull of a set, respectively. When F is bounded and closed, from [25], we know

$$\begin{aligned} {D}_{F}^* = \text {cone}\left\{ \begin{bmatrix} 1\\x \end{bmatrix}{\begin{bmatrix} 1\\x \end{bmatrix}}^T \in {\mathbb {S}}^{n+1}~ \Big |~ x \in {F}\right\} . \end{aligned}$$

When an equivalent conic reformulation problem is solved, the optimal value of the original problem may be obtained. However, there are two difficulties for solving the conic reformulation problem. One is that it could be hard to check whether a matrix belongs to ${D}_{F}$ (or ${D}_{F}^*$) for some given F. For example, when F is ${\mathbb {R}}_+^n$, Murty and Kabadi [29] proved that this checking is co-NP-complete. The other difficulty is that there is no guarantee that the conic reformulation and its dual are strictly feasible for the applicability of the interior-point methods [35]. For the problem (QLCP), unfortunately, we can prove that when $\frac{A+A^T}{2} \succeq 0$, the conic reformulation problem is not strictly feasible.

To overcome the two technical difficulties, we aim to design a feasible outer approximation G of $F_\text {LCP}$, i.e., $F_\text {LCP} \subseteq {G}$, for providing a corresponding conic relaxation. Hopefully, there is a polynomial-time algorithm for checking a matrix belongs to ${D}_{G}$ (or ${D}_{G}^*.$) or not. And, hopefully again, the conic relaxation problem and its dual become strictly feasible.

In this paper, we first provide a conic reformulation and its dual for problem (QLCP) such that these three problems are equivalent in the sense that they share the same optimal objective value. Moreover, when $F_{LCP}$ is nonempty and bounded, the conic reformulation problem becomes attainable. However, the conic reformulation is in general a hard problem. This leads us to consider some conic relaxations for the original problem. Under the assumption that there exists a vector $x \in {\mathbb {R}}^n$ satisfying $x >0$ and $Ax+b >0$, we can show that if $\frac{A+A^T}{2} \prec 0$, then both of the semidefinite relaxation and its dual for problem (QLCP) become strictly feasible. This implies that a lower bound for problem (QLCP) can be obtained by using the primal-dual interior point approach. For more general cases, by adaptively refining the feasible outer approximation, we provide a conic approximation algorithm for finding an optimal solution or an $\epsilon -$optimal solution to problem (QLCP). To illustrate the proposed approach, the binary quadratic program, which is a special case of problem (QLCP), is used to highlight some computational results. The proposed conic approximation algorithm can also be extended to handle quadratic programs with convex quadratic constraints and linear complementarity constraints.

The rest of the paper is organized as follows. In Sect. 2, a conic reformulation and its dual for problem (QLCP) are introduced. The strict feasibility issue is also discussed. We provide a sufficient condition under which the semidefinite relaxation and its dual are strictly feasible. Then, an idea of how to relax the feasible set for a better conic relaxation is given. In Sect. 3, we propose a conic approximation method with a convergence proof for finding an $\epsilon$-optimal solution to problem (QLCP). Some numerical examples are provided to illustrate the effectiveness of our proposed algorithm in Sect. 4 while a short conclusion is given in Sect. 5.

2 Conic reformulation and strict feasibility

The conic reformulation over the cone of nonnegative quadratic functions for quadratically constrained quadratic programs was first studied by Sturm and Zhang [33]. The conic reformulation problem is in general NP-hard. It is equivalent to a second-order conic or semidefinite positive programming problem in some special cases, and then can be solved in polynomial time. Burer [10] listed some special problems with this property in his recent review paper. With the matrix decomposition method provided in [33], the optimal solutions of some quadratic optimization problems can be obtained in polynomial time, e.g., quadratic programs with one quadratic inequality constraint, one strictly convex equality constraint, or the intersection of one convex quadratic inequality and one linear inequality constraint. For the cone of nonnegative quadratic functions over a given set $F \subseteq {\mathbb {R}}^n$, we have the following simple facts to be used in this paper:

Lemma 1

[25] If F is a nonempty, bounded, closed set, then

$$\begin{aligned} int({D}_{F}) = \left\{ U \in {\mathbb {S}}^{n+1} \Big | {\begin{bmatrix} 1\\x\end{bmatrix}}^T U \begin{bmatrix} 1\\ x\end{bmatrix} > 0,~\forall x \in F\right\} . \end{aligned}$$

Lemma 2

[25] If ${F} \subseteq {G} \subseteq {\mathbb {R}}^n$, then ${D}_{{G}} \subseteq {D}_{F}$ and ${D}_{{F}}^* \subseteq {D}_{{G}}^*$.

Lemma 3

[37] ${D}_{{\mathbb {R}}^n}={D}_{{\mathbb {R}}^n}^*={\mathbb {S}}_+^{n+1}$.

Lemma 4

[34] For ${G} \subseteq {\mathbb {R}}^n$, if G has an interior point, then ${D}_{G}$ and ${D}_{{G}}^*$ are proper cones, i.e., they are closed, convex, solid and pointed cones.

The term of “solid” here means a cone has interior points. The conic reformulation of problem (QLCP) becomes

$$\begin{aligned} V_{\text {QLCP-CR}}=\min \quad&\frac{1}{2} \begin{bmatrix}2c&f^T\\f&Q \end{bmatrix} \cdot Y\\ s.t.\quad&Y_{11} = 1,\\&Y \in {D}_{{F}_{\text {LCP}}}^*, \end{aligned}$$

(QLCP-CR)

where $Y_{11}$ represents the element in the first row and the first column of the matrix Y. The conic dual of problem (QLCP-CR) becomes

$$\begin{aligned} V_{\text {QLCP-DR}}=\max \quad&\sigma \\ s.t. \quad&\begin{bmatrix}c - \sigma&\frac{f^T}{2}\\ \frac{f}{2}&\frac{Q}{2} \end{bmatrix} \in {D}_{{F}_{\text {LCP}}},\\ \end{aligned}$$

(QLCP-DR)

It is not difficult to see that, following [13, 33], problems (QLCP), (QLCP-CR) and (QLCP-DR) share the same optimal objective value when ${F}_{LCP } \ne \emptyset$. We would like to know if problems (QLCP-CR) and (QLCP-DR) are attainable, i.e., there exists a feasible solution to achieve the optimal value. To answer this question, Ben-Tal et al. [5] indicate that for a conic optimization problem, if the primal problem is bounded and its feasible domain has at least one relative interior point, i.e., strictly feasible, then the dual problem is attainable and the primal and dual problems share the same optimal value. Hence, we investigate the strict feasibility of problems (QLCP-CR) and (QLCP-DR) in the next two results.

Theorem 1

If the feasible domain $F_{LCP }$ of problem (QLCP) is nonempty and bounded, then problem (QLCP-DR) is strictly feasible and bounded above. Consequently, problem (QLCP-CR) is attainable.

Proof

Notice that in this case ${F}_{\text {LCP}}$ is a nonempty, bounded, closed set and problem (QLCP) is bounded below. Hence problem (QLCP-DR) is bounded above. Let $\gamma = \min _{x \in {F}_{\text {LCP}}}\quad \frac{1}{2}{x^T Q x} + f ^T x + c$ and $\sigma = \gamma - 1$. Then Lemma 1 implies that

$$\begin{aligned} \begin{bmatrix}c - \sigma&\frac{f^T}{2}\\ \frac{f}{2}&\frac{Q}{2} \end{bmatrix} \in \text {int}({D}_{{F}_{\text {LCP}}}). \end{aligned}$$

Therefore, problem (QLCP-DR) is strictly feasible and bounded above. Following Ben-Tal et al. [5], we know the problem (QLCP-CR) is attainable.$\square$

However, since ${F}_{\text {LCP}}$ does not contain any relative interior points, problem (QLCP-CR) may not be strictly feasible. There is no guarantee that problem (QLCP-DR) is attainable. The next result shows such a case.

Theorem 2

If ${\frac{A+A^T}{2} \succeq 0}$, then problem (QLCP-CR) is not strictly feasible. Moreover, there is no feasible solution to problem (QLCP) that satisfies the inequality constraints strictly.

Proof

Since ${F}_{\text {LCP}} \subseteq {\mathbb {R}}^n$, from Lemmas 2 and 3, we know that ${D}_{{F}_{\text {LCP}}}^* \subseteq {\mathbb {S}}_+^{n+1}$, and then $Y \succeq 0$. Because $Y_{11}=1$, we can rewrite $Y = \begin{bmatrix}1&x^T\\x&X\end{bmatrix}$. By the definition of ${D}_{\text {LCP}}^*$, for any $Y \in {D}_{\text {LCP}}^*$, there exist $\tau _k \in {\mathbb {Z}}_+$, $\lambda _{jk} \ge 0$ and $x^{jk} \in F$, $j=1,2,\ldots ,\tau _k$, $k=1,2,\ldots ,+\infty$, satisfying $Y^k = \sum _{j=1}^{\tau _k} \lambda _{jk} \begin{bmatrix}1\\x^{jk} \end{bmatrix}{\begin{bmatrix}1\\x^{jk} \end{bmatrix}}^T$ and $Y=\lim _{k\rightarrow \infty } Y^k$. Since

$\begin{bmatrix}0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot \begin{bmatrix}1\\x^{jk} \end{bmatrix}{\begin{bmatrix}1\\x^{jk} \end{bmatrix}}^T = 0$, $\begin{bmatrix}0&\frac{e_i^T}{2}\\ \frac{e_i}{2}&0 \end{bmatrix} \cdot \begin{bmatrix}1\\x^{jk} \end{bmatrix}{\begin{bmatrix}1\\x^{jk} \end{bmatrix}}^T \ge 0$ and $\begin{bmatrix}b_i&\frac{a_i^T}{2} \\ \frac{a_i}{2}&0 \end{bmatrix} \cdot \begin{bmatrix}1\\x^{jk} \end{bmatrix}{\begin{bmatrix}1\\x^{jk} \end{bmatrix}}^T \ge 0$, for $j=1,2,\ldots ,\tau _k$ and $i=1,2,\ldots ,n$, we have $\begin{bmatrix}0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y = \frac{A+A^T}{2} \cdot X + b^T x = 0$, $\begin{bmatrix}0&\frac{e_i^T}{2}\\ \frac{e_i}{2}&0 \end{bmatrix} \cdot Y = x_i \ge 0$ and $\begin{bmatrix}b_i&\frac{a_i^T}{2} \\ \frac{a_i}{2}&0 \end{bmatrix} \cdot Y = a_i^T x + b_i \ge 0$. Since $\frac{A+A^T}{2}$ and $X-xx^T$ are both positive semidefinite, we know $\frac{A+A^T}{2} \cdot (X-xx^T) \ge 0$ and

$$\begin{aligned} 0 = \frac{A+A^T}{2} \cdot X + b^T x \ge \frac{A+A^T}{2} \cdot xx^T + b^T x = x^T (Ax + b). \end{aligned}$$

Hence, when $\frac{A+A^T}{2} \succeq 0$, we cannot find any Y satisfying $\begin{bmatrix}0&\frac{e_i^T}{2}\\ \frac{e_i}{2}&0 \end{bmatrix} \cdot Y = x_i > 0$ and $\begin{bmatrix}b_i&\frac{a_i^T}{2} \\ \frac{a_i}{2}&0 \end{bmatrix} \cdot Y = a_i^T x + b_i > 0$, for $i=1,2,\ldots ,n$. This means that we cannot find any $Y \in \text {int}({D}_{{F}_{\text {LCP}}}^*)$ and problem (QLCP-CR) is not strictly feasible. From Lemma 4, we conclude that there is no feasible solution to problem (QLCP) that satisfies the inequality constraints strictly.$\square$

As far as we know, there is no polynomial-time algorithm to verify whether a matrix belongs to ${D}_{{F}_{\text {LCP}}}^*$ or not. Nor can we guarantee that problem (QLCP-DR) is attainable. Therefore, we consider some conic relaxations. The idea is to find an outer approximation of $F_{\text {LCP}}$, i.e., ${F}_{\text {LCP}} \subseteq {G}$ such that there exists a polynomial-time algorithm to verify whether a matrix belongs to ${D}_{{G}}^*$ or not. If this is doable, then we have a computable conic relaxation problem to approximate problem (QLCP).

The simplest computable conic relaxation is to choose ${G} = {\mathbb {R}}^n$. In this case, we have the following semidefinite relaxation of problem (QLCP) [5, 27]:

$$\begin{aligned} \begin{aligned} \min \quad&\frac{1}{2} \begin{bmatrix}2c&f^T\\f&Q \end{bmatrix} \cdot Y,\\ s.t.\quad&Y_{11}=1, \\&\begin{bmatrix}0&\frac{e_i^T}{2} \\ \frac{e_i}{2}&0 \end{bmatrix} \cdot Y \ge 0,\quad i=1,2,\ldots ,n,\\&\begin{bmatrix}b_i&\frac{a_i^T}{2} \\ \frac{a_i}{2}&0 \end{bmatrix} \cdot Y \ge 0,\quad i=1,2,\ldots ,n,\\&\begin{bmatrix}0&\frac{b^T}{2} \\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y = 0,\\&Y \succeq 0. \end{aligned} \end{aligned}$$

(QLCP-SDP)

Notice that the proof of Theorem 2 shows that problem (QLCP-SDP) is not strictly feasible when $\frac{A+A^T}{2} \succeq 0$. It could diminish the effectiveness of the interior-point approach. However, the next result shows a case for problem (QLCP-SDP) to be strictly feasible.

Theorem 3

Assume that there exists an $x \in {\mathbb {R}}^n$ satisfying $x>0$ and $Ax+b > 0$. If $\frac{A+A^T}{2} \preceq 0$ and $\frac{A+A^T}{2} \ne 0$, then problem (QLCP-SDP) is strictly feasible. The problem remains strictly feasible when the constraint $X \ge 0$ is added.

Proof

Let $x \in {\mathbb {R}}^n$ satisfy $x>0$ and $Ax+b > 0$. We can find an $X \in {\mathbb {S}}^{n}$ such that $X \succ xx^T$ and $X > 0.$ For example, $X=xx^T + I_{n \times n}$. Since $\frac{A+A^T}{2} \preceq 0$ and $\frac{A+A^T}{2} \ne 0$, we know $\frac{A+A^T}{2} \cdot (X - xx^T) < 0$. Noticing that $\frac{A+A^T}{2} \cdot (X - xx^T) < 0$, $\frac{A+A^T}{2} \cdot X < \frac{A+A^T}{2} \cdot xx^T \le 0$, we have $\frac{A+A^T}{2} \cdot X + b^Tx < \frac{A+A^T}{2} \cdot xx^T + b^Tx$.

If $\frac{A+A^T}{2} \cdot X + b^Tx = 0$, then $Y = \begin{bmatrix} 1&x^T \\x&X \end{bmatrix}$ is a strictly feasible solution.

If $\frac{A+A^T}{2} \cdot X + b^Tx > 0$, then there exists an $\alpha > 1$ such that $\frac{A+A^T}{2} \cdot (\alpha X) + b^Tx = 0$ and $\alpha X \succeq xx^T$. Hence $Y = \begin{bmatrix} 1&x^T \\x&\alpha X \end{bmatrix}$ with $\alpha >1$ is a strictly feasible solution.

If $\frac{A+A^T}{2} \cdot X + b^T x < 0$, then $b^Tx > 0$. Otherwise, $A \cdot xx^T + b^Tx \le 0$, which contradicts the assumption of $x^T (Ax + b) > 0$. Let $k_1 = \frac{A+A^T}{2} \cdot xx ^T + b^Tx$, $k_2 = \frac{A+A^T}{2} \cdot X + b^Tx$ and $\alpha = \frac{k_2}{k_2 - k_1}$, then we have $\alpha k_1 + (1 - \alpha ) k_2 = 0$. Because $k_1 > 0$ and $k_2 < 0$, we know $1> \alpha > 0$. Moreover, $\frac{A+A^T}{2} \cdot (\alpha xx^T + (1 - \alpha ) X) + b^Tx = \alpha (\frac{A+A^T}{2} \cdot xx^T + b^Tx) + (1 - \alpha )(\frac{A+A^T}{2} \cdot X + b^Tx) = 0$ and $\alpha xx^T + (1 - \alpha )X -xx^T = (1-\alpha )(X - xx^T) \succ 0$. Then $Y = \begin{bmatrix} 1&x^T \\ x&\alpha xx^T + (1 - \alpha )X \end{bmatrix}$ with $1>\alpha >0$ becomes a strictly feasible solution.

As can be seen from the above process, if the additional constraint of $X \ge 0$ is added, the problem remains to be strictly feasible.$\square$

The conic dual of problem (QLCP-SDP) can be expressed as

$$\begin{aligned} \begin{aligned} \max \quad&\sigma \\ s.t. \quad&\begin{bmatrix}c - \sigma - \sum _{i=1}^n \lambda _i b_i&\frac{f^T - \sum _{i=1}^n \omega _i e_i^T - \sum _{i=1}^n \lambda _i a_i^T - \mu b^T}{2}\\ \frac{f - \sum _{i=1}^n \omega _i e_i - \sum _{i=1}^n \lambda _i a_i - \mu b}{2}&\frac{Q}{2} - \mu \frac{A+A^T}{2} \end{bmatrix} \succeq 0, \\&\omega _i \ge 0,\quad \lambda _i \ge 0,\quad i=1,2,\ldots ,n, \quad \mu \in {\mathbb {R}}. \end{aligned} \end{aligned}$$

(QLCP-SDD)

Notice that problem (QLCP-SDP) is relaxed from problem (QLCP-CR) with $F_{\mathrm{LCP}}$ being relaxed to ${\mathbb {R}}^n$. Because ${\mathbb {R}}^n$ is unbounded, the strict feasibility of problem (QLCP-SDD) cannot be inferred by Theorem 1. However, we can show that problem (QLCP-SDD) becomes strictly feasible when $\frac{A+A^T}{2} \prec 0$.

Theorem 4

If $\frac{A+A^T}{2} \prec 0$, then problem (QLCP-SDD) is strictly feasible.

Proof

When $\frac{A+A^T}{2} \prec 0$, there exists a sufficient large number $\mu > 0$ such that $\frac{Q}{2} - \mu \frac{A+A^T}{2} \succ 0$. For fixed $\omega _i >0$ and $\lambda _i>0$, $i=1,\ldots ,n$, if $-\sigma$ is a sufficiently large positive number, then we have $c - \sigma - \sum _{i=1}^n \lambda _i b_i >0$ and $4(c - \sigma - \sum _{i=1}^n \lambda _i b_i) - (f - \sum _{i=1}^n \omega _i e_i - \sum _{i=1}^n \lambda _i a_i - \mu b)^T (\frac{Q}{2} - \mu \frac{A+A^T}{2})^{-1} (f - \sum _{i=1}^n \omega _i e_i - \sum _{i=1}^n \lambda _i a_i - \mu b) > 0$. The Schur-complementary theorem then implies that problem (QLCP-SDD) is strictly feasible.$\square$

On one hand, we have good news that problem (QLCP-CR) is attainable whenever $F_{\text {LCP}}$ is nonempty and bounded, the semidefinite relaxation and its dual are computable when $\frac{A+A^T}{2} \prec 0$. On the other hand, the attainability of problem (QLCP-DR) is not guaranteed when $\frac{A+A^T}{2} \succeq 0$. All these results depend on the properties of $F_{\text {LCP}}$.

From the definition of cone of nonnegative quadratic functions, a key obstacle of solving problems (QLCP-CR) and (QLCP-DR) is the structure of ${F}_{\text {LCP}}=\{x \in {\mathbb {R}}^n|x \ge 0,~Ax+b \ge 0,~x^T(Ax+b)=0\}$. We would like to find a better outer approximation for ${F}_{\text {LCP}}$ based on its structure rather than simply relax it to ${\mathbb {R}}^n$. Later, we will discuss how to relax the set ${F}_{\text {LCP}}$ by a set G such that $D_G$ and $D_G^*$ can be checked in polynomial-time.

For problem (QLCP), if the set $\{x \in {\mathbb {R}}^n | x \ge 0,~Ax+b \ge 0\}$ is bounded, then we can choose a box ${T}=[u,v]$ with $u \in {\mathbb {R}}^n$ and $v \in {\mathbb {R}}^n$ to outer approximate the set $\{x \in {\mathbb {R}}^n |x \ge 0,~Ax+b \ge 0\}$. In this way, we have ${F}_{\text {LCP}} = \{x \in {\mathbb {R}}^n | x \ge 0,~Ax+b \ge 0\} \cap \{x \in {\mathbb {R}}^n | x^T(Ax+b)\le 0\}$, and then ${F}_{\text {LCP}} \subseteq {T} \cap \{x \in {\mathbb {R}}^n | x^T(Ax+b)\le 0\}$. An ellipsoid $H_T$ can be found such that $T \subseteq H_T$, consequently, ${F}_{\text {LCP}} \subseteq H_T \cap \{x \in {\mathbb {R}}^n | x^T(Ax+b)\le 0\}$ and $D_{{F}_{\text {LCP}}} \subseteq D_{H_T}^* \cap D_{\{x \in {\mathbb {R}}^n | x^T(Ax+b)\le 0\}}^*$. Based on $D_{H_T}^*$, using linear matrix inequality (LMI) representations [25] and relaxing $D_{\{x \in {\mathbb {R}}^n | x^T(Ax+b)\le 0\}}^*$ by $\left\{ Y \in {\mathbb {S}}^{n+1}\Big |\begin{bmatrix}0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y \le 0 \right\}$, we can obtain a conic relaxation for problem (QLCP). Lemmas 2 and 3 imply such conic relaxation could fit better than the semidefinite relaxation. In the next section, we provide details of how to find such a box T and an ellipsoid $H_T$, and how to improve the conic relaxation for a better lower bound.

3 Conic approximation algorithm for solving problem (QLCP)

In this section, we introduce a conic approximation algorithm for solving problem (QLCP) by adaptively refining the outer approximation G of the feasible domain ${F}_{\text {LCP}}$ under the assumption that ${F}_{\text {LCP}} \ne \emptyset$ and the set $\{x \in {\mathbb {R}}^n | x \ge 0,~Ax+b \ge 0\}$ is bounded.

Following our previous discussions, we need to construct an initial box T in order to find a good outer approximation of ${F}_{\mathrm{LCP}}$. For $i=1,\ldots ,n$, consider the following linear programs:

$$\begin{aligned} u_i=\min \quad&x_i \nonumber \\ s.t. \quad&x \ge 0,\\&Ax+b \ge 0,\nonumber \end{aligned}$$

(1)

and

$$\begin{aligned} v_i=\max \quad&x_i \nonumber \\ s.t. \quad&x \ge 0,\\&Ax+b \ge 0, \nonumber \end{aligned}$$

(2)

where $x_i$ represents the i-th element of variable $x \in {\mathbb {R}}^n$. Since they are linear programs, an initial box ${T}=[u,v]$ can be easily obtained.

Remark 1

If there exists a k such that $u_k=v_k$, then obviously $x_k=u_k=v_k$. We can construct a new quadratic program with linear complementarity constraints by letting $f_i=Q_{ik}x_k+f_i$, $b_i=b_i+A_{ik}x_k$, $i=1,\ldots ,n$, and $c=c+\frac{1}{2}Q_{kk}x_k^2+f_kx_k$. Due to the linear complementarity condition, when $x_k=0$, we need to add the linear constraint $\sum _{i=1}^n A_{ki}x_i+b_k \ge 0$. When $x_k>0$, we need to add $\sum _{i=1}^n A_{ki}x_i+b_k=0$ to the new problems. Delete the k-th row and k-th column of Q and A, and delete the k-th row of f and b. Then, we obtain a new problem whose dimensionality is $n-1$. Therefore, we may as well assume that $v_i>u_i$ for any $i=1,\ldots ,n$.

For $0<\theta < 1$, let

$$\begin{aligned}&{H}_{T} = \left\{ x \in {\mathbb {R}}^n \Big |\frac{4(x- \frac{u+v}{2})^T {\theta (Diag(v-u)^2)^{-1}} (x- \frac{u+v}{2})}{n} \le 1\right\} \end{aligned}$$

(3)

Then ${H}_{T}$ is an ellipsoidal set that outer approximates the box T [38]. Moreover, let

$$\begin{aligned} {J}=\{x \in {\mathbb {R}}^n | x^T(Ax+b)\le 0\} \end{aligned}$$

and define ${G}={H}_{T} \cap {J}$. The next result follows,

Theorem 5

If $F_{\mathrm{LCP}} \ne \emptyset$, $\{x \in {\mathbb {R}}^n | x^T(Ax+b)<0\} \ne \emptyset$ and the set $\{x \in {\mathbb {R}}^n | x \ge 0,~Ax+b \ge 0\}$ is bounded, then the outer approximation ${G}={H}_{T} \cap J$ contains an interior point.

Proof

When $F_{\mathrm{LCP}} \ne \emptyset$, there exists an $x^0 \in {F}_{\text {LCP}}$ such that $x^0 \ge 0$, $Ax^0+b \ge 0$ and $(x^0)^T (Ax^0+b)=0$. When $0<\theta <1$, we have $\{x \in {\mathbb {R}}^n | x \ge 0,~Ax+b \ge 0\} \subseteq \text {int}({H}_{{T}})$. Hence $x^0 \in \text {int}({H}_{{T}})$. Since $\{x \in {\mathbb {R}}^n | x^T(Ax+b)<0\} \ne \emptyset$ and ${H}_{{T}}$ is an ellipsoidal set, we can find an $x^*$ sufficiently close to $x^0$ such that it is interior to G. $\square$

Remark 2

(3) implies the smaller $\theta$ is, the larger $H_T$ becomes. When $\theta =1$, it is the smallest ellipsoid which covers the box T. However, it cannot be guaranteed that the outer approximation G contains an interior point when $\theta =1$. Hence, we choose $0<\theta <1$. Based on numerical experiments, we choose $=$ 0.95 in our algorithm.

Theorem 5 and Lemma 4 imply that $D_G^* \subseteq D_{{H}_{T}}^* \cap D_J^*$ and $D_G^*$ contains an interior point. By the definition of ${D}_{{J}}^*$, for any $Y \in {D}_{{J}}^*$, there exist $\tau _k \in {\mathbb {Z}}_+$, $\lambda _{ik} \ge 0$ and $x^{ik} \in {J}$, $i=1,2,\ldots ,\tau _k$, $k=1,2,\ldots ,+\infty$, satisfying $Y^k = \sum _{i=1}^{\tau _k} \lambda _{ik} \begin{bmatrix}1\\x^{ik} \end{bmatrix}{\begin{bmatrix}1\\x^{ik} \end{bmatrix}}^T$ and $Y=\lim _{k\rightarrow \infty } Y^k$. Since $\begin{bmatrix}0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot \begin{bmatrix}1\\x^{ik} \end{bmatrix}{\begin{bmatrix}1\\x^{ik} \end{bmatrix}}^T \le 0$, we have $\begin{bmatrix}0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y^k \le 0$ and $\begin{bmatrix}0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y \le 0$. Let

$$\begin{aligned} {B}=\left\{ Y \in {\mathbb {S}}^{n+1}\Big |\begin{bmatrix}0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y \le 0 \right\} , \end{aligned}$$

then $D_J^* \subseteq B$ and ${D}_{{{G}}}^* \subseteq {D}_{{H}_{T}}^* \cap {B}$.

Because ${H}_{{T}}$ is an ellipsoidal set, some linear matrix inequality (LMI) representations for ${D}_{{H}_{T}}^*$ can be provided as below.

Theorem 6

[25] For an ellipsoidal set ${H} = \left\{ x \in {\mathbb {R}}^n \Big | (x-d)^T P (x-d) \le 1 \right\}$ with $P \in {\mathbb {S}}_{++}^{n}$ and $d \in {\mathbb {R}}^n$, we have $Y \in {D}_{H}^*$ if and only if

$$\begin{aligned}&\begin{bmatrix}d^T P d - 1&-(Pd)^T \\ -Pd&P \end{bmatrix} \cdot Y \le 0,\\&Y \succeq 0. \end{aligned}$$

In order to discuss the improvement of ${D}_{G}^*$, we need the next known result.

Lemma 5

[34] Let ${G} = {G}_1 \cup {G}_2 \cup \cdots \cup {G}_m$ with ${G}_i \ne \emptyset$ for $i=1,2,\ldots ,m$, then ${D}_{G} = {D}_{{G}_1} \cap {D}_{{G}_2} \cap \cdots \cap {D}_{{G}_m}$ and ${D}_{{G}}^* = {D}_{{G}_1}^* + {D}_{{G}_2}^* + \cdots + {D}_{{G}_m}^*$.

Replacing ${D}_{{F}_{\text {LCP}}}^*$ by ${D}_{{H}_{T}}^* \cap {B}$ in problem (QLCP-CR), we can obtain a computable conic relaxation problem and achieve a lower bound for problem (QLCP). We further consider how to improve the lower bound. One intuitive idea is to partition the box T into a collection of m $(m>1)$ small boxes such that ${T} = {T}_1 \cup \cdots \cup {T}_m$ with ${T}_i =[u^i,v^i]$. Let $d^i = \frac{u^i+v^i}{2}$ and $P^i = \theta \frac{4}{n} (Diag(v^i-u^i)^2)^{-1}$, then

$$\begin{aligned} {H}_{{T}_i} = \left\{ x \in {\mathbb {R}}^n \Big | (x-d^i)^T P^i (x-d^i) \le 1 \right\} , \end{aligned}$$

$i=1,2,\ldots ,m$. Let ${G} = {G}_1 \cup \cdots \cup {G}_m$ with ${G}_i = {H}_{{T}_i} \cap {J}$, then ${D}_{{G}}^* = {D}_{{G}_1}^* + \cdots + {D}_{{G}_m}^* \subseteq ({D}_{{H}_{{T}_1}}^* \cap {B}) + \cdots + ({D}_{{H}_{{T}_m}}^* \cap {B})$. Using Lemma 5 and Theorem 6, we have the following conic relaxation for problem (QLCP):

$$\begin{aligned} \begin{aligned} V_{\mathrm{QLCP-Relax}}=\min \quad&\frac{1}{2} \begin{bmatrix}2c&f^T\\f&Q \end{bmatrix} \cdot Y\\ s.t.\quad&Y_{11}=1, \\&Y=Y^1 + \cdots + Y^m,\\&\begin{bmatrix}0&\frac{b^T}{2}\\\frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y^i\le 0,~i=1,\ldots ,m, \\&\begin{bmatrix}(d^i)^T P^i d^i - 1&-(P^i d^i)^T \\ -P^i d^i&P^i \end{bmatrix} \cdot Y^i \le 0,~i=1,\ldots ,m,\\&Y^i \succeq 0,~i=1,\ldots ,m. \end{aligned} \end{aligned}$$

(QLCP-Relax)

Notice that if every $G_i$, $i=1,\ldots ,m$, contains an interior point, then problem (QLCP-Relax) can be solved by an interior-point approach. We denote the optimal value as $V_{\mathrm{QLCP-Relax}}$ and the optimal solution as $Y^*$.

The next known result tells us how to decompose an optimal solution $Y^*$.

Theorem 7

[25] For the optimal solution $Y^*=(Y^1)^* + \cdots + (Y^m)^*$ of problem (QLCP-Relax), there exists a decomposition running in polynomial time such that

$$\begin{aligned} Y^* = \sum _{i=1}^m \sum _{j=1}^{r_i} \xi _{ij} \begin{bmatrix}1\\x^{ij} \end{bmatrix} {\begin{bmatrix}1\\x^{ij} \end{bmatrix}}^T \end{aligned}$$

satisfying $(x^{ij}-d^i)^T P^i (x^{ij}-d^i) \le 1$, $\xi _{ij} > 0$, for $i=1,2,\ldots ,m,$ $j=1,2,\ldots ,r_i,$ and $\sum _{i=1}^m \sum _{j=1}^{r_i} \xi _{ij} = 1$, where $r_i = rank(Y^i)$.

If there exists an $x^{ij}$ with $i \in \{1,2,\ldots ,m\}$ and $j \in \{1,\ldots ,r_i\}$ from the above decomposition such that $x^{ij} \ge 0$, $A x^{ij}+b \ge 0$, $x^{ij}(A x^{ij}+b)=0$ and $\frac{1}{2}(x^{ij})^T Q x^{ij} + f^T x^{ij} + c \le V_{\mathrm{QLCP-Relax}}$ , then it is an optimal solution of problem (QLCP). Otherwise, we need a partition of the box T in order to obtain a new outer approximation for ${F}_{\mathrm{LCP}}$. Define

$$\begin{aligned}&z^* = arg \min _{z \in \left\{ x^{ij} ,~i=1,\ldots ,m,~j=1,\ldots ,r_i \right\} } \frac{1}{2}z^T Q z + f^T z +c \end{aligned}$$

as a “sensitive point.” Note that the sensitive point may not be unique. If there are multiple sensitive points, we choose the one with the smallest $i \in \{1,\ldots ,m\}$ and smallest $j \in \{1,\ldots ,r_i \}$ as the sensitive point. Naturally, if the sensitive point is decomposed from $Y^t$, $t \in \{1,2,\ldots ,m\}$, then it belongs to the t-th box. The corresponding box is then called the sensitive box.

Assuming that ${T}_t = [u^t,v^t]$ is the sensitive box where $u^t, v^t \in {\mathbb {R}}^n$, we shall split it in half along the direction perpendicular to the longest edge. First, we find the longest edge by calculating $\max _{i=1,\ldots ,n} (v_i^t-u_i^t)$ and defining $id=\arg \max _{i=1,\ldots ,n} (v_i^t-u_i^t)$. Then ${T}_t$ can be split into two boxes: ${T}_{t1}=[u^{t1},v^{t1}]$ and ${T}_{t2}=[u^{t2},v^{t2}]$, with $u^{t1}=u^t$, $v_{i}^{t1}=v_i^t$, for $i \ne id$, $v_{id}^{t1}=\frac{u_{id}^t+v_{id}^t}{2}$ and $v^{t2}=v^t$, $u_i^{t2}=u_i^t$ for $i \ne id$, $u_{id}^{t2}=\frac{u_{id}^t+v_{id}^t}{2}$.

Considering the two new boxes, the newly added sets are

$$\begin{aligned} G_{tj}=\{x \in {\mathbb {R}}^n|(x-d^{tj})^T P^{tj} (x-d^{tj}) \le 1,~x^T(Ax+b) \le 0\}, j = 1, 2, \end{aligned}$$

with $d^{tj} = \frac{u^{tj}+v^{tj}}{2}$ and $P^{tj} = \theta \frac{4}{n} (Diag(v^{tj}-u^{tj})^2)^{-1}$ where $0<\theta <1$. To see ${\mathrm{int}}(G_{tj})=\emptyset$ or not, let us consider the following problem for $j=1,2$:

$$\begin{aligned} \gamma _j^*=\min \quad&(x-d^{tj})^T P^{tj} (x-d^{tj})-1\\ s.t.\quad&x^T(Ax+b) \le 0.\\ \end{aligned}$$

Using [33], we know the optimal value of the above problem can actually be found by solving the following problem in polynomial time:

$$\begin{aligned} \gamma _j^*=\min \quad&\begin{bmatrix}(d^{tj})^TP^{tj}d^{tj}-1&(P^{tj}d^{tj})^T\\P^{tj}d^{tj}&P^{tj}\end{bmatrix} \cdot Y \\ s.t.\quad&Y_{11}=1,\\&\begin{bmatrix}0&\frac{b^T}{2}\\\frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y \le 0,\\&Y \succeq 0. \end{aligned}$$

The next result tells us whether ${\mathrm{int}}(G_{tj})=\emptyset$ or not.

Theorem 8

Given any $0< \theta <1$, for $j=1,2$, ${\mathrm{int}}(G_{tj})=\emptyset ~~$ if and only if $~~\gamma _j^* \ge 0$.

Proof

If $\gamma _j^* \ge 0$, then it is clear that ${\mathrm{int}}(G_{tj}) \subseteq \{x \in {\mathbb {R}}^n | x^T(Ax+b) \le 0\} \cap {\text {int}}(\{x \in {\mathbb {R}}^n | (x-d^{tj})^T P^{tj} (x-d^{tj}) \le 1\})=\emptyset$.

If $\gamma _j^* < 0$, then there exists an $x^0$ such that $(x^0)^T(Ax^0+b) \le 0$ and $(x^0-d^{tj})^T P^{tj} (x^0-d^{tj}) <1$. Furthermore, if $(x^0)^T(Ax^0+b) < 0$, then $x^0 \in {\text {int}} (G_{tj}) = \{x \in {\mathbb {R}}^n |(x-d^{tj})^T P^{tj} (x-d^{tj})< 1,~ x^T(Ax+b) < 0\}$. Otherwise, since $(x^0-d^{tj})^T P^{tj} (x^0-d^{tj}) \le 1$ is an ellipsoidal constraint, we can find a point $x^*$ sufficiently close to $x^0$ such that $x^* \in {\text {int}}\{x \in {\mathbb {R}}^n |(x-d^{tj})^T P^{tj} (x-d^{tj}) \le 1,~ x^T(Ax+b) \le 0\} = {\mathrm{int}}(G_{tj})$.$\square$

Notice that when ${\mathrm{int}}(G_{tj})=\emptyset$, we have $F_{\mathrm{LCP}} \cap T_{tj} =\{x \in {\mathbb {R}}^n | x \ge 0,~Ax+b \ge 0,~x^T(Ax+b) \le 0,~v^{tj} \ge x \ge u^{tj}\} \subseteq \{x \in {\mathbb {R}}^n | x^T(Ax+b) \le 0\} \cap \text {int}(\{x \in {\mathbb {R}}^n | (x-d^{tj})^T P^{tj} (x-d^{tj}) \le 1\})=\emptyset$ with $1> \theta >0$. It means that the set $G_{tj}$ is redundant and we may eliminate it and the corresponding box $T_{tj}$. Therefore, we can manage the rectangle sets in T in the following way:

$$\begin{aligned}&{T}={T}\backslash \{{T}_t\}, \quad ~~~~~~~~~~~~~~~~~~~~~~~~{\mathrm{if}} ~\gamma _1^* \ge 0~\text { and}~ \gamma _2^* \ge 0; \end{aligned}$$

(4)

$$\begin{aligned}&{T}={T}\backslash \{{T}_t\}\cup \{{T}_{t2}\}, \quad ~~~~~~~~~~~~{\mathrm{if}}~ \gamma _1^* \ge 0~\text { and}~ \gamma _2^* < 0; \end{aligned}$$

(5)

$$\begin{aligned}&{T}={T}\backslash \{{T}_t\}\cup \{{T}_{t1}\}, \quad ~~~~~~~~~~~~{\mathrm{if}} ~\gamma _1^* < 0~\text { and}~ \gamma _2^* \ge 0; \end{aligned}$$

(6)

$$\begin{aligned}&{T}={T}\backslash \{{T}_t\}\cup \{{T}_{t1}\} \cup \{{T}_{t2}\}, \quad {\mathrm{if}}~ \gamma _1^*< 0~\text { and}~ \gamma _2^* < 0. \end{aligned}$$

(7)

Before the algorithm is designed, we notice that $Y=Y^1+\cdots +Y^m$, the objective and constraint functions are linear over Y in problem (QLCP-Relax). Hence, we have the next theorem.

Theorem 9

Solving problem (QLCP-Relax) is equivalent to finding the minimum of the following problems:

$$\begin{aligned} V_i=\min \quad&\frac{1}{2} \begin{bmatrix} 2c&f^T\\ f&Q \end{bmatrix} \cdot Y\nonumber \\ s.t.\quad&Y_{11}=1,\nonumber \\&\begin{bmatrix} 0&\frac{b^T}{2}\\ \frac{b}{2}&\frac{A+A^T}{2} \end{bmatrix} \cdot Y\le 0, \nonumber \\&\begin{bmatrix} (d^i)^T P^i d^i - 1&-(P^i d^i)^T \\ -P^i d^i&P^i \end{bmatrix} \cdot Y \le 0,\nonumber \\&Y \succeq 0, \end{aligned}$$

(8)

for $i=1,\ldots ,m$.

Proof

Denote $Y^*$ and $V^*$ as the optimal solution and optimal value of problem (QLCP-Relax), respectively. It is obvious that $V^* \le V_i$, for $i=1,\ldots ,m$. Conversely, if $V_k=\min \{V_i |i=1,\ldots ,m\}$ and the corresponding optimal solution is $Y^k$, then it is easy to prove that $Y^*=Y^1+\cdots +Y^m$, with $Y^i$ being the zero matrix for $i \ne k$, is the optimal solution of problem (QLCP-Relax).$\square$

By the previous theorem, in order to save computation time, when we solve problem (QLCP-Relax) for $G=G_1 \cup \cdots \cup G_m$, we just need to solve at most two new problems (8) where $i=t1$ and (or) $i=t2$ based on (4–7), then with the records of optimal solutions and optimal values for other $(V_i)s$, we can obtain the optimal value and optimal solution of problem (QLCP-Relax). Furthermore, when decomposing the optimal solution $Y^*$ for problem (QLCP-Relax), we only need to decompose the optimal solutions of the the two new problems where $i=t1$ and (or) $i=t2$. With the records of former decompositions, we can obtain a new decomposition for $Y^*$.

Summarizing the above analysis, we propose a conic approximation algorithm (CAA) for solving problem (QLCP).

We now provide a convergency proof of the proposed algorithm.

Theorem 10

Assume that $F_{LCP } \ne \emptyset$ and the set $\{x \in {\mathbb {R}}^n | x \ge 0,~Ax+b \ge 0\}$ is bounded. For any given $\epsilon >0$, the proposed conic approximation algorithm either returns an optimal solution to problem (QLCP) or there exists an integer $N_{\epsilon }>0$ such that $|V_{QLCP-Relax }-V_{QLCP }| \le \epsilon$ at the $N_{\epsilon }$-th iteration.

Proof

Notice that the objective function of problem (QLCP) is continuous. If a set F is bounded and closed, then for any given $\epsilon >0$, there exists a $\delta _{\varepsilon }>0$ such that $|\frac{1}{2}x^T Q x + f^T x + c-(\frac{1}{2}y^T Q y + f^T y + c)|< \epsilon$ for any $x\in F$, $y\in F$ and $\Vert x-y\Vert _{\infty } < \delta _{\varepsilon }$.

From the description of the proposed algorithm, there exists an integer $N_{\epsilon } > 0$, a sensitive point $z^*$ and a feasible point $z^0$ in the sensitive box $T_t$ such that after $N_{\epsilon }$ iterations, the length of the longest edge of the sensitive box ${T}_t$ is shorter than $\frac{2 \delta _{\varepsilon }\sqrt{\theta }}{\sqrt{n}}$. Following the structure of ${H}_{T_t}$, the length of its j-th axis of ${H}_{T_t}$ is equal to $\frac{\sqrt{n}}{2\sqrt{\theta }}$ times the length of its corresponding j-th edge of ${T}_t$. Then $\Vert z^*-z^0\Vert _{\infty } \le \delta _{\varepsilon }$ and $|V_{\text {{QLCP-Relax}}} - V_{\text {{QLCP}}}| \le |\frac{1}{2}(z^*)^T Q z^* + f^T z^* + c - (\frac{1}{2}(z^0)^T Q z^0 + f^T z^0 + c) | \le \epsilon$. $\square$

This convergency proof actually claims that under the stated assumptions, the proposed conic approximation algorithm either finds an optimal solution to the problem (QLCP) or eventually provides an $\epsilon$-optimal solution of problem (QLCP).

Remark 3

Suppose the initial box is [u, v]. From the partition, we know that, at each iteration, we split the sensitive box in half along the direction perpendicular to the longest edge to achieve two new boxes. Therefore, after taking at most

$$\begin{aligned} N_{\epsilon } = \left( \frac{\sqrt{n}}{2\delta _{\varepsilon }\sqrt{\theta }}\right) ^n \Pi _{i=1}^n (v_i-u_i) \end{aligned}$$

iterations, the length of the longest edge of the sensitive box ${T}_t$ is smaller than $\frac{2 \delta _{\varepsilon }\sqrt{\theta }}{\sqrt{n}}$.

For any given $\varepsilon >0$, we may calculate $\delta _{\varepsilon }$ as follows. If $x \in {\mathbb {R}}^n$, $u \le y \le v$ and $\Vert x-y\Vert _{\infty } \le \delta _{\varepsilon }$, we have $\max _{i=1}^n (x_i+y_i) \le 2v+\delta _{\varepsilon }$ and

$$\begin{aligned}&\left| \frac{1}{2}x^T Q x + f^T x + c-\left( \frac{1}{2}y^T Q y + f^T y + c\right) \right| \\&\quad \le \left| \frac{1}{2}x^T Q x -\frac{1}{2} x^T Q y + \frac{1}{2}x^T Q y -\frac{1}{2}y^T Q y\right| + |f^T (x-y)|\\&\quad \le \sum _{i,j=1}^n \frac{1}{2}|Q_{ij}| |x_i+y_i||x_j-y_j| + \sum _{i=1}^n |f_i| |x_i-y_i|\\&\quad \le \frac{1}{2}\left( \sum _{i,j=1}^n |Q_{ij}| \delta _{\varepsilon } (2v+\delta _{\varepsilon }) + 2\sum _{i=1}^n |f_i| \delta _{\varepsilon }\right) \end{aligned}$$

Then $\delta _{\varepsilon }$ can be taken as ${\frac{2\epsilon }{\sqrt{(\sum _{i,j=1}^n v|Q_{ij}|+\sum _{i=1}^n |f_i|)^2+2\epsilon \sum _{i,j=1}^n |Q_{ij}|}+(\sum _{i,j=1}^n v|Q_{ij}|+\sum _{i=1}^n |f_i|)}}$ such that $\frac{1}{2}(\sum _{i,j=1}^n |Q_{ij}| \delta _{\varepsilon } (2v+\delta _{\varepsilon }) + 2\sum _{i=1}^n |f_i| \delta _{\varepsilon }) \le \epsilon$. Consequently, in the worst case, we need to take

$$\begin{aligned}&N_{\epsilon } \\&\quad = \left( \frac{\sqrt{n} ({\sqrt{(\sum _{i,j=1}^n v|Q_{ij}|+\sum _{i=1}^n |f_i|)^2+2\epsilon \sum _{i,j=1}^n |Q_{ij}|}+(\sum _{i,j=1}^n v|Q_{ij}|+\sum _{i=1}^n |f_i|)})}{4\varepsilon \sqrt{\theta }}\right) ^n \\&\qquad \times \, \Pi _{i=1}^n (v_i-u_i) \end{aligned}$$

iterations.

3.1 Binary quadratic programming problems

The binary quadratic programming (BQP) problem is a special quadratic program with linear complementarity constraints. In this subsection, we show a customized partition for this problem.

Consider the following binary quadratic programming problem:

$$\begin{aligned} V_{\text {BQP}}=\min \quad&\frac{1}{2}x^T Q x + f^T x + c\\ s.t. \quad&x \in \{0,1\}^n, \end{aligned}$$

(BQP)

which can be rewritten as

$$\begin{aligned} \min \quad&\frac{1}{2}x^T Q x + f^T x + c\\ s.t. \quad&x \ge 0,\\&-I_n x+1_n \ge 0,\\&x^T(-I_n x+1_n)=0, \end{aligned}$$

where $1_n = {\begin{bmatrix} 1&\cdots&1\end{bmatrix}}_n^T$. Since $-I_n \prec 0$, the assumptions of Theorems 3 and 4 are satisfied. Then the semidefinite relaxation for problem (BQP) can be solved using an interior-point algorithm.

It is obvious that the initial box can be taken as $[0,1]^n$. Assuming ${T}^* = [u,v]$ is the sensitive box and $z^*$ is the sensitive point, we can provide a specific partition here.

Given $0<\rho \le 1$, $0<\theta <1$ and $\delta >0$, there are two cases. Here $\rho$ is used to speed up the convergence. Based on our numerical experiments, $\rho$ can be chosen as 0.2. Moreover, $\delta$ is decided by the precision level.

Case 1. $z^{*} \in [0,1]^n$.

(1) If $z^{*} \in {T}^*$, we define $id = arg\max _{1\le i\le n} \{\min (z_i^*-u_i, v_i-z_i^*)\}$. Then

$$\begin{aligned} w_{id}=\frac{2\rho \min (|z_{id}^*-u_{id}|, |z_{id}^*-v_{id}|)}{\frac{\sqrt{n}}{\sqrt{\theta }}+1}. \end{aligned}$$

We have ${T}_1^* = \{x | x \in {T}^*,~u_{id}+w_{id} \ge x_{id} \ge u_{id} \}$ and ${T}_2^* = \{x | x \in {T}^*,~v_{id} \ge x_{id} \ge v_{id}-w_{id} \}$.

(2) If $z^{*} \notin {T}^*$, we define $id = arg\max _{1\le i\le n} \{\max (u_i-z_i^*, z_i^*-v_i)\}$. Then

$$\begin{aligned} w_{id}=\frac{2 \rho \max (|z_{id}^*-u_{id}|,|z_{id}^*-v_{id}|)}{\frac{\sqrt{n}}{\sqrt{\theta }}+1}. \end{aligned}$$

When ${z_{id}^*}-v_{id}>0$, we have ${T}_1^* = \{x | x \in {T}^*,~u_{id}+w_{id} \ge x_{id} \ge u_{id} \}$. Otherwise, we have ${T}_1^* = \{x | x \in {T}^*,~v_{id} \ge x_{id} \ge v_{id}-w_{id} \}$.

Case 2. $z^{*} \notin [0,1]^n$.

Define $l = arg\max _{1\le i\le n} \{\max (-z_i^*, z_i^*-1)\}$.

(1) If $v_{l}-u_{l}< \delta$, then

$$\begin{aligned} id = arg\max _{1\le i\le n} \{\min (z_i^*-u_i, v_i-z_i^*)\}. \end{aligned}$$

If $\min (z_{id}^*-u_{id}, v_{id}-z_{id}^*) \le 0$, stop partitioning, $z^*$ is the approximate optimal solution. Otherwise, $w_{id}=\frac{2\rho \min (|z_{id}^*-u_{id}|, |z_{id}^*-v_{id}|)}{\frac{\sqrt{n}}{\sqrt{\theta }}+1}$. In this case, we have ${T}_1^* = \{x | x \in {T}^*,~u_{id}+w_{id} \ge x_{id} \ge u_{id} \}$ and ${T}_2^* = \{x | x \in {T}^*,~v_{id} \ge x_{id} \ge v_{id}-w_{id} \}$.

(2) If $v_{l}-u_{l} \ge \delta$, let $id=l$ and $w_{id}= \frac{2\rho \max (z_{id}^*-v_{id},u_{id}-z_{id}^*)}{\frac{\sqrt{n}}{\sqrt{\theta }}-1}$. If $z_{id}^*-1>0$ and $u_{id}>\delta$, then we have ${T}_1^* = \{x | x \in {T}^*,~v_{id} \ge x_{id} \ge v_{id}-w_{id} \}$. Otherwise, if $z_{id}^*<0$ and $v_{id}<1-\delta$, we have ${T}_1^* = \{x | x \in {T}^*,~u_{id}+w_{id} \ge x_{id} \ge u_{id} \}$. If $z_{id}^* \ge 0$, we have ${T}_1^* = \{x | x \in {T}^*,~v_{id} \ge x_{id} \ge v_{id}-w_{id} \}$ and ${T}_2^* = \{x | x \in {T}^*,~u_{id}+w_{id} \ge x_{id} \ge u_{id} \}$.

It is easy to see that when $0<\theta <1$, the outer approximation for the feasible set of problem (BQP) contains an interior point and this partition for problem (BQP) is more effective than (4–7) for general quadratic programs with linear complementarity constraints.

Remark 4

Actually, our conic approximation algorithm can also be applied to (BQP) with several linear constraints. For such case, we only need to add some linear matrix inequalities to the corresponding conic relaxation problem and the rest of the process is similar to solving (BQP).

3.2 Quadratic programs with convex quadratic constraints and linear complementarity constraints

Consider the following quadratic program with convex quadratic constraints and linear complementarity constraints:

$$\begin{aligned} \min \quad&\frac{1}{2} x^T Q_0 x + f_0^T x + c_0\\ s.t. \quad&\frac{1}{2} x^T Q_i x + f_i^T x + c_i \le 0,~i=1,\ldots ,s,\\&x \ge 0,\\&Ax+b \ge 0,\\&x^T(Ax+b)=0. \end{aligned}$$

where $Q_i \in {\mathbb {S}}_+^n$, $i=1,\ldots ,s$.

This problem is an extension of problem (QLCP) that can be solved by the proposed conic approximation algorithm with some modifications.

First, we notice that there exists a matrix $D_i$ such that $Q_i=D_i D_i^T$ for each $i =1,2,\ldots s$. Assume that $\{x \in {\mathbb {R}}^n|\frac{1}{2} x^T Q_i x + f_i^T x + c_i \le 0,~i=1,\ldots ,s,~x \ge 0,~Ax+b \ge 0\}$ is a bounded set. The method to find an initial box $T=[u,v]$ is similar to what we did for problem (QLCP). Consider the following problems:

$$\begin{aligned} u_j=\min \quad&x_j\\ s.t. \quad&\left\| \begin{bmatrix}D_i^Tx\\ \frac{f_i^Tx+c_i+2}{2} \end{bmatrix}\right\| _2 \le \frac{-f_i^Tx-c_i+2}{2},~i=1,\ldots ,s,\\&x \ge 0,\\&Ax+b \ge 0, \end{aligned}$$

and

$$\begin{aligned} v_j=\max \quad&x_j\\ s.t. \quad&\left\| \begin{bmatrix}D_i^Tx\\ \frac{f_i^Tx+c_i+2}{2} \end{bmatrix}\right\| _2 \le \frac{-f_i^Tx-c_i+2}{2},~i=1,\ldots ,s,\\&x \ge 0,\\&Ax+b \ge 0, \end{aligned}$$

for $j=1,\ldots ,n$ and $x_j$ represents the j-th element of variable $x \in {\mathbb {R}}^n$. Note that the above two convex programs can be effectively solved.

Similar outer approximation and partition processes of problem (QLCP) can also be extended to design a conic approximation algorithm for solving this problem.

4 Numerical examples

In this section, five numerical examples are provided to illustrate the proposed algorithm. All experiments are conducted using MATLAB 2012 on a PC with Intel Core 2 CPU of 2.26 Ghz and 3G memory to show its effectiveness. All convex programming problems are solved using a MATLAB software package CVX[17]. In the following examples, we choose $\theta =0.95$ and $\rho =0.2$.

Example 1

Consider the following problem:

$$\begin{aligned} \min \quad&-x_1^2-72x_1x_2+14x_2^2+53x_1-28x_2\\ s.t.\quad&x_2 \ge x_1 \ge 0,\\&x_1+x_2 \le 1,\\&x^T \left( \begin{bmatrix} -1&1\\ -1&-1 \end{bmatrix}x+ \begin{bmatrix} 0\\ 1 \end{bmatrix}\right) =0. \end{aligned}$$

The objective function is non-convex. Obviously, the feasible solutions are $(0,0)^T$, $(0,1)^T$ and $(0.5,0.5)^T$, the optimal solution is $(0,1)^T$ and optimal value is $-14$. Using the proposed conic approximation algorithm, after 12 iterations, we can obtain an approximate optimal solution $(0.0001,1.0000)^T$ with an approximate optimal value $-14.0014$. The CPU time is 5.4741 s.

Example 2

Consider the problem with $n=3$,

$$\begin{aligned} Q=\left[ \begin{array}{ccc} 18 &{} -1 &{} -1\\ -1 &{} -7 &{} 5\\ -1 &{} 5 &{} 19 \end{array} \right] ,\quad f=( -9,6,-3 )^T,\quad c=0. \end{aligned}$$

A and b are obtained from [15] such that

$$\begin{aligned} A=\left[ \begin{array}{ccc} 0 &{} -1 &{} 2\\ 2 &{} 0 &{} -2\\ -1 &{} 1 &{} 0 \end{array} \right] ,\quad b=(-3,6,-1 )^T. \end{aligned}$$

A linear constraint $x \le (0,10,10)^T$ is also added.

By solving problems (1) and (2), we have $u=(0,1,2)^T$, $v=(0,3,3)^T$ and ${T}=[u,v]$. Since $u_{1}=v_{1}=0$, we know $x_1=0$. Using Remark 1, a new 2-dimension quadratic program with linear complementarity constraints can be obtained. Using the proposed conic approximation algorithm, we obtain an approximate optimal solution $(0,1,3)^T$ with an approximation optimal value 93.9998 in 12 iterations. The CPU time is 6.0506 s.

Example 3

Consider an example from [11]. This example dose not completely fit the form of problem (QLCP), but it still can be solved by the proposed algorithm.

$$\begin{aligned} \min \quad&\frac{1}{2} (y-y_d)^T H (y-y_d)+\frac{\alpha }{2}(u-u_d)^T M (u-u_d)\\ s.t. \quad&Nu-Ay \ge 0,\\&Nu-Ay-Dy \ge 0,\\&(Nu-Ay)^T (Nu-Ay-Dy)=0,\\&Bu \le b. \end{aligned}$$

where variables $y \in {\mathbb {R}}^2$ and $u \in {\mathbb {R}}$, $M=\alpha =b=1$, $H=D= \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}$, $B=1$, $A=\begin{bmatrix} 2&-1\\ -1&2 \end{bmatrix}$ and $N=\begin{bmatrix}3\\ -1\end{bmatrix}$. The objective function is convex.

• (1) When $y_d=(0,1)^T$ and $u_d=1$, using the proposed conic approximation algorithm, we obtain an approximate optimal solution $( 0.5,0,0.5)^T$ with an optimal value 0.7500 in 1 iteration. The CPU time is 0.1623 s.

• (2) When $y_d=(0,-3)^T$ and $u_d=1$, using the proposed conic approximation algorithm, we obtain an approximate optimal solution $(0.4832, -0.0085,0.4860)^T$ with an optimal value 4.7233 in 79 iterations. The CPU time is 48.3613 s.

• (3) When $y_d=(0,1)^T$ and $u_d=0$, using the proposed conic approximation algorithm, we obtain an approximate optimal solution $(0.0010,-0.0000,0.0010)^T$ with an optimal value 0.5000 in 1 iteration. The CPU time is 0.1561 s.

• (4) When $y_d=(0,-\frac{1}{3})^T$ and $u_d=0$, using the proposed conic approximation algorithm, we obtain an approximate optimal solution $(-0.0475,-0.0095, -0.0285 )^T$ with an optimal value 0.0540 in 149 iterations. The CPU time is 83.5579 s.

Example 4

Consider the following example whose objective function and constraints are the same as those in Example 1 except that there is one more convex quadratic constraint:

$$\begin{aligned} \min \quad&-x_1^2-72x_1x_2+14x_2^2+53x_1-28x_2\\ s.t.\quad&x_2 \ge x_1 \ge 0,\\&x_1+x_2 \le 1,\\&x^T \left( \begin{bmatrix} -1&1\\ -1&-1 \end{bmatrix}x+\begin{bmatrix} 0\\ 1 \end{bmatrix}\right) =0,\\&x^T x \le 3/5. \end{aligned}$$

The optimal solution is $(0.5,0.5)^T$ and the optimal value is $-2.25$. We solve the problem using the proposed conic approximation algorithm. After taking 20 iterations, we can obtain an approximate optimal solution $( 0.5002,0.5002)^T$ with an optimal value $-2.2567$. The CPU time is 13.7047 s.

Table 1 Beasley instances [4] in Biq Mac Library [36]

Table 2 Billionnet and Elloumi instances [6] in Biq Mac Library [36]

Table 3 Randomly generated instances

Table 4 MAX-CUT instances generated using rudy [30] in Biq Mac Library [36]

Example 5

BQP and MAX-CUT problems. As stated in Sect. 3.1, BQP and MAX-CUT are binary quadratic programming problems which can be formulated as (QLCP). These problems are in general NP-hard and are usually used for efficiency test. We choose some BQP and MAX-CUT benchmarks in Biq Mac Library [36] to test the proposed conic approximation algorithm (CAA) through comparison with two existing algorithms - QCR and Q-MIST, where QCR represents a branch-and-bound method of [26] with lower bounds provided by the semidefinite relaxation proposed in [6] and Q-MIST is an abbreviation of the “Algorithm Q-MIST” in [7].

When CAA is applied to solve BQP, we may obtain an upper bound in each iteration by setting

$$\begin{aligned} x_i= {\left\{ \begin{array}{ll} 1, &{}z_i^*>1/2 \\ 0, &{}z_i^*\le 1/2, \quad {\mathrm{for}}\quad i=1,2,\ldots ,n, \end{array}\right. } \end{aligned}$$

(9)

as a feasible solution, where $z_i^*$ is the sensitive point obtained in Step 1 of CAA. For BQP problems, our testing instances include those Beasley [4] instances in Biq Mac Library [36], Billionnet and Elloumi [6] instances in Biq Mac Library [36], and some randomly generated instances. Each randomly generated BQP instance has an $n \times n$ real symmetric matrix Q with $Q_{ij}=Q_{ji}$ being uniformly distributed over [$-50,50$], and $f \in {\mathbb {R}}^n$ with $f_i$ being uniformly distributed over [$-100,100$]. The problem size n (number of discrete variables) goes from 10 to 120 with 20 instances being generated for each n. For MAX-CUT problems, testing instances are generated using rudy [30] shown in Biq Mac Library [36].

In the numerical experiments, each algorithm is terminated when the relative error $({\frac{|{\mathrm{upper bound-lower bound}}|}{|{\mathrm{lower bound}}|}})$ is less than 0.1 % or the iterations becomes greater than a maximum number, which is set to be 1000 for CAA and 200,000 for both“QCR” and “Q-MIST”. The computational results are reported in Tables 1, 2, 3 and 4, in which the symbol “-” means the instance cannot be solved within the given maximum iterations and “$\sharp$” indicates the actual number of iterations in Tables 1, 2, 4 and “the average number of 20 instances” in Table 3.

Some observations can be made from Tables 1, 2, 3 and 4:

• 1. In general, QCR is less effective than the proposed CAA and Q-MIST in solving BQP and MAX-CUT problems in our experiment, in particular, for large size problems.

• 2. For BQP problems, Table 2 shows that the proposed CAA clearly outperfoms Q-MIST for Billionnet and Elloumi instances [6] in Biq Mac Library [36], in particular, CAA runs orders faster than Q-MIST when $n = 120$. Table 1 shows that, for Beasley instances [4] in Biq Mac Library [36], Q-MIST outperforms CAA when $n=50$, but the situation reverts when n grows to 100. The same performance is further evidenced in Table 3 for those randomly generated instances with $n > 90$. Therefore, the proposed CAA is the most effective one for solving large-size BQP problems.

• 3. For MAX-CUT problems, Table 4 again shows that the proposed CAA clearly outperfoms Q-MIST in almost all of the instances, in particular, CAA runs orders faster than Q-MIST when $n > 80$.

• 4. The overall performance of the proposed CAA is the dominating one. CAA’s strategy of spending more computation time in each iteration for a tighter bound to reduce the total number of iterations works very well, in particular, for large-size problems.

5 Conclusion

In this paper, we have studied a quadratic program with linear complementarity constraints, its conic reformulation and conic dual problems. We have shown that when the feasible domain is nonempty and bounded, the conic reformulation problem becomes attainable. Since the conic reformulation problem is in general NP-hard, conic relaxations are further considered. Under the assumption that there exists a vector $x \in {\mathbb {R}}^n$ satisfying $x >0$ and $Ax+b >0$, we can further show that if $\frac{A+A^T}{2} \prec 0$, then both of the semidefinite relaxation and its dual for problem (QLCP) are strictly feasible. In this case, a primal-dual interior point approach becomes applicable for providing a lower bound in polynomial time. For more general cases, an adaptive conic approximation algorithm has been proposed with a convergence proof to find an optimal solution or an $\epsilon$-optimal solution to a quadratic optimization problem with bounded linear complementarity constraints. Numerical experiments supports the effectivess of the proposed conic approximation algorithm for large-size problems.