A semidefinite programming approach to robust truss topology optimization under uncertainty in locations of nodes

Abstract

This paper addresses truss topology optimization taking into account robustness to uncertainty in the truss geometry. Specifically, the locations of nodes are assumed not to be known precisely and the compliance in the worst case is attempted to be minimized. We formulate a semidefinite programming problem that serves as a safe approximation of this robust optimization problem. That is, any feasible solution of the presented semidefinite programming problem satisfies the constraints of the original robust optimization problem. Since a semidefinite programming problem can be solved efficiently with a primal-dual interior-point method, we can find a robust truss design efficiently with the proposed semidefinite programming approach. A notable property of the proposed approach is that the obtained truss is guaranteed to be stable. Numerical experiments are performed to illustrate that the optimal truss topology depends on the magnitude of uncertainty.

1 Introduction

Real-world structures inevitably encounter various uncertainties stemming from manufacturing variability, aging, degradation, limitation of knowledge of environments, etc. Reality can deviate from the design-base models and data. The concept of robustness to uncertainty is, therefore, central in structural design. This paper addresses truss topology optimization considering robustness to uncertainty in the geometry of a truss.

If reliable statistical property of uncertainty is available, then probabilistic reliability analysis can be performed. In such a case, reliability-based optimization can be employed in structural design; see, e.g., Beyer and Sendhoff (2007), Schuëller (2006), Schuëller and Jensen (2008) and Zang et al. (2005). In contrast, a possibilistic model of uncertainty might be applicable to problems without reliable stochastic information, because it requires only bounds for the input data to define the uncertainty and hence is often less information-intensive. In this paper we adopt a possibilistic model, rather than probabilistic one, to represent the uncertainty in the locations of nodes of a truss. The truss topology optimization problem, which attempts to minimize the maximum value of the compliance, is then treated within the framework of robust optimization (Ben-Tal and Nemirovski 1998; El Ghaoui et al. 1998), also called worst-case approach, bounded-but-unknown approach, or robust design optimization in structural optimization; see Ben-Tal et al. (2009) for comprehensive exposition of robust optimization.

Many studies have been done on robust optimization of structures under the assumption that uncertainty exists only in external loads. Early works include, among others, Elishakoff et al. (1994), Ganzerli and Pantelides (2000), Lombardi (1998) and Pantelides and Ganzerli (1998). The seminal work of Ben-Tal and Nemirovski (1997) considered the compliance minimization of a truss under uncertainty in the static external load. Specifically, the external load is assumed to take any value in a given ellipsoid centered at the origin. Then the maximal value of compliance (called the principal compliance by some authors (Cherkaev and Cherkaev 2003)) is minimized. Ben-Tal and Nemirovski (1997) showed that this robust optimization problem can be formulated as a semidefinite programming (SDP) problem. Under the same situation, the robust compliance optimization of a continuum was recast by (Takezawa et al. 2011) as a minimization problem of the maximum eigenvalue of a standard eigenvalue problem, provided that the stiffness matrix is nonsingular. Earlier, it was shown that the same robust optimization problem can be reformulated as a minimization problem of the maximum eigenvalue of a generalized eigenvalue problem; see Cherkaev (2003, 2008) and Brittain et al. (2012). The latter formulation was extended to the case where the center of the ellipsoid, that represents the uncertainty in the external load, is not necessarily at the origin (de Gournay et al. 2008). With this non-homogeneous model of uncertainty, it was shown that the robust compliance optimization of a truss can also be recast as an SDP problem; see Calafiore and Dabbene (2008) and Ben-Tal et al. (2009, section 8.2.2.2). Another extension of the SDP formulation for robust truss optimization is making use of some binary variables to address variation of truss topology in the course of optimization (Yonekura and Kanno 2010). Concerning structural performances other than compliance, a nonlinear SDP approach (Kanno and Takewaki 2006) and a mixed-integer linear programming approach (Kanno and Guo 2010) were proposed for robust truss optimization under load uncertainties. Here, a nonlinear SDP problem refers to an optimization problem of the form

$$\begin{array}{@{}rcl@{}} &\underset{\boldsymbol{x}}{\text{Minimize}} &\boldsymbol{b}^{\top} \boldsymbol{x} \end{array} $$

(1a)

$$\begin{array}{@{}rcl@{}} &\mathrm{subject \;\;to}\;\;\; &\mathit{G}(\boldsymbol{x}) \succeq \mathit{O},\;\; \end{array} $$

(1b)

$$\begin{array}{@{}rcl@{}} &&\boldsymbol{h}(\boldsymbol{x}) =\mathbf{0} , \end{array} $$

(1c)

where $\boldsymbol {x} \in \mathbb {R}^{n}$ is a variable vector to be optimized, $\boldsymbol {b}\in \mathbb {R}^{n}$ is a constant vector, $G:\mathbb {R}^{n} \to \mathcal {S}^{n}$ and ${\boldsymbol {h}}:\mathbb {R}^{n}\to \mathbb {R}^{l}$ are sufficiently smooth, $\mathcal {S}^{n}$ denotes the set of n × n real symmetric matrices and G(x) ≽ O means that matrix G(x) is positive semidefinite. If h is linear and G is given by

$${G}({\boldsymbol{x}}) = {C} - \sum\limits_{i=1}^{m} x_{i} {A}_{i} $$

with constant matrices A ₁,…, A _m, ${C} \in \mathcal {S}^{n}$, then problem (1) reduces to an SDP problem (which is also called a linear SDP problem by some authors to clarify the distinction from nonlinear SDP problems). We refer the reader to Anjos and Lasserre (2012) and Wolkowicz et al. (2000) for fundamentals of SDP; particularly for nonlinear SDP problems, see, e.g., Jarre (2000), Kanzow et al. (2005), Noll et al. (2004), Shapiro (1997) and Yamashita and Yabe (2012).

Compared with uncertainty in loads, studies addressing other sources of uncertainties in robust structural optimization have been rather limited. Concerning truss optimization, Guo et al. (2009) considered uncertainty in stiffness (or uncertainties in member cross-sectional areas) and formulated a nonlinear SDP problem that provides us with a safe approximation of the robust optimal solution. Besides the uncertainty in member cross-sectional areas, Guo et al. (2011) considered uncertainty in length of each member and formulated a nonlinear SDP problem as a safe approximation of the robust optimization problem. Also, the dynamic response under uncertain driving loads were handled in Guo et al. (2011). These nonlinear SDP formulations are considered extensions of the SDP formulation for computing a conservative bound for response of a structural system that possess various uncertainties (Kanno and Takewaki 2008, 2009).

Very recently increasing attention has been drawn to topology optimization of a continuum considering geometric uncertainties. In most of those studies, probabilistic approaches are adopted to address deviation of the geometry of the boundary of a continuum. Sigmund (2009) and Wang et al. (2011) proposed a robust topology optimization method considering uniform manufacturing errors. An application of such an uncertainty model is in representing errors in etching for MEMS (micro-electro-mechanical systems). This method takes into account errors stemming from uniform over-etching and uniform under-etching. Then the robust optimization problem is formulated according to the worst-case approach, where only three cases, i.e., the nominal, over-etched and under-etched cases, are considered. Schevenels et al. (2011) extended this method to the case where non-uniform manufacturing errors are considered in a probabilistic manner. The statistical moments of structural response were then estimated by Monte Carlo simulations. Since Monte Carlo simulation is time-consuming, the alternative methods were proposed by using stochastic perturbation (Lazarov et al. 2012b) and stochastic collocation (Lazarov et al. 2012a). Geometrical uncertainties have also been handled within the framework of level-set methods for topology optimization. Chen and Chen (2011) modeled the geometric uncertainty by combing the level-set equations with a random field of normal perturbation of the boundary. The statistical moments of structural response are then obtained by using the Karhunen–Loève expansion and the multivariate Gauss quadrature. As non-probabilistic approaches, Jang et al. (2012) considered uniform etching uncertainties within the framework of a level-set method. Also, Guo et al. (2013) modeled non-uniform uncertainty of the boundary geometry introducing a perturbation of a level-set function, where change in the structural volume due to the boundary perturbation is assumed to be bounded. Then the worst-case optimization problem was dealt with using the first-order approximation of structural performance, under the assumption that perturbation of the boundary is sufficiently small.

This paper is inspired by the work of Guest and Igusa (2008), in which the robust truss topology optimization under uncertainty in the truss geometry was dealt with in a probabilistic manner. There, the locations of nodes were assumed to be uncorrelated random variables and the expected value of the compliance was attempted to be minimized. Under the assumption that perturbation of node locations is sufficiently small, it was shown that the problem under consideration can be recast in the form of the optimization problem under load uncertainties using the notion of equivalent random forces.¹ In contrast, the present work addresses the compliance optimization of a truss with non-probabilistic uncertainty in the locations of nodes. Provided that node locations can take any value in a given ellipsoid, we attempt to minimize the worst value of the compliance of a truss, where design variables are the member cross-sectional areas. As pointed out by Guest and Igusa (2008), the robust compliance optimization with uncertain node locations is more difficult problem than that with uncertain external loads. In this paper we formulate an SDP problem that serves as a safe approximation of the original robust optimization problem, in the sense that the optimal solution of the SDP problem is feasible for the original robust optimization problem. Throughout the paper we assume small deformation and linear elasticity. Deviation of a node location from its nominal value can however be arbitrarily large. SDP is a class of convex optimization and the optimal solution of an SDP problem can be computed efficiently by using a primal-dual interior-point method (Anjos and Lasserre 2012; Wolkowicz et al. 2000). This is considered an advantage of the SDP approach developed in this paper over existing nonlinear SDP approaches to robust structural optimization, because nonlinear SDP problems formulated in Guo et al. (2009, 2011) and Kanno and Takewaki (2006) are nonconvex optimization problems and thereby quite difficult to be solved. As pointed out by Guest and Igusa (2008), uncertainties in nodal locations can possibly have significant effects in truss topology optimization, because the optimal truss obtained by the standard compliance optimization without taking into account uncertainties is often unstable. Indeed, we can show, under mild assumptions, that the optimal solution of the presented SDP problem is a stable truss.

The paper is organized as follows. Section 2 reviews an SDP formulation of the standard compliance optimization of a truss. We also present an explicit form of the stiffness matrix as a function of the node locations. Section 3 presents an SDP problem which serves as a safe approximation of the robust truss optimization under uncertainty in the locations of nodes. Section 4 explores two important properties of the presented SDP problem: The first is zeroing, i.e., the SDP problem coincides with the standard compliance optimization when the magnitude of uncertainty is set to zero and the second is stability of the truss obtained by solving the proposed SDP problem. Section 5 performs numerical experiments. Conclusions are drawn in Section 6. Appendix collects technical prerequisites.

A few words regarding notation. We use ${\mathcal {S}^{n}}$ to denote the set of n × n real symmetric matrices. For matrices X, $\mathrm {Y} \in \mathcal {S}^{n}$, notation X ≽ Y means that matrix X−Y is positive semidefinite. Particularly, notation X ≽ O means that X is positive semidefinite. We use I _n to denote the n × n identity matrix. For a block matrix, we often omit to write zero blocks. For instance, we write

The ℓ _p -norm (1 ≤ p ≤ ∞) of vector ${\boldsymbol {x}}\in \mathbb {R}^{n}$ is defined by

$$\| {\boldsymbol{x}} \|_{p} = \left\{\begin{array}{ll} \left( \sum\limits_{i=1}^{n} |x_{i}|^{p} \right)^{1/p} & \text{if } 1 \le p < \infty, \\ \max \{ |x_{1}|,\dots,|x_{n}| \} & \text{if } p= \infty. \end{array}\right. $$

For matrix $M \in \mathbb {R}^{m \times n}$, the operator norm of M induced by the Euclidean norm is defined by

$$\| M \|_{2} = \max_{{\boldsymbol{x}}\ne {\boldsymbol{0}}}{\frac{\|M{\boldsymbol{x}}\|_{2}}{\|{\boldsymbol{x}}\|_{2}}}. $$

Note that ∥M∥₂ is equal to the maximum singular value of M.

2 Fundamentals of compliance optimization

This section summarizes fundamentals of the standard compliance optimization of a truss structure, where issues of uncertainty are not taken into account. Attention is focused on the SDP formulation due to Ben-Tal and Nemirovski (1997). This formulation serves as a basis of our robust optimization approach that will be developed in Section 3. Section 2.1 introduces our notation for truss topology optimization. The stiffness matrix is expressed as a function of the node locations. This expression is extremely useful in the latter sections for development and analysis of our robust optimization approach. Section 2.2 recalls the SDP formulation of the conventional minimization problem of the compliance of a truss under the volume constraint.

2.1 Explicit formulation of stiffness matrix in terms of locations of nodes

Following the conventional ground structure approach, consider a truss consisting of many candidate members connected by nodes. Throughout the paper we assume small deformation and linear elasticity. Let d denote the dimension of space, i.e., d = 2 for a planar truss and d = 3 for a spatial truss. We use $\mathcal {V}$ and $\mathcal {E} \subseteq \mathcal {V} \times \mathcal {V}$ to denote the set of nodes and the set of members of the truss, respectively, where $|\mathcal {V}|=n$ and $|{\mathcal {E}}|=m$. Note that ${\mathcal {V}}$ includes some supports. If we adopt terminology of the graph theory, ${\mathcal {V}}$ and ${\mathcal {E}}$ correspond to the set of vertices and the set of edges, respectively, of a given graph $G=({\mathcal {V}},{\mathcal {E}})$. For node $\nu \in {\mathcal {V}}$, we denote by ${\boldsymbol {x}}^{(\nu )} \in \mathbb {R}^{d}$ its location in the space. We use a _i ≥ 0 to denote the cross-sectional area of member $i \in {\mathcal {E}}$ and write ${\boldsymbol {a}}=(a_{1},\dots ,a_{m})^{\top } \in \mathbb {R}^{m}$. Given $G=({\mathcal {V}},{\mathcal {E}})$ and ${\boldsymbol {x}}^{(\nu )}\,(\forall v\in \mathcal {V})$, we attempt to optimize a.

Let p denote the number of degrees of freedom of displacements. Define q by $q = d n = d|{\mathcal {V}}|$. Since ${\mathcal {V}}$ includes supports, we have that p < q. Let $\mathcal {V} = \{\nu _{1},\nu _{2},\dots ,\nu _{n} \}$. Define $\boldsymbol {x}\in \mathbb {R}^{q}$ by

$${\boldsymbol{x}} = \left[\begin{array}{ll} {\boldsymbol{x}}^{(\nu_{1})} \\ {\vdots} \\ {\boldsymbol{x}}^{(\nu_{n})} \\ \end{array}\right], $$

which is a vector consisting of the location vectors of nodes. In Section 3 and the subsequent sections we shall suppose that x is not known precisely. We use l _i (x) to denote the undeformed length of member $i \in \mathcal {E}$ and write ${\boldsymbol {l}}({\boldsymbol {x}}) = (l_{1}({\boldsymbol {x}}),\dots ,l_{m}({\boldsymbol {x}}))^{\top }\in {\mathbb {R}}^{m}$.

Since we will suppose that the locations of supports as well as the locations of free nodes are uncertain, expression of the stiffness matrix will become rather cumbersome. For clarity of exposition, we use the following two different coordinate systems. The first one, denoted $\mathcal {C}$, is the conventional global coordinate system of the displacements. The dimension of $\mathcal {C}$ is hence equal to the number of degrees of freedom, p. In coordinate system $\mathcal {C}$, we use $\boldsymbol {u} \in \mathbb {R}^{p}$ to denote the vector of nodal displacements. The second one, denoted $\check {\mathcal {C}}$, is the coordinate system in which all the nodes are supposed to be free nodes. The dimension of $\check {\mathcal {C}}$ is hence equal to q, i.e., the size of vector x. We use $\check {\boldsymbol {u}}\in \mathbb {R}^{q}$ to denote the vector of nodal displacements in coordinate system $\check {\mathcal {C}}$.

Let $T \in {\mathbb {R}}^{p\times q}$ denote the transformation matrix from coordinate system $\check {{\mathcal {C}}}$ to coordinate system ${\mathcal {C}}$. Note that the set of nodes, $\mathcal {V}$, is partitioned into three subsets, the set of pin supports, the set of roller supports and the set of free nodes. We use $\mathcal {V}_{\text {fix}} \subseteq \mathcal {V}$ to denote the set of pin supports. Without loss of generality we may suppose that ${\mathcal {V}}_{{\text {fix}}} = \{\nu _{\hat {n}+1},\dots ,\nu _{n} \}$ and ${\mathcal {V}} \setminus {\mathcal {V}}_{{\text {fix}}} = \{\nu _{1},\dots ,\nu _{\hat {n}} \} \,(\hat {n} < n)$. Then matrix T is of the form

(2)

Here, T ^(ν _j ) is a d × d orthogonal matrix if node ν _j is free, while it is a rectangular matrix with full row rank if node ν _j is a roller support. Then the transformation is written as

$${\boldsymbol{u}} = T\check{\boldsymbol{u}}, $$

and its inverse is

$$ \check{\boldsymbol{u}} = T^{\top}{\boldsymbol{u}}. $$

(3)

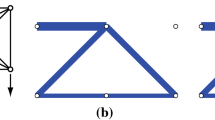
Example 1

Consider the truss shown in Fig. 1a. The truss lies in a plane, i.e., d = 2 and consists of m = 2 members connected to n = 3 nodes and hence q = 6. Node ν ₁ is a roller support, v ₂ is a free node and v ₃ is a pin support, i.e., $\mathcal {V}_{\text {fix}}=\{\nu _{3} \}$ and $\hat {n}=2$. The number of degrees of freedom of displacements is p = 3. Coordinate systems $\mathcal {C}$ and $\check {\mathcal {C}}$ can be defined, for instance, as depicted in Figs. 1a and b, respectively. The transformation matrix, $T \in \mathbb {R}^{3 \times 6}$, from $\check {{\mathcal {C}}}$ to ${\mathcal {C}}$ is given by

Thus T ^(ν ₁) is a 1 × 2 rectangular matrix and T ^(ν ₂) is a 2 × 2 orthogonal matrix.

Fig. 1

Definitions of the two coordinate systems. aCoordinate system C; and b coordinate system Č

In the following the stiffness matrix in the small deformation theory is formulated as an explicit function of the locations of nodes, x. We begin with the compatibility relation in coordinate system $\check {{\mathcal {C}}}$. Consider member $i=(\nu _{j},\nu _{k})\in {\mathcal {E}}$, which connects node ν _j and node ν _k . We use e _i to denote the elongation of this member. Observe that the directional cosine from node v _k towards node v _j is given by ${\boldsymbol {x}}^{(\nu _{j})}-{\boldsymbol {x}}^{(\nu _{k})}/l_{i}({\boldsymbol {x}})$. Define $\check {{\boldsymbol {b}}}_{i}({\boldsymbol {x}}) \in \mathbb {R}^{q}$ as a block-partitioned vector such that the block corresponding to node ν _j and ν _k are equal to the directional cosines of $\boldsymbol {x}^{(\nu _{j})}-\boldsymbol {x}^{(\nu _{k})}$ and $\boldsymbol {x}^{(\nu _{k})}-\boldsymbol {x}^{(\nu _{j})}$, respectively, and all the other blocks are zero vectors. Namely, $\check {\boldsymbol {b}}_{i}(\boldsymbol {x}) \in \mathbb {R}^{q}$ is of the form

(4)

and then the compatibility relation between e _i and $\check {{\boldsymbol {u}}}$ is given by

$$ e_{i} = \check{{\boldsymbol{b}}}_{i}({\boldsymbol{x}})^{\top}\check{{\boldsymbol{u}}}. $$

(5)

We define the stiffness matrix respect to coordinate system ${\mathcal {C}}$ as usual. By performing coordinate transformation (3), (5) is reduced to

$$ e_{i} = (T \check{{\boldsymbol{b}}}_{i}({\boldsymbol{x}}))^{\top} {\boldsymbol{u}}. $$

(6)

Let s _i denote the axial force of member i. Since linear elasticity is assumed, the constitutive law is given by

$$ s_{i} = \frac{E a_{i}}{l_{i}({\boldsymbol{x}})}e_{i} , $$

(7)

where E is the Young modulus. From (6) and (7), the stiffness matrix of the truss, denoted $K(\boldsymbol {a};\boldsymbol {x}) \in \mathcal {S}^{p}$, is written as

$$ K({\boldsymbol{a}};{\boldsymbol{x}}) = \sum\limits_{i \in {\mathcal{E}}} \frac{E a_{i}}{l_{i}({\boldsymbol{x}})^{3}} \left(T \check{{\boldsymbol{b}}}_{i}({\boldsymbol{x}})\right) \left(T \check{{\boldsymbol{b}}}_{i}({\boldsymbol{x}})\right)^{\top}. $$

(8)

Finally, we reduce $\check {{\boldsymbol {b}}}_{i}({\boldsymbol {x}})$ in (8) to a form useful in the subsequent discussions. Define $J_{i} \in \mathcal {S}^{q}\,(i \in \mathcal {E})$ as

(9)

i.e., it is a constant block matrix such that only the blocks related to nodes ν _j and ν _k are nonzero matrices. Then $\check {\boldsymbol {b}}_{i}(\boldsymbol {x})$ defined by (4) can be expressed as

$$ \check{{\boldsymbol{b}}}_{i}({\boldsymbol{x}}) = \frac{1}{l_{i}({\boldsymbol{x}})}J_{i}{\boldsymbol{x}}. $$

(10)

Substitution of (10) into (8) yields

$$ K({\boldsymbol{a}};{\boldsymbol{x}}) = \sum\limits_{i \in {\mathcal{E}}} \frac{E a_{i}}{l_{i}({\boldsymbol{x}})^{3}} (T J_{i} {\boldsymbol{x}}) (T J_{i} {\boldsymbol{x}})^{\top}. $$

(11)

We will use this form in the subsequent sections.

Note that coordinate system $\check {{\mathcal {C}}}$ is never used in the remainder of the paper. The global coordinate system is always taken as $\mathcal {C}$.

2.2 Semidefinite programming formulation for conventional compliance optimization

This section briefly recalls the conventional compliance optimization of trusses, without considering uncertainties and its SDP formulation in literature.

The compliance is a measure of flexibility of a structure. For given load f, member cross-sectional areas a and nodal coordinates x, the compliance of the truss is defined by

$$ \pi({\boldsymbol{a}};{\boldsymbol{x}}) = \sup\left\{ 2{\boldsymbol{f}}^{\top} {\boldsymbol{u}} - {\boldsymbol{u}}^{\top} K({\boldsymbol{a}};{\boldsymbol{x}}){\boldsymbol{u}} : {\boldsymbol{u}} \in {\mathbb{R}}^{p}\right\}. $$

(12)

We write ${\boldsymbol {x}} = \tilde {{\boldsymbol {x}}}$ to clarify that, in this section, x is supposed to be known without uncertainties. In the latter sections, $\tilde {{\boldsymbol {x}}}$ will be interpreted as the nominal value, or the best estimate, of x. The minimization problem of compliance under the volume constraint is then formulated as

$$\begin{array}{@{}rcl@{}} \underset{{\boldsymbol{a}}, \text{\textit{w}}}{\text{Minimize}} &&\;\;\text{\textit{w}} \end{array} $$

(13a)

$$\begin{array}{@{}rcl@{}} \text{subject to} &&\;\;\text{\textit{w}} \ge \pi({\boldsymbol{a}}; \tilde{{\boldsymbol{x}}}) \end{array} $$

(13b)

$$\begin{array}{@{}rcl@{}} &&\;\;{\boldsymbol{l}}(\tilde{{\boldsymbol{x}}})^{\top}{\boldsymbol{a}} \le V_{\mathrm{u}}, \end{array} $$

(13c)

$$\begin{array}{@{}rcl@{}} &&\;\;{\boldsymbol{a}} \ge {\boldsymbol{0}}, \end{array} $$

(13d)

where V _u > 0 is a specified upper bound for the structural volume. Note that ${\boldsymbol {a}} \in \mathbb {R}^{m}$ and $w \in \mathbb {R}$ are variables to be optimized. Constraint (13c) is satisfied with equality at the optimal solution of problem (13).

It is known that problem (13) can be recast as an SDP problem. More specifically, constraint (13b) can be written as a linear matrix inequality in terms of a and w. This fact corresponds to a special case of Lemma 2.2 of Ben-Tal and Nemirovski (1997), where the robust compliance constraint under load uncertainty was treated. Below we briefly restate this result for a fixed load. This SDP formulation serves as a basis of our SDP formulation for robust optimization developed in Section 3. From definition (12) of the compliance, we can see that constraint (13b) reads

$$\text{\textit{w}} \ge\sup \left\{2{\boldsymbol{f}}^{\top} {\boldsymbol{u}} - {\boldsymbol{u}}^{\top} K{\boldsymbol{u}} : {\boldsymbol{u}} \in {\mathbb{R}}^{p} \right\} , $$

which is equivalently rewritten as

$$\text{\textit{w}} \ge 2{\boldsymbol{f}}^{\top} {\boldsymbol{u}} - {\boldsymbol{u}}^{\top} K{\boldsymbol{u}} \quad (\forall {\boldsymbol{u}} \in {\mathbb{R}}^{p}). $$

This inequality is written of the quadratic form

(14)

By applying Lemma 8 in Appendix, (14) is equivalently rewritten as

(15)

In short, (13b) is equivalent to (15).

As a consequence of the discussion above, the truss optimization problem in (13) can be rewritten equivalently as

$$\begin{array}{@{}rcl@{}} \text{(TO)}: & \underset{{\boldsymbol{a}}, \text{\textit{w}}}{\text{Minimize}} &{\mathit{w}} \end{array} $$

(16a)

(16b)

$$ {\kern4.2pc}\boldsymbol{l}(\tilde{{\boldsymbol{x}}})^{\top}{\boldsymbol{a}} \le V_{\mathrm{u}}, $$

(16c)

$$ {\kern4.2pc}{\boldsymbol{a}} \ge {\boldsymbol{0}}. $$

(16d)

In this problem, the objective function in (16a) is a linear function of w. Also, constraints (16c) and (16d) are linear inequality constraints on a. Since $\tilde {\boldsymbol {x}}$ is fixed, we can see from (11) that the stiffness matrix depends linearly on a ₁,…, a _m. Hence, constraint (16b) is a linear matrix inequality in terms of a and w. Therefore, problem (16) is an SDP problem.

3 Robust optimization and its safe approximation

This section explores a robust optimization method of a truss subjected to uncertainties in locations of nodes. Section 3.1 defines the robust truss optimization problem. In Section 3.2 we propose an SDP problem that serves as a safe approximation of this robust truss optimization problem.

3.1 Robust optimization under uncertainty in locations of nodes

Since structures in the real world inevitably encounter various uncertainties in geometry caused by manufacturing errors, aging, deterioration, etc., robustness to geometrical uncertainties should be taken into account in structural design. This section defines a deterministic (i.e., non-statistical) model of uncertainty in x and formulates a robust optimization problem of a truss subjected to the uncertainty. This problem is considered a robust counterpart of the compliance minimization problem formulated in Section 2.2.

Uncertainty in the locations of nodes, x, is modeled as follows. Let $\tilde {{\boldsymbol {x}}}\in {\mathbb {R}}^{q}$ denote the nominal value, or the best estimate, of x. Suppose that x can possibly take any value in a compact convex set as

$$ {\boldsymbol{x}} \in {\mathcal{X}}_{r} , \quad {\mathcal{X}}_{r} = \{ \tilde{{\boldsymbol{x}}} + A{\boldsymbol{\zeta}} : \|{\boldsymbol{\zeta}}\|_{2} \le r \}. $$

(17)

Here, r ≥ 0 is a given constant, ${\boldsymbol {\zeta }} \in {\mathbb {R}}^{l}$ is a vector of uncertain variables that can take any value in the closed ball with radius r, i.e.,

$${\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r} , \quad {\mathcal{Z}}_{r} = \left\{ {\boldsymbol{\zeta}} \in {\mathbb{R}}^{l} : \|{\boldsymbol{\zeta}}\|_{2} \le r \right\} , $$

and $A\in {\mathbb {R}}^{q \times l}$ is a constant matrix satisfying

$$ \| A \|_{2} = 1. $$

(18)

Matrix A has a block structure corresponding to nodes ν ₁,…, ν _n as

$$ A = \left[\begin{array}{ll} A^{(\nu_{1})} \\ {\vdots} \\ A^{\nu} \\ \end{array}\right], $$

(19)

where $A^{(\nu )}\in {\mathbb {R}}^{d \times l}\,(\forall v\in {\mathcal {V}})$. For instance, by putting A = I _q , we suppose that the locations of all nodes are uncertain. As another example, if the location of node ν _j is supposed to be known without uncertainty, then we put A ^(ν _j ) = O. Constant r ≥ 0 is called the uncertainty parameter, which expresses the level of uncertainty in the following sense (Ben-Haim 2006):

• (i) ${\mathcal {X}}_{0} = \{ \tilde {{\boldsymbol {x}}}\}$ and

• (ii) r ≤ r ^′ implies ${\mathcal {X}}_{r} \subseteq {\mathcal {X}}_{r^{\prime }}$.

That is, (i) only the nominal case is considered at r = 0 and (ii) the range of possible scenarios of nodal locations increases as r increases.

Recall that the conventional topology optimization problem has been formulated as (TO) in (16). In the following we formulate a robust counterpart of (TO), when x undergoes the uncertainty in (17). Note that, in (TO), constraints (16b) and (16c) involve x. Both constraints can be converted to robust constraints. However, compared with the compliance constraint in (16b), the volume constraint in (16c) is considered a soft constraint, because the structural performance is related only to the compliance constraint. For this reason, throughout the paper we evaluate the structural volume at the nominal member lengths and, thence, constraint (16c) is not converted to a robust constraint. Only constraint (16b) is required to be satisfied all possible x’s. Then the robust topology optimization problem is formulated as

$$\begin{array}{@{}rcl@{}}&&{}\text{(RTO)}: \\ &&\underset{{\boldsymbol{a}}, \text{\textit{w}}}{\text{Minimize}}{\kern10pt} {\mathit{w}} \end{array} $$

(20a)

(20b)

$$ {\kern5pc}\boldsymbol{l}(\tilde{{\boldsymbol{x}}})^{\top}{\boldsymbol{a}} \le V_{\mathrm{u}}, $$

(20c)

$$ {\kern5pc}{\boldsymbol{a}} \ge {\boldsymbol{0}}. $$

(20d)

Here, ${\boldsymbol {a}} \in \mathbb {R}^{m}$ and w $\in \mathbb {R}$ are variables to be optimized.

In dealing with problem (20), a key is treatment of the stiffness matrix, K(a;x), in constraint (20b). Recall that K(a;x) is given by (11), where x is now supposed to follow the uncertainty model in (17), i.e., ${\boldsymbol {x}}=\tilde {{\boldsymbol {x}}}+{A}{\boldsymbol {\zeta }}$. Substitution of this equation into (11) yields

$$ K({\boldsymbol{a}};\tilde{{\boldsymbol{x}}}+A{\boldsymbol{\zeta}}) = \sum\limits_{i \in {\mathcal{E}}} a_{i} \kappa_{i}({\boldsymbol{\zeta}}) ({\boldsymbol{b}}_{i} + C_{i}{\boldsymbol{\zeta}}) ({\boldsymbol{b}}_{i} + C_{i}{\boldsymbol{\zeta}})^{\top} , $$

(21)

where $\kappa _{i}:\mathbb {R}^{l} \to \mathbb {R}$, ${\boldsymbol {b}}_{i} \in \mathbb {R}^{p}$ and $C_{i} \in \mathbb {R}^{p \times l}$ are defined by

$$ \kappa_{i}({\boldsymbol{\zeta}}) = \frac{E}{l_{i}(\tilde{{\boldsymbol{x}}}+A{\boldsymbol{\zeta}})^{3}} , $$

(22)

$$ {\boldsymbol{b}}_{i} = T J_{i} \tilde{{\boldsymbol{x}}} , $$

(23)

$$ C_{i} = T J_{i} A. $$

(24)

Particularly, at the nominal value, (21) is reduced to

$$ K({\boldsymbol{a}};\tilde{{\boldsymbol{x}}}) = \sum\limits_{i \in {\mathcal{E}}} a_{i} \kappa_{i}({\boldsymbol{0}}) {\boldsymbol{b}}_{i} {\boldsymbol{b}}_{i}^{\top}. $$

(25)

The difficulty of problem (20) stems from the high nonlinearity of the formulation in (21).

3.2 Safe approximation of robust optimization

The robust topology optimization problem (20) formulated in Section 3.1 is not tractable computationally, because it has infinitely many positive-semidefinite constraints in (20b). This motivates us to construct an optimization problem that serves as a safe approximation of problem (20) and can be solved easily. This section formulates an SDP problem, the optimal solution of which is guaranteed to satisfy all the constraints of the original robust optimization problem (20).

We first consider a lower bound for κ _i (ζ) defined by (22), when ζ is running through ${\mathcal {Z}}_{r}$. As seen in (21), κ _i (ζ) appears in the stiffness matrix as a coefficient. The following lemma, providing us with a lower bound, prepares our SDP formulation discussed in Theorem 1.

Lemma 1

Define $\breve {\kappa }_{i} \in \mathbb {R}$ by

$$ \breve{\kappa}_{i} = \frac{E}{(\tilde{l}_{i} + 2r)^{3}}. $$

(26)

Then we obtain $0 < \breve {\kappa }_{i} \le \min \{\kappa _{i}({\boldsymbol {\zeta }}) : {\boldsymbol {\zeta }}\in {\mathcal {Z}}_{r}\}$.

Proof

Since E > 0, $\tilde {l}_{i}>0$ and r ≥ 0 by definitions, it is clear that $\breve {\kappa }_{i} > 0$. With reference to (22) and (26), we see that the assertion of this lemma is obtained by showing

$$ l_{i}(\tilde{{\boldsymbol{x}}} + A {\boldsymbol{\zeta}}) \le \tilde{l}_{i} + 2r \quad (\forall {\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r}). $$

(27)

Recall that the location vector of node $v \in {\mathcal {V}}$ is given by

$${\boldsymbol{x}}^{(\nu)} = \tilde{{\boldsymbol{x}}}^{(\nu)} + {A}^{(\nu)} {\boldsymbol{\zeta}}. $$

Hence, concerning the length of member $i=(\nu _{j},\nu _{k})\in {\mathcal {E}}$, we obtain

$$\begin{array}{@{}rcl@{}} &&{}l_{i}(\tilde{{\boldsymbol{x}}}+A{\boldsymbol{\zeta}}) \\ &&= \| (\tilde{{\boldsymbol{x}}}^{(\nu_{j})}+A^{(\nu_{j})}{\boldsymbol{\zeta}}) -(\tilde{{\boldsymbol{x}}}^{(\nu_{k})}+A^{(\nu_{k})}{\boldsymbol{\zeta}}) \|_{2} \\ &&\le \| \tilde{{\boldsymbol{x}}}^{(\nu_{j})} - \tilde{{\boldsymbol{x}}}^{(\nu_{k})} \|_{2} + \|A^{(\nu_{j})}{\boldsymbol{\zeta}}\|_{2} + \|A^{(\nu_{k})}{\boldsymbol{\zeta}} \|_{2} \\ &&\le \tilde{l}_{i} + \|A^{(\nu_{j})}\|_{2} \|{\boldsymbol{\zeta}}\|_{2} + \|A^{(\nu_{k})}\|_{2} \|{\boldsymbol{\zeta}}\|_{2} , \end{array} $$

where the triangularity inequality and Lemma 6 (in Appendix) have been used. Furthermore, for any $v \in {\mathcal {V}}$, we have that

$$ \max \{ \|A^{(\nu)}\|_{2} \|{\boldsymbol{\zeta}}\|_{2} :{\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r} \} = \|A^{(\nu)}\|_{2} r $$

(28)

and

$$ \|A^{(\nu)}\|_{2}\le1 $$

(29)

due to assumption (18). By using (28) and (29), we obtain

$$\begin{array}{@{}rcl@{}} &&\hspace*{-8.9pt} \|A^{(\nu_{j})}\|_{2} \|{\boldsymbol{\zeta}}\|_{2}+ \|A^{(\nu_{k})}\|_{2} \|{\boldsymbol{\zeta}}\|_{2} \\&& \le (\|A^{(\nu_{j})}\|_{2} + \|A^{(\nu_{k})}\|_{2}) r\le 2r\quad (\forall {\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r}), \end{array} $$

and hence (27) holds. □;

We construct a safe approximation of the robust optimization problem by making use of value $\breve {\kappa }_{i}$ in Lemma 1. By using b _i given by (23), define $B_{i} \in {\mathbb {R}}^{p\times m}\,(\forall i \in {\mathcal {E}})$ by

$$\begin{array}{@{}rcl@{}} B_{i} = \begin{array}{c}\left[\,\,\,\, |\boldsymbol{b}_{i}|\,\,\,\, \right],\vspace*{-3pt}\end{array}\\ \begin{array}{c}\vspace*{-3pt} {}\uparrow \\ {}i\\ \end{array} \end{array} $$

(30)

i.e., it is a constant block matrix such that the ith column is equal to b _i and the other columns are zero vectors. Consider the following optimization problem:

$$\begin{array}{@{}rcl@{}} \mathrm{(ARTO)}: \\ &{}\underset{\boldsymbol{a}, \text{\textit{w}},{\boldsymbol{\lambda}}}{\text{Minimize}} &\mathit{w} \end{array} $$

(31a)

(31b)

$$ {\kern4pc}{\boldsymbol{l}}(\tilde{{\boldsymbol{x}}})^{\top}{\boldsymbol{a}} \le V_{\mathrm{u}}, $$

(31c)

$$ {\kern4pc}{\boldsymbol{a}} \ge {\boldsymbol{0}}, $$

(31d)

$$ {\kern4pc}{\boldsymbol{\lambda}} \ge {\boldsymbol{0}}. $$

(31e)

This is an SDP problem in variables ${\boldsymbol {a}} \in \mathbb {R}^{m}$, $w \in \mathbb {R}$ and ${\boldsymbol {\lambda }} \in \mathbb {R}^{m}$, because constraint (31b) is a linear matrix inequality in terms of these variables.

Problem (31) provides us with a conservative approximation of the optimal solution of (RTO) in (20). This key issue is formally proved in the following theorem.

Theorem 1

(ARTO) in (31) is a safe approximation of (RTO) in (20) , in the sense that if $({\boldsymbol {a}},\text {\textit {w}},{\boldsymbol {\lambda }})\in \mathbb {R}^{m} \times \mathbb {R} \times \mathbb {R}^{m}$ is feasible for (ARTO) then (a, w) is feasible for (RTO).

Proof

We shall show that ( a, w) is feasible for (20b) if there exists ${\boldsymbol {\lambda }} \in \mathbb {R}^{m}$ satisfying (31b) and (31e).

For simple presentation, we use the following notation. Define $\varOmega ({\boldsymbol {a}};{\boldsymbol {\zeta }}) \in \mathcal {S}^{p+1}$ by

(32)

so that constraint (20b) can be written as

$$ \varOmega({\boldsymbol{a}};{\boldsymbol{\zeta}}) \succeq {O} \quad (\forall {\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r}). $$

(33)

For each $i\in {\mathcal {E}}$, define $\hat {{\boldsymbol {b}}}_{i} \in {\mathbb {R}}^{p+1}$, $\hat {B}_{i} \in {\mathbb {R}}^{(p+1)\times m}$ and $\hat {C}_{i} \in {\mathbb {R}}^{(p+1)\times l}$ by

$$\begin{array}{@{}rcl@{}} \hat{{\boldsymbol{b}}}_{i} = \left[\frac{0}{\boldsymbol{b}_{i}}\right], \end{array} $$

(34a)

$$\begin{array}{@{}rcl@{}} \hat{B}_{i} = \left[\frac{\boldsymbol{0}^{\top}}{B_{i}} \right], \end{array} $$

(34b)

$$\begin{array}{@{}rcl@{}} \hat{C}_{i} = \left[\frac{\boldsymbol{0}^{\top}}{C_{i}}\right], \end{array} $$

(34c)

where b _i , B _i and C _i have been defined by (23), (30), (24), respectively. By using these vectors and matrices, define $\varOmega _{0}\in \mathcal {S}^{p+1}$ and $\varOmega _{i}({\boldsymbol {\zeta }})\in \mathcal {S}^{p+1}\,(i \in {\mathcal {E}})$ by

(35)

$$\varOmega_{i}({\boldsymbol{\zeta}}) =(\hat{{\boldsymbol{b}}}_{i} + \hat{C}_{i}{\boldsymbol{\zeta}}) (\hat{{\boldsymbol{b}}}_{i} + \hat{C}_{i}{\boldsymbol{\zeta}})^{\top}. $$

(36)

With reference to (21), we see that Ω(a;ζ) in (32) can be written as

$$ \varOmega({\boldsymbol{a}};{\boldsymbol{\zeta}}) = \varOmega_{0} + \sum\limits_{i\in{\mathcal{E}}}a_{i} \kappa_{i}({\boldsymbol{\zeta}})\varOmega_{i}({\boldsymbol{\zeta}}). $$

(37)

With the preparation above we derive a sufficient condition for constraint (20b), i.e., for (33). By definition of a positive semidefinite matrix, (33) is equivalently rewritten as

$${\boldsymbol{\xi}}^{\top} \varOmega({\boldsymbol{a}};{\boldsymbol{\zeta}}){\boldsymbol{\xi}} \ge 0 \quad (\forall {\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r},\ \forall {\boldsymbol{\xi}} \in {\mathbb{R}}^{p+1}). $$

This condition is also equivalent to

$$ \min_{{\boldsymbol{\zeta}}} \{ {\boldsymbol{\xi}}^{\top} \varOmega({\boldsymbol{a}};{\boldsymbol{\zeta}}){\boldsymbol{\xi}} : {\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r}\} \ge 0 \quad (\forall {\boldsymbol{\xi}} \in {\mathbb{R}}^{p+1}). $$

(38)

Substitution of (37) into (38) yields

$$\begin{array}{@{}rcl@{}} &&{}\min_{{\boldsymbol{\zeta}}} \left\{ {\boldsymbol{\xi}}^{\top} \varOmega_{0}{\boldsymbol{\xi}} +\sum\limits_{i\in{\mathcal{E}}} a_{i} \kappa_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}}^{\top} \varOmega_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}} :{\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r} \right\} \ge 0 \\ && \qquad\qquad (\forall {\boldsymbol{\xi}} \in {\mathbb{R}}^{p+1}). \end{array} $$

(39)

Condition (39) holds if

$$\begin{array}{@{}rcl@{}} &&{}{\boldsymbol{\xi}}^{\top} \varOmega_{0}{\boldsymbol{\xi}} +\sum\limits_{i\in{\mathcal{E}}}a_{i} \min_{{\boldsymbol{\zeta}}} \{\kappa_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}}^{\top} \varOmega_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}} :{\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\}\ge 0 \\ && {\kern3pc}(\forall {\boldsymbol{\xi}}\in {\mathbb{R}}^{p+1} ) \end{array} $$

(40)

is satisfied. Thus we see that (40) is a sufficient condition for (20b).

We next deal with the minimization problems included in (40). For fixed ${\boldsymbol {\xi }}\in \mathbb {R}^{p+1}$, we obtain

$$\begin{array}{@{}rcl@{}} &&{}\min \{ \kappa_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}}^{\top} \varOmega_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}} : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r} \} \\ &&{\kern-9.5pt}\ge \min \{ \kappa_{i}({\boldsymbol{\zeta}}) : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r} \} \min \{ {\boldsymbol{\xi}}^{\top} \varOmega_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}} : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\} \\ &&{}D\ge \breve{\kappa}_{i} \min \{{\boldsymbol{\xi}}^{\top} \varOmega_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}}: {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\} , \end{array} $$

(41)

where the last inequality follows from Lemma 1. Substitution of (36), i.e., the definition of Ω _i , into (41) yields

$$\begin{array}{@{}rcl@{}} &&{}\breve{\kappa}_{i}\min\left\{ {\boldsymbol{\xi}}^{\top} \varOmega_{i}({\boldsymbol{\zeta}}){\boldsymbol{\xi}}: {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\right\} \\ &&= \breve{\kappa}_{i} \min\left\{{\boldsymbol{\xi}}^{\top} (\hat{{\boldsymbol{b}}}_{i} + \hat{C}_{i}{\boldsymbol{\zeta}}) (\hat{{\boldsymbol{b}}}_{i} + \hat{C}_{i}{\boldsymbol{\zeta}})^{\top}{\boldsymbol{\xi}} : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r} \right\} \\ &&= \breve{\kappa}_{i} {\boldsymbol{\xi}}^{\top} \hat{{\boldsymbol{b}}}_{i} \hat{{\boldsymbol{b}}}_{i}^{\top} {\boldsymbol{\xi}} \\ && \qquad {+} \breve{\kappa}_{i} \min\left\{ 2 {\boldsymbol{\xi}}^{\top} \hat{C}_{i} {\boldsymbol{\zeta}} \hat{{\boldsymbol{b}}}_{i} {\boldsymbol{\xi}} + {\boldsymbol{\xi}}^{\top} \hat{C}_{i} {\boldsymbol{\zeta}} {\boldsymbol{\zeta}}^{\top} \hat{C}_{i}^{\top} {\boldsymbol{\xi}} : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\right\} \\ &&\ge \breve{\kappa}_{i} \left( {\boldsymbol{\xi}}^{\top} \hat{{\boldsymbol{b}}}_{i}\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}} + 2 |\hat{{\boldsymbol{b}}}_{i} {\boldsymbol{\xi}}| \min \left\{ (\hat{C}_{i}^{\top} {\boldsymbol{\xi}})^{\top} {\boldsymbol{\zeta}} : {\boldsymbol{\zeta}} \in {\mathcal{Z}}_{r} \right\} \right.\\ &&\left. \qquad {}+\min\left\{{\boldsymbol{\xi}}^{\top} \hat{C}_{i}{\boldsymbol{\zeta}}{\boldsymbol{\zeta}}^{\top} \hat{C}_{i}^{\top}{\boldsymbol{\xi}} : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\right\} \right) \\ &&\ge \breve{\kappa}_{i} \left({\boldsymbol{\xi}}^{\top} \hat{{\boldsymbol{b}}}_{i}\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}} -2r |\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}}| \|\hat{C}_{i}^{\top}{\boldsymbol{\xi}}\|_{2}\right) \\ &&= \breve{\kappa}_{i} \left( {\boldsymbol{\xi}}^{\top} \hat{{\boldsymbol{b}}}_{i}\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}} -2r\max_{\eta_{i}\in{\mathbb{R}}} \left\{\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}} \eta_{i} : |\eta_{i}| \le \|\hat{C}_{i}^{\top}{\boldsymbol{\xi}}\|_{2} \right\} \right).\\ \end{array} $$

(42)

Here, the second inequality follows from Lemma 5 (in Appendix) and

$$\begin{array}{@{}rcl@{}} &&{}\min\left\{ {\boldsymbol{\xi}}^{\top} \hat{C}_{i}{\boldsymbol{\zeta}}{\boldsymbol{\zeta}}^{\top} \hat{C}_{i}^{\top}{\boldsymbol{\xi}} : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\right\} \\ &&= \min \left\{ ({\boldsymbol{\zeta}}^{\top} \hat{C}_{i}^{\top}{\boldsymbol{\xi}})^{2} : {\boldsymbol{\zeta}}\in{\mathcal{Z}}_{r}\right\}=0 , \end{array} $$

while the last equality follows from Lemma 4 (in Appendix). It follows from (41) and (42) that (40) holds if

$$\begin{array}{@{}rcl@{}} &&{}{\boldsymbol{\xi}}^{\top} \varOmega_{0}{\boldsymbol{\xi}} \\ &&+\sum\limits_{i\in{\mathcal{E}}}a_{i} \breve{\kappa}_{i} \left( {\boldsymbol{\xi}}^{\top} \hat{{\boldsymbol{b}}}_{i}\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}} -2r\max_{\eta_{i}\in{\mathbb{R}}} \{\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}} \eta_{i} : |\eta_{i}| \le \|\hat{C}_{i}^{\top}{\boldsymbol{\xi}}\|_{2} \} \right) \\ && \ge 0 \quad (\forall {\boldsymbol{\xi}} \in {\mathbb{R}}^{p+1} ) \end{array} $$

(43)

is satisfied, i.e., (43) is a sufficient condition for (40). Condition (43) is equal to the condition that, for variables $\boldsymbol {\xi } \in \mathcal {R}^{p+1}$ and $\boldsymbol {\eta } \in \mathcal {R}^{m}$, the implication

$$\begin{array}{@{}rcl@{}} &&{}|\eta_{i}| \le \|\hat{C}_{i}^{\top}{\boldsymbol{\xi}}\|_{2} \ (\forall i\in{\mathcal{E}}) \\ && \Rightarrow\quad {\boldsymbol{\xi}}^{\top} \varOmega_{0}{\boldsymbol{\xi}} +\sum\limits_{i\in{\mathcal{E}}}a_{i} \breve{\kappa}_{i} \left({\boldsymbol{\xi}}^{\top} \hat{{\boldsymbol{b}}}_{i}\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}} -2r\eta_{i}\hat{{\boldsymbol{b}}}_{i}^{\top}{\boldsymbol{\xi}}\right) \ge 0 \end{array} $$

(44)

holds. Note that both sides of implication (44) are expressed as quadratic inequalities in terms of ξ and η. Indeed, by using constant matrices $E_{i,i} \in \mathcal {S}^{m}\,(i \in {\mathcal {E}})$ defined by

(45)

we can rewrite (44) as

(46)

Implication (46) clearly consists of quadratic inequalities of ξ and η. Then by applying Lemma 9 (in Appendix) we see that (46) holds if there exist nonnegative real numbers λ ₁,…, λ _m satisfying

(47)

By substituting the definitions of $\hat {{\boldsymbol {b}}}_{i}$, $\hat {B}_{i}$ and $\hat {C}_{i}$ (in (34)) and that of Ω ₀ (in (35)) into (47), this sufficient condition for (46) is written as

(48)

We thus conclude that condition (48), which corresponds to constraints (31b) and (31e), is a sufficient condition for constraint (20b). □;

Theorem 1 asserts that the optimal solution of (ARTO) (in (31)) is feasible for the original robust optimization problem, (RTO) in (20). Thus (ARTO) serves as a conservative approximation of (RTO). It is difficult to deal with (RTO) computationally, because (RTO) has infinitely many constraints in (20b). In contrast, (ARTO) is a conventional SDP problem and it can be solved efficiently with a primal-dual interior-point method. Since we do no resort to any approximation for formulating the stiffness matrix with uncertain node locations, conservativeness of the obtained solution is guaranteed for arbitrary large r, as shown in Theorem 1. Instead, the optimality of the obtained solution is not guaranteed, i.e., the optimal solution of (ARTO) is not optimal for (RTO) in general.

Remark 1

The size of (ARTO) in (31) is larger than the size of (TO) in (16). The number of variables is increased from m+1 to 2m+1. The size of matrix subjected to the positive-semidefinite constraint is increased from (p+1) × (p+1) to (p + m+1) × (p + m+1). However, all the coefficient matrices in (31b) are sparse matrices.

Remark 2

In the proof of Theorem 1 we have shown that (43) is a sufficient condition for constraint (20b). In this process, we use the fact that (40) is a sufficient condition for (39). Unlike (39), minimization in (40) is performed for each $i \in \mathcal {E}$. This means that, in (40), effect of uncertainty on each member is considered independently. This overestimates the effect of uncertainty, because the location of one node generally affects all members connected to that node. In other words, in (40) we consider an incompatible situation such that two members connected by a node in the nominal scenario are supposed not necessarily to be connected in the worst scenario. For this reason, it might probably happen that the optimal solution of (ARTO) is too conservative, compared with the optimal solution of (RTO). In Section 5.3, we shall use a small numerical example to investigate tightness of approximation of (ARTO).

4 Two properties of the proposed formulation

This section explores favorable properties of (ARTO), proving two theorems. The first, Theorem 2, establishes that, when r = 0, (ARTO) coincides with the standard compliance optimization, i.e., (TO) in (16). In this sense (ARTO) can be considered a natural extension of (TO). The second, Theorem 3, establishes, under fairly general conditions, that the truss obtained as the optimal solution of (ARTO) is stable. This might be considered a significant advantage of the proposed formulation, because the optimal solution of (TO) is often unstable and an unstable truss has no robustness against uncertainties in external forces as well as locations of nodes.

4.1 Nominal case

This section discusses a particular case, r = 0, which means that no uncertainty is supposed.

When r = 0, we can show that problem (31), which serves as a conservative approximation of the robust truss optimization problem, coincides with the nominal truss optimization problem, i.e., problem (16). More precisely, at r = 0, these two problems share the same optimal value and the optimal truss design of one problem is also optimal for the other problem. In this sense, the proposed formulation, (31), is considered a natural extension of the nominal optimization problem, (16). This equivalence follows straightforwardly from Theorem 2 presented below.

Theorem 2

Suppose r = 0. If ${\boldsymbol {a}}\in \mathbb {R}^{m}$ and ${\boldsymbol {\lambda }}\in \mathbb {R}^{m}$ satisfy (31b) and (31e) , then a satisfies (16b) . Conversely, if ${\boldsymbol {a}}\in \mathbb {R}^{m}$ satisfies (16b) , then there exists ${\boldsymbol {\lambda }}\in \mathbb {R}^{m}$ such that a and λ satisfy (31b) and (31e).

Proof

We begin by considering constraint (31b) at r = 0. Recall that $\breve {\kappa }_{i}$ in (31b) is defined by (26). With reference to definition (22) of κ _i , we see that $\breve {\kappa }_{i} = \kappa _{i}({\boldsymbol {0}})$ holds at r = 0. Therefore, when r = 0, constraint (31b) reads

(49)

Since the left-hand side of (49) is a block-diagonal matrix, (49) is equivalent to

$$ \text{diag}({\boldsymbol{\lambda}}) \succeq O, $$

(50a)

(50b)

Note that (50a) is equivalent to (31e). On the other hand, (16b) is rewritten as follows. Substitution of (25) into (16b) results in

(51)

As a consequence, the assertion of this theorem is obtained by showing that (50) is satisfied if and only if there exists λ satisfying (50a) and (31e).

Suppose that a satisfies (50). Then (50a) and (31e) are satisfied with λ = 0. This shows the “only if” part. The converse is shown as follows. Suppose that a and λ satisfy (50a) and (31e). Then we have that

This implies that a satisfies (50). □;

4.2 Stability of optimal truss

This section shows that the truss obtained by solving (ARTO) (in (31)) is stable (i.e., kinematically determinate). See, e.g., Kuznetsov (1988), Pellegrino (1993), Pellegrino and Calladine (1986) and (Tarnai 2001) for the notion of kinematical determinacy.

Stability of the optimal truss is formally defined as follows. Let $(\bar {{\boldsymbol {a}}},\bar {\text {\textit {w}}},\bar {{\boldsymbol {\lambda }}}) \in \mathbb {R}^{m} \times \mathbb {R} \times \mathbb {R}^{m}$ denote the optimal solution of (ARTO). Define $\mathcal {E}_{\text {opt}} \subseteq \mathcal {E}$ by

$${\mathcal{E}}_{{\text{opt}}} = \{ i \in {\mathcal{E}} : \bar{a}_{i} > 0 \} , $$

i.e., ${\mathcal {E}}_{{\text {opt}}}$ is the set of members that exist at the optimal solution. Define ${\mathcal {V}}_{{\text {opt}}} \subseteq {\mathcal {V}}$ as the set of nodes that are connected to a member belonging to $\mathcal {E}_{\text {opt}}$. In other words, if $i=(\nu _{j},\nu _{k}) \in \mathcal {E}_{\text {opt}}$, then ν _j , $\nu _{k} \in {\mathcal {V}}_{{\text {opt}}}$. Then graph $G_{{\text {opt}}}=({\mathcal {V}}_{{\text {opt}}},{\mathcal {E}}_{{\text {opt}}})$ corresponds to the topology of the optimal truss, $\bar {\boldsymbol {a}}$. We say that the optimal truss, $\bar {\boldsymbol {a}}$, is stable if any displacement vector $\boldsymbol {u} = (\boldsymbol {u}^{(\nu )} \mid \nu \in \mathcal {V})$ solving

$${K}(\bar{{\boldsymbol{a}}};\tilde{{\boldsymbol{x}}}) {\boldsymbol{u}} = {\boldsymbol{0}} $$

satisfies ${\boldsymbol {u}}^{(\nu )}={\boldsymbol {0}}\,(\forall \nu \in {\mathcal {V}}_{{\text {opt}}})$. Note that the stability is evaluated when the nodes exist at their nominal locations. Stability does not mean that $K(\bar {\boldsymbol {a}};\tilde {\boldsymbol {x}})$ has full rank, if some nodes are removed at $\bar {\boldsymbol {a}}$. We may consider a stiffness matrix only with the rows and columns corresponding to the degrees of freedom of the nodes belonging to ${\mathcal {V}}_{{\text {opt}}}$. Then stability of the optimal truss means that this newly-defined stiffness matrix has full rank (equivalently, it is positive definite).

To establish the main result stated in Theorem 3, we need the following assumption, which is unrestrictive from a practical point of view.

Assumption 1

• (i) Any node $v \in {\mathcal {V}}_{{\text {opt}}}$ is either pin-supported or free.

• (ii) For any member $i=(v_{j},v_{k})\in {\mathcal {E}}$ , matrix A ^(v _j ) −A ^(v _k ) has full row rank, i.e., $\text {rank}\left (A^{(v_{j})}-A^{(v_{k})}\right )=d$.

• (iii) r > 0.

Remark 3

Assumption 1 (i) means that the optimal truss does not have any roller support. This is, certainly, satisfied if the ground structure has no roller support.

Remark 4

Assumption 1 (ii) means that, for $i=(v_{j},v_{k})\in {\mathcal {E}}$, the location of node v _j can vary independently of the location of node v _k . For instance, if we choose A = I _p in (17), then this assumption is satisfied. Note that locations of pin supports are also considered uncertain.

Remark 5

Assumption 1 (iii) is natural because r = 0 means that no uncertainty is considered.

The following two lemmas prepare for the main result stated in Theorem 3.

Lemma 2

Suppose r>0. Let $(\bar {{\boldsymbol {a}}}, \bar {\text {\textit {w}}}, \bar {{\boldsymbol {\lambda }}}) \in \mathbb {R}^{m}\times \mathbb {R} \times \mathbb {R}^{m}$ denote the optimal solution of (ARTO) in (31) . Then $\bar {\lambda }_{i}>0\,(\forall i\in {\mathcal {E}}_{{\text {opt}}})$.

Proof

Since any principal submatrix of a positive semidefinite matrix is positive semidefinite, constraint (31b) implies

(52)

Suppose, for contradiction, that there exists member $\hat {i}\in {\mathcal {E}}_{{\text {opt}}}$ satisfying $\bar {\lambda }_{\hat {i}}=0$. Then (52) reads

which implies

$$ \bar{a}_{\hat{i}} \breve{\kappa}_{\hat{i}} r{\boldsymbol{b}}_{\hat{i}} = {\boldsymbol{0}}. $$

(53)

In contrast, from the assumption of this lemma we have that $\bar {a}_{\hat {i}} \ne 0$ and r ≠ 0. Furthermore, for any $i \in {\mathcal {E}}$, we see that b _i ≠ 0 and $\breve {\kappa }_{i} \ne 0$ from their definitions in (23) and (26). Therefore, $\bar {a}_{\hat {i}} \breve {\kappa }_{\hat {i}} r{\boldsymbol {b}}_{\hat {i}} \not = {\boldsymbol {0}}$, which contradicts (53). □;

Lemma 3

If Assumption 1 is satisfied, then any connected component of graph $G_{{\text {opt}}}=({\mathcal {V}}_{{\text {opt}}},{\mathcal {E}}_{{\text {opt}}})$ has at least one support.

Proof

Suppose, for contradiction, that G _opt has a connected component that has no support.

If no external load is applied to this connected component, then all the members in this connected component can be removed without changing the compliance of the total structure. This means that an optimal solution cannot have such a connected component. Hence, in the following, we suppose that some external forces are applied to the connected component. Note that no reaction is applied to the connected component, because we are assuming for contradiction that the connected component has no support. The proof proceeds by considering two cases.

• (a) Suppose that the external forces applied to the connected component are not in static equilibrium when ${\boldsymbol {x}}=\tilde {{\boldsymbol {x}}}$. Then the forces cause rigid-body motion in a direction of the unbalanced force. Therefore, the compliance is not bounded above. This contradicts the argument that $G_{{\text {opt}}}=({\mathcal {V}}_{{\text {opt}}},{\mathcal {E}}_{{\text {opt}}})$ is feasible for (ARTO).

• (b) Suppose that the external forces applied to the connected component are in static equilibrium when $\boldsymbol {x}=\tilde {\boldsymbol {x}}$. Choose a node at which an external force is applied. We use v to denote this node. From Assumption 1 (ii), the location of node v can be perturbed arbitrary with satisfying ${\boldsymbol {x}}\in {\mathcal {X}}_{r}$, when the locations of the other nodes are fixed. Here, the direction of the external force at node v is not changed. Therefore, there exists a location of v at which the equilibrium of moments of external forces will be violated. This location of the node yields the worst-case compliance, which is not bounded above. Such a solution is not feasible for (ARTO) and this contradicts the assumption of this lemma.

Thus contradiction arises in each case and hence any connected component of G _opt has at least one support. □

We are now in position to state the main result of this section.

Theorem 3

If Assumption 1 is satisfied, then the truss obtained as the optimal solution of (ARTO) in (31) is stable.

Proof

From (25), the stiffness matrix of the optimal solution with the nominal nodal locations, i.e., $\boldsymbol {x}=\tilde {\boldsymbol {x}}$ and ζ = 0, is given by

$$\sum\limits_{i\in{\mathcal{E}}} \bar{a}_{i} \kappa_{i}({\boldsymbol{0}}){\boldsymbol{b}}_{i}{\boldsymbol{b}}_{i}^{\top}. $$

Hence, the assertion of this theorem can be obtained by showing that any u solving

$$ \sum\limits_{i\in{\mathcal{E}}}\bar{a}_{i}\kappa_{i}({\boldsymbol{0}}){\boldsymbol{b}}_{i}{\boldsymbol{b}}_{i}^{\top}{\boldsymbol{u}} = {\boldsymbol{0}} $$

(54)

satisfies ${\boldsymbol {u}}^{(v)}={\boldsymbol {0}}\,(\forall v\in {\mathcal {V}}_{{\text {opt}}})$.

It follows from Lemma 1 and constraint (31b) of (ARTO) that the stiffness matrix satisfies

$$ \sum\limits_{i\in{\mathcal{E}}}\bar{a}_{i} \kappa_{i}({\boldsymbol{0}}){\boldsymbol{b}}_{i}{\boldsymbol{b}}_{i}^{\top} \succeq\sum\limits_{i\in{\mathcal{E}}}\bar{a}_{i}\breve{\kappa}_{i}{\boldsymbol{b}}_{i}{\boldsymbol{b}}_{i}^{\top} \succeq\sum\limits_{i\in{\mathcal{E}}}\bar{\lambda}_{i} C_{i} C_{i}^{\top}. $$

(55)

On the other hand, (54) implies

$$ {\boldsymbol{u}}^{\top} \left( \sum\limits_{i\in{\mathcal{E}}} \bar{a}_{i} \kappa_{i}({\boldsymbol{0}}){\boldsymbol{b}}_{i}{\boldsymbol{b}}_{i}^{\top} \right){\boldsymbol{u}} = 0. $$

(56)

By using (55), we see that (56) implies

$$ {\boldsymbol{u}}^{\top} \left(\sum\limits_{i\in{\mathcal{E}}}\bar{\lambda}_{i} C_{i} C_{i}^{\top}\right){\boldsymbol{u}} = \sum\limits_{i\in{\mathcal{E}}}\bar{\lambda}_{i} \left(C_{i}^{\top}{\boldsymbol{u}}\right)^{\top} \left(C_{i}^{\top}{\boldsymbol{u}}\right) = 0. $$

(57)

It follows from Lemma 2 that (57) implies

$$ C_{i}^{\top}{\boldsymbol{u}} = {\boldsymbol{0}} \quad (\forall i\in{\mathcal{E}}_{{\text{opt}}}). $$

(58)

In the following we show that any u solving (58) satisfies ${\boldsymbol {u}}^{\nu }={\boldsymbol {0}}\,(\forall v \in {\mathcal {V}}_{{\text {opt}}})$. Choose a connected component of G _opt arbitrarily. Lemma 3 asserts that this connected component has a support. Let v denote this support. Choose member $\hat {i}=(\nu ,\nu ^{\prime }) \in \mathcal {E}_{\text {opt}}$. From Assumption 1 (i), node v ^′ is either a support or a free node. If node v ^′ is a support, then $\bar {a}_{\hat {i}}=0$ holds at the optimal solution and hence $\hat {i} \not \in \mathcal {E}_{\text {opt}}$. Therefore, node ν is a free node. From (24) (see, also, (2), (9) and (19)), matrix $C_{\hat {i}} \in {\mathbb {R}}^{p\times l}$ is of the form

(59)

i.e., it is a block matrix such that only the block related to node v ^′ is a nonzero matrix. Here, $T^{(\nu ^{\prime })} \in \mathbb {R}^{d \times d}$ is an orthogonal matrix. From (59), equation $C_{\hat {i}}^{T}\boldsymbol {u} = \boldsymbol {0}$ in (58) is written as

$$ T^{(\nu^{\prime})}(A^{(\nu^{\prime})}-A^{(\nu)}){\boldsymbol{u}}^{(\nu^{\prime})} ={\boldsymbol{0}}. $$

(60)

It follows from Assumption 1 (ii) and the orthogonal property of $T^{(\nu ^{\prime })}$ that $T^{(\nu ^{\prime })}(A^{(\nu ^{\prime })}-A^{(\nu )})$ has full row rank. Therefore, (60) implies

$$ {\boldsymbol{u}}^{(\nu^{\prime})} = {\boldsymbol{0}}. $$

(61)

We next choose member $i^{\prime }=(\nu ^{\prime },\nu ^{\prime \prime })\in {\mathcal {E}}_{{\text {opt}}}$ such that node $\nu ^{\prime \prime }\in {\mathcal {V}}_{{\text {opt}}}$ is a free node. Then matrix $C_{i^{\prime }} \in \mathbb {R}^{p \times l}$ is of the form

Therefore, equation $C_{i^{\prime }}^{\top }{\boldsymbol {u}} = {\boldsymbol {0}}$ in (58) is reduced to

$$\begin{array}{@{}rcl@{}}&& T^{(\nu^{\prime})}\left(A^{(\nu^{\prime})}-A^{(\nu^{\prime\prime})}\right){\boldsymbol{u}}^{(\nu^{\prime})} + T^{(\nu^{\prime\prime})}\left(A^{(\nu^{\prime\prime})}-A^{(\nu^{\prime})}\right){\boldsymbol{u}}^{(\nu^{\prime\prime})} \\ && = T^{(\nu^{\prime\prime})}\left(A^{(\nu^{\prime\prime})}-A^{(\nu^{\prime})}\right){\boldsymbol{u}}^{(\nu^{\prime\prime})} ={\boldsymbol{0}} , \end{array} $$

(62)

where (61) has been used. From Assumption 1 (ii) we see that $T^{(\nu ^{\prime \prime })} \left (A^{(\nu ^{\prime \prime })}-A^{(\nu ^{\prime })}\right )$ has full row rank, because $T^{(\nu ^{\prime \prime })}$ is an orthogonal matrix. Therefore, (62) implies $\boldsymbol {u}^{(\nu ^{\prime \prime })}=\boldsymbol {0}$. By repeating this procedure, we can show that u ^(w) = 0 should be satisfied at any node w contained in the connected component.

The discussion above is valid for any connected component of G _opt. Therefore, we can conclude that any solution of (58) satisfies ${\boldsymbol {u}}^{(\nu )}={\boldsymbol {0}}\,(\forall v \in {\mathcal {V}}_{{\text {opt}}})$. □

The assumption required in Theorem 3 is not restrictive, as briefly discussed in Remark 3, Remark 4 and Remark 5. Since it is well known that standard compliance optimization often yields an unrealistic unstable truss design, guarantee of stability provided by the presented method is significant from a practical point of view.

5 Numerical experiments

This section presents various numerical examples. The proposed SDP problem, (ARTO) in (31), is solved to find robust truss designs. Section 5.1 considers some different uncertainty models and studies difference of optimal solutions. Section 5.2 discusses a relation between the level of uncertainty, r, and optimal topology. Section 5.3 studies a small example to estimate the tightness of approximation of the presented formulation. Section 5.4 collects examples with larger sizes.

Computation was carried out on a 2.6 GHz Intel Core i5 processor with 8 GB RAM. SDP problems were solved with SeDuMi ver. 1.3 (Pólik 2005; Sturm 1999) on MATLAB ver. 7.7. Note that SeDuMi implements a primal-dual interior-point method for linear programming problems over symmetric cones.

All the examples consider planar trusses, i.e., d = 2. The elastic modulus is 200 GPa. The upper bound constraint on the structural volume becomes active at the optimal solution of each example.

5.1 Example (I): Effect of difference of uncertainty models

This section studies variation in optimal solutions due to differences of uncertainty model.

Consider the ground structure shown in Fig. 2a. This truss consists of m = 38 members connected by n = 5 × 3 = 15 nodes and hence q = 30. The lengths of all horizontal member and vertical members are 1 m. The leftmost nodes, i.e., nodes ν ₁, ν ₂ and ν ₃, are pin-supported. The number of degrees of freedom of displacements is p = 24. A horizontal force of 10 N is applied at the rightmost node in the middle row, i.e., node ν ₇. The specified upper bound for the structural volume is V _u = 0.05m³.

Fig. 2

Example (I). a The ground structure; and b the nominal optimal solution (r = 0)

Figure 2b shows the trivial optimal solution of the conventional compliance optimization without considering uncertainty, i.e., r = 0. Four members with uniform cross-sectional areas are aligned on a straight line. This solution is certainly unstable.

As for the uncertainty models of node locations, we consider four cases:

• Model (i): Locations of all the nodes possess uncertainty ( l = q = n d = 30).

• Model (ii): Locations of nodes ν ₂, ν ₄, ν ₅, ν ₆ and ν ₇ possess uncertainty ( l = 5d = 10).

• Model (iii): Locations of nodes ν ₄, ν ₅ and ν ₆ possess uncertainty ( l = 3d = 6).

• Model (iv): Location of node ν ₄ possesses uncertainty ( l = 2).

Note that matrix A for model (i) is A = I _q . For models (ii), (iii) and (iv), ${A} \in \mathbb {R}^{q \times l}$ is of the form

$$ {A} = \left[\begin{array}{c} {I}_{l} \\ {O} \\ \end{array}\right]. $$

(63)

The level of uncertainty is r = 0.05m in all these cases. With probabilistic uncertainty setting, similar problem was solved by Guest and Igusa (2008, section 3.6).

5.1.1 Solution under uncertainty in all nodes (model (i))

Figure 3a shows the optimal solution of (ARTO) in (31) with model (i). The width of each member in this figure is proportional to its cross-sectional area. The computational results are listed in Table 1. The results in the nominal case, r = 0, is also listed in the bottom row of this table. Here, “Opt. val.” shows the optimal value and $\pi (\bar {{\boldsymbol {a}}};\tilde {{\boldsymbol {x}}})$ is the compliance when the nodes are located at the nominal positions, $\tilde {{\boldsymbol {x}}}$. Note that 1 J = 1 N⋅m.

Fig. 3

Robust optimal solutions of example (I) with r = 0.05 m. a Model (i); b model (ii); c model (iii); and d model (iv)

Table 1 Computational results of example (I)

As stated earlier, without considering uncertainty standard optimization yields an unstable truss design shown in Fig. 2b. When locations of existing nodes are perturbed in the vertical direction, this solution cannot equilibrate under the given external load. Therefore, this solution is not feasible for our robust optimization problem; thus unrealistically unstable truss designs are excluded by considering uncertainty in node locations. The same assertion was made by Guest and Igusa (2008) with probabilistic uncertainty setting. The robust optimal solution shown in Fig. 3a is stable, which agrees with Theorem 3.

5.1.2 Solutions under uncertainty in some nodes (models (ii)–(iv))

This section mentions the results with uncertainty models (ii), (iii) and (iv). Figs. 3b, c and d show the optimal solutions with models (ii), (iii) and (iv), respectively. Table 1 reports the optimal values and the values of compliance with the nominal locations of the nodes. In each case the computational time required by SeDuMi is less than 2 seconds. The member cross-sectional areas of the obtained solutions are reported in Table 2, where the member indices are defined in Fig. 2a. The solutions obtained with models (ii) and (iii) are stable and have the same topology as the solution with model (i).

Table 2 The obtained solutions of example (I)

In model (iv), the location of only one node is considered uncertain. The solution obtained with this model is unstable, where only members around the uncertain node are braced. This agrees with the result obtained by Guest and Igusa (2008) with probabilistic uncertainty setting.

5.2 Example (II): Effect of uncertainty magnitude

This section examines how the robust optimal solution varies when the magnitude of uncertainty, r, is changed.

Consider the initial truss shown in Fig. 4. The truss consists of m = 24 members connected by n = 9 nodes, where q = d n = 18. The lengths of all horizontal and vertical members are 1 m. The leftmost nodes are pin-supported. The number of degrees of freedom of displacements is p = 12. A horizontal force of 10N is applied at the rightmost node in the middle row. The upper bound for the structural volume is V _u = 0.01m³. Locations of all the nodes are supposed to be uncertain, where matrix A in (17) is A = I _q with l = q.

Fig. 4

Example (II). The ground structure

Figure 5 shows the variation of the optimal value, $\bar {w}$, with respect to the level of uncertainty, r. The trade-off relation between the worst compliance and the level of uncertainty is clearly captured from this curve, called the robustness curve (Ben-Haim 2006). Namely, the robustness cannot be improved (i.e., r cannot be larger) when the requirement of the performance becomes more severe (i.e., $\bar {\text {\textit {w}}}$ becomes smaller). As r is increased, the optimal topology changes in the five types shown in Fig. 6.

Fig. 5

The variation of the optimal value, $\bar {w}$, of example (II) with respect to the level of uncertainty, r

Fig. 6

The optimal topologies in Fig. 5. a Topology 1; b topology 2; c topology 3; d topology 4; and e topology 5

It is observed in Fig. 6 that, when r is small, thin braces are used to stabilize the two thick members in the middle row. As proved in Section 4.1, the optimal solution at r = 0 in Fig. 6a coincides with the optimal solution of (TO). When r is large, the optimal topology becomes a two-bar truss. As r becomes larger, the number of existing nodes becomes smaller. Thus the optimal topology depends on the level of uncertainty.

5.3 Example (III): Tightness of approximation

As already proved, the presented method provides us with a safe approximation of the robust optimal solution. Theoretically, in this paper we do not analyze tightness of approximation. In other words, we do not know how far the optimal solution of (ARTO) is from the optimal solution of (RTO). This section investigates the tightness numerically using a small example.

Consider the 2-bar truss shown in Fig. 7a. The two left nodes are pin-supported, i.e., p = 2. The location of the right free node is supposed to be uncertain, while the locations of two supports are supposed to be known precisely, i.e., the number of uncertain parameters is l = 2. Matrix A is given by (63) and the level of uncertainty is r = 0.01m. This means that the free node can exist at any points in and on a circle with radius r as shown in Fig. 7a. A horizontal force of 100 N is applied at the right free node. The upper bound for the structural volume is V _u = 0.01 m³.

Fig. 7

Example (III). a The 2-bar problem; b the nominal optimal solution; and c the robust optimal solution

The nominal optimal truss, i.e., the optimal solution of (TO) in (16), is trivially the one shown in Fig. 7b. The member cross-sectional areas are (10000,0) mm² and the optimal value is 5 J. Fig. 7c shows the optimal solution of (ARTO) in (31). The member cross-sectional areas of this solution are (9808.07,135.71)mm² and the optimal value is 5.658718 J.

We next generate many sample points for the locations of the free node. These samples are equally distributed points on the two-dimensional circle with radius r shown in Fig. 7a. The member cross-sectional areas are fixed as the optimal solution of (ARTO) and the compliance is computed. The curve in Fig. 8 depicts the compliance, where 𝜃 is the angle of the location of node to the horizontal axis. The maximum value of this curve is 5.311027 J, when we take 1000 samples. Thus the optimal value of (ARTO), 5.658718 J, overestimates the compliance in the worst scenario.

Fig. 8

The variation of the compliance of example (III) with respect to the location of the node

Finally, we perform the worst-case minimization using the generated samples. Namely, we solve the minimization problem of the maximum compliance among 1000 uniformly distributed samples on the two-dimensional circle shown in Fig. 7a. The optimal solution of this problem might be expected to be very close to the true optimal solution of (RTO) in (20). The member cross-sectional areas of this solution are (9807.18,136.34) mm² and the optimal value is 5.311025 J. It is worth noting that this optimal value is very close to the maximum value of the solid curve in Fig. 7a. Therefore, we may probably conclude that, in this particular example, the optimal truss design of (ARTO) is sufficiently close to the true optimal truss design of (RTO), although the optimal value of (ARTO) overestimates the true compliance in the worst scenario. This is, certainly, just one example that yields positive result on the quality of the optimal solution of (ARTO). It is true that the quality of a solution is not clear when (ARTO) is applied to more complex examples. However, for a larger problem, verification using simple sampling, such as what performed above, is difficult due to the curse of dimensionality.

5.4 More examples

This section collects numerical experiments with larger scale optimization problems.

5.4.1 Example (IV)

Consider the two ground structures shown in Fig. 9, where only the nodes are depicted. Any two nodes are connected by a member, but overlapping of members is avoided by removing the longer member when two members overlap. The truss in Fig. 9a has m = 418 members and p = 60 degrees of freedom of displacements. The one in Fig. 9b has m = 919 members and p = 96 degrees of freedom of displacements. In both structures, the leftmost nodes are pin-supported. A vertical force of 10 N is applied at the bottom rightmost node. The upper bound for the structural volume is V _u = 0.1 m³. Locations of all nodes are considered uncertain, i.e., l = q. Matrix A in (17) is A = I _q .

Fig. 9

Example (IV). The ground structures. a The 5 × 5-grid ground structure; and b the 8 × 5-grid ground structure

The nominal optimal solutions are shown in Figs. 10a and 11a. Figs. 10b, c, d, and 11b, c and d show the optimal solutions of (ARTO) in (31) with r = 0.02 m, r = 0.05 m and r = 0.1 m. The computational results are listed in Table 3, where “Time” means the computational time required by SeDuMi to solve an SDP problem.

Fig. 10

The solutions for the 5 × 5-grid problem of example (IV). a r = 0; b r = 0.02 m; c r = 0.05 m; and d r = 0.1m

Fig. 11

The solutions for the 8 × 5-grid problem of example (IV). a r = 0; b r = 0.02 m; c r = 0.05 m; and d r = 0.1m

Table 3 Computational results of example (IV)

The solution of Fig. 10b has all the members that exist in the solution of Fig. 10a. In other words, the set of existing members in Fig. 10b is a superset of the set of existing members in Fig. 10a. In contrast, the set of existing members in Fig. 10d is not a superset of that in Fig. 10a. The number of existing nodes in Fig. 10d is very small due to a large level of uncertainty in the locations of nodes. The solution in Fig. 11b has many more members than the nominal solution in Fig. 11a. This is because the nominal optimal solution is unstable due to the presence of collinear members and the robust optimal solution requires many thin members to achieve stability. The truss topologies in Figs. 11c and d are much different from the nominal optimal solution in Fig. 11a. Also, the solutions in Figs. 11c and d have few nodes, which avoids the effect of large uncertainty in the locations of nodes as far as possible.

5.4.2 Example (V)

Consider the three ground structures shown in Fig. 12. Any two nodes are connected by a member, but overlapping of members is avoided by removing the longer member when two members overlap. The truss in Fig. 12a consists of m = 140 members and has p = 36 degrees of freedom of displacements. The one in Fig. 12b has m = 386 members and p = 60 degrees of freedom. The final one, shown in Fig. 12c, has m = 748 members and p = 84 degrees of freedom. The leftmost nodes are pin-supported. A vertical force of 10 N is applied at the rightmost node in the middle row. The upper bound for the structural volume is V _u = 0.1 m³. The magnitude of uncertainty is r = 0.05 m. Locations of all nodes are supposed to be uncertain, i.e., l = q and A = I _q .

Fig. 12

Example (V). The ground structures. a The 6 × 2-grid ground structure; b the 6 × 4-grid ground structure; and c the 6 × 6-grid ground structure

The nominal optimal solutions for these three ground structures are shown in Figs. 13a, c and e. The optimal solutions obtained by solving (ARTO) in (31) are shown in Figs. 13b, d and f. The computational results are listed in Table 4.

Fig. 13

The solutions of example (V). a The 6 × 2 nominal optimal solution; b the 6 × 2 robust optimal solution; c the 6 × 4 nominal optimal solution; d the 6 × 4 robust optimal solution; e the 6 × 6 nominal optimal solution; and f the 6 × 6 robust optimal solution

Table 4 Computational results of example (V)

In contrast to the other examples in Section 5, the three nominal optimal solutions in Fig. 13 are stable. The nominal optimal solution in Fig. 13c is similar to its robust counterpart in Fig. 13d, but a middle node in the nominal optimal solution is missing in the robust optimal solution. Similarly, one node of the nominal optimal solution in Fig. 13e is not used in the robust optimal solution shown in Fig. 13f.

In Jalalpour et al. (2013, section 3.1.1), a reliability-based topology optimization problem of a similar cantilever truss was solved, where uncertainties in node locations were dealt with in a probabilistic manner. It was observed in the result of Jalalpour et al. (2013) that the number of members increases as the probability of failure is decreased. In contrast, it is observed in Fig. 13 that the optimal solutions of (ARTO) has less members than those of (TO).

6 Conclusions

The concept of robustness to uncertainty is central in structural design. This paper has addressed robust truss optimization considering geometrical uncertainties. We have formulated the SDP problem that provides us with a safe approximation of the optimal solution.

Theorem 1 establishes that any feasible solution of the proposed SDP problem is feasible for the original robust optimization problem. This assertion holds for arbitrarily large magnitude of uncertainty. Instead of this guaranteed safety, the optimal solution of the presented SDP problem is not optimal for the original robust optimization problem in general. In the numerical experiment in Section 5.3, it has been observed that these two optimal solutions are close enough, although no theoretical result is available for approximation ratio.

Two properties of the proposed SDP approximation have been explored. Theorem 2 shows zeroing of our SDP formulation, i.e., when the magnitude of uncertainty is equal to zero, the SDP problem truly coincides upper bound for the structural volume without considering uncertainties. Theorem 3 establishes, under mild assumptions, that the optimal solution of the SDP problem is a stable truss.

In the context of compliance optimization of trusses, guaranteed stability of the obtained solution might be considered a fairly distinguished feature of the proposed approach.² It is worth noting, on the other hand, that many nodes of the initial structure can possibly disappear in the solution obtained by the proposed approach, as illustrated in Section 5. Roughly speaking, the truss topology can vary in the course of optimization of the proposed approach. Stability of a truss in compliance optimization is also guaranteed by considering uncertainty in external loads (Ben-Tal and Nemirovski 1997), if all the nodes of the ground structure are subjected to uncertain external forces. In this case, however, all the nodes in the ground structure remain at the robust optimal solution. It is not obvious to guess the set of existing nodes at the robust optimal solution. One remedy is making use of discrete variables representing existence of members (Yonekura and Kanno 2010). However, such a method, based upon mixed-integer programming, is usually time consuming. In contrast, the method presented in this paper generates a stable truss by solving a single SDP problem.

Through the numerical experiments it has been illustrated that the optimal truss topology depends on the magnitude of uncertainty, as well as the set of uncertain nodes. Roughly speaking, when the nominal optimal truss is unstable and the level of uncertainty is small, the robust optimal truss often has many thin members that are used to stabilize the nominal optimal solution. In contrast, as the level of uncertainty is large, the number of nodes of the robust optimal solution decreases to avoid the effect of large uncertainty in the locations. If the nominal optimal truss is stable, then the robust optimal solution is often similar to the nominal one.

This paper was restricted to the compliance optimization of a truss. Other objective functions can be studied to optimize other structural performance. Also, extension of the presented method to other types of structures can be considered. Particularly, robust optimal design of micro compliant mechanisms (Jang et al. 2012; Schevenels et al. 2011; Sigmund 2009; Wang et al. 2011) could probably be a promising application. Furthermore, theoretical assessment of tightness of the proposed SDP approximation remains to be explored.

Appendix: Technical lemmas

This section summarizes technical prerequisites that are known in literature.

We begin with three lemmas related to vector and matrix norms. These lemmas are used in Section 3.2. For p satisfying 1 ≤ p ≤ ∞, define p ^∗ by

$$\frac{1}{p} + \frac{1}{p^{*}} = 1 , $$

where we use the convention 1/∞ = 0. The ℓ _p ^∗-norm is the dual norm of the ℓ _p -norm. For any x, $\boldsymbol {y} \in \mathbb {R}^{n}$, we have that

$$ {\boldsymbol{x}}^{\top}{\boldsymbol{y}} \le \|{\boldsymbol{x}}\|_{p} \|{\boldsymbol{y}}\|_{p^{*}}, $$

(64)

which is known as the Hölder inequality (Horn and Johnson 1985; Steele 2004). For any ${\boldsymbol {x}} \in \mathbb {R}^{n}$, there exists ${\boldsymbol {y}} \in \mathbb {R}^{n}$ satisfying (64) with equality and ∥y∥ _p ^∗=1. We denote this y by ψ _p (x).

Lemma 4

Let $\mathbb {R} \ni s \ge 0$ be a constant, ${\boldsymbol {x}}\in {\mathbb {R}}^{n}$ and 1 ≤ p ≤ ∞. Then

$$\max_{{\boldsymbol{y}}\in {\mathbb{R}}^{n}} \{ {\boldsymbol{x}}^{\top} {\boldsymbol{y}} : \|{\boldsymbol{y}}\|_{p^{*}} \le s \} = s \| {\boldsymbol{x}} \|_{p}. $$

Proof

For any ${\boldsymbol {x}}\in {\mathbb {R}}^{n}$ and ${\boldsymbol {y}}\in {\mathbb {R}}^{n}$ satisfying ∥y∥ _p ^∗ ≤ s, it follows from the Hölder inequality that

$${\boldsymbol{x}}^{\top} {\boldsymbol{y}} \le \left\|{\boldsymbol{x}}\right\|_{p} \left\|{\boldsymbol{y}}\right\|_{p^{*}} \le s \left\|{\boldsymbol{x}}\right\|_{p}. $$

Here, two inequalities are satisfied with equalities at y = s ψ _p (x), which concludes the proof. □;

Lemma 4 is used in the proof of Theorem 1 in Section 3.2.

Lemma 5

Let $x \in \mathbb {R}$ , ${\boldsymbol {y}} \in \mathbb {R}^{n}$ and $\mathbb {R} \ni r > 0$ . Then

$$\max_{{\boldsymbol{z}}\in {\mathbb{R}}^{n}} \{ x {\boldsymbol{y}}^{\top} {\boldsymbol{z}} : \|{\boldsymbol{z}}\|_{2} \le r \} = r|x| \| {\boldsymbol{y}} \|_{2}. $$

Proof

The Cauchy–Schwarz inequality implies

$$x {\boldsymbol{y}}^{\top} {\boldsymbol{z}} = {\boldsymbol{y}}^{\top} (x {\boldsymbol{z}}) \le \|{\boldsymbol{y}}\|_{2} \| x{\boldsymbol{z}}\|_{2}. $$

From ∥z∥₂ ≤ r, we obtain

$$\| x{\boldsymbol{z}} \|_{2} \le |x| \|{\boldsymbol{z}}\|_{2} \le |x| r. $$

These inequalities are satisfied with equalities at

$${\boldsymbol{z}} = \left\{\begin{array}{ll} r {\boldsymbol{\psi}}_{2}({\boldsymbol{y}}) & \text{if}\;\; x \ge 0, \\ -r {\boldsymbol{\psi}}_{2}({\boldsymbol{y}}) & \text{if} \;\;x < 0, \\ \end{array}\right. $$

which concludes the proof. □;

Lemma 5 is used in the proof of Theorem 1 in Section 3.2.

For $A \in \mathbb {R}^{m \times n}$, the matrix norm induced by the Euclidean vector norm is defined by

$$ \| A \|_{2} = \max_{{\boldsymbol{x}}\ne {\boldsymbol{0}}} \frac{\| A{\boldsymbol{x}} \|_{2}}{\|{\boldsymbol{x}}\|_{2}} , $$

(65)

which is equal to the largest singular value of A. From this definition we immediately obtain the following property.

Lemma 6

Let $A\in {\mathbb {R}}^{m \times n}$ and ${\boldsymbol {x}}\in {\mathbb {R}}^{n}$ . Then

$$\| A{\boldsymbol{x}} \|_{2} \le \|A\|_{2} \|{\boldsymbol{x}}\|_{2}. $$

Lemma 6 is used to show Lemma 1 in Section 3.2.

In the following we establish Lemma 9, which is used in Section 3.2 to formulate the conservative approximation of the robust optimization problem. Two lemmas, Lemma 7 and Lemma 8, prepare for Lemma 9. Firstly, we state the following fact, which is the obvious part of the well-known S-lemma; see, e.g., Boyd et al. (1987) and Pólik and Terlaky (2007).

Lemma 7

Let f ₀ , $f_{1},\dots ,f_{m}:\mathbb {R}^{n} \to \mathbb {R}$ be quadratic functions. The implication

$$ f_{1}({\boldsymbol{x}})\ge 0,\dots,f_{m}({\boldsymbol{x}})\ge 0 \quad\Rightarrow\quad f_{0}({\boldsymbol{x}})\ge 0 $$

(66)

holds if there exist t ₁ ,…,t _m ≥ 0 satisfying

$$f_{0}({\boldsymbol{x}})\ge \sum\limits_{i=1}^{m} t_{i}f_{i}({\boldsymbol{x}}) \quad (\forall {\boldsymbol{x}}\in{\mathbb{R}}^{n}). $$

Proof

Suppose that (66) does not hold, which means that there exists $\hat {{\boldsymbol {x}}} \in \mathbb {R}^{n}$ satisfying

$$f_{0}(\hat{{\boldsymbol{x}}}) < 0 , f_{1}(\hat{{\boldsymbol{x}}}) \ge 0 , {\dots} , f_{m}(\hat{{\boldsymbol{x}}}) \ge 0. $$

Then we obtain

$$f_{0}(\hat{{\boldsymbol{x}}}) < 0 \le \sum\limits_{i=1}^{m} t_{i} f_{i}(\hat{{\boldsymbol{x}}}) \quad (\forall t_{1},\dots,t_{m} \ge 0). $$

Thus the contraposition of Lemma 7 has been shown. □;

The following fact can be found, e.g., in Calafiore and El Ghaoui (2004).

Lemma 8

Let $Q\in {\mathcal {S}^{n}}$ , ${\boldsymbol {p}}\in {\mathbb {R}}^{n}$ and $r\in {\mathbb {R}}$ . Then the following two conditions are equivalent:

$$ \mathrm{(i)}\;\;\left[\begin{array}{l} 1 \\ {\boldsymbol{x}} \\ \end{array}\right]^{\top} \left[\begin{array}{l} r \;\;{\boldsymbol{p}}^{\top} \\ {\boldsymbol{p}} \;\;Q \\ \end{array}\right] \left[\begin{array}{c} 1 \\ {\boldsymbol{x}} \\ \end{array}\right] \ge 0, \quad \forall {\boldsymbol{x}}\in{\mathbb{R}}^{n}, $$

(67)

$$ \mathrm{(ii)} \;\;\left[\begin{array}{l} r \;\;{\boldsymbol{p}}^{\top} \\ {\boldsymbol{p}}\;\; Q \\ \end{array}\right] \succeq O. $$

(68)

Proof

It is trivial that (ii) implies (i). We show that (i) implies (ii) by contradiction. Suppose that (ii) does not hold, which means that there exists $(\hat {\xi }, \hat {{\boldsymbol {x}}}) \in \mathbb {R} \times \mathbb {R}^{n}$ satisfying

$$ \left[\begin{array}{c} \hat{\xi} \\ \hat{{\boldsymbol{x}}} \\ \end{array}\right]^{\top} \left[\begin{array}{c} r \;\;{\boldsymbol{p}}^{\top} \\ {\boldsymbol{p}} \;\;Q \end{array}\right] \left[\begin{array}{c} \hat{\xi} \\ \hat{{\boldsymbol{x}}} \\ \end{array}\right] < 0. $$

(69)

If $\hat {\xi } \not = 0$, then (69) is reduced to

$$\left[\begin{array}{c} \hat{{\boldsymbol{x}}}/\hat{\xi} \\ 1 \\ \end{array}\right]^{\top} \left[\begin{array}{l} r \;\;{\boldsymbol{p}}^{\top} \\ {\boldsymbol{p}} \;\;Q \\ \end{array}\right] \left[\begin{array}{c} \hat{{\boldsymbol{x}}}/\hat{\xi} \\ 1 \\ \end{array}\right] < 0 , $$

which contradicts with (i). Hence, suppose $\hat {\xi }=0$. Then (69) is reduced to

$$ \hat{{\boldsymbol{x}}}^{\top} Q \hat{{\boldsymbol{x}}} < 0. $$

(70)

Let $\gamma \in \mathbb {R}$ be a parameter and choose ${\boldsymbol {x}} = \gamma \hat {{\boldsymbol {x}}}$ in (i) to reduce the left-hand side to

$$ \left(\hat{{\boldsymbol{x}}}^{\top} {Q} \hat{{\boldsymbol{x}}}\right) \gamma^{2} + 2 \left({\boldsymbol{p}}^{\top} \hat{{\boldsymbol{x}}}\right) \gamma + r. $$

(71)

The left-hand side of (71) is a quadratic function of γ and (70) implies that (71) is not bounded below. Therefore, there exists γ such that (71) becomes negative, which contradicts (i). □;

The following fact is obtained as a straightforward corollary of Lemma 7 and Lemma 8.

Lemma 9

Let f ₀ , $f_{1},\dots ,f_{m} : \mathbb {R}^{n} \to \mathbb {R}$ be quadratic functions defined by

$$f_{i}({\boldsymbol{x}}) = \left[\begin{array}{c} 1 \\ {\boldsymbol{x}} \\ \end{array}\right]^{\top} \left[\begin{array}{c} r_{i} \;\;{\boldsymbol{p}}_{i}^{\top} \\ {\boldsymbol{p}}_{i}\;\; {Q}_{i} \end{array}\right] \left[\begin{array}{c} 1 \\ {\boldsymbol{x}} \\ \end{array}\right] , \quad i=0,1,\dots,m , $$

where ${Q}_{i} \in {\mathcal {S}}^{n}$ , ${\boldsymbol {p}}_{i} \in \mathbb {R}^{n}$ , $r_{i} \in \mathbb {R}\,(i=0,1,\dots ,m)$ . Then the implication

$$f_{1}({\boldsymbol{x}}) \ge 0,\dots,f_{m}({\boldsymbol{x}}) \ge 0 \quad\Rightarrow\quad f_{0}({\boldsymbol{x}}) \ge 0 $$

holds if there exist t ₁ ,…,t _m ≥ 0 satisfying

$$\left[\begin{array}{c} r_{0} \;\;{\boldsymbol{p}}_{0}^{\top} \\ {\boldsymbol{p}}_{0}\;\; {Q}_{0} \end{array}\right] \succeq\sum\limits_{i=1}^{m} t_{i} \left[\begin{array}{c} r_{i} \;\;{\boldsymbol{p}}_{i}^{\top} \\ {\boldsymbol{p}}_{i} \;\;{Q}_{i} \end{array}\right]. $$

Lemma 9 plays a key role in proving Theorem 1 in Section 3.2.