A family of periodic orbits in the three-dimensional lunar problem

Abstract

A family of periodic orbits is proven to exist in the spatial lunar problem that are continuations of a family of consecutive collision orbits, perpendicular to the primary orbit plane. This family emanates from all but two energy values. The orbits are numerically explored. The global properties and geometry of the family are studied.

1 Introduction

We consider the three-dimensional circular restricted three-body problem. This models the three-dimensional motion of a particle, $P_0$, of zero mass in the Newtonian gravitational field generated by two particles, $P_1, P_2$ of respective positive masses, $m_1, m_2$, in a mutual uniform circular motion. It is assumed that $m_1$ is much larger than $m_2$. This problem is studied in a rotating coordinate system that rotates with the same constant frequency $\omega$ of the circular motion of $P_1, P_2$, so that in this system $P_1$ and $P_2$ are fixed. Because $m_1$ is much larger than $m_2$, we refer to $P_1$ as the Earth and $P_2$ as the Moon, for convenience.

When $P_0$ moves about the larger particle, $P_1$, the motion of $P_0$ can be completely understood if, for example, $P_0$ is restricted to the two-dimensional plane of motion of $P_1, P_2$. In this case, with $m_2 = 0$, assume that $P_0$ has precessing elliptic motion, of elliptic frequency $\omega ^*$ about $P_1$, precessing with frequency $\omega$. Then the Kolmogorov–Arnold–Moser (KAM) theorem proves that this precessing motion persists if $m_2$ is sufficiently small and if $\omega$ and $\omega ^*$ are sufficiently noncommensurate. Otherwise, the motion is chaotic due to heteroclinic dynamics. That is, invariant KAM tori almost foliate the phase space. The motion of $P_2$ is proven to be stable (Siegel and Moser 1971). When the initial elliptic motion of $P_0$ is not in the same plane as $P_0, P_1$, then under similar assumptions KAM tori can be proven to exist, but stability cannot be guaranteed.

In this paper, we study the three-dimensional motion of $P_0$ about $P_2$. This is referred to as the three-dimensional, or spatial, lunar problem. Relatively little is proven in general about the motion of $P_0$ unless the initial motion starts infinitely close to $P_2$. The proof of existence of KAM tori in the three-dimensional lunar problem was obtained by M. Kummer under the assumption that the initial motion of $P_0$ lies infinitely near to $P_2$ (Kummer 1983, see also Yanguas et al. 2008).¹

The main result of this paper is to prove the existence of a special family of periodic orbits about $P_2$, nearly perpendicular to the primary orbit plane. More precisely, if we normalize $m_1 = 1 - \mu , m_2 = \mu$, then in the case of $\mu = 0$ there exists a family of periodic orbits on the $z-$axis through $P_2$, so perpendicular to the $P_1, P_2$ plane, parameterized by their energy h. This family consists of consecutive collision orbits: Starting at collision at $P_2$, they extend up the $z-$axis to a maximal distance $d=d(h)$, then fall back to $P_2$, and periodically repeat this oscillation, where d can have any positive value. We label these as $\phi ^*(t,h)$. These orbits have period $T^*(h)$. We prove that $\phi ^*(t,h)$ continuously varies as a function of $\mu$, sufficiently small, into a unique periodic orbit $\phi (t,\mu )$ of period $T = T(\mu ), ~T(0) = T^*$, on the associated Jacobi energy surface, provided a non-degeneracy condition holds. This condition is satisfied for every energy value except two. The resulting family periodic orbits is labeled, $\mathcal {F}(h, \mu )$. This family depends on $\mu ^{1/3}$ real analytically.

The method of proof of $\mathcal {F}(h, \mu )$ is to make use of the proof of existence of an analogous family of orbits about the primary mass $P_1$ (Belbruno 1981a). A three-dimensional regularization defined first in Belbruno (1981a) is performed. This uses a fractional linear Möbius transformation which can be represented elegantly using a Jordan algebra. We also exploit symmetry properties of the lunar problem.

The resulting family of orbits is numerically investigated and has interesting properties. The properties are analogous to those in Belbruno (1981b) for very negative energy, but differ markedly for larger energy. In particular, the polar orbit in this paper has hyperbolic rather than elliptic behavior for large Jacobi energy.

The main theorem for this paper is stated as Theorem 1 in Sect. 2. The proof is done in Sect. 3. In Sect. 4, we describe numerical results. These include stability properties as well as the evolution of the polar orbit as a function of the parameters. A theoretical justification for the evolution is given in Belbruno et al. (2018), based on the Rabinowitz functional (Rabinowitz 1978) and the contact property, proved by Albers et al. (2012) and by Cho and Kim (2018).

We conclude the introduction with brief summary of the role of the Hamiltonians that we shall use.

• H will denote the Hamiltonian of the restricted three-body problem with the origin at the center of mass. It is defined in (1).

• $H_m$ is the Hamiltonian of the restricted three-body problem with the origin at the second primary. It is defined in (4).

• $H^{\mu }$ is a rescaled version of $H_m$, still centered at the second primary, but zoomed in at the Hill’s region around the second primary. It is defined in Eq. (8) and simplified in Eq. (9). Both distances and energies are affected by this rescaling, but it still describes the restricted three-body problem.

As $\mu$ goes to 0, the Hamiltonian $H^\mu$ converges to the Hamiltonian of Hill’s lunar problem, which is given by $H^0$. One can also take the limit $\mu$ goes to 1 of $H^m$. This gives the rotating Kepler problem. The latter problem was used in Belbruno (1981a). We do not use the rotating Kepler problem except for comparison which we do in detail in Remark 1.

2 Spatial lunar problem and main result

The three-dimensional restricted three-body problem in a rotating coordinate system with coordinates $q = (q_1, q_2, q_3) \in \mathbb {R}^3$ and momenta, $p = (p_1, p_2, p_3) \in \mathbb {R}^3$, for the motion of the zero mass particle $P_0$ is defined by the Hamiltonian system,

$$\begin{aligned}&\displaystyle H = \frac{1}{2}|p|^2-\frac{\mu }{|q-m|}-\frac{1-\mu }{|q-e|}+ \omega (q_1 p_2-q_2p_1) , \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle \dot{q} = H_p , \quad \dot{p} = - H_q, \end{aligned}$$

(2)

$^. \equiv d/dt$, $t \in \mathbb {R}^1$ is time, $H_p \equiv \partial H/\partial p$, where the masses of $P_1, P_2$ are normalized to be $m_1 = 1 - \mu , \quad m_2 = \mu$, respectively, $\mu \in (0,1]$. The center of mass is placed at the origin. $P_1, P_2$ are fixed on the $q_1$-axis at the respective locations, $e=(-\mu ,0,0), \quad m=(1-\mu ,0,0)$, where e, m denotes Earth, Moon, respectively. $\omega$ is the frequency of the rotating frame that is normalized to be 1, where we use $\omega$ for generality. A solution $\phi = \phi (t) \in \mathbb {R}^6$ of (2) lies on the 5-dimensional energy surface

$$\begin{aligned} \varSigma _H = \{ (q,p) \in \mathbb {R}^6 | H(q,p) = -h \}, \end{aligned}$$

(3)

where $h \in \mathbb {R}^1$ is a constant. (In nonsymplectic coordinates, H can be written in another form called the Jacobi integral).

Definition

The spatial lunar problem is defined by viewing the motion of $P_0$ from (2) to lie near $P_2$ and assuming that $\mu$ is small.

We will now show how to derive the spatial lunar problem as a limit case of the restricted three-body problem following the computation on page 77 of Frauenfelder and van Koert (2018), see also page 143-144 of Meyer et al. (2009). A translation T is made to center the coordinates at $P_2$ by moving $P_1$ to $e_1=(0,0,0)$ and $P_2$ to the origin: $\mathbf{q}_\mathbf{1}'=\mathbf{q}_\mathbf{1}- \mathbf{m}_\mathbf{1}, ~\mathbf{q}_\mathbf{2}'=\mathbf{q}_\mathbf{2}, ~\mathbf{q}_\mathbf{3}'=\mathbf{q}_\mathbf{3},~ \mathbf{p}_\mathbf{2}'=\mathbf{p}_\mathbf{2} - \mathbf{m}_\mathbf{1}, ~ \mathbf{p}_\mathbf{1}'=\mathbf{p}_\mathbf{1}, ~ \mathbf{p}_\mathbf{3}'=\mathbf{p}_\mathbf{3}.$ This is a symplectic map yielding a Hamiltonian, $H(T^{-1}(q', p'))$. We add a constant, $\frac{(1-\mu )^2}{2}$ to this Hamiltonian as this does not change the Hamiltonian vector field, and end up with $H_m(q', p')= H(T^{-1}(q', p')) + \frac{(1-\mu )^2}{2}$. For simplicity of notation, we replace $q', p'$ by q, p, not to be confused with previous notation.

Thus, the spatial lunar problem in translated $P_2$ centered coordinates can be represented as a Hamiltonian system, with Hamiltonian,

$$\begin{aligned} H_m = \frac{1}{2}|p|^2-\frac{\mu }{|q|} + \omega (q_1p_2-q_2p_1)-(1-\mu )\bigg (\frac{1}{\sqrt{(q_1+1)^2+q_2^2+q_3^2}}+q_1\bigg ). \end{aligned}$$

(4)

The flow is given by,

$$\begin{aligned} \dot{q} = {H_m}_p , \quad \dot{p} = - {H_m}_q . \end{aligned}$$

(5)

The energy surface $\varSigma _H$ becomes,

$$\begin{aligned} \varSigma _{H_m}= \{ (q,p) \in \mathbb {R}^6 | H_m(q,p) = -h \}. \end{aligned}$$

(6)

In order to study the flow in the coordinates (q, p) defined by $H_m$ near $P_2$, we magnify the flow near $P_2$ by the map, $M: (q,p) \rightarrow (\hat{q}, \hat{p})$,

$$\begin{aligned} M: \quad \hat{p} = \mu ^{-{\frac{1}{3}}}p, \quad \hat{q} = \mu ^{-{\frac{1}{3}}}q. \end{aligned}$$

(7)

Thus, for $\mu$ small, as we are assuming for this paper, the coordinates $(\hat{q}, \hat{p})$ are defined in a magnified neighborhood about $P_2$. This implies that when solutions are found in these coordinates, in the original coordinates (q, p), the solutions lie close to $P_2$ as determined by (7).

The transformation given by (7) is not symplectic. In order to obtain a Hamiltonian system in the coordinates $(\hat{p},\hat{q})$, it is noted that M is conformally symplectic with constant conformal factor $\mu ^{2/3}$. It is verified that a new Hamiltonian incorporating this magnification is given by,

$$\begin{aligned} H^\mu (\hat{q},\hat{p})=\mu ^{-2/3}(H_m(M^{-1}(\hat{p},\hat{q}))+1-\mu ). \end{aligned}$$

This can be simplified using a Taylor expansion. This follows since,

$$\begin{aligned} \begin{aligned} H^\mu (\hat{q},\hat{p})&=\frac{1}{2}|\hat{p}|^2-\frac{1}{|\hat{q}|}+ \omega (\hat{q}_1\hat{p}_2-\hat{q}_2\hat{p}_1)\\&\quad -\frac{1-\mu }{\mu ^{2/3}}\bigg (\frac{1}{\sqrt{(\mu ^{1/3} \hat{q}_1+1)^2+\mu ^{2/3}\hat{q}_2^2+\mu ^{2/3}\hat{q}_3^2}}+\mu ^{1/3}\hat{q}_1-1\bigg ). \end{aligned} \end{aligned}$$

(8)

It is verified that the term within the square root in the last term of $H^\mu$ can be written as $1+2\mu ^{1/3}\hat{q}_1+\mu ^{2/3}|\hat{q}|^2$. Setting $x = 2\mu ^{1/3}\hat{q}_1+\mu ^{2/3}|\hat{q}|^2$, and using the formula,

$$\begin{aligned} \frac{1}{\sqrt{1+x}}=1-\frac{x}{2}+\frac{3x^2}{8}+\mathcal {O}(x^3) \end{aligned}$$

for $|x| < 1,$ which is satisfied for $\mu$ sufficiently small, it is verified that,

$$\begin{aligned} \begin{aligned} H^\mu (\hat{q},\hat{p})&= \frac{1}{2}|\hat{p}|^2-\frac{1}{|\hat{q}|}+ \omega (\hat{q}_1\hat{p}_2-\hat{q}_2\hat{p}_1) +\frac{1}{2}|\hat{q}|^2-\frac{3}{2}\hat{q}_1^2+\mathcal {O}( {\mu }^{1/3} ), \end{aligned} \end{aligned}$$

(9)

where the term $\mathcal {O}({\mu }^{1/3} )$ is a real analytic function of $\hat{q}$ and ${\mu }^{1/3}$, and depends continuously on $\mu$. The Hamiltonian flow is given by,

$$\begin{aligned} \dot{\hat{q}} = {{H^\mu }_{\hat{p}} } , \quad \dot{\hat{p}} = - {H^\mu }_{\hat{q}}. \end{aligned}$$

(10)

The Hamiltonian flow takes place on fixed energy surfaces,

$$\begin{aligned} \varSigma _{H^{\mu }}(h) = \{ (\hat{q},\hat{p}) \in \mathbb {R}^6 | H^{\mu }(\hat{q},\hat{p}) = -h \}. \end{aligned}$$

(11)

It is remarked that setting $\mu = 0$ defines Hill’s Problem. For small $\mu$, the (rescaled) restricted three-body problem represents a perturbation of order $\mu ^{\frac{1}{3}}$.

The function $H^\mu (\hat{p},\hat{q})$ has the form of a Hamiltonian for a perturbed rotating Kepler problem similar to what occurs in the restricted three-body problem about the primary mass point. As was studied in Belbruno (1981a) for motion about the primary mass point $P_1$, this system for $\mu = 0$ has the $\hat{q}_3$-axis as an invariant submanifold for the flow for $\hat{q}(t), \hat{p}(t)$.

Let $\hat{\phi }^*(t)$ represent the solution on the $\hat{q}_3$-axis for $\mu = 0$. Setting $\hat{q}_k = 0, \hat{p}_k = 0 , k= 1,2,$ one obtains an integrable Hamiltonian system of 1 degree of freedom in the variables $(\hat{q}_3,\hat{p}_3)$. After regularizing collisions, $P_0$ moves to some finite distance d(h) from the origin, where $\dot{\hat{q}}_3 = 0$, and then falls back to $P_2$ for another collision. It continues to do this in a periodic fashion for all time. This defines a periodic consecutive collision orbit with energy $-h$ and with period $T^*$. As h varies, $T^* = T^*(h)$ varies in a continuous manner. In contrast to the family studied in Belbruno (1981a), the family studied here exists for all energies h. In particular, as h increases to 0, the distance d remains bounded. The family extends to positive energy h, and d tends to $\infty$ as h goes to $\infty$.²

In summary, the family of consecutive collision orbits for $\mu =0$ for System (10) on the $\hat{q}_3$-axis with frequency $T^*(h)$ lies on the energy surface $\varSigma _{H^{\mu }}(h)|_{\mu =0}$. This family is denoted by $\mathcal {F}^*(h)$ and an orbit of this family is labeled $\hat{\phi }^*(t,h)$. This orbit moves a maximal distance d(h). In the original system given by (5) one has a similar family of consecutive collision orbits for $\mu =0$ on the energy surface $\varSigma _{H_m}$ given by (6) which move close to $P_2$ to within $\mathcal {O}(\mu ^{1/3} )$.

We will prove the following theorem,

Theorem 1

On each fixed energy surface $\varSigma _{H^{\mu }}(h)$ for System (10), there exists a unique periodic orbit, $\hat{\phi }(t,h,\mu )$, for $\mu$ sufficiently small, where $\hat{\phi }(t,h, 0) = \hat{\phi }^*(t,h)$ and whose period $T(\mu )$ continuously tends to $T(0) = T^*$, provided the orbit $\hat{\phi }(t,h, 0)$ is non-degenerate. ($\varDelta \ne 0$ (see (13).)) The orbits of this family, $\mathcal {F}(h, \mu )$, are symmetric to the $\hat{q}_2\hat{q}_3$-plane, and $\mathcal {F}(h, 0) = \mathcal {F}^*(h)$. $\mathcal {F}(h, \mu )$ and $T(\mu )$ depend continuously on $\mu$ and in a real analytic fashion on ${\mu }^{1/3}$.

We will refer to the orbits of this theorem as polar orbits.

Remark 1

We shall see in the numerical section that the non-degeneracy condition appears to fail only twice: once for $h\le 0$, or once for $h>0$, see Figs. 1 and 6. This is in contrast to the polar orbit in the rotating Kepler problem, which becomes degenerate infinitely many times. This may seem surprising given the similarities between the Hamiltonians of Hill’s lunar problem and the rotating Kepler problem. However, we point out several important differences:

• 1. The rotating Kepler problem is completely integrable, whereas Hill’s lunar problem $H^0$ is not: the additional terms in the potential describe a tidal and centrifugal force.

• 2. The period of the polar orbit in the rotating Kepler problem goes to infinity as the Jacobi energy goes to 0. For Jacobi energy $h>0$, a regularized orbit moving on the z-axis escapes to infinity. In Hill’s lunar problem, the region consisting of the intersection of the Hill’s region with the z-axis (containing the origin) is bounded for all energies h. As a result consecutive collision orbits in Hill’s lunar problem are periodic for all energies h.

• 3. From a physical point of view, there is a large difference between these problems. In the rotating Kepler problem, the rotational term $q_1p_2-q_2p_1$ is due to the rotating coordinate system centered at the larger primary in 0. In Hill’s lunar problem, the center of rotation is infinitely far away: the physical meaning of the rotational term is hence more complicated, resulting in additional terms corresponding to a tidal/centrifugal force.

• 4. The orbits in Hill’s lunar problem become unstable for large h. Intuitively, the instability in the polar orbits in Hill’s lunar problem for large energies is easy to understand: for sufficiently large energy h they spend a considerable time away from the smaller primary centered at the origin, so that the tidal forces can destabilize the orbit.

2.1 Distance of orbits to the Moon

The map M given by (7) scales the coordinates of the periodic orbits by $\mu ^{{\frac{1}{3}}}$ when mapping back to the original (q, p) coordinates of (5). Thus for $\mu$ small, the periodic orbits remain close to $P_2$ to within the distance, $\rho = \mathcal {O}(\mu ^{{\frac{1}{3}}})$. This distance, however, is significant and can extend to the $L_1, L_2$ Lagrange points.

2.1.1 Bounded period and existence for all energies

We estimate the period of the polar orbit in Hill’s lunar problem. The rotational term drops out on the z-axis, so the energy equals

$$\begin{aligned} E_H=\frac{1}{2}\dot{z}^2+V(z), \end{aligned}$$

where we take Hill’s lunar potential restricted to the z-axis, given by $V(z)=-\frac{1}{z} + \frac{1}{2}z^2$. Fix the energy to the value h. The particle moves between $z=0$ and $z=d(h)$, where d(h) is a solution to $V(z)=h$. This equation is equivalent to the cubic equation

$$\begin{aligned} z^3-2hz-2=0, \end{aligned}$$

which clearly has a unique, positive solution, which can be found with Cardano’s formula. Using the energy, we can compute the speed, and find for the period

$$\begin{aligned} T^*=2\int _0^{d(h)}\frac{1}{\sqrt{2h-V(z)}}\mathrm {d}z =2\int _0^{d(h)}\frac{1}{\sqrt{2h+\frac{2}{z}-z^2}}\mathrm {d}z. \end{aligned}$$

This integral can be evaluated exactly using elliptic integrals as one may verify with a computer algebra system such as Maple. The expression is not too illuminating, and we will only establish a period bound here. We compute

$$\begin{aligned} \begin{aligned} T^*&\underset{u=z/d(h)}{=} 2\int _0^1 \frac{1}{\sqrt{2h+\frac{2}{d(h) u} - d(h)^2 u^2}} d(h) \mathrm {d}u\\&\qquad \le 2\int _0^1 \frac{1}{\sqrt{\frac{2h}{d(h)^2}+\frac{2}{d(h)^3}-u^2 } } \mathrm {d}u = 2\int _0^1 \frac{1}{\sqrt{1-u^2}} \mathrm {d}u=\pi \end{aligned} \end{aligned}$$

In other words, the polar orbit in Hill’s lunar problem has a uniform period bound holding for all h. Furthermore, this period bound is so small that the polar orbit always closes up before the rotational term can finish even one revolution. We shall see that the orbit still becomes degenerate due to the tidal and centrifugal force terms.

3 Proof

In this section, we prove Theorem 1. It is necessary to regularize the flow since the consecutive collision orbits for $\mu = 0$ collide with $P_2$. After that is done, making use of the symmetry of the orbits allows a section to be defined. The existence of the periodic orbit family then results from an application of the implicit function theorem.

The main Hamiltonian, $H^\mu (\hat{q},\hat{p})$, (9), in this paper that we want to regularize has a form similar to the Hamiltonian in Belbruno (1981a; Eq. 1, p. 397). The differences are that roles of the $q_1$ and $q_2$ axis are reversed, and (9) has the extra term,

$$\begin{aligned} E = +\frac{1}{2}|\hat{q}|^2-\frac{3}{2}\hat{q}_1^2 . \end{aligned}$$

This term is smooth(real analytic) at $\hat{q} = 0$ and will not affect the regularization.

It is remarked that the additional term $-E_{\hat{p}}$ is introduced to the Hamiltonian differential equations for $\dot{\hat{p}}$ that are not present in the Hamiltonian differential equation of $\dot{p}$ for Belbruno (1981a; Eq. 1, p. 397). Another notable difference in the Hamiltonians is that the additional perturbation terms in Belbruno (1981a; Eq. 1, p. 397) are $\mathcal {O}(\mu )$, whereas the perturbation terms in (9) are $\mathcal {O}({\mu }^{1/3})$ for $\mu$ small.

The idea of regularization is to make a symplectic transformation of the coordinates,

$$\begin{aligned} \hat{q} = F(P,Q), \hat{p} = G(P,Q), \end{aligned}$$

where $Q \in \mathbb {R}^3, P \in \mathbb {R}^3$ and a transformation of time $t \rightarrow s$, so that in the new coordinates, the Hamiltonian flow is well defined at collision.

In three degrees of freedom, regularizations are considerably more complex than in two degrees of freedom, where, for example, the Levi-Civita transformation can be readily applied. A regularization for three degrees of freedom is developed and applied in Belbruno (1981a) that is ideal for the collision at $P_2$, since, as noted, the Hamiltonian H in Belbruno (1981a) is very close to $H^\mu (\hat{q},\hat{p})$.

The regularization in Belbruno (1981a) is a higher dimensional Möbius transformation. It is represented in a clear manner by defining a Jordan algebra that serves as a generalization of the complex numbers. This is a nonassociative algebra defined on the space $\mathbb {A}_{n}$ which is isomorphic to $\mathbb {R}^{n+1}$ as a vector space. Its product structure is defined as follows. Write $z \in \mathbb {A}_{n}$ as

$$\begin{aligned} z = z_0 + i_1z_1 +i_2z_2 + \cdots + i_n z_n, \end{aligned}$$

$z_i \in \mathbb {R}^1$ for $i = 1,2,\ldots ,n$. The $\mathbb {R}$-linear multiplication is then defined by imposing

$$\begin{aligned} i_\alpha i_\beta = - \delta _{\alpha \beta }. \end{aligned}$$

Conjugation is defined as

$$\begin{aligned} \bar{z} = z_0 - i_1z_1 -i_2z_2 - \cdots - i_n z_n. \end{aligned}$$

One then obtains, $z\bar{z} = |z|^2 = z_0^2 + z_1^2 + \cdots + z_n^2$. Division is defined as

$$\begin{aligned} \frac{1}{z} = \frac{\bar{z}}{|z|^2} \end{aligned}$$

Although this algebra is commutative, it is nonassociative. A measure of the non-associativity is the ’associator’ $a = x(yz) - (xy)z$, x, y, z are each in $\mathbb {A}_{n}$. Since our variables are of three components, the case $n=2$ is of relevance, where $a = (x_2z_1 - x_1z_2)(i_1 y_2 - i_2 y_1)$. Further details are in Belbruno (1981a).

With coordinates in this Jordan algebra $\mathbb {A}_{2}$, we will obtain a simple form for a symplectic transformation that regularizes collisions. Since the axes in this paper differ from those in Belbruno (1981a), we first interchange the first two components: $\tilde{q}\equiv (\hat{q}_2,\hat{q}_1,\hat{q}_3)$ and $\tilde{p}\equiv (\hat{p}_2,\hat{p}_1,\hat{p}_3)$. After that, we use the transformation

$$\begin{aligned} \tilde{p} = {\frac{1+ P}{1 -P}}, \tilde{q} = {\frac{Q}{2}}(1- \bar{P})^2 - (QP)\bar{P} + Q(P\bar{P}). \end{aligned}$$

As in Belbruno (1981a), we will see that the Hamiltonian $\varGamma$ given by

$$\begin{aligned} \varGamma = (1/2)|P - (1,0,0)|^2|Q| (H^\mu +h) \end{aligned}$$

regularizes the energy level $H^\mu =-h$; we use the time transformation $t \rightarrow s$ given by $t = \int ^s|q| d\tau = (1/2)\int ^s|P - (1,0,0)|^2|Q|d\tau$ for the rescaling of the Hamiltonian. The new level set of interest, corresponding to $H^\mu =-h$ will be denoted by

$$\begin{aligned} \varSigma _\varGamma = \{(P,Q) \in \mathbb {R}^6| \varGamma = 0 \}. \end{aligned}$$

The new Hamiltonian has the form of Belbruno (1981a)(Equ. 22) with the addition of the term $\tilde{E}(Q,P)$. Here $\tilde{E}(Q,P)= \frac{1}{8} |P - (1,0,0)|^4|Q|^2 - \frac{3}{2}f^2(Q,P)$, where f(Q, P) is the first component of the transformation of $\tilde{q}$:

$$\begin{aligned} \begin{aligned} \varGamma&= {\frac{|Q|}{4}}\{|P+(1,0,0)|^2 + 2(h + \omega \alpha (Q,P))|P-(1,0,0)|^2 \} \\&\quad - 1 + (1/2) \tilde{E}(Q,P)|P - (1,0,0)|^2|Q| + \mathcal {O}(\mu ^{1/3}). \end{aligned} \end{aligned}$$

The Hamiltonian flow is defined by,

$$\begin{aligned} Q^{'} = \varGamma _P , P^{'} = - \varGamma _Q , \end{aligned}$$

where $\phantom { }^{'} \equiv {\frac{d}{ds}}$. To check that the Hamiltonian flow $X(s) = (Q(s), P(s))$ is regular at collision orbits, we note that collision occurs when $\hat{\phi }^*(t,h) = (\hat{q}^*(t),\hat{p}^*(t))$ tends to $(0,0,0;0,0, \infty )$. In the coordinates Q, P, any collision point corresponds to $P=(1,0,0)$ and $|Q|=1$; the collision point $X(0)=(0,0,-1;1,0,0)$. We see that the Hamiltonian $\varGamma$ is smooth near collision points, so the collision orbit, which we label by $X^*(s)$, is indeed regularized and becomes a well-defined periodic orbit on $\varSigma _\varGamma$. We denote its period by $S^*$.

The existence of a unique periodic orbit $X(s,X_0, \mu )$ near $X^*(s)$, $X(0,X_0, \mu ) = X_0$, of period S near $S^*$ for $\mu$ sufficiently small is obtained by the implicit function theorem, applied to the subset of symmetric orbits, as we shall now see.

The Hamiltonian flow is symmetric with respect to the $\hat{q}_1,\hat{q}_3$-plane, because the Hamiltonian $H^\mu$ is invariant under the map

$$\begin{aligned} t \rightarrow -t, \qquad (\hat{q}_1,\hat{q}_2,\hat{q}_3,\hat{p}_1,\hat{p}_2, \hat{p}_3) \rightarrow (\hat{q}_1,-\hat{q}_2,\hat{q}_3,-\hat{p}_1,\hat{p}_2, -\hat{p}_3). \end{aligned}$$

Keeping in mind our interchange of components, this implies that the involution

$$\begin{aligned} s \rightarrow -s, \qquad (Q_1,Q_2,Q_3,P_1,P_2, P_3) \rightarrow (-Q_1,Q_2,Q_3,P_1,-P_2, -P_3). \end{aligned}$$

preserves $\varGamma$. Solutions that are symmetric with respect to this involution are characterized by the condition,

$$\begin{aligned} Q_1(0) = P_2(0) = P_3(0) = 0. \end{aligned}$$

This means that symmetric solutions are characterized by three initial values $Q_2(0), Q_3(0), P_1(0).$ This can be reduced to two initial values on the energy surface near $X^*(0)$. Namely at $X^*(0)$ we can verify that

$$\begin{aligned} { \frac{\partial \varGamma }{\partial Q_3 } }= -1\ne 0. \end{aligned}$$

(12)

Thus, by the implicit function theorem, near $X^*(0)$, we can eliminate the $Q_3$ coordinate and characterize symmetric solutions by two initial values,

$$\begin{aligned} Q_2(0), P_1(0). \end{aligned}$$

In addition, the time of intersection of solutions near $X^*(0)$ can be determined from (12) as $s = s(Q_2, Q_3, P_1)$ by the implicit function theorem for $\mu$ sufficiently small.

This defines a three-dimensional surface of section

$$\begin{aligned} \mathcal {S} = \{ Q_2, Q_3, P_1 | Q_1(0) = P_2(0) = P_3(0) = 0 \} . \end{aligned}$$

A solution starting on this section at time $s =0$, then reintersecting the section at time $s = S/2$ yields a symmetric periodic orbit of period S. This is satisfied by the consecutive collision orbit, $X^*(s)$ with $s = S^*/2$. For this to be satisfied near $X^*(s)$ for small $\mu$ by a solution $X(s,X_0, \mu )$ yields a periodic orbit of period $S(\mu )$ near $S^*$, such that $S(0) = S^*$. This can be satisfied provided the determinant

$$\begin{aligned} \varDelta = det { \frac{\partial (Q_1, P_2, P_3)}{\partial (S, Q_2(0), P_1(0)) } } \end{aligned}$$

(13)

does not vanish at $\mu = 0, S = S^*/2, X(0) = X^*(0)$. When $\varDelta \ne 0$ is satisfied, we say that the periodic orbit $\hat{\phi }(t,h,0)$ is non-degenerate. It is numerically shown next, in Sect. 4, that $\hat{\phi }(t,h,0)$ is non-degenerate except for two values of h.

This concludes the proof of Theorem 1.

4 Numerical results

We start with a summary of the numerical results. Throughout, we will be comparing Hill’s lunar problem with the rotating Kepler problem. The reason for this is twofold.

• The same type of polar orbit has been studied before in Belbruno (1981a). Comparison will hence clarify differences and similarities.

• We can consider the two types of polar orbits as part of a larger family of periodic orbits in the restricted three-body problem. Both the rotating Kepler problem and Hill’s lunar problem are limit cases where the polar orbit has a particularly simple form.

Here is a list of the main results. We will write $H^0$ for Hill’s lunar problem and K for the rotating Kepler problem.

4.1 Stability properties for fixed $\mu$:

$H^0$::

The polar orbit goes through four bifurcations for $h\in (-\infty ,\infty )$: they are a period doubling bifurcation, a simple degeneracy, another simple degeneracy, and a period halving bifurcation. The polar orbit is elliptic for $h<-1.03$ and complex hyperbolic for $h>0.11$.³

K::

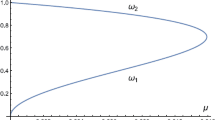
The polar orbit goes through infinitely many simple degeneracies for $h \in (-\infty ,0)$, and the orbit is elliptic for all $h<0$. Simple degeneracies occur whenever the period of the polar orbit is a multiple of $2\pi$, the rotation period of the coordinate system.

4.1.1 Variation of the family $\mathcal F(h, \mu )$ with fixed $\mu$ and varying h

We consider small deformations of Hill’s lunar Hamiltonian, i.e., small $\mu$ in $H^\mu$ and of the rotating Kepler problem, i.e., $\mu$ close to 1 in $H_m$.

$H^0$::

The polar orbit starts out as a very eccentric ellipse, staying near the z-axis: the projection to the xy-plane looks like an oval. After becoming degenerate twice, the orbit starts to develop a cusp in the yz-projection.

K::

The orbit also starts out as a very eccentric ellipse, near the z-axis: the projection to the xy-plane looks like an oval for very negative energy. As h increases, the shape ceases to be convex and the orbit becomes degenerate. With each degeneracy, the winding number of the polar orbit around 0 increases; in other words, the orbit accumulates loops as the Jacobi energy increases.

4.1.2 A bridge between polar orbits in the rotating Kepler problem and the restricted three-body problem near the light primary

Suppose that we are given a smooth 1-parameter family of vector fields depending on a parameter s. In analogy with the results of Schmidt (1972), we will refer to a smooth 1-parameter family of periodic orbits $\gamma _s$ of $X_s$ as a bridge for $\gamma _s$ varying between $\gamma _0$ and $\gamma _1$.

For energy $h\le -1.50$⁴ we will see that there is a bridge with constant Jacobi energy h connecting polar orbits near the smaller primary, meaning small $\mu$ in $H_m$, to polar orbits in the rotating Kepler problem, meaning $\mu =1$ for the Hamiltonian $H_m$. The orbits near the smaller primary can be continued to Hill’s lunar problem after rescaling the coordinates.

For very negative Jacobi energy, this bridge does not involve any dynamical transitions. For larger Jacobi energy, orbits near the light primary are hyperbolic, whereas orbits in the rotating Kepler problem are elliptic, so this bridge necessarily involves bifurcations.

4.1.3 Non-collision polar orbits in the Moon–Earth system

We continue the polar orbit into the Moon–Earth system where the polar orbit turns out to be a physical non-collision orbit for sufficiently high Jacobi energy. A plot of the periapsis and apoapsis as function of the energy is given in Fig. 13. It also undergoes a period doubling bifurcation, making a transition from stable to unstable in the same energy range.

4.2 Details concerning the numerical procedure

4.2.1 Regularization scheme

We will use the Moser–Belbruno–Osipov regularization scheme to regularize the flow. We use the incarnation due to Moser, which we will refer to as just Moser regularization, and the incarnation due to Belbruno specialized to collision orbits as in Belbruno (1981a), which we will refer to as Belbruno transform; this scheme is described in Sect. 3. Both schemes are detailed in the appendices.

As a short summary, the Moser scheme regularizes the energy hypersurface below the critical value to the unit cotangent bundle of the three-sphere and has the advantage that it is global, i.e., no local charts are needed (see Appendix). However, to do computations in the Moser scheme we need to impose constraints to stay on this space, which we view as a submanifold of $T^*\mathbb {R}^{4}$; this leads to a slightly larger computational effort.

The Belbruno transform uses a generalized Möbius transformation, based on the Jordan algebra described in Sect. 3. For this regularization scheme, the advantages and disadvantages as described above are reversed. The scheme is local and gives a chart, which some orbits could escape from. On the other hand, the Belbruno regularization does not require constraints.

4.2.2 Integration scheme

For numerical integration, we have used a Taylor integrator with both variable stepsize and order. The typical order with a double and long double, which corresponds to about 15–16 digits and 18–19 digits precision, respectively, was between 20 and 30. We have used three different implementations of the Taylor integrator: the Taylor translator described in Jorba and Zou (2005), the CAPD-library, CAPD (2018), and a homegrown Taylor library.

To find periodic orbits for $\mu >0$, we made use of a local surface of section and the familiar homotopy method to follow solutions from $\mu =0$ to the desired value of $\mu$ in sufficiently steps of $\mu$. We choose a linear surface of section perpendicular to the z-axis. This is useful to follow the orbits for large parameter changes. As usual, we followed the orbit until it crossed the surface of section and found a more accurate intersection by normalizing the flow.

For the stability analysis of the polar orbit, we choose a symmetric surface of section in line with the proof in Sect. 3. This has the advantage that the symmetry properties can be exploited more effectively.

A final remark concerning the Hamiltonian: for the lunar problem we use the regularization of $H^\mu$, the Hamiltonian given in (8), but some care has to be taken to deal with the catastrophic cancelation in the final term.

4.3 Detailed results

4.3.1 Non-degeneracy of the lunar and Kepler orbit for $h\le 0$

To apply the theorem, we need to know whether the non-degeneracy condition holds. To check this, we numerically compute the linearized return map transverse to the flow. We can represent this as a symplectic $4\times 4$-matrix, so its eigenvalues have some symmetry properties. Namely, if $\lambda$ is an eigenvalue of a symplectic $4\times 4$-matrix, then $\bar{\lambda }$, $1/\lambda$ and $1/\bar{\lambda }$ are also eigenvalues (possibly equal). In general, this leaves a lot of possibilities. However, it turns out that the linearized return map is elliptic, i.e., all eigenvalues lie on the unit circle, for very negative energies h. The behavior for the lunar problem, which is of primary interest here, turns out to differ from the behavior in the rotating Kepler problem studied in Belbruno (1981a).

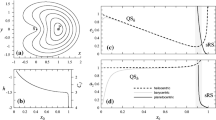
See Fig. 1 for the eigenvalues in the lunar problem. For very negative energies, the return map is elliptic. For $h\sim -1.03$, the orbit goes through a period doubling/halving bifurcation: the orbit goes from being purely elliptic to mixed elliptic/negative hyperbolic without becoming degenerate; its double cover does become degenerate.

At energy $h\sim -0.86$, the orbit itself becomes degenerate resulting in a positive hyperbolic/negative hyperbolic pair of eigenvalues.

Fig. 1

The real part of the four eigenvalues for $\mu =0$, the lunar problem, as a function of the energy h in the Hamiltonian $H^{\mu }$ for $h\le 0$. Bifurcations from an elliptic to a hyperbolic eigenvalue appear twice

This is in contrast to the situation for the rotating Kepler problem, where the orbit stays elliptic up to $h=0$. Furthermore, the polar orbit in the rotating Kepler problem becomes degenerate infinitely many times as the energy goes to 0, and its behavior changes every time when it does. This results in loops appearing in the perturbations of the rotating Kepler problem. This behavior was found by Belbruno in Belbruno (1981a). We include an illustration for the convenience of the reader in Fig. 3. Most of the other illustrations of the orbits will involve only projections to the xy- and yz-plane.

Fig. 2

The real part of two eigenvalues for $\mu =1$, the rotating Kepler problem, as a function of the energy h in the Hamiltonian $H_m$. All eigenvalues are elliptic, and bifurcations occur whenever an eigenvalue passes through 1

Remark 2

The plot in Fig. 2 was obtained through numerical means, and we want to point out that one can obtain an analytical expression for the eigenvalues of the linearized return map.

Fig. 3

A periodic polar orbit in RTBP for large mass ratio, close to the rotating Kepler problem. This orbit has picked up many loops as described in Sect. 4. On the right, the xy- and yz-projections of the orbit. The xz-projection can be found in Fig. 4

Fig. 4

The xz-projection of the orbit from Fig. 3

4.3.2 Stability properties of the polar orbit in the lunar problem for $h>0$

In Hill’s lunar problem, the polar orbit remains a periodic orbit for $h>0$, and its stability properties there are very interesting. To understand the situation, recall that eigenvalues of a symplectic matrix come with symmetries as mentioned in Sect. 4.2.1. In the spatial problem, there are four eigenvalues, and an orbit can lose stability without becoming degenerate by the following mechanism:

• 1. at parameter $h_1$ all eigenvalues are elliptic, i.e., on the unit circle.

• 2. as the parameter $h\rightarrow h_1$ the eigenvalues stay elliptic, but they collide in pairs: i.e., there are only two distinct eigenvalues (Fig. 4).

• 3. for $h>h_1$ the eigenvalues move off the unit circle as sketched in Fig. 5.

Fig. 5

Collision of eigenvalues

It turns out that this mechanism occurs in for Hill’s lunar problem for $h>0$.

Fig. 6

Bifurcation of the polar orbit for $h>0$ in Hill’s lunar problem: the real part of the four eigenvalues of the linearized return map

We briefly explain the bifurcation points in Fig. 6.

• a the orbit becomes degenerate and goes from being hyperbolic/negative hyperbolic to elliptic/negative hyperbolic for $h\sim 0.044$.

• b the orbit goes through a period doubling/halving bifurcation: it goes from elliptic/negative hyperbolic to elliptic/elliptic for $h\sim 0.091$.

• c the orbit goes through an eigenvalue collision for $h\sim 0.11$ and the eigenvalues move for away from the unit circle. They do not appear to return to the unit circle, so stability seems to be lost for large $h>0$. Beyond point c, the eigenvalues move “freely” in the complex plane, so the real part has then little meaning by itself. In particular, the additional “intersection” is not an intersection in the complex plane.

Remark 3

The same mechanism of losing stability takes place for small $\mu >0$.

4.4 Bifurcations

Let $\gamma _h$ denote the polar orbit in Hill’s lunar problem as a function of the energy h. We have found the following bifurcation behavior of $\gamma _h$:

• 1. a period doubling/halving bifurcation for $h\in [-1.025245,-1.025225]$ and in the interval [0.0909615, 0.0909616].

• 2. a simple degeneracy in two intervals, namely for $h\in [-0.85556,-0.85555]$ and for $h\in [0.043843, 0.043844]$.

• 3. an eigenvalue collision for $h\in [0.109989, 0.109990]$.

We verified this statement using a computer-assisted argument with interval arithmetic to obtain rigorous error bounds. This method was also used in for example Kapela and Simó (2007). The above bifurcations of the polar orbit $\gamma _h$ are recognized by noting that in each case we have a specific behavior of the eigenvalues of the linearized return map. Namely,

• 1. In this case, the linearized return map has an eigenvalue equal to $-1$ for some parameter in the given interval, and a pair of eigenvalues moves from the unit circle to the positive real axis or vice versa.

• 2. In this case, the linearized return map has an eigenvalue equal to 1 for some parameter in the given interval, and a pair of eigenvalues moves from the unit circle to the positive real axis or vice versa.

• 3. In this case, the linearized return map has two eigenvalues on the unit circle that are equal, and not equal to $-1$ or 1 for some parameter in the given interval, and in addition, the corresponding pairs of eigenvalues move away from the unit circle.

We have proceeded by making the proof from Sect. 3 more quantitative, and we have used the linearized flow to obtain a tight enclosure of the return map. Such a scheme is similar to the rigorous bifurcation results in the Rössler system obtained in Wilczak and Zgliczyński (2009). We will briefly outline how we deduced the bifurcations. After obtaining an enclosure for the return map using the linearized flow, we have computed the coefficients of the characteristic polynomial of the restriction of the linearized flow to a transverse slice. Let us denote this restriction by $\psi$. The characteristic polynomial of $\psi$ is given by

$$\begin{aligned} \chi (\psi )(x)=x^4-s_1(\psi )x+s_2(\psi )x^2-s_3(\psi )x+\det (\psi ). \end{aligned}$$

Here $s_i(\psi )$ denotes the elementary symmetric polynomial in the roots of the characteristic polynomial of degree i, so $s_1(\psi )=Tr(\psi )$. A $4\times 4$ symplectic matrix satisfies $\det (\psi )=1$ and $s_3(\psi )=s_1(\psi )$. Hence we can compute the entire characteristic polynomial by just computing $s_1$ and $s_2$. Using the standard formula for a quadratic polynomial, we find all roots with good error bounds. Based on numerical experiments, we obtain the following.

Observation 1

The orbit is elliptic for $h<-1.03$ and complex hyperbolic for $h>0.11$

Although we have checked the statement for some finite intervals using interval arithmetic, we do not have a full proof that works for all energies.

4.4.1 Evolution of the polar orbit as a function of the energy

Here we fix a small mass parameter $\mu >0$, namely $\mu =10^{-10}$ in the figures, and vary the energy. We plot the projection to the xy-plane and to the yz-plane, and look at the evolution as function of the energy. The typical situation for $h<0$ is drawn in Fig. 7. For $h\ge 0$, the typical situation is drawn in Fig. 8 with the pointed tip in the yz-plane becoming more pronounced as the energy increases.

Fig. 7

The xy- and the yz-projection of a periodic polar orbit in the lunar problem: $\mu =10^{-10}$ and $h=-1.5$

Fig. 8

The xy- and the yz-projection of a periodic polar orbit in the lunar problem: $\mu =10^{-10}$ and $h=+8.0$

Remark 4

Periodic polar solutions can be found in Hill’s lunar problem for all energies, even for $h>0$. Indeed, the Hill’s region becomes unbounded, but remains bounded in the z-direction. This is of course not true for the restricted three-body problem, which we will discuss next.

4.4.2 Solutions for the restricted three-body problem

The solutions we find for the rescaled Hamiltonian $H^\mu$ can be continued to larger $\mu$ as solutions for the unrescaled problem. The energy is rescaled, and periodic polar orbits do not exist for all energies anymore. Indeed, for $h>0$ the orbits will typically escape a given region around the masses.

For small $\mu$ and suitably rescaled energy, the behavior of the orbits is of course the same as before. We will just mention one case that is of particular interest, namely the case $\mu \sim 0.01215$, which is the mass ratio of the Moon/Earth. We found that the periodic polar orbit can be continued to sufficiently large $h\sim -1.52$ such that it is no longer a physical collision orbit. This value of the Jacobi energy exceeds that of the first critical value. A 3d-plot of this orbit is given in Fig. 9.

Fig. 9

A periodic polar orbit in RTBP for the mass ratio Moon–Earth. The minimal distance to the center of the Moon, the black ball, is 4389 km. This orbit is mixed elliptic/negative hyperbolic. Projections to the xy- and yz-plane are drawn on the right. The projection to the xz-plane is drawn in Fig. 10

Fig. 10

The projection to the xz-plane of the orbit from Fig. 9

We also remark that solutions in the restricted three-body problem include the families discussed in Belbruno (1981a). In the next section, we see that the new family from the main theorem is for some energies a continuation of an orbit found in Belbruno (1981a).

4.4.3 Evolution of the polar orbit as a function of $\mu$

Here we fix the Jacobi energy of the Hamiltonian $H_m$ and start at small, and small positive $\mu$ at a near collision orbit. We will investigate how the polar orbit $\gamma _\mu$ evolves as $\mu$ changes from small values to $\mu =1$. This gives part of a bridge connecting the polar orbits from this paper to the polar orbits from Belbruno (1981a).

Remark 5

We point out that the part of the bridge indicated in the figures here is in the unrescaled problem. In other words, we are using the Hamiltonian $H_m$ rather than $H^\mu$.

The bridge is constructed using a numerical homotopy. The homotopy becomes more difficult to carry out, i.e., smaller parameter steps are needed, for larger h. In particular, for h close to $-1.5$, the period of polar orbits near the smaller primary becomes very large.

We make the following observations

• When h is sufficiently negative, e.g., $h<-2$, there are no bifurcations in the evolution of the polar orbit as the mass parameter goes from small $\mu$ to large $\mu$. In particular, $\gamma _\mu$ is elliptic in this case.

• The projection of the orbit $\gamma _\mu$ to the xy-plane grows in area as $\mu$ increases until the area reaches a maximum near $\mu \sim 0.5$, after which the projection shrinks to a point for $\mu =1$ (which is collision orbit). This is illustrated in xy-projections of Figs. 11 and 12. Also note that the projection of the orbit does not bound a convex region for large $\mu$.

• For larger Jacobi energy h, the polar orbit in the lunar problem becomes hyperbolic, whereas the polar orbit in the rotating Kepler problem, i.e., $H_m$ with $\mu =1$, remains elliptic. For these values of h, a bridge involves bifurcations.

Fig. 11

The xy- and yz-projection of an orbit in the bridge from lunar to rotating Kepler: for $h=-2.0$ as $\mu$ varies from 0 to 0.5

Fig. 12

The xy- and yz-projection of an orbit in the bridge from lunar to rotating Kepler: for $h=-2.0$ as $\mu$ varies from 0.5 to 1.0

4.4.4 Periapsis, apoapsis for Moon–Earth system

We approximate the Moon–Earth system with the restricted three-body problem. For the distance Earth–Moon we take 386,000 km. Following the above scheme, we find the polar orbit as a function of the Jacobi energy. It turns out that the polar orbit does not collide with the Moon for sufficiently large energy. We have included a plot of the periapsis and of the apoapsis of the polar orbit.

Fig. 13

Periapsis (left) and apoapsis (right) in km as function of the Jacobi energy. At the light blue line, the orbit just hits the surface of the Moon (taken to have a radius of 1716 km), and at the dark blue line, the orbit reaches a periapsis that is at least 50 km above the surface

The stability properties of the polar orbit in the Moon-Earth system, though similar to those of the Hill’s lunar system, are plotted in Fig. 14. The bifurcation point indicates a period doubling/halving bifurcation.

Fig. 14

The real part of the eigenvalues of the linearized return map for the polar orbit in the Moon–Earth system as function of the Jacobi energy

The effect of the instability that appears after the period doubling/halving bifurcation is indicated in Fig. 15.

Fig. 15

An orbit starting close to the periodic polar orbit: it is shifted by about 400 km in the y-direction (orbits are fairly stable under shifts in the x-direction), and followed for five periods of the polar orbit

We make the following observation: the periapsis of the polar orbit exceeds 1766 km (just 50km above the surface of the Moon) just before losing stability. The values are so close though that the approximations we made (circular restricted three-body problem) most likely spoil stability of a physical non-collision orbit.

Appendices

Appendix: Regularization in coordinates

Moser regularization is based on $n-$dimensional stereographic projection. The position and momentum variables are given by $q = (q_1, q_2, \ldots , q_n) \in \mathbb {R}^n$ , $p = (p_1, p_2, \ldots , p_n) \in \mathbb {R}^n$. We denote by $(q,p) \in T^*\mathbb {R}^n$ a point in the (co)-tangent bundle of $\mathbb {R}^n$, where we think of $\mathbb {R}^n$ as a chart for $S^n = \{|\xi |^2 = \varSigma _{i=0}^{n} \xi _i^2 = 1\}$, $\xi = (\xi _0, \xi _1, \ldots , \xi _n)$. We set $x= - p$ and $y=q$, and define the (co)-tangent bundle of $S^n$ as

$$\begin{aligned} T^*S^n =\{ (\xi ,\eta ) \in T^*\mathbb {R}^{n+1} ~|~ |\xi |^2 =1 , \quad \langle \xi ,\eta \rangle \equiv \varSigma _{i=0}^{n} \xi _i \eta _i = 0 \}. \end{aligned}$$

To go from $T^*S^n$ to $T^*\mathbb {R}^n$ we use the map

$$\begin{aligned} \begin{aligned} x&= \frac{\tilde{\xi }}{1-\xi _0} \\ y&= \eta _0 \tilde{\xi } +(1-\xi _0) \tilde{\eta } , \end{aligned} \end{aligned}$$

(14)

where $\tilde{\xi } = (\xi _1, \xi _2, \ldots , \xi _n)$. Collision corresponds to $\xi _0 = 1$.

To go from $T^*\mathbb {R}^n$ to $T^*S^n$, we use the inverse given by

$$\begin{aligned} \begin{aligned} \xi _0&= \frac{|x|^2-1}{|x|^2+1} \\ \tilde{\xi }&= -\frac{2 x}{|x|^2+1} \\ \eta _0&= -\langle x,y \rangle \\ \tilde{\eta }&= \frac{|x|^2+1}{2}y - \langle x, y \rangle x . \end{aligned} \end{aligned}$$

(15)

The Belbruno transform employs a Möbius transformation which sends to the collision point $|p| = \infty$ to $P=(1,0,\ldots ,0)\in \mathbb {R}^n$. In coordinates for three dimensions (the index $j=2,3$), the forward Belbruno transformation is given by

$$\begin{aligned} \begin{aligned} Q_1&= \frac{1-|p|^2}{2}q_1 +\langle q, p\rangle (p_1+1) \\ Q_j&= \frac{|p|^2 + 1}{2}q_j + p_1 q_j - p_j q_1 - \langle q, p\rangle p_j\\ P_1&= \frac{|p|^2 -1 }{|p+1|^2} \\ P_j&= \frac{2p_j}{|p+1|^2} . \end{aligned} \end{aligned}$$

The inverse Belbruno transform is given by

$$\begin{aligned} \begin{aligned} q_1&= \frac{1-|P|^2}{2}Q_1 + \langle Q,P\rangle (P_1 - 1)\\ q_j&= \frac{|P|^2 +1}{2}Q_j - P_1 Q_j + P_j Q_1 - \langle Q,P\rangle P_j\\ p_1&= \frac{1-|P|^2}{ |P-1|^2 } \\ p_j&= \frac{2P_j}{ |P-1|^2 } . \end{aligned} \end{aligned}$$

Appendix: Hamiltonian vector field with constraints

The setup is the following. We are given a manifold M, which is a symplectic submanifold of the symplectic manifold $(N,\varOmega )$. We denote the inclusion by $\iota : M\rightarrow N$, and the induced symplectic form on M by $\omega :=\iota ^*\varOmega$. We assume that $M=f_1^{-1}(0) \cap f_2^{-1}(0)$. In addition, we are given a Hamiltonian function $H_N:N \rightarrow \mathbb {R}$, and we have the induced Hamiltonian $H_M=\iota ^*H_N$. In our case $N=T^*\mathbb {R}^{n+1}$ and $M:=T^*S^n$.

The functions that define M are

$$\begin{aligned} f_1=\frac{1}{2} |\xi |^2-\frac{1}{2},\quad f_2=\langle \xi ,\eta \rangle . \end{aligned}$$

In our case, the symplectic manifold $N=T^*\mathbb {R}^{n+1}$ has a global chart, but $T^*S^n$ has not. We will give a formula for the Hamiltonian vector field $X_H$ on M in terms of Hamiltonian vector field on N. In our example, this means that we can use the global coordinates on $N=T^*\mathbb {R}^{n+1}$. We have

$$\begin{aligned} X_H=X_{H_N}+c_1 X_{f_1}+c_2 X_{f_2}, \end{aligned}$$

(16)

where

$$\begin{aligned} \begin{aligned} X_{H_N}&=\sum _{j=0}^n \frac{\partial H_N}{\partial \eta _j} \frac{\partial }{\partial \xi _j}-\frac{\partial H_N}{\partial \xi _j} \frac{\partial }{\partial \eta _j} \\ X_{f_1}&=\sum _{j=0}^n \frac{\partial f_1}{\partial \eta _j} \frac{\partial }{\partial \xi _j}-\frac{\partial f_1}{\partial \xi _j} \frac{\partial }{\partial \eta _j} = -\sum _j \xi _j \frac{\partial }{\partial \eta _j}\\ X_{f_2}&=\sum _{j=0}^n \frac{\partial f_2}{\partial \eta _j} \frac{\partial }{\partial \xi _j}-\frac{\partial f_2}{\partial \xi _j} \frac{\partial }{\partial \eta _j} = \sum _j \xi _j \frac{\partial }{\partial \xi _j}-\eta _j \frac{\partial }{\partial \eta _j}\\ c_1&= \frac{df_2(X_{H_N})}{df_2(X_{f_1})} = -\frac{ \{ f_2,H_N\} }{\{ f_1,f_2\}} = -\{ f_2, H_N\} \\ c_2&= \frac{df_1(X_{H_N})}{df_1(X_{f_2})} = \frac{ \{ f_1,H_N\} }{\{ f_1,f_2\}} = \{ f_1, H_N\} . \end{aligned} \end{aligned}$$

The Poisson brackets defined by $\{ f, g\}:=\omega (X_f, X_g\}$ are of course not needed to do the computations, but they clarify the situation if M is a symplectic submanifold of higher codimension, where a matrix filled with $\{ f_i, f_j \}$ has to be inverted. A computation shows that the above vector field is tangent to the submanifold M and that it is the Hamiltonian vector field.