Optimal impulsive time-fixed transfers around the libration points of the restricted three-body problem

Abstract

A methodology is proposed to design optimal time-fixed impulsive transfers in the vicinity of the L2 libration point of the Earth-Moon system, taking the construction of a space station around the collinear libration points as the background. The approximate analytical expression of motions around the L2 point in the CRTBP is given, and the expression in the ERTBP is derived by linearizing the dynamical equations for the purpose of expanding the methodology from the CRTBP to the ERTBP. Thus, the approximate analytical solution of the transfer between two points is obtained by substituting the position vectors of the two points into the expression, which solves the Lambert problem in the three-body system. Furthermore, the transfer between different orbits is constructed by parameterization of the position vectors with the amplitudes and phases of the initial orbit and the final orbit. The transfers are optimized such that the total velocity increment required to implement the transfer exhibits a global minimum. The values of variables involved in the optimal transfers are determined by the unconstrained minimization of a function of one or nine variables using a multivariable search technique. To numerically ensure that the transfers are accurate and to eliminate the linearization bias, the differential correction and SQP method are employed. The optimality of the transfers is determined lastly by the primer vector theory. Simulations of point-to-point transfers, Lissajous-to-Lissajous transfers, halo-to-halo transfers and Lissajous-to-halo transfers are made. The results of this study indicate that the approximate analytical solutions, as well as the differential correction and SQP method, are valid in the design of the optimal transfers around the libration points of the restricted three-body problem.

1 Introduction

Deep space exploration has attracted increasing attention from scientists and engineers in recent years with the rapid development of aerospace technology. Different from the traditional near-Earth aerospace activities based on the two-body problem, deep space exploration is primarily based on the three-body problem, for which the most commonly used models of motion are the circular restricted three-body problem (CRTBP) and the elliptic restricted three-body problem (ERTBP). Due to the special positions of the libration points of the restricted three-body problem, the periodic or quasi-periodic orbits around these points can provide ideal sites to locate a space station, place astronomy telescopes, or perform other applications such that the Sun-Earth/Moon barycentre system and the Earth-Moon system have become the gateway of the Interplanetary Superhighway (IPS). Meanwhile, the construction of a space station on the periodic orbits in the vicinity of collinear libration points of the Earth-Moon system appears increasingly likely, for which the orbit rendezvous (or orbit transfer) technique is clearly necessary. With increasing interest in such trajectories, efficient transfers in the restricted three-body problem may offer more options and flexibility in trajectory design. Therefore, the study of orbit transfers in the three-body system is of great value, both in theory and for engineering applications.

Due to the dynamical properties of the three-body problem, orbit transfers around the libration points might be considerably more complex and significantly different from transfers between low Earth orbits. In comparison to a low Earth orbit, the libration point orbit is not centred by a heavy celestial body but by an equilibrium point; therefore, the gravitational field is notably shallow, and its periodic motion takes a considerably longer time than a low Earth orbit. Additionally, because of the non-dominant gravitational field, the position relation of the Sun or other planets with respect to the Earth and the Moon might affect the motion of the spacecraft.

However, considering the promising applications of libration points, some previous literature entries have involved transfer problems of libration point orbits. In general, there are two types of transfers, namely, impulsive transfers and low-thrust transfers.

With respect to impulsive transfers, Pernicka (1990) briefly examined superior transfers between two nearly periodic halo orbits about a collinear libration point in the ERTBP. The research utilizes a trial-and-error method to determine a path that approximately connects the specified departure and arrival locations. Gómez et al. (1991) used manifold theory to study an inferior transfer between halo orbits about a collinear libration point in the CRTBP. Sato et al. (2015) proposed a chaser’s rendezvous strategy by making a chaser phase along the reference halo orbit, similar to a rendezvous in a low Earth orbit. Hiday-Johnston and Howell (1996) developed a transfer methodology that uses a portion of a Lissajous orbit to connect the initial halo orbit and the final halo orbit. Gómez et al. (1991), Sato et al. (2015), and Davis (2009) used manifold theory to study the transfer between halo orbits about a collinear libration point in the CRTBP. Sukhanov and Prado (2004) solved the three-body Lambert problem by correcting the position vectors of the starting point and ending point simultaneously. Sun et al. (2017) utilized a genetic algorithm to improve the poor convergence of the current three-body Lambert algorithm. Zeng and Zhang (2016) applied the techniques associated with stable manifold and lunar flyby to the construction of optimal transfers to Earth-Moon L1/L2 libration point orbits.

With respect to low-thrust transfers, Peng et al. (2014) presented the nonlinear closed-loop feedback control strategy for the spacecraft rendezvous between libration point orbits in the Sun-Earth barycentre system with finite low thrust. Peng et al. (2011) transformed the nonlinear optimal control problem of rendezvous into a nonlinear two-point boundary value problem and solved it by symplectic adaptive algorithm. Lian and Tang (2013a, 2013b) and Lian et al. (2012) studied the problem of libration point orbit rendezvous using terminal sliding mode control. Qu et al. (2017) investigated a gradient-based design methodology for low-thrust trajectories with the help of invariant manifolds and halo orbit of LL1 point.

In addition, Zhang et al. (2013) studied the low-energy and low-thrust transfer between halo orbits associated with two coupled three-body systems through the invariant manifolds. Ulybyshev (2016) applied the pseudo-impulse set method to obtain the low-thrust rendezvous trajectories in the vicinity of the Earth-Moon L2 (EML2) libration point. Cao et al. (2017) presented a convenient procedure for designing the direct transfer trajectory from LL2 halo orbit to a low lunar orbit.

To summarize, although the study of orbit transfers in the three-body system still remains relatively unexplored, the literature regarding transfers in the three-body system has yielded some achievements through numerical methods or by transforming the transfer problem into a kind of control problem. Nevertheless, as is well-known, analytical methods play an important role in space missions, especially in orbit design. Hence, this research is directed towards developing a new, analytical and generalized methodology to design optimal impulsive time-fixed transfers in the vicinity of collinear libration points of the restricted three-body problem.

This paper is organized as follows. In Sect. 1, the background of the transfer problem in the restricted three-body problem and some previous literature entries are introduced. Section 2 illustrates the restricted three-body problem, including the CRTBP model, the ERTBP model, and the derived analytical expression of motion around the collinear libration points in both the CRTBP and ERTBP. In Sect. 3, the formulations of the impulsive time-fixed transfers between two points and between two orbits are respectively given, and the solutions for optimal transfers are then obtained theoretically. Four types of transfers, namely, point-to-point transfers, Lissajous-to-Lissajous transfers, halo-to-halo transfers and Lissajous-to-halo transfers, are simulated to verify the validity and generality of the methodology in Sect. 4. Finally, the conclusions of this study, as well as a brief discussion regarding future efforts, are presented in Sect. 5.

2 Restricted three-body problem

The restricted three-body problem (RTBP) describes the motion of an infinitesimal particle or spacecraft (called the third body), which is governed in the gravitational field generated by two massive primaries. Because the mass of the third body is too small, its gravitational attraction to the primaries can be ignored. Then, the motions of the primaries around their barycentre can be approximated as Keplerian orbits. The most commonly used models are the CRTBP and ERTBP. When the orbit of the primaries around their barycentre is circular, the problem is called the CRTBP. When the orbit of the primaries is elliptic, the problem is called the ERTBP. The Earth-Moon system is chosen to be the three-body system in this study.

2.1 Approximate analytical solutions in the CRTBP

The basic and most used model in the restricted three-body problem is the CRTBP, which is usually used to study the dynamic characteristic and the basic motions in the three-body problem; therefore, the model representing the actual forces acting on the spacecraft is first chosen to be the CRTBP model for the Earth-Moon system.

From the viewpoint of computation accuracy and simplification of equations of motion, the normalization is performed first by taking the total mass of the primaries, their distance, and reciprocal of the mean motion as unity, as shown in Eq. (1), such that the gravitational constant and the period of the motion of the primaries are 1 and $2\pi$, respectively.

$$ \left\{ \textstyle\begin{array}{l} M^{ *} = m_{1} + m_{2} \\ L^{ *} = L_{12} = a \\ T^{ *} = \sqrt{\frac{a^{3}}{G(m_{1} + m_{2})}} = \frac{1}{n} \end{array}\displaystyle \right. $$

(1)

where $M^{ *}$, $L^{ *}$, and $T^{ *}$ represent the unit of mass, length, and time, respectively. $m_{1}$ and $m_{2}$ denote the masses of the two primaries, $L_{12}$ denotes the distance between them, $a$ denotes the semi-major axis of the orbit of the primaries, $G$ denotes the gravitational constant, $n$ denotes the mean motion of the primaries.

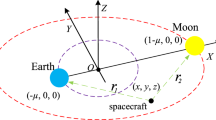
The dynamics of the CRTBP are usually studied in the barycentric synodic coordinate system $O - XYZ$ (see Fig. 1). In this coordinate system, the origin is located at the barycentre of the primaries, the $X$-axis joins the primaries and directs from the massive primary $m_{1}$ towards the secondary $m_{2}$, the $Z$-axis is parallel to the angular momentum vector of the primaries, and the $Y$-axis completes the right-handed triad.

Fig. 1

Barycentric synodic coordinate system $O - XYZ$ and L2-centred synodic coordinate system $L_{2} - xyz$

In the barycentric synodic coordinate system $O - XYZ$, $\boldsymbol{X} = [X,Y,Z]^{T}$ represents the position vector of a spacecraft, $\dot{\boldsymbol{X}} = [\dot{X},\dot{Y},\dot{Z}]^{T}$ represents the velocity vector, and the differential equations of motion of a spacecraft in the CRTBP take the form

$$ \left\{ \textstyle\begin{array}{l} \ddot{X} - 2\dot{Y} = \frac{\partial \Omega}{\partial X} \\ \ddot{Y} + 2\dot{X} = \frac{\partial \Omega}{\partial Y} \\ \ddot{Z} = \frac{\partial \Omega}{\partial Z} \end{array}\displaystyle \right. $$

(2)

where $\Omega$ denotes the pseudo-potential function, which is shown in Eq. (7).

To further study the motion of a spacecraft around the L2 point, another coordinate system is defined as the L2-centred synodic reference system $L_{2} - xyz$ (see Fig. 1), which is analogous to the synodic coordinate system $O - XYZ$ but centred at L2. Let $\boldsymbol{x} = [x,y,z]^{T}$ and $\dot{\boldsymbol{x}} = [\dot{x},\dot{y},\dot{z}]^{T}$ represent the position vector and velocity vector of a spacecraft in the L2-centred synodic reference system. The transformation between the two vectors $\boldsymbol{x} = [x,y,z]^{T}$ and $\boldsymbol{X} = [X,Y,Z]^{T}$ is shown below

$$ \left\{ \textstyle\begin{array}{l} x = (X - X_{2}) \\ y = Y \\ z = Z \end{array}\displaystyle \right. $$

(3)

where $X_{2}$ denotes the distance between the L2 and the barycentre $O$ of the system.

According to Gómez (2001), the approximate analytical expressions, obtained by linearizing the dynamical equations, for the motions around the collinear libration point can be written as

$$ \left\{ \textstyle\begin{array}{l} x(t) = A_{1}\mathrm{e}^{\lambda_{1}t} + A_{2}\mathrm{e}^{ - \lambda_{1}t} \\ \quad + A_{3}\cos (\operatorname{Im} (\lambda_{3})t) + A_{4}\sin (\operatorname{Im} (\lambda_{3})t) \\ y(t) = k_{1}A_{1}\mathrm{e}^{\lambda_{1}t} - k_{1}A_{2}\mathrm{e}^{ - \lambda_{1}t} \\ \quad - k_{2}A_{3}\sin (\operatorname{Im} (\lambda_{3})t) + k_{2}A_{4}\cos (\operatorname{Im} (\lambda_{3})t) \\ z(t) = A_{5}\cos (\operatorname{Im} (\lambda_{5})t) + A_{6}\sin (\operatorname{Im} (\lambda_{5})t) \end{array}\displaystyle \right. $$

(4)

where $A_{i}(i = 1, \ldots 6)$ are integration constants determined by the initial state of the spacecraft and represent the parameters of a Lissajous orbit in the following sections, and $\lambda_{1}, \lambda_{3}, \lambda_{5}$ are the eigenvalues of the linearized system.

Equation (4) will be used hereinafter to design the optimal impulsive time-fixed transfers when the model of motion is chosen to be the CRTBP.

2.2 Approximate analytical solutions in the ERTBP

The eccentricity of the motions of the primaries is taken into account in the ERTBP; therefore, the ERTBP is more accurate than the CRTBP. To expand the methodology from the CRTBP to the ERTBP, the model representing the actual forces acting on the spacecraft is subsequently chosen to be the ERTBP for the Earth-Moon system.

Similarly, the normalization is also performed first by taking the total mass of the primaries, their instantaneous distance, and reciprocal of the mean motion as unity, as shown in Eq. (5), such that the period of the motion of the primaries is $2\pi$.

$$ \left\{ \textstyle\begin{array}{l} M^{ *} = m_{1} + m_{2} \\ L^{ *} = L_{12} = \frac{a(1 - e^{2})}{1 + e\cos f} \\ T^{ *} = \sqrt{\frac{a^{3}}{G(m_{1} + m_{2})}} = \frac{1}{n} \end{array}\displaystyle \right. $$

(5)

where $L_{12}$ denotes the instantaneous distance between the primaries, $a$ denotes the semi-major axis of the orbit of the primaries, $e$ denotes the eccentricity, $f$ denotes the true anomaly and is taken as the time-like independent variable, $n$ denotes the mean motion of the primaries.

Obviously, the normalization is pulsating and beneficial to study basic characteristics of the motions in the ERTBP.

To successfully expand the methodology from the CRTBP to the ERTBP, the approximate analytical expressions for motions around the collinear libration point in the ERTBP must be obtained.

The dynamics of the ERTBP are usually studied in the barycentric pulsating synodic coordinate system (Szebehely 1967), which is defined in the same way as the barycentric synodic coordinate system in the CRTBP, so O-XYZ also represents the barycentric pulsating synodic coordinate system in the ERTBP. The differential equations of motion of a spacecraft in the ERTBP (Szebehely 1967) take the form

$$ \left\{ \textstyle\begin{array}{l} \ddot{X} - 2\dot{Y} = \frac{1}{1 + e\cos f}\Omega_{X} \\ \ddot{Y} + 2\dot{X} = \frac{1}{1 + e\cos f}\Omega_{Y} \\ \ddot{Z} + Z = \frac{1}{1 + e\cos f}\Omega_{Z} \end{array}\displaystyle \right. $$

(6)

where $\Omega$ is also the pseudo-potential function and is defined as

$$ \Omega = \frac{1}{2}[X^{2} + Y^{2} + Z^{2} + \mu (1 - \mu )] + \frac{1 - \mu}{r_{1}} + \frac{\mu}{r_{2}} $$

(7)

The pulsating normalization and the barycentric pulsating synodic coordinate system are two common techniques for the ERTBP when the eccentricity is relatively small, just like the Earth-Moon system.

More details about the equations of dynamics can be found in Szebehely (1967). According to Szebehely (1967), the positions of the five libration points in the pulsating synodic coordinate system in the ERTBP are the same as the positions of the five libration points in the synodic coordinate system in the CRTBP, so the next step is to linearize the dynamical model (6) at the collinear libration points $L_{i}(i = 1,2,3)$ in the L2-centred pulsating synodic reference system, which is defined in the same way as the L2-centred synodic reference system and also denoted as $L_{2} - xyz$.

$$ \dot{\boldsymbol{x}} = \frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}}|_{\boldsymbol{X} = \boldsymbol{X}_{L_{i}}}\boldsymbol{x} = D_{L_{i}}\boldsymbol{x} + \mathrm{H}.\mathrm{O}.\mathrm{T} $$

(8)

where H.O.T denotes High-Order-Terms and can be ignored; therefore, Eq. (8) can be expanded as

$$ \dot{\boldsymbol{x}} = \left[ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \Omega_{X,X} & \Omega_{X,Y} & \Omega_{X,Z} & 0 & 2 & 0 \\ \Omega_{X,Y} & \Omega_{Y,Y} & \Omega_{Y,Z} & - 2 & 0 & 0 \\ \Omega_{X,Z} & \Omega_{Y,Z} & \Omega_{Z,Z} & 0 & 0 & 0 \end{array}\displaystyle \right]\boldsymbol{x} $$

(9)

where $\Omega_{i,j}(i,j = X,Y,Z)$ denote the second partial derivatives of the pseudo-potential $\Omega$ with respect to three axes $X$, $Y$ and $Z$.

With regard to collinear libration points, substituting $Y = Z = 0$ into Eq. (9), yields

$$ \dot{\boldsymbol{x}} = \left[ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ g(1 + 2\bar{\mu} ) & 0 & 0 & 0 & 2 & 0 \\ 0 & g(1 - \bar{\mu} ) & 0 & - 2 & 0 & 0 \\ 0 & 0 & g( - \bar{\mu} ) + k & 0 & 0 & 0 \end{array}\displaystyle \right]\boldsymbol{x} $$

(10)

where

$$ \left\{ \textstyle\begin{array}{l} g = \frac{1}{1 + e\cos f}, k = \frac{ - e\cos f}{1 + e\cos f} \\ \bar{\mu} = \frac{1 - \mu}{\left| X + \mu \right|^{3}} + \frac{\mu}{\left| X + \mu - 1 \right|^{3}} > 1 \end{array}\displaystyle \right. $$

(11)

The eigenvalues ($\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4},\lambda_{5},\lambda_{6}$) of the linearized system are obtained through the ordinary differential equation theory, as shown in Eq. (12).

$$ \left\{ \textstyle\begin{array}{l} \lambda_{1} = - \lambda_{2} = \sqrt{\frac{2g + g\bar{\mu} - 4 + \sqrt{9g^{2}\bar{u}^{2} - 8g\bar{u} - 16g + 16}}{2}} \\ \lambda_{3} = - \lambda_{4} = i\sqrt{\frac{ - 2g - g\bar{\mu} + 4 + \sqrt{9g^{2}\bar{u}^{2} - 8g\bar{u} - 16g + 16}}{2}} \\ \lambda_{5} = - \lambda_{6} = i\sqrt{g\bar{u} - k} \end{array}\displaystyle \right. $$

(12)

The corresponding eigenvectors take the form shown in Eq. (13).

$$ \left\{ \textstyle\begin{array}{l} \boldsymbol{v}_{1} = \left[ \textstyle\begin{array}{cccccc} 1 & \eta_{1} & 0 & \lambda_{1} & \eta_{2} & 0 \end{array}\displaystyle \right]^{\mathrm{T}} \\ \boldsymbol{v}_{2} = \left[ \textstyle\begin{array}{cccccc} 1 & - \eta_{1} & 0 & - \lambda_{1} & \eta_{2} & 0 \end{array}\displaystyle \right]^{\mathrm{T}} \\ \boldsymbol{v}_{3} = \left[ \textstyle\begin{array}{cccccc} 1 & \eta_{3} & 0 & \lambda_{3} & \eta_{4} & 0 \end{array}\displaystyle \right]^{\mathrm{T}} \\ \boldsymbol{v}_{4} = \left[ \textstyle\begin{array}{cccccc} 1 & - \eta_{3} & 0 & - \lambda_{3} & \eta_{4} & 0 \end{array}\displaystyle \right]^{\mathrm{T}} \\ \boldsymbol{v}_{5} = \left[ \textstyle\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & \lambda_{5} \end{array}\displaystyle \right]^{\mathrm{T}} \\ \boldsymbol{v}_{6} = \left[ \textstyle\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & - \lambda_{5} \end{array}\displaystyle \right]^{\mathrm{T}} \end{array}\displaystyle \right. $$

(13)

where $\eta_{1},\eta_{2},\eta_{3},\eta_{4}$ can be obtained when calculating the corresponding eigenvectors.

Finally, the approximate analytical expressions for the motions around the collinear libration point in the ERTBP are obtained as shown in Eq. (14).

$$ \left\{ \textstyle\begin{array}{c} x(f) = A_{1}\mathrm{e}^{\lambda_{1}f} + A_{2}\mathrm{e}^{ - \lambda_{1}f} + \\ A_{3}\cos (\operatorname{Im} (\lambda_{3})f) + A_{4}\sin (\operatorname{Im} (\lambda_{3})f) \\ y(f) = k_{1}A_{1}\mathrm{e}^{\lambda_{1}f} - k_{1}A_{2}\mathrm{e}^{ - \lambda_{1}f} - \\ k_{2}A_{3}\sin (\operatorname{Im} (\lambda_{3})f) + k_{2}A_{4}\cos (\operatorname{Im} (\lambda_{3})f) \\ z(f) = A_{5}\cos (\operatorname{Im} (\lambda_{5})f) + A_{6}\sin (\operatorname{Im} (\lambda_{5})f) \end{array}\displaystyle \right. $$

(14)

As can be seen from Eq. (14) and Eq. (4), the expressions for motions around the collinear libration points in the ERTBP have the same forms as those in the CRTBP, with differences being that the independent variables are different and relevant parameters have different values. So, it can be assured that the method of constructing optimal impulsive time-fixed transfers in the CRTBP can also be applied into the ERTBP; therefore, in this instance, the CRTBP is taken as the research object to save space.

3 Formulation of the optimal impulsive time-fixed transfer

The essence of the impulsive orbit transfer problem is essentially the Lambert problem. Although it has been proved that there is no precise analytical solution for the three-body Lambert problem due to the strong-linearity and instability of the three-body problem, an approximate solution is derived here through the expression for motions around the collinear libration point in the restricted three-body problem. Considering that the basic case of the Lambert problem is transfer between two points, so point-to-point transfer is studied first.

3.1 Point-to-point transfer

Suppose that there are two points $A$ and $B$ around a collinear libration point and that the epochs are set to be $t_{1}$ and $t_{2}$, respectively; their states in the L2-centred synodic frame are denoted as $\boldsymbol{x}_{A}$ and $\boldsymbol{x}_{B}$.

$$ \left\{ \textstyle\begin{array}{l} \boldsymbol{x}_{A} = \left[ \textstyle\begin{array}{cccccc} x_{A} & y_{A} & z_{A} & V_{Ax} & V_{Ay} & V_{Az} \end{array}\displaystyle \right]^{\mathrm{T}} \\ \boldsymbol{x}_{B} = \left[ \textstyle\begin{array}{cccccc} x_{B} & y_{B} & z_{B} & V_{Bx} & V_{By} & V_{Bz} \end{array}\displaystyle \right]^{\mathrm{T}} \end{array}\displaystyle \right. $$

(15)

The transfer trajectory connecting $A$ and $B$ can be expressed by the expression for motions mentioned above, Eq. (4) for the CRTBP and Eq. (14) for the ERTBP. Both Eq. (4) and Eq. (14) contain six parameters [$A_{1},A_{2},A_{3},A_{4}, A_{5},A_{6}$], and after substituting the positions of $A$ and $B$ into Eq. (4), the formulation of the relation can be written as Eq. (16). And ($\lambda_{3},\lambda_{4},\lambda_{5},\lambda_{6}$) denote their imaginary part in Sect. 3.1 for simplification.

$$ \left\{ \textstyle\begin{array}{l} x_{A} = A_{1}\mathrm{e}^{\lambda_{1}t_{1}} + A_{2}\mathrm{e}^{ - \lambda_{1}t_{1}} + A_{3}\cos \lambda_{3}t_{1} + A_{4}\sin \lambda_{3}t_{1} \\ y_{A} = k_{1}A_{1}\mathrm{e}^{\lambda_{1}t_{1}} - k_{1}A_{2}\mathrm{e}^{ - \lambda_{1}t_{1}} \\ \quad - k_{2}A_{3}\sin \lambda_{3}t_{1} + k_{2}A_{4}\cos \lambda_{3}t_{1} \\ z_{A} = A_{5}\cos \lambda_{5}t_{1} + A_{6}\sin \lambda_{5}t_{1} \\ x_{B} = A_{1}\mathrm{e}^{\lambda_{1}t_{2}} + A_{2}\mathrm{e}^{ - \lambda_{1}t_{2}} + A_{3}\cos \lambda_{3}t_{2} + A_{4}\sin \lambda_{3}t_{2} \\ y_{B} = k_{1}A_{1}\mathrm{e}^{\lambda_{1}t_{2}} - k_{1}A_{2}\mathrm{e}^{ - \lambda_{1}t_{2}}\\ \quad - k_{2}A_{3}\sin \lambda_{3}t_{2} + k_{2}A_{4}\cos \lambda_{3}t_{2} \\ z_{B} = A_{5}\cos \lambda_{5}t_{2} + A_{6}\sin \lambda_{5}t_{2} \end{array}\displaystyle \right. $$

(16)

The six parameters [$A_{1},A_{2},A_{3},A_{4},A_{5},A_{6}$] can be calculated by solving Eq. (16), and the result is shown in Eq. (17).

$$ \left[ \textstyle\begin{array}{c} A_{1} \\ A_{2} \\ A_{3} \\ A_{4} \\ A_{5} \\ A_{6} \end{array}\displaystyle \right] = \left[\small \textstyle\begin{array}{cccccc} \mathrm{e}^{\lambda_{1}t_{1}} & \mathrm{e}^{ - \lambda_{1}t_{1}} & \cos \lambda_{3}t_{1} & \sin \lambda_{3}t_{1} & 0 & 0 \\ k_{1}\mathrm{e}^{\lambda_{1}t_{1}} & - k_{1}\mathrm{e}^{ - \lambda_{1}t_{1}} & - k_{2}\sin \lambda_{3}t_{1} & k_{2}\cos \lambda_{3}t_{1} & 0 & 0 \\ 0 & 0 & 0 & 0 & \cos \lambda_{5}t_{1} & \sin \lambda_{5}t_{1} \\ \mathrm{e}^{\lambda_{1}t_{2}} & \mathrm{e}^{ - \lambda_{1}t_{2}} & \cos \lambda_{3}t_{2} & \sin \lambda_{3}t_{2} & 0 & 0 \\ k_{1}\mathrm{e}^{\lambda_{1}t_{2}} & - k_{1}\mathrm{e}^{ - \lambda_{1}t_{2}} & - k_{2}\sin \lambda_{3}t_{2} & k_{2}\cos \lambda_{3}t_{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \cos \lambda_{5}t_{2} & \sin \lambda_{5}t_{2} \end{array}\displaystyle \right]^{ - 1} \left[ \textstyle\begin{array}{c} x_{A} \\ y_{A} \\ z_{A} \\ x_{B} \\ y_{B} \\ z_{B} \end{array}\displaystyle \right] $$

(17)

Differentiating Eq. (4) and substituting them with Eq. (17), the required velocities of $A$ and $B$ on the transfer trajectory are denoted as $[V_{xA},V_{yA},V_{zA}]^{T}$ and $[V_{xB},V_{yB}, V_{zB}]^{T}$, respectively, and can then be obtained by Eq. (18).

$$ \left[ \textstyle\begin{array}{c} V_{xA} \\ V_{yA} \\ V_{zA} \\ V_{xB} \\ V_{yB} \\ V_{zB} \end{array}\displaystyle \right] = \left[ \textstyle\begin{array}{cccccc} \lambda_{1}\mathrm{e}^{\lambda_{1}t_{1}} & - \lambda_{1}\mathrm{e}^{ - \lambda_{1}t_{1}} & - \lambda_{3}\sin \lambda_{3}t_{1} & \lambda_{3}\cos \lambda_{3}t_{1} & 0 & 0 \\ k_{1}\lambda_{1}\mathrm{e}^{\lambda_{1}t_{1}} & k_{1}\lambda_{1}\mathrm{e}^{ - \lambda_{1}t_{1}} & - k_{2}\lambda_{3}\cos \lambda_{3}t_{1} & - k_{2}\lambda_{3}\sin \lambda_{3}t_{1} & 0 & 0 \\ 0 & 0 & 0 & 0 & - \lambda_{5}\sin \lambda_{5}t_{1} & \lambda_{5}\cos \lambda_{5}t_{1} \\ \lambda_{1}\mathrm{e}^{\lambda_{1}t_{2}} & - \lambda_{1}\mathrm{e}^{ - \lambda_{1}t_{2}} & - \lambda_{3}\sin \lambda_{3}t_{2} & \lambda_{3}\cos \lambda_{3}t_{2} & 0 & 0 \\ k_{1}\lambda_{1}\mathrm{e}^{\lambda_{1}t_{2}} & k_{1}\lambda_{1}\mathrm{e}^{ - \lambda_{1}t_{2}} & - k_{2}\lambda_{3}\cos \lambda_{3}t_{2} & - k_{2}\lambda_{3}\sin \lambda_{3}t_{2} & 0 & 0 \\ 0 & 0 & 0 & 0 & - \lambda_{5}\sin \lambda_{5}t_{2} & \lambda_{5}\cos \lambda_{5}t_{2} \end{array}\displaystyle \right] \left[ \textstyle\begin{array}{c} A_{1} \\ A_{2} \\ A_{3} \\ A_{4} \\ A_{5} \\ A_{6} \end{array}\displaystyle \right] $$

(18)

Equation (18) is exactly the derived approximate analytical solution for the three-body Lambert problem. Although this approximate solution is not the precise analytical solution, it can be used to design the precise transfer in combination with the differential correction and sequential quadratic programming (SQP) method in the next sections.

Just like the two-body Lambert problem, the three-body Lambert problem is also only determined by the positions of $A$ and $B$, which are $[x_{A},y_{A},z_{A}]^{T}$ and $[x_{B},y_{B},z_{B}]^{T}$, respectively, and the time of flight (TOF) $\Delta t = t_{2} - t_{1}$.

Substituting Eq. (17) into Eq. (18), the more detailed expression for the velocities of $A$ and $B$ on the transfer trajectory, denoted as $[V_{xA},V_{yA},V_{zA}]^{T}$ and $[V_{xB},V_{yB},V_{zB}]^{T}$, respectively, are shown in Eq. (19).

$$ \left\{\textstyle\begin{array}{l} V_{xA} = \{ [2k_{2}^{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3}) - 2k_{1}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) + 2k_{1}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - \\ \quad 2k_{1}k_{2}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3})]x_{A} + [2k_{2}\lambda_{1} + 2k_{1}\lambda_{3} - 2k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) - \\ \quad 2k_{1}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) + 2k_{1}\lambda_{1}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1})]y_{A} + \\ \quad {} [2k_{1}^{2}\lambda_{3}\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}^{2}\lambda_{1}\sin (\Delta_{t}\lambda_{3}) + 2k_{1}k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3}) - 2k_{1}k_{2}\lambda_{1}\sinh (\Delta_{t}\lambda_{1})]x_{B} + \\ \quad {}[2k_{1}\lambda_{3}\cos (\Delta_{t}\lambda_{3}) - 2k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3}) + 2k_{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1}) - 2k_{1}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})]y_{B} \} / \\ \quad {}[4k_{1}k_{2} + 2k_{1}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 4k_{1}k_{2}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1})] \\ V_{yA} = - \{ [2k_{1}k_{2}^{2}\lambda_{3} - 2k_{1}^{2}k_{2}\lambda_{1} + 2k_{1}^{2}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) - 2k_{1}k_{2}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) + \\ \quad 2k_{1}k_{2}^{2}\lambda_{1}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) + 2k_{1}^{2}k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1})]x_{A} + {}[2k_{1}^{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3}) - \\ \quad 2k_{2}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{1}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) + 2k_{1}k_{2}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3})]y_{A} + \\ \quad {} [2k_{1}^{2}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3}) + 2k_{1}k_{2}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3}) - 2k_{1}^{2}k_{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1}) - 2k_{1}k_{2}^{2}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})]x_{B} + \\ \quad {} [2k_{2}^{2}\lambda_{3}\sinh (\Delta_{t}\lambda_{1}) - 2k_{1}^{2}\lambda_{1}\sin (\Delta_{t}\lambda_{3}) - 2k_{1}k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3}) + 2k_{1}k_{2}\lambda_{1}\sinh (\Delta_{t}\lambda_{1})]y_{B}\} / \\ \quad {} [4k_{1}k_{2} + 2k_{1}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 4k_{1}k_{2}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1})] \\ V_{zA} = \{ \lambda_{5}[z_{B} - \cos (\Delta_{t}\lambda_{5})z_{A}]\} /\sin (\Delta_{t}\lambda_{5}) \\ V_{xB} = \{ [2k_{1}k_{2}\lambda_{1}\sinh (\Delta_{t}\lambda_{1}) - 2k_{1}k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3}) + 2k_{2}^{2}\lambda_{1}\sin (\Delta_{t}\lambda_{3}) - 2k_{1}^{2}\lambda_{3}\sinh (\Delta_{t}\lambda_{1})]x_{A} + \\ \quad {} [ 2k_{1}\lambda_{3}\cos (\Delta_{t}\lambda_{3}) - 2k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3}) + 2k_{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1}) - 2k_{1}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})]y_{A} + \\ \quad {} [2k_{1}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}^{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3}) - 2k_{1}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) + \\ \quad 2k_{1}k_{2}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3})]x_{B} + [2k_{2}\lambda_{1} + 2k_{1}\lambda_{3} - 2k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) - \\ \quad 2k_{1}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) + 2k_{1}\lambda_{1}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1})]y_{B}\} / \\ \quad {} [4k_{1}k_{2} + 2k_{1}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 4k_{1}k_{2}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1})] \\ V_{yB} = - \{ [2k_{1}^{2}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3}) + 2k_{1}k_{2}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3}) - 2k_{1}^{2}k_{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1}) - 2k_{1}k_{2}^{2}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})]x_{A} + \\ \quad {} [2k_{1}^{2}\lambda_{1}\sin (\Delta_{t}\lambda_{3}) - 2k_{2}^{2}\lambda_{3}\sinh (\Delta_{t}\lambda_{1}) + 2k_{1}k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3}) - 2k_{1}k_{2}\lambda_{1}\sinh (\Delta_{t}\lambda_{1})]y_{A} + \\ \quad {}[2k_{1}k_{2}^{2}\lambda_{3} - 2k_{1}^{2}k_{2}\lambda_{1} + 2k_{1}^{2}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) - 2k_{1}k_{2}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1}) + \\ \quad 2k_{1}k_{2}^{2}\lambda_{1}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) + 2k_{1}^{2}k_{2}\lambda_{3}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1})]x_{B} + {} [2k_{2}^{2}\lambda_{3}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - \\ \quad 2k_{1}^{2}\lambda_{1}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3}) + 2k_{1}k_{2}\lambda_{1}\cos (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{1}k_{2}\lambda_{3}\cosh (\Delta_{t}\lambda_{1})\sin (\Delta_{t}\lambda_{3})]y_{B}\} / \\ \quad {} [4k_{1}k_{2} + 2k_{1}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 2k_{2}^{2}\sin (\Delta_{t}\lambda_{3})\sinh (\Delta_{t}\lambda_{1}) - 4k_{1}k_{2}\cos (\Delta_{t}\lambda_{3})\cosh (\Delta_{t}\lambda_{1})] \\ V_{zB} = - \{ \lambda_{5}[z_{A} - \cos (\Delta_{t}\lambda_{5})z_{B}]\} /\sin (\Delta_{t}\lambda_{5}) \end{array}\displaystyle \right. $$

(19)

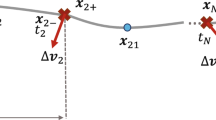
Suppose that $A$ is the starting point (or departure point) and $B$ is the ending point (or arrival point) on the transfer trajectory. The sketch map of the transfer trajectory is shown in Fig. 2.

Fig. 2

Sketch map of the transfer trajectory

Let $\boldsymbol{V}_{A0}= [V_{Ax}, V_{Ay}, V_{Az}]^{\mathrm{T}}$ and $\boldsymbol{V}_{B0}= [V_{Bx}, V_{By}, V_{Bz}]^{\mathrm{T}}$ represent the initial velocities (before transfer) of $A$ and $B$, respectively. The transfer trajectory is then patched between the two points $A$ and $B$ such that the entire resulting trajectory (starting point $A$, transfer path, ending point $B$) is continuous in position but contains two velocity discontinuities at the patch points. The two velocity differences of $A$ and $B$ are denoted as $\Delta \boldsymbol{V}_{A}$ and $\Delta \boldsymbol{V}_{B}$, representing the two velocity impulses required to implement the transfer, namely,

$$ \left\{ \textstyle\begin{array}{l} \Delta \boldsymbol{V}_{A} = \left[ \textstyle\begin{array}{ccc} V_{xA} & V_{yA} & V_{zA} \end{array}\displaystyle \right]^{\mathrm{T}} - \left[ \textstyle\begin{array}{ccc} V_{Ax} & V_{Ay} & V_{Az} \end{array}\displaystyle \right]^{\mathrm{T}} \\ \Delta \boldsymbol{V}_{B} = \left[ \textstyle\begin{array}{ccc} V_{Bx} & V_{By} & V_{Bz} \end{array}\displaystyle \right]^{\mathrm{T}} - \left[ \textstyle\begin{array}{ccc} V_{xB} & V_{yB} & V_{zB} \end{array}\displaystyle \right]^{\mathrm{T}} \end{array}\displaystyle \right. $$

(20)

The total velocity increment $\Delta V$ is the sum of two velocity impulses $\Delta \boldsymbol{V}_{A}$ and $\Delta \boldsymbol{V}_{B}$.

$$ \textstyle\begin{array}{l} \Delta V = \sqrt{(V_{xA} - V_{Ax})^{2} + (V_{yA} - V_{Ay})^{2} + (V_{zA} - V_{Az})^{2}} + \\ \sqrt{(V_{Bx} - V_{xB})^{2} + (V_{By} - V_{yB})^{2} + (V_{Bz} - V_{zB})^{2}} \end{array} $$

(21)

In practical engineering applications, the total velocity increment $\Delta V$ and TOF $\Delta t$, both required for a transfer trajectory, are two important mission parameters, especially in deep space exploration; therefore, a transfer accomplished with the greatest economy of fuel and the shortest TOF is always desirable. Hence, the optimality criterion is selected to be the sum of the velocity increment $\Delta V$ and the TOF $\Delta t$.

$$ J = p\Delta V + q\Delta t = F(\Delta t) $$

(22)

where $J$ denotes the cost function, $p$ and $q$ denote the weights of the total velocity increment $\Delta V$ and the TOF $\Delta t$, respectively.

In the problem of point-to-point transfer, although the positions of $A$ and $B$ are fixed, the TOF is variable, which means that different TOFs will result in different transfers; therefore, it is highly significant to obtain the optimal transfer trajectory by optimizing the TOF.

3.2 Orbit-to-orbit transfer

Practical orbit transfers in real space missions are transferring a spacecraft from one orbit to another, rather than the simple point-to-point transfer. Thus, it is necessary to study transfers between different orbits, and many more factors will be taken into account than point-to-point transfer, in which the only variable is the TOF.

In the restricted three-body problem, there are a total of three types of periodic and pseudo-periodic orbits around the collinear libration points, i.e., Lissajous orbits, halo orbits and Lyapunov orbits. From the view of the essence of the dynamics, halo orbits and Lyapunov orbits are bifurcations of Lissajous orbits, which means that halo orbits and Lyapunov orbits are actually two subsets of Lissajous orbits; therefore, the method used in Lissajous-to-Lissajous transfer is representative and must also be suitable for halo-to-halo transfer, Lyapunov-to-Lyapunov transfer, and even transfers between these three types of orbits. Therefore, to save space but without loss of generality, the orbit-to-orbit transfer takes the Lissajous-to-Lissajous transfer as an example to show the process of optimizing orbit-to-orbit transfer.

According to Gómez (2001) and Eq. (4), to construct periodic orbits, Eq. (23) must be satisfied.

$$ A_{1} = 0,A_{2} = 0 $$

(23)

Thus, the approximate analytical expressions for periodic orbits around the collinear libration points take the simpler form

$$ \left\{ \textstyle\begin{array}{c} x(t) = A_{3}\cos (\operatorname{Im} (\lambda_{3})t) + A_{4}\sin (\operatorname{Im} (\lambda_{3})t) \\ y(t) = - k_{2}A_{3}\sin (\operatorname{Im} (\lambda_{3})t) + k_{2}A_{4}\cos (\operatorname{Im} (\lambda_{3})t) \\ z(t) = A_{5}\cos (\operatorname{Im} (\lambda_{5})t) + A_{6}\sin (\operatorname{Im} (\lambda_{5})t) \end{array}\displaystyle \right. $$

(24)

Transforming Eq. (24) into the form of amplitudes and phases yields

$$ \left\{ \textstyle\begin{array}{c} x(t) = A_{x}\cos (\operatorname{Im} (\lambda_{3})t + \varphi_{0}) = A_{x}\cos \varphi \\ y(t) = - k_{2}A_{x}\sin (\operatorname{Im} (\lambda_{3})t + \varphi_{0}) = - k_{2}A_{x}\sin \varphi \\ z(t) = A_{z}\cos (\operatorname{Im} (\lambda_{5})t + \psi_{0}) = A_{z}\cos \psi \end{array}\displaystyle \right. $$

(25)

where $A_{x}$ denotes the $x$-amplitude, $A_{z}$ denotes the $z$-amplitude, $\varphi_{0}$ denotes the initial phase in the $xy$-plane, $\varphi$ denotes the real-time phase in the $xy$-plane, $\psi_{0}$ denotes the initial phase in the $z$-axis, and $\psi$ denotes the real-time phase in the $z$-axis.

$$ \left\{ \textstyle\begin{array}{l} \varphi = \operatorname{Im} (\lambda_{3})t + \varphi_{0} \\ \psi = \operatorname{Im} (\lambda_{5})t + \psi_{0} \end{array}\displaystyle \right. $$

(26)

Equation (25) is the approximate analytical expression of periodic and pseudo-periodic orbits, i.e., the Lissajous orbits, halo orbits, and Lyapunov orbits, in the form of amplitudes and phases. On this basis, when it comes to Lissajous-to-Lissajous transfer, we can see that the variables that need to be optimized are the amplitudes and phases of the initial orbit and final orbit, in the $xy$-plane and $z$-axis, and the TOF. Thanks to Eq. (25) and Eq. (26), the starting point $A$ and the ending point $B$ can be parameterized when calculating the optimal Lissajous-to-Lissajous transfer, that is, any point on the initial orbit and the final orbit can be described as a function of the amplitudes $A_{x},A_{z}$ and the phases $\varphi,\psi$.

Thus, the position vector of the starting point $A$ takes the form

$$ \left\{ \textstyle\begin{array}{l} x_{A}(t) = A_{x1}\cos \varphi_{1} \\ y_{A}(t) = - k_{2}A_{x1}\sin \varphi_{1} \\ z_{A}(t) = A_{z1}\cos \psi_{1} \end{array}\displaystyle \right. $$

(27)

where $A_{x1}$ denotes the $x$-amplitude of the initial orbit, $A_{z1}$ denotes the $z$-amplitude of the initial orbit, $\varphi_{1}$ denotes the phase of the starting point$A$in the $xy$-plane, and $\psi_{1}$ denotes the phase of the starting point$A$in the $z$-axis.

Then, the velocity vector of the starting point $A$ takes the form

$$ \left\{ \textstyle\begin{array}{l} V_{Ax}(t) = - \operatorname{Im} (\lambda_{3})A_{x1}\sin \varphi_{1} \\ V_{Ay}(t) = - \operatorname{Im} (\lambda_{3})k_{2}A_{x1}\cos \varphi_{1} \\ V_{Az}(t) = - \operatorname{Im} (\lambda_{5})A_{z1}\sin \psi_{1} \end{array}\displaystyle \right. $$

(28)

The position vector of the ending point $B$ takes the form

$$ \left\{ \textstyle\begin{array}{l} x_{B}(t) = A_{x2}\cos \varphi_{2} \\ y_{B}(t) = - k_{2}A_{x2}\sin \varphi_{2} \\ z_{B}(t) = A_{z2}\cos \psi_{2} \end{array}\displaystyle \right. $$

(29)

where $A_{x2}$ denotes the $x$-amplitude of the final orbit, $A_{z2}$ denotes the $z$-amplitude of the final orbit, $\varphi_{2}$ denotes the phase of the ending point $B$ in the $xy$-plane, and $\psi_{2}$ denotes the phase of the ending point $B$ in the $z$-axis.

Then, the velocity vector of the ending point $B$ takes the form

$$ \left\{ \textstyle\begin{array}{l} V_{Bx}(t) = - \operatorname{Im} (\lambda_{3})A_{x2}\sin \varphi_{2} \\ V_{By}(t) = - \operatorname{Im} (\lambda_{3})k_{2}A_{x2}\cos \varphi_{2} \\ V_{Bz}(t) = - \operatorname{Im} (\lambda_{5})A_{z2}\sin \psi_{2} \end{array}\displaystyle \right. $$

(30)

Substituting Eqs. (27)–(30) into Eq. (19), the total velocity increment $\Delta V$ of Lissajous-to-Lissajous transfer can be described as a function of $[A_{x1},\varphi_{1},A_{z1},\psi_{1},A_{x2},\varphi_{2},A_{z2}, \psi_{2},\Delta t]$; thus,

$$ \Delta V = f(A_{x1},\varphi_{1},A_{z1},\psi_{1},A_{x2},\varphi_{2},A_{z2},\psi_{2},\Delta t) $$

(31)

Therefore, the cost function $J$ of Lissajous-to-Lissajous transfer takes the new form

$$\begin{aligned} J = &p\Delta V + q\Delta t \\ = & F(A_{x1},\varphi_{1},A_{z1},\psi_{1},A_{x2},\varphi_{2},A_{z2},\psi_{2},\Delta t) \end{aligned}$$

(32)

3.3 Optimization of transfer

Now that the approximate analytical solution for transfer has been constructed, the approximate analytical transfer can then be automatically optimized by the unconstrained minimization of a function of one or nine variables using a multivariable search technique. Considering that Lissajous-to-Lissajous transfer is representative and much more complex, the Lissajous-to-Lissajous transfers are similarly taken here as an example to show how to obtain the theoretical optimal transfer, and the method is undoubtedly also suitable for point-to-point transfer, halo-to-halo transfer and Lissajous-to-halo transfer.

In the Lissajous-to-Lissajous transfer, the variables in the multivariate function are denoted as $\boldsymbol{\chi}$ and can be defined as

$$ \textstyle\begin{array}{l} \boldsymbol{\chi} = [x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9}] =\\ {} [A_{x1},\varphi_{1},A_{z1},\psi_{1},A_{x2},\varphi_{2},A_{z2},\psi_{2},\Delta t] \end{array} $$

(33)

Thus, the necessary condition for optimal transfer is that the Jacobian matrix of $F$ must be equal to zero.

$$ \mathrm{Jacobian}(F) = [\frac{\partial F}{\partial x_{1}},\frac{\partial F}{\partial x_{2}},\ldots,\frac{\partial F}{\partial x_{9}}] = 0 $$

(34)

The sufficient condition is that the Hessian matrix of $F$ must be positive definite.

$$ \mathrm{Hessian}(F) = \left[ \textstyle\begin{array}{cccc} \frac{\partial^{2}F}{\partial x_{1}^{2}} & \frac{\partial^{2}F}{\partial x_{1}\partial x_{2}} & \ldots & \frac{\partial^{2}F}{\partial x_{1}\partial x_{9}} \\ \frac{\partial^{2}F}{\partial x_{1}\partial x_{2}} & \frac{\partial^{2}F}{\partial x_{2}^{2}} & \ldots & \frac{\partial^{2}F}{\partial x_{2}\partial x_{9}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2}F}{\partial x_{1}\partial x_{9}} & \frac{\partial^{2}F}{\partial x_{2}\partial x_{9}} & \ldots & \frac{\partial^{2}F}{\partial x_{9}^{2}} \end{array}\displaystyle \right] > 0 $$

(35)

According to the necessary condition and the sufficient condition, the approximate analytical optimal Lissajous-to-Lissajous transfer can be obtained theoretically.

As can be seen from the above, there are a total of nine parameters $[A_{x1},\varphi_{1}, A_{z1},\psi_{1}, A_{x2},\varphi_{2}, A_{z2},\psi_{2},\Delta t]$ that determine the optimal Lissajous-to-Lissajous transfer. Considering the complexity of the expression of the solution, i.e., Eq. (34) and Eq. (35), it is usually very difficult to calculate the solution directly and analytically; therefore, a numerical method, such as the shooting method or Newton-Raphson method, is employed as a tool to calculate the optimal solution.

Although the approximate analytical optimal transfer can be obtained through the method mentioned above, the transfer trajectory unfortunately usually cannot arrive at the ending point $B$ accurately due to the linearization bias and the strong-nonlinearity. Thus, the differential correction is employed to slightly correct the velocity vector of the starting point $A$ step by step until the transfer trajectory arrives at the ending point $B$. Meanwhile, the correction of the velocity vector may destroy the optimality of the solution; therefore, the SQP method is utilized to guarantee the optimality and get rid of the linearization bias. Therefore, the differential correction and SQP method are employed to get rid of the linearization bias and further optimize the transfer numerically after the approximate analytical solution. The overall process of obtaining the optimal transfer is shown in Fig. 3.

Fig. 3

Flow chart of the proposed methodology for the optimal impulsive time-fixed transfers

4 Numerical results and discussion

Considering that the Earth-Moon L2 point is located beyond the far side of the Moon and has become a candidate location for the construction of a space station for lunar missions, the Earth-Moon L2 point is taken as the object of this study. If not otherwise stated, the optimum is defined to be the minimum velocity increments in this study, which means that $p = 1$, $q = 0$, in accordance with most of the previous literature. Other optimums can also certainly be defined as long as $p,q$ are assigned to other values.

To verify the validity of this method and obtain the characteristics of the optimal transfers around the collinear libration points of the restricted three-body problem, considering that Lissajous orbits and halo orbits are the basic and most used orbits around the collinear libration points, this section successively involves four types of optimal transfer trajectories, namely, point-to-point transfers, Lissajous-to-Lissajous transfers, halo-to-halo transfers, and Lissajous-to-halo transfers.

4.1 Point-to-point transfers

Among the four types of transfers, the point-to-point transfer is the basic and simplest case. To determine what effect the position of the starting point $A$ has on the optimal transfers, transfers from different starting points $A$ to the same ending point $B$ are examined.

To increase the persuasiveness of this section, three different starting points $A$ and one ending point $B$ are taken from the reference (Sun et al. 2017). These starting points are located on three different halo orbits, with $z$-amplitudes of 7000 km, 9000 km, and 11000 km, respectively, and phases in the $xy$-plane and $z$-axis are both zero, i.e., $\varphi_{A} = 0^{ \circ}$, $\psi_{A} = 0^{ \circ}$. The ending point $B$ is also located on a halo orbit characterized by a z-amplitude of 5000 km, and with a state of $[1.1533, 0.0819, -0.0084, 0.0655, -0.0599, -0.0205]$ in the barycentric synodic coordinate system $O - XYZ$, in dimensionless units (DU).

The analytical solution is obtained according to Sects. 3.1 and 3.3, and the results of the differential correction and SQP method are obtained according to Fig. 3.

As can be seen from Table 1, the optimal transfers obtained by the analytical solutions are not accurate enough, especially in the velocity increment $\Delta V$, but the results become very accurate after differential correction and SQP. This means that the differential correction is necessary to make the transfers accurate numerically and that SQP is necessary to get rid of the linearization bias and perform further optimization. Thus, the differential correction and SQP method are indispensable in obtaining the optimal transfers under the requirement that the precision and optimality must be guaranteed.

Table 1 Results of optimal transfers between two points with different starting points

Compared to the reference (Sun et al. 2017), when the z-amplitudes of the initial orbits are 7000 km, 9000 km, and 11000 km, although the TOFs of transfers increase by 5.84%, 4.53%, and 3.82%, respectively, the corresponding velocity increments decrease by 44.87%, 14.25%, and 2.71%, which proves the validity of the methodology that the TOF can be optimized to decrease the velocity increment $\Delta V$ and obtain the optimal transfer.

Figure 4 presents one of the three optimal transfer trajectories when the starting point $A$ is located on a halo orbit with a z-amplitude of 11000 km.

Fig. 4

Optimal transfer trajectory between two points

To further verify whether the transfers are optimal or not, Lawden (1963) proposed the primer vector theory for the impulsive transfer problems, and Chen (2016a, 2016b) derived the necessary condition and second-order optimality conditions for optimal control problems. For simplicity, the primer vector theory is employed, and the result is shown in Fig. 5. The magnitude of the primer vector is equal to one at the starting point and the ending point and less than one during the coast period, which means that the transfer is indeed optimal; thus, the optimality of the transfers is determined.

Fig. 5

Primer magnitude history of the transfer between two points when Az=11000 km

4.2 Lissajous-to-Lissajous transfers

Orbit-to-orbit transfers are much more complex than point-to-point transfers. Unlike point-to-point transfers, in which the only parameter is the TOF $\Delta t$, there are a total of nine parameters that determine the global optimal orbit-to-orbit transfer, which are the $x$-amplitude of the initial orbit $A_{x1}$, the phase in the $xy$-plane of the starting point $\varphi_{1}$, the $z$-amplitude of the initial orbit $A_{z1}$, the phase in the $z$-axis of the starting point $\psi_{1}$, the $x$-amplitude of the final orbit $A_{x2}$, the phase in the $xy$-plane of the ending point $\varphi_{2}$, the $z$-amplitude of the final orbit $A_{z2}$, the phase in the $z$-axis of the ending point $\psi_{2}$, and finally, the TOF$\Delta t$.

Obviously, if optimizing the orbit-to-orbit transfer as a whole, that is, considering the coupling between all of the parameters, the most general, complicated and comprehensive case is that all of the nine parameters $[A_{x1},\varphi_{1},A_{z1},\psi_{1}, A_{x2},\varphi_{2},A_{z2},\psi_{2},\Delta t]$ are variables that need to be optimized in orbit-to-orbit transfers. The most general, complicated and comprehensive optimal orbit-to-orbit transfer can be obtained with Eqs. (27)–(35) in Sect. 3.2. According to theoretical analysis and common sense, it can be assured that the optimal transfer is not unique and will occur when the starting point and the ending point are on the same orbit, i.e., $A_{x1} = A_{x2}$, $A_{z1} = A_{z2}$, such that the spacecraft can coast from the starting point to the ending point along the orbit without any velocity impulses, that is, the velocity increment $\Delta V$ equals zero.

Nevertheless, it is difficult to present the simulation of the nine-variable optimal orbit-to-orbit transfers, and there will be some constraints on the variables in real space missions. Thus, to show the process of optimizing the orbit-to-orbit transfers as a whole, clearly and without loss of generality, a simpler but representative and practical case, i.e., three-variable orbit-to-orbit transfers, is given below because, no matter how many variables there are, the solving process is the same.

According to most real cases of orbit transfers, the initial orbit and the final orbit are actually pre-determined before transfer, which means that the amplitudes $A_{x}$, $A_{z}$ of the initial orbit and the final orbit are fixed. Moreover, the phase in the $xy$-plane $\varphi$ and the phase in the $z$-axis $\psi$ are synchronous when varying over time according to Eq. (26); thus, $\psi$ can be replaced with $\varphi$. Supposing that the initial phases $\varphi_{0}$ and $\psi_{0}$ are zero, i.e., $\varphi_{0} = 0^{ \circ}, \psi_{0} = 0^{ \circ}$, both for the initial orbit and the final orbit, one can get $\psi = \varphi (\operatorname{Im} (\lambda_{5}) / \operatorname{Im} (\lambda_{3}))$. Therefore, the variables that need to be taken into account in this simulation are just three parameters, i.e., the phase of the starting point on the initial orbit $\varphi_{1}$, the phase of the ending point on the final orbit $\varphi_{2}$, and the TOF $\Delta t$. The values of the $x$-amplitudes $A_{x1},A_{x2}$ and $z$-amplitudes $A_{z1}$, $A_{z2}$ in dimensionless units (DU) are shown in Table 2.

Table 2 Parameters and result of the theoretical global optimal Lissajous-to-Lissajous transfer

First, the theoretical global optimal Lissajous-to-Lissajous transfer can be obtained by Eqs. (34)–(35) with the Newton-Raphson method. The result of the global optimal transfer is shown in Table 2, and the global optimal solution is marked as a cyan pentalpha in Fig. 6 (ii, iv).

Fig. 6

Simulation results of Lissajous-to-Lissajous transfers

Second, to further study the characteristics of Lissajous-to-Lissajous transfers numerically and verify the validity of the theoretical optimal transfer, simulations under various circumstances are made.

The phase of the starting point $\varphi_{1}$ is varied from 10° to 350° at intervals of 20° and the phase of the ending point $\varphi_{2}$ is varied from 20° to 360° at intervals of 20° such that the optimal TOF can be optimized for every pair of ($\varphi_{1},\varphi_{2}$) according to Fig. 3. The result of the global optimal transfer is shown in Table 3. The simulation results of the TOF and $\Delta V$ are shown in Fig. 6, and the global optimal solution is marked as a magenta pentalpha in Fig. 6 (ii, iv).

Table 3 Parameters and result of the numerical global optimal Lissajous-to-Lissajous transfer

According to the simulation results, the following conclusions can be summarized.

(i) As can be seen from Fig. 6(i, ii), the contour lines of the TOF are parallel to the diagonal of the diagram and also symmetric about the diagonal, which means that the optimal TOF, for every pair of ($\varphi_{1}$,$\varphi_{2}$), mainly depends on the absolute value of the difference between the phases of the starting point and ending point, i.e., $\left\| \varphi_{1} - \varphi_{2} \right\|$. Specifically, when the phases of the starting point $\varphi_{1}$ and ending point $\varphi_{2}$ are approximately equal, i.e., $\left\| \varphi_{1} - \varphi_{2} \right\| \approx 0^{ \circ}$, the TOF gets the approximate minimum, approximately 1.67 days, as the blue areas show in Fig. 6(ii). When the absolute value of the difference of the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$ increases, the TOF first increases and then decreases, and when the absolute value is approximately 200°, as the red areas show in Fig. 6(ii), the TOF gets the approximate maximum, 6.17 days.

(ii) As can be seen from Fig. 6(iii, iv), the total velocity increment $\Delta V$ also mainly depends on the absolute value of the difference between the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$. Specifically, when the phases are approximately equal, i.e., $\left\| \varphi_{1} - \varphi_{2} \right\| \approx 0^{ \circ}$, as the red area shows in Fig. 6(iv), $\Delta V$ gets the approximate maximum, 210 m/s; therefore, it is the most costly transfer in this situation. When the absolute value of the difference of the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$ increases, $\Delta V$ first decreases, then increases, and finally decreases, and when the absolute value is approximately 200° or 300°, as the blue areas show in Fig. 6(iv), $\Delta V$ gets the approximate minimum of 40 m/s; therefore, it is the least costly transfer in this situation.

(iii) The TOF and $\Delta V$ represent a pair of contradictions, as can be concluded from above. When the TOF increases, $\Delta V$ will decrease, and vice versa under the same transfer conditions. This is consistent with common sense.

(iv) As can be seen in Table 2 and Table 3, the global optimal Lissajous-to-Lissajous transfer occurs when the phases of the starting point $\varphi_{1}$ and ending point $\varphi_{2}$ are approximately 10° and 170°, respectively, and the minimum of $\Delta V$ is approximately 40 m/s. On the whole, the solution of the theoretical global optimal Lissajous-to-Lissajous transfer is consistent with the solution of the numerical global optimal transfer, in spite of a small difference between the two solutions. This can also be confirmed by the cyan pentalpha and magenta pentalpha in Fig. 6 (ii, iv), which are very close to each other. Moreover, Fig. 7 shows that the theoretical global optimal transfer trajectory and the numerical global optimal transfer trajectory have similar variation trends. The inconsistencies of the two transfers only indicate that the theoretical solution is not accurate enough and can be improved by a numerical process. Thus, in a word, the global optimal Lissajous-to-Lissajous transfer can be obtained by the theoretical method with a small error tolerance, and the precise global optimal transfer can be obtained by improving the theoretical solution with a numerical method.

Fig. 7

Global optimal Lissajous-to-Lissajous transfers obtained theoretically and numerically

4.3 Halo-to-halo transfers

Similar to Lissajous-to-Lissajous transfers, the fixed parameters in optimizing halo-to-halo transfers are also the $x$-amplitudes $A_{x1},A_{x2}$ and $z$-amplitudes $A_{z1},A_{z2}$ of the initial orbit and the final orbit, and the phases of the two orbits in the $z$-axis are also determined with the relation $\psi_{1,2} = \varphi_{1,2}(\operatorname{Im} (\lambda_{5}) / \operatorname{Im} (\lambda_{3}))$. The values of the $x$-amplitudes $A_{x1}$, $A_{x2}$ and $z$-amplitudes $A_{z1}$, $A_{z2}$ in dimensionless units (DU) are shown in Table 4.

Table 4 The parameters and result of the theoretical global optimal halo-to-halo transfer

First, the theoretical global optimal halo-to-halo transfer can be obtained by Eqs. (34)–(35) with the Newton-Raphson method. The result of the global optimal transfer is shown in Table 4, and the global optimal solution is marked as a cyan pentalpha in Fig. 8 (ii, iv).

Fig. 8

Simulation results of halo-to-halo transfers

Second, to further study the characteristics of halo-to-halo transfers numerically and verify the validity of the theoretical optimal transfer, simulations under various circumstances are performed.

The phase of the starting point $\varphi_{1}$ is varied from 10° to 350° at intervals of 20° and the phase of the ending point $\varphi_{2}$ is varied from 20° to 360° at intervals of 20° such that the optimal TOF can be optimized for every pair of ($\varphi_{1},\varphi_{2}$) according to Fig. 3. The result of the global optimal transfer is shown in Table 5. The simulation results of the TOF and $\Delta V$ are shown in Fig. 8, and the global optimal solution is marked as a magenta pentalpha in Fig. 8 (ii, iv).

Table 5 The parameters and result of the numerical global optimal halo-to-halo transfer

According to the simulation results, the following conclusions can be summarized.

(i) As can be seen from Fig. 8(i, ii), the contour lines of the TOF are very parallel to the diagonal of the diagram and also very symmetric about the diagonal, which means that the optimal TOF, for every pair of ($\varphi_{1},\varphi_{2}$), mainly depends on the absolute value of the difference between the phases of the starting point and ending point $\left\| \varphi_{1} - \varphi_{2} \right\|$. When the phases of the starting point $\varphi_{1}$ and ending point $\varphi_{2}$ are approximately equal, i.e., $\left\| \varphi_{1} - \varphi_{2} \right\| \approx 0^{ \circ}$, the TOF gets the approximate minimum of approximately 1.5 days, as the blue area shows in Fig. 8(ii). When the absolute value of the difference of the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$ increases, the TOF first increases and then decreases, and when the absolute value is approximately 200°, as the red areas show in Fig. 8(ii), the TOF gets the approximate maximum of 7.2 days.

(ii) As can be seen from Fig. 8(iii, iv), the total velocity increment$\Delta V$also mainly depends on the absolute value of the difference between the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$. Leaving out the special case of $\varphi_{1}\ = 10^{ \circ},\varphi_{2}\ = 360^{ \circ}$, when the absolute value of the difference between the phases equals zero or 200°, i.e., $\left\| \varphi_{1} - \varphi_{2} \right\| \approx 0^{ \circ}$ or $120^{ \circ}$, as the red areas show in Fig. 8(iv), $\Delta V$ obtains the approximate maximum of 140 m/s; therefore, it is the most costly transfer in this situation. When the absolute value of the difference of the phase $\left\| \varphi_{1} - \varphi_{2} \right\|$ increases, $\Delta V$ first decreases, then increases, and finally decreases, and when the absolute value is approximately 100° or 280°, as the blue areas show in Fig. 8(iv), $\Delta V$ gets the approximate minimum of 15 m/s; thus, it is the least costly transfer in this situation.

(iii) The TOF and $\Delta V$ are a pair of contradictions, as can be concluded from above. When the TOF increases, $\Delta V$ will decrease, and vice versa under the same transfer conditions. This is consistent with common sense.

(iv) As can be seen in Table 4 and Table 5, the global optimal halo-to-halo transfer occurs when the phases of the starting point $\varphi_{1}$ and ending point $\varphi_{2}$ are approximately 70° and 340°, respectively, and the minimum of $\Delta V$ is approximately 12 m/s. On the whole, the solution of the theoretical global optimal halo-to-halo transfer is consistent with the solution of the numerical global optimal transfer, in spite of a small difference between the solutions. This can also be confirmed by the cyan pentalpha and magenta pentalpha in Fig. 8(ii, iv), which are very close to each other. Moreover, Fig. 9 shows that the theoretical global optimal transfer and the numerical global optimal transfer have very similar variation trends. The inconsistencies of the two transfers only indicate that the theoretical solution is not accurate enough and can be improved by a numerical process. Thus, in a word, the global optimal halo-to-halo transfer can be obtained by the theoretical method with a small error tolerance, and the precise global optimal transfer can be obtained by improving the theoretical solution with a numerical method.

Fig. 9

Global optimal halo-to-halo transfers obtained theoretically and numerically

4.4 Lissajous-to-halo transfers

Similar to Lissajous-to-Lissajous transfers and halo-to-halo transfers, the fixed parameters in optimizing the Lissajous-to-halo transfers are also the $x$-amplitudes $A_{x1},A_{x2}$ and $z$-amplitudes $A_{z1},A_{z2}$ of the initial orbit and the final orbit, and the phases of the two orbits in the z-axis are also determined with the relation $\psi_{1,2} = \varphi_{1,2}(\operatorname{Im} (\lambda_{5}) / \operatorname{Im} (\lambda_{3}))$. The values of the $x$-amplitudes $A_{x1},A_{x2}$ and $z$-amplitudes $A_{z1},A_{z2}$ in dimensionless units (DU) are shown in Table 6.

Table 6 Parameters and result of the theoretical global optimal Lissajous-to-halo transfer

First, the theoretical global optimal Lissajous-to-halo transfer can be obtained by Eqs. (34)–(35) with the Newton-Raphson method. The result of the global optimal transfer is shown in Table 6, and the global optimal solution is marked as a cyan pentalpha in Fig. 10 (ii, iv).

Fig. 10

Simulation results of Lissajous-to-halo transfers

Second, to further study the characteristics of Lissajous-to-halo transfers numerically and verify the validity of the theoretical optimal transfer, simulations under various circumstances are performed.

The phase of the starting point $\varphi_{1}$ is varied from 10° to 350° at intervals of 20° and the phase of the ending point $\varphi_{2}$ is varied from 20° to 360° at intervals of 20° such that the optimal TOF can be optimized for every pair of ($\varphi_{1},\varphi_{2}$) according to Fig. 3. The result of the global optimal transfer is shown in Table 7. The simulation results of the TOF and $\Delta V$ are shown in Fig. 10, and the global optimal solution is marked as a magenta pentalpha in Fig. 10 (ii, iv).

Table 7 Parameters and result of the numerical global optimal Lissajous-to-halo transfer

According to the simulation results, the following conclusions can be summarized.

(i) As can be seen from Fig. 10(i, ii), the contour lines of the TOF are approximately parallel to the diagonal of the diagram and also symmetric about the diagonal, which means that the optimal TOF, for every pair of ($\varphi_{1},\varphi_{2}$), mainly depends on the absolute value of the difference between the phases of the starting point and ending point $\left\| \varphi_{1} - \varphi_{2} \right\|$. Specifically, when the phases of the starting point $\varphi_{1}$ and ending point $\varphi_{2}$ are approximately equal, i.e., $\left\| \varphi_{1} - \varphi_{2} \right\| \approx 0^{ \circ}$, the TOF gets the approximate minimum of 0.95 days, as the blue area shows in Fig. 10(ii). When the absolute value of the difference of the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$ increases, the TOF first increases and then decreases, and when the absolute value is approximately 200°, as the red areas show in Fig. 10(ii), the TOF gets the approximate maximum of 6.75 days.

(ii) As can be seen from Fig. 10(iii, iv), the total velocity increment$\Delta V$also mainly depends on the absolute value of the difference between the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$. Leaving out the special case of $\varphi_{1}\ = 10^{ \circ},\varphi_{2}\ = 360^{ \circ}$, when the phases are approximately equal, i.e., $\left\| \varphi_{1} - \varphi_{2} \right\| \approx 0^{ \circ}$, as the red areas show in Fig. 10(iv), $\Delta V$ obtains the approximate maximum of 200 m/s; therefore, it is the most costly transfer in this situation. When the absolute value of the difference of the phases $\left\| \varphi_{1} - \varphi_{2} \right\|$ increases, $\Delta V$ first decreases, then increases, and finally decreases, and when the absolute value is approximately 150° and 260°, as the blue areas show in Fig. 10(iv), $\Delta V$ gets the approximate minimum of 70 m/s; thus, it is the least costly transfer in this situation.

(iii) The TOF and $\Delta V$ represent a pair of contradictions, as can be concluded from above. When the TOF increases, $\Delta V$ will decrease, and vice versa under the same transfer conditions. This is consistent with common sense.

(iv) As can be seen in Table 6 and Table 7, the global optimal Lissajous-to-halo transfer occurs when the phase of the starting point $\varphi_{1}$ and ending point $\varphi_{2}$ are approximately 190° and 260°, respectively, and the minimum of $\Delta V$ is approximately 64 m/s. On the whole, the solution of the theoretical global optimal Lissajous-to-halo transfer is consistent with the solution of the numerical global optimal transfer, in spite of a small difference between the solutions. This can also be confirmed by the cyan pentalpha and magenta pentalpha in Fig. 10(ii, iv), which are very close to each other. Moreover, Fig. 11 shows that the theoretical global optimal transfer and the numerical global optimal transfer have very similar variation trends. The inconsistencies of the two transfers only indicate that the theoretical solution is not accurate enough and can be improved by a numerical process. Thus, in a word, the global optimal Lissajous-to-halo transfer can be obtained by the theoretical method with a small error tolerance, and the precise global optimal transfer can be obtained by improving the theoretical solution with a numerical method.

Fig. 11

Global optimal Lissajous-to-halo transfers obtained theoretically and numerically

As can be seen from above, the simulation results of Lissajous-to-Lissajous transfers, halo-to-halo transfers and Lissajous-to-halo transfers are similar from the perspective of the three-dimensional curved surface of the TOF and $\Delta V$. This finding is not surprising because the halo orbit is a bifurcation of the Lissajous orbit from the view of dynamics, as mentioned in Sect. 3.2; therefore, halo-to-halo and Lissajous-to-halo transfers are essentially two types of specific Lissajous-to-Lissajous transfers. Moreover, considering that the Lyapunov orbit is also a bifurcation of the Lissajous orbit, the transfers related to the Lyapunov orbit can also be obtained with the same method. Therefore, the problem of optimal impulsive time-fixed transfers between the three types of orbits around the collinear libration point of the restricted three-body problem is solved with the method proposed in this study.

5 Conclusions

This study involves the development of a methodology for the design of optimal time-fixed impulsive transfers in the vicinity of the L2 libration point of the Earth-Moon system. The approximate analytical solution of optimal transfers, along with the differential correction and SQP method, has been verified as valid through simulations of point-to-point transfers, Lissajous-to-Lissajous transfers, halo-to-halo transfers and Lissajous-to-halo transfers. The point-to-point transfers obtained in this study required the fewest velocity increments by optimizing the TOF. The Lissajous-to-Lissajous transfers, halo-to-halo transfers and Lissajous-to-halo transfers obtained a global optimal solution by optimizing the phases of the initial orbit and final orbit, as well as the TOF. Moreover, the theoretical global optimal solution has been verified as consistent with the results of the numerical simulations. The primer vector theory was also employed to further verify the optimality of these transfers. Therefore, the methodology is valid in designing optimal time-fixed impulsive transfers between points and between orbits in the vicinity of collinear libration points of the restricted three-body problem.

The solution for optimal transfers derived in this paper is actually an approximate analytical solution, which is based on the approximate analytical expression for motions around the collinear libration points of the CRTBP and ERTBP. Future works will further consider and take advantage of the nonlinearity of the restricted three-body problem and other numerical optimization techniques to obtain a more precise analytical solution.