Low-thrust transfer trajectory planning and tracking in the Earth–Moon elliptic restricted three-body problem

Abstract

In this work, the problem of low-thrust transfer between planar multi-revolution orbits at libration points near the secondary body in the Earth–Moon elliptic restricted three-body problem (ERTBP) is studied. Due to the presence of lunar orbital eccentricity, the ERTBP is closer to the real system than the circular restricted three-body problem (CRTBP). The stable and unstable invariant manifolds, associated with the libration point orbits in the CRTBP are used for the transfer trajectory planning. Different classes of heteroclinic connections are identified by the Poincaré section technique, which are used as initial trials for the calculation of energy-optimal low-thrust transfers. The trajectories are then switched to the ERTBP using continuous algorithms. We propose a computational strategy to match the non-autonomous dynamics of the ERTBP by coordinating the endpoints with the flight times of the transfer trajectories. Finally, a model predictive controller is designed for trajectory tracking in the real ephemeris that takes into account the actual lunar orbital eccentricity. The studies presented in this paper are more closely related to the requirements of practical lunar mission designs.

1 Introduction

The study of libration point orbits (LPOs) in the restricted three-body problem has become a hot topic of current research due to the proposal of related space missions like Lunar Orbital Platform-Gateway [1]. A spacecraft must be able to transfer in cislunar space if the selected LPO is already occupied by another spacecraft or if it intends to carry out several missions [2]. Among them, the transfer problem of LPOs in the vicinity of the Moon is more attractive.

The research of the Earth–Moon system can be performed in the circular restricted three-body problem (CRTBP) and the elliptic restricted three-body problem (ERTBP). A lot of researchers have investigated problems such as orbit formation, station-keeping, and transfer in the CRTBP [3,4,5]. With the advancement of low-thrust technology, the use of continuous low-thrust engines for deep space missions is gaining increasing relevance [6]. Russell [7] proposed an indirect optimization method for the low-thrust transfer problem in the CRTBP. Based on this, Zhang et al. [8] addressed the problem of low-thrust transfer to LPOs in cislunar space with time-, energy-, and propellant-optimal criteria. Peng and Wang [9] divided the transfer between LPOs into a mixed trajectory with an invariant manifold part and a low-thrust part, and developed a multi-objective optimization strategy to save propellant consumption for the transfer. Invariant manifolds can be conceived as tubes governing spatial dynamics and mass transfer [10]. Combining invariant manifolds with low-thrust propulsion for transfer in the CRTBP allows the benefits of both techniques to be examined simultaneously. Chupin et al. [11] used a low-thrust engine to connect the manifolds associated with LPOs at points L1 and L2, resulting in lower energy consumption for transfer. Du et al. [12] found that for the same transfer scenario, low-thrust transfer trajectories using manifold structures may perform better than typical transfer trajectories in terms of propellant consumption and time of flight (TOF).

An improperly calculated transfer trajectory may not be applied in practice, resulting in mission failure [13]. Due to the eccentricity of the lunar orbit, the transfer trajectories solved in the ERTBP are much more efficient than those in the CRTBP and are closer to the actual requirements [14]. In the ERTBP, there is a type of LPOs called multi-revolution orbits, which are essentially resonant orbits with the motion of the secondary body [15]. Ferrari and Lavagna [16] used differential corrections and eccentricity continuation techniques to produce multi-revolution orbits from orbits in the CRTBP. Neelakantan and Ramanan [17] designed multi-revolution orbits using differential evolution in the ERTBP framework. Peng and Xu [18] analyzed the stability of multi-revolution orbits by studying the distribution of the eigenvalues of the orbital monodromy matrix. The manifold transfer trajectories along the main stable directions are then constructed in the Earth–Moon ERTBP [19]. However, there have been few studies of the transfer problem between multi-revolution orbits. In order to be applicable to actual mission requirements and technological developments, it is necessary to calculate low-thrust transfer trajectories between multi-revolution orbits in the ERTBP.

In this paper, we study the problem of low-thrust transfer between multi-revolution orbits around points L1 and L2 in the Earth–Moon ERTBP using the invariant manifold construction. Due to the non-autonomous dynamics [14, 20] and the fact that the distribution of eigenvalues of the orbital monodromy matrix is different from that in the CRTBP [21], it is challenging to directly calculate and splice the manifolds in the ERTBP. Therefore, in this study, the invariant manifolds associated with the LPOs in the CRTBP are calculated to construct energy-optimal low-thrust transfer trajectories. The Poincaré section technique is used to identify the appropriate intersection points to splice the manifolds into heteroclinic connections. Depending on the type of heteroclinic connections, the transfer trajectories are classified into half-circle, single-circle, and double-circle configurations around the Moon. These trajectories are then transformed to the ERTBP case using continuous algorithms and by examining the transfer endpoint data and modifying the trajectory characteristics to match the non-autonomous dynamics. Finally, it should be noted that the eccentricity of the lunar orbit varies from moment to moment in the real ephemeris. In real-world settings, model errors, measurement noise, and other undesirable factors are frequent. If no action is taken to mitigate these detrimental consequences, the flight mission will fail [22]. To make the results in this study more applicable to actual missions, a constraint tightening technique for robust model predictive controller (MPC) is used to evaluate the effect of tracking transfer trajectories between multi-revolution orbits in the real ERTBP. The detailed description of the MPC will be presented in Sect. 4.

The structure of this paper is as follows: Sect. 2 introduces the dynamics of the Earth–Moon ERTBP and the formulation of the optimal low-thrust transfer problem. The optimal low-thrust transfer trajectories between periodic orbits around L1 and L2 points in the Earth–Moon ERTBP are computed in Sect. 3. Section 4 describes the trajectory tracking problem using a constraint tightening MPC algorithm. The conclusions of this study are presented in Sect. 5.

2 Theoretical formalism

This section is devoted to the description of the equations of motion for a spacecraft in the Earth–Moon CRTBP and ERTBP, introducing the concepts of invariant manifolds and multi-revolution orbits. Also, the energy-optimal low-thrust transfer problem is formulated.

2.1 Dynamics background

The units in Eq. (1) are used for non-dimensionalization in the ERTBP, which is different from the CRTBP case:

$$\begin{aligned} \begin{aligned}&\text {Distance Unit}: \qquad \ \ \textrm{DU}(f)=\frac{a\left( 1-\text {e}^{2}\right) }{1+e \cos f}, \\&\text {Acceleration Unit}: \quad \textrm{AU}(f)=\frac{G\left( m_{1}+m_{2}\right) }{\textrm{DU}^{2}(f)}, \\&\text {Time Unit}: \, \ {\tiny \textrm{TU}(f)=\left( \sqrt{\frac{G\left( m_{1}+m_{2}\right) }{a^{3}\left( 1-\text {e}^{2}\right) ^{3}}}(1+e \cos f)^2\right) ^{-1}}, \end{aligned} \end{aligned}$$

(1)

where e is the lunar orbit eccentricity, a is the lunar orbit semi-major axis, and f is the true anomaly; G is the gravitational constant; $m_1$ and $m_2$ represent the masses of the Earth and Moon, respectively.

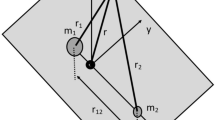
Thus, a synodic, non-uniformly rotating and pulsating frame is obtained (See Fig. 1) [17]. Note that the independent variable of the system is the true anomaly f. The Earth and Moon are located at points (-$\mu$,0,0) and (1-$\mu$,0,0), respectively, where $\mu =\frac{m_2}{m_1+m_2}$ is related to the mass of the Earth and Moon. As a result, the dimensionless equation for the motion of a spacecraft with a low-thrust engine in the pulsating synodic frame reads [14, 18]:

$$\begin{aligned} \begin{aligned} \ddot{x}-2 {\dot{y}}&=\frac{\partial \varOmega }{\partial x}+\frac{C_1 u T_{\max } \alpha _{x}}{(1+e \cos f)m},\\ \ddot{y}+2 {\dot{x}}&=\frac{\partial \varOmega }{\partial y}+\frac{C_1 u T_{\max } \alpha _{y}}{(1+e \cos f)m}, \\ \ddot{z}&=\frac{\partial \varOmega }{\partial z}+\frac{C_1 u T_{\max } \alpha _{z}}{(1+e \cos f)m}, \\ {\dot{m}}&=-C_{2} \frac{u T_{\max }}{I_{s p} g_{0}}, \end{aligned} \end{aligned}$$

(2)

where ${\varvec{r}}=[x,y,z]^\textrm{T}$ and ${\varvec{v}}=[v_x,v_y,v_z]^\textrm{T}$ are the spacecraft position and velocity vectors in the ERTBP, respectively, m is the mass of the spacecraft, $T_{\max }$ represents the maximum thrust produced by the engine, $I_\textrm{sp}$ is the engine specific impulse, and $g_0$ is the gravitational acceleration. The throttle factor $u \in [0,1]$ and the thrust direction unit vector $\varvec{\alpha } = [\alpha _{x},\alpha _{y},\alpha _{z}$] are organized as the control variables. In Eq. (2) we introduce the constant $C_1 = 1/\text {AU}(f)$ and $C_2 = \text {DU}(f)$ to non-dimensionalize the equation. $\varOmega$ is the pseudo-potential, defined as:

$$\begin{aligned} \begin{aligned}&\varOmega =U/(1+e \cos f),\\&U=\frac{1}{2}(x^{2}+y^{2} -z^2 e \cos f )+\frac{1-\mu }{r_{1}}+\frac{\mu }{r_{2}}, \end{aligned} \end{aligned}$$

(3)

where $r_{1}=\sqrt{(x+\mu )^{2}+y^{2}+z^{2}}$ and $r_{2}=\sqrt{(x+\mu -1)^{2}+y^{2}+z^{2}}$ shown in Fig. 1 are the distances from the spacecraft to the Earth and Moon, respectively.

In Eq. (2), the unit thrust direction vector $\varvec{\alpha }$ is determined by:

$$\begin{aligned} \varvec{\alpha }=\left[ \begin{array}{l} \alpha _{x} \\ \alpha _{y} \\ \alpha _{z} \end{array}\right] =\left[ \begin{array}{c} \cos \theta _{1} \cos \theta _{2} \\ \sin \theta _{1} \cos \theta _{2} \\ \sin \theta _{2} \end{array}\right] , \end{aligned}$$

(4)

where $\theta _{1}$ is the engine control angle between the Ox axis and the projection of the thrust in the xOy plane, $\theta _{2}$ is the control angle between the thrust vector and the xOy plane.

The other parameters used in this paper are listed in Table 1 below.

Fig. 1

Pulsating synodic Earth–Moon coordinate system

Table 1 Parameter list

2.1.1 Multi-revolution orbits

If the throttle factor u in Eq. (2) is set to zero, this equation represents the passive motion of the spacecraft in the Earth–Moon ERTBP. In the ERTBP framework, LPOs also exist, which are called multi-revolution orbits.

Fig. 2

The construction of a 3:1 multi-revolution orbit

Campagnola [23] introduced a sufficient periodicity criterion: a symmetric periodic orbit in the ERTBP must cross the x–z plane perpendicularly twice when primaries are at their apsides. When the LPO completes one period, the Earth–Moon phase (their true anomalies) must return to zero. This periodic orbit, known as multi-revolution orbit, is essentially a resonant orbit with an orbital period that is an integer ratio to the period of the Moon’s motion.

According to the criterion, multi-revolution orbits are characterized by periods that are integer multiples of the system non-dimensional period 2$\pi$ [17]. See Fig. 2 for a diagrammatic illustration of the setup for a multi-revolution orbit with a 3:1 resonance ratio.

The Moon moves from position 1 to position 2, and the trajectory completes one and a half revolutions with two perpendicular crossings on the x–z plane. Since the Moon returns in a symmetric way from position 2 to position 1, making the trajectory symmetric with respect to the x–z plane results in a 3:1 multi-revolution orbit. In Refs. [16, 17], it is described how multi-revolution orbits are created in the ERTBP. The transfer problem between them is the main subject of this research.

2.1.2 Invariant manifolds

Invariant manifolds can be conceived as tubes that dominate the space dynamics and mass transfer [10]. Its structure gives a geometrical basis for understanding the dynamics at different energies. Therefore, invariant manifolds are of great interest in terms of transfer in cislunar space, and most of the studies have been carried out within the CRTBP framework. Equation (2) degenerates to the equation of spacecraft motion in the CRTBP if e and u are set to 0.

Invariant manifolds are divided into unstable and stable manifolds, which are two sets of asymptotic trajectories. It is necessary to determine the eigenvectors of the monodromy matrix ${\textbf{M}}$ in order to obtain those manifolds. The definition of the monodromy matrix ${\textbf{M}}$ for the orbit in the CRTBP can be found in [24]. This matrix has six eigenvalues:

$$\begin{aligned} \begin{array}{c} \lambda _{1}, \lambda _{2}=\lambda _{1}^{-1}, \lambda _{3}=\lambda _{4}=1, \\ \lambda _{5}=\lambda _{6}^{*},\left| \lambda _{5}\right| =\left| \lambda _{6}\right| =1, \end{array} \end{aligned}$$

(5)

where $\lambda _{1}$ and $\lambda _{2}$ determine the local stability properties of orbits. For an unstable periodic orbit in the CRTBP, $\lambda _{1}>1$ and $\lambda _{2}<1$. $\lambda _{1}$ and its eigenvector ${\textbf{u}}_{u}$ represent an unstable component, while $\lambda _{2}$ and its eigenvector ${\textbf{u}}_{s}$ denote a stable component.

The unstable manifolds, represented by $W^u$, include all possible trajectories that a spacecraft in a nominal orbit may take if disturbed in the direction of the unstable eigenvector ${\textbf{u}}_{u}$. While the stable manifolds $W^s$ contain all alternative trajectories that a spacecraft may follow to reach the nominal orbit along the stable eigenvector direction ${\textbf{u}}_{s}$ [24]. Let’s discuss phase vectors ${\textbf{x}}_{u}$ and ${\textbf{x}}_{s}$, such that:

$$\begin{aligned} {\textbf{x}}_{u}={\textbf{x}}_{0} \pm \varepsilon {\textbf{u}}_{u}, \quad {\textbf{x}}_{s}={\textbf{x}}_{0} \pm \varepsilon {\textbf{u}}_{s}, \end{aligned}$$

(6)

where ${\textbf{x}}_{0}$ is the spacecraft state vector in a nominal orbit, and $\varepsilon$ is an initial tiny offset.

Integrating the state vectors ${\textbf{x}}_{u}$ and ${\textbf{x}}_{s}$ over time by Eq. (2) yields the invariant manifolds. Figure 3 depicts the unstable and stable invariant manifolds, associated with an L2 Lyapunov orbit. In this paper, the manifold transfer trajectory is calculated in the CRTBP as an initial trial for the low-thrust transfer.

Fig. 3

The sample of invariant manifolds in the Earth–Moon CRTBP

2.2 Formulation of the optimal control problem

The low-thrust optimal transfer problem can be classified into time-, energy- and propellant-optimal problems. For the energy- and propellant-optimal problems, the TOF is given. And they can be switched into each other via the homotopy process [25]. Since the TOF needs to be adjusted to match the non-autonomous nature of the ERTBP framework, we use energy-optimal control for transfer trajectory planning.

The performance index for the minimum-energy problem is represented as follows:

$$\begin{aligned} J_\textrm{e}=\frac{T_{\max }}{_\textrm{sp}g_0} \int _{{0}}^{t_{f}} u^2 \text {d}t. \end{aligned}$$

(7)

By introducing the costate vectors $\varvec{\lambda }=\left[ \varvec{\lambda }_\textrm{r}, \varvec{\lambda }_\textrm{v}, \lambda _\textrm{m}\right] ^\textrm{T}$, the Hamiltonian of the system is defined as follows:

$$\begin{aligned} \begin{aligned}&H=\varvec{\lambda }_\textrm{r}^\textrm{T} {\varvec{v}}+\varvec{\lambda }_{v}^\textrm{T}\left[ {\varvec{g}} ({\varvec{r}})+{\varvec{h}}({\varvec{v}}) +\frac{T_{\max } u C_1 \varvec{\alpha }}{m (1+e \cos f)}\right] \\&\quad - \lambda _\textrm{m} \frac{T_{\max } u C_2}{I_\textrm{sp}g_0}+\frac{T_{\max }C_2 u^2}{I_\textrm{sp}g_0}, \end{aligned} \end{aligned}$$

(8)

where

$$\begin{aligned} \begin{array}{l} \varvec{\lambda _\textrm{r}} =\left[ \lambda _{x}, \lambda _{y}, \lambda _{z}\right] ^\textrm{T},\\ \varvec{\lambda }_{v} =\left[ \lambda _{v_{x}}, \lambda _{v_{y}}, \lambda _{v_{z}}\right] ^\textrm{T},\\ {\varvec{g}}({\varvec{r}}) =-\left[ U_{x}, U_{y}, U_{z}\right] ^\textrm{T}/(1+e \cos f),\\ {\varvec{h}}({\varvec{v}}) =\left[ 2 v_{y},-2 v_{x}, 0\right] ^\textrm{T}.\\ \end{array} \end{aligned}$$

(9)

Table 2 Data on objective orbits (non-dimensional)

Fig. 4

Objective orbits in the Earth–Moon CRTBP and ERTBP

According to the optimal control theory [26], there are:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\varvec{\lambda }}_\textrm{r}=-\left( \frac{\partial {\varvec{g}}({\varvec{r}})}{\partial {\varvec{r}}}\right) ^\textrm{T} \varvec{\lambda }_{v}, \\ \dot{\varvec{\lambda }}_{v}=-\varvec{\lambda }_\textrm{r}-\left( \frac{\partial {\varvec{h}}({\varvec{v}})}{\partial {\varvec{v}}}\right) ^\textrm{T} \varvec{\lambda }_{v}, \\ {\dot{\lambda }}_\textrm{m}=\frac{C_1 u T_{\max }\varvec{\alpha } }{m^{2} \varvec{\lambda }_{v} (1+e \cos f)}, \\ \lambda _\textrm{m}\left( t_{f}\right) =0. \end{array}\right. \end{aligned}$$

(10)

Then using the Pontryagin Maximum Principle (PMP) to minimize the Hamiltonian in Eq. (8), we obtain that the optimal control variables u and $\varvec{\alpha }$ are determined as follows [27]:

$$\begin{aligned} \begin{array}{l} \varvec{ \alpha }^{*}=-\frac{\varvec{\lambda }_{v}}{\left\| \varvec{\lambda }_{v}\right\| },\\ u^{*}=\left\{ \begin{array}{ll} 0 &{} S>1, \\ (1-S)/2 &{} -1 \le S\le 1, \\ 1 &{} S<-1, \end{array}\right. \end{array} \end{aligned}$$

(11)

where $S=1-\frac{C_1\left\| \varvec{\lambda }_{v}\right\| I_\textrm{sp}g_0}{C_2m (1+e \cos f)}-\lambda _\textrm{m}$ is the switching function.

This yields a 14-dimensional spacecraft controlled motion equation in the ERTBP:

$$\begin{aligned} \begin{aligned}&\dot{\varvec{\varPhi }}={\mathcal {F}}(\varvec{\varPhi }) \Rightarrow \left[ \begin{array}{c} \dot{{\varvec{r}} }\\ \dot{{\varvec{v}}} \\ {\dot{m}} \\ \dot{\varvec{\lambda }}_\textrm{r} \\ \dot{\varvec{\lambda }}_{v} \\ {\dot{\lambda }}_\textrm{m} \end{array}\right] \\&\quad =\left[ \begin{array}{c} {\varvec{v}} \\ {\varvec{g}}({\varvec{r}})+{\varvec{h}}({\varvec{v}})-{\varvec{\lambda }_{v}}/{\lambda _{v}}\frac{C_1 u T_{\max }}{m (1+e \cos f )}\\ -C_2 u T_{\max } / (I_\textrm{sp}g_0) \\ -\partial {\varvec{g}}({\varvec{r}}) / \partial {\varvec{r}} \cdot \varvec{\lambda }_{v} \\ -\varvec{\lambda }_\textrm{r}-\partial {\varvec{h}}({\varvec{v}}) / \partial {\varvec{v}} \cdot \varvec{\lambda }_{v} \\ -C_1 \left\| \varvec{\lambda }_{v}\right\| u T_{\max } / [m^{2}(1+e \cos f)] \end{array}\right] , \end{aligned} \end{aligned}$$

(12)

where $\varvec{\mathbf {\varPhi }}$ is state vector, it consists of the spacecraft coordinate vector, the mass and the costate vector: $\mathbf {\varPhi }=[{\varvec{x}}, m, \varvec{\lambda }]^\textrm{T}$, ${\varvec{x}}=[{\varvec{r}}, {\varvec{v}}]$.

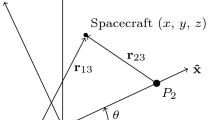
As a result, the optimal control problem reduces to a two-point boundary value problem (TPBVP) with 6 parameters. The transversality conditions are constructed by choosing two points M: ${\varvec{x}}_0=[{\varvec{r}}_0, {\varvec{v}}_0]$ and N: ${\varvec{x}}_\textrm{f}=[{\varvec{r}}_\textrm{f}, {\varvec{v}}_\textrm{f}]$, which are, respectively, on the departure and arrival orbits [12]:

$$\begin{aligned} \begin{array}{ll} {\varvec{r}}\left( t_{0}\right) ={\varvec{r}}_{0}, {\varvec{v}}\left( t_{0}\right) ={\varvec{v}}_{0}, m\left( t_{0}\right) =m_{0}, \\ {\varvec{r}}\left( t_{f}\right) ={\varvec{r}}_{f}, {\varvec{v}}\left( t_{f}\right) ={\varvec{v}}_{f}, {\lambda }\left( t_{f}\right) =0. \end{array} \end{aligned}$$

(13)

From this we can define the energy-optimal problem as follows:

$$\begin{aligned} \begin{aligned} \begin{array}{l} \min \ J_\textrm{e}\\ \text{ find } \varvec{\lambda } \text{ and } t_{f} \Rightarrow \text{ s.t. } \\ \left\{ \begin{array}{l} \dot{\mathbf {\varPhi }}={\mathcal {F}}(\mathbf {\varPhi }), \\ \mathbf {\varPhi }_{0}=\left[ {\varvec{x}}_{0}, m_{0}, \varvec{\lambda }_{0}\right] , \mathbf {\varPhi }_{f}=\left[ {\varvec{x}}_{f}, m_{f}, \varvec{\lambda }_{f}\right] , \\ {\varvec{x}}_0=[{\varvec{r}}_0, {\varvec{v}}_0], {\varvec{x}}_\textrm{f}=[{\varvec{r}}_\textrm{f}, {\varvec{v}}_\textrm{f}], \\ \lambda _\textrm{m}\left( t_{f}\right) =0. \end{array}\right. \end{array} \end{aligned} \end{aligned}$$

(14)

To solve this problem, we use a function called bvp4c integrated in MATLAB to create a collocation technique based on the Lobatto IIIA methods [28, 29], since it is difficult to make a reasonable initial approximation of $\varvec{\lambda }(t_0)$. The state and costate vectors of the spacecraft motion at each sample point are determined by this solver. This allows us to use the constructed manifold transfer trajectory data as an initial trial for the transfer problem in Eq. (14).

3 Low-thrust transfer simulation results

In this section, the problem of low-thrust transfer from L2 LPO to L1 LPO will be addressed in the ERTBP. For the L2 point departure orbit, a planar multi-revolution orbit with a resonance ratio of 7:4 is selected, while for the L1 arrival orbit, a 2:1 planar multi-revolution orbit is chosen. The orbital parameters are listed in Table 2, and the corresponding orbits are plotted in Fig. 4.

3.1 Manifolds splicing

Invariant manifolds can be spliced to generate transfer trajectories as initial trials for low-thrust transfers. For this purpose, the stable and unstable invariant manifolds, associated with L1 and L2 LPO in the CRTBP with the same Jacobi constant are calculated in Fig. 5. The Poincaré map is then created by selecting a surface of section ${\varvec{\Sigma }}$ (where the Moon is located) and recording the information on the states of manifolds at this surface (See Fig. 6a).

The intersection points on the Poincaré map indicate the same states of the stable and unstable manifolds at surface ${\varvec{\Sigma }}$, allowing the spliced trajectories to form heteroclinic connections (depicted in Fig. 6b). Depending on the type of heteroclinic connection, the transfer trajectories are classified into half-circle, single-circle, and double-circle configurations around the Moon.

Fig. 5

Stable and unstable manifolds, associated with L1 LPO and L2 LPO

Fig. 6

Poincaré map and corresponding heteroclinic connections

3.2 Transfer trajectories in the CRTBP

Initializing the function bvp4c using the heteroclinic connections shown in Fig. 6b, the manifold transfers can be switched to low-thrust energy-optimal transfers from L2-C to L1-C by continuous algorithms (see Fig. 7 for an example of a half-circle transfer trajectory configuration around the Moon).

In fact, we are only concerned with the configuration of the transfer trajectories, that is, obtaining trajectories with different numbers of circles around the Moon, to aid the subsequent calculations. The L1 LPO and L2 LPO used for splicing manifolds with the same Jacobi constant can be chosen arbitrarily. The parameters of the transfer trajectory given in Fig. 7, including the thrust magnitude and the TOF, are also unimportant. Note that in Fig. 7, the departure and arrival points of the low-thrust transfer trajectory are set at the points M and N, which are the farthest from the Moon, respectively. This is further explained by the following calculations.

Fig. 7

The low-thrust transfer trajectory from L2-C to L1-C using manifold technique

As we can see in Figs. 8 and 9, two cases are demonstrated when the departure and arrival points are fixed at M and N, respectively. And a time variable $\tau$, representing the position of a spacecraft on a periodic orbit, is defined as the ratio of the TOF for the spacecraft to move from a reference point to the current point along the orbit to the orbital period [12].

The point N is selected as the reference point for the objective orbit L1-C, and the negative value of $\tau$ corresponds to the red part of L1-C while the positive $\tau$ corresponds to the blue part of L1-C, as depicted in Fig. 8. The calculations reveal that if the arrival point falls into the red part, the thrust required for transfer is larger. However, the thrust required in the blue part does not change significantly, but the TOF increases with increasing $\tau$. The turning point occurs at $\tau$ = 0, that is, at the point N. As for L2-C, the reference point is set as the point M. The data in Fig. 9 show that the case is similar to Fig. 8, with the turning point also occurring at $\tau$ = 0, i.e. point M.

Fig. 8

Minimum thrust and corresponding minimum TOF for the transfer from point M to L1-C

Fig. 9

Minimum thrust and corresponding minimum TOF for the transfer from L2-C to point N

As a result, in order to avoid increasing the TOF and the thrust required for transfer, it is reasonable to choose the departure and arrival points at the points M and N in Fig. 7, respectively, as a preliminary analysis of the low-thrust transfer problem. In addition, the points M and N represent the inflection points of the x-component of the orbital coordinates, which are easier to identify.

3.3 Transfer trajectories between multi-revolution orbits

This part aims to construct low-thrust transfer trajectories between multi-revolution orbits in the Earth–Moon ERTBP. In order to switch from a transfer in the CRTBP to a transfer between L2-E and L1-E, the following two steps must be performed:

• 1. The transfer problems should be computed in the ERTBP.

• 2. The moments of the transfer endpoints should be adjusted to match the true anomalies of the Earth–Moon system.

For the first step, the non-dimensionalization in the ERTBP results in the same positions of the Earth and Moon in this rotating and pulsating frame as in the CRTBP case. It is therefore only necessary to gradually increase the eccentricity e from 0 to 0.0549 in the equation of spacecraft motion by continuous algorithms, using the low thrust transfer trajectory obtained in the CRTBP as an initial trial.

As for the second step, the ERTBP is non-autonomous and the information contained in each point on the multi-revolution orbit is not only the state, but also the true anomaly f. So, the f at the moment of departure and arrival, and the TOF should be constrained. The true anomalies at the transfer departure point M and arrival point N are defined as $f_{M}$ and $f_N$, respectively, and the transfer is completed if:

$$\begin{aligned} f_M+\text {TOF}_\text {{non-d}}=f_N + 2k\pi , \quad k=0,\pm 1,\pm 2... \quad . \end{aligned}$$

(15)

Variations of the x-component for L2-E and L1-E with true anomaly are shown in Fig. 10. The so-called points M and N in the CRTBP represent the vicinity of the local farthest point on the multi-revolution orbits from the Moon (point class M and point class N), and the corresponding true anomalies are labeled in Fig. 10.

Fig. 10

Variations of the x-component of L2-E and L1-E with f

Fig. 11

An example of low-thrust transfer from L2-E to L1-E: a in the barycenter ERTBP; b in the Moon-center ERTBP; c the time history of $\theta$; d the time history of u

Let’s look at the simplest case: the points M and N are placed at ${\textbf{x}}_{0}$ in Table 2, and the thrust is adjusted so that the non-dimensional TOF is equal to 2$\pi$. In this example, both $f_M$ and $f_N$ are set to 0, and k is equal to 1.

The final low-thrust transfer trajectory is plotted in Fig. 11, including the time history of the control variables u and thrust direction angle $\theta$ (Fig. 11c, d, $\theta = \theta _1$). Meanwhile, the trajectory is redrawn in the dimensional ERTBP framework with the Moon at the center to observe whether the trajectory matches the information of the transfer endpoints (see Fig. 11b). The data on transfer trajectory are listed in Table 3.

It can be seen that to satisfy the constraints of Eq. (15), the transfer requires a large magnitude of thrust and the trajectory appears to be kinked. This means that this trajectory may not be optimal, but it does give us a lot of inspiration. Since the energy-optimal transfer criterion is applied in this study with an engine throttle factor u that varies from 0 to 1, the same thrust magnitude corresponds to a range of TOF [2]. That is, if we calculate from the situation in Fig. 11, the TOF can be increased to a certain value with the throttle factor u reaching its maximum value at each moment, $u (t) \equiv 1$. Alternatively, the TOF can be gradually decreased, with the value of u first decreasing and then increasing to $u (t) \equiv 1$. The maximum TOF achievable with this thrust magnitude (200 mN) is called the “upper bound”, and the minimum TOF is called the “lower bound”.

Table 3 Data on transfer trajectory in Fig. 11

In Fig. 12, all low-thrust transfers from the point class M region to the point class N region are calculated for different initial true anomalies (one period, 2$\pi$). The blue area represents all transfer solutions obtained by changing the TOF, from which trajectories satisfying Eq. (15) can be selected. For example, the data listed in Table 4 are used to construct the transfer trajectories (points A and B in Fig. 12). During the change of TOF, if $u(t)<0.5$ at a particular transfer scenario, it is possible that in this case the thrust magnitude can be equivalently taken as $0.5\times 200$ mN = 100 mN.

Fig. 12

Distribution of TOF with respect to true anomaly

Table 4 The appropriate transfer parameters in Fig. 12

Therefore, two low-thrust transfer trajectories from L2-E to L1-E are calculated using the sets of parameters in Table 4 (See Figs. 13 and 14). The transfer parameters are listed in Table 5. It is found that a reasonable choice of the true anomaly for the departure and arrival points in the ERTBP leads to several feasible solutions for the transfer between multi-revolution orbits, including the acceptable thrust magnitude and the TOF. In fact, there are an infinite number of such solutions, depending on the requirements of different missions, and each parameter in Eq. (15) can be adjusted. The transfer departure and arrival points can also fall into the blue regions of the target orbits (Figs. 8 and 9) and will not be repeated here.

Fig. 13

Low-thrust transfer from L2-E to L1-E using set A: a the barycenter ERTBP; b the Moon-center ERTBP; b the time history of $\theta$; d the time history of u

Fig. 14

Low-thrust transfer from L2-E to L1-E using set B: a the barycenter ERTBP; b the Moon-center ERTBP; b the time history of $\theta$; d the time history of u

Table 5 Data on transfer trajectories in Figs. 13 and 14

The above procedure works equally well for single- and double-circle trajectory configurations around the Moon, for which the relevant transfer solutions are presented in Figs. 15 and 16, as well as in Table 6.

Fig. 15

Low-thrust transfers from L2-E to L1-E with single-circle around the Moon: a the barycenter ERTBP; b the Moon-center ERTBP

Fig. 16

Low-thrust transfers from L2-E to L1-E with double-circle around the Moon: a the barycenter ERTBP; b the Moon-center ERTBP

Table 6 Data on transfer trajectories in Figs. 15 and 16

As in the case of the CRTBP, the same three configurations exist for the transfer between different LPOs (multi-revolution orbits) near the secondary body in the ERTBP. The more revolutions the spacecraft makes around the Moon, the lower the magnitude of the thrust is required for the transfer, which leads to an increase in the TOF and the propellant consumption.

4 Transfer trajectory tracking

In practice, the lunar orbital eccentricity e varies from moment to moment [30]. Figure 17 depicts the projected curve for the lunar orbital eccentricity in 2023. In contrast, the low-thrust transfer trajectories in the existing studies are planned in an offline model, considering a constant mean eccentricity. The application of such transfer trajectories in the real ephemeris requires an effective trajectory tracking controller.

Fig. 17

The lunar orbital eccentricity in 2023

Model predictive control (MPC) is an online controller capable of solving constrained problems and counteracting the effects of disturbances [31, 32]. MPC has been studied in the context of aerospace exploration. For example, Chai et al. [33] suggested a centralized robust MPC controller for reentry vehicle flight to track the reference attitude trajectory. Sanchez et al. [34] implemented the spacecraft rendezvous problem on near rectilinear halo orbits using chance-constrained MPC. Thus, in this paper, we design an MPC-based controller for the low-thrust transfer trajectory tracking problem.

4.1 MPC controller design

This section expands on the use of MPC controller for low-thrust transfer scenarios in the Earth–Moon ERTBP to assess the performance of transfer tracking between multi-revolution orbits. The reference trajectory is selected from Fig. 14.

Let ${\varvec{x}}_\textrm{r}=[{\varvec{r}}_\textrm{r},{\varvec{v}}_\textrm{r},m_\textrm{r}]^\textrm{T}$ and ${\varvec{u}}_\textrm{r}=[u_\textrm{r},\theta _\textrm{r}]^\textrm{T}$ represent the states of the spacecraft and the control inputs along the reference trajectory, then the equation of planar reference motion for a spacecraft reads:

$$\begin{aligned} \begin{aligned}&\dot{{\varvec{x}}}_\textrm{r}=f\left( {\varvec{x}}_\textrm{r}, {\varvec{u}}_\textrm{r}\right) \Rightarrow \left[ \begin{array}{l} \dot{{\varvec{r}}}_\textrm{r} \\ \dot{{\varvec{v}}}_\textrm{r} \\ {\dot{m}}_\textrm{r} \end{array}\right] \\&\quad =\left[ \begin{array}{l} v_{x_\textrm{r}} \\ v_{y_\textrm{r}} \\ {\varvec{g}}({\varvec{r}}_\textrm{r})+{\varvec{h}}({\varvec{v}}_\textrm{r})+ \frac{C_{1} u_\textrm{r} T_{\max }}{m_\textrm{r} (1+e\cos f)} \cos \left( \theta _\textrm{r}\right) \\ {\varvec{g}}({\varvec{r}}_\textrm{r})+{\varvec{h}}({\varvec{v}}_\textrm{r})+\frac{C_{1} u_\textrm{r} T_{\max }}{m_\textrm{r} (1+e\cos f)} \sin \left( \theta _\textrm{r}\right) \\ -C_{2} u_\textrm{r} T_{\max } / (I_{s p} g_{0}) \end{array}\right] . \end{aligned} \end{aligned}$$

(16)

Equation (16) is then linearized at a reference point (${\varvec{x}}_\textrm{r}(t),{\varvec{u}}_\textrm{r}(t)$):

$$\begin{aligned}&\dot{{\varvec{x}}}(t) =f\left( {\varvec{x}}_\textrm{r}(t), {\varvec{u}}_\textrm{r}(t)\right) \nonumber \\ {}&\quad +\left. \frac{\partial f}{\partial {\varvec{x}}}\right| _{\begin{array}{l} {\begin{array}{c} {\varvec{x}}={\varvec{x}}_\textrm{r}(t)\\ {\varvec{u}}={\varvec{u}}_\textrm{r}(t) \end{array}} \end{array}}\left( {\varvec{x}}(t)-{\varvec{x}}_\textrm{r}(t)\right) +\left. \frac{\partial f}{\partial {\varvec{u}}}\right| _{\begin{array}{c} {\varvec{x}}={\varvec{x}}_\textrm{r}(t) \nonumber \\ {\varvec{u}}={\varvec{u}}_\textrm{r}(t) \end{array}}\left( {\varvec{u}}(t)-{\varvec{u}}_\textrm{r}(t)\right) \nonumber \\&=f\left( {\varvec{x}}_\textrm{r}(t) {\varvec{u}}_\textrm{r}(t)\right) +{\textbf{A}}_\textrm{e}(t)\left( {\varvec{x}}(t)-{\varvec{x}}_\textrm{r}(t)\right) \nonumber \\&\quad +{\textbf{B}}_\textrm{e}(t)\left( {\varvec{u}}(t)-{\varvec{u}}_\textrm{r}(t)\right) , \end{aligned}$$

(17)

where ${\textbf{A}}_\textrm{e}(t)$ and ${\textbf{B}}_\textrm{e}(t)$ are the Jacobians of the system $f(\cdot )$, evaluated at the reference point.

By means of defining state error ${\varvec{x}}_\textrm{e}(t)={\varvec{x}}(t)-{\varvec{x}}_\textrm{r}(t)$ and control input error ${\varvec{u}}_\textrm{e}(t)={\varvec{u}}(t)-{\varvec{u}}_\textrm{r}(t)$ between the actual trajectory and the reference trajectory, the error equation for the spacecraft motion is as follows by subtracting Eq. (16) from Eq. (17):

$$\begin{aligned} \dot{{\varvec{x}}}_\textrm{e}(t)={\textbf{A}}_\textrm{e}(t) {\varvec{x}}_\textrm{e}(t)+{\textbf{B}}_\textrm{e}(t) {\varvec{u}}_\textrm{e}(t). \end{aligned}$$

(18)

In this study, we discretize Eq. (18) using the Eulerian discretization method and obtain the following discrete equation for the spacecraft motion error:

$$\begin{aligned} {\varvec{x}}_\textrm{e}(t+1)={\textbf{A}}_\textrm{d}(t) {\varvec{x}}_\textrm{e}(t)+{\textbf{B}}_\textrm{d}(t) {\varvec{u}}_\textrm{e}(t), \end{aligned}$$

(19)

where ${\textbf{A}}_\textrm{d}(t)=\text {e}^{{\textbf{A}}_\textrm{e}(t) T_{s}}$ and ${\textbf{B}}_\textrm{d}(t)=\int _{0}^{T_{s}} \text {e}^{{\textbf{A}}_\textrm{e}(t) \tau } \textrm{B}_\textrm{e}(t) d \tau$ are the discretized time-varying system and the control matrices, respectively. $T_s$ is the sample time.

The actual controller input ${\varvec{u}}$ to the spacecraft at each sampling instant t is ${\varvec{u}}_\textrm{r}+{\varvec{u}}_\textrm{e}$. To bound the tracking error, the state error ${\varvec{x}}_\textrm{e}(t)$ and the control input error ${\varvec{u}}_\textrm{e}(t)$ are subjected to the following constraints:

$$\begin{aligned} \begin{array}{l} {\varvec{x}}_\textrm{e}(t) \in {\mathbb {X}}_\textrm{e}:=\left\{ {\varvec{x}}_\textrm{e} \mid {\varvec{x}}_{e \min } \le {\varvec{x}}_\textrm{e} \le {\varvec{x}}_{e \max }\right\} , \\ {\varvec{u}}_\textrm{e}(t) \in {\mathbb {U}}_\textrm{e}(t):=\left\{ {\varvec{u}}_\textrm{e} \mid {\varvec{u}}_{\min }-{\varvec{u}}_\textrm{r}\right. \\ \left. \le {\varvec{u}}_\textrm{e} \le {\varvec{u}}_{\max }-{\varvec{u}}_\textrm{r}\right\} . \end{array} \nonumber \\ \end{aligned}$$

(20)

As a result, the optimal low-thrust transfer trajectory tracking problem can be described as: the control rate ${\varvec{u}}_\textrm{e}(t)=\kappa ({\varvec{x}}_\textrm{e}(t))$ is designed so that the spacecraft moves along the reference trajectory ${\varvec{x}}_\textrm{r}$ and satisfies the state constraints ${\mathbb {X}}_\textrm{e}$ and control input constraints ${\mathbb {U}}_\textrm{e}(t)$.

At each moment, the MPC-based algorithm solves a finite-horizon control problem using the current state as the initialization. The control input is thus repeatedly calculated. However, taking into account the full system model as well as the state and control constraints imposes a significant computational cost on the solution process that cannot be tolerated in real-time [35, 36]. In general, to ensure the robustness of MPC, it is necessary to compute the terminal set and the terminal cost [37]. This procedure, however, involves operations on polytopes and is computationally complex. So, in this paper, we adopt a simple constraint tightening formulation to avoid the computation of terminal sets and terminal costs to improve the MPC controller’s capability for real-time online computing [38].

$$\begin{aligned} {\mathbb {X}}_\textrm{e}= & {} \left\{ {\varvec{x}}_\textrm{e} \in {\mathbb {R}}^{n} \mid H {\varvec{x}}_\textrm{e} \le {\textbf{1}}_\textrm{p}\right\} , \nonumber \\ {\mathbb {U}}_\textrm{e}= & {} \left\{ {\varvec{u}}_\textrm{e} \in {\mathbb {R}}^{m} \mid L {\varvec{u}}_\textrm{e} \le {\textbf{1}}_\textrm{q}\right\} . \end{aligned}$$

(21)

A simple constraint tightening based on the exponential decay rate $\rho$ and a scalar tunable factor $\epsilon \in {\mathbb {R}}_{>0}$ is described with a scalar tightening parameter according to Köhler et al. [38].

$$\begin{aligned} \epsilon _{k}=\epsilon \frac{1-\sqrt{\rho }^{k}}{1-\sqrt{\rho }}, \quad \epsilon _{0}=0,\quad k \in \{0, \ldots , N-1\}. \end{aligned}$$

(22)

The set of tightened constraints is given by:

$$\begin{aligned} \begin{array}{l} \overline{{\mathbb {X}}}_\textrm{e}=\left( 1-\epsilon _{k}\right) {\mathbb {X}}_\textrm{e}=\left\{ {\varvec{x}}_\textrm{e} \in {\mathbb {R}}^{n} \mid H {\varvec{x}}_\textrm{e} \le \left( 1-\epsilon _{k}\right) {\textbf{1}}_\textrm{p}\right\} , \\ \overline{{\mathbb {U}}}_\textrm{e}=\left( 1-\epsilon _{k}\right) {\mathbb {U}}_\textrm{e}=\left\{ {\varvec{u}}_\textrm{e} \in {\mathbb {R}}^{m} \mid L {\varvec{u}}_\textrm{e} \le \left( 1-\epsilon _{k}\right) {\textbf{1}}_\textrm{q}\right\} . \end{array}\nonumber \\ \end{aligned}$$

(23)

Assume that a complete measurement of the state ${\varvec{x}}$ is available at the current time t. Such we can formulate the MPC optimization problem ${\mathcal {P}}(t)$ by the constraint tightening:

$$\begin{aligned} \begin{aligned} \min _{U(t)}&\quad {\bar{V}}_{N}, \\ \text{ s.t. }&{\varvec{x}}_\textrm{e}(i+1 \mid t)={\textbf{A}}_\textrm{d}(t+i) {\varvec{x}}_\textrm{e}(i \mid t)\\&\quad +{\textbf{B}}_\textrm{d}(t+i) {\varvec{u}}_\textrm{e}(i \mid t), \\&{\varvec{x}}_\textrm{e}(i \mid t) \in \overline{{\mathbb {X}}}_\textrm{e}, {\varvec{u}}_\textrm{e}(i \mid t) \in \overline{{\mathbb {U}}}_\textrm{e}, i=0, \ldots N-1, \\&{\varvec{x}}_\textrm{e}(0 \mid t)={\varvec{x}}_\textrm{e}(t). \end{aligned} \end{aligned}$$

(24)

In Eq. (24) ${\bar{V}}_{N}=\sum _{i=0}^{N-1}\left( \left\| {\varvec{x}}_\textrm{e}(i \mid t)\right\| _{{Q}}^{2}+\left\| {\varvec{u}}_\textrm{e}(i \mid t)\right\| _\textrm{r}^{2}\right)$. Q and R are the positive definite state weighting and control weighting matrices, respectively. N is the receding horizon step for the MPC controller. The actual control input in the spacecraft motion error equation is $\kappa \left( {\varvec{x}}_\textrm{e}(t)\right) ={\varvec{u}}_{\textrm{e}}{ }^{*}(0 \mid t)$.

The solution of this optimization problem is performed using the MPT3 toolbox in the MATLAB environment [39].

4.2 The trajectory tracking simulation results

The transfer trajectory depicted in Fig. 14 is calculated for the case of $e \equiv$ 0.0549. Since the lunar orbital eccentricity is predictable, the true e can be computed in advance with a given date and applied to the reference trajectory. The transfer trajectory data indicates an initial lunar true anomaly of 4.47 radians for the transfer, with a selected date of 3 May 2023 at 14:34:17 ($E_0$). That is, the transfer trajectory is first calculated in the ideal ERTBP and then shifted into the real ephemeris model using continuous algorithms. The resulting trajectory is used as a reference trajectory for the real mission.

This section considers a trajectory tracking control problem with an initial orbit error of 40 km and a launch window error of 1 h. The constraints and parameter settings for the MPC controller are listed in Table 7.

Table 7 Parameter settings for the MPC controller

Fig. 18

The result of low-thrust transfer tracking: a the tracking trajectory; b the control inputs u and $\theta$

Fig. 19

The spacecraft state tracking errors

Figure 18 shows the result of tracking the energy-optimal low-thrust transfer trajectory between multi-revolution orbits in the real Earth–Moon ERTBP. Discrete trajectory tracking points are plotted as black circles, while the reference trajectory is represented by the blue curve. The spacecraft state tracking errors are shown in Fig. 19. As can be seen from Fig. 19, the initial orbit error is quickly eliminated, a position error of 1.53 km and a velocity error of 0.01 m/s are obtained at the end of the transfer.

It should be noted that, as explained at the beginning of Section 4.2, the implementation of this transfer mission requires a strict choice of the launch window. Due to the non-autonomous and periodic nature of the ERTBP, the initial lunar true anomaly is unique for a given transfer scenario, and if missing the launch window requires waiting for one more lunar period (about 27 days). Moreover, since the lunar orbital eccentricity is changing all the time, even if we wait until the next launch window, the algorithm may not converge due to the large difference between the values of actual e and that planned offline.

So, the Monte Carlo method is used for the simulation analysis of the error in the initial epoch of the transfer. By performing a large number of random calculations, we find that the trajectory tracking algorithm converges if the error between the initial moment of the transfer and $E_0$ is within 5 h. That is, the MPC-based controller designed in this paper can achieve a transfer trajectory tracking mission that satisfies a given tracking error within the ERTBP framework with an allowable launch window error of no more than 5 h.

5 Conclusion

In this paper, we study the low-thrust transfer between planar multi-revolution orbits in the Earth–Moon ERTBP near the secondary body. By splicing invariant manifolds associated with periodic orbits in the CRTBP, different types of heteroclinic connections are constructed using the Poincaré section technique as initial trials for the energy-optimal low-thrust transfers in the ERTBP. Indirect optimization is used to solve for the optimal control input. Investigations into this low-thrust transfer problem have led us to three conclusions:

• As in the case of the CRTBP, the same three trajectory configurations exist for the transfer between different collinear libration point orbits in the ERTBP. The more revolutions the spacecraft makes around the Moon, the lower the magnitude of the thrust is required for the transfer.

• To determine whether the transfer is complete, we propose a formula. This formula can be used to match the departure moment (the true anomaly of the Moon’s motion) and the transfer time, resulting in acceptable transfer trajectories with thrusts as low as a few tens of mN.

• The designed constraint tightening MPC controller is able to track the optimal transfer trajectory planned offline with the consideration of initial orbital errors and launch window errors in practice.

The concepts and procedures presented in this study for low-thrust transfer calculations in the ERTBP are more closely related to the requirements of practical lunar mission designs.