1 Introduction

Einstein (1916) proposed three tests of general relativity, subsequently called the classical tests of general relativity: the perihelion precession of Mercury’s orbit, the deflection of light by the Sun and the gravitational redshift of light. The deflection of light due to gravity of the massive object is known as gravitational lensing. Gravitational lensing has become an important tool for astronomy. It can give information about the source that is imaged, about the object acting as a lens, and about the intervening large-scale geometry of the universe when source, lens and observer at a cosmological distances from one another. The first paper on this subject, enabled “Nebulae as gravitational lenses” was published by Zwicky (1937). Zwicky clearly emphasized the role of galaxies as light-deflecting objects that could produce multiple images of background sources. In the 1960s and 1970s, Refsdal (1964, 1966), Barnothy and Barnothy (1968), Kristian and Sachs (1966), Bourass and Kantowski (1975), Dyer and Roeder (1974), Sanitt (1971) and several others published papers highlighting various aspects of gravitational lensing, ranging from purely theoretical investigations in general relativity to observational predictions in astronomy. For further details on problems of the theory and observations of gravitational lensing one can find in the book of Schneider et al. (1992).

Recently Bisnovatyi-Kogan and Tsupko (2010, 2015), Tsupko and Bisnovatyi-Kogan (2012) have studied propagation of light in the presence of massive gravitational lens surrounded by plasma. In these works it has been considered the deflection of light by the gravitation field and by the inhomogeneities of plasma self-consistently and showed that even in the homogeneous plasma the deflection angle depends on the frequency of light through the refractive index. In the paper of Morozova et al. (2013) it has been studied gravitational lensing in the vicinity of a slowly rotating massive object surrounded by a plasma. They have studied the influence of rotation of the gravitational lens on the deflection angle of the light ray in the presence of plasma.

In the present paper we consider effects of gravitational lensing by non-Schwarzschild space-time in the presence of homogeneous plasma. Present non-Schwarzschild space-time has been introduced by Yunes and Stein (2011) where they studied two large classes of alternative theories, modifying the action through algebraic, quadratic curvature invariants coupled to scalar fields, and found a deformation to the Schwarzschild metric that solved the modified field equations in the small coupling approximation. Afterwards Johannsen and Psaltis (2011) have been motivated by examining the no-hair theorem, they applied the Newman-Janis transformation (Newman and Janis 1965) and constructed a non-Kerr black hole metric with deformed parameter \(\epsilon\), which measures deviations from the Kerr geometry. The deformation parameter \(\epsilon\) can take quantities as \(\epsilon> 0\) or \(\epsilon<0\) corresponds to the cases in which the event horizon of compact object is more prolate or oblate than that of the Kerr one, respectively. The study of the astrophysical processes in the vicinity of deformed compact gravitational objects could provide an opportunity for constraining the allowed parameter space of solutions, and to provide a deeper insight into the physical nature and properties of the corresponding spacetime metric. For example Chen and Jing (2012) have studied the strong gravitational lensing in the background of a non-Kerr black hole and have found that the marginally circular stable orbit radius and deflection angle depend sharply on the deformation parameter \(\epsilon\) and rotation one \(a\). Recently in our preceding work (Atamurotov et al. 2013) it was shown that in addition to the specific angular momentum \(a\), the deformation parameter of non-Kerr spacetime essentially deformed the shape of the black hole shadow. Moreover recently Rayimbaev et al. (2015) have studied rotating magnetized neutron star with plasma magnetosphere described by non-Kerr spacetime metric in slow rotation approximation.

The main purpose of this paper is to study the weak gravitational lensing by a non-Schwarzschild compact object surrounded by homogeneous plasma and see how deformation parameter either plasma influence to the deflection angle in the weak field limit. Here we plan to extend the results of the paper of Bisnovatyi-Kogan and Tsupko (2010) to the case of deformed gravitational lens. We consider a light ray propagating in the vicinity of the massive Schwarzschild like object surrounded by plasma shell. Our goal is to investigate the deflection angle in the case when the metric of spacetime has deformation parameter.

The paper is organized as follow. In Sect. 2 we study deflection of light by non-Schwarzschild gravitational lensing object in a plasma. As a physical application of the obtained result in Sect. 3 we consider the influence of deformation parameter on the magnification of brightness of the star in the case of microlensing. We obtain the ratio of the magnification in the case of non-Schwarzschild and Schwarzschild lens, but the estimation of the effect using the typical parameters of the lensing systems shows that the effect of deformation is small. Finally in Sect. 4 we summarize our main findings.

Throughout, we use a space-like signature \((-,+,+,+)\). Greek indices run from 0 to 3 and Latin ones from 1 to 3.

2 Deflection of light by a non-Schwarzschild lensing object in a plasma

2.1 Equations of light propagation in deformed space-time

Here we assume that the gravitational field is weak and the space-time is asymptotically flat, mathematically it means

$$\begin{aligned}& g_{\alpha\beta}=\eta_{\alpha\beta}+h_{\alpha\beta}, \quad \eta _{\alpha\beta}=(-1,1,1,1), \\& h_{\alpha\beta}\ll1, \quad h_{\alpha\beta}\rightarrow0 \quad \mbox{under } x^{i}\rightarrow\infty, \end{aligned}$$
(1)

where \(g_{\alpha\beta}\) is the metric tensor of the \(ds^{2}=g_{\alpha\beta }dx^{\alpha}dx^{\beta}\) space-time metric, \(h_{\alpha\beta}\) is the flat space metric \((-1, 1, 1, 1)\) and is a small perturbation. And their contravariants are (see Landau and Lifshitz 1971)

$$ g^{\alpha\beta}=\eta^{\alpha\beta}-h^{\alpha\beta} , \quad h^{\alpha\beta}=h_{\alpha\beta} . $$
(2)

Synge (1960) suggested equivalent variational principle which might be taken as a base of the geometrical optics. He has shown that in the presence of the gravitational field the trajectories of photons can be taken from the variational principle

$$ \delta \biggl( \int p_{\alpha}dx^{\alpha}\biggr)=0 $$
(3)

by using following restriction condition

$$ n^{2}=1+ \frac{p_{\alpha}p^{\alpha}}{ (p^{0}\sqrt{-g_{00}} )^{2}} , $$

in the form

$$ W\bigl(x^{\alpha},p_{\alpha}\bigr)=\frac{1}{2} \bigl[g^{\alpha\beta }p_{\alpha}p_{\beta}-\bigl(n^{2}-1 \bigr) \bigl(p_{\alpha} V^{\alpha} \bigr)^{2} \bigr]=0 , $$
(4)

here \(p^{\alpha}\) is the photon momentum, \(V^{\alpha}\) is the 4-velocity of the medium and \(n\) is the refractive index of the medium, leads to the following system of differential equations

$$ \frac{dx^{\alpha}}{d\lambda}=\frac{\partial W}{\partial p_{\alpha}} ,\qquad \frac{dp_{\alpha}}{d\lambda}=-\frac{\partial W}{\partial x^{\alpha}} , $$
(5)

with the affine parameter \(\lambda\) which is changing along the photon’s trajectory.

Taking into account that in a static gravitational field for a static medium (see Synge 1960)

$$ p_{\alpha} V^{\alpha}=-\frac{\hbar\omega(x^{i})}{c} , $$
(6)

where \(\hbar\) is the Planck constant, \(\omega(x^{i})\) is the photon frequency, which depends on the spatial coordinates \(x^{i}\) due to the presence of the gravitational field, and \(c\) is the speed of light, the scalar function \(W(x^{\alpha},p_{\alpha})\) may be rewritten in the form

$$ W\bigl(x^{\alpha},p_{\alpha}\bigr)=\frac{1}{2} \biggl[g^{\alpha\beta}p_{\alpha}p_{\beta}-\bigl(n^{2}-1\bigr)\frac{\hbar^{2}\omega^{2}(x^{i})}{c^{2}} \biggr] . $$
(7)

Here a static inhomogeneous plasma with a refractive index \(n\) depends on \(x^{i}\) and \(\omega(x^{i})\) as

$$ n^{2}=1-\frac{\omega^{2}_{e}}{\omega^{2}(x^{i})} , \qquad\omega^{2}_{e}= \frac{4\pi e^{2} N}{m}\equiv K_{e}N , $$
(8)

where \(N=N(x^{i})\) is the electron concentration in an inhomogeneous plasma, \(e\) is the charge of the electron, \(m\) is the electron mass, \(\omega_{e}\) is the electron plasma frequency in this plasma. We denote the following notations for the values at infinity as \(\omega(\infty)=\omega\), \(\omega_{e}(\infty)=\omega_{0}\), \(n(\infty)=\sqrt{1-\omega^{2}_{0}/\omega^{2}}=n_{0}\).

From (7) and (8) one may write Eqs. (5) for the trajectory of the photon as

$$\begin{aligned}& \begin{aligned} &\frac{dx^{i}}{d\lambda}=g^{ik}p_{k} , \\ &\frac{dp_{i}}{d\lambda}=-\frac{1}{2}g^{lm}_{,i}p_{l}p_{m} -\frac{1}{2}g^{00}_{,i}p_{0}^{2} - \frac{1}{2}\frac{\hbar^{2} K_{e} N_{,i}}{c^{2}} . \end{aligned} \end{aligned}$$
(9)

Solution for the photon’s trajectory in flat space-time in vacuum is a straight line. The components of the 4-momentum of photon moving along the straight line along the \(z\)-axis are (see Bisnovatyi-Kogan and Tsupko 2010)

$$ p^{\alpha}= \biggl(\frac{\hbar\omega}{c},0,0,\frac{n_{0}\hbar\omega }{c} \biggr),\quad\quad p_{\alpha}= \biggl(-\frac{\hbar\omega}{c},0,0,\frac{n_{0}\hbar\omega }{c} \biggr) . $$
(10)

While there is weak gravitational field and small plasma inhomogeneity, we follow to the work of Bisnovatyi-Kogan and Tsupko (2010) and may consider the components (10) as null approximation for the trajectory of the photon. Using Eqs. (9) one gets in the left-hand side the first order deviation of the trajectory from a straight line as

$$ \frac{dp_{i}}{dz}=\frac{1}{2}\frac{n_{0}\hbar\omega}{c} \biggl(h_{33 ,i} + \frac{1}{n_{0}^{2}}h_{00 ,i} - \frac{K_{e} N_{,i}}{n_{0}^{2}\omega^{2}} \biggr) , $$
(11)

with

$$ \frac{dz}{d\lambda}=\frac{n_{0}\hbar\omega}{c} . $$
(12)

The deflection angle of the light ray in the plane perpendicular to the \(z\)-axis is equal to (see Bisnovatyi-Kogan and Tsupko 2009)

$$\begin{aligned}& \begin{aligned} &\hat{\alpha}_{k}=\bigl[p_{k}( \infty)-p_{k}(-\infty)\bigr]/p , \\ & p=\sqrt{p_{1}^{2}+p_{2}^{2}+p_{3}^{2}}=|p_{3}|= \frac{n_{0}\hbar\omega}{c} , \quad k=1,2, \end{aligned} \end{aligned}$$
(13)

and from Eq. (11) one can get

$$\begin{aligned}& \hat{\alpha}_{k}= \frac{1}{2} \int^{\infty}_{-\infty} \frac{\partial}{\partial x^{k}} \biggl(h_{33}+\frac{h_{00}\omega^{2}}{\omega^{2}-\omega^{2}_{0}} -\frac{K_{e}N}{\omega^{2}-\omega^{2}_{0}} \biggr)dz . \end{aligned}$$
(14)

2.2 Angle of deflection

The deformed Schwarzschild like metric which describes static and asymptotically flat vacuum spacetime, in the standard Boyer-Lindquist coordinates, may be expressed as (Yunes and Stein 2011)

$$\begin{aligned} ds^{2} = -f(1+h)c^{2}dt^{2}+f^{-1}(1+h)dr^{2}+r^{2}d \Omega, \end{aligned}$$
(15)

where

$$\begin{aligned}& f = 1-\frac{2\mathit{GM}}{c^{2}r}, \\& d\Omega = d\theta^{2}+\sin^{2}\theta d \phi^{2}. \end{aligned}$$

Together with the mass of lensing object, this spacetime metric contains parameters that measure potential deviations from the Schwarzschild metric and reduces to the Schwarzschild metric in Boyer-Lindquist coordinates in the case when \(h(r)=0\). The function \(h(r)\) can be chosen as

$$\begin{aligned} h(r)=\sum_{k=0}^{\infty}\epsilon_{k} \biggl(\frac{\mathit{GM}}{c^{2}r} \biggr)^{k}, \end{aligned}$$

and the constraints on \(\epsilon_{k}\) can be found from asymptotical properties of the metric (15). The requirement of the asymptotic flatness of the metric implies that \(\epsilon_{0}=\epsilon _{1}=0\). Here our choice of the function \(h(r)\) to be the third power of \((\mathit{GM}/c^{2}r)\) as in Johannsen and Psaltis (2011) is

$$\begin{aligned} h(r)=\epsilon \biggl(\frac{\mathit{GM}}{c^{2}r} \biggr)^{3} . \end{aligned}$$

As \(\epsilon=0\), the metric (15) is reduced to the typical Schwarzschild one well known in general relativity.

In the limit of large radii, the static and asymptotically flat spacetime non-Schwarzschild metric can be written as (Landau and Lifshitz 1971)

$$\begin{aligned} ds^{2} = ds^{2}_{0}+ \biggl(\frac{2\mathit{GM}}{c^{2}r}-h \biggr)c^{2}dt^{2}+ \biggl( \frac {2\mathit{GM}}{c^{2}r}+h \biggr)dr^{2} , \end{aligned}$$
(16)

where the flat part of the above metric is \(ds^{2}_{0}=-c^{2}dt^{2}+dr^{2}+r^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2})\).

In the Cartesian coordinates the components \(h_{\alpha\beta}\) are written as

$$\begin{aligned}& \begin{aligned} &h_{00}= \biggl(\frac{r_{g}}{r}-h \biggr), \\ &h_{ik}= \biggl(\frac{r_{g}}{r}+h \biggr)n_{i}n_{k}, \quad\quad h_{33}= \biggl(\frac{r_{g}}{r}+h \biggr)\cos^{2}\chi . \end{aligned} \end{aligned}$$
(17)

Here \(r_{g}=2\mathit{GM}/c^{2}\), \(n_{i}\) is the unit vector of 3-radius-vector \(r_{i} = (x_{1},x_{2},x_{3})\), the angle \(\chi\) is the polar angle between 3-vector \(r^{i}=r_{i}\) and \(z\)-axis, and \(n_{3}=\cos\chi= z/r = z/\sqrt{b^{2}+z^{2}}\). And the formula for the deflection angle of light for non-Schwarzschild lensing object in homogeneous plasma will be in the following form

$$\begin{aligned} \hat{\alpha}_{b} =&\int_{0}^{\infty}\frac{\partial}{\partial b} \biggl[ \biggl(\frac{r_{g}}{\sqrt{b^{2}+z^{2}}}+\epsilon\frac {(\mathit{GM}/c^{2})^{3}}{(b^{2}+z^{2})^{3/2}} \biggr) \frac{z^{2}}{b^{2}+z^{2}} \\ &{} +\frac{1}{1-\omega^{2}_{0}/\omega^{2}} \biggl(\frac{r_{g}}{\sqrt{b^{2}+z^{2}}} -\epsilon\frac{(\mathit{GM}/c^{2})^{3}}{(b^{2}+z^{2})^{3/2}} \biggr) \biggr]dz . \end{aligned}$$

One can calculate the deflection angle as

$$\begin{aligned} \hat{\alpha}_{b} =& \frac{r_{g}}{b} \biggl[ \biggl(1+ \frac{1}{1-\omega ^{2}_{0}/\omega^{2}} \biggr) \\ &{} -\epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} \biggl( \frac{1}{1-\omega ^{2}_{0}/\omega^{2}} -\frac{1}{3} \biggr) \biggr] . \end{aligned}$$
(18)

The above formula (18) is valid only for \(\omega>\omega_{0}\), because the waves with \(\omega<\omega_{0}\) do not propagate in the plasma (see Ginzburg 1970).

One can see from (18) when there is vacuum \(\omega_{0}=0\) and no deformation in spacetime \(\epsilon=0\) the gravitational deflection

$$\begin{aligned} \hat{\alpha}_{b}=\frac{2r_{g}}{b} , \end{aligned}$$
(19)

is the Schwarzschild one. In the presence of plasma and absents of the deformation of the spacetime, the formula (18) comes to

$$ \hat{\alpha}_{b}=\frac{r_{g}}{b} \biggl(1+\frac{1}{1-\omega^{2}_{0}/\omega ^{2}} \biggr) , $$
(20)

as it was shown by Bisnovatyi-Kogan and Tsupko (2010). One can easily see that in the absent of plasma the deflection angle by non-Schwarzschild spacetime will be:

$$ \hat{\alpha}_{b}=\frac{2r_{g}}{b} \biggl(1-\frac{1}{3} \epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} \biggr) . $$
(21)

For the clarity of importance of our research we compare the second term in the right hand side with deformation parameter of Eq. (18) for \(\hat{\alpha}_{b}\) with the first term by the order of magnitude. In the case \(\omega_{0}<<\omega\) the ratio of these terms is equal to

$$ -\frac{1}{3}\epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} , $$
(22)

which can be \(0.017\epsilon\) for the typical neutron star with the radius \(R=10~\mbox{km}\). For deformation parameter \(\epsilon=\pm6\) the ratio reaches \(10^{-1}\) as the ratio of term being responsible for the angular momentum to the one induced by the total mass for millisecond pulsars (see Morozova et al. 2013).

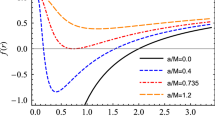
Let us now see how the deflection angle behaves in a weak field for the lens with a homogeneous plasma described by a non-Schwarzschild metric (15). From Fig. 1 one can see that as in the Schwarzschild case for all values of deformation parameter \(\epsilon\) the deflection angle decreases with the increasing impact parameter \(b\) either the lens is in vacuum figure (a) or surrounded with a plasma figure (b). Nevertheless the presence of the plasma increases the deflection angle by the lensing object. Let us note that the deflection can be strongest only for the radiowaves, when the frequency of the electromagnetic wave would be slightly exceeding the plasma frequency (see Bisnovatyi-Kogan and Tsupko 2009) and in other wave lengths when the frequency of the light much more bigger then the electron frequency plasma it comes to the Schwarzschild one (19). The change of deflection angle \(\alpha\) by the deformed lensing object with a square ratio of electron frequency plasma \(\omega_{0}\) to the frequency of photon \(\omega\) changes from zero to one is shown in Fig. 2, which tells us that the deflection angle is increasing monotonically with frequency \(\omega\) is approaching to the electron plasma frequency \(\omega_{0}\).

Fig. 1
figure 1

Deflection angle \(\alpha_{b}\) as a function of the impact parameter \(b\). In plots in vertical axes \(\alpha_{b}\) is taken in radians, and in horizontal axes \(b/M\) is considered as dimensionless parameter. Plot (a) corresponds to the vacuum case, while plot (b) has a plasma with a \(\varpi=\omega_{0}^{2}/\omega^{2}=0.5\)

Full size image
Fig. 2
figure 2

Variety of the deflection angle \(\alpha_{b}\) with the deformed parameter \(\epsilon\), where \(\varpi=\omega_{0}^{2}/\omega^{2}\)

Full size image

3 Amplification of brightness of the image source

In the classical model of gravitational lensing the traveling light is bent to the angle (19) which is called Einstein deflection angle, by the presence of a massive body. However in our deformed lens surrounded by the homogenous plasma case the deflection angle should be replaced by formula (18). In observational astronomy an Einstein ring is the inclination of the light from a source (such as a galaxy or star) into a ring through gravitational lensing of the source’s light by an object with an extremely large mass (such as another galaxy or a black hole). This occurs when the source, lens, and observer are all aligned. The size of an Einstein ring which is the angular half separation due to gravitational lensing, between the images of the source in vacuum (Schneider et al. 1992) is of the order of

$$ \theta_{0} = \sqrt{2 r_{g} \frac{D_{ds}}{D_{d} D_{s}}} , $$
(23)

where \(D_{d}\) is the angular diameter distance between the observer and the lens, \(D_{s}\) is the angular diameter distance between the observer and the source, \(D_{ds}\) is the angular diameter distance between the lens and the source. Non-Schwarzschild lensing in presence of a homogeneous plasma (18) leads to an angular half separation between images as

$$\begin{aligned} \bigl(\theta_{0}^{pl} \bigr)_{\epsilon} =& \biggl[ \biggl[ \biggl(1+\frac {1}{1-\omega^{2}_{0}/\omega^{2}} \biggr) \\ &{} -\epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} \biggl( \frac{1}{1 - (\omega _{0}^{2} / \omega^{2})}-\frac{1}{3} \biggr) \biggr] r_{g} \frac{D_{ds}}{D_{d} D_{s}} \biggr]^{1/2} \\ =&\theta_{0} \biggl[\frac{1}{2} \biggl( 1 + \frac{1}{1 - (\omega_{0}^{2} / \omega^{2})} \biggr) \\ &{} -\frac{1}{2}\epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} \biggl( \frac{1}{ 1 - (\omega_{0}^{2} / \omega^{2})}-\frac{1}{3} \biggr) \biggr]^{1/2} , \end{aligned}$$
(24)

or the formula (24) can be written in the following way

$$ \bigl(\theta_{0}^{pl} \bigr)_{\epsilon}= \sqrt { \bigl(\theta_{0}^{pl} \bigr)^{2}- \epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} \biggl( \frac{1}{1 - \omega_{0}^{2} / \omega^{2}}-\frac{1}{3} \biggr)\frac{\theta_{0}^{2}}{2}} , $$
(25)

where

$$ \theta_{0}^{pl}=\theta_{0}\sqrt{ \frac{1}{2} \biggl(1+\frac{1}{1-\omega_{0}^{2} / \omega^{2}} \biggr)} , $$
(26)

which is called, as plasma Einstein ring (see Bisnovatyi-Kogan and Tsupko 2010).

While gravitational lensing preserves surface brightness, lensing does change the apparent solid angle of a source. The amount of magnification is given by the ratio of the image area to the source area. The magnification effect enables us to observe objects which are too distant or intrinsically too faint to be observed without lensing. Lenses therefore act as “cosmic telescopes” and allow us to infer source properties far below the resolution limit or sensitivity limit of current observations. For a circularly symmetric lens, the magnification factor \(\mu\) is given by

$$ \mu=\frac{\theta}{\beta}\frac{d\theta}{d\beta} , $$

where the \(\beta\) is the angular position of the source and the \(\theta \) is the angular position of the appeared image relative to the line passing through the observer and the lens respectively.

Following to the book of Schneider et al. (1992) let the magnification factor of the primary image \(\mu_{+}\), located at the same side as the source relative to the lens, and of the secondary image \(\mu_{-}\), located at the opposite side, depend on the angular position of the source. Further corresponding expression for the magnification would be

$$\begin{aligned}& \mu_{+} = \frac{1}{4} \biggl[ \frac{y}{\sqrt{y^{2}+4}} + \frac{\sqrt{y^{2}+4}}{y} + 2 \biggr], \end{aligned}$$
(27)
$$\begin{aligned}& \mu_{-} = \frac{1}{4} \biggl[ \frac{y}{\sqrt{y^{2}+4}} + \frac{\sqrt {y^{2}+4}}{y} - 2 \biggr]. \end{aligned}$$
(28)

Here \(y = \beta/ \theta_{0}\), and the total magnification of the source is equal to

$$ \mu_{\Sigma} = \mu_{+} + \mu_{-} = \frac{y^{2} + 2}{y \sqrt{y^{2}+4}}. $$
(29)

We consider the total magnification which is the product of the individual values of each type of magnification used in combination with each other. Because it is important for the microlensing events when the separated images are not resolved, and the only observable effect is changing of the flux from the source due to lensing.

In the case of lensing in plasma we can rewrite these formulae, using \(\tilde{y} = \beta/ (\theta_{0}^{pl} )_{\epsilon}\) instead \(y\):

$$\begin{aligned}& \mu_{\epsilon+}^{pl} = \frac{1}{4} \biggl[ \frac{\tilde{y}}{\sqrt{\tilde {y}^{2}+4}} + \frac{\sqrt{\tilde{y}^{2}+4}}{\tilde{y}} + 2 \biggr], \end{aligned}$$
(30)
$$\begin{aligned}& \mu_{\epsilon-}^{pl} = \frac{1}{4} \biggl[ \frac{\tilde{y}}{\sqrt{\tilde {y}^{2}+4}} + \frac{\sqrt{\tilde{y}^{2}+4}}{\tilde{y}} - 2 \biggr], \end{aligned}$$
(31)
$$\begin{aligned}& \mu_{\Sigma}^{pl} = \mu_{+}^{pl} + \mu_{-}^{pl} = \frac{\tilde{y}^{2} + 2}{\tilde{y} \sqrt{\tilde{y}^{2}+4}}, \end{aligned}$$
(32)

where

$$\begin{aligned} \tilde{y} =& \frac{\beta}{ (\theta_{0}^{pl} )_{\epsilon}} \\ =& \frac{\beta}{\theta_{0}} \biggl[\frac{1}{2} \biggl( 1 + \frac{1}{1 - (\omega_{0}^{2} / \omega^{2})} \biggr) \\ &{}-\frac{1}{2}\epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} \biggl( \frac{1}{1 - \omega_{0}^{2} / \omega^{2}}-\frac{1}{3} \biggr) \biggr]^{-1/2} . \end{aligned}$$
(33)

At large \(\beta\) the total amplification factor goes to unity, because the influence of the lens on the light propagation becomes negligible. For both Schwarzschild and non-Schwarzschild lenses at a small angle \(\beta\), the amplification is inversely proportional to the angle \(\beta\), and is proportional to the angular radius of the Einstein ring, which increases with decreasing frequency, approaching infinity at the plasma frequency. As \(\beta\) goes to zero, the amplification increases, formally unrestrictedly for the point source.

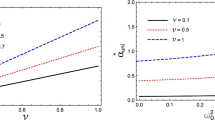
The ratio of the magnification of the primary image in presence of plasma \(\mu_{\epsilon+}^{pl}\) to the same value in vacuum \(\mu_{\epsilon+}\) with deformation parameters is given in Fig. 3, for \(\omega=\sqrt{2} \omega_{e}\), according to (27), (30). The upper curve in Fig. 3 is the ratio of the magnification of the secondary image in presence of plasma \(\mu_{\epsilon-}^{pl}\) to the same value in vacuum \(\mu _{\epsilon-}\), according to (28), (31).

Fig. 3
figure 3

The ratio \(\mu_{\epsilon+}^{pl}/\mu_{\epsilon+}\) of the magnification of the primary image in presence of plasma to the same value in vacuum (lower curve), and the ratio \(\mu_{\epsilon-}^{pl}/\mu_{\epsilon-}\) of the magnification of the secondary image in presence of plasma to the same value in vacuum (upper curve) with deformations parameter \(\epsilon\). Curves are plotted for \(\omega=\sqrt{2} \omega_{0}\)

Full size image

The deflection angle in presence of the plasma is larger, than in the vacuum, so the amplification for lower frequencies is larger, and in this situation the image spectrum differs from the original spectrum of the source, having more intensive the low-frequency part. The light in two lensing images is propagating through different media with different plasma density. Therefore, different images of the same source may have different spectra in the radio band.

Our purpose is to calculate \({\mu_{\Sigma\epsilon}^{pl}}/{\mu_{\Sigma}^{pl}}\) for the case when \(\beta\rightarrow0\) and see how deformation parameters affects the maximum value of the peak of magnification in the gravitational microlensing phenomena. Here \(\mu_{\Sigma\epsilon}^{pl}\) is the magnification by the deformed and \(\mu_{\Sigma}^{pl}\) by the non-deformed gravitational lenses surrounded by homogeneous plasma. The magnification in the case of the non-deformed lens surrounded by plasma was investigated in the work of Bisnovatyi-Kogan and Tsupko (2010) and for \(\beta\rightarrow0\) is equal to

$$ \mu_{\Sigma}^{pl} \big|_{\beta\rightarrow0}\rightarrow \frac{1}{2}\frac{\sqrt{2\theta^{2}_{0} (1+\frac{1}{1-\frac{\omega^{2}_{0}}{\omega^{2}}} )}}{\beta} . $$
(34)

One can obtain for the ratio \({\mu_{\Sigma\epsilon}^{pl}}/{\mu_{\Sigma}^{pl}}\) in the limit \(\beta\rightarrow0\) the following result

$$\begin{aligned} \frac{\mu_{\Sigma\epsilon}^{pl}}{\mu_{\Sigma}^{pl}} =& \biggl[1-\epsilon \biggl(\frac{\mathit{GM}}{c^{2}b} \biggr)^{2} \biggl(\frac{1}{1-\frac{\omega_{0}^{2}}{\omega^{2}}}-\frac{1}{3} \biggr) \\ &{} \times \biggl(1+\frac{1}{1-\frac{\omega_{0}^{2}}{\omega^{2}}} \biggr)^{-1} \biggr]^{\frac{1}{2}} , \end{aligned}$$
(35)

which is equal to 1 when there is vacuum \(\omega_{0}=0\) and no deformation \(\epsilon=0\), as it could be expected.

However, the effect of the deformation on the magnification appears to be of little significance as soon as we try to estimate it for the astrophysical situation. Assuming the lens to be a supermassive black hole with the following values of parameters e.g. deformation parameter between \((-20, 20)\) (see Chen and Jing 2012; Johannsen and Psaltis 2011; Atamurotov et al. 2013; Abdujabbarov et al. 2013), and the mass \(M=1\), with the impact parameter \(b=8.982\) (see Tsupko and Bisnovatyi-Kogan 2013), and the ratio of electron plasma frequency with the frequency of the light as \(\omega _{0}^{2}/\omega^{2}=(0, 0.01, 0.25, 0.5, 0.9)\) have the following orders Table 1.

Table 1 The contribution of the deformation parameter to the magnification of the brightness of the source. The ration of magnification with deformation parameter to the source without deformation parameter in plasma can be expressed like \(\mu_{\Sigma \epsilon}/\mu_{\Sigma}=1\pm\Delta\mu\), where \(\Delta\mu\) is presented in percentages \(\%\). Here in the table 0 means vacuum spacetime
Full size table

This give us conclusion that for the realistic situations the contribution of the deformation parameter of the gravitational lens to the magnification of the brightness of the source makes small changes as well as a plasma of the lens.

4 Conclusion

We have studied the gravitational lensing in a plasma surrounding deformed gravitational object and can summarize our main findings as the following.

  1. 1.

    The deflection angle of light by non-Schwarzschild gravitational source surrounded by plasma linearly depends on both the gravitational mass \(M\) and the deformation parameter \(\epsilon\) of the gravitational lens. For \(\epsilon=\pm6\) the ratio of term being responsible for the deformation to the one induced by the total mass may proportional to \(10^{-1}\) for the ordinary neutron stars.

  2. 2.

    We have studied influence of deformation parameter of gravitational lens to the magnification of brightness of the star in the case of microlensing and have shown that the deformation does not make noticeable contribution to the magnification.