Plasma magnetosphere of deformed magnetized neutron star

Abstract

The plasma magnetosphere surrounding a rotating magnetized neutron star described by non-Kerr spacetime metric in slow rotation approximation has been studied. First we have studied the vacuum solutions of the Maxwell equations in spacetime of slowly rotating magnetized non-Kerr star with dipolar magnetic configuration. Then for the magnetospheric model we have derived second-order differential equation for electrostatic potential from the system of Maxwell equations in spacetime of slowly rotating magnetized non-Kerr star. Analytical solutions of Goldreich-Julian (GJ) charge density along open field lines of slowly rotating magnetized non-Kerr neutron star have been obtained which indicate the modification of an accelerating electric field, charge density along the open field lines and radiating losses of energy of the neutron star by the deformation parameter.

1 Introduction

It is well known that the Kerr spacetime metric describes an external gravitational field of a rotating astrophysical black hole, which possesses two parameters as the total mass M and the specific angular momentum a of gravitational source. However in the regime of strong gravity, the general relativity could be broken down and as it has been shown in Johannsen and Psaltis (2011) that a deformed Kerr-like metric is suitable for the strong field of the no-hair theorem, which describes so called rotating non-Kerr compact gravitational source (Johannsen and Psaltis 2011). The study of the astrophysical processes in the vicinity of rotating non-Kerr compact gravitational objects could provide an opportunity for constraining the allowed parameter space of solutions, and to provide a deeper insight into the physical nature and properties of the corresponding spacetime metric. For example, in our preceding work (Abdujabbarov et al. 2013) a comparison of the numerical results of the innermost stable circular orbits (ISCOs) around a non-Kerr black hole with the observational data for the ISCO radius of rapidly rotating black holes have (Steiner et al. 2009) provided the upper limit for the deformation parameter. Moreover we have studied shadow of the non-Kerr black holes in Atamurotov et al. (2013). Therefore, in this work we have paid attention for studying the electromagnetic processes around rotating non-Kerr magnetized compact star.

The plasma magnetospheric model of the neutron stars was first presented in the pioneering paper by Goldreich and Julian (1969). Since many processes on the surface and magnetosphere of the neutron stars depend on several parameters of the neutron star, it is difficult theoretically describe the whole process. One direction of adequate description of the astrophysical process around neutron stars is to include the effects of the strong gravitational field. In general relativity, Beskin (1990) and, independently, Muslimov and Tsygan (1990) were the first to find that the frame dragging induced by general relativistic effects provides a source of additional electric field contributing to particle acceleration in the polar cap region. The accelerating component (parallel to the magnetic field) of the electric field is driven by deviations of the space density charge from the Goldreich-Julian (GJ) charge density, which is determined by the magnetic field geometry. As noted by several authors (Beskin 1990; Muslimov and Tsygan 1990; Muslimov and Harding 1997; Dyks et al. 2001; Mofiz and Ahmedov 2000; Morozova et al. 2008; Beskin 2009), the general relativistic frame dragging effects on the field geometry in the plasma magnetosphere of rotating neutron stars is a first-order effect, which has to be carefully included in any self-consistent model of pulsar magnetosphere, especially when computing the resulting electromagnetic radiation. In the paper (Muslimov and Tsygan 1992) influence of non-zero inclination angle of the neutron star to GJ charge density and accelerating electrical fields (parallel electric field to magnetic field lines)was checked for the small-polar angle approximation cases. As result of that work we can know the non zero inclination angle strongly affects to neutron star magnetosphere.

In one of our preceding papers (Morozova et al. 2008) the influence of nonvanishing Newman-Unti-Tamburino (NUT) parameter of the plasma magnetosphere of neutron stars was studied. The main result of it was that the NUT parameter strongly affects the GJ charge density, accelerating electric field and energy losses along the open magnetic field lines on a polar cap. Here we plan to extend it to the plasma magnetosphere of the deformed neutron star in slowly rotating geometry with the deformation parameter h. In Sect. 2 we have analyzed GJ charge density and found approximate solution of the second order Maxwell equation in the non-Kerr spacetime. In the next Sect. 3 we have solved second order differential Poisson equation for scalar potential using separating variables with help of so-called Fourier Bessel transformation method and as a consequence we have found analytical expression for the accelerating electrical field. Section 4 has been devoted to the losses energy of the slowly rotating deformed magnetized neutron stars. Finally the last Sect. 5 summarizes the main results obtained.

In recent work, we have used signatures (−,+,+,+) for the space-time and Gaussian system unit G=c=1 (However, for those expressions with an astrophysical application we have written the speed of light explicitly). Latin indices go from 1,2,3 and Greek ones from 0 to 3.

2 Charge density in the plasma magnetosphere of slowly rotating deformed star

The spacetime metric of a slowly rotating relativistic star with the deformation term h can be obtained from the solution for rotating non-Kerr compact gravitational source provided by Johannsen and Psaltis (2011) in the case when the quadratic angular momentum of star a ²→0 as (see e.g. Hartle and Thorne 1968)

$$\begin{aligned} \begin{aligned}[b] ds^2&=-N^2(1+h)dt^2+N^{-2}(1+h)dr^2 \\ &\quad +r^2 \bigl[d\theta^2+\sin^2\theta \bigl(d \phi^2 -2 \omega(1+h)d\phi dt\bigr) \bigr], \end{aligned} \end{aligned}$$

(1)

where lapse function is given as N ²≡(1−2M/r), ω=2aM/r ³ is the angular velocity of the dragging of inertial frames, h=ϵM ³/r ³ and ϵ is deformation coefficient of the star with total mass M.

Assuming that the magnetic field of a neutron star is stationary in the co-rotating frame one can get the Poisson equation for the scalar potential Φ as

$$ \boldsymbol{\nabla}\cdot \biggl(\frac{1}{N\sqrt{1+h}}\boldsymbol{\nabla} \varPhi \biggr)= -4\pi(\rho-\rho_{\mathit{GJ}}), $$

(2)

using expression derived by Muslimov and Tsygan (1992). Effective space charge density is given as ρ−ρ _GJ which is able to explain production of unscreened parallel electric field along the open magnetic field lines.

As it was shown by Goldreich and Julian (1969) that, neutron stars, which have a strong magnetic field and high conductivity, rotating around magnetic axis, would spontaneously build up a charged magnetosphere. One may analyze influence of the deformation of the spacetime to the Goldreich-Julian charge density ρ _GJ in magnetosphere of slowly rotating deformed neutron star. Using the metric vector g _i =−g _0i /g ₀₀ one can calculate the GJ charge density through the following modified expression (Muslimov and Tsygan 1992)

$$ \rho_{\mathit{GJ}}=-\frac{1}{4\pi}\boldsymbol{\nabla}(N\sqrt{1+h} {\mathbf{g}}\times\mathbf{B}), $$

(3)

where B is the magnetic field, g is the vector expression for slowly rotating non Kerr spacetime:

$$ {\mathbf{g}}=\frac{1}{N^2(1+h)} \bigl[(\boldsymbol{\Omega}- \boldsymbol{\omega})\times\mathbf{r} \bigr],$$

(4)

and Ω is the angular velocity of rotation of neutron star. Inserting (4) into the expression (3) for the Goldreich-Julian charge density ρ _GJ we obtain

$$ \rho_{\mathit{GJ}}=-\frac{1}{4\pi}\boldsymbol{\nabla} \biggl\{ \frac{1}{N \sqrt{1+h}} \biggl[1-\frac{\kappa}{ \eta^3}(1+h) \biggr] {\mathbf{u}}\times \mathbf{B} \biggr\} , $$

(5)

where u=Ω×r, η=r/R is the dimensionless radial coordinate, parameter κ≡εβ, ε=2M/R is the compactness parameter, and β=I/I ₀ is the stellar moment of inertia in the units of I ₀=MR ².

2.1 Vacuum solutions for dipolar magnetic field of slowly rotating deformed star

It is clear that magnetic field lines of neutron star depend on the spacetime structure. That is why we have to definite induction of magnetic fields for a slowly rotating neutron star in the spacetime possessing deformation parameter. For example, in the spacetime metric of the slowly rotating neutron star components of dipolar magnetic field have the form

$$\begin{aligned} & B^{\hat{r}}=B_0\frac{f(\eta)}{f(1)} \eta^{-3}\cos\theta, \end{aligned}$$

(6)

$$\begin{aligned} &B^{\hat{\theta}} =\frac{1}{2} B_0 N \biggl[-2 \frac{f(\eta)}{f(1)}+ \frac{3}{(1-\varepsilon/\eta)f(1)} \biggr]\eta^{-3}\sin\theta, \end{aligned}$$

(7)

with

$$ f(\eta)=-3 \biggl(\frac{\eta}{\varepsilon} \biggr)^3 \biggl[ \ln \biggl(1-\frac{\varepsilon}{\eta} \biggr)+\frac{\varepsilon}{\eta} \biggl(1+ \frac{\varepsilon}{2\eta} \biggr) \biggr], $$

(8)

where B ₀≡2μ/R ³ is the Newtonian value of the magnetic field at the pole of star, hats label the orthonormal components and μ is the magnetic moment. The solution of this type was first obtained by Ginzburg and Ozernoy (1964) and then reproduced by the number of authors, see for the details Rezzolla et al. (2001a, 2001b). The magnetic field configuration for compact magnetized stars in alternate theories of gravity has been studied in Ahmedov and Fattoyev (2008), Hakimov et al. (2013).

Radial component of the magnetic field in the spacetime (1) can be taken in the following form

$$ B^{\hat{r}}(\eta,\theta)=B_0\frac{\varPsi^{\hat{r}}(\eta)}{\eta^{3}} \cos\theta. $$

(9)

Then it is easy to show that in the spacetime (1) the Maxwell equation for the radial part of magnetic field takes the form

$$ \frac{\partial}{\partial \eta} \biggl(N^2 \frac{\partial}{\partial \eta} \bigl[\eta^2 \varPsi^{\hat{r}}(\eta) \bigr] \biggr)-2(1+h) \varPsi^{\hat{r}}(\eta)=0. $$

(10)

We look for solution of equation (10) in the following approximate form

$$ \varPsi^{\hat{r}}(\eta)=\frac{f(\eta)}{f(1)} (1+\alpha h ), $$

(11)

where α is correction coefficient being responsible for effect of the deformation parameter.

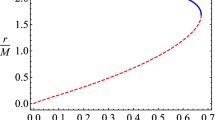
The Fig. 1 shows the ratio between numerical solution of equation (10) and approximate solution (11) for the different values of the correction coefficient α. One can see that when α=3/20 the difference between numerical and approximate solutions is minimal i.e. less than 0.12 %. It is meant that we can use expression (11) with α=3/20 as an approximate analytical solution of Eq. (10) since 0.12 % error is almost negligible. The asymptotical value of this solution coincides with the solution in the Newtonian spacetime.

Fig. 1

Relation between numerical solution of Eq. (10) and approximate solution (11) for the different values of the parameter α. Solid blue (red) line corresponds to α=3/4 (α=−3/4), dashed blue (red) line corresponds to α=3/10 (α=−3/10) and dot-dashed blue (red) corresponds to α=3/20 (α=−3/20). Thus top red colored side of the plot is for negative deformation ϵ=−20 and bottom is for ϵ=20

2.2 Goldreich Julian charge density in magnetosphere of slowly rotating deformed star

Form of the polar angle Θ

$$\begin{aligned} \begin{aligned}[c] &\sin\varTheta(\eta)=\sqrt{\eta\frac{1}{\varPsi^{\hat{r}}}}\sin \varTheta_{0} , \\ &\sin\varTheta_{0}=\sqrt{\frac{R}{R_{\mathit{LC}}f(1)(1+\alpha\tilde{\epsilon})}}, \end{aligned} \end{aligned}$$

(12)

is slightly different from the expression given by Muslimov and Tsygan (1991a) due to the presence of the spacetime deformation. Parameter Θ ₀ is responsible for the magnetic colatitude of the last open magnetic field line (or first closed magnetic field line) at the stellar surface, R _LC =c/Ω is the light-cylinder radius and $\tilde{\epsilon}=\epsilon {M^{3}}/{R^{3}}$.

It is obvious that from Eq. (12) one can get particle trajectory equation in the form dθ/dr. In Fig. 2 projection of particle trajectory to z=const plane on the polar cap for the different values of the deformation parameter is shown. For the positive values of deformation coefficient the particle leaves polar zone with larger (wider) step with compare to the case when ϵ is zero or negative.

Fig. 2

Projection to z=const plane of the path of the particles on the polar cap of the neutron star for the different values of the deformation parameter.

Performing further algebraic transformations on the Eq. (5) and taking into account Eq. (6) one can get the following expression for the GJ charge density

$$ \rho_{\mathit{GJ}}=-\frac{\varOmega B_0}{2\pi c } \frac{1}{N \sqrt{1+h}\eta^3} \varPsi^{\hat{r}} \biggl[1-\frac{\kappa}{\eta^3}(1+h) \biggr]. $$

(13)

In Fig. 3 the radial dependence of obtained general relativistic expression for the GJ charge density ρ _GJ normalized in its Newtonian expression for the different values of deformation parameter is presented. It can be found that even for comparatively small values of the deformation parameter its influence on the GJ charge density ρ _GJ  (13) plays an important role. The value of the GJ charge density ρ _GJ at the surface of the star is more sensitive to the deformation parameter. ρ _GJ is “inversely linear” proportional to the deformation parameter (see Eq. (13) where ρ∼(1−h)) at the surface of the star and for asymptotic values it reaches the Newtonian limit. For plotting the graphs we have selected the typical numbers for the neutron star parameters as R=10 km, M=2 km and P=0.1 s.

Fig. 3

Radial dependence of the Goldreich-Julian charge density normalized to the Newtonian expression for the different values of the deformation coefficient ϵ and dimensionless moment of inertia β of the star

3 Solution of Poisson equation in magnetosphere of slowly rotating deformed star

The charge density ρ in the relativistic plasma is proportional to the magnetic field with the proportionality coefficient being constant along the given magnetic field line (see, for example, Muslimov and Tsygan 1991b) that is

$$ \rho=\frac{\varOmega B_0}{2\pi c }\frac{1}{N \sqrt{1+h}\eta^3}\varPsi^{\hat{r}}A( \xi), $$

(14)

where ξ=θ/Θ is the dimensionless angular variable, A(ξ) is an unknown function to be defined from the boundary conditions.

Following to Muslimov and Tsygan (1991b) one could insert expressions (13) and (14) into the Poisson equation (2) and get the following differential equation

$$\begin{aligned} &\frac{1}{R^2\eta^2}\frac{\partial}{\partial\eta} \biggl(\eta^2 \frac{\partial}{\partial\eta}\varPhi \biggr) \\ &\qquad +\frac{1}{R^2 N^2 (1+h)\eta^2\theta} \biggl(\frac{\partial}{\partial\theta}\theta\frac{\partial}{\partial\theta}+ \frac{1}{\theta}\frac{\partial^2}{\partial\phi^2} \biggr)\varPhi \\ &\quad =-4\pi\frac{\varOmega B_0}{2\pi c}\frac{\varPsi^{\hat{r}}}{N^2 (1+h)\eta^3} \biggl[1-\frac{\kappa}{\eta^3}(1+h)+A( \xi) \biggr] \end{aligned}$$

(15)

in the approximation of small angles θ.

The further calculations are based on the extension of works Muslimov and Tsygan (1992) and Morozova et al. (2008) to the spacetime of deformed slowly rotating neutron star. Here one can introduce dimensionless function F=ηΦ/Φ ₀ in order to solve Eq. (15), where Φ ₀=ΩB ₀ R ² and variables η and ξ. We can then rewrite Eq. (2) for the dimensionless electrostatic potential as

$$\begin{aligned} & \biggl[\frac{d^2}{d\eta^2}+\varLambda^2(\eta) \frac{1}{\xi}\frac{\partial}{ \partial\xi} \biggl(\xi\frac{\partial}{\partial\xi} \biggr) \biggr]F \\ &\quad =-\frac{2}{\eta^2 N^{2}(1+h)}\varPsi^{\hat{r}} \biggl[1-\frac{\kappa}{\eta^3}(1+h)+A( \xi) \biggr], \end{aligned}$$

(16)

where $\varLambda(\eta)= [\eta\varTheta(\eta)N\sqrt{1+h} ]^{-1}$. As in Muslimov and Tsygan (1992) in order to get solution of Eq. (16) we have also used Fourier-Bessel transformation:

$$\begin{aligned} \begin{aligned}[b] &F(\eta,\xi)=\sum_{i=1}^{\infty}F_i( \eta)J_0(k_i\xi) \\ &\quad F_i(\eta)=\frac{2}{[J_1(k_i)]^2}\int^1_0 \xi F(\eta,\xi)J_0 (k_i\xi)d\xi, \end{aligned} \end{aligned}$$

(17)

use relation

$$ \sum_{i=1}^{\infty}\frac{2}{k_i J_1(k_i)}J_0(k_i \xi)=1 , $$

(18)

and obtain Eq. (16) in the form

$$\begin{aligned} & \biggl[\frac{d^{2}}{d\eta^{2}}-\gamma^{2}_{i}( \eta) \biggr]F_{i}= -\frac{2}{\eta^{2} N^{2}(1+h)}\varPsi^{\hat{r}}(\eta) \\ &\quad \times \biggl\{ \frac{2}{k_{i} J_{1}(k_{i})} \biggl[1-\frac{\kappa}{\eta^{3}}(1+h) \biggr]+A_{i} \biggr\} , \end{aligned}$$

(19)

where $\gamma^{2}_{i}=k^{2}_{i}\varLambda^{2}$, k _i are positive zeros of the functions J ₀, $A_{i}=(2/k_{i} J_{1}(k_{i}))\int^{1}_{0}\xi A(\xi) J_{0} (k_{i} \xi)d\xi$. Considering a region near to the surface of the star, where z=η−1≪1, and using following boundary conditions (that are the conditions of equipotentiality of the stellar surface and zero steady state electric field at r=R):

$$ F_i|_{z=0}=0,\qquad \frac{\partial F_i}{\partial z}\biggr|_{z=0}=0 $$

(20)

one can find the expression for the scalar potential Φ near to the surface of the star and corresponding to this potential component of the electric field E _∥, being parallel to the magnetic field (see the discourses of Muslimov and Tsygan (1992)):

$$\begin{aligned} \varPhi =&\frac{12\varPhi_0}{\eta}\kappa \varTheta^2_0\sum ^{\infty}_{i=0} \bigl[e^{-\gamma_i (1)(\eta-1)}-1 + \gamma_i (1) (\eta-1) \bigr] \\ &{}\times\frac{1}{\gamma_i(1)}\frac{J_0(k_i\xi)}{k_i^3J_1(k_i)}, \end{aligned}$$

(21)

here $\gamma_{i} (1)= {k_{i}}/({\varTheta_{0}\sqrt{(1-\varepsilon)(1+\tilde{\epsilon}})})$, $A_{i}= 2[k(1+ \tilde{\epsilon})-1] /(k_{i} J_{1}(k_{i}))$

$$ E_{\|}=-\frac{12\varPhi_0}{R}\kappa \varTheta^2_0 \sum^{\infty}_{i=0}\frac{J_0(k_i\xi)}{k_i^3 J_1(k_i)} \bigl[1-e^{-\gamma_i(1)(\eta-1)} \bigr]. $$

(22)

Analyzing the region Θ ₀≪η−1≪R _LC /R, where $|d^{2}F_{i}/d\eta^{2}|\ll\gamma^{2}_{i}(\eta)|F_{i}|$ one can see that equation (19) becomes

$$\begin{aligned} -\gamma^2_i(\eta)F_i =&-\frac{2}{\eta^2N^2 (1+h)} \varPsi^{\hat{r}}(\eta) \\ &{}\times \biggl\{ \frac{2}{k_i J_1(k_i)} \biggl[1-\frac{\kappa}{\eta^3}(1+h) \biggr]+A_i \biggr\} \end{aligned}$$

(23)

from which it right away follows

$$\begin{aligned} F_i=\theta^2(\eta)\varPsi^{\hat{r}}(\eta) \frac{4\kappa}{k^3_i J_1(k_i)} \biggl[1+\tilde{\epsilon}-\frac{1}{\eta^3}(1+h) \biggr]. \end{aligned}$$

(24)

The derived expression for F _i gives an opportunity to get expression for the scalar potential in the region at distances greater than the polar cap size as

$$\begin{aligned} \varPhi =&\frac{\varPhi_0}{\eta}F=2\varPhi_0\varTheta^2_0 \kappa \biggl[1+\tilde{\epsilon}-\frac{1}{\eta^3}(1+h) \biggr]\sum _i\frac{2J_0(k_i\xi)}{k^3_i J_1(k_i)} \\ =&\frac{1}{2}\varPhi_0\varTheta_0^2 \kappa \biggl[1+\tilde{\epsilon}-\frac{1}{\eta^3}(1+h) \biggr]\bigl(1- \xi^2\bigr) \\ =&\frac{1}{2} \varOmega R^2 B_0 \varTheta_0^2 \kappa \biggl[1+\tilde{\epsilon}- \frac{1}{\eta^3}(1+h) \biggr]\bigl(1-\xi^2\bigr). \end{aligned}$$

(25)

Component of electric field E _∥ produced by the gradient of this potential will look like

$$ E_{\|}=-\frac{1}{R}\frac{\partial\varPhi}{\partial\eta}\biggr|_{\xi=\mathit{const}}=- \frac{3}{2}E_{\mathit{vac}} \varTheta^2_0 \kappa \frac{1}{\eta^4}(1+2h) \bigl(1-\xi^2\bigr) , $$

(26)

where E _vac ≡(ΩR/c)B ₀ is the Newtonian value of the electric field generated near the surface of a neutron star rotating in vacuum (Deutsch 1955). In Fig. 4 it is shown radial dependence of the ratio between E _∥ and E _vac for the different values of deformation parameter.

Fig. 4

Radial dependence of accelerating electrical field for the different values of deformation coefficient

4 Energy losses of slowly rotating deformed magnetized neutron star

Now it is possible to calculate losses energy on the polar cap of the slowly rotating deformed neutron star. The total energy losses expression according to Muslimov and Harding (1997) is

$$ L_p=2\biggl(-c\int\rho\varPhi\, dS\biggr). $$

(27)

In the slowly rotating non Kerr spacetime with deformation parameter we have

$$\begin{aligned} {-}\rho\varPhi \approx&\frac{1}{4\pi} \biggl(\frac{\varOmega B_0}{c} \biggr)^2\frac{R^2 \varTheta^2_0}{N \sqrt{1+h}\eta^3}\varPsi^{\hat{r}} \\ &{}\times \kappa \bigl[1-\kappa(1+\tilde{\epsilon}) \bigr](1+\tilde{\epsilon}) \bigl(1- \xi^2\bigr). \end{aligned}$$

(28)

Maximal loss energy can be obtained by inserting (28) into (27) and taking the integral as

$$ (L_p)_{\mathit{max}}\approx\frac{3}{2}\kappa \bigl[1-\kappa(1+\tilde{\epsilon}) \bigr] \biggl[1+\biggl(\frac{1}{2}-\alpha \biggr)\tilde{\epsilon} \biggr]\dot{E}_{\mathit{rot}}, $$

(29)

where

$$ \dot{E}_{\mathit{rot}}\equiv\frac{1}{6}\frac{\varOmega^4 B_0^2 R^6}{c^3 f^2(1)}= \frac{1}{f^2(1)}(\dot{E}_{\mathit{rot}})_{\mathit{Newt}}, $$

(30)

and $(\dot{E}_{\mathit{rot}})_{\mathit{Newt}}$ is the standard Newtonian expression for the magneto-dipole losses in flat space-time approximation.

In general relativistic non deformation cases i.e. when ϵ→0, $\tilde{\epsilon}$ also tends to zero, then one could get the result of Muslimov and Harding (1997)

$$ (L_p)_{\mathit{max}\ (\epsilon=0)}=\frac{3}{2}\kappa(1- \kappa)\dot{E}_{\mathit{rot}}. $$

(31)

The ratio

$$ \frac{(L_p)_{\mathit{max}}}{(L_p)_{\mathit{max}\ (\epsilon=0)}}= \biggl[1+ \biggl(\frac{1}{2}-\alpha \biggr)\tilde{\epsilon} \biggr]\frac{1-\kappa(1+\tilde{\epsilon})}{1-\kappa} $$

(32)

as a function of deformation parameter is presented in Fig. 5. The dependence has a linear character and for small values of deformation parameter amount of the energy losses is increased. The amount of energy loss increases with the growth of deformation parameter and it is due to the fact that contributions into accelerating electric field produced by the effects of the different parameters have the same sign.

Fig. 5

Ratio of polar cap energy losses as a function of deformation coefficient for the typical neutron star with the different values of parameter β

Now for comparison with the astrophysical data on pulsars spin down Eq. (29) can be rewritten in terms of pulsar’s observable characteristics as the period P and its time derivative $\dot{P}\equiv dP/dt$:

$$\begin{aligned} (P\dot{P})_{\mathit{max}} =&\frac{3}{2}\kappa \bigl[1- \kappa(1+\tilde{\epsilon}) \bigr] \biggl[1+ \biggl(\frac{1}{2}-\alpha \biggr)\tilde{\epsilon} \biggr] \\ &{}\times \frac{I}{\tilde{I}} \frac{1}{f^2(1)}(P\dot{P})_{\mathit{Newt}}, \end{aligned}$$

(33)

where the expressions

$$ (L_p)_{\mathit{max}}=-\tilde{I}(\varOmega\dot{ \varOmega})_{\mathit{max}}, $$

(34)

and

$$ (P\dot{P})_{\mathit{Newt}}\equiv \biggl(\frac{2\pi^2}{3c^3} \biggr) \frac{R^6B^2_0}{I} $$

(35)

have been taken into account.

In Eq. (34) $\tilde{I}$ is the general relativistic moment of inertia of the star (see e.g. Rezzolla and Ahmedov 2004)

$$ \tilde{I}\equiv\int d^3\mathbf{x}\sqrt{\gamma}e^{-\varPhi(r)}\rho r^2\sin^2\theta, $$

(36)

where $e^{-\varPhi(r)}\equiv 1/\sqrt{-g_{00}}$, ρ(r) is the total energy density, γ is the determinant of the three metric and d ³ x is the coordinate volume element. Period of pulsar and it’s time derivative are very precisely measured quantities for a large number of pulsars (for example, in the paper of Kaspi et al. (2006) there is a $P-\dot{P}$ diagram for the 1403 catalogued rotation-powered pulsars). Thus, expression (33) for $P\dot{P}$ may indicate the possible existence and magnitude of deformation-parameter. It has been found in our preceding study Ahmedov et al. (2013) that in general relativity slow down due to the energy losses through charged particles outflow in plasma magnetosphere strongly depends on star’s compactness parameter and is more faster for the neutron star with comparison to that for the strange star of the same mass. Comparison with astrophysical observations on pulsars spin down precise data may provide important information about star’s compactness parameter and consequently an evidence for the strange star existence and, thus, serve as a test for distinguishing it from the neutron star. As it was mentioned the main difficulty encountered on this way nowadays is the uncertainty of estimation of the moment of inertia of the neutron star.

5 Conclusion

We have analyzed corrections from the spacetime deformation to the GJ charge density, electrostatic scalar potential and accelerating component of electric field being parallel to the magnetic field lines in the polar cap region of slowly rotating magnetized neutron star.

The presence of deformation parameter slightly modulates Goldreich-Julian charge density near the surface of the star. However as it is known the effective electric charge density i.e. difference between Goldreich-Julian charge density ρ _GJ (being proportional in the case of flat space-time to Ω⋅B) and electric charge density (being proportional to B) in the star magnetosphere is responsible for the generation of electric field being parallel to magnetic field lines. This difference is equal to zero at the surface of the star and changes with the distance from it due to the fact that ρ can not compensate ρ _GJ . General relativistic terms arising from the dragging of inertial frames and presence of the deformation parameter gives very important additional contribution to this difference. Both of these terms depend on the radial distance from the star as 1/r ³ and have equally important influence on the value of accelerating electric field component generated in the magnetosphere near the surface of the neutron star. The negative deformation increases value of GJ charge density and the positive deformation decreases it. It is also shown that accelerating electrical field being parallel to magnetic field lines is also increased (decreased) for the negative (positive) values of deformation parameter.

From the Fig. 3 one can see that GJ charge density near to the surface of the neutron star at negative values of the deformation coefficient has bigger value than that for the positive and zero deformations. It is clear from Eq. (2) that this feature will increase the values of the scalar potential and accelerating electrical field on the polar cap. This result has been shown in Fig. 4 and the higher accelerating electrical field will give the higher energy losses with compare to other cases (see Fig. 5). Moreover one we could see from Fig. 2 that for the negative deformation particles leave out from polar cap with the wider step than in the case with the positive and zero deformation.

There results are also repeated for energy losses which linearly depend on the deformation parameter. The obtained results have been applied to find an expression for electromagnetic energy losses along the open magnetic field lines of the slowly rotating non Kerr star. It is found that in the presence of deformation parameter an additional important term to the standard magneto-dipole energy losses expression appears. It is easy to see from Fig. 6 at ϵ=−22 amount of energy losses for typical neutron stars (compactness parameter ε=0.2) increases nearly for 20 per cents and for ϵ=22 it decreases up to 20 per cents. For neutron stars with the bigger compactness parameter ε=0.22 this value reaches up to 30 per cents.

Fig. 6

Dependence of the ratio of polar cap energy losses from the stellar compactness parameter. Left panel is for the different values of the deformation coefficient. In the right panel solid line corresponds to β=1, dashed and dotdashed lines correspond to β=1.1 and β=0.9, respectively