1 Introduction

Gravitational lensing is one of the direct consequences of the Einstein’s general theory of relativity. Light propagating from the source to the observer may be bent by intervening mass and come to the observation point through different pathways. The gravitating mass in this case acts as a lens and produces several different images of one radiating source object. Despite the fact that gravitational lensing is extremely complicated phenomena because light can be bent by many different objects (such as stars, galaxies or clusters of galaxies, “dark” objects) while propagating from the source to the observer, investigation of simple model cases remains an important task and gives us deeper understanding of the physics of the phenomena. Gravitational lensing serves as important astronomical tool because it can provide us the information about sources and lenses as well as about content and large-scale geometry of the Universe. One particular and very important case of gravitational lensing is microlensing, when different images of the source cannot be optically resolved but lensing affects the appeared brightness of the radiating object. Since the pioneering works of Paczyński (1986), Alcock et al. (1993), Aubourg et al. (1993), Udalski et al. (1993) various aspects of microlensing were studied by many authors (see for review, for example Paczyński 1996; Wambganss 2006).

Investigations of general relativistic effects connected with non-diagonal components of the metric tensor are proved to be fruitful and have important consequences in astrophysics. For example, as has been noted by several authors (e.g., Beskin 1990; Muslimov and Tsygan 1992; Muslimov and Harding 1997; Mofiz and Ahmedov 2000; Morozova et al. 2008; Beskin 2009), the effect of general relativistic frame dragging on the field geometry in the plasma magnetosphere of a rotating neutron star is a first-order effect, which has to be carefully included in a self-consistent model of pulsar magnetospheric structure and the associated electromagnetic radiation. General relativistic effects due to the frame dragging are crucial for the formation of the electric field component aligned with the magnetic field and particle acceleration in the magnetosphere (e.g. Beskin 1990; Muslimov and Tsygan 1992; Zanotti et al. 2012) and they are also important for the vacuum electromagnetic fields produced by slowly rotating magnetized neutron stars (Rezzolla et al. 2001a, 2001b).

In the papers of Bisnovatyi-Kogan and Tsupko (2009, 2010), Tsupko and Bisnovatyi-Kogan (2012) propagation of light in the presence of massive gravitational lens surrounded by plasma medium has been studied. In these works authors considered deflection of light by the gravitational field and by the inhomogeneities of plasma self-consistently and showed that even in the homogeneous plasma the deflection angle depends on the frequency of light through the refractive index.

In our paper we plan to extend the results of the paper of Bisnovatyi-Kogan and Tsupko (2010) to the case of rotating gravitational lens. Theoretical basis of the research is presented in the works of Bisnovatyi-Kogan and Tsupko (2009, 2010), where the equations of light propagation were derived in a general case for arbitrary medium with gravity. We consider a light ray propagating in the vicinity of the massive rotating object surrounded by plasma shell. Our goal is to investigate the deflection angle in the case when the metric of space time is non-diagonal and derive the terms being responsible for the rotation of the lensing object. For more details about Kerr black hole gravitational lensing and a discussion of its observational prospects, see the recent review article by Bozza (2010) and the references therein. There is the expectation that the direct observation of black holes will be possible in the near future (Zakharov et al. 2005a, 2005b; De Paolis et al. 2011). Optical properties of rotating braneworld black holes were studied by Schee and Stuchlik (2009).

In Sect. 2 we derive the expression for the deflection angle of light in non-diagonal spacetime in the presence of plasma. In Sect. 3 we study deflection of light by slowly rotating lensing object in a plasma. As a physical application of the obtained result in Sect. 3.2 we consider the influence of rotation on the magnification of brightness of the star in the case of microlensing. We obtain the ratio of the magnification in the case of rotating and static lens, but the estimation of the effect using the typical parameters of the lensing systems shows that the effect of rotation is negligibly small. Faraday effect in a plasma surrounding slowly rotating lensing object is studied in Sect. 3.3. In Sect. 4 we summarize our main findings.

Throughout, we use a space-like signature (−,+,+,+). Greek indices run from 0 to 3 and Latin ones from 1 to 3.

2 Equations of light propagation in non-diagonal space-time

We start from the metric of space-time

$$ ds^2=g_{\alpha\beta}dx^{\alpha}dx^{\beta}, $$
(1)

and assume that the gravitational field is week and the space-time is asymptotically flat, what mathematically means

(2)

and (see Landau and Lifshitz 1971)

$$ g^{\alpha\beta}=\eta^{\alpha\beta}-h^{\alpha\beta}, \quad h^{\alpha\beta}=h_{\alpha\beta}. $$
(3)

Note, however, that we don’t require the space-time to be static, as in the works of Bisnovatyi-Kogan and Tsupko (2009, 2010), but require it to be stationary. In particular, we assume the existence of non-zero time independent g 0i components of the metric, responsible for the rotation of the gravitating object. Henceforth in the paper we use the realistic assumption that the metric of the space-time is fixed and the influence of the propagating light on the gravitational background is neglected.

Following the preceding works on the topic we will base our calculation on the description of the geometrical optics in an arbitrary medium in the presence of gravity, given by Synge (1960). In his work Synge reformulated the Fermat’s least-time principle for the light ray propagation in the case when the dispresive medium is present. Using this principle Synge developed the Hamiltonian approach for the description of the geometrical optics. In particular, Synge has shown that the variational principle

$$ \delta\biggl(\int p_\alpha dx^\alpha\biggr)=0 $$
(4)

together with the restriction condition

$$ W\bigl(x^\alpha ,p_\alpha\bigr)=\frac{1}{2} \bigl[g^{\alpha\beta}p_\alpha p_\beta -\bigl(n^2-1 \bigr) \bigl(p_{\alpha} V^{\alpha} \bigr)^2 \bigr]=0, $$
(5)

where p α is the photon momentum, V α is the 4-velocity of the observer and n is the refractive index of the medium, give the following system of differential equations governing the trajectory of the photon

$$ \frac{dx^\alpha}{d\lambda}=\frac{\partial W}{\partial p_\alpha}, \qquad \frac{dp_\alpha}{d\lambda}=-\frac{\partial W}{\partial x^\alpha}, $$
(6)

where λ is the affine parameter along the photon’s trajectory. More information on the relativistic geometrical optics in dispersive media may be found in the book of Arifov (1983).

Taking into account that (see Synge 1960)

$$ p_{\alpha} V^{\alpha}=-\frac{\hbar\omega(x^i)}{c}, $$
(7)

where ħ is the Planck constant, ω(x i) is the photon frequency, which depends on the spatial coordinates x i due to the presence of the gravitational field, and c is the speed of light, the scalar function W(x α,p α ) may be rewritten in the form

(8)

Refractive index of a stationary inhomogeneous plasma n depends on x i and ω(x i) as

$$ n^2=1-\frac{\omega^2_e}{\omega^2(x^{i})}, \quad \omega^2_e= \frac{4\pi e^2 N}{m}\equiv K_{e}N , $$
(9)

where N=N(x i) is the electron concentration in plasma, e and m are the electron charge and mass correspondingly. Henceforth we will adopt the notations for the values at infinity as ω(∞)=ω, ω e (∞)=ω 0, \(n(\infty)=\sqrt{1-\omega^{2}_{0}/\omega^{2}}=n_{0}\).

Using (8) and (9) Eqs. (6) for the trajectory of the photon may be rewritten as

(10)

Solution for the photon’s trajectory in flat space-time in vacuum is a straight line. The components of the 4-momentum of photon moving along the straight line along the z-axis are (see Bisnovatyi-Kogan and Tsupko 2010)

$$ p^{\alpha}= \biggl(\frac{\hbar\omega}{c},0,0,\frac{n_0\hbar\omega}{c} \biggr), \qquad p_{\alpha}= \biggl(-\frac{\hbar\omega}{c},0,0,\frac{n_0\hbar\omega}{c} \biggr). $$
(11)

In the case of small plasma inhomogeneity and weak gravitational field, following the work of Bisnovatyi-Kogan and Tsupko (2010), we may consider the components (11) as null approximation for the trajectory of the photon. Inserting them into the right-hand side of Eq. (10) one gets in the left-hand side the first order deviation of the trajectory from a straight line as

$$ \frac{dp_{i}}{dz}=\frac{1}{2}\frac{n_0\hbar\omega}{c} \biggl(h_{33 ,i} + \frac{1}{n_0^2}h_{00 ,i}+\frac{1}{n_0}h_{03 ,i}- \frac{K_e N_{,i}}{n_0^2\omega^2} \biggr) $$
(12)

with

$$ \frac{dz}{d\lambda}=\frac{n_0\hbar\omega}{c}. $$
(13)

The deflection angle of the light ray in the plane perpendicular to the z-axis is equal to (see Bisnovatyi-Kogan and Tsupko 2009)

(14)

and from Eq. (12) one can get

(15)

3 Deflection of light by a slowly rotating lensing object in a plasma

3.1 Angle of deflection

Using expression (15) one can calculate the deflection angle of light propagating in the vicinity of a slowly rotating massive object surrounded by homogeneous plasma. In a general case the nondiagonal components of the metric tensor \(\vec{h}\equiv(h_{01},h_{02},h_{03})\) in the vicinity of the slowly rotating object with the total angular momentum J are given by (see Eq. (6.1.23) of Ciufolini and Wheeler 1995 with physical units of measurement restored)

$$ \vec{h}(\vec{r})\cong-\frac{2G}{c^3}\frac{\vec{J}\times\vec{r}}{|\vec{r}|^3} , $$
(16)

where G is the Newton’s gravitation constant. When the angular momentum is directed along the z-axis expression (16) gives in spherical coordinates h 0ϕ ≅−2GJsin2 θ/c 3 r, as in the more familiar form of the metric for the slowly rotating massive object (see Hartle and Thorne 1968)

(17)

where M is the total mass of the object, ω LT =2GMa/c 2 r 3=2GJ/c 3 r 3 is the Lense-Thirring angular velocity of the dragging of inertial frames, a=J/cM is the specific angular momentum of the object.

From the expression (16) one can see that in Cartesian coordinates the component h 03∼J x y−J y x vanishes if one assumes the angular momentum J to be parallel to the z-axis. The effect of the dragging of inertial frames contributes to the deflection angle (15) only by means of the projection J r of the angular momentum on the xy-plane. Introducing polar coordinates (b,χ) of the intersection point of the light ray with the xy-plane, where \(\chi=\angle(\vec{J}_{r}\vec{b})\), one obtains

$$ h_{03}=-2\frac{GJ_r \sin\chi}{c^3}\frac{b}{(b^2+z^2)^{3/2}}. $$
(18)

The deflection angle of light (15) will contain the following contributions due to the derivatives of h 03 with respect to b and χ (the integrals are taken from 0 to ∞ because the functions under integration are symmetric with respect to z)

(19)

and

(20)

Combining this with the result of Bisnovatyi-Kogan and Tsupko (2009) on the deflection angle of light in the case of Schwarzschild space-time one gets the final expression for the deflection angle by the slowly rotating gravitational source surrounded by homogeneous plasma as

(21)

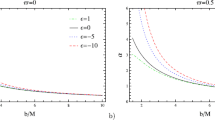
For the clarity of importance of our research we compare the second term in the right hand side of Eq. (21) for \(\hat{\alpha}_{b}\) with the first term by the order of magnitude. In the case ω 0≪ω the ratio of these terms is equal to

$$ \frac{J_r\sin\chi}{2 b c M}\sim\frac{\varOmega R}{c}\frac{R}{b} $$
(22)

which can be of the order of 10−1 for the millisecond neutron star with the radius R=10 km and period of rotation P=10−3 s. Observational data for the innermost stable circular orbits (ISCO) radius of rotating black holes (see Steiner et al. 2009; Shafee et al. 2008) show that the black holes are almost extremely rotating and the effect of dragging of inertial frames on the deflection angle may become very significant.

3.2 Amplification of brightness of the image source

Next we are going to apply the obtained Eq. (21) for the deflection angle to calculate possible significant physical effects of dragging of inertial frames. For simplicity further in this subsection we will neglect the effect due to the azimuthal deflection of light and investigate the influence of the polar deflection of light on the microlensing effect. This result will strictly apply to the case of \(\vec{b}\perp\vec{J_{r}}\), while in general case the simple picture presented below will be distorted by the azimuthal deflection.

The main equation of the gravitational lensing theory is the lens equation, which relates the angle β of the real object from the observer-lens axis, the angle θ of the appeared image of this object from the observer-lens axis and the deflection angle α (the angles are assumed to be small)

$$ \theta D_s=\beta D_s + \alpha D_{ls} , $$
(23)

where D s and D ls are the distances from observer to the source and from the lens to the source correspondingly. Taking into account that in the small angles approximation b≈D l θ, where D l is the distance from the observer to the lens, one can write the lens equation for the case of rotating source in the following form:

(24)

With the help of the substitution

$$ \theta_E= \biggl(\frac{4GM}{c^2}\frac{D_{ls}}{D_lD_s} \biggr)^{1/2} $$
(25)

Eq. (24) becomes

(26)

Solutions of the lens equation give (in our case three) positions θ of the appeared images of the object due to the presence of the lens. Figure 1 gives a schematic representation of the considered system, however, one needs to notice that the separation between the images and the bending angles of the light rays in the figure are exaggerated for the visualization purpose. θ E  is called the Einstein angle and sets the characteristic angular scale for gravitational lensing phenomena (for details see, for example, Hartle 2003). For many cases (lensing by the stars and stellar mass objects) the Einstein angle is too small to be resolved with modern telescopes. However even the lensing by such small objects like a star can be detectable because it changes the appeared brightness of the source. This situation is called microlensing. The magnification of brightness of the star can be calculated through the formula

$$ \mu_{\varSigma}=\frac{I_{tot}}{I_{\ast}}=\sum _k \biggl{|} \biggl(\frac{\theta_k}{\beta} \biggr) \biggl( \frac{d\theta_k}{d\beta} \biggr) \biggr{|} ,\quad k=1,2,\ldots, s , $$
(27)

where s is the amount of images, I tot is the total brightness of all the images and I ∗ is the unlensed brightness of the source. This function is always greater than unity and may be significant for small values of β. In this way gravitational lenses can be detected and used even when the individual images cannot be resolved.

Fig. 1
figure 1

Schematic representation of the gravitating lensing system. The background source, which is indicated as black star is lensed by the central black hole. D s  is the distance between observer (below) and the source (star). D ls is the distance from the lens (black hole) to the source. D l is the distance between observer and lens. χ represents the inclination angle between the projection of the vector J to xy plane and vector b

Full size image

Introducing new variable \(\theta=x+\frac{\beta}{3}\) one can reduce Eq. (26) to the form

$$ x^3+px+q=0 , $$
(28)

where

$$ p=-\frac{\beta^2}{3}-\frac{1}{2}\theta^2_E \biggl(1+\frac{1}{1-\frac{\omega^2_0}{\omega^2}} \biggr) $$
(29)

and

$$ \begin{aligned}[b] q&=-2\frac{\beta^3}{27}-\frac{\beta}{6} \theta^2_E \biggl(1+\frac{1}{1-\frac{\omega^2_0}{\omega^2}} \biggr) \\ &\quad {} -\frac{1}{2}\theta^2_E\frac{J_r}{MD_lc}\sin \chi\frac{1}{\sqrt{1-\frac{\omega^2_0}{\omega^2}}}. \end{aligned} $$
(30)

Equation (28) has three different real roots if the condition

$$ \frac{q^2}{4}+\frac{p^3}{27}<0 $$
(31)

satisfies, which takes place in our case. Our goal is to calculate μ Σrot /μ Σ for the case when β→0 and see how rotation affects the maximum value of the peak of magnification in the gravitational microlensing phenomena. Here μ Σrot is the magnification by the rotating and μ Σ by the non-rotating gravitational lenses. The magnification in the case of the non-rotating lens surrounded by plasma was investigated in the work of Bisnovatyi-Kogan and Tsupko (2010) and for β→0 is equal to

$$ \mu_{\varSigma} {|}_{\beta\rightarrow 0}\rightarrow \frac{1}{2} \frac{\sqrt{2\theta^2_E \Bigl(1+\frac{1}{1-\frac{\omega^2_0}{\omega^2}} \Bigr)}}{\beta}. $$
(32)

Solution of Eq. (28) looks like

$$ x=2\sqrt[3]{r}\cos{\frac{\phi+2k\pi}{3}} ,\quad(k=0,1,2) , $$
(33)

where

$$ r=\sqrt{-\frac{p^3}{27}} ,\quad \cos\phi=-\frac{q}{2r}. $$
(34)

The magnification for the case of slowly rotating gravitational lens surrounded by plasma can be obtained as

(35)

where the subscript β denotes the derivatives of the corresponding variables with respect to β. For the case when β→0 one has

(36)

Using Eqs. (36) one can obtain for the ratio μ Σrot /μ Σ in the limit β→0 the following result

(37)

which is equal to 1 in the case when J r =0 as it could be expected.

However, the effect of the dragging of inertial frames on the magnification appears to be insignificant as soon as we try to estimate it for the astrophysical situations. Assuming the lens to be a supermassive black hole with the mass M=1010 M ⨀, J r /Mc≡a r =0.2M, D l ∼D s ∼D ls ∼1019 km (this corresponds to few Mpc, typical distance to the nearby galaxies), sinχ=1 and ω 0/ω=0.5, the value of |q/2r| has the order of 10−6. This brings us to a conclusion that for the realistic situations the rotation of the gravitational lens surrounded by a plasma makes no significant additional contribution to the magnification of the brightness of the source.

3.3 Faraday effect in a plasma surrounding slowly rotating lensing object

General relativity predicts the rotation of polarization plane of a light wave in vacuum in the curved spacetime as a result of parallel translation of the polarization vector along the null geodesic (e.g. Sereno 2004). This effect is known as gravitational Faraday-Rytov-Skrotskii rotation (Skrotskii 1957; Brodutch et al. 2011). Due to the presence of the so-called gravitomagnetic field in the spacetime with the nonvanishing nondiagonal components of the metric tensor (see e.g. Ciufolini and Wheeler 1995), linearly polarized electromagnetic radiation propagating in a Kerr spacetime (Ishihara et al. 1988), Friedman-Robertson-Walker flat metric (Morales and Saez 2007) experiences a rotation of the polarization plane which is very similar to the Faraday rotation of the polarization plane that occurs when the light during its propagation in the continuous medium is distorted by the presence of a magnetic field. Due to this reason in the presence of the magnetized plasma around intervening lenses such as rotating gravitating compact objects, the propagation of polarized radiation through plasma is accompanied by the rotation of the polarization plane caused by the Faraday effect (Faraday 1846; Thorman 2001). Comprehensive reviews on astrophysical magnetic fields and magnetic fields of compact stars can be found in Brandenburg and Subramanian (2005) and Geppert (2009), respectively.

In this subsection we aim to give the estimation of the angle of Faraday rotation of polarization plane for the radiation propagating in plasma in the background of compact object and external magnetic field.

Following Narasimha and Chitre (2008) or Sereno (2004) the angle of rotation of the plane of polarization during propagation in a plasma is given by

$$ \Delta\varphi= {e^3\over 2\pi m_e^2 c^4}\int_{L} B_\parallel (l) n_e(l) \lambda^2 dl , $$
(38)

where n e is the electron number density, λ is the wavelength of the radiation as seen by the absorber medium, B ∥ is the line of sight component of the magnetic field and the integral is over the path length through the intervening absorbers. It should be noted that relativistic electrons of Lorentz factor γ contribute to n e in approximate proportion to γ −2.

From multi-wavelength observations of the polarization, it is found that a majority of sources have measured φ that vary over a wide range of wavelength such that Δφ=φ(λ)−φ(0), where the intrinsic position angle φ(0) is the zero-wavelength value. The constant RM is called the rotation measure and is a “polarized emission-weighted” mean of the Faraday depth.

The rotation measure, as measured by the observer at zero redshift is given by

$$ \mathit{RM}={\Delta\varphi\over \lambda^2_{obs}}= {e^3\over 2\pi m_e^2 c^4}\int B_\parallel (l) n_e(l) \biggl[{\lambda(l)\over \lambda_{obs}} \biggr]^2 dl . $$
(39)

For the Faraday Rotation produced by a deflector at redshift z, the rotation measure of the intervening galaxy with the average line of sight magnetic field component,

$$ \langle B_\parallel \rangle = {\int n_e (z) B_\parallel (z) dl (z)\over \int n_e (z) dl (z)} , $$
(40)

and the electron column density, N e =∫n e (z)dl(z) may be expressed as

$$ \mathit{RM} \simeq 2.6\times 10^{13} \frac{ \langle B_\parallel\rangle N_e}{(1+z)^2}\ \mbox{rad\,m}^{-2} . $$
(41)

One can estimate RM for a plasma density in a vicinity of the lensing SMBH with mass M=1010 M ⨀ of the order N e =5×104 cm−3 and magnetic field background with strength B ∥=104 Gauss as

$$ \mathit{RM} \simeq 1.3 \times 10^{22} (1+z)^{-2}\ \mbox{rad}/\mbox{m}^{2}. $$
(42)

Even though the Faraday Rotation may be caused by the source, the intervenor and the Milky Way, the difference in the rotation angle between the multiple images is practically due to the lens which is contained in Eq. (41). Consequently, the magnitude of the difference in rotation measures (RM) between images turns out to be a valuable probe for estimating the average line of sight component of magnetic field in the lenses.

Faraday rotation measure (RM) maps of the central parsecs of quasars and radio galaxies hosting relativistic jets (Saikia and Salter 1988) also reveal that the medium on parsec scales surrounding AGNs could be significantly magnetized (Zavala and Taylor 2003).

Let us estimate the value of the Faraday angle using evaluation data given by Bisnovatyi-Kogan and Tsupko (2010) for the frequency of radiation ν=3.27×106 Hz, plasma density in the vicinity of the lensing SMBH with mass M=1010 M ⨀ of the order of N e =5×104 cm−3 and magnetic field background with strength B ∥=104 Gauss, at the distance L=1.48×1015 cm. The estimation of the Faraday angle gives

$$ \Delta\varphi=1.62 \times 10^{15} \ \mbox{rad}. $$
(43)

Observational data of the multi-frequency VLA polarization can be found in Patnaik et al. (2001).

It has to be mentioned that estimates of magnetic fields for active galactic nuclei can be based on the observed polarization degrees (Silant’ev et al. 2013a). The distribution of magnetic field around black hole and polarization in accretion discs of AGN is studied in Gnedin et al. (2012). The dependence of the degree of polarization on the spin of the central black hole is studied in Silant’ev et al. (2013b). The approximate analytical expressions for the polarization of the radiation from a magnetized disk around black hole can be found in Silant’ev (2002, 2005), Silant’ev et al. (2009).

4 Conclusion

We have studied the gravitational lensing in a plasma surrounding slowly rotating gravitational object and can summarize our main findings as the following.

  1. 1.

    The deflection angle of light by the slowly rotating gravitational source surrounded by plasma linearly depends on both the gravitational mass M and the angular momentum J of the gravitational lens. The ratio of term being responsible for the angular momentum to the one induced by the total mass may reach 10−1 for the millisecond pulsars.

  2. 2.

    We have studied influence of rotation of gravitational lens to the magnification of brightness of the star in the case of microlensing and have shown that the rotation does not make noticeable contribution to the magnification.

  3. 3.

    The effect of the Faraday rotation of the polarization plane of a light wave propagating in plasma surrounding slowly rotating lensing object is considered. An estimation of the angle of the Faraday rotation and Rotation measure for the case of the rotating black hole surrounded by plasma is represented.