Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ cosmological models in a modified theory of gravity with variable $\varLambda$

Abstract

Spatially homogeneous Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ perfect fluid cosmological models in $f(R,T)$ modified theory of gravity have been investigated for a special choice of $f(R,T)=f_{1}(R)+f_{2}(T)$ with $f_{1}(R)=\lambda_{1}R$ and $f_{2}(T)=\lambda_{2}T$. This special choice leads to a cosmological constant $\varLambda$, which depends on stress energy tensor of matter source. To get the deterministic model of Universe, we assume that the expansion scalar ($\theta$) in the model is proportional to shear scalar ($\sigma$). This condition leads to relation between metric potentials, which yields a time dependent deceleration parameter. Various physical and geometrical features of the models are also discussed.

1 Introduction

The recent scenario of accelerated expansion of the Universe supported by astronomical observations (Riess et al. 1998; Perlmutter et al. 1999) has been playing a vital role in modern cosmology. It is now believed that dark energy is the best candidate to explain cosmic acceleration. The Universe consists of 76 % dark energy and 20 % dark matter. The exact nature of the dark energy is still a mystery. It supposed that dark energy has a strong negative pressure to explain the observed acceleration in the expansion rate of the Universe.

In recent years, dark energy models are attracting more and more attention of researchers. In particular, models with variable equation of state (EoS), that is $\omega(t)=\frac{p}{\rho}$, where $p$ is the pressure and $\rho$ is the energy density of the Universe. The cosmological constant $\varLambda$ and a scalar field with some potential known as the quintessence matter are supposed to be the most favorite candidates for the ‘dark energy’, the agent driving this alleged expansion. However, the cosmological constant $\varLambda$ is facing the coincidence problem. Another option is to explain the late time acceleration to modify Einstein’s theory of gravitation termed as “modified gravity approach”. Hence there have been several modifications of general relativity to provide natural gravitational alternative for dark energy. The modifications are based on the Einstein–Hilbert action to obtain alternative theories of Einstein such as $f(R)$ gravity (Carroll et al. 2004; Nojiri et al. 2006), $f(T)$ gravity (Bengocheu et al. 2009; Linder 2010) and $f(G)$ gravity (Bamba et al. 2010a, 2010b; Rodrigues et al. 2014; Nojiri and Odintsov 2011a, 2011b) where $R$, $T$ and $G$ are the scalar curvature, the torsion scalar and the Gauss-Bonnet scalar respectively. The maximal extension of the Hilbert-Einstein action have been proposed by Harko and Lobo (2010) by considering the gravitational Lagrangian as a arbitrary function of Ricci scalar $R$ and of the matter Lagrangian $L_{m}$. The relativistic covariant model of interacting dark energy based on the principle of least action is given in $f(R,L_{m})$ gravity (Poplawski 2006). In this theory, the cosmological constant is a function of trace of the energy tensor and hence the model was denoted “$\varLambda(T)$ gravity”. This is more general than the $f(R)$ gravity as it reduces to the latter when we neglect the pressure. A detailed review of $f(R)$ gravity and their properties with different models are discussed in detail by many authors (Lobo 2009; Felice and Tsujikawa 2010; Nojiri and Odintsov 2011a, 2011b).

Recently, Harko and Lobo (2010) proposed a new $f(R,T)$ modified theory of gravity, wherein the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar $R$ and the trace of the stress-energy tensor $T$. Several authors have investigated different cosmological models in $f(R,T)$ modified theory of gravitation. Rao and Neelima (2013) have obtained Bianchi type-$\mathit{VI}_{0}$ Universe filled with perfect fluid in $f(R,T)$ gravity. Reddy and Santhi Kumar (2013) have discussed some anisotropic cosmological models in a modified theory of gravitation. Reddy et al. (2013) have studied LRS Bianchi type-$\mathit{II}$ Universe with cosmic strings and bulk viscosity in a modified theory of gravity. Reddy et al. (2014) have investigated anisotropic bulk viscous cosmological models in a modified gravity. Mishra and Sahoo (2014) have studied Bianchi type-$\mathit{VI}_{h}$ perfect fluid cosmological model in $f(R,T)$ gravity. Shri Ram and Chandel (2015) have discussed dynamics of magnetized string cosmological model in $f(R,T)$ gravity theory. Rao and Divya Prasanthi (2015) have investigated Kantowski-Sachs bulk viscous string cosmological models in $f(R,T)$ theory of gravity. Ahmed and Pradhan (2014), Rao and Suryanarayana (2015) and Rao et al. (2015) have obtained various cosmological models in $f(R,T)$ gravity with specific choice of $f(R,T)=f_{1}(R)+f_{2}(T)$.

Bianchi type cosmological models are important in the sense that these are homogeneous and anisotropic, from which the process of isotropization of the Universe is studied through the passage of time. The simplicity of the field equations and relative ease of solutions made Bianchi space times useful in constructing models of spatially homogeneous and anisotropic cosmologies. The anomalies found in the cosmic microwave background (CMB) and large scale structure observations stimulated a growing interest in anisotropic cosmological models of the Universe. Rao et al. (2008) have studied Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ cosmological model in Saez-Ballester theory of gravitation. Rao and Vijaya Santhi (2012) have obtained Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ magnetized cosmological models in Brans-Dicke theory of gravitation. Rao and Sireesha (2012) have studied Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ string cosmological models with bulk viscosity in a scalar tensor theory of gravitation. Recently, Rao et al. (2014) have studied perfect fluid cosmological models in a modified theory of gravitation. Katore (2015) has discussed Bianchi type $\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ string cosmological models in $F(R)$ gravity.

Very recently, Sahoo and Sivakumar (2015) have studied LRS Bianchi type-$I$ cosmological model in $f(R,T)$ theory of gravity with $\varLambda(T)$. Sahoo et al. (2015) have investigated Kaluza-Klein cosmological model in $f(R,T)$ gravity with $\varLambda (T)$. So, in this work we investigate Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ cosmological models in $f(R,T)$ modified theory gravitation. Here we consider a special choice of the function $f(R,T)=f_{1}(R)+f_{2}(T)$ (Harko et al. 2011), where $f_{1}(R)=\lambda _{1}R$ and $f_{2}(T)=\lambda_{2}T$. This choice leads us to an evolving cosmological constant ($\varLambda$) which depends on trace of the energy momentum tensor.

2 $f(R,T)$ theory of gravitation

In $f(R,T)$ modified theory of gravity, the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar $R$ and the trace of the stress-energy tensor $T$. The field equations of $f(R,T)$ gravity are derived from the Hilbert-Einstein type variation principle. The action for the $f(R,T)$ gravity is

$$ S=\frac{1}{16\pi} \int{f(R,T)\sqrt{-g}d^{4}x}+ \int{L_{m}\sqrt{-g}d^{4}x}, $$

(1)

where $f(R,T)$ is an arbitrary function of Ricci scalar $R$ and $T$ be the trace of stress-energy tensor $(T_{ij})$ of the matter. $L_{m}$ is the matter Lagrangian density. The energy momentum tensor $T_{ij}$ is defined as

$$ T_{ij}=- \biggl(\frac{2}{\sqrt{-g}} \biggr)\frac{\delta(\sqrt {-g})L_{m}}{\delta{g^{ij}}}. $$

(2)

Here we assume that the dependence of matter Lagrangian is merely on the metric tensor $g_{ij}$ rather than its derivatives, we obtain

$$ T_{ij}=g_{ij}L_{m}-\frac{\partial{L_{m}}}{\partial{g^{ij}}}. $$

(3)

The $f(R,T)$ gravity field equations are obtained by varying the action $S$ with respect to metric tensor $g_{ij}$

$$\begin{aligned}& f_{R}(R,T)R_{ij}-\frac{1}{2}f(R,T)g_{ij}+(g_{ij} \square-\nabla_{i}\nabla_{j})f_{R}(R,T) \\& \quad=8\pi T_{ij}-f_{T}(R,T)T_{ij}-f_{T}(R,T) \varTheta_{ij}, \end{aligned}$$

(4)

where

$$ \varTheta_{ij}=-2T_{ij}+g_{ij}L_{m}-2g^{\alpha\beta} \frac{\partial^{2}L_{m}}{\partial{g^{ij}}\partial{g^{\alpha\beta}}}. $$

(5)

Here $f_{R}(R,T)=\frac{\partial{f(R,T)}}{\partial{R}}$, $f_{T}(R,T)=\frac {\partial{f(R,T)}}{\partial{T}}$ and $\Box=\nabla^{\mu} \nabla_{\mu}$, where $\nabla_{\mu}$ denotes the covariant derivative.

From Eq. (4), we get

$$\begin{aligned}& f_{R}(R,T)R+3{\square}f_{R}(R,T)-2f(R,T) \\& \quad=8{ \pi}T-(T+\varTheta)f_{T}(R,T), \end{aligned}$$

(6)

where $\varTheta=\varTheta_{i}^{i}$. Equation (6) gives a relation between Ricci scalar $R$ and the trace of energy momentum tensor $T$.

Then with the use of (5), we obtain the variation of stress-energy. Using matter Lagrangian $L_{m}$, the stress-energy tensor of the matter given by

$$ T_{ij}=(\rho+p)u_{i}u_{j}-pg_{ij}, $$

(7)

where $u^{i}=(0,0,0,1)$ is the four velocity and satisfies the condition $u^{i}u_{i}=1$ and $u^{i}\nabla_{j}u_{i}=0$, where $\rho$ and $p$ are the energy density and pressure of the fluid respectively. Here the matter Lagrangian can be taken as $L_{m}=-p$ since, there is no unique definition of the matter Lagrangian.

Then with the use of (5), we obtain for the variation of stress-energy of perfect fluid as

$$ \varTheta_{ij}=-2T_{ij}-pg_{ij}. $$

(8)

On the physical nature of the matter field, the field equations also depend through the tensor $\varTheta_{ij}$. Hence in the case of $f(R,T)$ gravity depending on the nature of the matter source, we obtain several theoretical models corresponding to different matter contributions for $f(R,T)$ gravity. However, Harko et al. (2011) gave three classes of these models:

$$f(R,T)= \left \{ \textstyle\begin{array}{l} R+2f(T)\\ f_{1}(R)+f_{2}(T)\\ f_{1}(R)+f_{2}(R)f_{3}(T). \end{array}\displaystyle \right . $$

In this paper, we focus on second case, i.e $f(R,T)=f_{1}(R)+f_{2}(T)$, where $f_{1}(R)$ and $f_{2}(T)$ are the arbitrary functions of Ricci scalar $R$ and the trace of stress-energy tensor $T$ respectively. If the matter source is a perfect fluid then the gravitational field equations (4) of $f(R,T)$ gravity reduced to

$$\begin{aligned}& f_{1}{'}(R)R_{ij}- \frac{1}{2}f_{1}(R)g_{ij} \\& \quad= 8\pi T_{ij}+f_{2}{'}(T)T_{ij}+ \biggl[f_{2}{'}(T)p+\frac{1}{2}f_{2}(T) \biggr]g_{ij}, \end{aligned}$$

(9)

where prime denotes differentiation with respect to the argument. The equation for standard $f(R)$ gravity can be recovered for $p=0$ (the dust case) and $f_{2}(T )=0$.

If we consider a particular form of the functions $f_{1}(R)=\lambda _{1}R$ and $f_{2}(T)=\lambda_{2}T$, where $\lambda_{1}$ and $\lambda _{2}$ are constants, then $f(R,T)=\lambda_{1}R+\lambda_{2}T$. Thus, the field equations (2) will reduce to

$$ R_{j}^{i}-\frac{1}{2} \delta_{j}^{i} R= \biggl(\frac{8\pi+ \lambda_{2}}{\lambda_{1}} \biggr)T_{j}^{i} + \frac{\lambda_{2}}{\lambda_{1}} \biggl(p+ \frac{1}{2} T \biggr)\delta_{j}^{i}. $$

(10)

Einstein field equations with cosmological constant term are usually expressed as

$$ R_{ij}-\frac{1}{2}Rg_{ij}=-8\pi T_{ij}+\varLambda g_{ij} $$

(11)

By comparing Eqs. (10) and (11), we observed that

$$ \varLambda=\varLambda(T)=\frac{\lambda_{2}}{\lambda_{1}} \biggl(p+ \frac{1}{2} T \biggr);\quad\quad -8\pi=\frac{8\pi+ \lambda _{2}}{\lambda_{1}} $$

(12)

i.e., $p+\frac{1}{2}T$ behaves as cosmological constant and rather than simply being a constant it evolves through the cosmic expansion. Poplawski (2006) has discussed the dependence of the cosmological constant $\varLambda$ on the trace of the energy momentum tensor $T$, where cosmological constant in the gravitational Lagrangian is considered as a function of the trace energy-momentum tensor, and consequently the model is denoted as gravity model. Recent observational data favoring the cosmological model with variable cosmological constant.

3 Metric and field equations

We consider the anisotropic Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ space-times in the form

$$ ds^{2}=dt^{2}-R^{2}\bigl[d \theta^{2}+f^{2}(\theta)d\phi^{2} \bigr]-S^{2}\bigl[d\varphi+h(\theta)d\phi\bigr]^{2} $$

(13)

where $(\theta,\phi,\varphi)$ are the Eulerian angles, and $R$ and $S$ are functions of time $t$ only.

It represents, Bianchi type $\mathit{II}$ if $f(\theta)=1$ and $h(\theta )=\theta$, Bianchi type $\mathit{VIII}$ if $f(\theta)=\mathrm{cosh}\theta$ and $h(\theta )=\mathrm{sinh}\theta$, and Bianchi type $\mathit{IX}$ if $f(\theta)=\sin \theta$ and $h(\theta)=\cos \theta$.

The Universe is assumed to be filled with a distribution of perfect fluid represented by the energy-momentum tensor

$$ T_{ij}=(\rho+p)u_{i}u_{j}-pg_{ij}, $$

(14)

where $u^{i}=(0,0,0,1)$ is the four velocity and satisfies the condition $u^{i}u_{i}=1$, $\rho$ and $p$ are the energy density and isotropic pressure of the fluid respectively.

Using comoving coordinates and Eq. (14), the field equations (10) for the metric (13) can be written as

$$\begin{aligned}& \frac{\ddot{R}}{R}+\frac{\ddot{S}}{S}+\frac{\dot{R}\dot{S}}{RS}+ \frac{S^{2}}{4R^{4}}= \biggl(\frac{8 \pi+ \lambda_{2}}{\lambda_{1}} \biggr)p-\varLambda \end{aligned}$$

(15)

$$\begin{aligned}& 2\frac{\ddot{R}}{R}+\frac{\dot{R}^{2}+\delta}{R^{2}}-\frac {3S^{2}}{4R^{4}}= \biggl(\frac{8 \pi+ \lambda_{2}}{\lambda_{1}} \biggr)p-\varLambda \end{aligned}$$

(16)

$$\begin{aligned}& 2\frac{\dot{R}\dot{S}}{RS}+\frac{\dot{R}^{2}+\delta }{R^{2}}-\frac{S^{2}}{4R^{4}}= \biggl(\frac{8 \pi+ \lambda_{2}}{\lambda_{1}} \biggr)\rho+\varLambda \end{aligned}$$

(17)

Using the transformation $dt=R^{2}S\,d\tau$, the field equations (15)–(17) can be written as

$$\begin{aligned}& \frac{1}{R^{4}S^{2}} \biggl(\frac{R''}{R}+\frac{S''}{S}-2 \frac{R'S'}{RS}-2\frac{R^{\prime\,2}}{R^{2}}-\frac{S^{\prime\,2}}{S^{2}} \biggr)+ \frac{S^{2}}{4R^{4}} \\& \quad= \biggl(\frac{8 \pi+ \lambda_{2}}{\lambda_{1}} \biggr)p-\varLambda \end{aligned}$$

(18)

$$\begin{aligned}& \frac{1}{R^{4}S^{2}} \biggl(2\frac{R''}{R}-3 \frac{R^{\prime\,2}}{R^{2}}-2\frac{R'S'}{RS} \biggr)+\frac{\delta}{R^{2}}- \frac{3S^{2}}{4R^{4}} \\& \quad= \biggl(\frac{8 \pi+\lambda_{2}}{\lambda_{1}} \biggr)p-\varLambda \end{aligned}$$

(19)

$$\begin{aligned}& \frac{1}{R^{4}S^{2}} \biggl(\frac{R^{\prime\,2}}{R^{2}}+2\frac{R'S'}{RS} \biggr)+\frac{\delta}{R^{2}}-\frac{S^{2}}{4R^{4}} \\& \quad = \biggl(\frac{8 \pi +\lambda_{2}}{\lambda_{1}} \biggr) \rho+\varLambda \end{aligned}$$

(20)

where dot denotes differentiation with respect to time and prime $(\,'\,)$ denotes the differentiation with respect to $\tau$.

4 Solution of the field equations

In order to solve the field equations completely, we assume that the shear scalar ($\sigma$) in the models is proportional to expansion scalar ($\theta$), this condition leads us to write

$$ R=S^{n} $$

(21)

where $R$ and $S$ are the metric potentials and $n$ is an arbitrary constant.

Using above condition (21), in field equations (18) and (19), we get

$$ \frac{S''}{S}-\frac{S^{\prime\,2}}{S^{2}}+\delta\biggl( \frac{S^{2n+2}}{n-1} \biggr)-\frac{S^{4}}{n-1}=0 $$

(22)

4.1 Bianchi type-$\mathit{II}$ ($\delta=0$) cosmological model

If $\delta=0$, Eq. (22) can be written as

$$ \frac{S''}{S}-\frac{S^{\prime\,2}}{S^{2}}-\frac{S^{4}}{n-1}=0, \quad \mbox{where } n\neq1 $$

(23)

From Eq. (23), we get

$$ S= \bigl[c_{1}\mathrm{cosech}(k_{2}-2\tau k_{1}) \bigr]^{\frac{1}{2}} $$

(24)

where $c_{1}=k_{1}\sqrt{2(n-1)}$ and $k_{1}$, $k_{2}$ are integrating constants.

From Eqs. (21) and (24), we get

$$ R= \bigl[c_{1}\mathrm{cosech}(k_{2}-2\tau k_{1}) \bigr]^{\frac{n}{2}} $$

(25)

Now the metric (13) can be rewritten as

$$\begin{aligned} ds^{2} =&dt^{2}- \bigl[c_{1}\mathrm{cosech}(k_{2}-2 \tau k_{1}) \bigr]^{n}\bigl[d\theta^{2}+d \phi^{2}\bigr] \\ &{}- \bigl[c_{1}\mathrm{cosech}(k_{2}-2\tau k_{1}) \bigr] [d\varphi+\theta d\phi]^{2} \end{aligned}$$

(26)

From Eqs. (19), (20), (24) and (25), we get

$$\begin{aligned} \varLambda =&\frac{\lambda_{2}}{4(8\pi+\lambda_{2})} \biggl(\frac{c_{1}^{2}-2(3n+1)k_{1}^{2}}{c_{1}^{2n+1}} \biggr) \\ &{}\times \bigl[\mathrm{cosech}(k_{2}-2\tau k_{1}) \bigr]^{1-2n} \end{aligned}$$

(27)

Using Eqs. (24) and (25) in field equations (19)–(20), we get

$$\begin{aligned} p =&\frac{\lambda_{1}}{8\pi+\lambda_{2}} \\ &{}\times \biggl\{ \frac {k_{1}^{2}}{2} \biggl( \frac{(2-n)(1+n)\mathrm{coth}^{2}(k_{2} {-} 2\tau k_{1})-2(3n+1)}{(c_{1}\mathrm{cosech}(k_{2}-2\tau k_{1}))^{2n+1}} \biggr) \\ &{} - \biggl(\frac{\lambda _{2}(c_{1}^{2}-2(3n+1)k_{1}^{2})}{(8\pi+\lambda_{2})c_{1}^{2n+1}}-\frac {1}{4} \biggr) \\ &{}\times \bigl(c_{1}\mathrm{cosech}(k_{2}-2\tau k_{1}) \bigr)^{1-2n} \biggr\} \end{aligned}$$

(28)

$$\begin{aligned} \rho =&\frac{\lambda_{1}}{8\pi+\lambda_{2}} \biggl\{ \biggl(\frac{\lambda_{2}(c_{1}^{2}-2(3n+1)k_{1}^{2})}{(8\pi+\lambda_{2})c_{1}^{2n+1}}- \frac{1}{4} \biggr) \\ &{}\times\bigl(c_{1}\mathrm{cosech}(k_{2}-2\tau k_{1})\bigr)^{1-2n} \\ &{} - \biggl(\frac{n(n+2)k_{1}^{2}\mathrm{coth}^{2}(k_{2}-2\tau k_{1})}{(c_{1}\mathrm{cosech}(k_{2}-2\tau k_{1}))^{2n+1}} \biggr) \biggr\} . \end{aligned}$$

(29)

Thus the metric (26) together with (27), (28) and (29) constitutes a homogeneous and anisotropic Bianchi type-$\mathit{II}$ perfect fluid cosmological model in $f (R,T)$ gravity with cosmological constant ($\varLambda$).

Figure 1 explains behavior of pressure and energy density in terms of $\tau$. It is observed that pressure is varying in negative region through out the evolution of Universe. As it is evident from host of the observational data believed that dark energy is the best candidate to explain cosmic acceleration and it is supposed that dark energy has a strong negative pressure to explain the observed acceleration of the Universe. Also, we observed that energy density is decreasing function of $\tau$ and vanishes for large values of $\tau$. Figure 2 depicts the character cosmological constant in terms $\tau$, it is observed that cosmological constant is varying from negative to positive region and attains a value in positive region. Which is in accordance with the lambda cold dark matter ($\varLambda\mbox{CDM}$) model where a positive value of the cosmological constant is required to explain the accelerated nature of the Universe. So one can select the positive value of $\varLambda$ consistent with the observational data.

Fig. 1

Plot of pressure and energy density versus $\tau$

Fig. 2

Evolution of cosmological constant versus $\tau$

4.2 Bianchi type-$\mathit{VIII}$ ($\delta=-1$) cosmological model

If $\delta=-1$, then Eq. (22) can be written as

$$ \frac{S''}{S}-\frac{S^{\prime\,2}}{S^{2}}- \biggl(\frac{S^{2n+2}}{n-1} \biggr)-\frac{S^{4}}{n-1}=0. $$

(30)

We can solve the above equation and get the deterministic solution only for $n=-1$.

So from Eq. (30), we get

$$ {S}^{\prime\,2}=(c_{2}S)^{2}-S^{6} $$

(31)

where $c_{2}=\sqrt{k_{3}-1}$ and $k_{3}$ is an integration constant.

From Eq. (31), we get

$$\begin{aligned} S= \bigl[c_{2}\mathrm{sech}(2c_{2}\tau +k_{4}) \bigr]^{\frac{1}{2}} \end{aligned}$$

(32)

where $k_{4}$ is an integrating constant.

Consequently from Eq. (21), we get

$$ R= \bigl[c_{2}\mathrm{sech}(2c_{2}\tau +k_{4}) \bigr]^{-\frac{1}{2}} $$

(33)

Now the metric (13) can be rewritten as

$$\begin{aligned} ds^{2} =&dt^{2}- \bigl[c_{2}\mathrm{sech}(2c_{2} \tau+k_{4}) \bigr]^{-1}\bigl[d\theta^{2}+\mathrm{cosh}^{2} \theta d\phi^{2}\bigr] \\ &{}- \bigl[c_{2}\mathrm{sech}(2c_{2} \tau+k_{4}) \bigr] [d\varphi+\mathrm{sinh}\theta d\phi]^{2} \end{aligned}$$

(34)

From Eqs. (19), (20), (32) and (33), we get cosmological term

$$\begin{aligned} \varLambda =&\frac{\lambda_{2}c_{2}^{2}}{4(8\pi+\lambda_{2})} \bigl\{ \bigl[4c_{2}\mathrm{sech}(2c_{2} \tau+k_{4}) \\ &{}-c_{2}^{2}\mathrm{sech}^{2}(2c_{2} \tau+k_{4})-3 \bigr]\mathrm{sech}^{2}(2c_{2}\tau +k_{4}) \bigr\} \end{aligned}$$

(35)

Using Eqs. (32) and (33) in field equations (19)–(20), we get pressure and energy density

$$\begin{aligned} p =&\frac{\lambda_{1}c_{2}^{3}\mathrm{sech}^{2}(2c_{2}\tau +k_{4})}{4(8\pi+\lambda_{2})^{2}} \biggl[ \biggl(\frac{24\pi+7\lambda _{2}}{8\pi+\lambda_{2}} \biggr)\mathrm{sech}(2c_{2}\tau+k_{4}) \\ &{}- \bigl(3+2\mathrm{sech}^{2}(2c_{2} \tau+k_{4}) \bigr) \biggr] \end{aligned}$$

(36)

$$\begin{aligned} \rho =&\frac{\lambda_{1}c_{2}\mathrm{sech}(2c_{2}\tau +k_{4})}{4(8\pi+\lambda_{2})^{2}} \\ &{}\times \bigl\{ \bigl[-3+(\lambda_{2}-24 \pi)c_{2}\mathrm{sech}(2c_{2}\tau+k_{4}) \\ &{}- \lambda_{2}c_{2}^{2}\mathrm{sech}^{2}(2c_{2} \tau+k_{4}) \bigr] \bigl(c_{2}\mathrm{sech}(2c_{2}\tau+k_{4}) \bigr) \\ &{}+4\bigl(c_{2}^{2}+1\bigr) (8\pi+\lambda_{2}) \bigr\} . \end{aligned}$$

(37)

Thus the metric (34) together with (35)–(37) constitutes a homogeneous and anisotropic Bianchi type-$\mathit{VIII}$ perfect fluid cosmological model in $f(R,T)$ gravity with cosmological constant.

The behavior of pressure and energy density versus $\tau$ is plotted in Figs. 3 and 4 respectively. We observed that pressure have negative values throughout the evolution, this behavior is similar to Bianchi type-$\mathit{II}$ case. Energy density is decreasing function $\tau$ and vanishes for large values of $\tau$.

Fig. 3

Plot of pressure versus $\tau$

Fig. 4

Evolution of energy density versus $\tau$

4.3 Bianchi type-$\mathit{IX}$ ($\delta=1$) cosmological model

If $\delta=1$, then Eq. (22) can be written as

$$ \frac{S''}{S}-\frac{S^{\prime\,2}}{S^{2}}+ \biggl(\frac{S^{2n+2}}{n-1} \biggr)-\frac{S^{4}}{n-1}=0. $$

(38)

Here also, we can solve the above equation and get the deterministic solution only for $n=-1$.

So from Eqs. (30) and (38), we get

$$ {S}^{\prime\,2}=(c_{3}S)^{2}-S^{6} $$

(39)

where $c_{3}=\sqrt{k_{5}+1}$. From Eq. (39), we get

$$\begin{aligned} S= \bigl[c_{3}\mathrm{sech}(2c_{3}\tau +k_{6}) \bigr]^{\frac{1}{2}} \end{aligned}$$

(40)

where $k_{4}$ is an integrating constant.

Consequently from Eq. (21), we get

$$ R= \bigl[c_{3}\mathrm{sech}(2c_{3}\tau +k_{6}) \bigr]^{-\frac{1}{2}}. $$

(41)

Now the metric (13) can be rewritten as

$$\begin{aligned} ds^{2} =&dt^{2}- \bigl[c_{3}\mathrm{sech}(2c_{3} \tau+k_{6}) \bigr]^{-1}\bigl[d\theta^{2}+\sin ^{2} \theta d\phi^{2}\bigr] \\ &{}- \bigl[c_{3}\mathrm{sech}(2c_{3} \tau+k_{6}) \bigr] [d\varphi+\cos \theta d\phi]^{2}. \end{aligned}$$

(42)

From Eqs. (19), (20), (40) and (41), we get cosmological term

$$\begin{aligned} \varLambda =&\frac{\lambda_{2}c_{3}^{2}}{4(8\pi+\lambda_{2})} \bigl\{ \bigl[4c_{3}\mathrm{sech}(2c_{3} \tau+k_{6}) \\ &{} -c_{3}^{2}\mathrm{sech}^{2}(2c_{3} \tau+k_{6})+3 \bigr]\mathrm{sech}^{2}(2c_{3}\tau +k_{6}) \bigr\} . \end{aligned}$$

(43)

Using Eqs. (40) and (41) in field equations (19)–(20), we get pressure and energy density

$$\begin{aligned} p =&\frac{\lambda_{1}c_{3}^{3}\mathrm{sech}^{2}(2c_{3}\tau +k_{6})}{4(8\pi+\lambda_{2})^{2}} \biggl[ \biggl(\frac{24\pi+7\lambda _{2}}{8\pi+\lambda_{2}} \biggr)\mathrm{sech}(2c_{3}\tau+k_{6}) \\ &{}+ \bigl(3-2\mathrm{sech}^{2}(2c_{3} \tau+k_{6}) \bigr) \biggr] \end{aligned}$$

(44)

$$\begin{aligned} \rho =&\frac{\lambda_{1}c_{3}\mathrm{sech}(2c_{3}\tau +k_{6})}{4(8\pi+\lambda_{2})^{2}} \\ &{}\times \bigl\{ \bigl[3+(\lambda_{2}-24 \pi)c_{3}\mathrm{sech}(2c_{3}\tau+k_{6}) \\ &{}- \lambda_{2}c_{3}^{2}\mathrm{sech}^{2}(2c_{3} \tau+k_{6}) \bigr] \bigl(c_{3}\mathrm{sech}(2c_{3}\tau+k_{6}) \bigr) \\ &{}+4\bigl(c_{3}^{2}-1\bigr) (8\pi+\lambda_{2}) \bigr\} . \end{aligned}$$

(45)

Thus the metric (42) together with (43)–(45) constitutes a homogeneous and anisotropic Bianchi type-$\mathit{IX}$ perfect fluid cosmological model in $f(R,T)$ gravity with cosmological constant.

Figure 5 describes the behavior of pressure and energy density versus $\tau$. We observed that pressure and energy density are decreasing functions of $\tau$, and vanishes for large values of $\tau$. From Fig. 6, it is observed that the cosmological constant have positive values throughout the evolution. This behavior is consistent with the cosmological constant is a small but positive value is required to explain the present day scenario of accelerated expansion given by lambda cold dark matter ($\varLambda\mbox{CDM}$) model.

Fig. 5

Plot of pressure and energy density versus $\tau$

Fig. 6

Evolution of cosmological constant versus $\tau$

5 Some other important properties of the models

5.1 Bianchi type-$\mathit{II}$ ($\delta=0$) cosmological model

The spatial volume and average scale factor for the model are

$$\begin{aligned}& V=\sqrt{-g}= \bigl(c_{1}\mathrm{cosech}(k_{2}-2k_{1} \tau) \bigr)^{\frac{2n+1}{2}} \end{aligned}$$

(46)

$$\begin{aligned}& a=V^{1/3}= \bigl(c_{1}\mathrm{cosech}(k_{2}-2k_{1} \tau) \bigr)^{\frac{2n+1}{6}} \end{aligned}$$

(47)

The expansion scalar ($\theta$) for flow vector ($u^{i}$) and shear scalar ($\sigma^{2}$) are given by

$$\begin{aligned}& \theta=u^{i}_{;i}=\frac{k_{1}(2n+1)\mathrm{cot}(k_{2}-2k_{1}\tau)}{ (c_{1}\mathrm{cosech}(k_{2}-2k_{1}\tau) )^{\frac{2n+1}{2}}} \end{aligned}$$

(48)

$$\begin{aligned}& \sigma^{2}=\frac{1}{2}\sigma^{ij} \sigma_{ij}=\frac{7k_{1}^{2}(2n+1)^{2}\mathrm{cot}^{2}(k_{2}-2k_{1}\tau)}{18 (c_{1}\mathrm{cosech}(k_{2}-2k_{1}\tau) )^{2n+1}} \end{aligned}$$

(49)

The Hubble’s parameter ($H$) is given by

$$ H=\frac{\dot{a}}{a}=\frac{k_{1}(2n+1)\mathrm{cot}(k_{2}-2k_{1}\tau )}{3 (c_{1}\mathrm{cosech}(k_{2}-2k_{1}\tau) )^{\frac{2n+1}{2}}} $$

(50)

The deceleration parameter ($q$) is given by

$$ q=\frac{-a\ddot{a}}{\dot{a}^{2}}=-3 \biggl(\frac{2\mathrm {sech}^{2}(k_{2}-2k_{1}\tau)}{2n+1}-1 \biggr) \frac{\mathrm{sinh}(k_{2}-2k_{1}\tau)}{c_{1}}. $$

(51)

5.2 Bianchi type-$\mathit{VIII}$ ($\delta=-1$) cosmological model

The spatial volume and average scale factor for model (34) are

$$\begin{aligned}& V=\sqrt{-g}= \bigl[c_{2}\mathrm{sech}(2c_{2}\tau +k_{4}) \bigr]^{\frac{-1}{2}}\mathrm{cosh}\theta \end{aligned}$$

(52)

$$\begin{aligned}& a=V^{1/3}= \bigl\{ \bigl[c_{2}\mathrm{sech}(2c_{2} \tau+k_{4}) \bigr]^{\frac{-1}{2}}\mathrm{cosh}\theta\bigr\} ^{\frac{1}{3}} \end{aligned}$$

(53)

The expansion scalar ($\theta$) for flow vector ($u^{i}$) and shear scalar ($\sigma^{2}$) are given by

$$\begin{aligned}& \theta=u^{i}_{;i}= \bigl(c_{2}\mathrm{tanh}(2c_{2} \tau+k_{4}) \bigr)\sqrt{c_{2}\mathrm{sech}(2c_{2}\tau +k_{4})} \end{aligned}$$

(54)

$$\begin{aligned}& \sigma^{2}=\frac{1}{2}\sigma^{ij} \sigma_{ij} \\& \phantom{\sigma^{2}}=\frac{7}{18} \bigl(c_{2}\mathrm{tanh}(2c_{2} \tau+k_{4}) \bigr)^{2} \bigl({c_{2}\mathrm{sech}(2c_{2} \tau+k_{4})} \bigr) \end{aligned}$$

(55)

The Hubble’s parameter ($H$) is given by

$$ H=\frac{\dot{a}}{a}=\frac{ (c_{2}\mathrm{tanh}(2c_{2}\tau+k_{4}) )\sqrt{c_{2}\mathrm{sech}(2c_{2}\tau+k_{4})}}{3} $$

(56)

The deceleration parameter ($q$) is given by

$$\begin{aligned} q =&\frac{-a\ddot{a}}{\dot{a}^{2}} \\ =&\frac{ (\mathrm {sech}(2c_{2}\tau+k_{4}) )^{\frac{1}{3}}}{c_{2}} \bigl[1-6\mathrm{cosech}^{2}(2c_{2} \tau+k_{4}) \bigr] \end{aligned}$$

(57)

5.3 Bianchi type-$\mathit{IX}$ ($\delta=1$) cosmological model

The spatial volume and average scale factor for model (37) are

$$\begin{aligned}& V = \sqrt{-g}= \bigl[c_{3}\mathrm{sech}(2c_{3}\tau +k_{6}) \bigr]^{\frac{-1}{2}}\sin \theta \end{aligned}$$

(58)

$$\begin{aligned}& a = V^{\frac{1}{3}}= \bigl\{ \bigl[c_{3}\mathrm{sech}(2c_{3} \tau+k_{6}) \bigr]^{\frac{-1}{2}}\sin \theta\bigr\} ^{\frac{1}{3}} \end{aligned}$$

(59)

The expansion scalar ($\theta$) for flow vector ($u^{i}$) and shear scalar ($\sigma^{2}$) are given by

$$\begin{aligned}& \theta = u^{i}_{;i}= \bigl(c_{3}\mathrm{tanh}(2c_{3} \tau+k_{6}) \bigr)\sqrt{c_{3}\mathrm{sech}(2c_{3}\tau +k_{6})} \end{aligned}$$

(60)

$$\begin{aligned}& \sigma^{2} = \frac{1}{2}\sigma^{ij} \sigma_{ij} \\ & \phantom{\sigma^{2} }=\frac{7}{18} \bigl(c_{3}\mathrm{tanh}(2c_{3} \tau+k_{6}) \bigr)^{2} \bigl({c_{3}\mathrm{sech}(2c_{3} \tau+k_{6})} \bigr) \end{aligned}$$

(61)

The Hubble’s parameter ($H$) is given by

$$ H=\frac{\dot{a}}{a}=\frac{ (c_{3}\mathrm{tanh}(2c_{3}\tau+k_{6}) )\sqrt{c_{3}\mathrm{sech}(2c_{3}\tau+k_{6})}}{3} $$

(62)

The deceleration parameter ($q$) is given by

$$\begin{aligned} q =&\frac{-a\ddot{a}}{\dot{a}^{2}} \\ =&\frac{ (\mathrm {sech}(2c_{3}\tau+k_{6}) )^{\frac{1}{3}}}{c_{3}} \bigl[1-6\mathrm{cosech}^{2}(2c_{3} \tau+k_{6}) \bigr] \end{aligned}$$

(63)

6 Conclusions

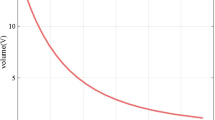
In this paper we have presented Bianchi type-$\mathit{II}, \mathit{VIII}$ and $\mathit{IX}$ cosmological models in $f(R,T)$ modified theory of gravitation proposed by Harko et al. (2011) for an appropriate choice of the function $f(R,T)=f_{1}(R)+f_{2}(T)=\lambda_{1}R+\lambda _{2}T$ with variable $\varLambda(T)$. We have shown that the field equations in this model reduce to the usual Einstein field equations for $\frac{\lambda_{2}}{1+\lambda_{1}}=-8\pi$ with an time-dependent cosmological constant which can be expressed in terms of the energy density and pressure. From Fig. 7, it is observed that the volume of Bianchi type-$\mathit{II}$, $\mathit{VIII}$ and $\mathit{IX}$ models zero for small values of $\tau$ whereas all the remaining physical parameters are diverge at this initial epoch and tend to zero as $\tau\rightarrow \infty$, which shows that at early stages the Universe starts evolving with zero volume and expands continuously approaching to infinite volume at late times. All three models have point type singularity (MacCallum 1971) at $\tau=0$. The pressure has negative values for Bianchi type-$\mathit{II}$ and $\mathit{VIII}$ models, which shows that the Universe is accelerated expanding for late times with the dominance of dark energy. The energy density of the three models positive throughout the evolution of the Universe and vanishes for large values of $\tau$. Also, we found that the cosmological constant has attains positive value for Bianchi type-$\mathit{II}$ and $\mathit{IX}$ models, this is consistent with the $\varLambda CDM$ model. The deceleration parameter is depends on $\tau$ for all three models, from Fig. 8, we observed that for Bianchi type-$\mathit{II}$ model the deceleration parameter is positive at the early stages and negative at late times, i.e., the Universe exhibits transition from deceleration to acceleration, which is consistent with the observations made by Perlmutter et al. (1999) and Riess et al. (1998) and the present day Universe is undergoing accelerated expansion. For Bianchi type-$\mathit{VIII}$ and $\mathit{IX}$ models the deceleration parameter is initially negative but later on they attain a constant positive value, i.e. the models represent acceleration in early times and deceleration in later times, however they will accelerate in finite time due to cosmic re-collapse (Nojiri and Odintsov 2003). So these Bianchi type-$\mathit{VIII}$ and $\mathit{IX}$ models are also useful to explain early stages of evolution of the Universe.

Fig. 7

Plot of volume versus $\tau$

Fig. 8

Plot of Deceleration parameter versus $\tau$