1 Introduction

Dusty plasmas occur frequently in astrophysical and space environments, such as asteroid zones, planetary atmospheres, interstellar media, circumstellar disks, dark molecular clouds, cometary tails, nebulae, and the Earth’s environment (Mamun and Hassan 2000). In a dusty plasma, the dust grains are charged by the collection of the plasma particles flowing onto their surfaces (Shukla and Mamun 2002). The difference of dusty plasmas from many component plasmas is that charged dust grains immersed in a plasma can exhibit charge fluctuations in response to oscillations in the plasma currents flowing into them.

In the literature, there are two approaches to study the dust charge fluctuations arising due to the wave-motion-induced oscillations in the plasma currents that flow to the grains. In the first category, using kinetic theory, longitudinal dielectric permittivity has been obtained from the Vlasov equation. For example, effects of dust charge fluctuations on the Langmuir waves (Ma and Yu 1994a) and dust ion-acoustic waves (Ma and Yu 1994b) have been investigated. The kinetic Alfven waves (Zubia et al. 2007) and dust-lower-hybrid waves (Salimullah et al. 2003) have been studied taking into account dust charge fluctuations. Effects of uniform magnetic field, the plasma inhomogeneity, and the dust charge fluctuations on the drift waves have been investigated in a nonuniform dusty magnetoplasma (Salimullah et al. 2004). In the second category, fluid theory has been used to find a fluctuating part of the dust charge. For example, dissipative phenomena has been found, which can damp the usual ion waves (Jana et al. 1993). It has been shown that the low frequency longitudinal waves such as the ion-acoustic waves and electrostatic-ion-cyclotron waves are damped, while the high frequency longitudinal Langmuir wave grows (Li et al. 1994). The criterion of instability and the growth rate of the ion-acoustic waves have been obtained (Lee 2004). The dust charge fluctuation instability in a dusty plasma in the presence of equilibrium density and external static magnetic field inhomogeneities has been examined (Salimullah et al. 2007). Current-driven electrostatic ion-cyclotron instability has been studied in a collisional magnetized dusty plasma (Sharma et al. 2013). Effects of dust charge fluctuations on current-driven dust-ion-acoustic waves have been investigated (Vranjes et al. 2001). Dust kinetic Alfvén waves with finite Larmor radius effects have been examined rigorously in a uniform dusty plasma in the presence of an external magnetic field (Rubab et al. 2009). Expressions for the charging currents have been derived using kappa and generalized (r,q) distribution functions (Rubab and Murtaza 2006). Effects of dust charge fluctuations on nonlinear dust ion-acoustic waves have been studied (Alinejad 2011). It has been shown that the effects of suprathermality of ions/electrons and dust charge fluctuation significantly modify the basic properties of dust acoustic shock wave (Shahmansouri and Alinejad 2013). Dust acoustic shock waves have been investigated in a dusty plasma having a high-energy-tail electron distribution (Shahmansouri and Tribeche 2013). Dust-ion-acoustic shock waves due to dust charge fluctuation in magnetized nonthermal dusty plasma have been studied (Shahmansouri and Mamun 2014).

In this paper, using kinetic theory, we investigate the dust ion-acoustic (DIA) waves by considering the dust charge fluctuations arising due to the wave-motion-induced oscillations in the plasma currents that flow to the grains. Since balance between the electron and ion currents flowing to the dust grains is disturbed by the wave potential, the dust grain charge can fluctuate around an equilibrium value. It is assumed that the time scales of the phenomena are much shorter than the time that the plasma particles attach to the dust grains. We obtain the longitudinal dielectric permittivity for a collisionless unmagnetized dusty plasma consisting of electrons, ions and massive charged dust grains. We consider a Maxwellian distribution for electrons and ions in the equilibrium and assume that drift speeds of the plasma particles are equal to zero. It is found that the dust charge fluctuations lead to either damping or growing of the DIA waves. This instability is quite different from the one due to the drift speed of the plasma particles and it can occur even in the presence of Landau damping. These results have been found in Ma and Yu (1994b). We numerically investigate the growth rate of DIA waves and a critical wave number above which these waves are unstable. In addition, we compare the results of kinetic theory with those of fluid theory.

The paper is organized as follows. In Sect. 2, the longitudinal dielectric permittivity and dispersion relations of electrostatic waves are obtained taking into account the dust charge fluctuations. In Sect. 3, the dispersion relation of the DIA waves is investigated. In Sect. 4, the numerical results are discussed. Section 5 contains the conclusions.

2 Dust charge fluctuations

The elementary processes that lead to the charging of dust grains depend on the environment around the dust grains. When dust grains are immersed in a plasma, the plasma particles are collected by the dust grains. The dust grain charge q d is determined by dq d /dt=∑ j I j where j represents the plasma species and I j is the current associated with the species j. Since in dusty plasmas whose constituents are electrons and ions, the electron thermal velocity is much larger than the ion thermal velocity, the electrons reach the dust grain surface much more rapidly than the ions. Thus, the surface potential of dust grain Φ d0 becomes negative. The charging current I j to the dust grain carried by the plasma particle j has been calculated with the orbit-limited motion approach (j equals e for electrons and i for ions) (Shukla and Mamun 2002)

$$ I(\vec{r},t,q_{d}) = \sum_{j = e,i} q_{j} \int v \sigma_{j}(q_{d},v) f_{j} ( \vec{r},v,t ) d^{3}p, $$
(1)

where f j and q j are, respectively, the velocity distribution and charge of the plasma species j and σ j is the cross section for charging collisions between the dust and the plasma particle species j. The ion (electron) charge is e(−e).

Perturbation of the form \(e^{i(\vec{k}.\vec{r} - \omega t)}\) is assumed, where ω is the frequency and \(\vec{k}\) is the wavevector, it can change the distribution function \(f_{j} ( \vec{r},\vec{v},t ) = f_{j0} ( v ) + f_{j1} ( \vec{r},\vec{v},t )\), where f j0 and f j1 are, respectively, the equilibrium and perturbed distribution functions (f j0≫f j1). The perturbation can also change cross section σ j (q d ,v)=σ j (q d0,v)+σ j (q d1,v), where the equilibrium dust charge q d0 is related to the grain potential, i.e. q d0=cΦ d0 (c is the capacitance of the spherical dust grain), q d1 is the perturbed dust charge (q d0≫q d1), and the perturbed cross section is \(\sigma_{j}(q_{d1},v) = q_{d1} \partial \sigma_{j}(q_{d},v) / \partial q_{d} \vert _{q_{d} = q_{d0}}\). Therefore, the charging current is \(I(\vec{r},t,q_{d}) = I_{0}(q_{d0}) + I_{1}(\vec{r},t,q_{d})\), where I 0 is the equilibrium current

$$\begin{aligned} I_{0}(q_{d0}) =& \sum_{j = e,i} I_{j0}(q_{d0}) \\ =& \sum_{j = e,i} q_{j} \int d^{3}p f_{j0} ( v )v \sigma_{j}(q_{d0},v) = 0. \end{aligned}$$
(2)

One can find the perturbed current (I 1≪I 0)

$$ \begin{aligned}[b] I_{1}(\vec{r},t,q_{d}) & = \sum _{j = e,i} q_{j} \int d^{3}p v \bigl[ \sigma_{j}(q_{d0},v)f_{j1} ( \vec{r},\vec{v},t ) \\ &\quad {}+\sigma_{j}(q_{d1},v) f_{j0} ( v )\bigr], \end{aligned} $$
(3)

where the equilibrium cross section is equal to

$$ \sigma_{j}(q_{d0},v) = \pi a_{d}^{2} \biggl(1 - \frac{2 q_{j} q_{d0}}{c m_{j} v^{2}}\biggr)H\biggl(1 - \frac{2 q_{j} q_{d0}}{c m_{j} v^{2}} \biggr), $$
(4)

in which H represents the Heaviside function, m j is the mass of the plasma species j and a d is the dust grain radius. The capacitance of the spherical dust grain in a plasma is equal to a d for a d ≪λ D (Shukla and Mamun 2002).

The Fourier transform of the perturbed distribution function is obtained from the linearized Vlasov equation (Ma and Yu 1994a, 1994b; Alexandrov et al. 1984)

$$ f_{j1}(\vec{k},\omega,\vec{v}) = - \frac{q_{j}}{m_{j}}\frac{\varPhi_{1}}{\omega - \vec{k}.\vec{v}} \vec{k}.\frac{\partial f_{j0}(v)}{\partial \vec{v}}, $$
(5)

where Φ 1 is the Fourier transform of the perturbed potential.

Substituting (4) and (5) into (3), we obtain

$$\begin{aligned} I_{1}(\vec{k},\omega,q_{d}) =& \sum_{j = e,i} m_{j}^{3}q_{j} \int v \biggl[ - \sigma_{j}(q_{d0},v) \\ &{}\times \frac{q_{j}}{m_{j}} \frac{\varPhi_{1}}{\omega - \vec{k}.\vec{v}}\vec{k}.\frac{\partial f_{j0}}{\partial \vec{v}} \\ &{}+ \frac{\partial \sigma_{j}(q_{d},v)}{\partial q_{d}} \bigg\vert _{q_{d0}} q_{d1}f_{j0} \biggr]d^{3}v. \end{aligned}$$
(6)

We can simplify equation (6) as

$$\begin{aligned} I_{1}(\vec{k},\omega,q_{d}) =& - \sum _{j = e,i} m_{j}^{2}q_{j}^{2} \int v \varPhi_{1}\frac{\sigma_{j}(q_{d0},v)}{\omega - \vec{k}.\vec{v}} \\ &{}\times \vec{k}.\frac{\partial f_{j0}(v)}{\partial \vec{v}} d^{3}v \\ &{} + q_{d1} \sum_{j = e,i} \frac{\partial I_{j0}(q_{d})}{\partial q_{d}} \bigg\vert _{q_{d} = q_{d0}}. \end{aligned}$$
(7)

The Fourier transform of the dust charge fluctuation q d1 can be obtained by taking the Fourier transform of ∂q d /∂t=∑ j I j together with Eq. (7)

$$ q_{d1} = \frac{e^{2}\varPhi_{1}}{\nu_{ch} - i\omega} \biggl(\frac{\nu_{i}}{T_{i}} + \frac{\nu_{e}}{T_{e}}\biggr), $$
(8)

where T j is the thermal energy of the plasma species j and ν ch is the charging frequency of the dust particle

$$ \nu_{ch} \equiv - \sum_{j = e,i} \frac{\partial I_{j0}(q_{d})}{\partial q_{d}} \bigg\vert _{q_{d} = q_{d0}}, $$
(9)

the coefficients ν e , ν i are

$$ \nu_{e} \equiv - \int m_{e}^{2}v \frac{ \sigma_{e}(q_{d0},v)}{\omega - \vec{k}.\vec{v}}T_{e}\vec{k}.\frac{\partial f_{e0}(v)}{\partial \vec{v}} d^{3}v, $$
(10)
$$ \nu_{i} \equiv - \int m_{i}^{3}v \frac{\sigma_{i}(q_{d0},v)}{\omega - \vec{k}.\vec{v}}T_{i}\vec{k}.\frac{\partial f_{i0}(v)}{\partial \vec{v}} d^{3}v. $$
(11)

We consider a Maxwellian velocity distribution for electrons and ions

$$ f_{j0} ( v ) = \frac{n_{j0}}{(2 \pi m_{j} T_{j})^{3 / 2}}\exp \biggl( - \frac{m_{j} v^{2}}{2 T_{j}} \biggr), $$
(12)

where n j0 is the equilibrium number density. Therefore, the ion and electron equilibrium currents are obtained (Shukla and Mamun 2002)

$$ I_{i0} = a_{d}^{2} e n_{i0} \biggl( \frac{8 \pi T_{i}}{m_{i}}\biggr)^{\frac{1}{2}} \biggl(1 - \frac{e q_{d0}}{c T_{i}} \biggr), $$
(13)
$$ I_{e0} = - a_{d}^{2} e n_{e0} \biggl( \frac{8 \pi T_{e}}{m_{e}}\biggr)^{\frac{1}{2}} \exp \biggl(\frac{e q_{d0}}{c T_{e}}\biggr). $$
(14)

At equilibrium, the net current flowing onto the dust grain surface becomes zero, i.e. (I i0=|I e0|).

Substituting (13) and (14) into (9), the charging frequency is obtained

$$ \nu_{ch} = \frac{e\vert I_{e0} \vert }{c}\biggl(\frac{1}{T_{e}} + \frac{1}{T_{i} - e \varPhi_{d0}}\biggr). $$
(15)

One can calculate ν e and ν i as a function of ω, \(\vec{k}\) for a Maxwellian distribution of particles as follows (Shukla and Mamun 2002; Ma and Yu 1994a, 1994b)

for ω≪kv Tj ,

$$ \nu_{e} = - \frac{\vert I_{e0} \vert }{e}, $$
(16)
$$ \nu_{i} = - \frac{\vert I_{e0} \vert }{e}, $$
(17)

for ω≫kv Tj ,

$$ \nu_{e} = \frac{2}{3} \frac{k^{2} v_{Te}^{2}}{\omega^{2}} \biggl(2 - \frac{e \varPhi_{d0}}{T_{e}}\biggr) \frac{\vert I_{e0} \vert }{e}, $$
(18)
$$ \nu_{i} = \frac{2}{3} \frac{k^{2} v_{Ti}^{2}}{\omega^{2}} \frac{(2 - \frac{e \varPhi_{d0}}{T_{i}})}{(1 - \frac{e \varPhi_{d0}}{T_{i}})} \frac{\vert I_{e0} \vert }{e}, $$
(19)

where \(v_{Tj} = \sqrt{T_{j} / m_{j}}\) is the thermal velocity of the plasma species j.

To study electrostatic waves, we can use Fourier transform of Poisson’s equation

$$ k^{2} \varPhi_{1} = 4\pi (en_{i1} - en_{e1} + q_{d0}n_{d1} + q_{d1}n_{d0}), $$
(20)

where n j1 is the number density perturbation of the plasma species j.

$$ n_{j1} = \int f_{j1} d^{3}p. $$
(21)

Substituting (5) into (21) and then substituting (21) and (8) into (20) and assuming that the charging frequency is much smaller than the wave frequency ν ch ≪ω, the longitudinal dielectric permittivity is obtained

$$ \begin{aligned}[b] \varepsilon^{lo}(\omega,k) &= 1 + \chi_{d} + \chi_{i} + \chi_{e} \\ &\quad {}- \frac{i n_{d0}}{\omega n_{e0}}\biggl(\frac{\nu_{e}}{ k^{2}\lambda_{De}^{2}} + \frac{n_{e0}\nu_{i}}{n_{i0} k^{2}\lambda_{Di}^{2}}\biggr) = 0, \end{aligned} $$
(22)

where λ Dj is Debye length (\(\lambda_{Dj} = \sqrt{T_{j} / 4\pi n_{j0}q_{j}^{2}}\)) and χ j is the plasma dielectric susceptibility of the plasma species j (Shukla and Mamun 2002)

$$ \chi_{j} = - \frac{4\pi q_{j}n_{j1}}{k^{2}\varPhi_{1}} = \frac{4\pi q_{j}^{2}}{k^{2}}\int m_{j}^{2}\frac{d^{3}v}{\omega - \vec{k}.\vec{v}}\vec{k}.\frac{\partial f_{j0}(v)}{\partial \vec{v}}. $$
(23)

The plasma dielectric susceptibility for the Maxwellian velocity distribution is

$$ \chi_{j} = \frac{1}{k^{2}\lambda_{Dj}^{2}}\biggl[1 - I_{ +} \biggl( \frac{\omega}{ kv_{Tj}}\biggr)\biggr], $$
(24)

with asymptotic behavior (Alexandrov et al. 1984)

$$\begin{aligned} I_{ +} \biggl(\frac{\omega}{kv_{Tj}}\biggr) = \left\{ \begin{array}{l@{\quad}l} 1 + (\frac{kv_{Tj}}{\omega} )^{2} + 3 (\frac{kv_{Tj}}{\omega} )^{4} +\cdots \\ \ {}- i\sqrt{\frac{\pi}{2}} \frac{\omega}{kv_{Tj}}\exp [ - \frac{1}{2}(\frac{\omega}{kv_{Tj}})^{2}] & \omega \gg kv_{Tj} , \\ - i\sqrt{\frac{\pi}{2}} \frac{\omega}{kv_{Tj}} & \omega \ll kv_{Tj}. \end{array} \right. \end{aligned}$$
(25)

For ω=ω r +iδ, the real and imaginary parts of the frequency can be found under the condition ω r ≫δ as follows (Alexandrov et al. 1984)

$$ \operatorname{Re} \bigl\{ \varepsilon^{lo}(\omega_{r},k) \bigr\} = 0, $$
(26)
$$ \delta = - \frac{\operatorname{Im} \{ \varepsilon^{lo}(\omega_{r},k)\}}{ \frac{\partial \operatorname{Re} \{ \varepsilon^{lo}(\omega_{r},k)\}}{\partial \omega_{r}}}. $$
(27)

When δ>0, the medium transfers its energy to the wave.

3 DIA waves

In this section, the dispersion relation of the DIA waves is investigated by including the effect of dust charge fluctuations. The dust grains are considered immobile, but their charge can fluctuate. We assume that these waves propagate along the z-axis. The phase velocity of the DIA waves is much smaller (larger) than the electron thermal velocity (ion and dust thermal velocities) (v Td , v Ti ≪ω/k≪v Te ). Thus, we choose ν e and ν i from (16) and (19), respectively. Therefore, the real and imaginary parts of the longitudinal dielectric permittivity are obtained

$$ \operatorname{Re} \bigl\{ \varepsilon^{lo}(\omega,k)\bigr\} = 1 + \frac{1}{k^{2}\lambda_{De}^{2}} - \frac{\omega_{pi}^{2}}{\omega^{2}} - \frac{\omega_{pd}^{2}}{\omega^{2}}, $$
(28)
$$ \begin{aligned}[b] \operatorname{Im} \bigl\{ \varepsilon^{lo}(\omega,k) \bigr\} & = \sqrt{\frac{\pi}{2}} \frac{1}{k^{2}\lambda_{De}^{2}}\frac{\omega}{ kv_{Te}} \\ &\quad {}+ \sqrt{\frac{\pi}{2}} \frac{1}{k^{2}\lambda_{Di}^{2}}\frac{\omega}{kv_{Ti}}\exp \biggl[ - \frac{1}{2}\biggl(\frac{\omega}{kv_{Ti}}\biggr)^{2}\biggr] \\ &\quad {}+ \frac{1}{\omega} \biggl(\frac{\beta_{e}}{k^{2}\lambda_{De}^{2}} - \frac{\beta_{i}\omega_{pi}^{2}}{\omega^{2}} \biggr), \end{aligned} $$
(29)

where \(\omega_{pj} = \sqrt{4 \pi n_{j0} q_{j}^{2} / m_{j}}\) is the plasma frequency associated with the plasma species j. The first and second terms in \(\operatorname{Im} [\varepsilon^{lo}(\omega,k)]\) are due to the thermal effects of electrons and ions, respectively. The last term is caused by dust charge fluctuation effects, here β i and β e are

$$ \beta_{i} \equiv \frac{\omega^{2}}{\omega_{pi}^{2}}\frac{n_{d0}}{n_{i0} k^{2}\lambda_{Di}^{2}} \nu_{i} = \frac{n_{d0}}{n_{i0}} \alpha \frac{\vert I_{e0} \vert }{e}, $$
(30)
$$ \beta_{e} \equiv - \biggl(\frac{n_{d0}}{n_{e0}}\biggr)\nu_{e} = \frac{n_{d0}}{n_{e0}} \frac{\vert I_{e0} \vert }{e}. $$
(31)

The coefficient α obtained from kinetic theory is

$$ \alpha = \frac{2}{3}\frac{(2 + \frac{\vert e \varPhi_{d0} \vert }{T_{i}})}{(1 + \frac{\vert e \varPhi_{d0} \vert }{T_{i}})}. $$
(32)

Letting ω=ω r +iδ, where ω r ≫δ, the real and imaginary parts of the frequency are obtained

$$ \omega_{r}^{2} = \frac{k^{2}\lambda_{De}^{2}(\omega_{pi}^{2} + \omega_{pd}^{2})}{1 + k^{2}\lambda_{De}^{2}} \approx \frac{k^{2}\lambda_{De}^{2} \omega_{pi}^{2}}{1 + k^{2}\lambda_{De}^{2}}, $$
(33)
$$ \delta = \delta_{L} + \delta_{f}, $$
(34)

here δ consists of two parts, one is

$$ \begin{aligned}[b] \delta_{L} & = - \sqrt{\frac{\pi}{8}} \frac{1}{1 + k^{2}\lambda_{De}^{2}}\frac{\omega_{r}^{2}}{kv_{Te}} \\ &\quad {}- \sqrt{\frac{\pi}{8}} \frac{1}{k^{2}\lambda_{Di}^{2}\omega_{pi}^{2}}\frac{\omega_{r}^{4}}{kv_{Ti}}\exp \biggl[ - \frac{1}{2}\biggl(\frac{\omega_{r}}{kv_{Ti}}\biggr)^{2}\biggr], \end{aligned} $$
(35)

in which the first and second terms are Landau damping of the DIA waves due to the electrons and ions, respectively, the second part δ f is caused by dust charge fluctuation effects. Using (30) and (31), we have

$$ \delta_{f} = - \frac{1}{2} \frac{n_{d0}}{n_{e0}} \frac{\vert I_{e0} \vert }{e}\biggl(\frac{\omega_{r}^{2}}{\omega_{pi}^{2}} \frac{1}{k^{2}\lambda_{De}^{2}} - \alpha \frac{n_{e0}}{n_{i0}}\biggr). $$
(36)

The terms in parentheses in Eq. (36) reduce to 1−αn e0/n i0 when kλ De ≪1, while the result obtained from fluid theory in Jana et al. (1993) has shown that the imaginary part of the frequency is proportional to 1−n e0/n i0=Z d n d0/n e0. In Li et al. (1994), by using fluid theory it has been shown that the imaginary part of the frequency is proportional to \(R = n_{d_{0}}\vert q_{d0} \vert / (n_{e0}e)\). Note that the condition ν ch ≪ω has not been considered in Li et al. (1994).

The dust charge fluctuations play an important role in the instability of the DIA waves, i.e. when the condition

$$ \frac{\beta_{i}}{2} - \frac{\beta_{e}}{2 (1 + k^{2}\lambda_{De}^{2})} + \delta_{L} > 0 $$
(37)

is fulfilled, the DIA waves are unstable due to the dust charge fluctuations. When the inequality in Eq. (37) is reversed, the dust charge fluctuations increase the damping of the waves.

The imaginary part of the frequency can be zero for a critical wave number k=k cr . When the condition k>k cr is fulfilled, the instability of the DIA waves can occur. We consider the limit δ L ≪δ f to obtain the normalized critical wave number K cr as follows

$$ K_{cr} = k_{cr}\lambda_{De} = \sqrt{ \frac{n_{i0}}{\alpha n_{e0}} - 1}. $$
(38)

When condition δ L ≪δ f is not fulfilled, the critical wave number is larger than K cr obtained from Eq. (38). One can compare this equation with the result obtained from fluid theory in Lee (2004), where it has been shown that the critical wave number is \(K_{cr} = \sqrt{n_{i0} / n_{e0} - 1} = \sqrt{Z_{d0}n_{d0} / n_{e0}}\). If the coefficient α in Eq. (38) is equal to 1, the results of kinetic theory approach those of fluid theory.

A comparison between the results of kinetic theory—Eqs. (36) and (38)—and those of fluid theory (Jana et al. 1993; Li et al. 1994; Lee 2004) indicates that the coefficient α is equal to 1 in fluid theory, while in the frame work of kinetic theory it is a function of the plasma parameters through Φ d0 and accepts values between 2/3 and 4/3.

4 Numerical results

In this section, the instability of the DIA waves is investigated numerically. We introduce the dust density parameter p=Z d n d0/n e0 and the dust parameter \(p_{de} = 4 \pi n_{d0} a_{d} \lambda_{De}^{2}\) that covers a rather broad range, especially in the case of astrophysical and space dusty plasmas. The dust parameter is 10−4 for Saturn’s E ring, 10 for Saturn’s G ring, and 1 for Jupiter’s ring (Melandso et al. 1993; Bhatt and Pandey 1994).

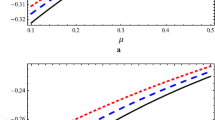
The normalized critical wave number K cr is plotted as a function of p in Fig. 1 for chosen plasma parameters. It should be noted that α is a function of the plasma parameters, while α is equal to 1 in fluid theory. In this figure, the solid line shows K cr obtained from kinetic theory (Eq. (38)) and the dashed line shows K cr obtained from fluid theory (Lee 2004). The shadowed regions are the stability and instability regions in kinetic theory and fluid theory, respectively. It is obvious that K cr of kinetic theory is larger than that of fluid theory. Figure 1 also shows that as p increases, the instability can occur for shorter wavelengths.

Fig. 1
figure 1

K cr as a function of p for kinetic model (solid line) and fluid model (dashed line) for T i /T e =0.01

Full size image

The imaginary part of the frequency obtained from (34) consists of two terms, Landau damping and dust charge fluctuation terms. The term of Landau damping always leads to the damping of the wave, but the term of the dust charge fluctuation leads to either damping or growing of the wave.

Figure 2 shows the normalized imaginary part of the frequency as a function of kλ De . One can see that considering the dust charge fluctuation leads to the increase of the damping rate in long-wavelength limit and instability of the DIA waves in the short-wavelength limit, i.e. damping (growing) of these waves can occur for small (large) values of kλ De . This figure also shows that the growth rate continues to increase with kλ De .

Fig. 2
figure 2

Normalized imaginary part of the frequency as a function of kλ De . The dashed line, dot-dashed and solid line are δ f /ω pi , δ L /ω pi , and δ/ω pi respectively. The other parameters are p=1.5, T i /T e =0.005, a d /λ De =0.005

Full size image

The dependence of the imaginary part of the frequency on the plasma parameters is investigated in Figs. 3 and 4. The normalized imaginary part of the frequency δ/ω pi as a function of p is plotted in Fig. 3 for two values of a d /λ De . This figure shows that the growth rate is not a monotonic growing function of p and increases with the increase of a d /λ De .

Fig. 3
figure 3

δ/ω pi as a function of p. The dashed line is a d /λ De =0.005 and the solid line is a d /λ De =0.003. The other parameters are T i /T e =0.01, kλ De =2.5

Full size image
Fig. 4
figure 4

δ/ω pi as a function of p de . The dashed line is T i /T e =0.001 and the solid line is T i /T e =0.01. The other parameters are a d /λ De =0.01, kλ De =2. (a) α=1, (b) α is a function of Φ d0

Full size image

Figure 4 displays the normalized imaginary part of the frequency δ/ω pi as a function of p de for two values of T i /T e . The results of fluid and kinetic theories are, respectively, depicted in Figs. 4(a) and (b) (substituting α=1 into the results of kinetic theory, we find those of fluid theory).

It is obvious from these figures that the growth rate of the DIA waves increases with the increase of p de . Figure 4(a) shows that the growth rate of the DIA waves decreases with the increase of T i /T e . Figure 4(b) obtained from kinetic theory shows that the slope of the growth rate line for the DIA waves decreases with the increase of T i /T e . The reason is the dependence of α to the plasma parameters. Therefore, behavior of δ in Fig. 4(b) becomes different from its behavior in Fig. 4(a).

Since the condition ν ch ≪ω must be satisfied, we investigate the ratio ν ch /ω for the chosen plasma parameters. In Fig. 2, ν ch /ω accepts values between 0.075 and 0.365. In Fig. 3, the inequalities 0.053<ν ch /ω<0.069 and 0.032<ν ch /ω<0.04 are fulfilled for the dashed line and solid line, respectively. In Fig. 4, we have 0.305<ν ch /ω<0.315 for the dashed line and 0.182<ν ch /ω<0.188 for the solid line. Hence, the condition ν ch ≪ω is fulfilled for these figures.

5 Conclusions

In this paper, we have investigated the instability of the DIA waves in the presence of the dust charge fluctuations by using kinetic theory. The dispersion relation of the DIA waves is obtained in collisionless unmagnetized dusty plasmas by assuming that the wave frequency is much larger than the attachment rate of the charged particles to the dust grains. It has been shown that the instability can occur even if we consider Landau damping and it is different from the instability due to the drift speed of the plasma particles. There is a critical wave number above which the instability of the DIA waves can occur. We have analytically found this critical wave number in kinetic theory for the limit δ L ≪δ f . In the framework of kinetic theory, there is the coefficient α depending on plasma parameters, while there is not this coefficient in the results of fluid theory. In addition, our results have shown that the growth rate of the DIA waves increases with the increase of the dust parameter, dust grain radius, and wave number. In kinetic theory, the growth rate increases (decreases) with the increase of the ratio of ion temperature to electron temperature for large (small) values of the dust parameter, while in fluid theory, substituting α=1 into the result of kinetic theory, the growth rate decreases with the increase of this ratio.