1 Introduction

Dusty plasma is an electron-ion plasma with an additional component of small micron sized highly charged dust (Shukla and Mamun 2002). The presence of this charged dust component does not only modify the existing plasma wave spectra, but also introduces new eigen-modes, such as dust- acoustic (DA) mode (Rao et al. 1990; Melandso et al. 1993; Rosenberg 1993; Barkan et al. 1995; D’Angelo 1995), dust- ion acoustic (DIA) mode (Shukla and Silin 1992), dust cyclotron mode (Shukla and Rahman 1998), dust drift mode (Shukla et al. 1991), dust lattice mode (Melandso 1996; Farokhi and Shahmansouri 2009; Shahmansouri and Farokhi 2012), etc. The DIA mode, which is one of the most important low frequency electrostatic dust associated modes, is first predicted theoretically by Shukla and Silin (1992), and observed experimentally by Barkan et al. (1996). The experimental observation of the DIA waves is more convenient than that of the DA waves. These waves exist not only in laboratory devices, but also in various space and astrophysical plasma systems. Therefore, the DIA waves have attracted a great deal of attention in the last few decades.

The electron distribution function may be significantly modified by the localized dust- ion-acoustic potential structures via generating fast or energetic or nonthermal electron population. The electrostatic solitary structures associated with density depression have been observed by the Viking spacecraft (Boström 1992) and Freja satellite (Shukla and Mamun 2002) at the lower part of in the magnetosphere or upper part of the ionosphere. These observations motivated Cairns et al. (1995) to study the effect of nonthermal electrons on the nature of ion acoustic solitary waves. Their results were in good agreement with those observed by Viking and Freja. The influence of nonthermal distribution of plasma particles on the collective processes in plasma has been discussed by a number of authors (Ghosh et al. 2002; Ghosh et al. 2004; Zhang and Xue 2005; El-Taibany and Sabry 2005; Zhang and Wang 2006; El-Taibany and Kourakis 2006; Roy et al. 2006; El-Taibany et al. 2007; El-Taibany and Wadati 2007; Chaudhuri et al. 2007; Tribeche and Amour 2007; Tribeche and Boumezoued 2008).

A large number of theoretical investigations (Duha and Mamun 2009; Sarma and Nakamura 2009; Mamun et al. 2009; Mamun and Shukla 2009; Mamun and Shukla 2010) have been made on the effects of dust charge fluctuation on the nonlinear propagation of the DIA waves in a collisionless dusty plasma during the last few couple of years very seriously. They are termed ‘collisionless’ in the sense that no viscous or damping effects resulting from collisions between dust and plasma particles are involved. Mamun and Shukla (2002) studied the DIA solitary and shock waves in dusty plasma with charge fluctuating dust. They explained clearly the necessary conditions for the formation of DIA solitary and shock waves as well as their properties. Moslem (2006) investigated the DIA solitary and shock waves in charge varying dusty plasma in the presence of transverse perturbations. It was showed that the DIA waves governed by the Kadomtsev–Petviashivili–Burgers (KPB) equation. Berbri and Tribeche (2009) have revisited the model of Mamun and Shukla (2002) in the presence of nonthermal electrons. The dusty plasma system with Maxwellian electrons supports only compressive DIA solitary waves, while that with nonthermal electrons supports both compressive and rarefactive DIA solitary waves. Duha et al. (2011) studied the DIA shock and solitary waves in a multi-ion plasma with trapped electrons. They discussed the implications of their findings in space and laboratory dusty multi-ion plasmas.

It is well known that the external magnetic field can modify the propagation properties of the electrostatic solitary structures. The effect of an ambient external magnetic field on the electrostatic waves has been studied by a number of authors (Alinejad and Mamun 2011; Mamun and Hassan 2000; Zhang and Xue 2005; Shahmansouri and Alinejad 2013a, 2013b; Choi et al., 2005a, 2005b; Anowar and Mamun 2008a, 2008b; Shalaby et al. 2009; Anowar et al. 2011; Shahmansouri and Alinejad 2012). D’Angelo (1990) studied two possible electrostatic modes, namely, electron-ion cyclotron and dust-ion acoustic in a magnetized dusty plasma. Yinhua and Yu (1994) investigated the influence of static dust particles on both large- and small-amplitude obliquely propagating ion acoustic solitons. They showed that the dust particles increase the region of permitted soliton speed as well as the soliton width. Anowar and Mamun (2008a) studied the oblique propagation of the DIA solitons in hot adiabatic magnetized dusty plasma. They also investigated the multi-dimensional instability of obliquely propagating DIA solitary waves in a magnetized dusty plasma (Anowar and Mamun 2008b). Shalaby et al. (2009) investigated the DIA solitary waves governed by the Zakharov–Kuznetsov (ZK) equation in a collisional magnetized dusty plasma, and discussed their stability. Recently, Shahmansouri and Alinejad (2012) studied obliquely propagating large amplitude DIA waves in magnetized superthermal dusty plasma. The characteristics of linear and nonlinear structures are found to depend significantly on the different types of electron distribution function.

Zhang and Xue (2005) studied DA shock waves in magnetized dusty plasma with dust charge fluctuations and nonthermal ion effects. They used the reductive perturbation technique to derive a KdV-Burgers equation. Recently, Tribeche and Bacha (2012) studied the DA shock waves in magnetized superthermal dusty plasma with application to the Halley’s Comet. More recently, we studied oblique propagation of IA shock waves in a magnetized plasma consisting of a cold viscous ion fluid and Maxwellian electrons. We showed that the combined effects of ion-viscosity, obliqueness and magnitude of the external magnetic field significantly modify the basic properties of the IA shock waves (Shahmansouri and Mamun 2013).

The aim of the present work is to examine the combined effects of external static magnetic field, obliqueness, nonthermal electron distribution and dust charge fluctuation on the basic properties of the DIA shock waves in a magnetized dusty plasma system in which the charge fluctuating dust grains are immobile, ions are inertial fluid and electrons follow the nonthermal distribution of Cairns et al. (1995).

The manuscript is organized as follows. Theoretical model and basic equations are provided in Sect. 2. The KdV-Burgers equation is derived in Sect. 3. The shock stationary shock wave solution is obtained and is numerically analyzed in Sect. 4. A brief discussion is presented in Sect. 5.

2 Theoretical model

We consider a collisionless magnetized dusty plasma consisting of charge fluctuating negatively charged static dust, inertial ion fluid, and nonthermal electrons of densities n d , n i , and n e , respectively. At equilibrium, the charge neutrality condition reads n e0+Z d0 n d0=n i0, from which we define f=n e0/n i0=1−Z d0 n d0/n i0. We assume this system is immersed in an external magnetic field (\(B_{0} \Vert \hat{z}\); \(\hat{z} \) is a unit vector along the z-axis). Thus, the nonlinear dynamics of the DIA waves can be described by

$$ \frac{\partial n_{i}}{\partial t} + \nabla \cdot (n_{i}\mathbf{u}_{i}) = 0, $$
(1)
$$ \frac{\partial \mathbf{u}_{i}}{\partial t} + (\mathbf{u}_{i} \cdot \nabla ) \mathbf{u}_{i} = - \nabla \phi + \omega_{c_{i}} \mathbf{u}_{i} \times \hat{z}, $$
(2)
$$ \nabla^{2}\phi = fn_{e} - n_{i} + (1 - f)Z_{d}, $$
(3)

where u i is the ion fluid velocity normalized by \(C_{s} = \sqrt{T_{e}/m_{i}} \), ϕ is the electrostatic wave potential normalized by T e /e, the time variable (t) is normalized by \(1/\omega_{pi} = \sqrt{m_{i}/4\pi n_{i0}e^{2}} \), the plasma species number density n j (j=e,i,d) is normalized by its equilibrium value n j0, the space variable (r) is normalized by λ D =C s /ω pi , and ω ci is the ion-cyclotron frequency normalized by ω pi .

To model the electron distribution with fast or nonthermal particles, we employ the nonthermal electron velocity distribution function of Cairns et al. (1995). The latter allow us to express the electron density n e as

$$ n_{e}(\phi ) = \biggl\{ 1 - \beta \frac{e\phi}{T_{e}} + \beta \frac{e^{2}\phi^{2}}{T_{e}^{2}} \biggr\} \exp \biggl(\frac{e\phi}{ T_{e}}\biggr), $$
(4)

where β=4α/(1+3α) and α determines the number of nonthermal electrons. It may be mentioned here that Eq. (4) is correct for an assumption: The magnetic field is so strong that the electron Larmor radius is very small in comparison with the size of the structures under consideration, i.e. the electrons are moving parallel to the strong magnetic field.

We note that the dust grain is charged by the plasma currents at the grain surface. The charging current originates from electrons and ions hitting the grain surface. It must be noted that the nonthermal electron distribution significantly modify the electron current flowing to the spherical dust grain surface. The modified expressions for electron and ion charging currents are expressed as (Berbri and Tribeche 2009)

$$\begin{aligned} I_{e} =& - \frac{\pi r_{d}^{2}en_{e0}}{1 + 3\alpha} \sqrt{\frac{8T_{e}}{\pi m_{e}}} \exp \biggl(\frac{e\phi}{T_{e}} - \frac{e^{2}Z_{d}}{r_{d}T_{e}}\biggr) \\ &{}\times \biggl\{ 1 + \frac{4\alpha}{5}\biggl(6 - \frac{20}{3} \frac{e\phi}{T_{e}} + \frac{4e^{2}Z_{d}}{r_{d}T_{e}} + 5\frac{e^{2}\phi^{2}}{T_{e}^{2}} \\ &{} - \frac{10}{3} \frac{e^{3}Z_{d}\phi}{r_{d}T_{e}^{2}} + \frac{e^{4}Z_{d}^{2}}{r_{d}^{2}T_{e}^{2}}\biggr) \biggr\} , \end{aligned}$$
(5)
$$ I_{i} = \pi r_{d}^{2}en_{i}\sqrt{ \frac{8T_{i}}{\pi m_{i}}} \biggl(1 + \frac{2e^{2}Z_{d}}{T_{i}r_{d}}\biggr), $$
(6)

where r d is the dust radius. We assume that the dust grain radius is smaller than the electron gyro-radius, thus the external magnetic field do not significantly affects the charging characteristics (Chang and Spariosu 1993; Rubinstein and Laframboise 1982). Then the variable dust charge is determined self-consistently by the following normalized charging equation

$$\begin{aligned} \eta \biggl(\frac{\partial Z_{d}}{\partial t} + u_{d}\frac{\partial Z_{d}}{\partial x}\biggr) =& \gamma \exp \biggl(\frac{e\phi}{T_{e}} - \frac{e^{2}Z_{d}}{r_{d}T_{e}}\biggr) \\ &{}\times \biggl\{ 1 + \frac{4\alpha}{5}\biggl(6 - \frac{20}{3}\frac{e\phi}{T_{e}} + \frac{4e^{2}Z_{d}}{r_{d}T_{e}} \\ &{} + 5\frac{e^{2}\phi^{2}}{T_{e}^{2}} - \frac{10}{3}\frac{e^{3}Z_{d}\phi}{ r_{d}T_{e}^{2}} + \frac{e^{4}Z_{d}^{2}}{r_{d}^{2}T_{e}^{2}}\biggr) \biggr\} \\ &{}- \chi n_{i}\biggl(1 + \frac{2\alpha Z_{d}}{\sigma} \biggr), \end{aligned}$$
(7)

where \(\eta = \sqrt{k_{ \circ} m_{e}(1 - f)/2m_{i}} \), \(\gamma = \mu (r_{d}/n_{d0}^{ - 1/3})^{3/2} / (1 + 3\alpha ) \), \(\chi = (r_{d}/n_{d0}^{ - 1/3})^{3/2}\sqrt{m_{e}\sigma /m_{i}} \), σ=T i /T e , and k ∘=Z d0 e 2/r d T e . Equation (7) is an additional equation which is coupled self-consistently to the plasma equations through the plasma currents. For nonadiabatic dust charge fluctuations (Shukla and Mamun 2002), the ratio ω pi /ν ch can be considered small but finite, and in the theory of adiabatic dust charge fluctuations we have ω pi /ν ch ≈0, in that ν ch is dust charging frequency defined as \(\nu_{ch} = r_{d}^{ - 1}T_{e}^{ - 1}\partial (I_{e} + I_{i}) / \partial Z_{d} \). The influence of the dust charging rates on the propagation of low frequency DIA waves is dependent on the dust charging frequency, ν ch in comparison to the plasma frequency ω pi . If the dust charging frequency becomes much greater than that of the plasma frequency, the dust charge reaches equilibrium value at each point. But for non-negligible values of ω pi /ν ch , the dust charge fluctuations play the role of a dissipative mechanism. Thus, the dust charge fluctuations modify the dynamical behavior of system and finally it can lead to the formation of collisionless shock waves. Furthermore, the charge neutrality at equilibrium conditions (Z d =1,ϕ=0) leads to the following constraint:

$$ f = \sqrt{\frac{\sigma m_{e}}{m_{i}}} \frac{(1 + 2k_{ \circ} /\sigma )(1 + 3\alpha )\exp (k_{ \circ} )}{1 + \frac{4\alpha}{5}(6 + 4k_{ \circ} + k_{ \circ}^{2})} . $$
(8)

The above equation indicates that how the equilibrium density ratio depends on the plasma parameters.

3 Derivation of KdV Burger equation

To study the small amplitude DIA shock waves in magnetized nonthermal dusty plasmas, we adopt the standard reductive perturbation method. The stretched coordinates for this method are defined as (Washimi and Taniuti 1996)

$$ \xi = \varepsilon^{1/2}(l_{x}x + l_{y}y + l_{z}z - V_{0}t) ,\qquad \tau = \varepsilon^{3/2}t , $$
(9)

where ε is a real and small parameter which measures the weakness of the amplitude or dispersion, V 0 is the normalized phase velocity, and l x , l y , and l z are, respectively, the directional cosines of the wave vector \(\vec{k} \) along the x,y, and z axes, so that \(l_{x}^{2} + l_{y}^{2} + l_{z}^{2} = 1 \). The expansion of dependent variables are considered as (Washimi and Taniuti 1996)

$$ n_{i} = 1 + \varepsilon n_{1} + \varepsilon^{2}n_{2} + \cdots, $$
(10a)
$$ u_{ix} = \varepsilon^{3/2}u_{x1} + \varepsilon^{2}u_{x2} + \cdots, $$
(10b)
$$ u_{iy} = \varepsilon^{3/2}u_{y1} + \varepsilon^{2}u_{y2} + \cdots, $$
(10c)
$$ u_{iz} = \varepsilon u_{z1} + \varepsilon^{2}u_{z2} + \cdots, $$
(10d)
$$ Z_{d} = 1 + \varepsilon Z_{d1} + \varepsilon^{2}Z_{d2} + \cdots , $$
(10e)
$$ \phi = \varepsilon \phi_{1} + \varepsilon^{2}\phi_{2} + \cdots . $$
(10f)

We note that for non-adiabatic dust charge fluctuations the ratio ω pi /ν ch can be considered small but finite. We assume that η≈ε 1/2 η ∘, (Ghosh et al. 2002) where η ∘ is a finite parameter of the order of unity. Now, substituting the above expansions, along with the stretched coordinates, into Eqs. (1)–(3) and (7), and collecting the terms in different powers of ε, the lowest order of ε leads to

$$ n_{1} = \frac{l_{z}}{V_{0}}u_{z1},\qquad u_{z1} = \frac{l_{z}}{V_{0}}\phi_{1}, $$
(11a)
$$ n_{1} = f(1 - \beta )\phi_{1} + (1 - f)Z_{d1}, $$
(11b)
$$ Z_{d1} = b_{1}\phi_{1} - b_{2}n_{1}. $$
(11c)

The set of Eqs. (11a–11c) allows us to express the wave velocity V 0 as

$$ V_{0} = l_{z}\sqrt{\frac{1 + (1 - f)b_{2}}{f(1 - \beta ) + (1 - f)b_{1}}} , $$
(12)

where

$$\begin{aligned} & {b_{1} = \gamma \biggl[ \frac{8\alpha k_{ \circ}}{15} - \frac{8\alpha}{15} + 1 + \frac{4\alpha k_{ \circ}^{2}}{5} \biggr] / b_{0}, }\\ & {b_{2} = \chi \biggl(1 + \frac{2k_{ \circ}}{\sigma} \biggr)\exp (k_{ \circ} ) / b_{0}, }\\ & { b_{0}= \gamma \biggl[ k_{ \circ} + \frac{8\alpha k_{ \circ}}{5} + \frac{8\alpha k_{ \circ}^{2}}{5} + \frac{4\alpha k_{ \circ}^{3}}{5} \biggr] + \frac{2k_{ \circ} \chi}{\sigma} \exp (k_{ \circ} ). } \end{aligned}$$

On the other hand, the x and y components of the momentum equation to the lowest order in ε, take the following form

$$ u_{x1} = - \frac{l_{y}}{\omega_{ci}}\frac{\partial \phi_{1}}{\partial \xi}\quad \mbox{and}\quad u_{y1} = \frac{l_{x}}{\omega_{ci}}\frac{\partial \phi_{1}}{\partial \xi} $$
(13)

The above equation indicates the components of the electric field drift. Now, the next higher order in ε leads to the following set of equations

$$ \frac{\partial n_{2}}{\partial \xi} = \frac{1}{V_{0}}\frac{\partial n_{1}}{\partial \tau} + \frac{1}{V_{0}} \frac{\partial}{\partial \xi} (l_{x}u_{x2} + l_{y}u_{y2} + l_{z}u_{z2} + l_{z}n_{1}u_{z1}), $$
(14a)
$$ \frac{\partial u_{z2}}{\partial \xi} = \frac{1}{V_{0}}\frac{\partial u_{z1}}{\partial \tau} + \frac{1}{2} \frac{l_{z}}{V_{0}}\frac{\partial (u_{z1}^{2})}{\partial \xi} + \frac{l_{z}}{V_{0}}\frac{\partial \phi_{2}}{\partial \xi}, $$
(14b)
$$ \frac{\partial^{2}\phi_{1}}{\partial \xi^{2}} = f\biggl[(1 - \beta )\phi_{2} + \frac{1}{2} \phi_{1}^{2}\biggr] - n_{2} + (1 - f)Z_{d2}, $$
(14c)
$$ Z_{d2} = b_{1}\phi_{2} - b_{2}n_{2} + b_{3}\frac{\partial \phi_{1}}{\partial \xi} + b_{4}\phi_{1}^{2}, $$
(14d)
$$ u_{x2} = \frac{V_{0}l_{x}}{\omega_{ci}^{2}}\frac{\partial^{2}\phi_{1}}{\partial \xi^{2}}, $$
(14e)
$$ u_{y2} = \frac{V_{0}l_{y}}{\omega_{ci}^{2}}\frac{\partial^{2}\phi_{1}}{\partial \xi^{2}}, $$
(14f)

where

$$b_{3} = V_{0}\eta \bigl(b_{1} - b_{2}l_{z}^{2}/V_{0}^{2} \bigr)\exp (k_{ \circ} )/b_{0}, $$
$$\begin{aligned} b_{4} =& \frac{\gamma}{b_{0}} \biggl[ \frac{16\alpha}{15} - \frac{16\alpha k_{ \circ}}{15} + \frac{1}{2} + \frac{2\alpha k_{ \circ}^{2}}{5} \biggr] \\ &{} - \frac{2k_{ \circ} \chi}{\sigma} \frac{l_{z}^{2}}{V_{0}^{2}} \biggl(b_{1} - b_{2}\frac{l_{z}^{2}}{V_{0}^{2}}\biggr) \frac{\exp (k_{ \circ} )}{b_{0}} \\ &{} + \frac{\gamma k_{ \circ}}{b_{0}} \biggl(b_{1} - b_{2}\frac{l_{z}^{2}}{V_{0}^{2}}\biggr) \biggl[ \frac{16\alpha}{15} + \frac{16\alpha k_{ \circ}}{15} - 1 - \frac{4\alpha k_{ \circ}^{2}}{5} \biggr]. \end{aligned}$$

Now, using Eqs. (11a–11c)–(14a–14f), and after some straight forward mathematical steps, we can eliminate the second perturbed quantities and obtain the following KdV-Burgers equation for the first perturbed term of the electrostatic potential as

$$ \frac{\partial \phi_{1}}{\partial \tau} + A\phi_{1}\frac{\partial \phi_{1}}{\partial \xi} + B \frac{\partial^{3}\phi_{1}}{\partial \xi^{3}} = C\frac{\partial^{2}\phi_{1}}{\partial \xi^{2}}, $$
(15)

where

$$\begin{aligned} & {A = \biggl[ - \frac{V_{0}^{3}}{2l_{z}^{2}}f + \frac{3l_{z}^{2}}{2V_{0}}g_{ \circ} - \frac{V_{0}^{3}}{l_{z}^{2}}b_{4}(1 - f) \biggr] \Big/ g_{ \circ}, }\\ & {B = \frac{V_{0}^{3}}{2l_{z}^{2}} \biggl[ 1 + \frac{1 - l_{z}^{2}}{\omega_{ci}^{2}}g_{ \circ} \biggr] \Big/ g_{ \circ}, }\\ & { C = V_{0}^{3}(1 - f)b_{3} / 2l_{z}^{2}g_{ \circ},g_{ \circ} = \bigl[ 1 + (1 - f)b_{2} \bigr]. } \end{aligned}$$

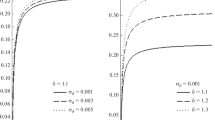
The above equation (15) represents the KdV- Burgers equation which describes the nonlinear evolution of the DIA shock wave including the obliqueness, electron nonthermality effects, and dust charge fluctuation. The structure of shock-like solution of Eq. (15) depends upon the competition between the coefficients A, B and C. Here, the nonlinear coefficient A, the dispersion coefficient B, and the dissipation coefficient C are strongly influenced by the nonthermal parameter α, obliqueness and dust charge fluctuation. We note that in the absence of dust charge fluctuation, the dissipation coefficient tends to zero and Eq. (15) reduces to the well known KdV-equation. Thus, it can be anticipated that the relation between the plasma parameters β, l z , ω ci and σ may control the behavior of the solution of Eq. (15). Figure 1 shows the effect of different parameters (such as obliqueness θ, nonthermal parameter α and magnitude of the magnetic field ω ci ) on the ratio of dissipation to dispersion coefficients C/B as a function of the obliqueness θ. In the Fig. 1a, we consider C/B with different values of α, for the case ω ci =0.5. It can be observed that C/B decreases with θ. Furthermore, the nonthermal parameter α has a reducing effect on C/B. But we see that in all curves C is very larger than B, as we have C≫B. Figure 1b shows variation of C/B as a function of obliqueness for different values of magnitude of the magnetic field with α=0.1. It is clear that an increase in ω ci increases C/B. Thus, in the presence of a weak magnetic field, when DIA shock wave goes more oblique neither dispersion nor dissipation are not negligible. We discuss this case with more details in the next section.

Fig. 1
figure 1

Ratio of the dissipation coefficient to the dispersion coefficient, as a function of obliqueness θ, (a) for different values of α with ω ci =0.5; (b) for different values of ω ci with α=0.1

Full size image

4 Shock wave solution

The electrostatic shock-like solutions of the Eq. (15) depends on the competition between the coefficients of KdV-Burgers equation. It is found from Fig. 1 that for high values of ω ci (i.e. strong magnetic field), the dispersion coefficient is very smaller than the dissipation coefficient, while for lower values of ω ci (i.e. weak magnetic field), when the waves propagate obliquely, the dispersion coefficient can be comparable with the dissipation coefficient. Therefore, Fig. 1 leads us to consider two different physical situations, namely dispersive case (low values of ω ci ) and weakly dispersive case (high values of ω ci ), to solve the KdV-Burgers.

1 st case: A Dispersive case (low values of ω ci and high values of θ)

Let us consider a special case for low values of ω ci and high values of θ, in which C/B is in order of unity (Fig. 2a). To study the shock-like solution of Eq. (15), in this case we consider a reference frame moving with the shock speed. Now, transforming the independent variables ξ and τ to ς=(ξ−Vτ′)/L and τ′=τ, one can find, under the steady-state condition, a third order differential equation for ϕ 1, which after integrating once, reduces to

$$ \frac{A}{2} [ \phi_{1} ]^{2} + \frac{B}{L^{2}} \frac{d^{2}\phi_{1}}{d\varsigma^{2}} = \frac{C}{L}\frac{d\phi_{1}}{d\varsigma} + V\phi_{1}, $$
(16)

where V is the shock speed (in the reference frame), i.e. the shock speed is V shock =c s +V, L indicates the shock width. To obtain Eq. (16), we have used the appropriate boundary conditions, namely ϕ 1→0, dϕ 1/dς→0, d 2 ϕ 1/dς 2→0 at ς→∞. The differential Eq. (16) is similar to the equation of motion of a damped an-harmonic oscillating particle of a unit mass with speed dϕ 1/dς and position ϕ 1. The above boundary conditions show that Eq. (16) has two singular points dϕ 1/dς=0 at ϕ 1=0 and dϕ 1/dς=0 at ϕ 1=2V/A. If we assume that the particle was located at ϕ 1=0 for ς→+∞, then for ς→−∞ we have ϕ 1=2V/A. Thus, under the condition that ϕ 1 is bounded by ς→±∞, the solution of Eq. (16) describes a shock-like structure. There are several techniques to solve the nonlinear partial differential equations (for example, Hirota bilinear formalism, inverse scattering method, Backlund transformation, tanh method, etc). It should be noted that in the systems including the combined effect of dispersion and dissipation, “tanh” technique is the most convenient technique. Thus, the analytical stationary solution of Eq. (16) by adopting “tanh” approach (Malfliet 1992; Malfliet 2004; Sultana et al. 2012) can be obtained as

$$ \phi_{1}(\xi,\tau ) = \varPhi_{\max} \biggl\{ 1 - \frac{1}{4} \biggl[ 1 + \tanh \biggl(\frac{\xi - V\tau}{L}\biggr) \biggr]^{2} \biggr\} , $$
(17)

where Φ max=12C 2/25AB is the shock amplitude, L=10B/C is the shock width and V=6C 2/25B is the shock speed. Since V>0, this solution corresponds to a shock traveling toward the +ς axis. It should be noted that all the shock relevant parameters are the function of the plasma parameters such as α, l z , ω ci ,σ and V 0.

Fig. 2
figure 2

(a) Ratio of the dissipation coefficient to the dispersion coefficient, as a function of obliqueness θ with α=0.5 and ω ci =0.1. (b) The threshold curve for the oscillatory shock profiles as a function of obliqueness θ. The triangles refer to the ratio C/V 3/2 as a function of θ. The parameters are similar to the panel (a)

Full size image

To investigate the stability of a small perturbation around the exact solution given in Eq. (17), we consider a perturbed solution in the form of ϕ 1(ς)=Φ(ς)+εΦ 1, where ε is a real small parameter. Then following the approach given in Mamun and Shukla (2002), Sultana et al. (2012) via the substitution of ϕ 1 in Eq. (16), and after linearizing with respect to Φ 1, we obtain a differential equation in the form

$$ \frac{B}{L^{2}}\frac{d^{2}\varPhi_{1}}{d\varsigma^{2}} - \frac{C}{L}\frac{d\varPhi_{1}}{d\varsigma} + \varPhi_{1}(A\varPhi - V) = 0. $$
(18)

The general solution of Eq. (18) is an exponential function in the form exp(λς), and it is easy to show that the parameter λ admits the following condition

$$ \lambda = \frac{CL \pm \sqrt{C^{2}L^{2} - 4BL^{2}(A\varPhi - V)}}{ 2B}. $$
(19)

Due to the behavior of the parameter λ the shock structure can take oscillatory or monotonic behavior. An imaginary value of the parameter λ leads to an oscillatory behavior, whereas for the real value of λ, the perturbation around the exact solution represents an exponentially behavior. Now, substituting Φ obtained from (17) into Eq. (19) we see that the parameter λ take always real values. Thus, in the 1st case the present model supports excitation of the monotonic shock structures, which are unstable with respect to an external perturbation.

2 nd case: Weakly dispersive case (high values of ω ci )

It is shown that in the 2nd situation the effect of dispersion is almost negligible compared to that of dissipation (Fig. 1), that this is a dominate effect in the present model. Thus, we proceed by neglecting the dispersion coefficient in Eq. (16). The latter reduces to

$$ \frac{A}{2} [ \phi_{1} ]^{2} - V\phi_{1} = \frac{C}{L}\frac{d\phi_{1}}{d\varsigma}. $$
(20)

This equation is analytically solvable and exhibits a monotonic shock wave solution in the following form

$$ \phi_{1}(\xi,\tau ) = \varPhi_{w}\biggl[1 - \tanh \biggl( \frac{\xi - V\tau}{ L_{w}}\biggr)\biggr], $$
(21)

where Φ w =V/A and L w =2C/V represent the amplitude and the width of the shock waves, respectively. In a particular case, according to Fig. 2a, when shock wave propagates more obliquely, the dispersion coefficient increases and thus for large values of θ we cannot neglect it. This is similar to the propagation of the shock wave from a non-dispersive zone (small θ) to a dispersive one (large θ). The behavior of shock solution (21) through such propagation (from non-dispersive to dispersive zone), has been investigated in Sultana et al. (2012). Similarly, we substitute Eq. (21) into Eq. (16) and obtain the following expression

$$ - \frac{BV^{3}}{2AC^{2}}\tanh \biggl(\frac{\xi - V\tau}{ L_{w}}\biggr)\biggl[ \tanh^{2}\biggl(\frac{\xi - V\tau}{L_{w}}\biggr) - 1\biggr] = 0, $$
(22)

To preserve the stability of the DIA shock waves (which are stable in the non-dispersive zone) in the dispersive zone, the condition (22) must be fulfilled. For an arbitrary ς, the above condition can be satisfied for BV 3/2AC 2≪1. This means that in the presence of weak dispersion or strong dissipation a shock structure preserve its stability through the propagation in the dispersive zone. We can obtain a θ-dependent form from Eq. (22), which determines the essential condition for the monotonic or oscillating shock profile when it propagates through the dispersive zone. The condition is

$$ \frac{C}{V^{3/2}} \gg \sqrt{\frac{1 + \frac{1 - l_{z}^{2}}{\omega_{ci}^{2}}g_{ \circ}}{ - 2f + \frac{6l_{z}^{4}}{V_{0}^{4}}g_{ \circ} - 4b_{4}(1 - f)}}. $$
(23)

It is seen from Figs. 1 that the dispersion term is negligible in comparison with the dissipation term, and therefore in this case the solution (21) satisfies Eq. (16). But in Fig. 2a, when shock wave propagates more obliquely, the dispersion term will be comparable with dissipation term. This is equivalent to a fact that the wave is propagating from a non-dispersive zone to a dispersive one. In this case we consider a stable shock profile (21) for θ≪1 and employ the above condition (23) to check the stability of shock profile in the dispersive zone (θ→25). Figure 2b shows the behavior of C/V 3/2 as a function of θ, for the parameters similar to Fig. 2a (the blue triangles). The threshold curve for the oscillatory shock profiles (the red line) is depicted in Fig. 2b where the right hand side of Eq. (23) is used. It can be seen that for all the values of θ, all the blue triangles lay below the threshold curve, and thus the condition (23) is not satisfied. This means that for this typical plasma parameters (which have been used in Fig. 2) when the shock structure propagates more obliquely (from non-dispersive zone to the dispersive zone) the shock structure may be shows an oscillatory behavior. Therefore, only in this special case the DIA shock wave shows an oscillatory behavior and in the other cases the behavior of shock structures are monotonic. A similar treatment has been reported by Mamun and Shukla (2002) DIA shock waves in unmagnetized dusty plasma.

To investigate the influence of the obliqueness, dust charge fluctuations, and nonthermal electron distribution on the basic properties of DIA shock waves, we have numerically analyzed the shock solution. The typical dusty plasma parameters (Mamun and Shukla 2002), viz. Z d0=103, r d =1–6 μm, σ=0.05–0.1 have been chosen so that the non-adiabatic condition ω pd /ν ch ≠0 is fulfilled.

To trace the effect of nonthermal parameter α on the shock profile, we have shown variation of the nonlinear coefficient with α in Fig. 3. We see that as we increase the nonthermal parameter α, the nonlinear coefficient decreases and tends to zero at a certain critical value α crit =0.118. This means that the present plasma model supports existence of both compressive and rarefactive shock structures. It turns out that the shock profile depends significantly on the nonthermal parameter. Samanta et al. (2007) reported a similar kind of result for the DA solitary waves in a magnetized dusty plasma with nonthermal ions. The obliqueness do not affects the critical value of the nonthermal parameter α crit .

Fig. 3
figure 3

Variation of the nonlinear coefficient as a function of nonthermal parameter α, for different values of obliqueness.

Full size image

Figure 4 shows the effect of obliqueness (θ) on the shock structures for the compressive shock structure (Fig. 4a) with α=0.1 and for the rarefactive shock structures (Fig. 4b) with α=0.3. It can be seen that as we increase θ, the height (thickness) of both the compressive and rarefactive shock waves increases (decreases). Thus obliqueness makes the shock structures more spiky. This is identical to that observed by Zhang and Xue (2005) for the DA shock wave in a magnetized dusty plasma. Mamun (1998) has shown a similar result for the study of obliquely propagating DA solitary waves in a magnetized dusty plasma with nonthermal ions. Recently, Tribeche and Bacha (2012) investigated the DA shock waves in a charge variable magnetized dusty plasma with superthermal electrons and reported a similar kind of effect of the obliqueness on the DA shock structures.

Fig. 4
figure 4

The behavior of DIA shock profile as a function of obliqueness θ, for (a) α=0.1, and (b) α=0.3 with ω ci =0.5

Full size image

The dependency of the DIA shock profiles on nonthermal electron is investigated in Fig. 5 for the compressive (Fig. 5a) and rarefactive (Fig. 5b) profiles. It can be seen that deviations of electrons from thermodynamics equilibrium, via an increase in the nonthermal parameter α, leads to an increase (decrease) in the shock amplitude of compressive (rarefactive) profile.

Fig. 5
figure 5

The behavior of (a) compressive and (b) rarefactive DIA shock profile as a function of nonthermal parameter α, with l z =0.95 and ω ci =0.5

Full size image

5 Discussion

The present investigation describe the formation and basis properties of small but finite amplitude compressive and rarefactive DIA shock waves in a magnetized dusty plasma whose constituents are charge fluctuating (negatively charged) static dust, inertial ions, and nonthermal electrons. The reductive perturbation technique has been employed to derive the KdV-Burgers equation. The latter has been then analyzed analytically and numerically. It is shown that the dust charge fluctuation is a source of dissipation, and is responsible for the formation of the DIA shock structures. It is found that the nonthermal index α modifies all the nonlinear, dispersion, and damping coefficients of the KdV-Burgers equation. An increase in the nonthermal parameter α, induces a decrease of the nonlinearity coefficient, as it tends to zero at a critical value α crit =0.118. This means that nonthermal plasma supports the existence of compressive and rarefactive shock structures. The dispersion coefficient is shown to be dependent upon the magnitude of the external magnetic field B 0, while the nonlinear and dissipation coefficients are independent of B 0. We have also found that the amplitude (width) of the DIA shock waves increases (decreases) with the increase the obliqueness θ. It appears appropriate here to add a comment that the reductive perturbation technique restricts the validity region of our investigation to the small but finite amplitudes limit. Thus, the present investigation is only valid for the small angles θ. We note that when θ→90∘, the width tends to zero and amplitude tends to infinity. It is likely that for large angles the assumption that the waves are electrostatic in nature is no longer valid one, and one should look for fully electromagnetic structures.

It is more appropriate to compare our results to those of Mamun and Shukla (2002) where thermal (Maxwell–Boltzmann) electrons have been used for space dusty plasma parameters. Mamun and Shukla (2002) reported the existence of only compressive solitary DIA waves. The present model, due to the nonthermal electron distribution, supports compressive as well as rarefactive DIA shock waves. Similarly, they found only monotonic DIA shock waves. On the other hand, Berbri and Tribeche (2009) extended the work of Mamun and Shukla (2002) to the situation in which electrons satisfy a nonthermal distribution in the presence of ion streaming velocity. They also reported formation of compressive as well as rarefactive DIA shock waves with monotonic behavior for 0.22<α<1. We found that the basic properties of the DIA shock waves have been significantly modified in the presence of external magnetic field and nonthermal electron distribution. We expect that the present investigation should be useful for understanding the localized electrostatic disturbances in magnetized space dusty plasma.