1 Introduction

There has been a great deal of interest in collective processes in dusty plasmas due to their vital role in the study of astrophysical and space environments, such as cometary tails, Saturn’s rings, asteroid zones, the gossamer ring of Jupiter, planetary rings, the interstellar clouds, the earth’s mesosphere and ionosphere, etc. (Verheest 1996). It has been shown that the dust charge dynamics introduces new eigenmodes, such as dust- acoustic (DA) mode (Rao et al. 1990; Barkan et al. 1995), dust-ion acoustic mode (Shukla and Silin 1992), dust cyclotron mode (Shukla and Rahman 1998), dust drift mode (Shukla et al. 1991) and dust lattice mode (Melandso 1996; Farokhi et al. 2009; Shahmansouri and Farokhi 2012).

A number of authors have studied nonlinear DA waves (Mamun 1999a, 1999b; Ghosh et al. 2001; El-Labany et al. 2010; Rahman et al. 2008; Pakzad 2010; Das and Devi 2010; Tribeche and Benzekka 2011; Mayout and Tribeche 2011; Shahmansouri and Tribeche 2012). However, most of these studies have been confined to Maxwell-Boltzmann distributed electrons and ions, while observations show that astrophysical and space plasmas have particle distribution function which are quasi-Maxwellian up to the mean thermal velocities, and possess non-Maxwellian suprathermal tails at the high velocities or energies (Pierrard and Lemaire 1996; Maksimovic et al. 1997). Such suprathermal plasmas are existed naturally in the magnetosphere of Earth, Saturn, Mercury, Uranus, and in the solar wind (Maksimovic et al. 1997), and may be modeled by the so-called kappa or suprathermal distribution (Summers and Thorne 1991; Baluku and Helberg 2008; Helberg et al. 2009), since it fits both the thermal as well as the suprathermal parts of the observed velocity spectra (Pierrard and Lemaire 1996; Maksimovic et al. 1997; Krimigis et al. 1983).

To model the fast suprathermal particles, we adopt three-dimensional generalized Lorentzian or kappa distribution function, which it takes the form,

(1)

where θ 2=2T j (κ−3/2)/κm j is the effective thermal speed, Γ is the gamma function, j(=e,i) refers to type of particles, and κ is a spectral index. The spectral index measures deviation from Maxwellian distribution, as the smaller values of κ denotes the more suprathermal particles in the distribution function tail (and the harder energy spectrum). In the limit of κ→∞, the kappa distribution recovers the Maxwellian distribution.

On the other hand appearance of an anomalous dissipation in the collisionless dusty plasma, can leads to possibility of the existence of a new kind of the shock waves. This type of dissipation originates from the dust charging processes, and they are termed collisionless in the sense that no viscous or damping effects resulting from collisions between dust and plasma particles are involved (Popel et al. 1996; Nakamura et al. 1999). Recently, Tribeche et al. (2009), Tribeche and Bacha (2010) investigated the influence of electron/ion suprathermality on DA waves in a charge varying dusty plasma. It has been shown that the dust charge variation may provide an alternate physical mechanism causing dissipation and, as a consequence, leads to the formation of shock waves (Ghosh et al. 2006). The influence of the dust charge fluctuation on the formation of DA shock waves has been studied by many authors (Gupta et al. 2001; Tribeche and Bacha 2010). Tribeche and Bacha (2010) found that the effect of decreasing the spectral index κ makes the solitary structure spikier, also they shown that as the ion suprathermal character becomes important, the dust grain charge becomes less negative and the dust grains accumulation more effective. The effect of dust charge fluctuation and suprathermality on DIA shock waves in a dusty plasma has been examined by Alinejad et al. (2011). They found that the presence of superthermal electrons does not only significantly modify the basic properties of shock waves, but also causes the existence of shock profile with only positive potential in such plasma with parameter ranges corresponding to Saturn’s rings. They also showed that the strength and steepness of the shock waves decrease with increase of the size of dust grains and ion temperature.

Motivated by the results arrived in the work of Baluku and Helberg (2008), we propose here to study weak amplitude DA waves in a charge varying dusty plasma with kappa-distributed ions as well as electrons. As the aim of our study we investigate the basic properties of DA shock waves in a complex plasma in which the dust grains are modeled as a cold, inertial fluid and the electrons and ions have a kappa distribution. A new Burgers equation is derived by employing the standard reductive perturbation technique. The influence of suprathermality effects and dust charge fluctuation on structure of DA shock waves is investigated.

The structure of this paper is as follows. After introduction the basic set of dynamical equations governing our plasma model is presented in Sect. 2. A Burgers equation is derived for the nonlinear propagation of DA shock waves in Sect. 3. The DA shock wave solution is investigated numerically in Sect. 4. Finally, a discussion is provided in Sect. 5.

2 Model and basic equations

Let us consider a collisionless, unmagnetized charge variable dusty plasma having electrons, positive ions, and dust grains of densities n e , n i , and n d , respectively. We assume that all the grains have the same negative charge q d =−Z d e, where Z d is number of charge residing on the dust grain. At equilibrium, the charge neutrality reads as n e0+Z d0 n d0=n i0, from which we define f=n e0/Z d0 n d0=n i0/Z d0 n d0−1. In this case, the nonlinear dynamics of this low frequency, purely electrostatic perturbation can be described by

(2)
(3)
(4)

where we use the following non-dimensional variables x→x/λ Dd , t→tω pd , n j →n j /n j0, u j →u j /C d , and ϕ→eϕ/T i , where \(\omega_{pd} = \sqrt{4\pi n_{d0}e^{2}Z_{d0}^{2}/m_{d}}\) is the dust plasma frequency, \(C_{d} = \sqrt{k_{B}T_{i}Z_{d0}/m_{d}}\) the dust-acoustic speed, and λ Dd =C d /ω pd the dust Debye length. Here j=i,e,d denotes, respectively, ions, electrons, and dust grains, the subscript “0” stands for equilibrium quantities, and the variables have their usual meaning.

In order to find an electron density as well as ion distribution with suprathermal particles, we integrate the kappa distribution function (1) over velocity space. Then, the normalized electron and ion number density are accordingly expressed as

(5)
(6)

We note that the dust grain is charged by the plasma currents at the grain surface. The charging current originates from electrons and ions hitting the grain surface. According to the standard orbit-limited probe model, the electron (Tribeche and Bacha 2010) and ion (Tribeche et al. 2009) charging currents are as follow

(7)
(8)

where α=Z d0 e 2/r d T e . Then the variable dust charge is determined self-consistently by the following normalized charging equation

(9)

where r d is the dust radius, σ=T i /T e and

$$\gamma_{e,i} = \sqrt{\frac{2r_{d}^{4}n_{i0}^{2}T_{i}m_{d}}{m_{i}n_{d0}Z_{d0}^{4}e^{2}}} \frac{\kappa_{e,i}}{\kappa_{e,i} - 1}\sqrt{\frac{\kappa_{e,i} - 3/2}{\kappa_{e,i}^{4}}} \frac{\varGamma (\kappa_{e,i} + 1)}{\varGamma (\kappa_{e,i} - 1/2)}. $$

The above equation, as an additional equation which is coupled self-consistently to the plasma equations through the plasma currents.

The charge neutrality at equilibrium conditions (Z d =1, ϕ=0) leads to the following constraint:

(10)

We can also define the normalized dust charging frequency as

(11)

For nonadiabatic dust charge fluctuations (Shukla and Mamun 2002), the ratio 1/ν ch can be considered small but finite, and in the theory of adiabatic dust charge fluctuations we have 1/ν ch ≈0. Here we have

(12)

The influence of the dust charging rates on the propagation of low frequency DA waves is dependent on the dust charging frequency, ν ch , in comparison to the plasma frequency, ω pd . If the dust charging frequency becomes much greater than that of the plasma frequency, the dust charge reaches equilibrium value at each point. But for non-negligible values of 1/ν ch , the dust charge fluctuations play the role of a dissipative mechanism. Thus, the dust charge fluctuations modify the dynamical behavior of system and finally it can lead to the formation of collisionless shock waves (Ghosh et al. 2006).

3 Derivation of Burger equation

In order to investigate dynamical equation of nonlinear DA waves, we employ the standard reductive perturbation technique. In the reductive perturbation method, the main assumption is that ϕ 1≪1. This means that the perturbation theory is used for the study of small but finite amplitude limit. The advantage of small but finite amplitude limit is that we can clearly compare analytical analysis with numerical one. This limit also allows us to clearly identify the basic features of DA shock waves in the dusty plasma under consideration (please see Karpman et al. 2005, after Eq. (20) on p. 204). The stretched coordinates are defined as (Mace et al. 1991; Verheest 2000)

$$ \xi = \varepsilon(x - V_{0}t) ,\qquad \tau = \varepsilon^{2}t, $$
(13)

where ε is a real and small parameter which shows the strength of nonlinearity, and V 0 is the normalized phase velocity. The expansion of dependent variables are considered as

(14a)
(14b)
(14c)
(14d)
(14e)
(14f)

Substituting set of Eqs. (14a)–(14f) along with the stretched coordinates into Eqs. (2)–(4) and (9), and collecting the terms in different powers ofε, the lowest order of ε leads to

(15a)
(15b)

where b 1=(2κ i −1)/(2κ i −3), c 1=(2κ e −1)σ/(2κ e −3), d 1=d u /d d ,

The linear dispersion relation of system can be obtained from set of Eqs. (15a), (15b)

$$ V_{0} = \frac{1}{\sqrt{fc_{1} + (1 + f)b_{1} + d_{1}}} . $$
(16)

It is obvious that the dispersion relation of system is modified by the presence of dust charge fluctuation and suprathermality effects. If we set (κ e ,κ i )→∞ and d 1=0 in Eq. (16), it reduces to the familiar expression that obtained in (Rao et al. 1990; Ma and Liu 1997; Verheest et al. 2005), for Boltzmann ions and electrons, i.e., \(V_{0}^{2} = 1/[f\sigma + (1 + f)]\). Figure 1 shows that phase velocity present an increasing behavior with both electron and ion suprathermal index. The phase velocity values always are smaller than unit, i.e. it is subsonic. It is clear that in the limit of two component e-i plasma (i.e., f→∞), V 0→0. In an electron depleted dusty plasma (i.e., f→0), Eq. (16) is independent of κ e and σ. In the absence of charge fluctuation (i.e., d 1=0) dispersion relation is corresponded to the results of model of Baluku and Helberg (2008). Furthermore, Eq. (16) indicates that the actual DA speed in the plasma under consideration can be shown to be C dκ =ω pd λ Dg , where the global Debye length is given by

$$ \frac{1}{\lambda_{Dg}} = \frac{1}{\sqrt{\frac{4\pi n_{e0}e^{2}}{T_{e}}\frac{2\kappa_{e} - 1}{2\kappa_{e} - 3} + \frac{4\pi n_{i0}e^{2}}{T_{i}}\frac{2\kappa_{i} - 1}{2\kappa_{i} - 3} + \frac{4\pi Z_{d0}e^{2}n_{d0}d_{1}}{T_{i}}}}. $$
(17)

Equation (17) reduces to the usual expression for the Debye length when (κ e ,κ i )→∞ and d 1=0. In the Maxwellian case (i.e., (κ e ,κ i )→∞), Eq. (17) takes the form of Debye length which obtained by Mamun and Hassan (2000). In the absence of the charge variation, Eq. (17) recovers the result of (Baluku and Helberg 2008).

Fig. 1
figure 1

The variation of phase velocity with respect to electron and ion suprathermal index, for parameters: σ=0.1, r d =6 μm, Z d0=1×104

Full size image

Finally for the next power of ε, the conditions for annihilation of secular terms by using Eq. (16), lead to the Burgers equation

$$ \frac{\partial \phi_{1}}{\partial \tau} + A\phi_{1}\frac{\partial \phi_{1}}{\partial \xi} = B\frac{\partial^{2}\phi_{1}}{\partial \xi^{2}}, $$
(18)

where

Equation (18) is the Burgers equation which describes evolution of the nonlinear DA shock wave including the suprathermality effect of particles and dust charge fluctuation. The Burgers Eq. (18) has also a stationary shock wave solution which describes a wave moving without deformation at constant velocity U 0 (Karpman 1975). So, We are now interested in looking for the stationary shock wave solutions of (18) by introducing ζ=ξ−U 0 τ′ and τ′=τ, where U 0 is the shock speed (in the reference frame). This leads us to write (18), under the steady state condition , \(\frac{\partial}{\partial \tau'} = 0\) as

$$ - U_{0}\frac{\partial \phi_{1}}{\partial \zeta} + A\phi_{1} \frac{\partial \phi_{1}}{\partial \zeta} = B\frac{\partial^{2}\phi_{1}}{\partial \zeta^{2}} $$
(19)

It can be easily shown that (19) describes the shock waves (Karpman 1975; Hasegawa 1975), whose speed U 0 is related to the extreme values ϕ 1(−∞) and ϕ 1(∞) by \(\phi_{1}(\infty) - \phi_{1}( - \infty) = \frac{2U_{0}}{A}\). Thus under the condition that ϕ 1 is bounded at ζ=±∞, the shock wave solution of (19) is (Karpman 1975; Hasegawa 1975)

$$ \phi_{1} = \phi_{m}\biggl[ 1 - \tanh \biggl( \frac{\zeta}{L} \biggr) \biggr] , $$
(20)

where the thickness and amplitude of the shock wave are defined as L=2B/U 0 and ϕ m =U 0/A, respectively. It must be noted that the mutual balance between dissipation and nonlinearity leads to formation of this type of shock solution. It is clear that an increase in U 0 enhances the height of shock wave, and decreases its width.

4 Numerical results

In order to investigate the influence of the dust charge fluctuations and suprathermality effects on the basic properties of DA shock waves in this model, we have numerically analyzed the shock solution. The following parameters: Z d0=103–106, r d =1–6 μm, σ=0.01–0.1 have been chosen so that the nonadiabatic condition ω pd /ν ch ≠0 is fulfilled; these values of parameters are in accordance to Saturn’s rings (E-ring and F-ring) (Mendis and Rosenberg 1994; Smith et al. 1982). The results are displayed in Figs. 2, 3 and 4.

Fig. 2
figure 2

The profile of the DA shock, for different values of κ e ; where κ i =2, σ=0.1, r d =6 μm, Z d0=1×104

Full size image
Fig. 3
figure 3

The profile of the DA shock, for different values of κ i ; where κ e =2, σ=0.1, r d =6 μm, Z d0=1×104

Full size image
Fig. 4
figure 4

The influence of ion temperature on the DA shock structure, with (a) κ e =κ i =2 and (b) κ e =κ i =10; where r d =6 μm, Z d0=1×104

Full size image

It must be added that the effect of Jean frequency may be important when this frequency is comparable to ω pd . However one can neglect this frequency for dust acoustic wave satisfying in condition ω J ≪ω pd . In the present model, we found that \(\omega_{pd}/\omega_{J} = \sqrt{e^{2}Z_{d0}^{2}/Gm_{d}\varepsilon_{ \circ}} \ll 1\), thus the Jeans frequency is negligible.

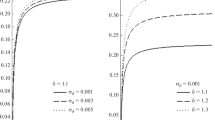
Figure 2 shows the effect of suprathermality of electrons on the shock structures via κ e value, when κ e increases from 2 to 3 and for κ i =2. The choice we have made clearly indicates what happens ifκ e increase from smaller to larger values. It can be seen that deviations of electrons from Maxwellian behavior, via a decrease in the suprathermal index κ e , leads to increase of the shock strength and decrease of its thickness. These results are the same as obtained by Tribeche and Bacha (2010) for arbitrary DA waves in a charge varying dusty plasma with suprathermal electrons.

The dependency of the DA shock amplitude and width on ion suprathermality is investigated in Fig. 3. It is found that a decrease in κ i enhances the amplitude of the shock front. This also means that deviations of ions from Maxwellian behavior lead to the existence of DA shock waves with larger amplitude. This is a result similar to that obtained by Tribeche et al. (2009) for DA waves in a charge variable dusty plasma with superthermal ions. The comparison of Figs. 2 and 3 shows that deviation from Maxwellian behavior leads to the narrower profile.

Also, similar results have been obtained for DA solitons by Baluku and Helberg (2008) for arbitrary amplitude DA solitary waves in a dusty plasma with superthermal ions and electrons.

To investigate the influence of ion temperature on the behavior of DA shock waves, we have plotted variation of ϕ 1 with respect to ζ and σ in Fig. 4, for different values of κ e and κ i . Where in Figs. 4a and 4b we have (κ e ,κ i )=(2,2) and (κ e ,κ i )=(10,10), respectively. It is clear that the DA shock amplitude decreases with σ. This shows that the ion temperature is destructive for the formation of DIA shock waves in such a dusty plasma, and may render its spatial less steeper. The comparison of Figs. 4a and 4b show that as deviations from Maxwellian behavior increases, via a decrease in the spectral indexes κ e and κ i , the influence of σ on DA shock profile becomes more important. Similar behavior is observed for dust ion acoustic in a charge varying dusty plasma with electrons having a high-energy-tail electron distribution (Alinejad et al. 2011) or having a vortex-like velocity distribution (Alinejad and Tribeche 2010). Moreover, these results are qualitatively similar to those obtained for DA in a charge variable dusty plasmas with Maxwell-Boltzmann or polytropic electrons and ions. However there are some quantitative differences, arising from the type of distribution function that we have chosen to obtain the number density of particles. Although the kappa distribution is a nonthermal distribution, but when one of the hot plasma species has a different nonthermal distribution, the results would be different. For instance here it is shown that only negative DA shock waves will be excited in this system. But, Zhang and Xue (2005) have investigated the properties of DA shock waves in a charge variable dusty plasma comprising nonthermal ions (satisfying Cairns distribution). They showed that for negative dust, positive DA shock waves could be found. This differences in results may be depends to deviation of the distribution function from Maxwellian. As for the kappa distribution the main change with respect to the Maxwellian would be restrict to the “tail” region, unlike the case of the Cairns distribution. A similar behavior also occurs for DA solitary waves which has described by Baluku and Helberg (2008).

5 Conclusion

The present study describe the properties and formation of weak amplitude DA shock waves in a charge variable dusty plasma whose constituents are cold dust fluid, super thermal ions and electrons.

A kappa distribution for electrons/ions is considered corresponding to deviation from the Maxwellian behavior through an increase in the suprathermal electrons/ions components and a concomitant decrease in the thermal part of the electron/ion velocity distribution function. It is found that as deviations of electrons from Maxwellian behavior increases, via a decrease in the suprathermal index κ e , the amplitude of DA shock wave increases, but it decreases the DA shock thickness. Also it is evidence that as the suprathermal character of ions is increased, the potential amplitude enhances. It is shown that deviation from Maxwellian behavior leads to the narrower profile. The influence of ion temperature on DA shock waves is enhancement of the amplitude of the shock front when σ is decreasing. We have also observed that as deviations from Maxwellian behavior increases, via a decrease in the suprathermal index κ e and κ i , the effect of σ on DA shock profile becomes more important. This shows that the ion temperature is destructive for the formation of DA shock waves in such dusty plasma.

The above results should be applicable to the formation of nonlinear DA shock wave structures in regions in which dust grains are embedded in a kappa distribution plasma, such as, Saturn’s magnetosphere. Furthermore they may also explain the strong spiky waveforms observed in auroral electric field measurements (Ergun et al. 1998) and already predicted by Lotko and Kennel (1983). Specially, according to the observations of both κ-distributed electrons and ions in Saturn’s magnetosphere (Krimigis et al. 1983; Schippers et al. 2008), these results may be applicable in description of the dust acoustic shock waves in Saturn’s magnetosphere.