Semi-supervised node classification via graph learning convolutional neural network

Abstract

Graph convolutional neural networks (GCNs) have become increasingly popular in recent times due to the emerging graph data in scenes such as social networks and recommendation systems. However, engineering graph data are often noisy and incomplete or even unavailable, making it challenging or impossible to implement the de facto GCNs method directly on them. Current efforts for tackling this issue either require an overparameterized model that is hard to scale, or simply re-weight the existing edges for different downward tasks. In this work, we tackle this problem through introducing a graph learning convolutional neural network (GLCNN), which can be employed on both Euclidean space data and non-Euclidean space data. The similarity matrix is learned by a supervised method in the graph learning layer of the GLCNN. Moreover, graph pooling and distilling operations are utilized to reduce over-fitting. Comparative experiments are done on three different datasets: citation dataset, knowledge graph dataset, and image dataset. Results demonstrate that the GLCNN can improve the accuracy of the semi-supervised node classification by mining useful relationships among nodes. The performance is more obvious especially on datasets of Euclidean space. Specifically, GLCNN outperforms the best baseline by 3.1% and 1.1% on MNIST and SVHN datasets. Moreover, the robustness is explored by adding noises on the edge of the graph. Sensitive analysis and visualizations are performed to demonstrate effects of some key parameters.

1 Introduction

Deep learning (DL) has achieved enormous success in the past ten years due to the increased GPU computing power, the much-expanded data scale, and the effectiveness of increasingly complex models in extracting information on the Euclidean space data. In recent years, the application of machine learning algorithms on graph data has received widespread attention, and the GCNs have been developed rapidly. It has been used in the recommendations system [1, 2], the image segmentation [3], and drug discovery [4] et al. However, GCNs can only be used when the graph structure of data is available. Most models assume that the initial graph structure can accurately reflect the relationship between nodes, however, real-world graph are not suitable for different downstream tasks due to the incomplete or presence of noise. Therefore, GCNs based on such idealized assumptions will inevitably lead to sub-optimal results. Neglecting that is an intrinsic shortcoming of many GCN methods.

Recently, Deng et al. [5] constructed a weighted graph in the process of graph embedding. They manually converted the initial attribute matrix into an attribute graph by selecting k-nearest-neighbors after the spectral graph clustering. This typical unsupervised method was highly subjective. Yu et al. [6] raised a graph-revised module using GCN. The change of the original graph structure was done by changing the weights of existing edges and adding new edges. The experiment proved that this module was effective when the graph was incomplete or when the labeling rate was low. However, it learned one fixed graph for all the subsequent GCN layers. More recently, Franceschi et al. [7] proposed an advanced method that could learn the parameters of GCN and the graph simultaneously by solving a bilevel program. The idea was inspiring, however, this approach suffered from a scalability problem. It needs to lean the ${N}^{2}$ parameters of the N-node graph. The existing methods that manually construct an adjacent matrix or learn a fixed adjacent matrix for the rest layer have a limited effect on the downstream task. In this paper, GLCNN for semi-supervised node classification is proposed. The network can be employed when the graph structure has large noise or when the adjacent relationship is unknown. The GLCNN contains the input layer, graph learning layer, and prediction layer. It can update the node representation and the adjacent matrix simultaneously in the graph learning layer. Through the graph distilling and pooling operations, it can reduce the over-fitting effect. The prediction layer outputs node labels, which allows the calculation of classification accuracy. The experiments show that the learned graph structure is effective especially on the Euclidean dataset.

We mainly have the following three contributions. First, the graph learning layer is defined to dynamically adjust the adjacent relationship, which is more effective in fully mining the hidden connection information in the graph. Second, graph distilling operation is defined to further remove noise. Experiments show that our method can achieve robustness at a low labeling rate. Lastly, GLCNN can handle datasets where the graph structure is not known such as images, and experiment results indicate its effectiveness. The codes used in our experiments will be uploaded at https://github.com/LeeKangjie after publication.

The next four sections are arranged as follows. Some related works about GCN and graph learning are listed in Section 2. The GLCNN details are interpreted in Section 3. The results of the experiments and comparison on different datasets are given in Section 4. The summary and outlook are made in the last section.

2 Related works

2.1 Graph convolutional neural networks

Most researches about GCN can be categorized into spectral-based and spatial-based methods [8]. They have all developed rapidly in recent years. For example, Monti et al. [9] proposed MoNet, a unified framework that could generalize the CNN architecture to non-Euclidean domains like manifolds and graphs. They showed that several existing non-Euclidean CNN methods could be regarded as specific examples of their framework. Kipf et al. [10] raised a scalable network for semi-supervised learning on graph data. It employed the 1st order truncation of Chebyshev polynomials of spectral graph convolutions. However, the computation was non-parallel and suffered from a Laplacian smoothing problem. Hamilton et al. [11] proposed GraphSAGE, which could generate node embeddings by sampling and aggregating the representations from its neighborhood. In order to overcome the limited range of neighborhood aggregation procedure, Xu et al. [12] proposed a JK-net inspired by the random walk. It could learn structure-aware node representations by leveraging different neighborhood ranges. However, it could not fully use the graph information by random-walk strategy. Petar et al. [13] presented graph attention networks (GATs) by assigning different weights to different neighborhoods. It leveraged a masked self-attentional layer without costly matrix operations. As the spectral-based GCNs cannot be directly implemented on the directed graph, Ma et al. [14] proposed an improved approach by making use of refined Laplacians, which had a stronger ability to extract features from directed graphs. In order to convert graph structure data into grid structure, Gao et al. [15] proposed a learnable graph convolutional layer (LGCL), which selected a fixed number of neighboring nodes when calculating each feature. However, it could not perform down-sampling on graphs and is mainly applied to generic graph data. To resolve the challenge of applying GCN on the dynamic graph, Pareja et al. [16] proposed EvolveGCN, which adjusted the model along the temporal dimension. Chen et al. [17] studied the shallow-structure problem of most GCN models and proposed the GCNII to relieve the problem of over-smoothing. To obtain a more efficient convolution layer, Fu et al. [18] introduced Hessian graph convolutional networks (HesGCN) and optimized the one-order spectral graph Hessian convolutions.

2.2 Graph learning methods

As for graph learning, when a graph structure is unavailable, a simple approach is to create a k-nearest neighbor (kNN) graph [19] using the measurement of the similarity between two nodes. For instance, Deng et al. [5] generated a kNN graph based on the l2-norm distance between the representations of two nodes. Tang et al. [20] devised a method to dynamically learn the graphs that could adapt to the underlying structure of node representations in various layers. However, the graph creation and parameter learning steps were independent. The graph could not guarantee to best facilitate GCN learning. Lately, more and more approaches to automatically build a graph is explored. Henaff et al. [21] proposed a fully connected network to learn the graph in a supervised manner. But the learning process was separated from the parameter learning in GCN, which could not guarantee to be useful to the downstream task. Jiang et al. [22] proposed a graph learning convolutional network (GLCN), which learned an optimal graph by integrating graph convolution and graph learning in one network architecture. But it could not deal with situations when the adjacent matrix was noisy. In order to use data of different graph structure as the input, Li et al. [23] raised a generalized and flexible GCN. It could learn a task-driven adaptive graph by learning the distance metric. The graph learning quality directly influences the semi-supervised classification task. Lin et al. [24] proposed a deep graph learning to find better node feature by learning the global structure and local structure simultaneously. In order to apply GCN-based graph learning on a large-scale graph, Yang et al. [25] presented Node2Grids to map the coupled graph data into grid-like data, which could save memory and computational resource. Pu et al. [26] proposed an innovative graph learning method that could incorporate node-side and observation-side knowledge together. It could improve the durability of graph learning on missing and incomplete graph data.

3 Methodology

We first present notation and preliminary knowledge of the graph theory and graph convolutional neural networks. We then describe the proposed GLCNN and its architecture, which is split into the input layer, graph learning layer, and prediction layer. A detailed explanation of the implementation details is given last.

3.1 Notation and preliminary

Consider a graph G which includes a node set $V=\left\{ v_{1},...,v_{N}\right\}$ and an edge set $E_{1,..,M}\subseteq {V}\times {V}$ , where N and M are the nodes and edges numbers. The connectivity relationship of the nodes in the graph can be expressed as the adjacent matrix A with a size of ${N}\times {N}$ . If nodes $v_{i}$ and $v_{j}$ are connected, $A_{i,j}$ is 1, otherwise, it is 0. The Laplacian matrix of the graph is calculated as $L=D-A$, where $D_{i,i}=\mathop { \sum }\nolimits _{j}A_{i,j}$. If $i\ne j$,$D_{i,j}=0$. The degree matrix D is used to perform the normalization of A as shown later.

GCNs are a very important type of machine learning model used on graph structure data. All GCNs have two common inputs. The first is the node representation matrix $H\subset \mathbb {R}^{{N \times n}}$, where n is the dimension of the node representation. The second is the adjacent matrix A. Given a training set $V_{train}$, the aim is to train a mapping function f, that is $f(H,A)\rightarrow Y$ , to minimize the loss function:

$$\begin{aligned} {Loss={ \sum \limits _{v \in V_{train}}{l ( f ( H,A ) _{v},y_{v} ) + {\varOmega } ( W ) }}} \end{aligned}$$

(1)

where W is the weight matrix in the mapping function f, $f(H,A)_{v}$ is the predicted label of all nodes in the training set. l is the loss function, which is commonly the cross-entropy loss. ${\varOmega }$ is the regularization function, which is used to prevent over-fitting. Otherwise the network will remember the training dataset and produce a large bias on the test datasets. For example, Kipf et al. [10] proposed a two-layer GCN as the mapping f, as shown in the following expression:

$$\begin{aligned} {f(H,A)={\mathrm{Softmax}(A^{*}\mathrm{Relu}(A^{*}HW_{1})W_{2})}} \end{aligned}$$

(2)

where$A^{*}=D^{-1/2}(A+I)D^{-1/2}$, D is the diagonal matrix with$D_{i,i}=1+\sum _{j}{A_{i,j} }$.

The major notations used in the present paper are summarized in Table 1.

Table 1 Major notations and description

3.2 GLCNN architecture

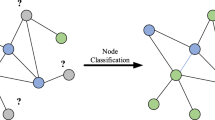
Some recognition tasks in the non-Euclidean domain might not have prior knowledge of graph structure. It is necessary to estimate a similarity matrix first [27]. The problem to be solved by the GLCNN can be described as follows. For data with a graph structure, it optimizes the graph structure by mining the association relationship and further applies the relationship to downstream tasks. For data without graph structure, it firstly uses kNN to build a graph and then optimizes the graph. The schematic diagram of the whole process is shown in Fig. 1.

Fig. 1

Schematic illustration of the overall process of GLCNN computation

The GLCNN is used to mine the similarity matrix and validate the effectiveness of the graph learning process. It contains the input layer, graph learning layer, and prediction layer as shown in Fig. 2. A more detailed description of each layer is provided in subsections.

Fig. 2

The architecture of the proposed method. From left to right, it includes an input layer, $n^{th}$ graph learning layers, and a prediction layer. The loss function includes two parts: node classification loss and graph learning loss

3.2.1 The input layer

The topological structures are rich sources of discriminative features. Some recognition tasks defined in non-Euclidean domains can make use of prior knowledge about graph structure [28]. However, many practical problems do not have such knowledge. Therefore, the input layer should be able to deal with two situations, that is, with and without a known adjacent matrix.

Currently, there are two types of methods for constructing the similarity matrix: unsupervised and supervised methods. The first step in unsupervised methods is to calculate the distance between features i and j:

$$\begin{aligned} {d(i,j)={{\Vert h_i-h_j\Vert }^2}} \end{aligned}$$

(3)

where $h_i$ and $h_j$ are the representative vectors of features i and j respectively. This is the simplest way to calculate the distance. It can also be calculated by first regularizing the features. After obtaining the distance value, it is necessary to calculate the strength of the relationship between nodes using a Gaussian diffusion kernel [29]:

$$\begin{aligned} {S(i,j)={\mathrm{exp}^{-d(i,j)/{\sigma }^2}}} \end{aligned}$$

(4)

where $\sigma$ is the variance of the distance. The advantage of this unsupervised method is that there is no need to label data. Therefore, it can be used to estimate the similarity between data with the same characteristics. However, the estimated similarity between features depends on the chosen kernel function and distance calculation criteria, which may not be suitable for specific classification tasks. Besides, the distance calculation method in the Euclidean space is not necessarily suitable for the calculation of the similarity in the non-Euclidean space, for example, some nodes with small distances calculated using (3) may not actually be connected. This is due to that the features used to calculate the distance may be unprocessed raw data that may not truly reflect the characteristics. For example, some physical connections are inherent, which are not related to similarity calculations. Therefore, the similarity matrix established through unsupervised methods is not suitable for the subsequent supervised learning process.

Therefore, we choose to use supervised methods to calculate the similarity between nodes. The calculation is carried out in the graph learning step inside the input layer structure we designed. The entire input layer is shown in Fig. 3.

Fig. 3

Input layer structure

The inputs are the initial $H_0$ and $A_0$. The outputs are $H_1$ and $A_1$. In the case when the initial $A_0$ is unavailable, kNN is used to construct $A_0$. Note that a modifying step is needed before outputting $A_1$. In kNN calculation, the distance between any two nodes is first calculated according to Formulas (4) and (5), and then only the top k closest values are retained as $A_0$:

$$\begin{aligned} A_0=\left\{ \begin{aligned} s_{ij},s_{ij}\in \mathrm{topK}(S_i), \\ 0, s_{ij}\notin \mathrm{topK}(S_i). \end{aligned} \right. \end{aligned}$$

(5)

where topK$(S_i)$ is the set of the top k points closest to $S_i$.

In the graph learning step, we use a single-layer neural network to calculate the similarity relationship:

$$\begin{aligned} {S_{ij}=\frac{\mathrm{exp}(\mathrm{ReLU}(a^T|H_i-H_j|))}{\sum _{j=1}^{n}{\mathrm{exp}(\mathrm{ReLU}(a^T|H_i-H_j|))}}} \end{aligned}$$

(6)

where a is the weight vector, which needs to be obtained through the back-propagation algorithm. Assuming $H_0\in \mathbb {R}^{n\times p}$ , then $a\in \mathbb {R}^{p\times 1}$ , ReLU is the single activation function in the neural network. $S_{ij}$ reflects the strength of the connection between nodes i and j.

When the input node representation has a large dimension, the vector a will have a large dimension and the calculation of $s_{ij}$ will be computationally intensive. To improve computational efficiency, we add a convolution (Conv) step before Graph learning step. We multiply $H_0$ by a low-dimensional embedding matrix $P\in \mathbb {R}^{p\times d}$ so that the input of Graph learning has a lower dimension d.

$$\begin{aligned} {{H_0^{*}}=H_0P} \end{aligned}$$

(7)

In the Modifying step, we sum the similarity matrix S and $A_0$ learned by Graph learning so that the output $A_1$ still contains the relationship information in $A_0$.

$$\begin{aligned} {A_1=A_0+{\gamma }_{1}S} \end{aligned}$$

(8)

where ${\gamma }_{1}$ is the weight coefficient between $A_0$ and S. In summary, the pseudo-code of the input layer is shown below. It uses a kind of nonlinear function to compute the neighborhood similarities between pairs.

3.2.2 The graph learning layer

The structure is shown in Fig. 4. Similarly, the adjacent matrix $A_{i-1}$ and node representation $H_{i-1}$ of the previous layer are used as the input, the adjacent matrix $A_i$ and node representation $H_i$ of the current i layer are the output. In addition to GNN operation, graph Distilling and Pooling steps are introduced in the layer to reduce the overfitting of the algorithm. The adjacent matrix of each layer can be dynamically changed, which can make it adaptive to the calculation of different layers.

Fig. 4

Graph learning architecture

The graph learning steps are the same as those of the input layer. The calculation of GNN adopts the graph convolution formula:

$$\begin{aligned} {Z_{i-1}=\mathrm{ReLU}(A_{i-1}^{*})H_{i-1}W_{i-1}} \end{aligned}$$

(9)

where $W_{i-1}$ is the weight matrix to be learned in this layer.

In the Distilling step, first, $A_{i-1}$ and $S_{i-1}$ are added in the graph learning step. Then the new $A_i$ is obtained through the following distillation formula:

$$\begin{aligned} {\overset{-}{A}_{i-1}=A_{i-1}+\gamma _{2}S_{i-1}} \end{aligned}$$

(10)

$$\begin{aligned} {A_i(p,q)=\mathrm{sparsemax}(\overset{-}{A}_{i-1}(p,q))=[\overset{-}{A}_{i-1}(p,q)-T(\overset{-}{A}_{i-1})]_+} \end{aligned}$$

(11)

where ${\gamma }_{2}$ is the weighting between $A_{i-1}$ and $S_{i-1}$, The sparsemax() function [30] returns all the values in the matrix that are greater than a certain threshold, and the remaining values all become 0, $[x]_+=max\{0,x\}$. T() is the distillation function, and returns the temperature value [31] that needs to be distilled according to the input matrix. Usually, the distillation temperature value is set to be a number that is proportional to the size of the input matrix. Assuming that the distillation function returns a constant temperature value of 0%, then $A_i=\overset{-}{A}_{i-1}$. If it returns a larger temperature value, such as 90%, the size of the adjacent matrix will be reduced by 90%, which means the largest 90% values in the matrix are removed. The distillation is an important step because it eliminates many weak connections in the adjacent matrix that deteriorate the accuracy and efficiency of subsequent calculations.

In the Pooling step, the node representation output by GNN is pooled bitwise. Assuming that $z_v\in Z_{i-1}$ is a node representation vector to be pooled and taking the jth bit of the vector as an example, the pooling step replaces the jth bit of this vector by the maximum value of the jth bit of all neighboring node representations. This calculation is expressed as follows.

$$\begin{aligned} {\overset{-}{h}_v(j)=\mathrm{max}(\{h_v(j),h_k(j),\forall h_k \in N(h_v)\})} \end{aligned}$$

(12)

where $N(h_v)$ is the set of all neighboring nodes of node $h_v$. The pooling step defined above is the same as the maximum pooling in the convolutional neural network. It does not need to rely on additional parameters, so it is easier to implement in graph convolution. In summary, the pseudo-code of the graph learning layer is shown in Algorithm 2.

3.2.3 The prediction layer

In the final layer, we employ the softmax classifier to classify the node label.

$$\begin{aligned} H_{out}=\mathrm{softmax}(A^{*}H^{*}W^{*}) \end{aligned}$$

(13)

where $H^*$ represents the input node representation, and $W^*$ represents the weight matrix to be trained in the prediction layer. The number of columns in $H_{out}$ is b, which is the same as the number of categories in the classification problem.

To train the neural network shown in Fig. 2, it is necessary to define a loss function, which is the combination of the node classification loss $L_{pred}$ and the graph learning loss $L_{gl}$: $L = L_{pred}+ L_{gl}$.

The node classification loss $L_{pred}$ is defined as the cross-entropy loss:

$$\begin{aligned} L_{pred}=-\sum \limits _{i\in Y_L}\sum \limits _{j=1}^{b}F_{ij}\mathrm{log} H_{ij}^{out} \end{aligned}$$

(14)

where $Y_L$ represents the set of nodes with labels in the classification problem, F is the mask matrix. If node i belongs to the class j, then $F_{ij}$ is 1, otherwise, it is 0.

The graph learning loss $L_{gl}$ is formulated based on two prior pieces of knowledge: (1) Sparsity: The useful association relationships in the graph structure are sparse; (2) Smoothness: nodes that have similar representations have a strong connection relationship, otherwise, they have a weak connection relationship. Hence the graph learning loss contains two parts:

$$\begin{aligned} {L_{gl}=\sum _{i,j=1}^{n}||h_i-h_j||_2^2S_{ij}+\gamma _3||S||_F^2} \end{aligned}$$

(15)

where $||.||_2$ represents the 2-norm of the vector, $||.||_F$ represents the Frobenius norm of the matrix. In the first part of the loss function, when the distance between node representations $h_i$ and $h_j$ is large, it is encouraged to learn a small $S_{ij}$ value. With this optimization, the network becomes smooth. The second part controls the sparsity of the learned S. The denser the network is, the larger the result of this part becomes. When the data scale is large, the running resources may be exhausted. In this case, the second part can be removed. For example, the second part needs to be removed when running Pubmed citation data.

4 Experiment and analysis

The effectiveness of the GLCNN is tested on both Euclidean datasets and non-Euclidean datasets. Firstly, we present the experiment setup. Then we compare the node classification results and perform an ablation study. Finally, parameter sensitivity analysis is conducted. All experiments are implemented on a Win10 professional server with 4 GPUs and 32 GB RAM.

4.1 Experiment setup

The experiments are carried out on two kinds of datasets. One of them is in non-Euclidean space, in which the adjacent matrix is known in advance. The other is image datasets [32] in Euclidean space such as MINIST and SVHN. Here we utilize the first one thousand images of the full public dataset. The numbers of the datasets are listed in Table 2. Each node in a citation dataset represents a paper, and the edge represents the citation relationship between papers. The class is the research field of different papers. The Pubmed data set is currently the data set with the lowest labeling rate, and it has nearly 20,000 nodes and is large in scale. It is closer to the real environment where there is a lot of data but the labeling rate is very low. In the knowledge graph, the node represents the text description of things, and the edges represent the relationship between things. The NELL dataset represents another situation, that is, the number of classes is large but the average number of data used for training in each class is small, which makes training on that data very challenging. In an image dataset, each node is an image, and the feature is the RGB value of the image pixel. Since the image dataset has no edge, one needs to generate the initial adjacent matrix according to kNN in advance. The choice of k is 10, which corresponds to ten digits of 0-9. The purpose of using image datasets is to verify the applicability of the similarity mining process proposed in the previous section.

Table 2 Details of the datasets used in present work

Figure 5 shows the image dataset, MNIST, which is a binary graph and SVHN, which is an image dataset with RGB three channels. Figure 5 (c) and (d) are the 2-dimensional visualizations of these two datasets using a dimension reduction algorithm. The ten colors represent ten numbers: 0-9. The dimension reduction is performed using the t-SNE algorithm [33]. It is a non-linear dimensionality reduction method, which finds the structure in the data based on the probability distribution of random walk on the neighborhood. It can be seen that images that have the same value trend to cluster together.

Fig. 5

Image data representations and t-SNE of MNIST, and SVHN. (a) MNIST. (b) SVHN. (c) t-SNE of MNIST.(d)t-SNE of SVHN

After tuning, the hyper-parameters are set as follows: the number of the graph learning layer is 1, dropout value is 0.6, weight decay is set to 1e-4 except for the case of Citeseer dataset, in which the weight decay is 1e-3. The last 10% of the similarity matrix value is set to 0 according to the descending order. The dimension of node representation embedding in the input layer is 70, and the dimension of GNN output in the graph learning layer is 30.

4.2 Node classification results

Table 3 summarizes the accuracy of the node classification results of different algorithms. The calculations of means and variances are based on the result of 20 runs. Transductive learning is used in this work because the node representation of the validation set and the test set have been used in training. In the table, n/a means that this method is not applicable for the image dataset in Euclidean space. The number in parentheses indicates that accuracy is calculated using the adjacent matrix constructed by kNN as input. The symbol - means that the accuracy cannot be obtained because their code is not public available.

Table 3 Results of node classification in terms of accuracies on various datasets in the transductive setting

It can be seen that Deepwalk and Planetoid have a relatively poor performance, because they are all random-walk based algorithms, which cannot effectively mine graph structure information. Compared with GCN, the accuracies of GLCNN are higher in most datasets. This advantage is more obvious on the Euclidean dataset. That is because our graph learning layer can learn the association relations useful for downstream classification tasks, and further, make the node representations of the output layer more distinctive. The performance of the GLCNN is better than that of the GAT in all datasets except Citeseer for the same reason, which further demonstrates its advantages in graph data representation and learning. JLGCN and Graphzoom all have a compression operation in learning node representation, which may lose part of the node information. They also have a process of dynamically adjusting the similarity matrix, but generally, they are still inferior to our algorithm. The GLCN algorithm cannot dynamically adjust the similarity relationship during the learning process. Although good results have been achieved on Cora and Citeseer, it still has certain limitations in processing Euclidean-space data, which our work is superior. Compared with HGAT, although the effect is not very prominent on graph datasets, significant progress has been made on image datasets. The possible reason is that the hierarchical method can better learn the node representation in non-Euclidean space. Most recently, some works like GCNII [17] are said to achieve the best results on the first three datasets in the table. However, they are pre-print work, which is lacks of validation. So we did not list them. In a nutshell, even though our algorithm could not achieve the best results on all non-Euclidean datasets, we believe it is at least a competitive one. And we emphasize it has a significant improvement on the Euclidean dataset compared with other graph neural networks, indicating the effectiveness of graph learning layer.

In addition to the accuracy, we also further compared the propagation model, the generation method of the adjacent matrix and the time complexity of the proposed method with the other GCN work as listed in Table 4. The propagation model is the main indicator that distinguishes different GCN algorithms. We briefly listed them in the table, the specific meaning of each formula can refer to the references. Different propagation models essentially result in different ways to handle the adjacent matrix. Whether the adjacent matrix A is directly given or calculated using the subsequent weighted method, it cannot be dynamically adjusted according to different downstream tasks in the multi-layer connection. The opposite is the adaptive method, where each layer dynamically adjusts the A structure. This is why our method is better than others. The time complexity in the table refers to the relationship between the running time of the algorithm and the node number N. It can be seen that the GAT-based methods need to calculate the attention layer $\alpha$, and the calculation time increases quadratically with the number of nodes N. Our proposed method and other GCN methods have a linear complexity.

Table 4 Comparison of different aspects of the proposed method

Before showing the learned similarity relationship, the input and the output of node representation are visualized to illustrate the mechanism of classification. Taking the Cora dataset as an example, the visualization are shown in Fig. 6. In the representation of output nodes, the separation between different classes is clearer than that of the input. Hence, the classification ability of the GLCNN algorithm in node representation and in semi-supervised classification is expected to be improved.

Fig. 6

t-SNE visualization of node representation of Cora. (a) Node representation of inputs. (b) Node representation of outputs

To illustrate the change of the similarity matrix after the graph learning layer intuitively, we use the heat map to visualize it, which is plotted in Fig. 7. In this case, only the values of the first 50 nodes are shown in the graph. The change of values of the adjacent matrix can be seen clearly in the two enlarged regions. This demonstrates that the graph learning layer can dynamically adjust the similarity matrix in the graph so that the subsequent node classification can have higher accuracy.

Fig. 7

Heat maps of the adjacent matrix of Cora. (a) The loaded similarity matrix. (b) The similarity matrix learned after the Graph learning layer

4.3 Ablation study

To illustrate the role of the graph learning layer, an ablation experiment is conducted to compare the accuracy of the GLCNN algorithm on three datasets with and without the learning layer.

Table 5 The comparative experiments on three different type datasets

It can be seen from Table 5 that the accuracy of classification decreased slightly after removing the graph learning layer, indicating the graph learning layer proposed in this work has a certain effect. The training and validation accuracies of GLCNN and GLCNN without graph learning layer on Cora dataset are plotted in Fig. 8. It can be seen the difference between the validation set and training set is smaller, which shows that the graph distilling and pooling can effectively improve the accuracy of similarity matrix mining by avoiding over-fitting.

Fig. 8

Algorithm training loss and accuracy curves. (a) GLCNN. (b) GLCNN-w/o graph learning layer

4.4 Parameter study

In order to assess the robustness of GLCNN on noisy graphs, we build graphs with random edge deletions or additions. The experiments are conducted on Cora and MNIST datasets. On the Cora dataset, the number of edges is randomly removed or added by 25%, 50%, and 75% of the original total number, respectively. On the MNIST dataset, we randomly add the number of edges by 5%, 15%, and 25% of the original total number, and remove the number of edges by 25%, 50%, and 75% of the original total number.

Testing accuracies of the GLCNN on various “noisy” Cora and MNIST datasets are plotted in Figs. 9 and 10 respectively. Results show that on the Cora dataset, the accuracies of both GLCNN and GCN algorithms decrease significantly with the deleted edges, but the declining speed of the GLCNN is lower than that of the GCN because the graph learning layer can offset part of the edge pruning effect. When new edges are added, the accuracy of the GLCNN remains nearly unchanged, while the accuracy of the GCN declines significantly, indicating that the GLCNN is much more robust than GCN. As for the MNIST dataset, contrary to our intuition, the test accuracy does not decrease monotonically with the number of deleted edges. The reason might be that for the data in this non-Euclidean space, the initial adjacency matrix is generated by the kNN algorithm, so it may contain a lot of invalid information. When the proportion of deleted edges increases to 75%, most of the invalid connections are filtered out. Although some effective connections are also likely to be filtered out, the remaining effective connections are enough to allow the algorithm to achieve higher accuracy. For the case with increased edges, both GLCNN and GCN show an obvious decreasing trend, however, the declining speed of GLCNN is slower than that of GCN, which shows that the graph learning layer still works, but the effect is not as large as that on Cora.

Fig. 9

The relationship between the test accuracy (±standard deviation) and (a) the ratio of the removed edges and (b) the ratio of the added edges on the Cora dataset

Fig. 10

The relationship between the test accuracy (±standard deviation) and (a) the ratio of the removed edges and (b) the ratio of the added edges on the MNIST dataset

The number of graph learning layers and distillation degree are two key parameters in GLCNN. In order to explore their influence on the accuracy of results, sensitivity analyses are conducted on two datasets. The number of layers varies from 1 to 2, and the distilling temperature value is set to be 5%, 10%, and 25% respectively.

Table 6 Impact of the number of layers and distillation degree on the accuracy of classification results

It can be seen from Table 6 that the classification accuracies of cases with two graph learning layers are not as good as that of the single layer. It may be due to the Laplacian smoothing phenomenon caused by twice convolution [37], which reduces the classification accuracy. When the distillation degree is 5%, the accuracy is less than that of 10%. Because many noises in the correlation are not removed. However, when the distillation degree is too large, for example, 25%, the accuracy rate shows a downward trend, possibly due to the fact that the useful connection information is also distilled away. The results of the bilevel graph learning layer on the MNIST dataset are different. The accuracy rate increases with the increased distillation degree, which indicates that the positive benefit of distillation is greater than the negative effect caused by Laplacian smoothing.

5 Conclusions and future work

In this paper, we present a similarity matrix learning method and establish a novel graph learning convolutional neural network. The experiment results verify the effectiveness of the GLCNN to the downstream node classification tasks. It can be implemented on both Euclidean and non-Euclidean datasets. In the graph learning layer, the node representation and similarity matrix can update simultaneously, which helps to mine the hidden connectivity and to boost the algorithm performance. Graph distilling and pooling operations are proposed to reduce over-fitting. The experiments show that GLCNN achieves competitive results among state-of-the-art methods. It obtains a relatively higher classification accuracy on most of the datasets, and the advantageous are more obvious on non-graph structured datasets. Future work can be carried out along the following directions. Firstly, the proposed GLCNN algorithm is only compared with the previous GCN algorithm on image datasets. There is still a big gap with the traditional CNN method, which is also the direction to be improved in the future. Secondly, for Euclidean datasets with an unknown category number, the k value of kNN in the input layer will have a great impact on downstream tasks. The development of a systematic approach to select k is also one of the directions of follow-up research. More recently, spiking neural network (SNN) is developed by imitating the communication mechanism of biological neurons [38, 39]. It is a highly energy-efficient network and suitable for hardware implantation. However, due to its discrete input, the training procedure is not as straightforward as that of the conventional neural networks. It has not been popularized in various tasks like CNN and is still in the development stage. Our method belongs to the conventional neural network, which uses straightforward backpropagation to train. Converting the architecture and weight of GCN to SNN directly could avoid the difficulty in training SNN. It might also be possible to combine the advantages of both and make our method run more efficiently on the hardware. It can be an interesting research direction in the future.