1 Introduction

At present, deep learning has performed well in solving computer vision [24], image processing [12], speech recognition [1] and other tasks [33]. Among different types of deep learning models, convolutional neural networks (CNNs) have been widely studied and applied because of its high performance in various tasks. LeCun et al. [20] and others established the basic framework of CNN model inspired by the cognitive mechanism of biological natural vision. Krizhevsky et al. [19] proposed the AlexNet network and won the championship in the 2012 ImageNet, making CNNs become the core algorithm model in image classification. After that, CNNs developed rapidly. Many CNNs models, such as ResNet [13], NasNet [33] and GoogleNet [27], have been proposed by researchers, which show strong recognition ability in target detection, digital classification and other tasks.

In particular, although CNNs have good performance and high efficiency, it also has great limitations. CNNs can only process data of the grid type. In the real world, the data we collect are often defined on irregular grids, even in non-Euclidean spaces, such as biomolecular networks, social networks, etc. Unlike image data and time series on regular grid, it is obvious that we can process these data better in the form of graph. However, there are some challenges in using CNNs to perform regular convolution operation in graph structure tasks. The convolution kernel of CNNs require that the number of adjacent nodes of each node remain unchanged, and the number of nodes is orderly. In graph structure data, each node has different number of adjacent nodes and the positions of nodes are different. In social networks, for example, each person has different relations. Therefore, it is impossible to directly use fixed rectangular filter to process graph structure data. For this reason, Researchers try to modify the convolution kernel to extract the features of irregular graph structure data and propose a variety of graph convolutional networks (GCNs) methods. Generally speaking, GCNs are divided into spatial-based and the spectral-based strategies. For spatial-based strategies, GCNs define convolution kernels directly on the connection relationship of each node, which is similar to the convolution kernel of traditional CNNs. Hamilton et al. [11] proposed a new representation of graph nodes by aggregating the features of neighbor nodes. Atwood and Towsley [3] proposed a diffusion based representation learning method, which extends CNNs to solve general graph structure data. For spectral-based strategies, the convolution operation on topological graph is realized by the theory of spectrum. Bruna et al. [4] proposed to define the graph convolution in the Fourier domain based on the characteristic decomposition of the graph Laplacian matrix. Besides, Defferrard et al. [7] proposed to get the filter through the approximate expansion of the Chebyshev polynomial of Laplacian, which reduced the computational complexity. Kipf and Welling [18] used the first-order approximation of the Chebyshev polynomial to get the kernel convolution, and proposed a simple graph convolution network.

The above GCNs have been widely used in various classification tasks, but these methods rarely pay attention to the development of graph structures. There is no doubt that one of the core of GCNs is the graph which can describe the neighborhood relationship of original data. A proper graph structure plays an important role in GCNs learning. In deep learning tasks, we often provide GCNs with a known graph structure, such as biomolecular network and social network. However, the graph structure obtained from domain knowledge may not be accurate or even available. For instance, in a social network, a user may have thousands of friends, but only a few close friends. When analyzing such social network data, it is not appropriate to create thousands of edges for the user to represent the nearest neighbor relationship. Therefore, how to construct a more suitable graph based on the known graph for GCNs classification is valuable. Futhermore, in some cases, the graph structure of the data may be unknown. We can use the traditional graph data model (such as k NN to build the graph) to obtain the graph structure of the data. But k NN only considers the binary relationship between data, and the data collected in reality often contain complex multivariate relationships. Complex relationships are simply represented as paired relationships,which can easily lead to the loss of important relevant information [32]. For the sake of overcoming the information loss problem of traditional graph model in the knowledge of complex multiple relationship, hypergraph model came into being. Yu et al. [29] proposed to generate a set of hyperedges for each image by changing the size of the neighborhood to achieve the image classification task. Jiang et al. [16] introduced a network evolution method based on a hypergraph model with multi-dimensional connections, and further explore the new relationship between data through the features extracted by graph convolution.

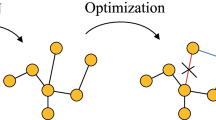
Inspired by these views, We consider the advantages of hypergraphs and how to create an ideal graph structure, and propose a novel GCNs of reconstructed graph structure with constrained Laplacian rank. First of all, we build a hypergraph of data as the initial adjacency matrix. Furthermore, by imposing some constraints, we learn a new graph matrix based on the initial graph matrix, making the new graph matrix more suitable for subsequent semi-supervised classification tasks on GCNs. Extensive experiments show that the graph generated by this method is superior to other common graphs in semi-supervised classification tasks and our method has the following advantages:

  • In view of the current GCNs methods, it is not necessarily the most appropriate to obtain graphs from the knowledge domain. This paper introduce a novel GCNs of reconstructed graph structure with constrained Laplacian rank. By introducing hypergraphs and Laplace rank constraints, we construct a graph structure that is more suitable for subsequent classification tasks of GCNs. Experiments on multiple data sets show that our proposed method has achieved more competitive results in semi-supervised classification tasks compared with the comparison method.

  • The traditional graph structure only considers the binary relationship between data. In practical application, there are many complex relationships between nodes. The traditional method of constructing graph can not describe the complex relationship between data effectively, which affects the quality of graph. In this paper, we use hypergraph to define the initial graph and consider the multiple relations of data.

The rest of this paper is arranged as follows. In Section 2, we briefly introduce the related knowledge of hypergraph learning and GCNs. In Section 3 and Section 4, we describe our proposed method of constructing optimal graph and related experimental results, respectively. Conclusion and future work are presented at the end of the paper.

2 Related work

In this section, we describe graph learning and hypergraph related knowledge, and further introduce a main model of GCNs.

2.1 Hypergraph and graph learning

With the progress of technology and the richness of social life, the real data collected is no longer a two-dimensional grid structure or even a simple one-dimensional structure. But high-dimensional complex structure data, such as biomolecular network data and commodity recommendation data, how to effectively analyze and apply these data with high-dimensional complex structure has become a challenge for current researches [14]. As a kind of generalized data structure, The graph is used to described the complicated node relations among samples. Many machine learning methods try to use graph structure to represent complex data [31]. For example, in the field of chemical analysis, people use graph structure to describe the relationship between chemical molecules [6], and in the commodity recommendation system, people use graph structure to describe the relationship among different people’s hobbies and commodities [21]. Real graph network is often high-dimensional and difficult to process. Researchers have proposed LLE [25], SDNE [28], Node2Vec [10] and other graph embedding methods. For example, Hu et al. [14] and Zhu et al. [31] designed novel graph embedding methods for SVM classification and spectral clustering, respectively. The traditional graph structure only considers the binary relationship between data. In practical application, the structure of data is often complex multiple relationship, so the traditional point-to-point graph structure cannot effectively describe the complex relationship between data, thus affects the quality of the graph. The hypergraph is the generalization of the common binary graph [30]. The hypergraph algorithm is initially applied to the very large-scale integrated electricity [2]. Zhou et al. [30] extended spectral clustering to hypergraphs and carried out tasks such as classification and clustering. In the deep learning task, Shi et al. [26] proposed to use hypergraph to establish the high-order correlation of visual data for CNNs vision classification . In this paper, hypergraph with multiple information is used to replace the ordinary graph of binary relation. A large number of literatures show that the richer the information learned from the data, the better the performance of real experiments [5, 30].

2.2 GCNs model

We review the GCNs for semi-supervised proposed by kipf and welling [18]. GCNs are similar to CNNs and other neural network architectures, including multiple graph convolutional hidden layers. Given data set \(\mathbf {X}=\{{{\textbf {x}}_{1}},{{\textbf {x}}_{2}},...,{{\textbf {x}}_{n}}\}\in {{\mathbb {R}}^{n\times d}}\), n and d represent the number of samples and features respectively. The graph adjacency matrix \(\mathbf {A}\in {{\mathbb {R}}^{n\times n}}\) corresponding to data set X. Then GCNs propagate layer by layer according to the following functions:

$$ \textbf{X}^{(k)} = \sigma (\boldsymbol{\tilde{D}}^{- \frac{1}{2}}\boldsymbol{\tilde{A}}\boldsymbol{\tilde{D}}^{-\frac{1}{2}} \textbf{X}^{(k-1)} \textbf{U}^{(k-1)}) , $$
(1)

where k is the number of hidden layers, \(\boldsymbol {\tilde {A}} = {\textbf {A}} + {{\textbf {I}}_{N}}\) is an adjacency matrix with a ring undirected graph, and D is a diagonal matrix with \({\tilde {\textbf {d}}_{i}} = \sum {_{j = 1}^{n}{{\tilde {\textbf {A}}}_{ij}}} \). \(\sigma (\centerdot )\) is an activation function. \({{\mathbf {U}}^{(k-1)}}\in {{\mathbb {R}}^{{{d}_{k-1}}\times {{d}_{k}}}}\) is defined the k − 1 layer’s weight matrix that changes iteratively with the number of layers. We apply softmax function to the output feature X(K) of the final K-layer to obtain the prediction label of each sample:

$$ \mathbf{P}=\text{softmax}(\mathbf{X}^{(K)}), $$
(2)

where \(\mathbf {P}\in \mathbb {R}^{n\times c}\) is the predicted label matrix, c is the number of real classes, and Pi is the prediction label of the i-th sample. For semi-supervised classification tasks, The weight matrices {U1,U2,...,UK} are updated by the cross entropy loss function, which is as follows:

$$ \begin{array}{l} Loss=\sum\limits_{i\in \mathbf{L}}\sum\limits_{j=1}^{c} \tilde{p}_{ij} \ln p_{ij}, \end{array} $$
(3)

where pij represents the i-th label predicted as j-th class and \(\tilde {p}_{ij}\) shows the i-th belonging to the real j-th class. and L is the set of labeled samples.

3 Our method

In this section, for the convenience of understanding, we define some notations in this paper, and then describe the proposed method in Section 3.2, Section 3.3, respectively. Besides, we introduce the corresponding optimization steps in Section 3.4.

3.1 Notations

For the convenience of understanding, we have the following definitions. For a matrix S, the i-th row and the i,j-th of matrix S are denoted as si and sij. We denote the Frobenius norm of matrix S as \(||\mathbf {S}||_{F} = \sqrt {\sum \nolimits _{ij} |s_{ij}|^{2}}\). Finally, we denote ST and tr(S) as the transpose of matrix S and the trace of matrix S, respectively.

3.2 Initial graph

Graph representation learning is widely used in machine learning and artificial intelligence tasks. However, the traditional graph structure has some limitations in the expression of data correlation. Data correlation may be more complex than point-to-point relationship. The traditional graph structure modeling does not describe the complex relationship between data sufficiently [30]. In this case, the traditional graph restricts the application of graph convolution neural network. For the sake of overcoming this limitation, hypergraph model came into being [30].

Hypergraph \(\textbf {G} = \left (\textbf {V},\textbf {E},\textbf {W} \right )\) contains three parts: vertex set V, hyperedge set E, and hyperedge weight matrix W. it is defined that hyperedge e has a weight w(e). the link relationship of hypergraph G is expressed as the correlation matrix \(\textbf {H} \in \mathbb {R}^{\left | V \right |\times \left | E \right |}\), which is defined as follows:

$$ h(v,e)=\left\{ \begin{array}{ll} 1 \qquad v\in e, \\ 0 \qquad v\notin e. \end{array} \right. $$
(4)

The above formula shows that if a vertex v is located in a hyperedge e, then h(v,e) = 1, otherwise h(v,e) = 0. According to the definition of correlation matrix, the degree matrix of hypergraph vertex and hyperedge can be further expressed as:

$$ \begin{array}{l} d\left( v \right) = \sum\limits_{e \in \textbf{E}} {w(e)} {h}(v,e)\\ \delta (e) = \sum\limits_{v \in\textbf{V}} {{{h}}(v,e)} . \end{array} $$
(5)

Furthermore, we define two diagonal matrices Dv and De to represent the diagonal degree matrix of hypergraph vertex and hyperedge respectively. Based on spectral graph theory and literature knowledge [30] , we define the adjacency matrix A of hypergraph as follows:

$$ \begin{array}{l} \textbf{A} = \textbf{HW} \textbf{H}^{T} - \textbf{D}_{v}, \end{array} $$
(6)

In this paper, the diagonal elements of W are all defined as one. Hypergraph has been proved to be able to completely represent the relationship between objects compared with ordinary graph [26, 30]. In this paper, we choose hypergraph as the initial graph adjacency matrix to reserve the multivariate relationship of data.

3.3 Adaptive graph learning

In graph learning theory, many works have proposed how to design a high quality graph structure. Nie et al. introduced the CLR method to learn the similarity matrix of data for clustering task and achieved excellent results [23]. In this paper, we use hypergraph as initial adjacency matrix \(\mathbf {A}\in {{\mathbb {R}}^{n\times n}}\) and CLR model to learn a graph matrix \(\mathbf {S}\in {{\mathbb {R}}^{n\times n}}\) more suitable for our subsequent semi-supervised classification tasks on GCNs. First, we define the minimum loss function between the optimal graph S and the initial graph A by establishing the l2-norm distance formula, that is, to minimize the following regularization terms. Besides, it is worth considering that some rows of the matrix S obtained in the above formula may be all zero. We construct the constraint condition \({{\textbf {s}}_{i}^{T}}{\textbf {1}} = 1\), thus we have:

$$ \begin{array}{l} \min\limits_{\textbf{S}} \left\| \textbf{S} - \textbf{A} \right\|_{F}^{2} .\\ s.t.\quad \textbf{s}_{i}^{T} \textbf{1} = 1,\textbf{s}_{i} \ge 0 \end{array} $$
(7)

In order to allow the adjacency matrix suitable for classification tasks, we apply Laplacian rank constraint rank(LS) = n − c to the matrix S. According to the properties of Laplace matrix, the number of zero eigenvalues of Laplace matrix LS is equal to the number of connected domains of affinity matrix. So the adjacency matrix just has c connected components. We can get:

$$ \begin{array}{l} \underset{\mathbf{S}}{\min} \left\| \mathbf{S}-\mathbf{A} \right\|_{F}^{2} . \\ s.t. \quad \textbf{s}_{i}^{T} \textbf{1} = 1, \textbf{s}_{i} \ge 0, rank(\textbf{L}_{S}) = n - c \end{array} $$
(8)

Because the rank constraint to matrix S is a complex constraints, in order to facilitate the subsequent optimization, according to the literature method [22, 23], it is assumed that ωi is the i-th smallest eigenvalue of Laplacian matrix LS. Since LS is a semi-positive definite matrix, if there is a sufficiently large value λ, Eq. (8) can be further equivalent to:

$$ \begin{array}{l} \underset{\mathbf{S}}{\min} \left\| \mathbf{S}-\mathbf{A} \right\|_{F}^{2}+2\lambda \sum\limits_{i}^{c} \omega_{i} . \\ s.t.\quad \textbf{s}_{i}^{T} \textbf{1} = 1, \textbf{s}_{i} \ge 0 \end{array} $$
(9)

Further, according to KyFan’s Theorem [8], we know that \(\sum \limits _{i}^{c} \omega _{i}=\underset {\mathbf {Y}^{T}\mathbf {Y}=\mathbf {I}} {\min \limits } tr(\mathbf {Y}^{T} \mathbf {L}_{S} \mathbf {Y})\) and \(\mathbf {Y}\in \mathbb {R}^{n\times c}\), and finally we get our objective function as follows:

$$ \begin{array}{l} \min\limits_{\textbf{S},\textbf{Y}} \left\| \textbf{S} - \textbf{A} \right\|_{F}^{2} + 2\lambda tr(\textbf{Y}^{T} \textbf{L}S \textbf{Y}) ,\\ s.t. \textbf{s}_{i}^{T} \textbf{1} = 1, \textbf{s}_{i} \ge 0, \mathbf{Y}^{T} \mathbf{Y}=\mathbf{I} \end{array}\\ $$
(10)

where the matrix S is a higher quality graph, A is the initial adjacency matrix introduced in Section 3.2 and LS is the Laplace matrix about the matrix S.

Based on the above objective function (10) , we can get an ideal matrix S by introducing S into GCNs model for classification task, Therefore, the convolution layer of GCNs changes as follows:

$$ \textbf{X}^{(k)} = \sigma (\boldsymbol{\tilde{D}}^{- \frac{1}{2}} \textbf{S} \boldsymbol{\tilde{D}}^{- \frac{1}{2}} \textbf{X}^{(k-1)} \textbf{U}^{(k-1)}) , $$
(11)

where S represents a new graph structure that is more suitable for subsequent classification tasks. It is obtained by alternating iterative optimization of Eq. (10), and D is a diagonal matrix with \(\tilde {\textbf {d}}_{i} = {\sum }_{j = 1}^{n} \textbf {S}_{ij}\).

3.4 Optimization

In this part, we mainly optimize and solve the objective function Eq. (10) to get the final matrix S.

  1. 1)

    Optimize Y by fixing S

    When S is fixed, the objective function Eq. (10) becomes:

    $$ \begin{array}{l} \underset{\mathbf{Y}}{\min} tr(\mathbf{Y}^{T} \mathbf{L}_{S} \mathbf{Y}) , \\ s.t. \mathbf{Y}^{T} \mathbf{Y}=\mathbf{I} \end{array} $$
    (12)

    The closed form solution of Y consists of c eigenvectors corresponding to c minimum eigenvalues of LS.

  2. 2)

    Optimize S by fixing Y

    When Y is fixed, for the second term in the formula, we can get:

    $$ \begin{array}{l} tr(\textbf{Y}^{T} \textbf{L}_{S} \textbf{Y}) =\frac{1}{2}\sum\limits_{i,j} \left\| \textbf{y}_{i} - \textbf{y}_{j} \right\|_{2}^{2}{s_{ij}} . \end{array} $$
    (13)

It is easy to understand that the value of matrix S is independent for each i. for Eq. (11), it is expanded by components as follows:

$$ \begin{array}{l} \min\limits_{\textbf{S}} \sum\limits_{j} (s_{ij} - a_{ij})^{2} + \lambda \sum\limits_{j} \left\| \textbf{y}_{i} - \textbf{y}_{j} \right\|_{2}^{2}{s_{ij}} .\\ s.t. \textbf{s}_{i}^{T} \textbf{1} = 1,{s_{ij}} \ge 0 \end{array} $$
(14)

We define vector \(\textbf {u}_{i} = \left \|\textbf {y}_{i} - \textbf {y}_{j} \right \|_{2}^{2}\), and the above formula is expanded by vector as follows:

$$ \begin{array}{l} \min\limits_{\textbf{S}} \left\| \textbf{s}_{i} - (\textbf{a}_{i} - \frac{\lambda}{2} \textbf{u}_{i}) \right\|_{2}^{2} .\\ s.t. \textbf{s}_{i}^{T} \textbf{1} = 1,{s_{ij}} \ge 0 \end{array} $$
(15)

Equation (15) can be solved by an iterative algorithm [15]. To sum up, we optimize and obtain the ideal graph S for semi-supervised classification on GCNs, and the related pseudo code is described in algorithm 1.

figure a

4 Experimental

We set up several groups of experiments to verify the performance of our proposed method. In Section 4.1 , we introduce the data sets and experimental methods used in the experiment, and in Section 4.2 , based on the experimental results, we analyze the superiority of the proposed method.

4.1 Datasets and experimental methods

To verify the performance of the proposed method on classification tasks, we test it on 10 real datasets, including the handwriting recognition datasets (MinistData05 and MinistData10), sound datasets (Waveform), etc. We describe information about all data sets in Table 1 , and the public data sets were collected from UCI Machine Learning Repository Footnote 1 and the CSDN blog Footnote 2 .

Table 1 Details of the public datasets
Full size table

About the experimental setup, we refer to some of the experimental settings of the previous work [9, 18]. Because of the different sizes of data sets, for all data sets, we randomly selected 10%, 20% and 30% samples as labeled samples, and used another 10% samples as validation samples. The remaining 80%, 70% and 60% were used as test samples. We use the Adam optimization method [17] to define that the number of training iterations using GCNs model is no more than 200, and set the learning rate to 0.01. If the cross entropy loss value of the validation set remains unchanged for 20 consecutive times, the training is stopped. Besides, we set dropout rate to 0.5. For the comparison methods, we set up KNN-GCN (KGCN) and Hypergraph-GCN (HGCN) methods respectively. For the KGCN method, k NN method is used to define the graph adjacency matrix of data, while the HGCN method uses Section 3.2 method to define the graph adjacency matrix of data. In addition, we set the neighborhood size of all datasets to 15. We mainly used ACC as the evaluation index of the experiment, and all the reported results were the average results with different training, verification and test data segmentation in 10 times.

4.2 Experiment results

The experiment results of the comparison methods KGCN, HGCN and the proposed method in this paper are shown in Table 2 and Fig. 1 respectively. Table 2 shows the average accuracy and the corresponding standard deviation of all models for 10 datasets under three different data partitions. It can be clearly seen that our proposed model has achieved the best or more advantageous results in all data sets. For example, For Musk2 datasets, when the label rate is 10%, our method is higher than HGCN and KGCN by 0.16% and 0.08% respectively, and when the label rate is 20%, our method is higher than HGCN and KGCN by 0.25% and 0.17% respectively. Besides, with the label rate growing up, the classification performance of our method is also improving. In addition, the accuracy of our method is 81.19%, 81.48%, 85.02% and 97.26% on Chess, Waveform, Ministdata10 and Ozone datasets, respectively. This further shows that our method has excellent performance on semi-supervised classification tasks. This is because this paper not only considers the multiple information between the data, but adaptively assigns the optimal neighborhood to each node through the Laplacian rank constraint. Finally, we get the most suitable data graph representation matrix for GCNs.

Table 2 Mean classification results (ACC ± Std (%)) under 10 different datasets, and the best performance are indicated by bold
Full size table
Fig. 1
figure 1

2D T-SNE visualization of the features output by KGCN, HGCN and our proposed method are performed on Dig1-10 dataset and Ministdata10 dataset

Full size image

Figure 1 shows the 2D T-SNE visualization with the convolution output feature of KGCN, HGCN and our method on Dig1-10 dataset and Ministdata10 dataset respectively. Through comparison, the data distribution of different types is more clear in our method, while several types of data distribution in KGCN show aggregation distribution, which represents that our method has better performance in graph node representation and semi-supervised classification tasks.

5 Conclusion

We propose a novel GCN of reconstructed graph structure with constrained Laplacian rank in this paper. First of all, we use hypergraph with complex multivariate relations to establish the initial graph between data. Based on the initial graph, we construct a new graph representation matrix which is more suitable for semi-supervised classification tasks on GCNs. Different from the previous methods, Our method is more general, especially when the graph structure of data is missing and unavailable. The experimental results on 10 real datasets show that the method has excellent performance compared with the comparison methods. In future work, we will try to embed the graph learning method proposed in this paper into the hidden layer of GCNs, so as to dynamically adjust the graph representation matrix in each iteration. In addition, we can build a better adaptive graph model to improve the performance and practicability for semi-supervised classification on GCNs.