Chaotic arithmetic optimization algorithm

Abstract

Arithmetic Optimization Algorithm (AOA) is a meta-heuristic algorithm. Its main idea is to use the distribution behavior of the four main mathematical operators of addition(A), subtraction(S), multiplication(M) and division(D). Chaotic mapping strategy was introduced into the optimization process of AOA. Firstly, ten chaotic maps are separately embedded into two parameter Arithmetic Optimization Accelerator (MOA) and Arithmetic Optimization Probability (MOP) that affect the exploration and balance of AOA so as to enhance its ergodicity and non-repeatability, and improve its convergence speed and accuracy. Then a combination test was carried out by embedding ten chaotic maps into MOA and MOP at the same time, and their advantages and disadvantages were compared with the chaotic maps embedded separately. 26 benchmark functions in CEC-BC-2017 are used to examine the performance of the proposed chaotic arithmetic optimization algorithm (CAOA). Finally, four engineering design issues are optimized, involving three-bar truss design problem, welded beam design problem, pressure vessel design problem and spring design problem. The experimental results reveal that CAOA can obviously solve the function optimization and engineering optimization problems. AOA based on the chaotic interference factors has the merit of balancing the exploration and exploitation in the optimization process and enhances the convergence accuracy.

1 Introduction

In recent decades, with the development of society, a series of problems and challenges have arisen, and people’s demand for reliable optimization technology is also increasing [1]. Optimization is the process of finding the best solution among all available solutions for a specific problem. Considering the nature of optimization algorithms [2], these algorithms can be roughly divided into two kinds, namely definite algorithms and random intelligent algorithms [3]. In the case of a deterministic algorithm, if the initial value is the same when solving the same problem, the same solution will be produced. These are gradient searching methods, strictly towards the optimal solution. Contrary to deterministic algorithms, haphazard intelligent algorithms are usually non-gradient techniques, in which irregular steps are used to obtain the optimal value. In this case, the optimization process is repetitive in any situation. Random intelligent optimization algorithms can be further divided into heuristic algorithms and meta-heuristic algorithms [3]. As the name implies, heuristic algorithm is the course of finding a solution through trial and error method [4]. Meta-heuristic optimization algorithms have two vital searching tactics: exploration and exploitation [5]. Exploration is the ability to probe the searching room on a global scale. When the algorithm tries to find a promising area in the searching space as widely as possible, the exploration phase occurs [6]. This capability is related to avoiding partial optima and solving partial optima. On the contrary, the development is to explore the vicinity to improve the local optimization ability [7]. The outstanding performance of the algorithm requires an apposite balance between these two traits [8,9,10,11]. All swarm-based intelligent optimization algorithms adopt these traits, but use unequal operation operators and searching mechanisms. Many heuristic algorithms are utilized in the field of optimization. For instance, the Bat Swarm Optimization Algorithm (BSO) [5], Hill Climbing [6] and Simulated Annealing [12]. In short, the idea of meta-heuristic algorithm is to use the prior knowledge of random search to solve the optimization problem randomly. This is an iterative optimization process, starting from a random initial solution and then randomly exploring and using the searching space with a clearly probability. So far, many meta-heuristic algorithms have been proposed by scholars such as Particle Swarm Optimization (PSO) [13], Genetic Algorithm (GA) [14], Rat Swarm Optimizer (RSO) [15], Archimedes Optimization Algorithm(AOA) [16], Equilibrium Optimizer (EO) [17], Ant lion optimizer (ALO) [18, 19], Gravitational Search Algorithm (GSA) [20], Harmony Search (HS) [21], Covariance Matrix Adaptive Evolution Strategy (CMA-ES) [22], Butterfly Optimization Algorithm (BOA) [23], Gray Wolf Optimization (GWO) [24] and Grasshopper Optimization Algorithm (GOA) [25], and so on.

With the continuous research and development of nonlinear theory, chaos theory has been widely used to improve exploration and exploitation [26]. As one of the characteristics of nonlinear systems, chaos is defined as randomness generated by simple real systems in the field of mathematics [27, 28]. So far, chaos theory has successfully solved the premature convergence problem of many meta-heuristic algorithms [29, 30]. Some scholars have added chaos mapping mechanism to different meta-heuristic algorithms to enhance the algorithm’s ability to search for optimal solutions, enhance random diversification and strengthen the ability to achieve optimal or sub-optimal solutions in complex multi-modal situations [31]. In fact, many algorithms have been improved by using chaotic mapping. Hassan, B.A integrates the chaotic forms of the sine cosine algorithm (SCA) and the firefly algorithm (FF), and proposes the chaotic sine cosine firefly algorithm to improve the convergence speed and efficiency [17]. Juliano Pierezan et al. proposed an improved COA (MCOA) method based on the chaotic sequence generated by Tinkerbell mapping to adjust the scattering and correlation probability [32]. M.S. Sanaj et al. embedded chaotic mapping in the squirrel search algorithm, and proposed four derivative search behaviors, which significantly improved the convergence speed and accuracy [33]. In order to enhance the capability of the water cycle algorithm (WCA), A. A. Heidari proposed a method of incorporating chaotic patterns in the random process of WCA [34]. S. Gupta proposed a chaotic grey wolf optimizer (GWO) based on opposition (OCS-GWO), which improves the performance of GWO [35]. S. Saha et al. proposed a quasi-opposite chaotic ant colony optimizer (QOCALO) for solving global optimization problems [36]. Gandomi et al. introduced chaos in the variant particle swarm optimization (PSO) algorithm to enhance the global search capability [37]. Gandomi et al. used chaotic mapping to adjust the gravitational coefficient and light absorption coefficient of the Firefly algorithm (FA) [29]. Arora et al. replaced the chaotic number to control the switching probability of the global and local search capabilities, and improved the performance of the butterfly optimization algorithm [38]. Han et al. used chaos to generate noisy signals combined with genetic algorithms and proved its effectiveness in reducing different types of noise [39]. Chen et al. proposed a WOA based on the quasi-opposite learning chaos mechanism (OBCWOA). Firstly, the chaos mechanism was used to generate the initial value to improve the convergence speed of the algorithm. Then the learning method based on opposition was used to balance the exploration and exploitation capabilities of the algorithm [27]. Saha et al. simplified the basic symbiosis search algorithm (SOS) and incorporated chaos into the local searching to form a chaotic SOS (CSOS), which improved the optimization accuracy and convergence mobility of the SOS algorithm, which have successfully solved the real-world power system problems [28]. Yu et al. controlled the steps of chaotic mapping through thresholds, and used the velocity inertia weights to synchronize the speed of the agents. This improves the stability and convergence speed of the bat algorithm. Finally, it was excellently applied to three engineering optimization problems [31].You et al. used chaotic sequences to obtain dynamic parameter settings in DE, and designed a chaotic local search (CLS) operator to solve DED problem to help DE effectively avoid premature convergence [40, 41]. Pan et al. proposed a chaotic local search algorithm with a probabilistic jumping scheme, and embedded it into the proposed harmony search (HS) algorithm to enhance its local search ability [42]. Ewees et al. integrated chaotic behavior into the locust optimization algorithm (GOA) to form the chaotic locust optimization algorithm (CGOA), which was used as a trainer for learning multi-layer perceptual neural networks (MLPNN) to improve its prediction accuracy [43]. Talatahari et al. used different chaotic operators to improve the movement steps of the imperialist competition algorithm and proved its superiority [44]. Talatahari et al. introduced chaos into the charging system to increase its global search mobility to achieve better global optimization [45]. Alatas used chaotic mapping to change the Big Bang, Big Crunch stage of the Big Crunch optimization algorithm, and achieved good results [28, 46]. In the artificial bee colony (ABC) algorithm, Wu et al. used chaotic searching behavior on the candidate food positions generated to improve the convergence characteristics and prevent ABC from falling into local optimum [47]. Jordehi embeds the chaotic map into the artificial immune algorithm to alleviate its premature convergence problem [48]. Li et al. used chaotic sequences to replace the random parameters in the catfish particle swarm algorithm, which greatly improved its performance [49]. Saremi adopts chaos operators to define the probability of biogeographic optimization algorithm selection, emigration and mutation, and the algorithm produces high performance [50]. Xiao et al. mapped chaos to the gravitational constant in the gravity search algorithm (GSA), avoiding the problem of premature convergence [51]. Niknam et al. improved the shuffled frog-leapfrog algorithm (SFLA) by using chaotic mapping to solve the multi-objective OPF problem [52]. Dharmbir Prasad et al. embedded the chaotic map into two parameters of whale optimization algorithm (WOA) to solve OPF problem better [53]. Gandomi et al. proposed four different chaotic bat algorithm variants for global optimization [54]. Mukherjee et al. used the chaotic krill algorithm to solve the optimal reactive power dispatch (ORPD) problem of the power system [55]. In addition, the chaos theory has applications in cryptography [56, 57], DNA computing [58], image processing [59], non-linear circuits [60], etc. All these attempts have proved that in different fields of engineering application, this newly constructed algorithm has better performance and higher beneficial accuracy than its standard algorithm.

Arithmetic Optimization Algorithm (AOA) is a meta-heuristic algorithm that its main idea is to use the distribution behavior of the four main mathematical operators of addition(A), subtraction(S), multiplication(M) and division(D) [1]. This paper integrates 10 chaotic maps into AOA so as to extensively study the effectiveness of chaos lore in improving the exploration and exploitation. Our main intention is to map the chaotic sequence into two key parameters of AOA. Various chaotic mapping operators have been proposed to replace linear decreasing or increasing sequences, in this way to balance the exploration and exploitation of AOA. It aims to speed up the global convergence speed and prevent the algorithm from falling into the local optimum. Firstly, 10 chaotic maps are embedded into MOA and MOP respectively, and then they are embedded in MOA and MOP at the same time. Then 26 test functions in CEC-2017 are compared and optimized. At the same time, some winning algorithms optimized for CEC2017 are selected for comparison. Finally, four engineering design issues are optimized, involving three-bar truss design problem, welded beam design problem, pressure vessel design problem and spring design problem. The simulation results show that the improved algorithm has obvious advantages compared with the original algorithm.

2 Basic principles of arithmetic optimization algorithm (AOA)

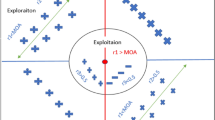
The swarm-based algorithm starts its optimization process from a set of randomly generated candidate solutions. This set of generated solutions is incrementally improved via some optimization rules, and iteratively evaluated through a specific objective function. Since the swarm-based algorithm seeks to find the optimal solution to the optimization problem randomly, it cannot guarantee that one solution will be obtained in one run. However, for a given problem, through a sufficient number of random solutions and optimization iterations, the probability of obtaining the global optimal solution increases [23]. The arithmetic optimization algorithm (AOA) is proposed through the arithmetic operators in mathematical operations, namely addition (+), subtraction (−), multiplication (x) and division (/). AOA is a swarm-based meta-heuristic algorithm that can solve optimization problems without calculating its derivatives. Arithmetic is not only a basic part of number theory, but also the cornerstone of modern mathematics, similar to algebra, geometry, analysis. Arithmetic operators (addition, subtraction, multiplication, and division) are usually used to study numbers and are a traditional and classic calculation method [27]. We use these simple operators as mathematical optimization ideas to determine the best elements that meet certain criteria from a set of candidate solutions The use of arithmetic operators in arithmetic problems is the main inspiration proposed by AOA. In the following subsections, we will discuss the specific influence of the arithmetic operators (addition, subtraction, multiplication and division) in the arithmetic optimization algorithm (AOA) on the algorithm. Figure 2 shows the search strategy and hierarchical structure of arithmetic operators from outside to inside.

• (1) Initialization phase

The optimization process of the arithmetic optimization algorithm (AOA) starts with a set of randomly generated candidate solutions, which is shown in Eq. (1). In the optimization process, an optimal candidate solution is obtained in each iteration, and the optimal solution is regarded as obtained optimal solution or the solution close to the optimal solution so far.

$$ X=\left(\begin{array}{ccc}{x}_{1,1}& \dots & {x}_{1,n}\\ {}\vdots & \ddots & \vdots \\ {}{x}_{N,1}& \cdots & {x}_{N,n}\end{array}\right) $$

(1)

Before AOA starts to work, it first enters the searching phase, that is to say the exploration or exploitation phase. Therefore, the mathematical optimization accelerator (MOA) determines its searching phase through calculation. The calculation formula is described as follows.

$$ MOA\left(C\_ Iter\right)=\mathit{\operatorname{Min}}+C\_ Iter\times \left(\frac{\mathit{\operatorname{Max}}-\mathit{\operatorname{Min}}}{M\_ Iter}\right) $$

(2)

where, MOA(C _ Iter) denotes the function value at the lth iteration; C _ Iter represents the current iteration, which is between 1 and the maximum number of iterations M _ Iter. Min and Max denote the minimum and maximum values of the accelerated function, respectively. At the same time, the mathematical optimizer probability (MOP) coefficient shown in Eq. (3) is introduced as follows:

$$ MOP\left(C\_\boldsymbol{Iter}\right)=1-\frac{C\_{\boldsymbol{Iter}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\partial $}\right.}}{M\_{\boldsymbol{Iter}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\partial $}\right.}} $$

(3)

where, MOP(C _ Iter) denotes the function value at the lth iteration, ∂ a is a sensitive parameter, which defines the accuracy of iterative development. Then a random number r1 is set, whose range is between (0, 1). When r1 > MOA, the algorithm is under the exploratory stage and when r1 < MOA, the algorithm is under the exploration stage.

• (2) Exploration Stage

In this searching stage, according to the arithmetic operators, the division (D) operator and the multiplication (M) operator are adopted to explore the searching mechanism. At the same time, the random number is set to determine whether it is updated by multiplication or division. Its location is updated by the following strategy.

$$ {X}_{i,j}\left(C\_ Iter+1\right)=\left\{\begin{array}{c} best\left({x}_j\right)\div \left( MOP+\epsilon \right)\times \mu +{LB}_j,\kern5.50em r2<0.5\\ {} best\left({x}_j\right)\times MOP\times \left(\left({UB}_j-{LB}_j\right)\times \mu +{LB}_j\right),\kern0.5em otherwise\end{array}\right. $$

(4)

where,r2is a random number between (0,1), which is used to switch multiplication and division operators; X_{i, j}(C _ Iter) indicates the j-th position of the i-th solution in the operating iteration; best(x_j) represents the j-th position in the best solution so far; ∈ is a smaller integer number; UB_j and LB_j denote to the upper bound and lower bound values of the j-th position respectively; μ is a control parameter to adjust the searching process, which is fixed equal to 0.5.

• (3) Exploitation Stage

In this development stage, according to the arithmetic operators, when using subtraction or addition, the result of the operation is relatively dense. Unlike other operators, addition operators and subtraction operators have the characteristics of low dispersion, which determines that they can more easily approach the search target. Using search operators (S and A) often tries to avoid falling into the local search area. This process helps to explore the searching strategy to find the optimal solution and maintain the diversity of candidate solutions. Random values are generated in each iteration, whether it is the first iteration or the last iteration, it keeps exploring. This can avoid falling into a local optimal stagnation, especially in the final iteration. Its location is updated according to Eq. (5).

$$ {X}_{i,j}\left(C\_ Iter+1\right)=\left\{\begin{array}{c} best\left({x}_j\right)- MOP\times \left(\left({UB}_j-{LB}_j\right)\times \mu +{LB}_j\right),\kern1.00em r3<0.5\kern0.75em \\ {}\begin{array}{cc} best\left({x}_j\right)+ MOP\times \left(\left({UB}_j-{LB}_j\right)\times \mu +{LB}_j\right),& otherwise\end{array}\end{array}\right. $$

(5)

where, r3 represents a random number between (0,1), which is used to switch addition and subtraction search; X_{i, j}(C _ Iter + 1) indicates the j-th position of the i-th solution in the next iteration; best(x_j) represents the j-th position in the best solution so far; LB_j and UB_j denote the lower bound and upper bound values of the j-th position respectively; μ is a control parameter to adjust the searching process, which is fixed equal to 0.5.

In a nutshell, the optimization process of AOA starts by generating a set of random candidate solutions. In the iterative process, A S, D, and M estimate the feasible position close to the optimal solution, and each solution updates its position from the optimal solution. In order to better distinguish between exploration and development, the parameter MOA is linearly increased from 0.2 to 0.9. When r1 > MOA, the candidate solution seeks to deviate from the near-optimal solution. When r1 < MOA, the candidate solution seeks to converge to a near-optimal solution. In the end, AOA stops due to the end-point criterion being met. The searching strategy of AOA is shown in Fig. 1.

Fig. 1

Searching strategy of arithmetic optimization algorithm

3 Chaotic arithmetic optimization algorithm

3.1 Chaotic mapping

Generally speaking, chaos is a deterministic and random-like method that exists in non-linear, dynamic, aperiodic, non-convergent and bounded systems. From a mathematical point of view, chaos is a deterministic dynamic system of randomness, and chaotic systems can be considered as the source of randomness. [29]. The nature of chaos is obviously random and unpredictable, but it also contains certain laws in randomness. Chaos is based on chaotic variables, not random variables [38]. Therefore, it can perform a thorough search at a higher speed than a random search that mainly relies on probability [35]. Even for very long sequences, only a few functions (chaotic mapping) and a few parameters (initial conditions) are needed [61]. In addition, once the initial conditions are changed, many different sequences are generated. The characteristics of these sequences are reproducible and deterministic. It can be seen that it is very sensitive to parameters and initial conditions [62]. On the basis of chaos theory, various chaotic maps have been derived in the field of optimization [38, 63]. In the current research work, there are 10 chaotic maps that are widely used by scholars [64]. The visualization graphs of these ten chaotic maps are given below, as shown in Fig. 2, and their mathematical expressions are described as follows.

• (1) Chebyshev map (CH)

Fig. 2

Visualization graphs of ten chaotic mapping strategies

The chaotic map expression is as follows:

$$ {x}_{k+1}=\mathit{\cos}\left(k{\mathit{\cos}}^{-1}\left({x}_k\right)\right) $$

(6)

• (2) Circle map (CI)

The chaotic map expression is as follows:

$$ {x}_{k+1}=\left({x}_k+b-\left(\frac{a}{2\pi}\right)\mathit{\sin}\left(2\pi {x}_k\right)\right)\mathit{\operatorname{mod}}(1) $$

(7)

where, a = 0.5, b = 0.2.

• (3) Gauss map (GA)

The chaotic map expression is as follows:

$$ {\displaystyle \begin{array}{c}{x}_{k+1}=\left\{\begin{array}{cc}0& {x}_{k=0}\\ {}\frac{1}{x_k\mathit{\operatorname{mod}}(1)}& \boldsymbol{otherwise}\end{array}\right.\\ {}\frac{1}{x_k\mathit{\operatorname{mod}}(1)}=\frac{1}{x_k}-\left[\frac{1}{x_k}\right]\end{array}} $$

(8)

• (4) Iterative map (IT)

The chaotic map expression is as follows:

$$ {x}_{k+1}=\mathit{\sin}\left(\frac{a\pi}{x_k}\right) $$

(9)

where, a ∈ (0, 1).

• (5) Logistic map (LO)

The chaotic map expression is as follows:

$$ {x}_{k+1}={ax}_k\left(1-{x}_k\right) $$

(10)

where, x_k is the k − thchaotic number, k is the number of iterations, x ∈ (0, 1), x₀ ∉ (0, 0.25, 0.5, 0.75, 1), a is a real number, a = 4.

• (6) Piecewise map (PI)

The chaotic map expression is as follows:

$$ {x}_{k+1}=\left\{\begin{array}{c}\frac{x_k}{p}\kern2.75em 0\le {x}_k<p\\ {}\frac{x_k-p}{0.5-p}\kern2.25em p\le {x}_k<\frac{1}{2}\\ {}\begin{array}{c}\frac{1-p-{x}_k}{0.5-p}\kern0.5em \frac{1}{\kern0.75em 2}\le {x}_k<1-p\\ {}\frac{1-{x}_k}{p}\kern1em 1-p\le {x}_k<1\end{array}\end{array}\right. $$

(11)

where, p ∈ (0, 1) is the control parameter, x ∈ (0, 1).

• (7) Sine map (SI)

The chaotic map expression is as follows:

$$ {x}_{k+1}=\frac{a}{4}\mathit{\sin}\left(\pi {x}_k\right) $$

(12)

where, a ∈ (0, 4].

• (8) Singer map (SG)

The chaotic map expression is as follows:

$$ {x}_{k+1}=\mu \left(7.86{x}_k-23.31{x_k}^2+28.75{x}_k^3-13.302875{x}_k^4\right) $$

(13)

where, μ ∈ (0.9, 1.08).

• (9) Sinusoidal map (SO)

The chaotic map expression is as follows:

$$ {x}_{k+1}={ax}_k^2\mathit{\sin}\left(\pi {x}_k\right) $$

(14)

where, a=2.3.

• (10) Tent map (TE)

The chaotic map expression is as follows:

$$ {X}_{k+1}\left\{\begin{array}{cc}\frac{x_k}{\alpha }& {x}_k<\alpha \\ {}\frac{\left(1-{x}_k\right)}{1-\alpha }& {x}_k\ge \alpha \end{array}\right. $$

(15)

where, α ∈ (0, 1).

3.2 Chaotic arithmetic optimization algorithm

3.2.1 MOA and MOP based on chaotic interference factors

Through the analysis of the original arithmetic optimization algorithm, two parameters (MOA and MOP) play an important role in the optimization process, and directly determine whether the algorithm is in the stage of exploration or exploitation. MOA determines which searching strategy the algorithm chooses, and MOP affects its location update. Figure 3 shows the changing trend of these two parameters. At the same time, the images of using chaotic factors to influence two parameters (MOA and MOP) respectively, which are shown in Figs. 4 and 5, respectively.

Fig. 3

MOA and MOP operators

Fig. 4

MOA with chaotic factors

Fig. 5

MOP with chaotic factors

3.2.2 Flowchart of chaotic arithmetic optimization algorithm

In order to increase the randomness of searching operators, the chaotic interference factors are added in MOA so as to expand the possibility of searching for promising areas. At the same time, the chaotic interference factor is added to affect the mathematical optimizer probability (MOP) in order to affect its position update, so that it has a certain volatility. This article takes Logistic map chaotic mapping as an example and embeds it in the parameters to update the position, the proposed chaotic interference factor are calculated by Eq. (16)–(20).

$$ MOA={x}_{t+1}\times \boldsymbol{Value}1 $$

(16)

$$ MOP={x}_{t+1}\times \boldsymbol{Value}2 $$

(17)

$$ {x}_{t+1}={ax}_t\left(1-{x}_t\right) $$

(18)

$$ \boldsymbol{Value}1={\left(\frac{C\_\boldsymbol{Iter}}{M\_\boldsymbol{Iter}}\right)}^{\frac{1}{6}} $$

(19)

$$ \boldsymbol{Value}2=1-{\left(\frac{C\_\boldsymbol{Iter}}{M\_\boldsymbol{Iter}}\right)}^{\frac{1}{2}} $$

(20)

where t is the current iteration number, a = 4, x ∈ (0, 1), x₀ ∉ (0, 0.25, 0.5, 0.75, 1).

This paper adopts chaotic interference factors to improve AOA so as to designs three different chaotic AOA. Firstly, the chaotic interference factors are alone used to interfere with MOA. The second is to use chaotic interference factors alone to interfere with MOP. Finally, a combination test is performed, that is to say that the chaotic interference factors are used to interfere with MOA and MOP at the same time. The AOA flowchart is shown in Fig. 6. Let’s take the last idea as an example and give the pseudo code of the improved AOA.

Fig. 6

Flowchart of AOA

Initialize the Arithmetic Optimization Algorithm parameters α, μ.

Initialize the solutions’ positions randomly. (Solutions: i = 1, ..., N.)

Return the best solution (x).

3.2.3 Computational complexity of chaos arithmetic optimization algorithm

This section analyzes the complexity of the Chaos Arithmetic Optimization Algorithm (CAOA) proposed in this paper. Its computational complexity is mainly composed of three aspects, namely the dimension D of the problem, the population size N and the maximum number T of iterations [65]. According to the optimization process of CAOA, the number of operations at each step will be calculated. First, in the initialization phase, the time complexity of initializing N search agents in the D-dimensional search space is O(2ND). Secondly, the function fitness value of N individual agents needs to be calculated, and the time complexity of the fitness function is O(ND). When selecting the best fitness value, a quick sort algorithm is adopted, and its computational complexity is O(NlogN) and O(N2) in the best and worst cases respectively. The computational complexity of MOA and MOP are O((N − 1)²). In the exploration phase of CAOA, the time complexity of all individual location updates and boundary control strategies is O(2ND). In the development phase of CAOA, the time complexity of all individual location updates and boundary control strategies is O(2ND). The simplified definition of overall complexity is described as follows.

$$ O\left(2 ND\right)+O(ND)+O(N2)+O(TlogN)+O\left(T{\left(N-1\right)}^2\right)+O\left(2 TND\right)+O\left(2 TND\right)\approx O\left(T\ast \left(N2+4 ND\right)\right) $$

(21)

4 Simulation experiments and result analysis

4.1 Function optimization

This paper selects 26 test functions in CEC-BC-2017 to test the performance of chaotic arithmetic optimization algorithms. These test functions are divided into four categories: unimodal function, multimodal function, mixed function and composite function. Through the optimization results of these four testing functions, the superiority of the chaotic AOA is fully proved. In order to ensure the fairness and reliability of the test experiment, the population size of the arithmetic optimization algorithm and the arithmetic optimization algorithm based on chaotic mapping is unified to 30, and the maximum number of iterations is unified to 1000. The specific parameter settings of each algorithm are shown in Table 1.

Table 1 Parameter settings of all algorithms

4.1.1 CEC2017 testing functions

This paper uses 26 functions listed in the CEC-BC-2017 [66,66,68]. The dimension of these testing functions is 10. Table 2 lists the expression of the function. Range means the range of the function is [−100,100], fmin means the optimal solution of the function. These functions are divided into four categories: unimodal functions f₁-f₃, multimodal functions f₄-f₁₀, mixed functions f₁₁, f₁₄-f₂₀, and composite functions f₂₁-f₂₃, f₂₅-f₂₈.

Table 2 CEC-BC-2017 test functions (Dim = 10)

4.1.2 Chaotic arithmetic optimization algorithm to optimize CEC-BC-2017 testing functions

For the selected 26 CEC-BC-2017 test functions, simulation experiments are carried out by adopting three proposed improved AOA. The dimension of all functions is 10, each algorithm is run 10 times and the optimal solution among ten times is recorded. This paper performs mathematical statistics on the experimental results to facilitate the comparison of the performance of the arithmetic optimization algorithm and the chaotic arithmetic optimization algorithm proposed in this paper. In order to analyze the experimental results more intuitively, this article chooses the average and variance for statistics. The obtained variance, optimal, average values are listed in Table 3, 4 and 5. The convergence curves of the experimental simulation are shown in Figs. 7, 8 and 9 respectively. It can be seen from figures and tables that the chaotic AOA has better convergence effect on most function optimizations than the standard AOA.

• (1) MOA with Chaos Factors

Fig. 7

AOA with chaotic MOA to optimize testing functions

Fig. 8

AOA with Chaotic MOP to optimize testing functions

Fig. 9

AOA with Chaotic MOA and MOP to optimize testing functions

Figure 7 shows the the convergence curves obtained by using AOA with MOA to optimize test functions. Table 3 is the experimental results obtained by simulation. From the results in Table 3, we can get the following conclusions. In terms of mean and minimum,the average values of GAAOA on function f₃ and f₄ are the closest to the optimal value. At the same time, the optimal and average values of function f₁, f₂, f₃, f₄, f₇, f₈, f₁₄, f₂₃ and f₂₈ obtained by GAAOA are the best. The optimal and average value of function f₁₀ and f₁₁ obtained by SIAOA are the smallest. The optimal and average values obtained by ITAOA to optimize the function f₆ and f₂₅ are the smallest. In terms of average value, CHAOA to optimize function f₅, PIAOA to optimize function f₉, LOAOA to optimize function f₁₅ and SIAOA to optimize function f₁₆ obtain the smallest average value. TEAOA only has a minimum value on function f₁₈. In terms of the minimum and optimal values on function f₁₅ and f₂₆, CHAOA obtains the smallest among the improved algorithms. For function f₉ and f₁₆, ITAOA has the best minimum value. TEAOA to optimize function f₂₂, SGAOA to optimize function f₅ and CIAOA to optimize function f₁₈ all achieve the minimum value. GAAOA only shows slight superiority on f₆, f₉ and f₂₆. At the same time, this paper has made a ranking of the optimization performance of each test function. When considering embedding the chaotic map into the parameter MOA separately, comparing their average rankings, we can intuitively see that GAAOA has the best optimization performance and ranks the first. On the other hand, SIAOA and CHAOA rank the second and third, respectively.

Table 3 Simulation results of AOA with chaotic MOA to optimize CEC-2017 testing functions

• (2) MOP with Chaos Factors

Figure 8 shows the convergence curves obtained by using AOA with the chaotic MOP to optimize test functions. Table 4 is the experimental results obtained by simulation. From the results in Table 4, we can get the following conclusions. In terms of mean and minimum, the average values of CHAOA on function f₆, ITAOA on functionf₈ and SIAOA on function f₁₁ are the closest to the optimal value. Among them, the average, optimal and standard deviation values obtained by PIAOA on functionf₂ are the smallest. The optimal and average value of function f₆ and f₇ obtained by CHAOA are the best. At the same time, the average and optimal values of SIAOA on function f₁₁, SOAOA on function f₃, PIAOA on function f₂₄ and GAAOA on function f₂₇ are the smallest. Seen from the mean and standard deviation values together, the average and standard deviation values of CHAOA on function f₂₈, GAAOA on function f₁₄, LOAOA on function f₉ and f₁₇ are the best. It means they are more stable. SOAOA only has a minimum value on function f₅, f₉ and f₂₃. From the average point of view, GAAOA is not as effective as the original algorithm on function f₁, f₂ and f₃. SOAOA only shows slight superiority on f₉, f₁₇ and f₂₀. At the same time, this paper has made a ranking of the performance of each algorithm optimization test functions. When considering embedding the chaotic map into the parameter MOP separately, comparing their average rankings, we can intuitively see that SIAOA has the best optimization performance and ranks the first. LOAOA and CHAOA rank the second and third, respectively.

Table 4 Simulation results of AOA with chaotic MOP to optimize CEC-2017 testing functions

• (3) MOA and MOP with Chaos Factors

Figure 9 shows the convergence curves obtained by using chaotic factors to interfere with the MOA and MOP at the same time to optimize testing functions. Table 5 is the experimental results obtained by simulation. From the results in Table 5, we can get the following conclusions. In terms of mean and minimum, the average values of ITAOA on f₃,LOAOA on f₁₆,SIAOA on f₅ are the closest to the optimal value. It is worth mentioning that the average, optimal and standard deviation values obtained by ITAOA to optimize function f₁, and f₂ are the smallest. CHAOA optimizing functionf₃ and f₁₄also gets the smallest average value, optimal value and standard deviation. At the same time, the optimal and average values of function f₁₁ obtained by TEAOA are the best. Looking at the mean and standard deviation values together, the average and standard deviation of CHAOA on function f₄,f₉, f₁₅,f₁₇,f₂₀and f₂₆, TEAOA on function f₁₁,ITAOA on function f₂₇are the smallest. It shows that they are more stable. GAAOA only has a minimum value on function f₄. Meanwhile, from the average point of view, GAAOA only shows slight superiority on f₂, f₁₁, f₁₅ and f₂₃. At the same time, this article has made a ranking of the performance of each algorithm optimization test function. When considering embedding the chaotic map into the parameters MOA and MOP at the same time, comparing their average rankings, we can intuitively see that CHAOA has the best optimization performance and ranks the first. ITAOA and TEAOA rank the second and third, respectively.

Table 5 Simulation results of AOA with chaotic MOA and MOP to optimize CEC-2017 testing functions

Based on the above figures and tables, it is not difficult to see that the use of chaotic interference factors to dynamically adjust the parameters on AOA has achieved better results. By further comparing the average values of three improved schemes, for most of the testing functions, the performance of AOA with chaotic interference factor alone to affect MOP is not as effective as AOA with chaotic interference factor alone to affect MOA. When using chaotic interference factors to affect MOA and MOP at the same time, the effect is better than using chaotic interference factors to affect MOA alone. By further comparing the average ranking of the optimization performance of each algorithm, it can be found that CHAOA ranks the first in these three improved schemes. Especially in the last winning scheme, CHAOA’s optimization performance leads the other algorithms, ranked first. Therefore, we have reason to believe that CHAOA is the best optimization performance in these algorithm variants.

In the above simulation experiments, this article runs the optimization process of each function independently for ten times, and determines its performance based on the minimum, average, and variance of the three indicators, but it is still impossible to determine the authenticity of each experimental result. In order to show the significance of each optimization result more fully and intuitively, a non-parametric test was performed on the results. The Wilcoxon rank sum test is used in this article. Table 6 describes the p value of the Wilcoxon rank sum test. In Table 6, based on the arithmetic optimization algorithm, the improved AOA based on the chaotic interference factor is tested.It can be found that, except for GAAOA, all p-values are less than 0.05. It shows that the improved AOA is significantly different from the original AOA.

Table 6 Results of Wilcoxon test (p ≥ 0.05)

4.1.3 Comparison with other intelligent optimization algorithms

In this section, this article selects some intelligent optimization algorithms that perform well in optimizing the CEC-2017 test functions, and compares them with AOA based on the chaotic interference factor. These competing algorithms include MPA, L-SHADE, LSHADE-EpSin, HHO, EO, WHO, WOA and PSO. Through the previous experimental analysis, it can be seen that the CHAOA algorithm in which the chaotic interference factor is embedded in the parameters MOP and MOA at the same time has the best effect. So this improved AOA is chosen as a representative to compare with other algorithms. Table 7 quotes the data in references [17, 68, 69]. By analyzing the data listed in Table 7, it can be seen that the optimization performance of LSHADE-EpSin and MPA are the best, and CHAOA proposed in this paper ranks third. For most of the test functions, the optimized value of CHAOA is very close to MPA. The fourth and fifth places are LSHADE and EO. Based on the data analysis in the Table 7, the performance of LSHADE-EpSin, MPA and CHAOA is far superior to other methods. This fact shows that CHAOA can be classified as a high-performance optimizer.

Table 7 Results of CEC - 2017 test suite

4.2 Engineering optimization design problems

4.2.1 Three-bar truss design problem

The design problem of the three-bar truss is to minimize the weight of the truss under certain constraints. Figure 10 shows the model diagram of the three-bar truss design problem. The constraints of the truss mainly refer to buckling constraints, stress and deflection.

Fig. 10

Model of three-bar truss design problem model

The specific constraints and objective functions of this problem are listed as follows:

$$ \mathrm{Objective}\ \mathrm{function}\colon\colon f(X)=\left(2\sqrt{2}{X}_1+{X}_2\right)\ast l $$

$$ {\displaystyle \begin{array}{c}\mathrm{Constraint}\ \mathrm{conditions}:\kern0.5em {\mathrm{g}}_1(X)=\frac{\sqrt{2}{X}_1+{X}_2}{\sqrt{2}{X}_1+2{X}_1{X}_2}P-\sigma \le 0\\ {}\begin{array}{cc}& {\mathrm{g}}_2(X)=\frac{X_2}{\sqrt{2}{X}_1+2{X}_1{X}_2}P-\sigma \le 0\end{array}\\ {}\begin{array}{cc}& {\mathrm{g}}_3(X)=\frac{1}{\sqrt{2}{X}_2+{X}_1}P-\sigma \le 0.\end{array}\end{array}} $$

where, the variables X₁ and X₂ are the cross-sectional areas of rod 1 and rod 2 respectively, 0 ≤ X₁, X₂ ≤ 1, l = 100 cm, P = 2 KN/cm, σ = 2 KN/cm.

Figure 11 shows the convergence curves of AOA and chaotic AOA to optimize the three-bar truss design problem. Table 8 records he best values of the original AOA algorithm and the arithmetic optimization algorithm based on the chaotic interference factor to optimize the three-bar truss problem. Each algorithm is run ten times, and then their average and variance are recorded in Table 9, and the best data in the table is bolded. It can be seen from Table 9 that SIAOA optimizing the three-bar truss design problem to obtain the best value, followed by the optimization results of CHAOA and SOAOA. From the average results, it can be seen that CIAOA optimizing three-bar truss problem is the best, but GAAOA is not good, and its volatility is relatively large.

Fig. 11

Convergence curves of three-bar truss problem optimized by chaotic AOA

Table 8 Best solution obtained from chaotic AOA on the three-bar truss design problem

Table 9 Simulation results obtained from chaotic AOA on the three-bar truss design problem

Table 10 lists the experimental results of other competing algorithms to optimize the design of three-bar truss. Since CIAOA performed well in this engineering problem, the improved algorithm is chosen for comparison. Judging from the data in Table 10, CIAOA has obtained the best parameter values and the best objective function value. From the average point of view, the optimization effect of EO and PSO is relatively good, and CIAOA ranks third.

Table 10 Results obtained from competitor algorithms for the three-bar truss design problem

4.2.2 Welded beam problem

The problem of cantilever beam design is to minimize the manufacturing cost function under certain constraints. Figure 12 shows the model diagram of the cantilever beam design problem. The constraints of the engineering problem include buckling load on the steel bar, shear stress and bending stress in the beam, deflection of the end of the beam, and side constraints. The specific constraints and objective functions of this problem are listed as follows:

$$ \mathrm{Objective}\ \mathrm{function}:f(X)=1.1047{X}_1^2{X}_2+0.04811{X}_3{X}_4\left(14.0+{X}_2\right) $$

$$ {\displaystyle \begin{array}{c}\mathrm{Constraint}\ \mathrm{conditions}:\kern0.5em {\mathrm{g}}_1(X)=\tau (X)-{\tau}_{\mathrm{max}}\le 0\\ {}\begin{array}{cc}& {\mathrm{g}}_2(X)=\sigma (X)-{\sigma}_{\mathrm{max}}\le 0\end{array}\\ {}\begin{array}{c}\begin{array}{cc}& {\mathrm{g}}_3(X)=\delta (X)-{\delta}_{\mathrm{max}}\le 0\end{array}\\ {}\begin{array}{cc}& {\mathrm{g}}_4(X)={X}_1-{X}_4\le 0\end{array}\\ {}\begin{array}{c}\begin{array}{cc}& {\mathrm{g}}_5(X)=P-{P}_c(X)\le 0\end{array}\\ {}\begin{array}{cc}& {\mathrm{g}}_6(X)=0.125-{X}_1\le 0\end{array}\\ {}\begin{array}{cc}& {\mathrm{g}}_7(X)=1.10471{X}_1^2+0.04811{X}_3{X}_4\left(14.0+{X}_2\right)-5.0\le 0\end{array}\end{array}\end{array}\end{array}} $$

where, $\tau (X)=\sqrt{{\left(\tau \prime \right)}^2+2\tau^{\prime}\tau^{\prime\prime}\frac{X_2}{2R}+{\left(\tau \prime \prime \right)}^2}$, $\tau^{\prime }=\frac{P}{\sqrt{2}{X}_1{X}_2}$, $\tau^{\prime\prime }=\frac{MR}{J}$, $M=P\left(L+\frac{X_2}{2}\right)$, $R=\sqrt{\frac{X_2^2}{4}+{\left(\frac{X_1+{X}_3}{2}\right)}^2}$, $J=2\left\{\sqrt{2}{X}_1{X}_2\left[\frac{X_2^2}{4}+{\left(\frac{X_1+{X}_3}{2}\right)}^2\right]\right\}$, $\sigma (X)=\frac{6 PL}{X_4{X}_3^2}$, $\delta (X)=\frac{6{PL}^3}{EX_3^2{X}_4}$, ${P}_c(X)=\frac{4.013E\sqrt{\frac{X_3^2{X}_4^6}{36}}}{L^2}\left(1-\frac{X_3}{2L}\sqrt{\frac{E}{4G}}\right)$,

Fig. 12

Model of welded beam design problem

P = 6000lb., L = 14in, δ_max = 0.25 in, E = 30 × 1⁶psi, G = 12 × 10⁶psi, τ_max = 13600psi, σ_max = 30000psi. X₁ is the thickness of the weld (0.1 ≤ X₁ ≤ 2), X₂ is length of attached part of bar (0.1 ≤ X₂ ≤ 10), X₃ represents the height of the bar (0.1 ≤ X₃ ≤ 10) and X₄ is the thickness of the bar (0.1 ≤ X₄ ≤ 2).

Figure 13 shows the convergence curves of AOA and the improved AOA based on the chaotic interference factor to optimize the welded beam design problem. Table 11 records the best values of the original AOA algorithm and the arithmetic optimization algorithm based on the chaotic interference factor to optimize the cantilever beam design problem. Each algorithm is run ten times, and then their average and variance are recorded in Table 12, and the best data in the table is bolded. It can be seen from Table 12 that the improved AOA on the welded beam problem has achieved better results. The best performance of optimizing the welded beam design problem is CHAOA, and the data result obtained by PIAOA ranks second. PIAOA runs ten times to get the best results.

Fig. 13

Convergence curves of welded beam problem optimized by chaotic AOA

Table 11 Best solution obtained from chaotic AOA on the welded beam problem

Table 12 Simulation results obtained from chaotic AOA on the welded beam problem

Table 13 refers to the experimental results of other competing algorithms to optimize the cantilever problem [16]. Because PIAOA performed well in this engineering problem, the improved algorithm is chosen for comparison. Judging from the data in Table 13, MPA has obtained the best parameter values and the best objective function value. From the average point of view, the optimization effects of MPA and EO are relatively good, and PIAOA ranks third.

Table 13 Results obtained from competitor algorithms for the welded beam problem

4.2.3 Pressure vessel problem

The goal of the problem based on pressure vessel design is to minimize the manufacturing cost function. Figure 14 shows a model diagram of the pressure vessel problem. The container contains four design variables, and the manufacturing cost includes the material of the container, the molding of the container and the welding of the container. The specific constraints and objective functions of this problem are listed as follows:

$$ \mathrm{Objective}\ \mathrm{function}:f(X)=0.6224{X}_1{X}_3{X}_4+1.7781{X}_2{X}_3^2+3.1661{X}_1^2{X}_4+19.84{X}_1^2{X}_3 $$

$$ {\displaystyle \begin{array}{c}\mathrm{Constraint}\ \mathrm{condition}:\kern0.5em {g}_1(X)=0.0193{X}_3-{X}_1\le 0\\ {}\begin{array}{cc}& {g}_2(X)=0.00954{X}_3-{X}_2\le 0\end{array}\\ {}\begin{array}{c}\begin{array}{cc}& {g}_3(X)=1296000-\pi {X}_3^2{X}_4-\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi {X}_3^3\le 0\end{array}\\ {}\begin{array}{cc}& {g}_4(X)={X}_4-240\le 0\end{array}\end{array}\end{array}} $$

where, X₁ and X₂ are head (Th) and cylinder wall thickness (Ts), 0.0625 ≤ X₁, X₂ ≤ 6.1875; X₃ is the radius of the cylinder and head (R), X₄ is the cylinder length (L), 10 ≤ X₃, X₄ ≤ 200. Among the four variables, X₁ and X₂ are uniformly discrete variables with an interval of 0.0625, X₃ and X₄ are continuous variables.

Fig. 14

Model of pressure vessel design problem

Figure 15 shows the convergence curves of AOA and the improved AOA based on the chaotic interference factor to optimize the pressure vessel problem. Table 14 records the best values of the original AOA algorithm and the arithmetic optimization algorithm based on the chaotic interference factor to optimize the pressure vessel design problem. Each algorithm is run ten times, and then their average and variance are recorded in Table 15, and the best data in the table is bolded. It can be seen from Table 15 that the optimization of improved AOA on the pressure vessel design problem has achieved better results. GAAOA optimizes the pressure vessel design problem to obtain the smallest minimum value. But from the average and variance point of view, SIAOA ranks first in the optimization process.

Fig. 15

Convergence curves of pressure vessel problem optimized by chaotic AOA

Table 14 Best solution obtained from chaotic AOA on the pressure vessel problem

Table 15 Simulation results obtained from chaotic AOA on the pressure vessel problem

Table 16 refers to the experimental results of other competing algorithms to optimize the pressure vessel problem [16]. Since SIOAA performed well in this engineering problem, the improved algorithm is chosen for comparison. Judging from the data in Table 16, SIOAA has obtained the best parameter values and the best objective function value. From the average point of view, SIAOA is equally excellent, and its standard deviation is also the smallest, ranking first in the listed algorithms, and MPA and EO are ranked second and third respectively.

Table 16 Results obtained from competitor algorithms for the pressure vessel problem

4.2.4 Tension spring problem

The goal of the tension spring design problem is to minimize the weight of the compression spring under certain constraints. Figure 16 shows the model diagram of the tension spring design problem. The design problem has three design variables. Constraints include vibration frequency, minimum deflection and shear stress. The specific constraints and objective functions of this problem are listed as follows:

$$ \mathrm{Objective}\ \mathrm{function}:f(X)=\left({X}_3+2\right){X}_2{X}_1^2 $$

$$ {\displaystyle \begin{array}{c}\mathrm{Constraint}\ \mathrm{condition}:\kern0.5em {g}_1(X)=1-\frac{X_2^3{X}_3}{71785{X}_1^4}\le 0\\ {}\begin{array}{cc}& {g}_2(X)=\frac{4{X}_2^2-{X}_1{X}_2}{12566\left({X}_2{X}_1^3-{X}_1^4\right)}+\frac{1}{5108{X}_1^2}\le 0\end{array}\\ {}\begin{array}{c}\begin{array}{cc}& {g}_3(X)=1-\frac{140.45{X}_1}{X_2^2{X}_3}\le 0\end{array}\\ {}\begin{array}{cc}& {g}_4(X)=\frac{X_1+{X}_2}{1.5}-1\le 0\end{array}\end{array}\end{array}} $$

where, X₁ is wire diameter (0.05 ≤ X₁ ≤ 2.00), X₂ is the average coil diameter (0.25 ≤ X₂ ≤ 1.30), and X₃ represents the number of effective coils (2.00 ≤ X₃ ≤ 15.0).

Fig. 16

Model of tension spring design problem

Figure 17 shows the convergence curves of AOA and AOA based on the chaotic interference factor to optimize the tension spring design problem. Table 17 records the best values of the original AOA algorithm and the arithmetic optimization algorithm based on the chaotic interference factor to optimize the tension spring design problem. Each algorithm is run ten times, and then their average and variance are recorded in Table 18, and the best data in the table is bolded. It can be seen from Table 18 that the improved algorithms in the optimization of the tension spring design problem have achieved better results. The optimal value obtained by SIAOA for optimizing the tension spring design problem is the smallest when the constraints are met, followed by the optimal value by CHAOA. At the same time, the average value of SIAOA to optimize the spring design problem is the smallest and SOAOA is more stable.

Fig. 17

Convergence curves of tension spring problem optimized by chaotic AOA

Table 17 Best solution obtained from chaotic AOA on the tension spring problem

Table 18 Simulation results obtained from chaotic AOA on the tension spring problem

Table 19 refers to the experimental results of other competing algorithms to optimize the tension spring problem [16]. Since SIOAA performed well in this engineering problem, the improved algorithm was chosen for comparison. Judging from the data in Table 19, SIOAA has obtained the best parameter values and the best objective function value. From the average point of view, SIAOA is equally excellent, ranking first in the listed algorithms, and MPA and EO are ranked second and third respectively.

Table 19 Results obtained from competitor algorithms for the tension spring problem

Through the above comparison with competing algorithms, it can be found that the improved algorithm proposed in this paper performs well in solving actual engineering optimization problems. Among the four engineering problems, three can obtain the best parameter values, so as to obtain the best objective function value. They are the three-bar truss problem, the pressure vessel problem, and the spring tension problem. In terms of the average optimization effect, for the four engineering problems, the proposed improved algorithm in this paper can be ranked in top three. Especially when solving the pressure vessel problem and the spring tension problem, it ranked first. The optimization effects of MPA and EO are also relatively good.

5 Conclusions

The improved AOA based on chaotic interference factors adopted in this paper improves the ability of the AOA to balance exploration and exploitation, avoids falling into local optimization, and improves the accuracy of convergence. This article has designed three schemes to carry out simulation experiments to test their performance. The optimization experiment results of unimodal functions, multimodal functions, mixed functions and complex functions show that the optimization performance of AOA based on chaotic interference factors are good. The optimization results show that the optimized average value of the arithmetic optimization algorithm based on the chaotic interference factor is lower than the initial algorithm in most of the test functions. By further comparing the optimization rankings of different chaotic variants, the CHAOA algorithm in which the chaotic interference factor is embedded in MOP and MOA at the same time has achieved the best effect among many chaotic variants. When compared with other optimization algorithms, the chaotic arithmetic optimization algorithm also has the upper hand. On the other hand, the convergence performance of the chaotic AOA to optimize the engineering design problem is also excellent. Among them, the optimized three-bar truss problem and the welded beam design problem are the most stable and the best is CIAOA and PIAOA respectively. For pressure vessel and spring design problems, the convergence speed and accuracy of the SIOA algorithm make it stand out. By comparing with other competing algorithms, the algorithm proposed in this article performs well in solving practical engineering problems.

It the future work, we plan to apply chaos theory to other optimization algorithms, not only considering the existing 2-dimensional chaos, but also considering the application of chaotic systems for optimization in order to extensively compare the performance of chaos in different heuristic algorithms. In addition, we will extend the application of the improved algorithm. First of all, the improved algorithm can be applied to the Frequent Itemsets Mining (FIM) [70] technology and the field of mining top-k most frequent association rules [71]. Secondly, CAOA can be applied to the recently more popular deep learning to optimize neural network parameters and improve the efficiency of network training. Finally, extending the algorithm to multi-objective optimization to solve combinatorial optimization problems can also be seen as a future contribution.