1 Introduction

Meta-heuristic optimization algorithms have been often used to solve the problems which are usually impossible to solve with conventional mathematical methods [1]. The main purpose of the optimization algorithms is to find a global optimum in a solution space. Local optima are also used to find the global optimum. Optimization methods send continuous random values to the target function to solve problems and thus keep the best values in memory [2, 3].

Researchers consider various branches of science, for instance, natural sciences, biology, mathematics, physics, chemistry, space science, and etc. to propose a new efficient meta-heuristic optimization technique [1, 4]. One of the commonly used algorithms by researchers is the genetic algorithm. Genetic algorithms were inspired by the theory of evolution and biology [5, 6]. Differential evolution algorithm is a particle-based algorithm which uses genetic algorithm operators [7]. In addition, there are a number of meta-heuristic optimization algorithms aiming to find global optimum by modeling animal behaviors [1]. These algorithms include ant colony algorithm [8], artificial bee colony algorithm [9], cuckoo bird search algorithm [10], firefly algorithm [11], cricket algorithm [2], bat optimization algorithm [12], particle swarm optimization algorithm [9], and the cat algorithm [13]. These algorithms try to model animal behaviors such as pathfinding, decision-making, communication, peer selection [2]. Besides, there is an animal behavioral algorithm proposed in the literature to model the behavior of all animals [14]. The basic rationale of the animal behavior algorithm is to model how animals interact with each other in a cubic field. Some optimization techniques have been developed based on plants. These algorithms have been exemplified as root growth optimization algorithm and seedling growth algorithm. One of the most comprehensive sources of the algorithm based on plant development was presented by Akyol and Alatas [15].

Optimization techniques inspired by physics, chemistry, mathematics, and even sports are often used. Basic mathematical algorithms among them were formed combining the mathematical programming and meta-heuristic algorithms [16]. One of the extensive studies in this area was carried out by Ozbay and Alatas [17]. The Sine Cosine algorithm, one of the optimization algorithms inspired by mathematics, was used to solve problems that were actually difficult to solve [18].

Chaotic maps are one of the frequently used methods for problem-solving in optimization techniques. Chaotic maps are important functions for nonlinear systems and are also used in methods such as image encryption, key generation, random number generation, and data steganography. The vast majority of these methods have used chaotic maps to generate random numbers. The algorithms, which are classified as COA, have aimed to find global optimum by using chaotic map equations.

The logistic map-based chaotic method had high success in solving the problem of particle swarm and sine-cosine optimization. Therefore, a new optimization technique with a logical-sine base was proposed. The proposed optimization technique used a hybrid 1D chaotic map. This map was previously used to encrypt the image [4]. It is known that the random nature of the logical-sine was good enough. Therefore, a particle-based logistic-sine chaotic optimization technique called as Logistic-Sine Chaotic Optimization Algorithm (LS-COA) is proposed. The proposed method was written in the most ideal software terms. In order to test the performance of this method using MATLAB, fitness functions that were frequently used in optimization methods were preferred. The results obtained were compared with other optimization techniques that are frequently used in the literature.

The main contributions of the proposed logistic-sine map-based chaotic optimization method are given as below.

  • As known from the literature, the hybrid chaotic maps have better random distribution capability than other chaotic maps and they have been generally used in image encryption methods. However, there are no hybrid chaotic map-based optimization technique. In this article, a novel logistic-sine map-based optimization technique is proposed and this method is tested by using 16 numerical functions. The results of a hybrid chaotic map are examined for optimization. The proposed method is the first hybrid chaotic map-based optimization method in the literature as we know.

  • Chaotic maps have been used to generate random values in most of the optimization methods. The most of the optimization methods have generally used a nature-inspired velocity formula to optimize parameters or values. To achieve high performance using chaos, a novel particle-based search strategy is proposed. This search strategy uses logistic-sine map and a differential method to update particles. The main aim of this search strategy was to use the effectiveness of the chaos directly. The experiments clearly indicated the effectiveness of the proposed search strategy.

  • The proposed optimization algorithm has a simple mathematical background. Hence, it is a very simple and effective method. It can be basically applied to real-world problems.

The remainder of this paper is organized as follows. Section 2 outlines the previous works related to this study, while Sect. 3 gives the background of this study. The benchmark functions are listed in Sect. 4. Section 5 explains the details of the proposed method; experimental results are given in Sect. 6. The results are discussed in Sect. 7. Section 8 outlines the conclusions of this study.

2 Related work

The majority of previous studies performed for the chaotic optimization algorithms were mostly used to generate random values. Classical optimization methods are rarely good global optimization methods. Optimization by heuristics has been effectively used for global optimization for several decades, and classical optimization methods are typically invalid for global optimization. Studies in the literature have shown the effectiveness of chaotic maps. Furthermore, the use of chaotic maps in both search strategies and speed parameters increases this efficiency. There are many studies in the literature based on the chaotic optimization method, and some of them are shown in Table 1.

Table 1 A new generation of academic studies using chaotic systems
Full size table

3 Background

In this study, a novel 1D hybrid chaotic map-based optimization method is presented. The main aim of this study is to achieve high performance in the meta-heuristic optimization. As we know from the literature, chaos is a phenomenon of the nonlinear dynamics and chaotic maps show good statistical results for random number generation. Therefore, many optimization methods use chaotic maps as random number generator. In order to directly use positive effect of the chaos, mathematical definition of the logistic-sine map is utilized as particle updating function. Therefore, the main component (Logistic-Sine Chaotic Map) of this paper is given in Sect. 3.1.

3.1 Logistic-sine chaotic map

The logistic-sine map is a chaotic map that uses both the logistic map and the sine map. Therefore, it is called as hybrid chaotic map. The main attribute of this map is that the chaotic interval is higher than the sine map and the logistic map. Mathematical description of the logistic map, sine map, and logistic-sine map is given in Eqs. 1–3 [32, 33].

$$x_{i + 1} = rx_{i} \left( {1 - x_{i} } \right)$$
(1)
$$x_{i + 1} = { \sin }\left( {\pi x_{i} } \right)$$
(2)
$$x_{i + 1} = \left( {rx_{i} \left( {1 - x_{i} } \right) + \frac{{\left( {4 - r} \right)\sin \left( {\pi x_{i} } \right)}}{4}} \right)\left( {\bmod 1} \right)$$
(3)

where x is a randomly generated number sequence and r is a multiplier of chaos. In Eqs. 1–2, logistic map and sine map are mathematically defined, respectively. In the Eq. 3, mathematical notation of the logistic-sine map is given.

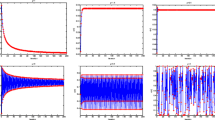
The bifurcation diagrams of the logistic map, sine map, and logistic-sine map are also shown in Fig. 1.

Fig. 1
figure 1

Bifurcation diagrams a logistic map, b sine map, c logistic-sine map [x = (0, 1) and r = (0, 4)]

Full size image

As seen from Fig. 1, the logistic-sine map provides better random distribution and the chaotic properties are stronger than the logistic map and sine map. Therefore, the logistic-sine map is chosen to design our proposed chaotic optimization algorithm.

4 Benchmark functions

In this section of the article, the fitness functions which are often used in the literature were used to test the performance of the proposed logistic-sine map-based chaotic optimization method. These fitness functions are called as F1–F16. A test suite is constructed using these functions. The numerical benchmark functions used are divided into two classes. These are unimodal and multimodal functions [42, 43]. Graphical representation of them is also given in Fig. 2. In here, 8 unimodal and 8 multimodal functions are used. The multimodal functions are F8–F15, and the others are unimodal. The main aim of the proposed hybrid chaotic map-based swarm optimization method is to achieve the optimal point of these functions [34,35,36,37,38,39,40,41,42,43].

Fig. 2
figure 2figure 2figure 2

The used numerical benchmark functions

Full size image

5 The proposed logistic-sine map-based meta-heuristic optimization algorithm

Chaotic optimization techniques generally use 1D chaotic maps such as sine, logistic, gauss, tent maps. In this study, the logistic-sine map, a hybrid chaotic map, was used to provide a high performance. The proposed logistic-sine map based on chaotic optimization technique is a particle-based. The flow diagram of the logistic-sine chaotic optimization technique is shown in Fig. 3.

Fig. 3
figure 3

Flow diagram of logistic-sine map-based optimization technique

Full size image

The steps of the proposed logistic-sine optimization method are given below.

Step 1 Generate initial population randomly by using lower bound and upper bound values.

$$p = \left( {{\text{UB}} - {\text{LB}}} \right) \times {\text{rand}}\left[ {0,1} \right] + {\text{LB}}$$
(4)

UB is upper bound, LB was lower bound, and rand [0, 1] was randomly generated number with range of [0, 1].

Step 2 Calculate step value.

$${\text{step}} = \frac{{{\text{UB}} - {\text{LB}}}}{{P_{\text{num}} }}$$
(5)

\(p_{\text{num}}\) number of particles.

Step 3 Calculate personal best by using the fitness function.

Step 4 Generate random numbers using logistic-sine map.

Step 5 Update particles.

$$p_{i}^{t + 1} = p_{i}^{t} + x_{i} \left( {p_{\text{best}}^{t} - p_{i}^{t} } \right) \times {\text{step}}$$
(6)

Step 6 If particles exceed lower or upper bounds, set position of it using personal best value.

$$p_{i} = p_{\text{best}}$$
(7)

Step 7 Update personal best value.

Step 8 Repeat steps 4–7 until reached desired values or maximum number of iteration.

For comparison’s sake, 16 fitness functions given in Sect. 4 were used in swarm optimization algorithms.

6 Experimental results

Sixteen commonly used numerical benchmark functions are used to obtain the performance of the proposed method in this section. Also, the proposed method was programmed by MATLAB 2018a using a personal computer (PC). This PC has 8 GB RAM, Intel i7 7500 CPU with 2.7 GHz and Windows 10.1 operating system. In order to obtain results, the maximum number of cycles, dimension, and particle size are chosen as 500, 30, and 40 respectively to compare other methods. The obtained results of the proposed logistic-sine map-based chaotic optimization method are listed in Table 2. The initial parameters of the proposed method are given as follows. The chaotic multiplier and initial value are selected as 0.86.

Table 2 Results of the proposed logistic-sine map-based chaotic optimization method by using the defined benchmark functions
Full size table

In Table 2, SD represents standard deviation. Table 2 shows the results of the used 16 benchmark functions by using the proposed logistic-sine map-based chaotic optimization method. The global optimum value of these functions is 0. As seen from Table 2, the proposed chaotic optimization method achieved global optimum value for 9 fitness functions which are Sphere (F1), Schwefel 2.22 (F2), Schwefel 1.2 (F3), Schwefel 2.1 (F4), Rosenbrock (F5), Step (F6), Rastrigin (F8), Trid (F15), and Dixon Price (F16) functions.

The proposed logistic-sine map-based method is also compared with Sine Cosine Algorithm (SCA) [18], Whale Optimization Algorithm (WOA) [3], and Grasshopper Optimization Algorithm (GOA) [44] Particle Swarm Optimization (PSO) [40] Gray Wolf Optimization (GWO) [45], Multi-Verse Optimization (MVO) [46, 47], and chaotic dynamic weight particle swarm optimization (CDW-PSO) [48] and the results obtained are listed in Table 3. In Table 3, the widely used 12 numerical functions are used and results of them are listed. The values less than 10−50 are assumed to be 0 in Table 3.

Table 3 Performance comparison results
Full size table

Table 3 shows the comparison results of the proposed hybrid chaotic map-based optimization method and the other widely used optimization methods. Twelve benchmark functions were used. According to Table 3, the proposed method achieved the best results for 10 numerical benchmark functions. The proposed LS-COA has not achieved the best result for F7 (Noise) and F10 (Griewank), because CDW-PSO achieved optimal result in these functions.

Minimization curves of the used function for comparisons are shown in Fig. 4.

Fig. 4
figure 4figure 4

Minimization curves of selected functions

Full size image

We showed the minimization curves of some numerical functions of the proposed method and the other previously presented methods. As seen in Fig. 4, the minimization capability of the proposed method is superior to others. The proposed LS-COA reached 0 for F5 function in the first or second step. Therefore, we cannot show it in the Fig. 4. It has wonderful minimization performance for F5 function.

To show the effectiveness of the proposed logistic-sine map-based chaotic optimization method, an engineering problem is used and it is called as compression spring design problem. It is a constrained engineering problem because the optimum value is searched in a limited space. The mathematical definitions of this problem are given below [49] (Fig. 5).

$$f\left( {x_{1} ,x_{2} ,x_{3} } \right) = \left( {x_{3} + 2} \right)x_{1}^{2} x_{2}$$
(8)
$$g_{1} \left( {x_{1} ,x_{2} ,x_{3} } \right) = 1 - \frac{{x_{2}^{3} x_{3} }}{{71785x_{1}^{4} }} \le 0$$
(9)
$$g_{2} \left( {x_{1} ,x_{2} ,x_{3} } \right) = \frac{{x_{2} \left( {4x_{2} - x_{1} } \right)}}{{12566x_{1}^{3} \left( {x_{2} - x_{1} } \right)}} + \frac{1}{{5108x_{1}^{2} }} \le 0$$
(10)
$$g_{3} \left( {x_{1} ,x_{2} ,x_{3} } \right) = 1 - \frac{{140.45x_{1} }}{{x_{2}^{2} x_{3} }} \le 0$$
(11)
$$g_{4} \left( {x_{1} ,x_{2} } \right) = \frac{{2x_{1} + 2x_{2} }}{3} - 1 \le 0$$
(12)
$$x_{1} \in \left[ {0.05,2} \right], \quad x_{2} \in \left[ {0.25,1.3} \right], \quad x_{3} \in \left[ {2,15} \right]$$
(13)

In Eqs. 8–13, this engineering problem is mathematically defined. As seen from these equations, this problem has 3 inputs which are called as \(x_{1}\), \(x_{2}\) and \(x_{3}\) and the output functions are \(f\left( {x_{1} ,x_{2} ,x_{3} } \right)\). \(g_{1} \left( {x_{1} ,x_{2} ,x_{3} } \right)\), \(g_{2} \left( {x_{1} ,x_{2} ,x_{3} } \right)\), \(g_{3} \left( {x_{1} ,x_{2} ,x_{3} } \right)\), and \(g_{4} \left( {x_{1} ,x_{2} ,x_{3} } \right)\) are restrictive functions. The main aim of this problem is to minimize \(f\left( {x_{1} ,x_{2} ,x_{3} } \right)\) function. In order to show effectiveness of the proposed logistic-sine map-based chaotic optimization method, a comparison table is given and our results are compared with SCA [18], PSO [40], Ant Colony Optimization [8] (ACO) and WOA [3] are chosen. The comparatively results of this problem are listed in Table 4.

Fig. 5
figure 5

Graphical representation of the compression spring design problem [50]

Full size image
Table 4 Comparatively results of the compression spring design problem
Full size table

Table 4 clearly shows that the proposed LS-COA achieved the best result among the selected methods.

7 Discussion

The proposed chaotic optimization algorithm used one dimensional (1D) hybrid chaotic map to update particles. LS-COA is a particle-based method. The fitness functions frequently used in the literature were used in comparisons. The displacement of particles in the LS-COA method is calculated using the logistic-sine map. The seed value of the logistic-sine map was obtained using the best particle. The fact that both the logistic-sine map has good random properties and that the seed value is produced from the best particle makes LS-COA produce optimum results better. In order to test the proposed LS-COA, 16 numerical benchmark functions extensively used in the literature were chosen, and the results obtained were compared with the other state of art methods. These are SCA [18], WOA [3], GOA [44], PSO [40], GWO [45], MVO [46], and CDW-PSO [48]. LS-COA achieved the best result in 10 of the 12 numerical benchmark functions. Additionally, the minimization curves showed that the LS-COA has a good minimization ability. In order to show the effectiveness of the proposed LS-COA, the compression spring design problem was used. This problem is a real-world optimization problem, and the proposed LS-COA achieved high performance in this problem. The advantages of the proposed hybrid chaotic map-based optimization algorithm are given below.

  • The proposed method has faster minimization abilities (see Fig. 4).

  • To compare the results of the proposed method, the commonly used 12 numerical benchmark functions are used. According to the results, the proposed method outperforms.

  • The mathematical structure and algorithm of the proposed method are clear and simple. Hence, it can be basically used to solve real-world problems.

  • The proposed method is the first hybrid chaotic map-based optimization method as we know. This situation clearly shows the originality of the proposed method.

  • Compression spring design problem was also used to test the proposed hybrid chaotic map-based optimization method and high success rate was obtained. The obtained result shows that the proposed method can be used to solve other real-world engineering problems (see Table 4).

8 Conclusions

In this study, a new chaotic optimization method is proposed based on the logistic-sine map. The proposed method is a meta-heuristic swarm optimization technique and the logistic-sine map, a hybrid chaotic map, is used to update the particle. The chaotic range of the logistic-sine map was found to be higher than the logistic map and sine map and showed better properties than the logistic map and sine map. The proposed LS-COA was used to perform such processes as initial particles generation, step calculation, seed value determination, random value (r) generation particle updating, finding personal best value, and calculating the best value sections by using the logistic-sine map. The proposed method is an effective method based on simple mathematical principles. To test the performance of this method, the widely used numerical benchmark functions and compression spring design problem were used. Experimental results showed that the proposed chaotic optimization method performed successfully. This study has shown that optimum solutions of mathematically unsolvable problems can be found in real-life by using the proposed logistic-sine-based optimization method.

In this study, success of the 1D hybrid chaotic map on the optimization problem was shown. In the future works, different chaotic maps can be utilized as optimization methods instead of image encryption method. Otherwise, other real-world non-polynomial (NP) problems can be solved by using the proposed logistic-sine-based chaotic optimization method. In the machine learning, one of the most important problems is to select distinctive features. This method can be utilized as feature selector in the machine learning methods.