An efficient intuitionistic fuzzy MULTIMOORA approach based on novel aggregation operators for the assessment of solid waste management techniques

Abstract

This paper intends to propose a multi-attribute group decision making (MAGDM) methodology based on MULTIMOORA under IFS theory for application in the assessment of solid waste management techniques. The present work is divided into three folds. The first fold is that some novel operational laws for intuitionistic fuzzy numbers are introduced and a series of aggregation operators based on them are developed. The properties related to new operations are discussed in detail. The second fold is that particle swarm optimization (PSO) algorithm is applied for attribute weight determination by formulating a non-linear optimization model with the goal of maximizing the distance of each alternative from negative ideal solution and minimizing the distance from positive ideal solution. Lastly, a MAGDM method based on MULTIMOORA is put forward and is applied in ranking different solid waste management techniques by taking various social, economical, environmental and technological factors into consideration. The reliability and effectiveness of the proposed methodology is explored by comparing the obtained results with several existing studies. The sensitivity analysis is done by taking different parameter values in order to show the stability of the proposed method.

1 Introduction

The solid waste management (SWM) is need of the hour because it is emerging as one of the major issues in almost all countries and has become a crucial factor in environment protection and natural resources conservation. Effective SWM is a necessary step to be taken in this growing world in order to prevent the earth’s ecosystem from damaging and to preserve the health of living beings. Keeping in view the growing need of SWM, nowadays a wide variety of methods such as composting, recycling, pyrolysis, landfills etc. are being used for the disposal of solid waste. It has been analyzed that most often different methods lead to conflicting objectives within the selected attribute set. Therefore, the proper assessment of various SWM techniques is essential in order to choose the optimal waste disposal methods. However, the process of ranking different methods of SWM requires proper administration as the various methods vary in cost, time, reliability, technology and affect different range of population. Often these parameters of SWM are uncertain in nature and the ignorance of uncertainty in such parameters may lead us to wrong selection of SWM technique. For instance, the preference values given by decision makers while assessing SWM techniques may be in approximate form. The exact values may not be given and the values may lie within a range. Also, the data may not be represented using precise scientific terms but rather is given using linguistic terms such as “high”, “medium” and “low”. Hence, the issue of SWM is becoming more and more serious due to the presence of uncertainty in almost all system variables. The uncertainties have made it complex to figure out reasonable improvement technique for SWM. This issue can be handled by utilizing fuzzy set theory and its various extensions [40, 46].

MAGDM is a tool in which more than one individuals make a decision regarding the available alternatives before them which are characterized by different attribute (criteria). The final decision made is then no longer attributable to any single individual of the group as all the members collectively contribute to the outcome. Recently, many researchers applied multi-attribute decision making (MADM) methods in the area of SWM. For instance, [1] applied three MADM methods namely TOPSIS (“Technique for order preference by similarity to ideal solution”), PROMETHEE (“preference ranking organization method for enrichment evaluations”) and fuzzy TOPSIS in order to evaluate ten disposal alternatives which are further assessed under eighteen criteria. Cheng et al. [14] integrated MADM and inexact mixed integer linear programming methods for optimal selection of landfill site alternatives considered in the SWM problem. Mir et al [36] applied TOPSIS in order to obtain the most optimal SWM method by comparing and ranking the scenarios. Wang et al. [46] developed MAGDM method in order to prioritize municipal SWM techniques and also developed a technique for determining criteria weights objectively. Generowicz et al. [27] applied multi-criteria decision analysis in order to develop a method which gives the planning procedure of waste management system in European cities or regions. In addition to these, many other researchers and scholars [15, 43, 52] applied MADM methods in SWM field.

In every real world system, due to undeniable presence of uncertainty, the task of handling imprecise and imperfect information is becoming more and more challenging. As the complexities in the socio-economic environments are increasing day by day therefore, dealing with uncertain information has become a basic concern. In order to incorporate uncertainty into system description efficiently, numerous models [2, 53] have been designed and introduced so far. For instance, in light of handling such complexities and uncertainties, [53] put forward the theory of fuzzy sets (FSs) in which a unique real number, belonging to [0,1], is assigned to each entity of the universal set and this number is called as membership degree (MD). The FS theory was put forward on the basis of the fundamental assumption that if any element of the universal set is assigned a MD, say z ∈ [0,1] then, automatically the non-membership degree (NMD) of that element is considered to be 1 − z. However, [2] pointed out that due to the presence of hesitation degree in human decisions and judgements, sum of MDs and NMDs is not necessarily one always. In light of this fact, [2] introduced an intuitionistic fuzzy set (IFS) theory characterized by NMDs, MDs and hesitation degrees and this theory proved quite successful in modeling uncertain and vague information more efficiently and effectively.

Nowadays, the fundamental aspect for all types of knowledge based systems, from image processing to decision-making (DM), from pattern recognition to machine learning is aggregation and fusion of information. In most of the practical MADM problems, it is often required to accumulate some numerical values and this is when aggregation operators (AOs) play a fundamental role. More generally, it can be said that the process of aggregation makes use of distinct information pieces to make it possible to reach at some conclusion or decision. Various scholars and researchers have presented their theories and methodologies [8, 19, 28, 45, 60] for analyzing the problems of DM and applied it to the various different disciplines. From these works, it is evident that the two major aspects of MADM process are: (i) how to aggregate the information (ii) how to obtain the criteria weights objectively. A great attention is paid towards aggregating uncertain information using AOs. For instance, [31] proposed intuitionistic fuzzy (IF) geometric interaction averaging AOs and applied them in the MADM process. Garg [22] proposed generalized interactive geometric interaction operators using einstein operations under IFS theory and further developed interactive AOs in [23]. Huang et al. [33] gave the hamachar operational laws and averaging and ordered averaging operators based on proposed operations. Garg [24] improved the existing Einstein operations and developed new operators based on improved operations. Ye [51] developed hybrid AOs and gave a DM approach of mechanical design scheme. Besides these, numerous authors and researchers [3, 21, 25, 30, 48, 49] presented their theories and methodologies for analyzing the problems of DM. Towards the second aspect of MADM process, [12] proposed a method for determination of criteria weight based on PSO [34] under interval-valued IFS environment, which was further improved in [11]. Das and Guha [17] proposed criteria weights determination technique based on multi-objective optimization problem [18, 50], PSO and penalty function [4] under IFS environment. Xu [47] proposed a method for determining ordered weighted averaging operator weights based on normal distribution.

Recently, a wide variety of new MADM methods have been developed and applied in various DM problems under different environments. For instance, [13] developed MADM method based on TOPSIS and similarity measures under IFS environment. Peng and Ma [37] put forward a novel score function, a MADM method based on it and combinative distance-based assessment (CODAS) using pythagorean fuzzy sets and applied their proposed technique for making decision regarding teaching evaluation system. [44] proposed multi-attributive border approximation area comparison (MABAC) based MAGDM method under q-rung orthopair fuzzy environment and further applied it in choosing construction projects. Stanujkic and Karabasevic [42] extended weighted aggregated sum product assessment (WASPAS) technique for IF numbers and applied it in a case of website evaluation. Further, [54] extended the WASPAS approach under interval-valued IFS theory. Apart from these MADM methods, [5] developed the multi-objective optimization by ratio analysis (MOORA) and further extended it to MOORA plus the full multiplicative form (MULTIMOORA) [6]. MULTIMOORA is a technique having characteristics of three MADM approaches which include additive utility functions, multiplicative utility functions and the reference point approach. Zhang et al. [59] proposed MULTIMOORA approach for IF numbers which facilitates the aggregation of different parts of MULTIMOORA and further applied it for assessing energy storage technologies. Zavadskas et al. [55] developed MULTIMOORA approach for interval-valued IF numbers and applied it in engineering problems. Dahooie et al [16] enhanced the performance of MULTIMOORA by giving correlation coefficient and standard deviation based objective weight determination method. Hafezalkotob et al. [29] utilized interval numbers based fuzzy logic concept for developing new approach based on MULTIMOORA. Stanujkic et al. [41] gave a new extension of the MULTIMOORA approach under bipolar FS environment. Zavadskas et al. [56] proposed novel DM method based on MULTIMOORA for m-generalized q-neutrosophic sets. Further, [57] applied MULTIMOORA approach and interval valued neutrosophic sets to present a novel heuristic evaluation methodology. Recently, many researchers and scholars applied MULTIMOORA technique in various environmental problems [26, 35, 38, 39].

From these works, it is noticed that MULTIMOORA approach is an effective approach utilized for solving real life environmental problems as this method combines the features of three MADM methods. Also, it is analyzed that in our everyday life, we experience various situations, where we need a mathematical function having the ability to reduce a set of numbers into a unique representative one. Therefore, the study of AOs is a significant part of MADM problems. Information aggregation has become basic concern in MADM process. Recently, the issue of how to aggregate information has gained much attention of many authors due to their extensive uses in various fields for example environmental issues, pattern recognition, image processing and information retrieval. After reviewing the existing AOs under IFS environment, it is noted that most of the fusion processes are based on simple algebraic operations. Therefore, the task of developing new AOs is still a meaningful and challenging task. The development of new operations may provide more choice to decision maker during the process of aggregation in order to take a sound decision. Motivated by these, the principle theoretical and practical contributions of the presented work are:

• 1) Novel operational laws for IF numbers are proposed and their properties are investigated in detail. Further, based on these operations, novel IF weighted averaging/geometric (IFWA/IFWG), IF ordered weighted averaging/geometric (IFOWA/IFOWG) and IF hybrid weighted averaging/ geometric (IFHWA/IFHWG) operators are proposed. The proposed operators depend on a parameter k which may assume any real value greater than 1. The influence of the parameter k on the decision results is discussed in detail.

• 2) A new method for determining attribute weights with the goal of maximizing the distance of alternatives from negative ideal and minimizing the distance from positive ideal simultaneously is proposed. As these targets lead to formulation of multi-objective optimization problem (MOOP) therefore, these are converted to single objective optimization problem by constructing appropriate membership functions corresponding to each fuzzy objective [9, 61]. The proposed methodology for weight determination leads to formulation of non-linear optimization problem and is solved using PSO, which is one of the most efficient and widely used evolutionary algorithm [20]. The PSO algorithm has a wide advantages over the other algorithm such as Genetic algorithm (GA). For instance, PSO algorithm helps in improving the solution at every stage and its characteristic helps in fast convergence towards the solutions whereas other metaheuristic algorithm such as GA does not provide such guidance mechanism. Also, in PSO, it does not require any additional parameter to tune the algorithm while the GA needs some parameters such as crossover, mutation etc. Further, PSO utilizes memory for storing the previous best solutions achieved by each candidate. This feature stops the candidate from diverting in unwanted direction as if some candidate starts moving towards unwanted path and the solution quality starts degrading then the solutions are directed to the previous stage through the pbest component.

• 3) A MAGDM approach based on MULTIMOORA and the proposed novel AOs is developed which combines the features of three MADM techniques namely additive utility functions (the ratio system approach (RSA)), multiplicative utility functions (the full multiplicative form (FMF)) and the reference point method (RPM). The final ranking of the alternatives is done by using dominance property [7].

• 4) The proposed methodology is applied in assessing various SWM techniques which are characterized by economic, social, technological and environmental criteria. The effectiveness of the presented approach results is demonstrated by comparing them with several most widely used MADM methods based on TOPSIS [13], CODAS [37], MABAC [44] and WASPAS [42]. The detailed sensitivity analysis by taking different parameter values k, utilized in the proposed AOs, is done. The influence of the parameter k, on different parts of MULTIMOORA and hence on final ranking of alternatives is discussed.

The remaining work is categorized into seven main sections. Section 2 recapitulates some brief ideas on IFS, MOOP and PSO. In Section 3, novel operational laws are proposed and their properties are discussed in detail. Based on these novel operations, IFWA, IFWG, IFOWA, IFOWG, IFHWA and IFHWG AOs are developed and their properties are investigated in Section 4. Further, Section 5 represents a method for determination of attribute weights objectively based on non-linear optimization problem and PSO. Section 6 presents a MAGDM methodology based on MULTIMOORA, novel AOs and PSO. The assessment of SWM techniques is done using proposed MAGDM approach in Section 7 and its results are compared with existing studies for validating the presented approach. Section 8 communicates the concluding comments.

2 Preliminaries

Some basic concepts related to IFS theory, MOOP and PSO are reviewed in this Section. Throughout the section, $\mathcal {U}$ represents the universal set.

2.1 Basic concepts

Definition 1

[2] An IFS, $\mathcal {I}$ on $\mathcal {U}$, is given as $\mathcal {I}=\{(x,\chi (x),\varphi (x)) \mid x \in \mathcal {U} \},$ where $\chi , \varphi : \mathcal {U} \rightarrow [0,1]$ represent the membership and non-membership functions respectively and satisfy the relation 0 ≤ χ(x) + φ(x) ≤ 1 ∀ $x \in \mathcal {U}$ and h(x) = 1 − χ(x) − φ(x) represents the hesitation degree of x in $\mathcal {I}$. If $\mathcal {U}$ contains only one element, then, for convenience, IFS $\mathcal {I}$ over $\mathcal {U}$ is written as (χ,φ) where χ,φ ∈ [0,1] and 0 ≤ χ + φ ≤ 1 and is called IF number (IFN).

Definition 2

[2] For two IFSs $\mathcal {I}_{1}=\{(x,\chi _{1}(x),\varphi _{1}(x)) \mid x \in \mathcal {U}\}$ and $\mathcal {I}_{2}=\{(x,\chi _{2}(x),\varphi _{2}(x)) \mid x \in \mathcal {U}\}$ defined on $\mathcal {U}$, we have:

• (i) $\mathcal {I}_{1}\subseteq \mathcal {I}_{2}$ if χ₁(x) ≤ χ₂(x), φ₁(x) ≥ φ₂(x) ∀ $x \in \mathcal {U}$.

• (ii) $\mathcal {I}_{1}=\mathcal {I}_{2}$ ⇔ $\mathcal {I}_{1}\subseteq \mathcal {I}_{2}$ and $\mathcal {I}_{2}\subseteq \mathcal {I}_{1}$.

• (iii) $\mathcal {I}_{1}^{c}=\{(x,\varphi _{1}(x),\chi _{1}(x)) \mid x \in \mathcal {U}\}$.

Definition 3

[2] For two IFSs $\mathcal {I}_{1}=\{\left (x,\chi _{1}(x),\varphi _{1}(x)\right ) \mid x \in \mathcal {U}\}$ and $\mathcal {I}_{2}=\{\left (x,\chi _{2}(x),\varphi _{2}(x)\right ) \mid x \in \mathcal {U}\}$ defined on $\mathcal {U}$, we have:

• (i) $\mathcal {I}_{1} \cup \mathcal {I}_{2}=\left \{\left (x,\max \limits \left (\chi _{1}(x),\chi _{2}(x)\right ),\min \limits \left (\varphi _{1}(x),\varphi _{2}(x)\right )\right ) \mid x \in \mathcal {U}\right \}$

• (ii) $\mathcal {I}_{1} \cap \mathcal {I}_{2}=\left \{\left (x,\min \limits \left (\chi _{1}(x),\chi _{2}(x)\right ),\max \limits \left (\varphi _{1}(x),\varphi _{2}(x)\right )\right ) \mid x \in \mathcal {U}\right \}$

• (iii) $\mathcal {I}_{1} \oplus \mathcal {I}_{2}=\left \{\left (x,\chi _{1}(x)+\chi _{2}(x)-\chi _{1}(x)\chi _{2}(x),\varphi _{1}(x)\varphi _{2}(x)\right ) \mid x \in \mathcal {U}\right \}$

• (iv) $\mathcal {I}_{1} \otimes \mathcal {I}_{2}=\left \{\left (x,\chi _{1}(x)\chi _{2}(x),\varphi _{1}(x)+\varphi _{2}(x)-\varphi _{1}(x)\varphi _{2}(x)\right ) \mid x \in \mathcal {U}\right \}$

Definition 4

[49] The score $\mathcal {S}$ and an accuracy ${\mathscr{H}}$ functions are given as

$$ \begin{array}{@{}rcl@{}} \mathcal{S}(\mathcal{I}_{1})&=&\chi_{1}-\varphi_{1} \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} \text{and~~} \mathcal{H}(\mathcal{I}_{1})&=&\chi_{1}+\varphi_{1} \end{array} $$

(2)

for an IFN $\mathcal {I}_{1}=(\chi _{1},\varphi _{1} )$. Further, depending on $\mathcal {S}$ and ${\mathscr{H}}$ functions, a comparison law between two IFNs $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$ is defined as, if $\mathcal {S}(\mathcal {I}_{1}) > \mathcal {S}(\mathcal {I}_{2})$ then, $\mathcal {I}_{1} \succ \mathcal {I}_{2}$ and if $\mathcal {S}(\mathcal {I}_{1}) = \mathcal {S}(\mathcal {I}_{2})$ then, calculate ${\mathscr{H}}(\mathcal {I}_{1})$ and ${\mathscr{H}}(\mathcal {I}_{2})$. If ${\mathscr{H}}(\mathcal {I}_{1}) >{\mathscr{H}}(\mathcal {I}_{2})$ then, $\mathcal {I}_{1} \succ \mathcal {I}_{2}$. Here, the symbol ‘≻’ stands for ‘preferred to’.

Definition 5

[49] For ‘n’ IFNs $\mathcal {I}_{v}=(\chi _{v}, \varphi _{v} )$ (v = 1,2,…,n), the IF weighted averaging (IFWA) and IF weighted geometric (IFWG) operators are defined as:

$$ \begin{array}{@{}rcl@{}} \text{IFWA}\left( \mathcal{I}_{1},\mathcal{I}_{2}, \ldots, \mathcal{I}_{n}\right) &=& \left( 1-\prod\limits_{v=1}^{n} \left( 1-\chi_{v}\right)^{\psi_{v}}, \prod\limits_{v=1}^{n}\left( \varphi_{v}\right)^{\psi_{v}}\right) \\ \text{IFWG}\left( \mathcal{I}_{1},\mathcal{I}_{2}, \ldots, \mathcal{I}_{n}\right) &=& \left( \prod\limits_{v=1}^{n}\left( \chi_{v}\right)^{\psi_{v}}, 1-\prod\limits_{v=1}^{n} \left( 1-\varphi_{v}\right)^{\psi_{v}}\right) \end{array} $$

where $\psi =\left (\psi _{1},\psi _{2},\ldots ,\psi _{n}\right )^{T}$ is the weight vector associated with ‘n’ IFNs $\mathcal {I}_{v}$ such that ψ_v > 0 and $\sum \limits _{v=1}^{n} \psi _{v}=1$.

Definition 6

[21] For IFNs $\mathcal {I}_{v}=\left (\chi _{v}, \varphi _{v}\right )$ (v = 1,2), the following operational laws are defined:

• (i) $\mathcal {I}_{1} \oplus \mathcal {I}_{2} =\left (\frac {\chi _{1}+\chi _{2}-2\chi _{1}\chi _{2}}{1-\chi _{1}\chi _{2}},\frac {\varphi _{1}\varphi _{2}}{\varphi _{1}+\varphi _{2}-\varphi _{1}\varphi _{2}}\right )$

• (ii) $\mathcal {I}_{1} \otimes \mathcal {I}_{2} =\left (\frac {\chi _{1}\chi _{2}}{\chi _{1}+\chi _{2}-\chi _{1}\chi _{2}},\frac {\varphi _{1}+\varphi _{2}-2\varphi _{1}\varphi _{2}}{1-\varphi _{1}\varphi _{2}}\right )$

Definition 7

[48] For two IFSs $\mathcal {I}_{1}=\{(x,\chi _{1}(x),\varphi _{1}(x)) \mid x \in \mathcal {U}\}$ and $\mathcal {I}_{2}=\{(x,\chi _{2}(x),\varphi _{2}(x)) \mid x \in \mathcal {U}\}$ defined on $\mathcal {U}=\left \{x_{1},x_{2},\ldots , x_{n} \right \}$, the weighted euclidean distance among them is defined as:

$$ d\left( \mathcal{I}_{1},\mathcal{I}_{2}\right)=\sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{1}(x_{v})-\chi_{2}(x_{v})\right)^{2} +\left( \varphi_{1}(x_{v})-\varphi_{2}(x_{v})\right)^{2}+\left( h_{1}(x_{v})-h_{2}(x_{v})\right)^{2}\right]\right\}} $$

(3)

where ψ_v is the weight of the elements $x_{v} \in \mathcal {U}$ such that ψ_v > 0 and $\sum \limits _{v=1}^{n} \psi _{v}=1$.

2.2 Multi-objective optimization problem

A MOOP is concerned with mathematical optimization problem which involve more than one objective function to be optimized. Generally, MOOP can be formulated as follows:

$$ \left. \begin{aligned} &\max/\min f=\left( f_{1}(x),f_{2}(x), \ldots, f_{Q}(x)\right) \\ &\text{subject to} ~~\mathcal{A}_{p}(x) \leq 0 \quad \quad p=1,2, \ldots, P ;\\ &~~~~~~~~~~~~~~~~~~\mathcal{B}_{k}(x)=0 \quad \quad k=1,2, \ldots, K ;\\ &~~~~~~~~~~~~~~~ x_{r}^{(l)} \leq x_{r} \leq x_{r}^{(u)} \quad r=1,2, \ldots, n . \end{aligned} \quad \right\} $$

Here f₁(x),f₂(x),…,f_Q(x) are individual objective functions and $x=(x_{1},x_{2},\ldots , x_{n}) \in \mathbb {R}^{n}$ is a vector of decision variables. The MOOP is designed to find a feasible $x \in \mathbb {R}^{n}$ which gives optimal value of objective function $f=\left (f_{1}(x),f_{2}(x), \ldots , f_{Q}(x)\right )$. In MOOP, no single feasible solution exists which optimizes all objective functions simultaneously. Therefore, it leads us to find the best compromise solution, also known as pareto optimal solution [18] and is defined as follows:

Definition 8

[18] A feasible solution $x^{*} \in \mathbb {R}^{n}$ is said to be pareto optimal, if it satisfies the following conditions.

• (i) There does not exist any $x \in \mathbb {R}^{n}$ satisfying f_q(x) ≥ f_q(x^∗) $\left (f_{q}(x) \leq f_{q}(x^{*})\right )$ ∀ q = 1,2,…,Q in case of maximization (minimization) problem.

• (ii) There exists at least one objective function f_q satisfying f_q(x^∗) > f_q(x) $\left (f_{q}(x^{*}) < f_{q}(x)\right )$ in case of maximization (minimization) problem for q ∈{1,2,…,Q}.

Further, for solving a constrained optimization problem, penalty functions are used. Penalty function replaces a constrained optimization problem to an unconstrained optimization problem whose solution ideally converge to the solution of the original constrained problem. In order to formulate penalty function, consider the following optimization problem:

$$ \left. \begin{aligned} &\max/\min ~\mathcal{F}(x)\\ &\text{subject to} ~~\mathcal{A}_{p}(x) \leq 0 \quad \quad p=1,2, \ldots, P \end{aligned} \quad \right\} $$

(4)

If there are equality constraints in the optimization problem such as ${\mathscr{B}}_{k}(x)=0$, then, these can be converted to inequality constraints as ${\mathscr{B}}_{k}(x) \leq 0$ and $-{\mathscr{B}}_{k}(x)\leq 0$.

Yang et al. [50] defined the penalty function as

$$ \mathbb{F}(x)=\mathcal{F}(x)+y(t)\mathcal{H}(x) $$

(5)

Here $\mathcal {F}(x)$ is the original objective function, y(t) is penalty value which is dynamically modified, t is the current iteration number of the algorithm and ${\mathscr{H}}(x)$ is penalty factor given as:

$$ \mathcal{H}(x)=\sum\limits_{p=1}^{P} {{{\varOmega}}}\left( \mathcal{Z}_{p}(x)\right)\times \left( \mathcal{Z}_{p}(x)\right)^{\gamma\left( \mathcal{Z}_{p}(x)\right)} $$

(6)

where $\mathcal {Z}_{p}(x)=\max \limits \left \{0,\mathcal {A}_{p}(x)\right \}$ ∀ p = 1,2,…,P; $\mathcal {A}_{p}(x)$ are the constraints defined in optimization problem (4). The functions y, Ω and γ depend on the optimization problem and can be chosen accordingly.

2.3 Particle swarm optimization

PSO is one of the most successful and widely used algorithms utilized in solving non linear optimization problems. The concept of PSO was introduced by [34] and it was inspired by the flocking and schooling patterns of birds and fish. PSO is based on the communication and interaction i.e., members (particles) of the population (swarm) exchange information among them. It is a method that optimizes the problem by iteratively trying to improve a solution with respect to given measure of quality. During movement, each particle modifies its best position (local best) in accordance with its own previous best position and the best position of its neighbor particles (global best). PSO begins with a swarm of particles whose positions are initial solutions and velocities are arbitrarily given in the search space. In view of the local best and the global best data, the particles keeps on updating their velocities and positions.

Each particle updates its position and velocity, in each iteration, using the following equation:

$$ \begin{array}{@{}rcl@{}} \text{vel}_{v}^{(t+1)} &=& \omega^{(t)} \text{vel}_{v}^{(t)}+c_{1} r_{v1}^{(t)} \left( P_{v}^{(t)}-x_{v}^{(t)}\right)\\ &&+c_{2} r_{v2}^{(t)} \left( P_{g}^{(t)}-x_{v}^{(t)}\right) \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} x_{v}^{(t+1)} &=& x_{v}^{(t)}+\text{vel}_{v}^{(t+1)} \end{array} $$

(8)

In the above Eq. (7), v = 1,2,…,N, where N is the size of population, $\text {vel}_{v}^{(t+1)}$ is the velocity of the v th particle in (t + 1)th iteration, ω^(t) is the inertia weight, c₁ and c₂ are positive constants known as cognitive and social parameters respectively, $r^{(t)}_{v1}$ and $r^{(t)}_{v2}$ are random parameters belonging to [0,1] used during iteration number t. Also, $P^{(t)}_{v}$ represents the best position of the particle achieved so far and $P^{(t)}_{g}$ represents the particle having smallest/largest fitness value (objective function value), in accordance with $\min \limits /\max \limits$ problem, acquired till iteration t. A brief description of a pseudo code of PSO for maximizing a function f is given in Algorithm 1 that can be divided into two main phases: (i) Initialization of particles, velocity and global best positions (ii) Updation of particle position, particle velocity, personal best and global best. At initialization phase, the initial positions and velocities for each particle are initialized. If there are M number of variables (unknowns) to be optimized then, the time complexity for this phase is O(MN). In the second phase, the position and velocity of each particle is updated and fitness value is computed for each iteration t. Let the maximum number of iterations be denoted by Z. Hence, the time complexity for this phase is O(MNZ).

3 New operational laws of IFNs

In this section, with the goal of enriching the base of IF operations, we propose new operations of IFNs based on logarithmic and exponential functions and investigate their properties in detail.

Definition 9

For IFNs $\mathcal {I}_{v}=\left (\chi _{v},\varphi _{v}\right )$, (v = 1,2), we define their operations as follows:

• (i) $\mathcal {I}_{1} \oplus \mathcal {I}_{2} = \left (\!1 - \frac {1}{1+ \log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right )}, \frac {1}{1+\log _{k}\left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}+k^{\frac {1-\varphi _{2}}{\varphi _{2}}}\! - 1\right )} \right )$;

• (ii) $\mathcal {I}_{1} \otimes \mathcal {I}_{2} = \left (\! \frac {1}{1+\log _{k}\left (k^{\frac {1-\chi _{1}}{\chi _{1}}}+k^{\frac {1-\chi _{2}}{\chi _{2}}}-1\right )}, 1-\frac {1}{1+ \log _{k}\left (k^{\frac {\varphi _{1}}{1-\varphi _{1}}}+k^{\frac {\varphi _{2}}{1-\varphi _{2}}} - 1\right )} \right )$

where k > 1 is a real number.

Remark 1

Consider the two functions $a(x,y)=1-\frac {1}{1+ \log _{k}\left (k^{\frac {x}{1-x}}+k^{\frac {y}{1-y}}-1\right )}$ and $b(x,y)=\frac {1}{1+\log _{k}\left (k^{\frac {1-x}{x}}+k^{\frac {1-y}{y}}-1\right )}$ where 0 ≤ x,y ≤ 1. Then, it is analyzed that b(x,y) = 1 − a(1 − x,1 − y). Therefore, the operations defined in Definition 9 can be re-written as $\mathcal {I}_{1} \oplus \mathcal {I}_{2}=\left (a\left (\chi _{1},\chi _{2}\right ),b\left (\varphi _{1},\varphi _{2}\right )\right )$ and $\mathcal {I}_{1} \otimes \mathcal {I}_{2}=\left (b\left (\chi _{1},\chi _{2}\right ),a\left (\varphi _{1},\varphi _{2}\right )\right )$ and hence, these operations satisfy the rule of constructing AOs given in [3].

Further, by taking k = 2, the values of the functions a(x,y) and b(x,y) are described in Fig. 1a and b respectively. These figures depict that the functions a(x,y) and b(x,y) are commutative, monotonically increasing with respect to x and y and are bounded as well. Also, these functions are defined for extreme values of x and y as depicted in the figures whereas the addition and multiplication operations defined in Definition 6 become undefined for extreme degrees of membership and non-membership.

Fig. 1

Values of functions a(x,y) and b(x,y) for different values of x and y

Theorem 1

For IFNs $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$, $\mathcal {I}_{1} \oplus \mathcal {I}_{2}$ and $\mathcal {I}_{1} \otimes \mathcal {I}_{2}$ are also IFNs.

Proof

Let $\mathcal {I}_{v}=\left (\chi _{v},\varphi _{v}\right )$, (v = 1,2) be two IFNs. Then, by definition of IFNs, we have 0 ≤ χ_v,φ_v,χ_v + φ_v ≤ 1 for each v = 1,2. Further, assume that $\mathcal {I}_{3}=\mathcal {I}_{1} \oplus \mathcal {I}_{2}= \left (\chi _{3},\varphi _{3}\right )$. By using Definition 9, we have $\chi _{3}=1-\frac {1}{1+ \log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right )}$ and $\varphi _{3}=\frac {1}{1+\log _{k}\left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}+k^{\frac {1-\varphi _{2}}{\varphi _{2}}}-1\right )}$. Now, in order to prove that $\mathcal {I}_{3}$ is IFN, it is sufficient to show that 0 ≤ χ₃,φ₃ ≤ 1 such that 0 ≤ χ₃ + φ₃ ≤ 1. Since, k > 1 and 0 ≤ χ₁,χ₂ ≤ 1. Therefore, $\log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right ) \geq 0$ ⇒ $1+ \log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right ) \geq 1$ ⇒ $0 \leq \frac {1}{1+ \log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right )} \leq 1$ ⇒ $0 \leq 1-\frac {1}{1+ \log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right )} \leq 1$. Also, as 0 ≤ φ₁,φ₂ ≤ 1 therefore, $\log _{k}\left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}+k^{\frac {1-\varphi _{2}}{\varphi _{2}}}-1\right )\geq 0$ ⇒ $1+\log _{k}\left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}+k^{\frac {1-\varphi _{2}}{\varphi _{2}}}-1\right ) \geq 1$ ⇒ $0 \leq \frac {1}{1+\log _{k}\left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}+k^{\frac {1-\varphi _{2}}{\varphi _{2}}}-1\right )} \leq 1$. Hence, 0 ≤ χ₃,φ₃ ≤ 1. Further, since 0 ≤ χ_v + φ_v ≤ 1 for each v = 1,2. Therefore, $\frac {\chi _{v}}{1-\chi _{v}} \leq \frac {1-\varphi _{v}}{\varphi _{v}}$ ⇒ $1+\log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right ) \leq 1+\log _{k}\left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}+k^{\frac {1-\varphi _{2}}{\varphi _{2}}}-1\right )$ ⇒ $\frac {1}{1+\log _{k}\left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}+k^{\frac {1-\varphi _{2}}{\varphi _{2}}}-1\right )} \leq \frac {1}{1+\log _{k}\left (k^{\frac {\chi _{1}}{1-\chi _{1}}}+k^{\frac {\chi _{2}}{1-\chi _{2}}}-1\right )}$. Hence,

$$ \begin{array}{@{}rcl@{}} \chi_{3}+\varphi_{3} &=& 1-\frac{1}{1+ \log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)} \\ &&+\frac{1}{1+\log_{k}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}+k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right)} \\ &\leq& 1-\frac{1}{1+ \log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)} \\ &&+\frac{1}{1+\log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)} =1 \end{array} $$

Also, χ₃,φ₃ ≥ 0 implies that χ₃ + φ₃ ≥ 0. Thus, 0 ≤ χ₃ + φ₃ ≤ 1. Hence, $\mathcal {I}_{3}=\mathcal {I}_{1} \oplus \mathcal {I}_{2}$ is an IFN. Proceeding in the similar manner, we can prove that $\mathcal {I}_{1} \otimes \mathcal {I}_{2}$ is also an IFN. □

Theorem 2

For two IFNs $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$, we have

• (i) $(\mathcal {I}_{1} \oplus \mathcal {I}_{2})^{c}=\mathcal {I}_{1}^{c} \otimes \mathcal {I}_{2}^{c}$;

• (ii) $(\mathcal {I}_{1} \otimes \mathcal {I}_{2})^{c}=\mathcal {I}_{1}^{c} \oplus \mathcal {I}_{2}^{c}$.

Proof

Here we prove the part (i) only, while part (ii) can be obtained in the similar manner. Using Definitions 2 and 9, we have

$$ \begin{array}{@{}rcl@{}} (\mathcal{I}_{1} \oplus \mathcal{I}_{2})^{c} &=& \left( 1-\frac{1}{1+ \log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)}, \frac{1}{1+\log_{k}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}+k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right)} \right)^{c} \\ &=& \left( \frac{1}{1+\log_{k}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}+k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right)}, 1-\frac{1}{1+ \log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)}\right) \\ &=& \left( \varphi_{1},\chi_{1}\right) \otimes \left( \varphi_{2},\chi_{2}\right) \\ &=& \mathcal{I}_{1}^{c} \otimes \mathcal{I}_{2}^{c} \end{array} $$

□

Theorem 3

For IFNs $\mathcal {I}_{1}$, $\mathcal {I}_{2}$ and $\mathcal {I}_{3}$, we have

• (i) $\mathcal {I}_{1} \oplus \mathcal {I}_{2}=\mathcal {I}_{2} \oplus \mathcal {I}_{1}$;

• (ii) $\mathcal {I}_{1} \otimes \mathcal {I}_{2}=\mathcal {I}_{2} \otimes \mathcal {I}_{1}$;

• (iii) $\mathcal {I}_{1} \oplus (\mathcal {I}_{2} \oplus \mathcal {I}_{3})=(\mathcal {I}_{1} \oplus \mathcal {I}_{2}) \oplus \mathcal {I}_{3}$;

• (iv) $\mathcal {I}_{1} \otimes (\mathcal {I}_{2} \otimes \mathcal {I}_{3})=(\mathcal {I}_{1} \otimes \mathcal {I}_{2}) \otimes \mathcal {I}_{3}$.

Proof

It is trial. □

Theorem 4

Let $\textbf {1}=\left (1,0\right )$ and $\textbf {0}=\left (0,1\right )$. Then, for any IFN $\mathcal {I}=\left (\chi ,\varphi \right )$, we have

• (i) $\mathcal {I} \oplus \textbf {1}=\textbf {1}$;

• (ii) $\mathcal {I} \otimes \textbf {0}=\textbf {0}$;

• (iii) $\mathcal {I} \oplus \textbf {0}=\mathcal {I}$;

• (iv) $\mathcal {I} \otimes \textbf {1}=\mathcal {I}$.

Proof

Follow from the Definition 9. □

Theorem 5

For IFNs $\mathcal {I}_{v}=\left (\chi _{\mathcal {I}_{v}},\varphi _{\mathcal {I}_{v}}\right )$ and $\mathcal {J}_{v}=\left (\chi _{\mathcal {J}_{v}},\varphi _{\mathcal {J}_{v}}\right )$ (v = 1,2) satisfying $\chi _{\mathcal {I}_{v}} \leq \chi _{\mathcal {J}_{v}}$ and $\varphi _{\mathcal {I}_{v}} \geq \varphi _{\mathcal {J}_{v}}$ for each v, we have

• (i) $\mathcal {I}_{1} \oplus \mathcal {I}_{2} \subseteq \mathcal {J}_{1} \oplus \mathcal {J}_{2}$;

• (ii) $\mathcal {I}_{1} \otimes \mathcal {I}_{2} \subseteq \mathcal {J}_{1} \otimes \mathcal {J}_{2}$.

Proof

Here we prove the part (i) only, while part (ii) can be obtained similarly. Let $\mathcal {I}_{1} \oplus \mathcal {I}_{2}=\left (\chi _{\mathcal {I}},\varphi _{\mathcal {I}}\right )$; $\mathcal {J}_{1} \oplus \mathcal {J}_{2}=\left (\chi _{\mathcal {J}},\varphi _{\mathcal {J}}\right )$; $\mathcal {A}=k^{\frac {\chi _{\mathcal {I}_{1}}}{1-\chi _{\mathcal {I}_{1}}}}+k^{\frac {\chi _{\mathcal {I}_{2}}}{1-\chi _{\mathcal {I}_{2}}}}-1$; ${\mathscr{B}}=k^{\frac {\chi _{\mathcal {J}_{1}}}{1-\chi _{\mathcal {J}_{1}}}}+k^{\frac {\chi _{\mathcal {J}_{2}}}{1-\chi _{\mathcal {J}_{2}}}}-1$; $\mathcal {C}=k^{\frac {1-\varphi _{\mathcal {I}_{1}}}{\varphi _{\mathcal {I}_{1}}}}+k^{\frac {1-\varphi _{\mathcal {I}_{2}}}{\varphi _{\mathcal {I}_{2}}}}-1$ and $\mathcal {D}=k^{\frac {1-\varphi _{\mathcal {J}_{1}}}{\varphi _{\mathcal {J}_{1}}}}+k^{\frac {1-\varphi _{\mathcal {J}_{2}}}{\varphi _{\mathcal {J}_{2}}}}-1$. Since, $\chi _{\mathcal {I}_{v}} \leq \chi _{\mathcal {J}_{v}}$ ⇒ $1-\chi _{\mathcal {I}_{v}} \geq 1-\chi _{\mathcal {J}_{v}}$ ⇒ $\frac {1}{1-\chi _{\mathcal {I}_{v}}} \leq \frac {1}{1-\chi _{\mathcal {J}_{v}}}$ ⇒ $\frac {\chi _{\mathcal {I}_{v}}}{1-\chi _{\mathcal {I}_{v}}} \leq \frac {\chi _{\mathcal {J}_{v}}}{1-\chi _{\mathcal {J}_{v}}}$ ⇒ $k^{\frac {\chi _{\mathcal {I}_{v}}}{1-\chi _{\mathcal {I}_{v}}}} \leq k^{\frac {\chi _{\mathcal {J}_{v}}}{1-\chi _{\mathcal {J}_{v}}}}$ ⇒ $\mathcal {A} \leq {\mathscr{B}}$⇒ $\log _{k}\left (\mathcal {A}\right ) \leq \log _{k}\left ({\mathscr{B}}\right )$ ⇒ $1+\log _{k}\left (\mathcal {A}\right ) \leq 1+\log _{k}\left ({\mathscr{B}}\right )$⇒ $\frac {1}{1+\log _{k}\left (\mathcal {A}\right )} \geq \frac {1}{1+\log _{k}\left ({\mathscr{B}}\right )}$ ⇒ $1-\frac {1}{1+\log _{k}\left (\mathcal {A}\right )} \leq 1-\frac {1}{1+\log _{k}\left ({\mathscr{B}}\right )}$ ⇒ $\chi _{\mathcal {I}} \leq \chi _{\mathcal {J}}$. Also, $\varphi _{\mathcal {I}_{v}} \geq \varphi _{\mathcal {J}_{v}}$⇒ $1-\varphi _{\mathcal {I}_{v}} \leq 1-\varphi _{\mathcal {J}_{v}}$ ⇒ $\frac {1-\varphi _{\mathcal {I}_{v}}}{\varphi _{\mathcal {I}_{v}}} \leq \frac {1-\varphi _{\mathcal {J}_{v}}}{\varphi _{\mathcal {J}_{v}}}$ ⇒ $k^{\frac {1-\varphi _{\mathcal {I}_{v}}}{\varphi _{\mathcal {I}_{v}}}} \leq k^{\frac {1-\varphi _{\mathcal {J}_{v}}}{\varphi _{\mathcal {J}_{v}}}}$ ⇒ $\mathcal {C} \leq \mathcal {D}$ ⇒ $\log _{k}\left (\mathcal {C}\right ) \leq \log _{k}\left (\mathcal {D}\right )$ ⇒ $1+\log _{k}\left (\mathcal {C}\right ) \leq 1+\log _{k}\left (\mathcal {D}\right )$ ⇒ $\frac {1}{1+\log _{k}\left (\mathcal {C}\right )} \geq \frac {1}{1+\log _{k}\left (\mathcal {D}\right )}$ ⇒ $\varphi _{\mathcal {I}} \geq \varphi _{\mathcal {J}}$. Hence, by using Definition 2, we have $\mathcal {I}_{1} \oplus \mathcal {I}_{2} \subseteq \mathcal {J}_{1} \oplus \mathcal {J}_{2}$. □

Remark 2

The operations defined in Definition 9 are monotonically increasing as depicted by Theorem 5. Therefore, for IFNs $\textbf {1}=\left (1,0\right )$, $\textbf {0}=\left (0,1\right )$, $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$, we have $\textbf {0}=\textbf {0}\oplus \textbf {0} \subseteq \mathcal {I}_{1} \oplus \mathcal {I}_{2} \subseteq \textbf {1} \oplus \textbf {1} =\textbf {1}$ and $\textbf {0} = \mathcal {I}_{1} \otimes \textbf {0} \subseteq \mathcal {I}_{1} \otimes \mathcal {I}_{2} \subseteq \textbf {1} \otimes \textbf {1} =\textbf {1}$. It implies that, the proposed operations $\mathcal {I}_{1} \oplus \mathcal {I}_{2}$ and $\mathcal {I}_{1} \otimes \mathcal {I}_{2}$ are bounded as well.

Theorem 6

Based on the addition operation defined in Definition 9, for any natural number ρ, we have

$$ \rho\mathcal{I}_{1} = \left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}\right) $$

(9)

Proof

We will prove the Eq. (9) by applying principle of mathematical induction on ρ.

• Step 1: For ρ = 2, using the addition operation defined in Definition 9, we have

  $$ \begin{array}{@{}rcl@{}} \mathcal{I}_{1} \oplus \mathcal{I}_{1}&=&\left( \chi_{1},\varphi_{1}\right) \oplus \left( \chi_{1},\varphi_{1}\right)\\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)}, \frac{1}{1+\log_{k}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}+k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)} \right) \\ &=&\left( 1-\frac{1}{1+ \log_{k}\left( 2k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)}, \frac{1}{1+\log_{k}\left( 2k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)}\right)\\ &=&\left( 1-\frac{1}{1+ \log_{k}\left( 2\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( 2\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}\right) \end{array} $$

  Hence, the Eq. (9) is true for ρ = 2.

• Step 2: Consider that the Eq. (9) holds for any natural number ρ = ρ₀. Then, for ρ = ρ₀ + 1, we have

  $$ \begin{array}{@{}rcl@{}} \left( \rho_{0}+1\right)\mathcal{I}_{1} &=& \underbrace{\mathcal{I}_{1}\oplus\mathcal{I}_{1}\oplus {\ldots} \oplus \mathcal{I}_{1}}_{(\rho_{0}+1) ~\text{times}} \\ &=& \left( \underbrace{\mathcal{I}_{1}\oplus\mathcal{I}_{1}\oplus {\ldots} \oplus \mathcal{I}_{1}}_{(\rho_{0}) ~\text{times}}\right)\oplus \mathcal{I}_{1} \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \rho_{0}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho_{0}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}\right) \oplus \left( \chi_1,\varphi_1\right) \\ &=& \left( 1-\frac{1}{1+\mathcal{A}},\frac{1}{1+\mathcal{B}}\right) \oplus \left( \chi_{\mathcal{I}_{1}},\varphi_{\mathcal{I}_{1}}\right) ~~~ \text{where}~~~ \mathcal{A}=\log_{k}\left( \rho_{0}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right) ~~\text{and}~~ \mathcal{B}=\log_{k}\left( \rho_{0}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)\\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( k^{\left( \frac{1-\frac{1}{1+\mathcal{A}}}{\frac{1}{1+\mathcal{A}}}\right)}+k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)}, \frac{1}{1+\log_{k}\left( k^{\left( \frac{1-\frac{1}{1+\mathcal{B}}}{\frac{1}{1+\mathcal{B}}}\right)}+ k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)} \right) \\ &=&\left( 1-\frac{1}{1+ \log_{k}\left( k^{\mathcal{A}}+k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)}, \frac{1}{1+\log_{k}\left( k^{\mathcal{B}}+k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)}\right) \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \rho_{0}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+k^{\frac{\chi_{1}}{1-\chi_{1}}}\right)}, \frac{1}{1+\log_{k}\left( \rho_{0}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+k^{\frac{1-\varphi_{1}}{\varphi_{1}}}\right)} \right) \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \left( \rho_{0}+1\right)\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \left( \rho_{0}+1\right)\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}\right) \end{array} $$

  Thus, the Eq. (9) is true for ρ = ρ₀ + 1. Hence, by principle of mathematical induction, the Eq. (9) holds for all natural numbers ρ.

□

Theorem 7

Based on the multiplication operation defined in Definition 9, for any natural number ρ, we have

$$ \begin{array}{@{}rcl@{}} \mathcal{I}_{1}^{\rho}&=&\underbrace{\mathcal{I}_{1}\otimes\mathcal{I}_{1}\otimes {\ldots} \otimes \mathcal{I}_{1}}_{\rho ~\text{times}} \\ &=& \left( \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\chi_{1}}{\chi_{1}}}-1\right)+1\right)}, 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\varphi_{1}}{1-\varphi_{1}}}-1\right)+1\right)}\right)\\ \end{array} $$

(10)

Proof

It can be obtained similarly as Theorem 6. □

The results of the Theorems 6 and 7 can be generalized to any positive real number as stated in the following Definition 10.

Definition 10

For IFN $\mathcal {I}_{1}$ and positive real number ρ, we have

• (i) $\rho \mathcal {I}_{1} = \left (1-\frac {1}{1+ \log _{k}\left (\rho \left (k^{\frac {\chi _{1}}{1-\chi _{1}}}-1\right )+1\right )}, \frac {1}{1+\log _{k}\left (\rho \left (k^{\frac {1-\varphi _{1}}{\varphi _{1}}}-1\right )+1\right )}\right )$;

• (ii) $\mathcal {I}_{1}^{\rho }=\left (\frac {1}{1+\log _{k}\left (\rho \left (k^{\frac {1-\chi _{1}}{\chi _{1}}}-1\right )+1\right )}, 1-\frac {1}{1+ \log _{k}\left (\rho \left (k^{\frac {\varphi _{1}}{1-\varphi _{1}}}-1\right )+1\right )}\right )$

Theorem 8

For IFN $\mathcal {I}_{1}$ and positive real number ρ, $\rho \mathcal {I}_{1}$ and $\mathcal {I}_{1}^{\rho }$ are also IFNs.

Proof

It can be obtained similarly as the proof of the Theorem 1. □

Theorem 9

For two IFNs $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$ and positive real number ρ, we have

• (i) $\left (\mathcal {I}_{1}^{c}\right )^{\rho }=\left (\rho \mathcal {I}_{1}\right )^{c}$.

• (ii) $\rho \left (\mathcal {I}_{1}^{c}\right )=\left (\mathcal {I}_{1}^{\rho }\right )^{c}$.

Proof Here we prove the part (i) only, while part (ii) can be obtained in the similar manner. Using Definitions 2 and 10, we have

$$ \begin{array}{@{}rcl@{}} \left( \mathcal{I}_{1}^{c}\right)^{\rho}&=&\left( \varphi_{1},\chi_{1}\right)^{\rho} \\ &=&\left( \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}, 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}\right) \\ &=&\left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}\right)^{c} \\ &=& \left( \rho \mathcal{I}_{1}\right)^{c} \end{array} $$

Theorem 10

For two IFNs $\mathcal {I}_{1}$ and $\mathcal {I}_{2}$ and positive real numbers ρ, ρ₁, ρ₂, we have

• (i) $\rho \left (\mathcal {I}_{1} \oplus \mathcal {I}_{2}\right )=\rho \mathcal {I}_{1} \oplus \rho \mathcal {I}_{2}$;

• (ii) $\left (\mathcal {I}_{1} \otimes \mathcal {I}_{2}\right )^{\rho }=\mathcal {I}_{1}^{\rho } \otimes \mathcal {I}_{2}^{\rho }$;

• (iii) $\left (\rho _{1}+\rho _{2}\right )\mathcal {I}_{1}=\rho _{1}\mathcal {I}_{1} \oplus \rho _{2}\mathcal {I}_{1}$;

• (iv) $\mathcal {I}_{1}^{\rho _{1}+\rho _{2}}=\mathcal {I}_{1}^{\rho _{1}} \otimes \mathcal {I}_{1}^{\rho _{2}}$.

Proof Here we prove the part (i) only, while others can be obtained in the similar manner. Using the operations defined in Definitions 9 and 10, we obtain that

$$ \begin{array}{@{}rcl@{}} \rho \left( \mathcal{I}_{1} \oplus \mathcal{I}_{2}\right) &=& \rho \left( 1-\frac{1}{1+ \log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)}, \frac{1}{1+\log_{k}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}+k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right)} \right) \\ &=& \rho \left( 1-\frac{1}{1+\mathcal{A}},\frac{1}{1+\mathcal{B}}\right) ~~~ \text{where}~~ \mathcal{A}=\log_{k}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right) ~~ \text{and}~~ \mathcal{B}=\log_{k}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}+k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right) \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\left( \frac{1-\frac{1}{1+\mathcal{A}}}{\frac{1}{1+\mathcal{A}}}\right)}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\left( \frac{1-\frac{1}{1+\mathcal{B}}}{\frac{1}{1+\mathcal{B}}}\right)}-1\right)+1\right)}\right) \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\mathcal{A}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\mathcal{B}}-1\right)+1\right)}\right) \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}+k^{\frac{\chi_{2}}{1-\chi_{2}}}-2\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}+k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-2\right)+1\right)}\right) \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+\rho\left( k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+\rho\left( k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right)+1\right)}\right) \\ &=& \left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}\right) \\ && \oplus \left( 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)+1\right)}, \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right)+1\right)}\right) \\ &=& \rho \mathcal{I}_{1} \oplus \rho \mathcal{I}_{2} \end{array} $$

Theorem 11

For IFN $\mathcal {I}_{1}$ and real number ρ > 0, the operation $\rho \mathcal {I}_{1}$ is monotonically increasing with respect to (w.r.t) $\mathcal {I}_{1}$ and ρ and the operation $\mathcal {I}_{1}^{\rho }$ is monotonically increasing w.r.t $\mathcal {I}_{1}$ and is decreasing w.r.t ρ

Proof

Consider the two functions

$$ c(x,y)=1-\frac{1}{1+ \log_{k}\left( x\left( k^{\frac{y}{1-y}}-1\right)+1\right)}~~ \text{and} ~~ s(x,y)=\frac{1}{1+\log_{k}\left( x\left( k^{\frac{1-y}{y}}-1\right)+1\right)} $$

where x > 0 and 0 ≤ y ≤ 1. Now, differentiating the functions “c” and “s” partially w.r.t x and y, we get

$$ \begin{array}{@{}rcl@{}} && \frac{\partial c}{\partial x}=\frac{\left( k^{\frac{y}{1-y}}-1\right)\log_{k}(e)}{\left( 1+ \log_{k}\left( x\left( k^{\frac{y}{1-y}}-1\right)+1\right)\right)^{2} \left( x\left( k^{\frac{y}{1-y}}-1\right)+1\right)} \geq 0 \quad;\quad \frac{\partial c}{\partial y}=\frac{ x \left( k^{\frac{y}{1-y}}\right)}{\left( 1+ \log_{k}\left( x\left( k^{\frac{y}{1-y}}-1\right)+1\right)\right)^{2} \left( x\left( k^{\frac{y}{1-y}}-1\right)+1\right) \left( 1-y\right)^{2}} \geq 0 ~; \\ && \frac{\partial s}{\partial x}=\frac{-\left( k^{\frac{1-y}{y}}-1\right)\log_{k}(e)}{\left( 1+ \log_{k}\left( x\left( k^{\frac{1-y}{y}}-1\right)+1\right)\right)^{2} \left( x\left( k^{\frac{1-y}{y}}-1\right)+1\right)} \leq 0 \quad;\quad \frac{\partial s}{\partial y}=\frac{ x \left( k^{\frac{1-y}{y}}\right)}{y^{2}\left( 1+ \log_{k}\left( x\left( k^{\frac{1-y}{y}}-1\right)+1\right)\right)^{2} \left( x\left( k^{\frac{1-y}{y}}-1\right)+1\right) } \geq 0. \end{array} $$

It gives that the function “c” is increasing w.r.t both x and y and the function “s” is increasing w.r.t y and is decreasing w.r.t x. Now, consider the two IFNs $\mathcal {I}_{v}=\left (\chi _{1},\varphi _{1}\right )$ (v = 1,2) such that $\mathcal {I}_{1} \subseteq \mathcal {I}_{2}$. Then, by using Definition 2, we have χ₁ ≤ χ₂ and φ₁ ≥ φ₂. Further, using the monotone properties of functions “c” and “s”, we obtain that

$$ \begin{array}{@{}rcl@{}} c\left( \rho,\chi_{1}\right)=1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)} &\leq & 1-\frac{1}{1+ \log_{k}\left( \rho\left( k^{\frac{\chi_{2}}{1-\chi_{2}}}-1\right)+1\right)}=c\left( \rho,\chi_{2}\right) \\ s\left( \rho,\varphi_{1}\right)=\frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)} &\geq& \frac{1}{1+\log_{k}\left( \rho\left( k^{\frac{1-\varphi_{2}}{\varphi_{2}}}-1\right)+1\right)}=s\left( \rho,\varphi_{2}\right) \end{array} $$

It implies that $\rho \mathcal {I}_{1} \subseteq \rho \mathcal {I}_{2}$. Similarly, it can be obtained that $\mathcal {I}_{1}^{\rho } \subseteq \mathcal {I}_{2}^{\rho }$ when $\mathcal {I}_{1} \subseteq \mathcal {I}_{2}$. Hence, the operations $\rho \mathcal {I}_{1}$ and $\mathcal {I}_{1}^{\rho }$ are increasing w.r.t $\mathcal {I}_{1}$. Further, consider two real numbers ρ₁ and ρ₂ such that 0 < ρ₁ ≤ ρ₂. Again, using the monotone properties of functions “c” and “s”, we obtain that

$$ \begin{array}{@{}rcl@{}} c\left( \rho_{1},\chi_{1}\right)=1-\frac{1}{1+ \log_{k}\left( \rho_{1}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)} &\leq & 1-\frac{1}{1+ \log_{k}\left( \rho_{2}\left( k^{\frac{\chi_{1}}{1-\chi_{1}}}-1\right)+1\right)}=c\left( \rho_{2},\chi_{1}\right) \\ s\left( \rho_{1},\varphi_{1}\right)=\frac{1}{1+\log_{k}\left( \rho_{1}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)} &\geq& \frac{1}{1+\log_{k}\left( \rho_{2}\left( k^{\frac{1-\varphi_{1}}{\varphi_{1}}}-1\right)+1\right)}=s\left( \rho_{2},\varphi_{1}\right) \end{array} $$

It gives that $\rho _{1}\mathcal {I}_{1} \!\subseteq \! \rho _{2}\mathcal {I}_{1}$. In the similar manner, it can be proved that $\mathcal {I}_{1}^{\rho _{2}} \subseteq \mathcal {I}_{1}^{\rho _{1}}$ when ρ₁ ≤ ρ₂. Hence, the operations $\rho \mathcal {I}_{1}$ and $\mathcal {I}_{1}^{\rho }$ are increasing and decreasing respectively w.r.t ρ. □

Moreover, by taking k = 2, the values of the function c(x,y) and s(x,y) are described in Fig. 2a and b respectively. In the figures, we have taken 0 < x ≤ 10 and 0 ≤ y ≤ 1. The monotonic behavior of the functions c(x,y) and s(x,y) is also depicted in the figures, which validates the Theorem 11.

Fig. 2

Values of functions c(x,y) and s(x,y) for different values of x and y

Remark 3

Using the Theorem 11, for IFNs $\textbf {1}=\left (1,0\right )$, $\textbf {0}=\left (0,1\right )$, $\mathcal {I}_{1}$ and real number ρ > 0, we have $\textbf {0}=\rho \textbf {0}\subseteq \rho \mathcal {I}_{1} \subseteq \rho \textbf {1}=\textbf {1}$ and $\textbf {0} = \textbf {0}^{\rho } \subseteq \mathcal {I}_{1}^{\rho } \subseteq \textbf {1}^{\rho }=\textbf {1}$. It implies that, the proposed operations $\rho \mathcal {I}_{1}$ and $\mathcal {I}_{1}^{\rho }$ are bounded also.

4 Aggregation operators of IFNs based on new operations

In this section, we develop averaging and geometric AOs, based on new introduced operations, under IFS theory for a collection of IFNs, denoted by Θ. Consider a collection of “n” IFNs $\mathcal {I}_{v}=\left (\chi _{v},\varphi _{v}\right )$, (v = 1,2,…,n) and the associated weight vector $\psi =\left (\psi _{1},\psi _{2}, \ldots , \psi _{n}\right )^{T}$, such that ψ_v > 0 and $\sum \limits _{v=1}^{n}\psi _{v}=1$.

Definition 11

A map $\text {IFWA}: {{{\varTheta }}}^{n} \rightarrow {{{\varTheta }}}$, defined as

$$ \begin{array}{@{}rcl@{}} \text{IFWA}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) &=& \psi_{1}\mathcal{I}_{1} \oplus \psi_{2}\mathcal{I}_{2} \oplus {\ldots} \oplus \psi_{n}\mathcal{I}_{n} \end{array} $$

(11)

is called as IF weighted averaging (IFWA) operator.

Theorem 12

The aggregated value acquired after applying IFWA operator on IFNs $\mathcal {I}_{v}$ (v = 1,2,…,n), is still IFN and is given as

$$ \text{IFWA}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) = \left( \!\!1 - \frac{1}{1 + \log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{\chi_{v}}{1-\chi_{v}}}\right)}, \frac{1}{1 + \log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{1-\varphi_{v}}{\varphi_{v}}}\!\right)}\!\!\right) $$

(12)

Proof

It can be obtained using Eq. (11) and the operations defined in Definitions 9 and 10. □

Definition 12

An IFWG operator is a map $\text {IFWG}: {{{\varTheta }}}^{n} \rightarrow {{{\varTheta }}}$, given as

$$ \begin{array}{@{}rcl@{}} \text{IFWG}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) &=& \mathcal{I}_{1}^{\psi_{1}} \otimes \mathcal{I}_{2}^{\psi_{2}} \otimes {\ldots} \otimes \mathcal{I}_{n}^{\psi_{n}} \end{array} $$

(13)

Theorem 13

The unique value obtained on using IFWG operator on IFNs $\mathcal {I}_{v}$ (v = 1,2,…,n), is still an IFN and is given as

$$ \text{IFWG}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) = \left( \!\frac{1}{1 + \log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{1-\chi_{v}}{\chi_{v}}}\right)},1 - \frac{1}{1 + \log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{\varphi_{v}}{1-\varphi_{v}}}\right)}\!\right) $$

(14)

In order to illustrate the working of the proposed IFWA and IFWG operator, we give an example as follows:

Example 1

Consider the four IFNs $\mathcal {I}_{1}=\left (0.2,0.3\right )$, $\mathcal {I}_{2}=\left (0.7,0.2\right )$, $\mathcal {I}_{3}=\left (0.5,0.1\right )$ and $\mathcal {I}_{4}=\left (0.3,0.2\right )$ and let $\psi =\left (0.25,0.30,0.15,0.30\right )^{T}$ be the weight vector associated with these IFNs. Without loss of generality, we choose k = 2. Based on these values, we have

$$ \begin{array}{@{}rcl@{}} \sum\limits_{v=1}^{4} \psi_{v} k^{\frac{\chi_{v}}{1-\chi_{v}}} &=& \psi_{1} k^{\left( \frac{\chi_{1}}{1-\chi_{1}}\right)}+\psi_{2} k^{\left( \frac{\chi_{2}}{1-\chi_{2}}\right)}+\psi_{3} k^{\left( \frac{\chi_{3}}{1-\chi_{3}}\right)}\\ &&+\psi_{4} k^{\left( \frac{\chi_{4}}{1-\chi_{4}}\right)} \\ &=& 0.25 \times 2^{\left( \frac{0.2}{1-0.2}\right)} + 0.30 \times 2^{\left( \frac{0.7}{1-0.7}\right)}\\ &&+0.15 \times 2^{\left( \frac{0.5}{1-0.5}\right)}+ 0.30 \times 2^{\left( \frac{0.3}{1-0.3}\right)} \\ &=& 0.25 \!\times\! 2^{0.2500} + 0.30 \times 2^{2.3333}+0.15 \\ &&\times 2^{1.0000}+0.30 \times 2^{0.2860} \\ &=& 0.25 \times 1.1892+0.30 \!\times\! 5.0397 + 0.15\\ &&\times 2.0000+0.30 \times 1.3459 \\ &=& 2.5130 \\ \text{and}~~ \sum\limits_{v=1}^{4} \psi_{v} k^{\frac{1-\varphi_{v}}{\varphi_{v}}} &=& \psi_{1} k^{\left( \frac{1-\varphi_{1}}{\varphi_{1}}\right)}+\psi_{2} k^{\left( \frac{1-\varphi_{2}}{\varphi_{2}}\right)}+\psi_{3} k^{\left( \frac{1-\varphi_{3}}{\varphi_{3}}\right)}\\ &&+\psi_{4} k^{\left( \frac{1-\varphi_{4}}{\varphi_{4}}\right)} \\ &=& 0.25 \times 2^{\left( \frac{1-0.3}{0.3}\right)} + 0.30 \times 2^{\left( \frac{1-0.2}{0.2}\right)}\\ &&+0.15 \times 2^{\left( \frac{1-0.1}{0.1}\right)}+ 0.30 \times 2^{\left( \frac{1-0.2}{0.2}\right)} \\ &=& 0.25 \times 2^{2.3333} + 0.30 \times 2^{4.0000}+0.15\\ &&\times 2^{9.0000}+0.30 \times 2^{4.0000} \\ &=& 0.25 \times 5.0397+0.30 \times 16.0000\\ &&+0.15 \times 512.0000+0.30 \times 16.0000 \\ &=& 87.6599 \end{array} $$

Further, using the Eq. (12), we have

$$ \begin{array}{@{}rcl@{}} \text{IFWA}\left( \mathcal{I}_{1}, \mathcal{I}_{2}, \mathcal{I}_{3}, \mathcal{I}_{4}\right) &=& \left( \!1 - \frac{1}{1 + \log_{2}\left( 2.5130\right)},\frac{1}{1 + \log_{2}\left( 87.6599\right)}\right) \\ &=& \left( 0.5707,0.1342\right) \end{array} $$

Proceeding in the similar manner, on utilizing Eq. (14), we obtain that $\text {IFWG}\left (\mathcal {I}_{1}, \mathcal {I}_{2}, \mathcal {I}_{3}, \mathcal {I}_{4}\right )=\left (0.2750,0.2172\right )$.

Further, it is noticed that the proposed IFWA and IFWG operators satisfy certain properties which are elaborated for IFWA operator as follows:

Property 1

(Idempotency) Let $\mathcal {I}_{0}$ be an IFN such that $\mathcal {I}_{v}=\mathcal {I}_{0}$ ∀ v. Then,

$$ \text{IFWA}(\mathcal{I}_{1}, \mathcal{I}_{2} {\ldots} \mathcal{I}_{n})= \mathcal{I}_{0} $$

Proof

Let $\mathcal {I}_{0}=\left (\chi _{0},\varphi _{0}\right )$. Since, $\mathcal {I}_{v}=\mathcal {I}_{0}$ ∀ v. It implies that χ_v = χ₀ and φ_v = φ₀ ∀ v. Further, using the fact that $\sum \limits _{v=1}^{n} \psi _{v}=1$ and Eq. (12), we have

$$ \begin{array}{@{}rcl@{}} \text{IFWA}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n})\!\! &=&\!\! \left( \!1 - \frac{1}{1 + \log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{\chi_{0}}{1-\chi_{0}}}\right)}, \frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{1-\varphi_{0}}{\varphi_{0}}}\!\right)}\!\right) \\ &=& \left( 1-\frac{1}{1+\log_{k}\left( k^{\frac{\chi_{0}}{1-\chi_{0}}}\right)}, \frac{1}{1+\log_{k}\left( k^{\frac{1-\varphi_{0}}{\varphi_{0}}}\right)}\right) \\ &=& \left( 1-\frac{1}{1+\frac{\chi_{0}}{1-\chi_{0}}}, \frac{1}{1+\frac{1-\varphi_{0}}{\varphi_{0}}}\right)=\left( \chi_{0},\varphi_{0}\right) \end{array} $$

Hence, $\text {IFWA}(\mathcal {I}_{1}, \mathcal {I}_{2}, \ldots , \mathcal {I}_{n})=\mathcal {I}_{0}$. □

Property 2

(Monotonicity) Let $\mathcal {I}_{v}$ and $\mathcal {J}_{v}$ be two collections of IFNs satisfying $\mathcal {I}_{v} \subseteq \mathcal {J}_{v}$ for each v. Then, we have

$$\text{IFWA}(\mathcal{I}_{1},\mathcal{I}_{2},\ldots,\mathcal{I}_{n}) \subseteq \text{IFWA}(\mathcal{J}_{1},\mathcal{J}_{2}, \ldots, \mathcal{J}_{n}).$$

Proof

Since, $\mathcal {I}_{v} \subseteq \mathcal {J}_{v}$ for each v. Then, by utilizing Theorem 5, we obtain that $\psi _{1}\mathcal {I}_{1} \oplus \psi _{2}\mathcal {I}_{2} \oplus {\ldots } \oplus \psi _{n}\mathcal {I}_{n} \subseteq \psi _{1}\mathcal {J}_{1} \oplus \psi _{2}\mathcal {J}_{2} \oplus {\ldots } \oplus \psi _{n}\mathcal {J}_{n}$. Hence, $\text {IFWA}(\mathcal {I}_{1},\mathcal {I}_{2},\ldots ,\mathcal {I}_{n}) \subseteq \text {IFWA}(\mathcal {J}_{1},\mathcal {J}_{2}, \ldots , \mathcal {J}_{n}).$□

Property 3

(Boundedness) Let $\mathcal {I}^{-}$ and and $\mathcal {I}^{+}$ be lower and upper bounds of a collection of “n” IFNs $\mathcal {I}_{v}$. Then,

$$\mathcal{I}^{-} \subseteq \text{IFWA}(\mathcal{I}_{1}, \mathcal{I}_{2} {\ldots} \mathcal{I}_{n}) \subseteq \mathcal{I}^{+} $$

Proof

Since, $\mathcal {I}^{-} \subseteq \mathcal {I}_{v} \subseteq \mathcal {I}^{+}$ ∀ v. Therefore, on utilizing Property 2, we have $\text {IFWA}(\mathcal {I}^{-}, \mathcal {I}^{-}, \ldots , \mathcal {I}^{-})\subseteq \text {IFWA}(\mathcal {I}_{1},$ $\mathcal {I}_{2}, \ldots , \mathcal {I}_{n}) \subseteq \text {IFWA}(\mathcal {I}^{+}, \mathcal {I}^{+}, \ldots , \mathcal {I}^{+})$. Further, by using Property 1, we obtain that $\mathcal {I}^{-} \subseteq \text {IFWA}(\mathcal {I}_{1}, \mathcal {I}_{2} {\ldots } \mathcal {I}_{n}) \subseteq \mathcal {I}^{+}$, which completes the proof. □

Further, we define ordered weighted averaging and geometric operators for aggregating IFNs. These operators have an associated weight vector and assign weights to the ordered positions of IFNs whereas in IFWA and IFWG operators weightage is given to IFNs itself.

Definition 13

A map $\text {IFOWA}: {{{\varTheta }}}^{n} \rightarrow {{{\varTheta }}}$, having associated weight vector $\phi =\left (\phi _{1},\phi _{2}, \ldots , \phi _{n}\right )^{T}$ satisfying ϕ_v > 0; $\sum \limits _{v=1}^{n} \phi _{v}=1$ and defined as

$$ \text{IFOWA}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) = \phi_{1}\mathcal{I}_{\tau(1)} \oplus \phi_{2}\mathcal{I}_{\tau(2)} \oplus {\ldots} \oplus \phi_{n}\mathcal{I}_{\tau(n)} $$

(15)

is called as IF ordered weighted averaging (IFOWA) operator. Here $\left (\tau (1), \tau (2), \ldots , \tau (n) \right )$ is an arrangement of (1,2,…,n) such that $S\left (\mathcal {I}_{\tau (v-1)}\right ) \geq S\left (\mathcal {I}_{\tau (v)}\right )$ for each v = 2,3,…,n.

Theorem 14

The aggregated value acquired after applying IFOWA operator on IFNs $\mathcal {I}_{v}$ (v = 1,2,…,n), is still an IFN and is given as

$$ \text{IFOWA}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n})= \left( 1-\frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{\chi_{\tau(v)}}{1-\chi_{\tau(v)}}}\right)}, \frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{1-\varphi_{\tau(v)}}{\varphi_{\tau(v)}}}\right)}\right) $$

(16)

Proof

It can be obtained by implementing the Eq. (15) and the operations given in Definitions 9 and 10. □

Definition 14

An IFOWG operator is a map $\text {IFOWG}: {{{\varTheta }}}^{n} \rightarrow {{{\varTheta }}}$, having associated weight vector $\phi =\left (\phi _{1},\phi _{2}, \ldots , \phi _{n}\right )^{T}$ satisfying ϕ_v > 0; $\sum \limits _{v=1}^{n} \phi _{v}=1$ and is defined as

$$ \text{IFOWG}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) = \mathcal{I}^{\phi_{1}}_{\tau(1)} \otimes \mathcal{I}^{\phi_{2}}_{\tau(2)} \otimes {\ldots} \otimes \mathcal{I}^{\phi_{n}}_{\tau(n)} $$

(17)

Theorem 15

On applying IFOWG operator on IFNs $\mathcal {I}_{v}$ (v = 1,2,…,n), the acquired value remains an IFN and is given as

$$ \text{IFOWG}(\mathcal{I}_{1}, \mathcal{I}_{2}, {\ldots} , \mathcal{I}_{n}) = \left( \frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{1-\chi_{\tau(v)}}{\chi_{\tau(v)}}}\right)},1-\frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{\varphi_{\tau(v)}}{1-\varphi_{\tau(v)}}}\right)}\right) $$

(18)

The working of the presented IFOWA and IFOWG operator is demonstrated through an example given as follows:

Example 2

Consider the four IFNs $\mathcal {I}_{1}=\left (0.2,0.3\right )$, $\mathcal {I}_{2}=\left (0.7,0.2\right )$, $\mathcal {I}_{3}=\left (0.5,0.1\right )$ and $\mathcal {I}_{4}=\left (0.3,0.2\right )$ and let $\phi =\left (0.19,0.28,0.31,0.22\right )^{T}$ be the weight vector associated with IFOWA operator. Further assume that k = 2. In order to aggregate IFNS $\mathcal {I}_{v}$(v = 1,2,3,4), we need to permute these IF numbers. For this, firstly we calculate their score values using (1) and these are obtained as $\mathcal {S}(\mathcal {I}_{1})=-0.1$, $\mathcal {S}(\mathcal {I}_{2})=0.5$, $\mathcal {S}(\mathcal {I}_{3})=0.4$ and $\mathcal {S}(\mathcal {I}_{4})=0.1$. Thus, $\mathcal {S}(\mathcal {I}_{2})>\mathcal {S}(\mathcal {I}_{3})>\mathcal {S}(\mathcal {I}_{4})>\mathcal {S}(\mathcal {I}_{1})$ which implies that $\mathcal {I}_{\tau (1)}=\left (0.7,0.2\right )$; $\mathcal {I}_{\tau (2)}=\left (0.5,0.1\right )$; $\mathcal {I}_{\tau (3)}=\left (0.3,0.2\right )$ and $\mathcal {I}_{\tau (4)}=\left (0.2,0.3\right )$. Now, proceeding as in Example 1, we obtain that $\sum \limits _{v=1}^{4} \phi _{v} k^{\frac {\chi _{\tau (v)}}{1-\chi _{\tau (v)}}}=2.1964$ and $\sum \limits _{v=1}^{4} \phi _{v} k^{\frac {1-\varphi _{\tau (v)}}{\varphi _{\tau (v)}}}= 152.4687$. Hence, using the Eq. (16), we have

$$ \begin{array}{@{}rcl@{}} \text{IFOWA}\left( \mathcal{I}_{1}, \mathcal{I}_{2}, \mathcal{I}_{3}, \mathcal{I}_{4}\right) &=& \left( 1-\frac{1}{1+\log_{2}\left( 2.1964\right)},\frac{1}{1+\log_{2}\left( 152.4687\right)}\right) \\ &=& \left( 0.5316,0.1212\right) \end{array} $$

Similarly, on utilizing Eq. (18), we obtain that $\text {IFOWG}(\mathcal {I}_{1},$ $\mathcal {I}_{2}, \mathcal {I}_{3}, \mathcal {I}_{4})= \left (0.2809,0.2030\right )$.

Remark 4

The Properties 1, 2 and 3 are also satisfied by the proposed IFOWA and IFOWG operators.

Since, in IFWA/IFWG operator weightage is assigned to IFNs itself whereas IFOWA/IFOWG operator has an associated weight vector which weights the ordered positions of IFNs and not the IFNs itself. Thus, in the AOs IFWA/IFWG and IFOWA/IFOWG, weight vector represent different aspects. In order to combine the characteristics of both IFWA/IFWG and IFOWA/IFOWG operators, in the next, we define IF hybrid weighted averaging and geometric operators.

Definition 15

A map $\text {IFHWA}: {{{\varTheta }}}^{n} \rightarrow {{{\varTheta }}}$, having associated weight vector $\phi =\left (\phi _{1},\phi _{2}, \ldots , \phi _{n}\right )^{T}$ satisfying ϕ_v > 0; $\sum \limits _{v=1}^{n} \phi _{v}=1$ and defined as

$$ \text{IFHWA}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) = \phi_{1}\dot{\mathcal{I}}_{\tau(1)} \oplus \phi_{2}\dot{\mathcal{I}}_{\tau(2)} \oplus {\ldots} \oplus \phi_{n}\dot{\mathcal{I}}_{\tau(n)} $$

(19)

is called as IF hybrid weighted averaging (IFHWA) operator. Here $\left (\tau (1), \tau (2), \ldots , \tau (n) \right )$ is an arrangement of (1,2,…,n) such that $S\left (\dot {\mathcal {I}}_{\tau (v-1)}\right ) \geq S\left (\dot {\mathcal {I}}_{\tau (v)}\right )$ for each v = 2,3,…,n. Also, $\dot {\mathcal {I}}_{v}=n\psi _{v} \mathcal {I}_{v}$ and ψ_v is the weightage corresponding to IFNs $\mathcal {I}_{v}$ for each v ∈{1,2,…,n}.

Theorem 16

The aggregated value acquired after applying IFHWA operator on IFNs $\mathcal {I}_{v}$ (v = 1,2,…,n), is still an IFN and is given as

$$ \text{IFHWA}(\mathcal{I}_{1}, \mathcal{I}_{2}, {\ldots} , \mathcal{I}_{n}) = \left( 1-\frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{\dot\chi_{\tau(v)}}{1-\dot\chi_{\tau(v)}}}\right)}, \frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{1-\dot\varphi_{\tau(v)}}{\dot\varphi_{\tau(v)}}}\right)}\right) $$

(20)

Proof

By implementing the Eq. (19) and the operations defined in Definitions 9 and 10, it can be obtained easily. □

Definition 16

An IFHWG operator is a map $\text {IFHWG}: {{{\varTheta }}}^{n} \rightarrow {{{\varTheta }}}$, having associated weight vector $\phi =\left (\phi _{1},\phi _{2}, \ldots , \phi _{n}\right )^{T}$ satisfying ϕ_v > 0; $\sum \limits _{v=1}^{n} \phi _{v}=1$ and is defined as

$$ \text{IFHWG}(\mathcal{I}_{1}, \mathcal{I}_{2}, \ldots, \mathcal{I}_{n}) = \left( \dot{\mathcal{I}}_{\tau(1)}\right)^{\phi_{1}} \otimes \left( \dot{\mathcal{I}}_{\tau(2)}\right)^{\phi_{2}} \otimes {\ldots} \otimes \left( \dot{\mathcal{I}}_{\tau(n)}\right)^{\phi_{n}} $$

(21)

Here $\left (\tau (1), \tau (2), \ldots , \tau (n) \right )$ is a permutation of (1,2,…,n) such that $S\left (\dot {\mathcal {I}}_{\tau (v-1)}\right ) \geq S\left (\dot {\mathcal {I}}_{\tau (v)}\right )$ for each v = 2,3,…,n. Also, $\dot {\mathcal {I}}_{v}=\left (\mathcal {I}_{v}\right )^{n\psi _{v}}$ and ψ_v is the weightage corresponding to IFNs $\mathcal {I}_{v}$ for each v ∈{1,2,…,n}.

Theorem 17

The value obtained after applying IFHWG operator on IFNs $\mathcal {I}_{v}$ (v = 1,2,…,n), is still an IFN and is given as

$$ \text{IFHWG}(\mathcal{I}_{1}, \mathcal{I}_{2}, {\ldots} , \mathcal{I}_{n}) = \left( \frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{1-\dot\chi_{\tau(v)}}{\dot\chi_{\tau(v)}}}\right)},1-\frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \phi_{v} k^{\frac{\dot\varphi_{\tau(v)}}{1-\dot\varphi_{\tau(v)}}}\right)}\right) $$

(22)

In order to demonstrate the working of the proposed IFHWA and IFHWG operators, we illustrate an example as follows:

Example 3

Consider the four IFNs $\mathcal {I}_{1}=\left (0.2,0.3\right )$, $\mathcal {I}_{2}=\left (0.7,0.2\right )$, $\mathcal {I}_{3}=\left (0.5,0.1\right )$ and $\mathcal {I}_{4}=\left (0.3,0.2\right )$. Let $\phi =\left (0.19,0.28,0.31,0.22\right )^{T}$ be the weight vector associated with IFHWA operator and the vector $\psi =\left (0.25,0.30,0.15,0.30\right )^{T}$ represents weightage corresponding to IFNs $\mathcal {I}_{v}$ (v = 1,2,3,4). Further, assume that k = 2. Now, using the Definition 15, we have $\dot {\mathcal {I}}_{v}=n\psi _{v} \mathcal {I}_{v}$. It gives that $\dot {\mathcal {I}}_{1}=(4\times 0.25) \mathcal {I}_{1}=1\left (0.2,0.3\right )=\left (0.2,0.3\right )$. Further, $\dot {\mathcal {I}}_{2}=(4\times 0.30) \mathcal {I}_{2}=1.2\left (0.7,0.2\right )$. Now, on utilizing the operation, defined in Definition 10, we obtain that

$$ \begin{array}{@{}rcl@{}} \dot{\mathcal{I}}_{2}&=&\left( 1-\frac{1} {1+\log_{2}\left( 1+1.2\left( 2^{\left( \frac{0.7}{1-0.7}\right)}-1\right)\right)},\frac{1}{1+ \log_{2}\left( 1+1.2\left( 2^{\left( \frac{1-0.2}{0.2}\right)}-1\right)\right)}\right) \\ &=&\left( 1-\frac{1}{1+\log_{2}\left( 5.8476\right)},\frac{1}{1+\log_{2}\left( 19.0000\right)}\right) \\ &=&\left( 0.7181,0.1906\right) \end{array} $$

Similarly, we obtain that $\dot {\mathcal {I}}_{3}=\left (0.4041,0.1079\right )$ and $\dot {\mathcal {I}}_{4}=\left (0.3337,0.1906\right )$. Now, using Eq. (1), it can be easily computed that $\mathcal {S}\left (\dot {\mathcal {I}}_{1}\right )=-0.1000$, $\mathcal {S}\left (\dot {\mathcal {I}}_{2}\right )=0.5276$, $\mathcal {S}\left (\dot {\mathcal {I}}_{3}\right )=0.2961$ and $\mathcal {S}\left (\dot {\mathcal {I}}_{4}\right )=0.1432$. Thus, $\mathcal {S}\left (\dot {\mathcal {I}}_{2}\right )>\mathcal {S}\left (\dot {\mathcal {I}}_{3}\right )>\mathcal {S}\left (\dot {\mathcal {I}}_{4}\right )> \mathcal {S}\left (\dot {\mathcal {I}}_{1}\right )$ which implies that $\dot {\mathcal {I}}_{\tau (1)}=\left (0.7181,0.1906\right )$, $\dot {\mathcal {I}}_{\tau (2)}=\left (0.4041,0.1079\right )$, $\dot {\mathcal {I}}_{\tau (3)}=\left (0.3337,0.1906\right )$ and $\dot {\mathcal {I}}_{\tau (4)}=\left (0.2000,0.3000\right )$. Further, on utilizing Eq. (20), we obtain that $\text {IFHWA}(\mathcal {I}_{1}, \mathcal {I}_{2},\mathcal {I}_{3} , \mathcal {I}_{4})=\left (0.5705,0.1305\right )$. Proceeding in the similar manner, using Eq. (22), we may acquire that $\text {IFHWG}(\mathcal {I}_{1}, \mathcal {I}_{2},\mathcal {I}_{3} , \mathcal {I}_{4})=\left (0.2702,0.2215\right )$.

Remark 5

The proposed IFHWA and IFHWG operators also satisfy the properties of idempotency, monotonicity and boundedness.

5 Weight determination by PSO technique

In order to determine the attribute weights objectively, we consider a DM problem comprising of “m” alternatives $\mathcal {T}_{u}$ (u = 1,2,…,m) which are characterized by “n” criteria $\mathcal {C}_{v}$ (v = 1,2,…,n) such that each alternative is assessed in terms of IFNs $\mathcal {I}_{uv}=\left (\chi _{uv},\varphi _{uv}\right )$. Let ψ = (ψ₁,ψ₂,…,ψ_n)^T be the weight vector associated with “n” attributes such that ψ_v > 0 and $\sum \limits _{v=1}^{n} \psi _{v}=1$. If the weight vector ψ is partially known or completely unknown then, in order to determine attribute weights, we propose a method based on the target of minimizing the distance of each alternative from positive ideal $\mathcal {T}^{+}$ and maximizing the distance of each alternative from negative ideal $\mathcal {T}^{-}$ simultaneously.

For this, firstly we calculate the positive ideal alternative (PIA) $\mathcal {T}^{+}=\left (\mathcal {C}^{+}_{v}\right )_{1\times n}$ and the negative ideal alternative (NIA) $\mathcal {T}^{-}=\left (\mathcal {C}^{-}_{v}\right )_{1\times n}$ where $\mathcal {C}^{+}_{v}=\left (\chi ^{+}_{v},\varphi ^{+}_{v}\right )=\left (\max \limits _{u}\left \{\chi _{uv}\right \}, \min \limits _{u}\left \{\varphi _{uv}\right \}\right )$ and $\mathcal {C}^{-}_{v}=\left (\chi ^{-}_{v},\varphi ^{-}_{v}\right )=\left (\min \limits _{u}\left \{\chi _{uv}\right \}, \max \limits _{u}\left \{\varphi _{uv}\right \}\right )$. Then, by utilizing Eq. (3), we calculate the distance of each alternative $\mathcal {T}_{u}$ from PIA $\mathcal {T}^{+}$ and NIA $\mathcal {T}^{-}$ as given below:

$$ \begin{array}{@{}rcl@{}} d^{+}_{u}&=&d\left( \mathcal{T}_{u},\mathcal{T}^{+}\right)= \sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{+}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{+}_{v}\right)^{2}+\left( h_{uv}-h^{+}_{v}\right)^{2}\right]\right\}} \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} d^{-}_{u}&=&d\left( \mathcal{T}_{u},\mathcal{T}^{-}\right)= \sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{-}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{-}_{v}\right)^{2}+\left( h_{uv}-h^{-}_{v}\right)^{2}\right]\right\}} \end{array} $$

(24)

where $h^{+}_{v}=1-\chi ^{+}_{v}-\varphi ^{+}_{v}$ and $h^{-}_{v}=1-\chi ^{-}_{v}-\varphi ^{-}_{v}$ are hesitation degrees of $\mathcal {C}^{+}_{v}$ and $\mathcal {C}^{-}_{v}$ respectively. For determining the weights objectively, we minimize $d^{+}_{u}$ and maximize $d^{-}_{u}$ corresponding to each alternative $\mathcal {T}_{u}$. In order to do so, we formulate the following multi-objective optimization model, corresponding to each alternative, given as:

$$ (\text{Model-1}:) \quad \begin{cases} a_{u}=\min\limits_{\psi} d^{+}_{u}=\sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{+}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{+}_{v}\right)^{2}+\left( h_{uv}-h^{+}_{v}\right)^{2}\right]\right\}} \\ b_{u}=\max\limits_{\psi}d^{-}_{u}= \sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{-}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{-}_{v}\right)^{2}+\left( h_{uv}-h^{-}_{v}\right)^{2}\right]\right\}} \\ \text{subject to} \quad \psi_{v} \in \bigtriangleup \quad,\quad \sum \limits_{v=1}^{n} \psi_{v}=1 \quad,\quad \psi_{v} \geq 0 \end{cases} $$

(25)

Here △ is the set of partial information about the weight vector. However, if there is no partial information available about the criteria weight then, △ becomes empty set. Since, the problem given in is (25) is MOOP, so it cannot have optimal solution for all the objectives simultaneously. Therefore, we need to find such a solution which satisfies all the objectives to some extent and such a solution is known as pareto optimal solution [18] or best compromise solution. In this perspective, because of the fuzziness present in the human judgements, it is normal to expect that the decision-maker may have fuzzy objective for each objective function. [9] and [17] optimized such fuzzy objectives, corresponding to each objective function, by constructing membership functions.

Now, in order to construct membership functions, we solve two single objective optimization problems corresponding to each objective function $d^{+}_{u}$ and $d^{-}_{u}$ (u = 1,2,…,m). For instance, for objective function $d^{+}_{u}$, we solve the following two optimization problems, given in Eqs. (26) and (27), separately.

$$ \begin{cases} \max\limits_{\psi} d^{+}_{u}=\sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{+}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{+}_{v}\right)^{2}+\left( h_{uv}-h^{+}_{v}\right)^{2}\right]\right\}} \\ \text{subject to} \quad \psi_{v} \in \bigtriangleup \quad,\quad \sum \limits_{v=1}^{n} \psi_{v}=1 \quad,\quad \psi_{v} \geq 0 \end{cases} $$

(26)

and

$$ \begin{cases} \min\limits_{\psi} d^{+}_{u}=\sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{+}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{+}_{v}\right)^{2}+\left( h_{uv}-h^{+}_{v}\right)^{2}\right]\right\}} \\ \text{subject to} \quad \psi_{v} \in \bigtriangleup \quad,\quad \sum \limits_{v=1}^{n} \psi_{v}=1 \quad,\quad \psi_{v} \geq 0 \end{cases} $$

(27)

On solving the problems given in the above Eqs. (26) and (27), we get two values ${a^{L}_{u}}$ and ${a^{U}_{u}}$, minimum and maximum values respectively of the objective function $d^{+}_{u}$. Similarly, by solving minimization and maximization problems for the objective function $d^{-}_{u}$, stated in Eqs. (28) and (29), we obtain ${b^{L}_{u}}$ and ${b^{U}_{u}}$ as minimum and maximum values respectively.

$$ \begin{cases} \max\limits_{\psi} d^{-}_{u}=\sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{-}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{-}_{v}\right)^{2}+\left( h_{uv}-h^{-}_{v}\right)^{2}\right]\right\}} \\ \text{subject to} \quad \psi_{v} \in \bigtriangleup \quad,\quad \sum \limits_{v=1}^{n} \psi_{v}=1 \quad,\quad \psi_{v} \geq 0 \end{cases} $$

(28)

and

$$ \begin{cases} \min\limits_{\psi} d^{-}_{u}=\sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{-}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{-}_{v}\right)^{2}+\left( h_{uv}-h^{-}_{v}\right)^{2}\right]\right\}} \\ \text{subject to} \quad \psi_{v} \in \bigtriangleup \quad,\quad \sum \limits_{v=1}^{n} \psi_{v}=1 \quad,\quad \psi_{v} \geq 0 \end{cases} $$

(29)

Further, we introduce membership functions $\mu \left (d^{+}_{u}\right )$ and $\mu \left (d^{-}_{u}\right )$ corresponding to each objective function $d^{+}_{u}$ and $d^{-}_{u}$ respectively as follows:

$$ \mu\left( d^{+}_{u}\right)= \begin{cases} 1, &\text{if}~ d^{+}_{u} \leq {a^{L}_{u}} \\ 1-\frac{d^{+}_{u}-{a^{L}_{u}}}{{a^{U}_{u}}-{a^{L}_{u}}}, &\text{if}~ {a^{L}_{u}} < d^{+}_{u} \leq {a^{U}_{u}} \\ 0, &\text{otherwise} \end{cases} $$

(30)

and

$$ \mu\left( d^{-}_{u}\right)= \begin{cases} 1, &\text{if}~ d^{-}_{u} \geq {b^{U}_{u}} \\ 1-\frac{{b^{U}_{u}}-d^{-}_{u}}{{b^{U}_{u}}-{b^{L}_{u}}}, &\text{if}~ {b^{L}_{u}} \leq d^{-}_{u} < {b^{U}_{u}} \\ 0, &\text{otherwise} \end{cases} $$

(31)

Now, using these characteristic functions, we transform the MOOP, given in Eq. (25), to the following optimization problem.

$$ \begin{cases} \max\left( \mu\left( d^{+}_{1}\right),\mu\left( d^{+}_{2}\right), \ldots, \mu\left( d^{+}_{m}\right),\mu\left( d^{-}_{1}\right),\mu\left( d^{-}_{2}\right), \ldots, \mu\left( d^{-}_{m}\right)\right) \\ \text{subject to} \quad \psi_{v} \in \bigtriangleup \quad,\quad \sum \limits_{v=1}^{n} \psi_{v}=1 \quad,\quad \psi_{v} \geq 0 \end{cases} $$

(32)

Further, in order to transform the above multi-objective model, given in Eq. (32), to single objective optimization problem, we aggregate the membership values of the objective function. In other words, the objective function of the above optimization problem can be transformed to $g\left (\max \limits \left (\mu \left (d^{+}_{1}\right ),\mu \left (d^{+}_{2}\right ), \ldots , \mu \left (d^{+}_{m}\right ),\mu \left (d^{-}_{1}\right ),\mu \left (d^{-}_{2}\right )\right .\right .$, $\left .\left .\ldots , \mu \left (d^{-}_{m}\right )\right )\right )$ where g indicates an aggregation function. There are several choices to aggregate objective function such as max operator, min operator, arithmetic mean and geometric mean. Out of these choices, available for function g, we utilize min operator, motivated by the work [61]. Hence, multi-objective optimization problem, stated in Eq. (32), is transformed into the following single objective non-linear optimization model:

$$ (\text{Model-2}:) \quad \begin{cases} &\max \lambda \\ &\text{subject to}~ \lambda \leq \mu\left( d^{+}_{u}\right),~ \lambda \leq \mu\left( d^{-}_{u}\right), \\ & \psi_{v} \in \bigtriangleup \quad,\quad \sum \limits_{v=1}^{n} \psi_{v}=1 \quad,\quad \psi_{v} \geq 0 \end{cases} $$

(33)

Since, the terms $d^{+}_{u},d^{-}_{u}$ used in Eq. (33) are non-linear therefore, the nature of the Model 2 becomes non-linear too and some effective algorithms are required to find the global solution of such optimization problems. There are many methods available in the literature so far in order to find the global solution of such problems. Out of these techniques, one of the most efficient process is evolutionary algorithm (EA) approach [20]. The main benefit of utilizing EA technique is that any sort of pre-assumptions such as continuity and differentiability of the objective function are not required in it.

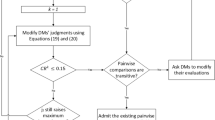
In this manuscript, we employ EA technique, namely PSO [34], in order to find the solution of Model 2. Since, the problem presented in Model 2 is constrained optimization problem therefore, firstly convert it to unconstrained optimization problem using penalty function as given in Eq. (5). Then, utilize PSO technique for solving this unconstrained non-linear optimization problem by using Algorithm 1 in MATLAB and obtain the optimal weight vector ψ = (ψ₁,ψ₂,…,ψ_n)^T.

6 Multiattribute group decision-making approach based on MULTIMOORA

This section presents an MAGDM approach in order to evaluate the available alternatives characterized by different criteria under IFS environment.

Consider a set $\{\mathcal {T}_{1}, \mathcal {T}_{2}, \ldots , \mathcal {T}_{m}\}$ of ‘m’ alternatives characterized by another collection $\{\mathcal {C}_{1}, \mathcal {C}_{2}, \ldots , \mathcal {C}_{n}\}$ of ‘n’ criteria is to be evaluated with the corresponding criteria weight vector ψ = (ψ₁,ψ₂,…,ψ_n)^T such that ψ_v > 0 and $\sum \limits _{v=1}^{n} \psi _{v}=1$. The given alternatives $\mathcal {T}_{u}$ are evaluated by ‘l’ different experts $\left \{\mathcal {E}^{(1)}, \mathcal {E}^{(2)}, \ldots , \mathcal {E}^{(l)}\right \}$ who give their rating values in terms of IFNs $\mathcal {I}^{(z)}_{uv}=\left (\chi ^{(z)}_{uv},\varphi ^{(z)}_{uv}\right )$ where $0 \leq \chi ^{(z)}_{uv}, \varphi ^{(z)}_{uv}, \chi ^{(z)}_{uv}+\varphi ^{(z)}_{uv} \leq 1$ for each z = 1,2,…,l; u = 1,2,…,m and v = 1,2,…n. The main objective of the problem is to order the alternatives from the most favorable to the least favorable ones. For this, we develop a MAGDM method, which involves the following steps:

• Step 1: (Construction of IF decision matrices:) Construct the IF decision matrices ${\mathscr{M}}^{(z)}=\left (\mathcal {I}^{(z)}_{uv}\right )_{m \times n}$ representing information related to all alternatives for the different criteria, given by ‘l’ experts, as:

  

  (34)

• Step 2: (Normalization:) Normalize the data by Eq. (35)

  $$ \mathcal{I}^{(z)}_{uv}= \begin{cases} \left( \chi^{(z)}_{uv},\varphi^{(z)}_{uv}\right) & ; \quad \text{if}~ \mathcal{C}_{v} ~ \text{is of benefit type} \\ \left( \varphi^{(z)}_{uv},\chi^{(z)}_{uv}\right) & ; \quad \text{if}~ \mathcal{C}_{v} ~ \text{is of cost type} \end{cases} $$

  (35)

• Step 3: (Aggregation of individual decision matrices into collective one:) Aggregate the individual IF decision matrices ${\mathscr{M}}^{(z)}=\left (\mathcal {I}^{(z)}_{uv}\right )_{m \times n}$, (z = 1,2,…,l) into collective one ${\mathscr{M}}=\left (\mathcal {I}_{uv}\right )_{m \times n}$ by utilizing either proposed IFOWA operator i.e.,

  $$ \begin{array}{@{}rcl@{}} \mathcal{I}_{uv}&=& \text{IFOWA}\left( \mathcal{I}^{(1)}_{uv},\mathcal{I}^{(2)}_{uv}, \ldots, \mathcal{I}^{(l)}_{uv}\right)\\ &=&\left( \chi_{uv},\varphi_{uv}\right) \\ &=& \!\!\left( \!1 - \frac{1}{1 + \log_{k}\!\left( \!\sum\limits_{z=1}^{l} \phi_{z} k^{\frac{\chi^{\tau(z)}_{uv}}{1-\chi^{\tau(z)}_{uv}}}\!\right)}, \frac{1}{1 + \log_{k}\left( \sum\limits_{z=1}^{l} \phi_{z} k^{\frac{1-\varphi^{\tau(z)}_{uv}}{\varphi^{\tau(z)}_{uv}}}\right)}\right)\\ \end{array} $$

  (36)

  or proposed IFOWG operator i.e.,

  $$ \begin{array}{@{}rcl@{}} \mathcal{I}_{uv}&=& \text{IFOWG}\left( \mathcal{I}^{(1)}_{uv},\mathcal{I}^{(2)}_{uv}, \ldots, \mathcal{I}^{(l)}_{uv}\right)\\ &=&\left( \chi_{uv},\varphi_{uv}\right) \\ &=& \!\!\!\left( \!\frac{1}{1 + \log_{k}\left( \sum\limits_{z=1}^{l} \phi_{z} k^{\frac{1-\chi^{\tau(z)}_{uv}}{\chi^{\tau(z)}_{uv}}}\!\right)}, 1 - \frac{1}{1 + \log_{k}\left( \sum\limits_{z=1}^{l} \phi_{z} k^{\frac{\varphi^{\tau(z)}_{uv}}{1-\varphi^{\tau(z)}_{uv}}}\!\right)}\!\right)\\ \end{array} $$

  (37)

  Here the weight vector $\phi =\left (\phi _{1},\phi _{2}, \ldots , \phi _{l}\right )^{T}$ associated with IFOWA/IFOWG operator can be obtained using normal distribution method [47] given as:

  $$ \phi_{z}=\frac{\exp\left[-\frac{\left( z-\frac{l+1}{2}\right)^{2}}{2{\sigma^{2}_{l}}}\right]}{\sum\limits_{z^{\prime}=1}^{l} \exp\left[-\frac{\left( z^{\prime}-\frac{l+1}{2}\right)^{2}}{2{\sigma^{2}_{l}}}\right]} \qquad \text{where} \quad \sigma_{l}=\sqrt{\frac{1}{l}\sum\limits_{z=1}^{l} \left( z-\frac{l+1}{2}\right)^{2}} $$

  (38)

• Step 4: (Computation of criteria weight vector:) Compute PIA, NIA, $d^{+}_{u}$ and $d^{-}_{u}$ for each u. Solve the optimization problems, corresponding to each alternative, given in Eqs. (26)–(29). Based on the solutions of these problems, develop the membership functions as described in Eqs. (30) and (31). Further, solve the non-linear optimization problem given in Eq. (33) by applying PSO Algorithm 1 and obtain the criteria weight vector ψ = (ψ₁,ψ₂,…,ψ_n)^T.

• Step 5: (The RSA:) It is based on the additive utility function. It involves the following two steps:

  • Step 5a: Aggregate the IF values $\mathcal {I}_{uv}$ into collective one $\mathcal {I}_{u}$ by utilizing proposed IFWA operator i.e.,

    $$ \begin{array}{@{}rcl@{}} \mathcal{I}_{u}&=&\text{IFWA}\left( \mathcal{I}_{u1},\mathcal{I}_{u2}, \ldots, \mathcal{I}_{un}\right) \\ &=& \left( \chi_{u},\varphi_{u}\right) \\ &=& \left( 1-\frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{\chi_{uv}}{1-\chi_{uv}}}\right)}, \frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{1-\varphi_{uv}}{\varphi_{uv}}}\right)}\right) \end{array} $$

    (39)

  • Step 5b: Obtain the score values of accumulated IFNs $\mathcal {I}_{u}$ using the Eq. (1). However if any two of the score values are equal then, calculate accuracy values using the Eq. (2). Further, rank the alternatives $\mathcal {T}_{u}$ using the Definition 4.

• Step 6: (The RPM:) It includes the following steps:

  • Step 6a: Identify the reference point i.e., PIA $\mathcal {T}^{+}\!\!=$ $\left (\mathcal {C}^{+}_{v}\right )_{1\times n}$ where $\mathcal {C}^{+}_{v} = \left (\chi ^{+}_{v},\varphi ^{+}_{v}\right )=(\max \limits _{u}$ $\left \{\chi _{uv}\right \}, \min \limits _{u}\left \{\varphi _{uv}\right \})$.

  • Step 6b: Calculate the distance of accumulated value $\mathcal {I}_{uv}$, corresponding to every alternative $\mathcal {T}_{u}$, from PIA $\mathcal {T}^{+}$ by using the Eq. (40) given as:

    $$ d\left( \mathcal{T}_{u},\mathcal{T}^{+}\right)=\sqrt{\frac{1}{2}\sum\limits_{v=1}^{n}\left\{\psi_{v}\left[\left( \chi_{uv}-\chi^{+}_{v}\right)^{2} +\left( \varphi_{uv}-\varphi^{+}_{v}\right)^{2}+\left( h_{uv}-h^{+}_{v}\right)^{2}\right]\right\}} $$

    (40)

  • Step 6c: Rank the alternatives in accordance with the increasing values of $d\left (\mathcal {T}_{u},\mathcal {T}^{+}\right )$.

• Step 7: (The FMF:) It is based on multiplicative utility function and consists of the following steps:

  • Step 7a: By utilizing proposed IFWG operator, accumulate the IF values $\mathcal {I}_{uv}$ into collective one $\mathcal {I}_{u}$ i.e.,

    $$ \begin{array}{@{}rcl@{}} \mathcal{I}_{u}&=&\text{IFWG}\left( \mathcal{I}_{u1},\mathcal{I}_{u2}, \ldots, \mathcal{I}_{un}\right) \\ &=& \left( \chi_{u},\varphi_{u}\right) \\ &=& \left( \frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{1-\chi_{uv}}{\chi_{uv}}}\right)}, 1-\frac{1}{1+\log_{k}\left( \sum\limits_{v=1}^{n} \psi_{v} k^{\frac{\varphi_{uv}}{1-\varphi_{uv}}}\right)}\right) \end{array} $$

    (41)

  • Step 7b: Calculate the score values of accumulated IFNs $\mathcal {I}_{u}$ using the Eq. (1). However if any two of the score values are equal then, obtain the accuracy values using the Eq. (2). Furthermore, obtain the ranking order of the alternatives $\mathcal {T}_{u}$ using the Definition 4.

• Step 8: (The final ranking:) Based on the ranking order of alternatives, obtained in Steps 5b, 6c and 7b, obtain the final ranking order of alternatives by applying dominance theory [7].

7 Ranking solid waste management techniques using proposed approach

In this section, we apply the proposed MAGDM approach based on MULTIMOORA in order to rank various techniques of SWM. Also, we compare the results of the proposed method with some of the prevailing IFS studies in order to show the validity and superiority of the proposed work.

7.1 Description and solution of the problem

With the growing human population, urbanization has increased rapidly [32, 58] and the production of solid waste has increased immensely. Therefore, nowadays the SWM has become a major concern in the urban areas particulary in the developing countries [38]. SWM is defined as the discipline associated with control of generation, storage, collection, transport or transfer, processing and disposal of solid waste materials in a way that best addresses the range of public health, conservation, economic, aesthetic, engineering, and other environmental considerations. One of the major environmental problems that developing nations are confronting nowadays is poor management and disposal of solid waste [10, 40]. It has been a significant environmental issue since the industrial revolution. The recognized techniques (labeled as alternatives), which are used for SWM, are described as follows:

• $\mathcal {T}_{1}$ Composting: This technique is a biological process in which micro-organisms, specifically fungi and bacteria, convert degradable organic waste into substances like humus. It gives formation a soil like product which is high in carbon and nitrogen. Good quality and environmental friendly manure is produced from the compost which is an excellent medium for growing plants and can be utilized for agricultural purposes as well.

• $\mathcal {T}_{2}$ Pyrolysis: In this method, solid wastes are chemically decomposed by heat without the presence of oxygen. It usually occurs under pressure and at temperatures of up to 430 degrees Celsius. The solid wastes are changed into gasses, solid residue of carbon, ash and small quantities of liquid.

• $\mathcal {T}_{3}$ Incineration: This method involves the burning of solid wastes at high temperatures until the wastes are turned into ashes. Incinerators are made in such a way that they do not give off extreme amounts of heat when burning solid wastes.

• $\mathcal {T}_{4}$ Recovery and Recycling: This technique is the way toward taking valuable however discarded things for the next use. Plastic bags, tins, glass and containers are often recycled automatically since, in many situations, they are likely to be scarce commodities.

• $\mathcal {T}_{5}$ Sanitary Landfill: In this technique, garbage is basically spread out in thin layers, compressed and covered with soil or plastic foam. If landfills are managed efficiently, it is an ensured sanitary waste disposal method.

Suppose that we are interested in ranking the above mentioned techniques $\mathcal {T}_{u}$ (u = 1,2,…,5) of SWM. The goal is to order these techniques $\mathcal {T}_{u}$ in descending order from the most important to least important. It is evident that in the process of techniques assessment, a number of quantitative and qualitative factors play a significant role. Therefore, we have considered four dimensions (Economy, Environmental, Technology and Society) and seven criteria $\mathcal {C}_{v}$ (v = 1,2,…,7) which influence the techniques $\mathcal {T}_{u}$, in the ranking process. The hierarchical structure of the considered criteria is described in the Fig. 3.

Fig. 3

The hierarchical structure of the criteria $\mathcal {C}_{v}$

We consult with four experts $\mathcal {E}^{(z)}$, (z = 1,2,3,4) who assess the SWM techniques $\mathcal {T}_{u}$ under criteria $\mathcal {C}_{v}$ and give their rating values in terms of IFNs.

The main procedure steps in order to rank the techniques $\mathcal {T}_{u}$, using proposed MAGDM method based on MULTIMOORA, described in the above section, are summarized as follows:

• Step 1: The rating values of each technique, given by four experts, are tabulated in Table 1. As the rating value of $\mathcal {T}_{1}$ under factor $\mathcal {C}_{1}$, given by $\mathcal {E}^{(1)}$, is $\left (0.1,0.8\right )$ which means that the membership term reveals that the expert $\mathcal {E}^{(1)}$ is 10 percent satisfied with the cost of technique $\mathcal {T}_{1}$ and 80 percent is not satisfied. In the similar manner, the rest of the data can be interpreted.

• Step 2: As the criteria $\mathcal {C}_{1}-\mathcal {C}_{4}$ and $\mathcal {C}_{7}$ are of cost type. Therefore, we convert them to benefit type using Eq. (35). The obtained normalized data values are tabulated in Table 2.

• Step 3: Using Eq. (38), the weight vector, corresponding to ordered weighted averaging/geometric operator is obtained as ϕ = (0.1550,0.3450, 0.3450,0.1550)^T. Further, without loss of generality (WLOG), by using Eq. (36) with k = 2, the rating values $\mathcal {I}^{(z)}_{uv}$, (z = 1,2,3,4) given by four experts are aggregated into collective one $\mathcal {I}_{uv}$. The acquired values corresponding to each technique $\mathcal {T}_{u}$ (u = 1,2,3) are depicted in Table 3.

  Further, using Eqs. (23) and (24), we have

  $$ \begin{array}{@{}rcl@{}} d^{+}_{1}=\sqrt{\frac{1}{2}\left\{0.0110 \psi_{1}+0.0000 \psi_{2}+0.0080 \psi_{3}+0.0646 \psi_{4}+0.0127 \psi_{5}+0.0000 \psi_{6}+0.0001 \psi_{7}\right\}}\\ d^{+}_{2}=\sqrt{\frac{1}{2}\left\{0.0435 \psi_{1}+0.0019 \psi_{2}+0.0000 \psi_{3}+0.0009 \psi_{4}+0.0329 \psi_{5}+0.0488 \psi_{6}+0.0008 \psi_{7}\right\}}\\ d^{+}_{3}=\sqrt{\frac{1}{2}\left\{0.1611 \psi_{1}+0.0514 \psi_{2}+0.0494 \psi_{3}+0.0000 \psi_{4}+0.0000 \psi_{5}+0.0926 \psi_{6}+0.0735 \psi_{7}\right\}}\\ d^{+}_{4}=\sqrt{\frac{1}{2}\left\{0.0518 \psi_{1}+0.1167 \psi_{2}+0.0965 \psi_{3}+0.0229 \psi_{4}+0.0742 \psi_{5}+0.0001 \psi_{6}+0.0635 \psi_{7}\right\}}\\ d^{+}_{5}=\sqrt{\frac{1}{2}\left\{0.0001 \psi_{1}+0.1242 \psi_{2}+0.1006 \psi_{3}+0.0001 \psi_{4}+0.0136 \psi_{5}+0.0447 \psi_{6}+0.0590 \psi_{7}\right\}}\\ d^{-}_{1}=\sqrt{\frac{1}{2}\left\{0.1131 \psi_{1}+0.1233 \psi_{2}+0.0489 \psi_{3}+0.0000 \psi_{4}+0.0446 \psi_{5}+0.0926 \psi_{6}+0.0750 \psi_{7}\right\}}\\ d^{-}_{2}=\sqrt{\frac{1}{2}\left\{0.0669 \psi_{1}+0.1275 \psi_{2}+0.0965 \psi_{3}+0.0512 \psi_{4}+0.0290 \psi_{5}+0.0155 \psi_{6}+0.0599 \psi_{7}\right\}}\\ d^{-}_{3}=\sqrt{\frac{1}{2}\left\{0.0000 \psi_{1}+0.0197 \psi_{2}+0.0094 \psi_{3}+0.0646 \psi_{4}+0.0741 \psi_{5}+0.0000 \psi_{6}+0.0000 \psi_{7}\right\}}\\ d^{-}_{4}=\sqrt{\frac{1}{2}\left\{0.0847 \psi_{1}+0.0001 \psi_{2}+0.0000 \psi_{3}+0.0165 \psi_{4}+0.0000 \psi_{5}+0.0922 \psi_{6}+0.0020 \psi_{7}\right\}}\\ d^{-}_{5}=\sqrt{\frac{1}{2}\left\{0.1587 \psi_{1}+0.0001 \psi_{2}+0.0089 \psi_{3}+0.0639 \psi_{4}+0.0336 \psi_{5}+0.0231 \psi_{6}+0.0008 \psi_{7}\right\}} \end{array} $$

  Now, based on (25), Model 1 is formulated as:

  $$ \begin{array}{@{}rcl@{}} &&a_{u}=\min\limits_{\psi} d^{+}_{u}~;~ b_{u}=\max\limits_{\psi} d^{-}_{u} \quad \forall~ u=1,2,\ldots,5 \\ \text{subject to} && 0.10 \leq \psi_{1} \leq 0.40, \qquad 0.05 \leq \psi_{2} \leq 0.45, \qquad 0.10 \leq \psi_{3} \leq 0.35, \\ && 0.15 \leq \psi_{4} \leq 0.50, \qquad 0.05 \leq \psi_{5} \leq 0.35, \qquad 0.10 \leq \psi_{6} \leq 0.40, \\ && 0.15 \leq \psi_{7} \leq 0.35, \qquad \sum \limits_{v=1}^{7} \psi_{v}=1, \qquad \psi_{v} \geq 0 \quad \forall~ v=1,2, \ldots, 7 \end{array} $$

  (42)

  Table 1 Preferences given by experts $\mathcal {E}^{(1)}$, $\mathcal {E}^{(2)}$, $\mathcal {E}^{(3)}$ and $\mathcal {E}^{(4)}$

  Table 2 Normalized data values

  Table 3 Aggregated values of experts obtained by using IFOWA operator

• Step 4: Consider that, the partial information about the weight vector ψ, associated with criteria $\mathcal {C}_{v}$, is given as: △ = {0.10 ≤ ψ₁ ≤ 0.40, 0.05 ≤ ψ₂ ≤ 0.45,0.10 ≤ ψ₃ ≤ 0.35,0.15 ≤ ψ₄ ≤ 0.50,0.05 ≤ ψ₅ ≤ 0.35,0.10 ≤ ψ₆ ≤ 0.40,0.15 ≤ ψ₇ ≤ 0.35}. In order to determine the criteria weights firstly, PIA and NIA are formulated from the accumulated data values tabulated in Table 3 and are given as:

	$\mathcal {C}_{1}$	$\mathcal {C}_{2}$	$\mathcal {C}_{3}$	$\mathcal {C}_{4}$	$\mathcal {C}_{5}$	$\mathcal {C}_{6}$	$\mathcal {C}_{7}$
$\mathcal {T}^{+}$	$\left (0.8653,0.1025\right )$	$\left (0.8656,0.1025\right )$	$\left (0.8643,0.1000\right )$	$\left (0.8891,0.1024\right )$	$\left (0.7628,0.1107\right )$	$\left (0.8646,0.1025\right )$	$\left (0.8893,0.1000\right )$
$\mathcal {T}^{-}$	$\left (0.5495,0.3360\right )$	$\left (0.5810,0.2148\right )$	$\left (0.6116,0.2067\right )$	$\left (0.6831,0.2275\right )$	$\left (0.5495,0.2719\right )$	$\left (0.6162,0.2275\right )$	$\left (0.6831,0.1343\right )$

As the problem formulated using Model 1, in Eq. (42), is MOOP with 10 objective functions (2 objectives corresponding to each alternative). Now, in order to obtain maximum and minimum value corresponding to each objective function, we solve 20 single objective optimization problems, which are formulated on the basis of Eqs. (26)-(29). The results acquired, obtained on solving these problems using PSO Algorithm 1, are summarized as

Optimization	Objective functions
	$d^{+}_{1}$	$d^{+}_{2}$	$d^{+}_{3}$	$d^{+}_{4}$	$d^{+}_{5}$	$d^{-}_{1}$	$d^{-}_{2}$	$d^{-}_{3}$	$d^{-}_{4}$	$d^{-}_{5}$
Maximization	0.1239	0.1137	0.2147	0.1833	0.1693	0.1988	0.2008	0.1370	0.1551	0.1976
Minimization	0.0782	0.0761	0.1482	0.1367	0.1231	0.1560	0.1533	0.0875	0.1012	0.1260

While obtaining the solutions, parameters in Algorithm 1 are set as N = 25,c₁ = 2.05,c₂ = 2.10. The inertia weight ω^(t), during each iteration t, is calculated using the following Eq. (43).

$$ \omega^{(t)} = \omega_{max}-\frac{t}{\text{maximum no. of iterations}}\left( \omega_{max}-\omega_{min}\right) $$

(43)

The maximum no. of iterations were set equal to 40; ω_max = 0.9; ω_min = 0.3 and 50 runs were performed for each problem. The penalty function parameters Ω and γ, as given in Eq. (6), were taken same as in [50] and the function y, used in Eq. (5), is set as $y(t)=\sqrt {t}$. Further, in order to describe the fuzziness included in each objective, the membership functions are formulated using Eqs. (30) and (31) as given below:

$$ \begin{array}{@{}rcl@{}} \mu\left( d^{+}_{1}\right)= \begin{cases} 1, &\text{if}~ d^{+}_{1} \leq 0.0782 \\ 1-\frac{d^{+}_{1}-0.0782}{0.1239-0.0782}, &\text{if}~ 0.0782 < d^{+}_{1} \leq 0.1239 \\ 0, &\text{otherwise} \end{cases} ~&;&~\mu\left( d^{+}_{2}\right)= \begin{cases} 1, &\text{if}~ d^{+}_{2} \leq 0.0761 \\ 1-\frac{d^{+}_{2}-0.0761}{0.1137-0.0761}, &\text{if}~ 0.0761 < d^{+}_{2} \leq 0.1137 \\ 0, &\text{otherwise} \end{cases} \end{array} $$

(44)

$$ \begin{array}{@{}rcl@{}} \mu\left( d^{+}_{3}\right)= \begin{cases} 1, &\text{if}~ d^{+}_{3} \leq 0.1482 \\ 1-\frac{d^{+}_{3}-0.1482}{0.2147-0.1482}, &\text{if}~ 0.1482 < d^{+}_{3} \leq 0.2147 \\ 0, &\text{otherwise} \end{cases} ~&;&~\mu\left( d^{+}_{4}\right)= \begin{cases} 1, &\text{if}~ d^{+}_{4} \leq 0.1367 \\ 1-\frac{d^{+}_{4}-0.1367}{0.1833-0.1367}, &\text{if}~ 0.1367 < d^{+}_{4} \leq 0.1833 \\ 0, &\text{otherwise} \end{cases} \end{array} $$

(45)

$$ \begin{array}{@{}rcl@{}} \mu\left( d^{+}_{5}\right)= \begin{cases} 1, &\text{if}~ d^{+}_{5} \leq 0.1231 \\ 1-\frac{d^{+}_{5}-0.1231}{0.1693-0.1231}, &\text{if}~ 0.1231 < d^{+}_{5} \leq 0.1693 \\ 0, &\text{otherwise} \end{cases} ~&;&~\mu\left( d^{-}_{1}\right)= \begin{cases} 1, &\text{if}~ d^{-}_{1} \geq 0.1988 \\ 1-\frac{0.1988-d^{-}_{1}}{0.1988-0.1560}, &\text{if}~ 0.1560 \leq d^{-}_{1} < 0.1988 \\ 0, &\text{otherwise} \end{cases} \end{array} $$

(46)

$$ \begin{array}{@{}rcl@{}} \mu\left( d^{-}_{2}\right)= \begin{cases} 1, &\text{if}~ d^{-}_{2} \geq 0.2008 \\ 1-\frac{0.2008-d^{-}_{2}}{0.2008-0.1533}, &\text{if}~ 0.1533 \leq d^{-}_{2} < 0.2008 \\ 0, &\text{otherwise} \end{cases} ~&;&~ \mu\left( d^{-}_{3}\right)= \begin{cases} 1, &\text{if}~ d^{-}_{3} \geq 0.1370 \\ 1-\frac{0.1370-d^{-}_{3}}{0.1370-0.0875}, &\text{if}~ 0.0875 \leq d^{-}_{3} < 0.1370 \\ 0, &\text{otherwise} \end{cases} \end{array} $$

(47)

$$ \begin{array}{@{}rcl@{}} \mu\left( d^{-}_{4}\right)= \begin{cases} 1, &\text{if}~ d^{-}_{4} \geq 0.1551 \\ 1-\frac{0.1551-d^{-}_{4}}{0.1551-0.1012}, &\text{if}~ 0.1012 \leq d^{-}_{4} < 0.1551 \\ 0, &\text{otherwise} \end{cases} ~&;&~ \mu\left( d^{-}_{5}\right)= \begin{cases} 1, &\text{if}~ d^{-}_{5} \geq 0.1976 \\ 1-\frac{0.1976-d^{-}_{5}}{0.1976-0.1260}, &\text{if}~ 0.1260 \leq d^{-}_{5} < 0.1976 \\ 0, &\text{otherwise} \end{cases} \end{array} $$

(48)

Now, by utilizing Eqs. (44)-(48) and Model 2 as given in Eq. (33), the single objective optimization problem is formulated as:

$$ \begin{array}{@{}rcl@{}} &&\max \lambda \\ &&\text{subject to} \\ &&0.0457 \lambda-0.1239+\sqrt{\frac{1}{2}\left\{0.0110 \psi_{1}+0.0000 \psi_{2}+0.0080 \psi_{3}+0.0646 \psi_{4}+0.0127 \psi_{5}+0.0000 \psi_{6}+0.0001 \psi_{7}\right\}} \leq 0 \\ &&0.0376 \lambda-0.1137+ \sqrt{\frac{1}{2}\left\{0.0435 \psi_{1}+0.0019 \psi_{2}+0.0000 \psi_{3}+0.0009 \psi_{4}+0.0329 \psi_{5}+0.0488 \psi_{6}+0.0008 \psi_{7}\right\}} \leq 0 \\ &&0.0665 \lambda-0.2147+\sqrt{\frac{1}{2}\left\{0.1611 \psi_{1}+0.0514 \psi_{2}+0.0494 \psi_{3}+0.0000 \psi_{4}+0.0000 \psi_{5}+0.0926 \psi_{6}+0.0735 \psi_{7}\right\}} \leq 0\\ &&0.0466 \lambda-0.1833+\sqrt{\frac{1}{2}\left\{0.0518 \psi_{1}+0.1167 \psi_{2}+0.0965 \psi_{3}+0.0229 \psi_{4}+0.0742 \psi_{5}+0.0001 \psi_{6}+0.0635 \psi_{7}\right\}} \leq 0 \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&0.0462 \lambda-0.1693+\sqrt{\frac{1}{2}\left\{0.0001 \psi_{1}+0.1242 \psi_{2}+0.1006 \psi_{3}+0.0001 \psi_{4}+0.0136 \psi_{5}+0.0447 \psi_{6}+0.0590 \psi_{7}\right\}} \leq 0 \\ &&0.0428 \lambda+0.1560-\sqrt{\frac{1}{2}\left\{0.1131 \psi_{1}+0.1233 \psi_{2}+0.0489 \psi_{3}+0.0000 \psi_{4}+0.0446 \psi_{5}+0.0926 \psi_{6}+0.0750 \psi_{7}\right\}} \leq 0 \\ &&0.0475 \lambda+0.1533-\sqrt{\frac{1}{2}\left\{0.0669 \psi_{1}+0.1275 \psi_{2}+0.0965 \psi_{3}+0.0512 \psi_{4}+0.0290 \psi_{5}+0.0155 \psi_{6}+0.0599 \psi_{7}\right\}} \leq 0 \\ &&0.0495 \lambda+0.0875-\sqrt{\frac{1}{2}\left\{0.0000 \psi_{1}+0.0197 \psi_{2}+0.0094 \psi_{3}+0.0646 \psi_{4}+0.0741 \psi_{5}+0.0000 \psi_{6}+0.0000 \psi_{7}\right\}} \leq 0 \\ &&0.0539 \lambda+0.1012-\sqrt{\frac{1}{2}\left\{0.0847 \psi_{1}+0.0001 \psi_{2}+0.0000 \psi_{3}+0.0165 \psi_{4}+0.0000 \psi_{5}+0.0922 \psi_{6}+0.0020 \psi_{7}\right\}} \leq 0 \\ &&0.0716 \lambda+0.1260-\sqrt{\frac{1}{2}\left\{0.1587 \psi_{1}+0.0001 \psi_{2}+0.0089 \psi_{3}+0.0639 \psi_{4}+0.0336 \psi_{5}+0.0231 \psi_{6}+0.0008 \psi_{7}\right\}} \leq 0 \\ && 0.10 \leq \psi_{1} \leq 0.40, 0.05 \leq \psi_{2} \leq 0.45, 0.10 \leq \psi_{3} \leq 0.35, \\ && 0.15 \leq \psi_{4} \leq 0.50, 0.05 \leq \psi_{5} \leq 0.35, 0.10 \leq \psi_{6} \leq 0.40, \\ && 0.15 \leq \psi_{7} \leq 0.35, \sum \limits_{v=1}^{7} \psi_{v}=1, \psi_{v} \geq 0 \quad \forall~ v=1,2, \ldots, 7 \\ && 0 \leq \lambda \leq 1 \end{array} $$

(49)

	$\mathcal {C}^{+}_{1}$	$\mathcal {C}^{+}_{2}$	$\mathcal {C}^{+}_{3}$	$\mathcal {C}^{+}_{4}$	$\mathcal {C}^{+}_{5}$	$\mathcal {C}^{+}_{6}$	$\mathcal {C}^{+}_{7}$
$\mathcal {T}^{+}$	$\left (0.8653,0.1025\right )$	$\left (0.8656,0.1025\right )$	$\left (0.8643,0.1000\right )$	$\left (0.8891,0.1024\right )$	$\left (0.7628,0.1107\right )$	$\left (0.8646,0.1025\right )$	$\left (0.8893,0.1000\right )$

Solving the above non-linear optimization problem by PSO, we obtain that ψ=(0.2700,0.0500, 0.1860, 0.1500, 0.0940, 0.1000, 0.1500)^T.

• Step 5: (The RSA:)

  • Step 5a: Using Eq. (39), by taking k = 2, the aggregated values $\mathcal {I}_{u}$ are obtained as: $\mathcal {I}_{1}=\left (0.8549,0.1098\right )$, $\mathcal {I}_{2}=\left (0.8483,0.1139\right )$, $\mathcal {I}_{3}=\left (0.8438,0.1280\right )$, $\mathcal {I}_{4}=\left (0.7864,0.1125\right )$ and $\mathcal {I}_{5}=\left (0.8572,0.1186\right )$.

  • Step 5b: The score values, corresponding to the accumulated values acquired in Step 5a, are obtained as: $\mathcal {S}\left (\mathcal {I}_{1}\right )=0.7451$, $\mathcal {S}\left (\mathcal {I}_{2}\right )=0.7344$, $\mathcal {S}\left (\mathcal {I}_{3}\right )=0.7159$, $\mathcal {S}\left (\mathcal {I}_{4}\right )=0.6739$ and $\mathcal {S}\left (\mathcal {I}_{5}\right )=0.7387$. Further, using the Definition 4, the ranking order of techniques $\mathcal {T}_{u}$, corresponding to the RSA, becomes: $\mathcal {T}_{1} \succ \mathcal {T}_{5} \succ \mathcal {T}_{2} \succ \mathcal {T}_{3} \succ \mathcal {T}_{4}$.

• Step 6: (The RPM:)

  • Step 6a: The reference IFN $\mathcal {T}^{+}$ is obtained as

  • Step 6b: By using the Eq. (40), the distance of accumulated values $\mathcal {I}_{uv}$, corresponding to every alternative $\mathcal {T}_{u}$, from PIA $\mathcal {T}^{+}$ is obtained as: $d\left (\mathcal {T}_{1},\mathcal {T}^{+}\right )=0.0876$, $d\left (\mathcal {T}_{2},\mathcal {T}^{+}\right )=0.1002$, $d\left (\mathcal {T}_{3},\mathcal {T}^{+}\right )=0.1943$, $d\left (\mathcal {T}_{4},\mathcal {T}^{+}\right )=0.1699$ and $d\left (\mathcal {T}_{5},\mathcal {T}^{+}\right )=0.1407$.

  • Step 6c: Hence, the ranking order of the techniques $\mathcal {T}_{u}$, corresponding to the RPM, is obtained as: $\mathcal {T}_{1} \succ \mathcal {T}_{2} \succ \mathcal {T}_{5} \succ \mathcal {T}_{4} \succ \mathcal {T}_{3}$.

• Step 7: (The FMF:)

  • Step 7a: Using Eq. (41), for k = 2, the accumulated values $\mathcal {I}_{u}$ are obtained as: $\mathcal {I}_{1}=\left (0.7809,0.1316\right )$, $\mathcal {I}_{2}=\left (0.7658,0.1209\right )$, $\mathcal {I}_{3}=\left (0.6543,0.2191\right )$, $\mathcal {I}_{4}=\left (0.6770,0.1546\right )$ and $\mathcal {I}_{5}=\left (0.7287,0.1268\right )$.

  • Step 7b: Using the Eq. (1), the score values of aggregated values $\mathcal {I}_{u}$, acquired in Step 7a, are obtained as: $\mathcal {S}\left (\mathcal {I}_{1}\right )=0.6493$, $\mathcal {S}\left (\mathcal {I}_{2}\right )=0.6449$, $\mathcal {S}\left (\mathcal {I}_{3}\right )=0.4352$, $\mathcal {S}\left (\mathcal {I}_{4}\right )=0.5224$ and $\mathcal {S}\left (\mathcal {I}_{5}\right )=0.6019$. Hence, by using the Definition 4, the ordering position of techniques $\mathcal {T}_{u}$, corresponding to the FMF, is obtained as: $\mathcal {T}_{1} \succ \mathcal {T}_{2} \succ \mathcal {T}_{5} \succ \mathcal {T}_{4} \succ \mathcal {T}_{3}$.

• Step 8: Finally, by applying the dominance theory [7] on the ordering positions acquired in Steps 5b, 6c and 7b, the final ranking order of SWM techniques is obtained as: $\mathcal {T}_{1} \succ \mathcal {T}_{2} \succ \mathcal {T}_{5} \succ \mathcal {T}_{4} \succ \mathcal {T}_{3}$.

7.2 Comparison with existing TOPSIS, CODAS, MABAC and WASPAS methods

In order to validate the reliability and effectiveness of the proposed MAGDM approach we compare it with several existing DM techniques [13, 37, 42, 44]. We apply IF TOPSIS method [13], pythagorean fuzzy CODAS method [37], q-rung orthopair fuzzy MABAC method [44] and IF extended WASPAS method [42] on the problem, described in the Section 7.1 and compare the obtained outcomes with the proposed approach results. The results obtained on employing the prevailing DM techniques [13, 37, 42, 44] and the proposed MAGDM method are tabulated in the Table 4.

Table 4 Comparative studies results

The results presented in the Table 4 depict that the most favorable and the least favorable SWM technique obtained on applying the existing methods [13, 37, 42, 44] is identical with the proposed one. Furthermore, the computational differences among the prevailing methods [13, 37, 42, 44] and the proposed approach are highlighted as follows:

• 1) Although, the ordering position of all the techniques $\mathcal {T}_{u}$ obtained on applying [13]’s method based on TOPSIS is identical with the proposed approach results but there are computational differences among the proposed method and IF TOPSIS method [13]. Chen et al. [13]’s ranking method is based on the distances of alternatives from PIA and NIA. It prefers those alternatives which have minimum distance from PIA and maximum distance from NIA. On the other hand, in the the proposed method the ranking of the alternatives is obtained by considering the score values obtained using averaging operator, the geometric operator and the distance of the alternatives from PIA simultaneously.

• 2) [37]’s approach based on CODAS gives identical outcomes for the ordering position of techniques $\mathcal {T}_{1}$, $\mathcal {T}_{4}$, $\mathcal {T}_{3}$ and states the technique $\mathcal {T}_{5}$ to be more superior than $\mathcal {T}_{2}$ whereas in accordance with the proposed MAGDM method based on MULTIMOORA $\mathcal {T}_{2}$ is superior than $\mathcal {T}_{5}$. The reason behind this change may be that in the pythagorean fuzzy CODAS method [37], the hamming and euclidean distances of score values of each alternative under every criteria are evaluated from the negative ideal score values and then, these distances are aggregated. Whereas, in the proposed MAGDM method the rating values corresponding to each alternative under every criteria are accumulated firstly using averaging and geometric AOs in the RSA and FMF respectively. Afterwards, the alternatives are ranked in accordance with decreasing order of score values. In the RPM of the proposed approach, the weighted Euclidean distance of each alternative is calculated from PIA and then, the alternatives are ranked on the basis of the increasing order of these distance values. The final ranking is done by applying the dominance property on the ranking orders obtained using the RSM, the RPM and the FMF.

• 3) The ordering position of the techniques $\mathcal {T}_{1}$, $\mathcal {T}_{2}$ and $\mathcal {T}_{3}$ obtained using [44]’s method based on MABAC and [42]’s method based on WASPAS is identical with the proposed approach results whereas the ranking order of $\mathcal {T}_{4}$ and $\mathcal {T}_{5}$ differs. The q-rung orthopair MABAC [44] approach is based on the principle of calculating the distance of each criteria from the border approximation area. Further, the alternatives are placed in the border, upper and lower approximation areas and are ranked accordingly. The IF WASPAS [42] method is combination of weighted sum and weighted product decision making approaches. On the other hand, the proposed method is based on MULTIMOORA which is combination of the RSM, the RPM and the FMF and gives final results by considering three assessment indices simultaneously.

Also, in order to have a more straightforward comparison, the correlation coefficients among the ranking orders obtained by applying the proposed method and existing IF TOPSIS method [13], pythagorean fuzzy CODAS method [37], q-rung orthopair fuzzy MABAC method [44], IF extended WASPAS method [42] are computed using spearman’s rank correlation coefficient formula and the acquired results are tabulated in Table 5.

Table 5 Correlation coefficients among the ranking orders obtained using different methods

From the values tabulated in Table 5, it is analyzed that the correlation among the ranking order of the proposed method and the existing methods [13, 37, 42, 44] is significantly high. Also, there is much significant correlation among the prevailing approaches [13, 37, 42, 44] themselves. Besides these, it has been analyzed that the proposed approach determines the weights corresponding to criteria objectively. Moreover, in our presented MAGDM method, the criteria weights are determined by keeping in view the ultimate goal of maximizing the distance of each alternative from NIA and minimizing the distance of each alternative from PIA simultaneously. Since the attribute weights play an important role in DM process therefore, the method of determining and choosing weights affects the ranking results directly. The random choice of criteria weights may lead us to wrong decision results. In the DM methods proposed in [13, 37, 42, 44] weights are chosen subjectively. Therefore, our presented approach is more reliable as compared to the approaches of [13, 37, 42, 44]. In addition to these, MAGDM approaches proposed in [42, 44] and the presented method can handle group DM problems. Moreover, by taking l = 1, our developed approach can handle single decision-maker problems as well. Therefore, the presented MAGDM method is more generalized as it can handle both single and group DM problems.

7.3 Sensitivity Analysis

In this section, we perform a sensitivity analysis in order to depict the influence of the parameter k, used in the proposed AOs, on the different parts of proposed MAGDM approach based on MULTIMOORA. We take five different values of k i.e., k = 2,4,6,8,10 in the proposed AOs and discuss the impact of these values on the ranking order of alternatives obtained via three different parts of MULTIMOORA namely the RSA, the RPA and the FMF. The results obtained by taking different values of k are depicted in Fig. 4.

Fig. 4

The utility values corresponding to different parts of MULTIMOORA in the proposed AOs

The Fig. 4 represent the utility values corresponding to each alternative $\mathcal {T}_{u}$ for three different parts of MULTIMOORA. These values are obtained by fixing the weight vector ψ=(0.2700, 0.0500, 0.1860, 0.1500, 0.0940, 0.1000, 0.1500)^T. These figures depict that with the change in the parameter k the utility values associated with every alternative, for each of the three parts of MULTIMOORA, vary greatly. The utility values corresponding to each alternative with respect to the RSA and the FMF increase with the rise in the parameter k while decreases by RPA. Besides this, the influence of the parameter k on utility values obtained using the RSA and the FMF is more as comparison to the RPA. This is due to the fact that in the RPA, the parameter k plays role in aggregating different decision matrices ${\mathscr{M}}^{(z)}$ into single one ${\mathscr{M}}$ i.e., in Step 3 only of the proposed MAGDM approach whereas in RSA the parameter k influences Steps 3 and 5. Also, in the FMF, the parameter k plays its part in two Steps 3 and 7. In addition to these, it is analyzed that as the value of the parameter k rises the changes in the utility values with respect to different parts of MULTIMOORA becomes small. Furthermore, the impact of the parameter k on the ranking order of the alternatives obtained using the RSA, the RPA and the FMF and hence on the final ordering position is depicted in the Table 6.

Table 6 Impact of k on the ranking order of the alternatives

The values tabulated in the Table 6 depict that the ranking order of alternatives with respect to three different parts of MULTIMOORA changes with the change in the value of the parameter k but the final ranking order of alternatives remains same. Also, if someone wants to utilize very few operators to model large number of situations, then the AOs have to be adaptable to the specific context. The proposed AOs and method have the characteristics of adaptability due to the parameter present in it. Existing min/max and averaging operators can not be used in such situations. The choice of the parameter k in the proposed AOs depends upon the preferences of the experts and the nature of the MAGDM problem. This influence of the parameter k on the utility values of different parts of MULTIMOORA makes the proposed MAGDM method more flexible as the expert(s) can choose the parameter in accordance with their preferences and practical situations.

7.4 Discussion

This paper aspires to present a MAGDM method based on MULTIMOORA and novel AOs under IFS environment. The proposed AOs are based on the parameter k and the presence of this parameter makes the proposed aggregation operations flexible and adaptable. Large number of situations can be modeled using the developed AOs by taking different values of parameter k. The efficiency of the proposed approach is demonstrated by applying it in an emerging issue i.e., assessment of SWM techniques. It has been done by capturing the uncertainty in the judgements using IF data values. Five techniques represented by $\mathcal {T}_{u}$ (u = 1,2,…,5) are taken and are assessed on the basis of economical, environmental, technological and social factors which are further sub-divided into seven criteria. The application of the proposed approach gives the ranking order of SWM techniques as $\mathcal {T}_{1} \succ \mathcal {T}_{2} \succ \mathcal {T}_{5} \succ \mathcal {T}_{4} \succ \mathcal {T}_{3}$. The results of the presented work are further compared with existing IF TOPSIS method [13], pythagorean fuzzy CODAS method [37], q-rung orthopair fuzzy MABAC method [44] and IF extended WASPAS method [42] in Section 7.2. The comparison analysis highlights the superiorities and various computational differences among the proposed work and the existing approaches [13, 37, 42, 44]. The proposed approach combines the features of three MADM techniques namely additive utility functions (RSA), multiplicative utility functions (FMF) and the reference point method (RPM) and therefore, it is more effective and reliable. Further, the effect of the parameter k on the proposed approach results is deeply discussed in Section 7.3.

8 Conclusion

Implementation of effective and proper SWM techniques is urgent necessity in order to control different types of pollution, to stop the spread of various infectious diseases, to conserve environmental resources and to recycle hazardous wastes. This has led various researchers and scholars to work in the direction of SWM. The presence of uncertainty in almost each real world system has compelled researchers to address the issue of SWM using fuzzy set theory and its extensions. In this work, we have proposed MAGDM method based on MULTIMOORA and new AOs in which criteria weights are determined objectively and have given its application for the assessment of SWM techniques by capturing the uncertainty using IF data values. On applying the proposed methodology, the ranking order of SWM techniques $\mathcal {T}_{u}$ is obtained as: $\mathcal {T}_{1} \succ \mathcal {T}_{2} \succ \mathcal {T}_{5} \succ \mathcal {T}_{4} \succ \mathcal {T}_{3}$. These results are obtained by considering three assessment indices simultaneously and therefore are more reliable.

The main contribution of the proposed work is outlined as follows:

• 1. New operational laws are proposed in this study and their properties are discussed in detail. Based on these operations, novel operators IFWA, IFOWA, IFHA, IFWG, IFOWG and IFHG are developed. The proposed AOs are based on a parameter k which may assume any real value greater than 1. It is proved that the proposed AOs satisfy the properties of idempotency, monotonicity and boundedness which are helpful in fusing multiple IF information.

• 2. A novel non-linear optimization model is established in order to determine attribute weights. This model is established with the main objective of maximizing the distance of each alternative from NIA and minimizing the distance from PIA simultaneously. The results of the proposed weight generation method are computed by employing one of the most effective evolutionary algorithms i.e., PSO scheme.

• 3. A MAGDM method based on MULTIMOORA, the proposed AOs and PSO is put forward. Unlike other MADM/MAGDM approaches, MULTIMOORA is not based on single assessment index. It combines the features of three MADM techniques namely the RSA, the RPA and the FMF. Therefore, the proposed DM method is more effective as this approach gives results by considering three assessment indices simultaneously.

• 4. The assessment of various SWM techniques is done by applying the proposed methodology. The various social, environmental, economical and technological factors are considered during the assessment process. The results of the proposed method are compared with several existing approaches which reveal the effectiveness of the presented work. Furthermore, sensitivity analysis by taking different parameter values is done. The influence of the parameter values on the ordering position of alternatives obtained via different parts of MULTIMOORA and hence on the final ranking order is discussed.

In the future, we will utilize the proposed AOs and MAGDM approach in order to solve other environmental issues such as greenhouse gas emissions, health-care SWM and green supplier selection. We will integrate the proposed MAGDM method with one of the other MADM techniques such as WASPAS, CODAS, TOPSIS and MABAC. Also, we have established the AOs in the present study in order to fuse independent arguments and therefore, in the future work we will try to develop operations for aggregating dependent IF numbers.