Research on a dynamic full Bayesian classifier for time-series data with insufficient information

Abstract

Small sample time-series data with insufficient information are ubiquitous. It is challenging to improve the classification reliability of small sample time-series data. At present, the dynamic classifications for small sample time-series data still lack a tailored method. To address this, we first setup the architecture of dynamic Bayesian derivative classifiers, and then establish a dynamic full Bayesian classifier for small sample time-series data. The joint density of attributes is estimated by using multivariate Gaussian kernel function with smoothing parameters. The dynamic full Bayesian classifier is optimized by splitting the smooth parameters into intervals, optimizing the parameters by constructing a smoothing parameter configuration tree (or forest), then selecting and averaging the classifiers. The dynamic full Bayesian classifier is applied to forecast turning points. Experimental results show that the resultant classifier developed in this paper is more accurate when compared with other nine commonly used classifiers.

1 Introduction

Many classifiers have been developed and widely applicated in the past decades, such as the Support Vector Machine [1], BP Neural Network [2], Decision Tree [3]. However, these classifiers are mainly oriented to non-time-series data with an underlying assumption that the data records are independent and identically distributed. Therefore, when the data records are not independent and identically distributed, the classifiers referred to are difficult to use for processing time-series data. In addition, models applicable to econometric time-series forecasting such as ARIMA [4] and GARCH [5] are suitable for regression, but not suitable for classification. The dynamic Bayesian classifier [6] is a temporal extension to the Bayesian classifier [7], it can be used to solve the classification problems over large sample time-series data. However, there exist many forecasts that need to be made based on small sample time-series data in practice. For example, long-term global economy growth and monetary policy rules are usually predicted based on annual data such as GDP and CPI [7, 8]. There is little tailored research on finding a dynamic Bayesian classifier for processing small sample data at present. Therefore, in this paper, we propose a dynamic Bayesian derivative classifier which is predicated on the need to cater for classification problems related specifically to small sample time-series data.

The last few decades have seen many Bayesian classifiers [9] designed and proposed that can be divided principally into two classes: some with discrete attributes and others with continuous attributes. In relation to the classifiers with discrete attributes or the discretization of continuous attributes, Chow and Liu (1968) [10] proposed the Dependency Tree classifier. Friedman et al. (1997) [11] proposed the TAN (Tree augmented naïve Bayes) classifier. Domingos and Pazzani (1997) [12] optimized the simple Bayesian classifier under 0–1 loss. Campos et al. (2016) [13] proposed an extended version of the TAN classifier by relaxing the independence assumption. Cheng and Greiner (1999) [14] designed a Bayesian network classifier based on dependency analysis to determine the network structure. Petitjean et al. (2018) [15] presented a hierarchical Dirichlet process to estimate accurate parameters for a Bayesian network classifier. Yager (2006) [16] provided an algorithm to obtain the weights associated with the extended naïve Bayesian classifier. Webb et al. (2005) [17] presented a classifier with an aggregating one-dependence estimator. Flores et al. (2014) [18] proposed the semi-naïve Bayesian network classifier. Daniel and Aryeh (2015) [19] examined the consistency of the optimal naïve Bayesian classifier for weighted expert majority votes under the small set of samples. Wang et al. (2013) [20], Sathyaraj and Prabu (2018) [21], Yang and Ding (2019) [22] and Kuang et al. (2019) [23] proposed Bayesian network classifiers based on search and scoring.

In respect of classifiers with continuous attributes, two aspects need to receive particular attention: one is setting up the classifier structure; the other is estimating the attribute density function. The structure of the Bayesian classifier with continuous attributes is similar to that with discrete ones. Currently, Gaussian function [24], Gaussian kernel function [25] and Copula function [26] are the main functions adopted to estimate the density of attributes [27]. John and Langley (1995) [28] established two naïve Bayesian classifiers by using Gaussian function and Gaussian kernel function to estimate the marginal density of attributes. The work is widely perceived as establishing the extended naïve Bayesian classifiers based on continuous attribute density estimation. Pérez et al. (2006, 2009) [24, 25] improved the estimation of Gaussian kernel function by introducing and optimizing the smoothing parameter. He et al. (2014) [29], Luis et al. (2014) [30] and Zhang et al. (2018) [31] developed the naïve Bayesian and the full Bayesian classifiers by using Gaussian function or Gaussian kernel function to estimate attribute density and applied them to fault diagnosis and spectroscopy analysis. Xiang et al. (2016) [32] used Gaussian kernel function to estimate attribute marginal density to set up an attribute weighted naïve Bayesian classifier. Wang et al. (2016) [33] presented a Bayesian network classifier by using Gaussian kernel function to estimate attribute conditional density.

The above-mentioned Bayesian classifiers are not suitable for time-series data classification (especially for small sample time-series data).

The research that we present here on dynamic Bayesian classifiers is mainly focused on classification with discrete attributes and need large sample time-series data for learning. Dang et al. (2016) [34] proposed a new method for the early detection of emergent topics, based on Dynamic Bayesian Networks in micro-blogging networks. Xiao et al. (2017) [35] proposed a novel time-series prediction model using a dynamic Bayesian network based on a combination of the Kalman filtering model (KFM) and echo state neural networks (ESN). Premebida et al. (2017) [36] addressed a time-based Dynamic Bayesian Mixture Model (DBMM) and applied it to solve the problem of semantic place categorization in mobile robotics. Extensive experiments were performed to highlight the influence of the number of time-slices and the effect of additive smoothing on the classification performance, and the results showed the effectiveness and competitive performance of the DBMM under different scenarios and conditions. Rishu et al. (2019) [37] developed a smartphone-based context-aware driver behavior classification using a Dynamic Bayesian Network (DBN) system, which demonstrated competitive performance when considering cost-effectiveness. Song et al. (2020) [38] proposed a Dynamic Hesitant Fuzzy Bayesian Network (DHFBN) to solve the optimal port investment decision-making problem of the “21st Century Maritime Silk Road”.

Almost all the dynamic Bayesian network classifiers developed at present need large sample discrete time-series data for learning, which is not available for small sample time-series data problems. In this paper, a dynamic full Bayesian ensemble classifier with continuous attributes fitting for small sample data classification is proposed. The structure of the Bayesian classifier has been developed, and the density of attributes has been estimated. In addition, the classifier is applied in forecasting the turning points for indexes. The experimental results indicate that the classifier proposed in this paper has good classification accuracy in dealing with small sample time-series problems.

The main contributions of this paper are as follows:

• (1) Dislocated transformation between variables and classes is utilized in developing the temporal asynchronous (non-synchronous) dynamic Bayesian derivative classifiers with continuous attributes.

• (2) The multivariate Gaussian kernel function with smoothing parameters is used to estimate the joint density of attributes. Based on that, we develop a synchronous dynamic full Bayesian ensemble classifier to solve the multivariate small sample time-series data classification problems.

• (3) We propose the architecture of the dynamic Bayesian derivate classifiers by extending the dependency of variables and dislocated transforming of variables based on dynamic Bayesian classifiers, dynamic full Bayesian classifiers and dynamic Bayesian network classifiers, which provides support for further research on dynamic Bayesian derivate classifiers.

This paper is organized as follows: Section 1 reviews and analyses on the research of Bayesian classifiers and dynamic Bayesian classifiers; Section 2 presents the definition and representation of Bayesian classifiers and dynamic Bayesian classifiers, as well as the structure of dynamic Bayesian derivative classifiers; Section 3 presents the definition and representation of dynamic full Bayesian classifier, the estimation method for attribute joint density, classification accuracy criterion for the time-series progressiveness, an algorithm for constructing a smoothing parameter configuration tree and the ensemble of dynamic full Bayesian classifiers; Section 4 conducts the experiments and analysis on small sample time-series dataset problems; Section 5 concludes this work with further directions.

2 Architecture of dynamic Bayesian derivative classifier

Definitions for Bayesian classifiers and dynamic Bayesian classifiers (both synchronous and asynchronous) are given firstly in this section, and on this basis, the architecture of dynamic Bayesian derivative classifiers is established.

2.1 Dynamic Bayesian classifier

Suppose that the attribute and class variables of a non-time-series dataset are denoted as X₁, …, X_n and C, and x₁, …, x_n, c are their specific values. Let D be a non-time-series dataset with N instances.

Definition 1

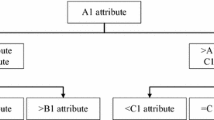
We call the classifier with the structure shown in Fig. 1 the Bayesian classifier (BC) [9].

Fig. 1

The structure of the Bayesian classifier

According to the Bayesian network theory [39], a BC can be represented as:

$$ \underset{c\left({x}_1,\dots, {x}_n\right)}{argmax}\left\{p\left(c|{x}_1,\dots, {x}_n\right)\right\} $$

(1)

We use X₁[t], X₂[t], …, X_n[t] and C[t] for attribute and class variables of a time-series dataset, and x₁[t], x₂[t], …, x_n[t], c[t] to denote specific values taken by those variables. Dataset sequences in cumulative time-duration are denoted by D[1], D[2], …, D[t], where D[1] ⊂ D[2] ⊂ … ⊂ D[t], the number of instances in the corresponding time-series dataset is denoted by N[1], N[2], …, N[t], where 1 ≤ t ≤ T. A dynamic Bayesian classifier is an extension of the Bayesian classifier for dealing with time-series problems. It can be defined in many forms, and we give the following definition:

Definition 2

The classifier with the structure given in Fig. 2 is labelled the dynamic Bayesian classifier (DBC) [6].

Fig. 2

The structure of the dynamic Bayesian classifier

The above dynamic Bayesian classifier may also be called the synchronous dynamic Bayesian classifier (SDBC), in which the attributes and class change synchronously in time. According to Bayesian network theory [39] and the conditional independencies contained in Fig. 2, we can get:

$$ p\left(c\left[t\right]|c\left[1\right],\dots, c\left[t-1\right],{x}_1\left[1\right],\dots, {x}_n\left[1\right],\dots, {x}_1\left[t\right],\dots, {x}_n\left[t\right]\right) $$

$$ =p\left(c\left[t\right]|c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right) $$

The DBC (or SDBC) can be expressed as:

$$ \underset{c\left[t\right]\left(c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)}{argmax}\left\{p\Big(c\left[t\right]|c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\Big)\right\} $$

(2)

Based on the synchronous dynamic Bayesian classifier, the asynchronous (non-synchronous) dynamic Bayesian classifier can be constructed by dislocated transformation of variables (between attributes and class) in time series.

Definition 3

The classifier with the structure given in Fig. 3 is called the asynchronous dynamic Bayesian classifier (ADBC), where the classifier order φ > 0.

Fig. 3

The structure of the asynchronous dynamic Bayesian classifier

With the same method, the ADBC can be expressed as:

$$ \underset{c\left[t+\varphi \right]\left(c\left[t+\varphi -1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)}{argmax}\left\{p\Big(c\left[t+\varphi \right]|c\left[t+\varphi -1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\Big)\right\} $$

(3)

2.2 Dynamic Bayesian derivative classifier

We label classifiers derived from a dynamic Bayesian classifier as the dynamic Bayesian derivative classifiers (DBDC). The DBDCs can be divided into two parts: the synchronous classifiers and the asynchronous classifiers. The synchronous classifier can be transformed into the corresponding asynchronous classifier by the dislocated transformation between attributes and classes over time series. According to the definition of the dynamic Bayesian derivative classifier, the structural changes in a time point (or a time slice) can be absorbed into the naïve structure, the full structure, and the Bayesian network structure (the other structures). By increasing the dependency between attributes and class over time points (or time slices), we can obtain the extended structure of temporal dependency; all these structures are synchronous classifiers. In the same way, the asynchronous classifier structures can be obtained by the dislocated transformation between attributes and class over time series. The specific structure is shown in Fig. 4.

Fig. 4

The architecture of the DBDCs

Figure 4 shows the internal relationships between different dynamic Bayesian derivative classifiers. Future systematic and in-depth study of these dynamic Bayesian derivative classifiers can be performed based on the structure of the DBDCs.

3 Dynamic full Bayesian ensemble classifier

The information contained in small sample time-series data is very limited, and it is hard to effectively perform the classifier structure learning and parameter estimation of the parameter model. Therefore, we promote a synchronous dynamic full Bayesian classifier with continuous attributes to deal with this kind of classification problem, i.e., when operating with insufficient information. Instead of “by structure learning”, the classifier can make full use of each record of information within datasets by estimating the joint density of attributes based on multivariate Gaussian kernel function. The classifier optimization is further improved by adjusting the smoothing parameters. The synchronous dynamic full Bayesian classifier is a kind of dynamic Bayesian derivative classifier that can make full use the information provided by attributes to improve the classification accuracy.

3.1 The definition and expression of the dynamic full Bayesian classifier

Definition 3

The classifier with the structure given in Fig. 5 is called as the dynamic full Bayesian classifier (DFBC).

Fig. 5

The structure of the DFBC

According to the probability formula, the Bayesian network theory [39] and the conditional independencies shown in Fig. 5, we can show that:

$$ {\displaystyle \begin{array}{c}p\left(c\left[t\right]|c\left[1\right],\dots, c\left[t-1\right],{x}_1\left[1\right],\dots, {x}_n\left[1\right],\dots, {x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)\\ {}=p\left(c\left[t\right]|c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)\\ {}\begin{array}{c}=\frac{p\left(c\left[t\right],c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)}{p\left(c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)}\\ {}=\alpha p\left(c\left[t\right]|c\left[t-1\right]\right)f\left({x}_1\left[t\right],\dots, {x}_n\left[t\right]|c\left[t\right]\right)\end{array}\end{array}} $$

(4)

where α is a normalization coefficient, which is independent of C[t]; p(c[t]| c[t − 1]) denotes the transition probability of class and f(·) denotes the attribute density function.

The DFBC can be expressed as:

$$ \underset{c\left[t\right]\left(c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)}{argmax}\left\{p\Big(c\left[t\right]|c\left[t-1\right]\left)f\right({x}_1\left[t\right],\dots, {x}_n\left[t\right]|c\left[t\right]\Big)\right\} $$

(5)

From the definition and expression of the DFBC, we can determine that the core is to estimate the joint density of attributes f(x₁[t], …, x_n[t]| c[t]).

3.2 Estimation of joint attributes density function

In this section, we will use the multivariate kernel function with a diagonal smoothing parameter matrix to estimate the attribute density. This method performs well in local fitting to small sample time-series data, and it also has good anti-noise performance for dealing with time-series data classification.

For the dataset D with N records, the multivariate kernel function with smoothing parameter is denoted as [27]:

$$ \phi \left({x}_1,\cdots, {x}_n|D\right)=\frac{1}{N{\rho}_1\cdots {\rho}_n}{\sum}_{m=1}^N{\prod}_{i=1}^n{K}_i\left(\frac{x_i-{x}_{im}}{\rho_i}\right) $$

(6)

where K_i(·) is the kernel function of X_i, ${K}_i\left(\frac{x_i-{x}_{im}}{\rho_i}\right)=\frac{1}{\sqrt{2\pi }{\rho}_i}\mathit{\exp}\left[-\frac{{\left({x}_i-{x}_{im}\right)}^2}{2{\rho}_i^2}\right]$, ρ₁, …, ρ_n are the smoothing parameters (or the bandwidth), and x_im is the value of the mth record of X_i in dataset D, 1 ≤ i ≤ n, 1 ≤ m ≤ N.

In this section, we will use the kernel function with diagonal smoothing parameter matrix to estimate the attribute density.

Let $\hat{f}\left({x}_1\left[t\right],\dots, {x}_n\left[t\right]|c\left[t\right],D\left[t\right]\right)$ denote the estimation of f(x₁[t], …, x_n[t]| c[t]), which is an attribute conditional probability density function in temporal extension to ϕ(x_1,⋯, x_n| D) under the classification, then

$$ \hat{f}\left({x}_1\left[t\right],\dots, {x}_n\left[t\right]|c\left[t\right],D\left[t\right]\right)=\frac{1}{{\left(2\pi \right)}^{n/2}N\left(c\left[t\right]\right){\rho}_1^2\cdots {\rho}_n^2}{\sum}_{v=1}^t\left\{ signa\left(c\left[v\right]\right){\prod}_{i=1}^n\mathit{\exp}\left[-\frac{{\left({x}_i\left[t\right]-{x}_i\left[v\right]\right)}^2}{2{\rho}_i^2}\right]\right\} $$

(7)

where N(c[t]) is the number of the instances when C[t] = c[t] in D[t], and $signa\left(c\left[v\right]\right)=\left\{\begin{array}{c}1,c\left[v\right]=c\left[t\right]\\ {}0,c\left[v\right]\ne c\left[t\right]\end{array}\right.$.

The DFBC can be denoted as:

$$ \underset{c\left[t\right]\left(c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)}{argmax}\left\{\frac{N\left(c\left[t\right],c\left[t-1\right]\right)}{{\left(2\pi \right)}^{n/2}N\left(c\left[t\right]\right)N\left(c\left[t-1\right]\right){\rho}_1^2\cdots {\rho}_n^2}{\sum}_{v=1}^t\left\{ signa\left(c\left[v\right]\right){\prod}_{i=1}^n\mathit{\exp}\left[-\frac{{\left({x}_i\left[t\right]-{x}_i\left[v\right]\right)}^2}{2{\rho}_i^2}\right]\right\}\right\} $$

(8)

where N(c[t − 1]) are the numbers of the instances when C[t − 1] = c[t − 1] in D[t], and N(c[t], c[t − 1]) are the numbers of the instances when both C[t] = c[t] and C[t − 1] = c[t − 1] in D[t], respectively.

The smoothing parameters that shape the curve (or surface) of a Gaussian function will have great influence on the performances of a DFBC. To balance the training and generalization of the DFBC, we construct a smoothing parameter configuration tree (or forest) to optimize the DFBC, where the scoring and search method is used under the time-series progressiveness classification accuracy criterion.

3.3 Information analysis of attributes providing for class

In dynamic Bayesian derivative classifiers, attributes can provide three kinds of dependency information for class, namely transitive dependency information, directly induced dependency information and indirectly induced dependency information [20, 39]. The attributes of a dynamic naïve Bayesian classifier can only provide transitive dependency information, but the attributes of a dynamic full Bayesian classifier (DFBC) can provide all three kinds of dependency information, hence the DFBCs have better performance in relation to classification accuracy. Figure 6 shows the way in which the different dependency information that attribute variables providing for class variable among dynamic Bayesian derivative classifiers with different network structures.

Fig. 6

The dependency information provided by attributes in dynamic naïve, dynamic tree and dynamic full Bayesian classifiers. a dynamic naïve Bayesian classifier, b dynamic tree Bayesian classifier, c dynamic full Bayesian classifier

In the dynamic naïve Bayesian classifier that is shown in Fig. 6(a), the attributes only provide transitive dependency information for class, although this kind of information is the primary one for classification, the other two kinds of information cannot be ignored. In the dynamic tree Bayesian classifier shown in Fig. 6(b), apart from transitive dependency information, X₁[t] and X₂[t] also provide direct induced dependency information for C[t]. In the dynamic full Bayesian classifier (DFBC) shown in Fig. 6(c), C[t − 1] and X₅[t] provide only transitive dependency information for C[t], whereas X₁[t], X₂[t], X₃[t] and X₄[t] provide all the three kinds of dependency information.

3.4 Classification accuracy criterion of time-series progressiveness

For the time-series dataset D[T], the threshold of initial prediction time point (or time slice) T₀ can be determined according to the time-series size, class probability validity, and attribute density estimation, or actual needs. We use D[t − 1] as the training set, x₁[t], …, x_n[t] as the input and ρ = (ρ₁, ⋯, ρ_n) as the smoothing parameter vector, and denote the classification accuracy, classification result, and true numerical result of c[t] in DFBC as accuracy(ρ, D[T], T₀), c_prediction[t], and c_true[t], respectively. Then we have:

$$ ac\mathrm{c} uracy\left( dfbc,\boldsymbol{\rho}, D\left[T\right],{T}_0\right)=\frac{1}{T-{T}_0+1}{\sum}_{t={T}_0}^T signb\left({c}_{prediction}\left[t\right],{c}_{true}\left[t\right]\right) $$

(9)

where

$$ signb\left({c}_{prediction}\left[t\right],{c}_{true}\left[t\right]\right)=\left\{\begin{array}{c}1,{c}_{prediction}\left[t\right]={c}_{true}\left[t\right]\\ {}0,{c}_{prediction}\left[t\right]\ne {c}_{true}\left[t\right]\end{array}\right.. $$

3.5 Optimization of smoothing parameters

When dealing with time-series data, since a close relationship exists between the same class variable over different time points (or time slices), the classifier that can accurately classify the most adjacent class values in time sequences should be the most reliable. Inspired by this fact, the smoothing parameter configuration tree (or forest) is established over adjacent time points (or slices), and the smoothing parameters are optimized based on the configured tree (or forest).

The smoothing parameters that shape the curve (or surface) of a Gaussian function will directly affect the performance of a classifier. The smaller the value of the smoothing parameter and the steeper the density curve is, the better fit between classifier and data is achieved, although the generalization ability will appear worse. To trade-off between the fit and generalization ability of the classifier, we construct a smoothing parameter configuration tree (or forest) and use it to optimize the smoothing parameter configuration. The depth-first search method is adopted to build the smoothing parameter configuration tree (or forest), and the optimal synchronous change parameter is used to initialize all smoothing parameters. We take the latest class value as the starting point to search under the cumulative classification accuracy criterion of time-series progressiveness. If the cumulative classification accuracy(dfbc, ρ, D[T], T₀) = 1, then ${\rho}^{\ast }=\underset{\boldsymbol{\rho}}{argmax}\left\{ accuracy\left( dfbc,\boldsymbol{\rho}, D\left[T\right],{T}_0\right)=1\right\}$, that is, the generalization ability of the classifier is improved by taking the maximum value of smoothing parameter configuration; otherwise, the branch search ends.

When it is necessary to search space for the smoothing parameters, the final set-up construction is a smoothing parameter configuration tree (or forest) with or without repeated searches, which depends on whether, or not, the search space includes the smoothing parameters that have assigned values. Although more search space is needed to build a smoothing parameter configuration tree (or forest) with repeated searches, the results gained by repeated searches present a better investment. By repeated search space experiments, we found that the interval of smoothing parameters with the greatest influence on the DFBC classification accuracy is (0, 1].

We use H = {ρ¹, ρ², …, ρ^L} to denote the set of values for each smoothing parameter and ${\rho}_i^j\left(1\le i\le j,1\le j\le L\right)$ to denote the jth value of the smoothing parameter ρ_i of the attribute X_i, where L denotes the numbers of values obtained by discretizing each smoothing parameter with interval (0, 1] in the step (step size 0.001) In the following, we give the algorithm to construct a smoothing parameter configuration tree by combining classification accuracy criterion of time-series progressiveness and non-repeated search.

L is independent of n or T. Based on the classification accuracy estimation equation, the time complexity of the algorithm constructing a smoothing parameter configuration tree (or forest) is O(nT²), and that of the algorithm calculating a Gaussian function is O(n²T³).

The smoothing parameter configuration tree (or forest) formed by repeated search will be more complex than that of a non-repeated search. A new configuration tree can be derived by resetting the smoothing parameter in an existing configuration tree. Therefore, the final smoothing parameter configuration formed by repeated search is commonly denoted a forest. When constructing a smoothing parameter configuration tree (or forest) by repeated search, we avoid the possible looping situation (although the possibility is small) by limiting the number of generated subtrees. Additionally, by limiting the number of generated subtrees, the time complexity of the algorithm constructing the smoothing parameter configuration tree (or forest) based on repeated search will be the same as that based on a non-repeated search. We can also improve the smoothing parameter configuration tree (or forest) by using a repeated search and a non-repeated search strategy and adjust the classification accuracy criterion from completely cumulative accurate into partially accurate, which forms the basis for future work that we will do.

3.6 Ensemble DFBC by model averaging

Let ρ¹, ⋯, ρ^U denote the smoothing parameter configuration vector with minimum threshold and DFBC_u denote the corresponding dynamic full Bayesian classifier with the parameter configuration ρ^u(1 ≤ u ≤ U). Dynamic full Bayesian ensemble classifier (DFBEC) is established by averaging these classifiers, the structure of DFBEC is shown in Fig. 7.

Fig. 7

The structure of DFBEC

DFBEC can be expressed as:

$$ \underset{c\left[t\right]\left(c\left[t-1\right],{x}_1\left[t\right],\dots, {x}_n\left[t\right]\right)}{argmax}\frac{1}{U}{\sum}_{u=1}^U\left\{\frac{N\left(c\left[t\right],c\left[t-1\right]\right)}{{\left(2\pi \right)}^{n/2}N\left(c\left[t\right]\right)N\left(c\left[t-1\right]\right){\left({\rho}_1^u\right)}^2\cdots {\left({\rho}_n^u\right)}^2}{\sum}_{v=1}^t\left\{ signa\left(c\left[v\right]\right){\prod}_{i=1}^n\mathit{\exp}\left[-\frac{{\left({x}_i\left[t\right]-{x}_i\left[v\right]\right)}^2}{2{\left({\rho}_i^u\right)}^2}\right]\right\}\right\} $$

(10)

where ${\rho}_i^u$ is the ith component of ρ^u.

4 Experiment and analysis

We use time-series datasets from the UCI [40] Machine Learning Repository and the Wind Economic Database for experiments. The indexes are selected as class variables, and the related factors that affect these indexes are selected as attribute variables. Each index g(t) is binary discretized over the time-series and fall into the class labeled c[t]: if g(t) reaches an extremum at t_j, then c[t] = 1, and t_j is the turning point or extreme point; or else c[t] = 0, and t_j is the non-turning or non-extreme point. We repair records for the missing data using a moving average method, discretizing the class variables over the time-series according to the turning points and normalizing the attribute variables over the time-series. The experiment is comprised of five experimental modules: (1) the construction of a smoothing parameter configuration tree (or forest); (2) the comparison of classification accuracy (or error rate); (3) the influence of smoothing parameter changes on classification accuracy; (4) the influences of the minimum and maximum smoothing parameter configurations on classification accuracy and (5) the anti-disturbance of DFBEC.

4.1 Construction of smoothing parameter configuration tree and forest

We choose the GDP annual data to create the smoothing parameter configuration tree (or forest). Setting the threshold for the initial perdition time point or time slice (threshold for short) T₀ = 15 and H = {0.002 + 0.002k| 0 ≤ k ≤ 500}, we obtain the initial configuration of smoothing parameters ρ₀ = 1, and T₀ = 23. Next, we present the smoothing parameter configuration tree with non-repeated searches and repeated searches, respectively.

• (a) Construction of smoothing parameter configuration tree with non-repeated searches

The smoothing parameter configuration tree of GDP on one path with non-repeated searches is shown in Fig. 8.

Fig. 8

The smoothing parameter configuration tree of GDP

In the smoothing parameter configuration tree, each path from the root to the leaf corresponds to a configuration vector. We form a DFBC from each smoothing parameter configuration vector. The minimum threshold T₀ = 17 is found by traversing the smoothing parameter configuration tree, and the corresponding configuration vectors are as follows:

$$ \left(1,1,1,1,\mathrm{0.036,1},\mathrm{0.016,1},\mathrm{0.088,1},1,1,\mathrm{0.09,1},1,1,1\right) $$

$$ \left(\mathrm{0.132,1},1,1,\mathrm{0.036,1},\mathrm{0.016,1},1,1,1,1,\mathrm{0.052,1},1,1,1\right) $$

$$ \left(1,1,1,1,\mathrm{0.036,1},\mathrm{0.016,0.03,1},1,1,\mathrm{1,0.052,1},1,1,1\right) $$

$$ \left(1,1,1,1,\mathrm{0.022,1},\mathrm{1,0.01,0.036,1},1,1,1,1,1,1,1\right) $$

We can obtain 4 DFBCs from the above 4 smoothing parameter configuration vectors, and the DFBEC is formed by averaging these classifiers. The restriction of the minimum threshold can also be extended. If we select T₀ = 19 as the threshold, we will obtain 13 smoothing parameter configuration vectors and the corresponding 13 DFBCs.

• (b) Construction of smoothing parameter configuration forest with repeated searches

When we repeat the search space for a smoothing parameter, we can obtain a smoothing parameter configuration forest. One of the configuration trees of the forest is shown in Fig. 9.

Fig. 9

The smoothing parameter configuration tree of GDP with repeated searches

Where the nodes with “*” will produce the new trees. The tree derived by (*)ρ₇ = 0.076(6) is shown in Fig. 10(a). The trees derived by (*)ρ₁₄ = 1(61) and (*)ρ₁₆ = 0.034(62) from Fig. 10(a) are shown in Fig. 10(b) and 10(c), respectively.

Fig. 10

Derivative trees from (*)h₇ = 0.076(6). a Derivative tree of No. 6, b. Derivative tree of No. 61, c Derivative tree of No. 62

We find the minimum threshold T₀ = 12 by traversing the smoothing parameter configuration forest, and the corresponding configuration vectors are as follows:

$$ \left(\mathrm{0.136,1},\mathrm{0.064,1},\mathrm{0.036,1},\mathrm{0.076,1},1,1,1,1,1,1,\mathrm{0.056,0.034,1}\right) $$

$$ \left(\mathrm{0.116,1},1,1,\mathrm{0.036,1},\mathrm{0.052,1},\mathrm{0.246,1},1,1,\mathrm{0.254,1},\mathrm{0.072,1},1\right) $$

$$ \left(\mathrm{0.116,1},1,1,\mathrm{0.036,1},1,1,\mathrm{0.08,1},1,1,1,1,\mathrm{0.048,1},1\right) $$

$$ \left(\mathrm{0.116,1},1,1,\mathrm{0.036,1},\mathrm{0.052,1},\mathrm{0.142,1},1,1,1,1,\mathrm{0.072,0.032,1}\right) $$

The restriction of the minimum threshold can also be extended. If we select 19, 18, 17, 16, 15, 14 and 13 as the thresholds T₀, we will obtain 26, 19, 15, 12, 11, 9 and 6 smoothing parameter configuration vectors and DFBCs, respectively.

4.2 Comparison of classification accuracy

We choose 9 commonly used classifiers together with DFBEC classifier for comparing classification accuracy. 21 time-series datasets from the UCI and 24 time-series datasets from the Wind database are selected for experiments. Firstly, we select a dataset of 30 in front of the time-series dataset to establish the smoothing parameter configuration tree and determine the parameter configuration. Then, we take the latest 113 (or 103) data in the time-series dataset as the testing set to carry out a sliding test, with a fixed window size (training set size) of 30.

Descriptions of the comparison classifiers are as follows:

• GDNBC:dynamic naïve Bayesian classifier based on Gaussian density [33]

• KDNBC:dynamic naïve Bayesian classifier based on Gaussian kernel density [6, 33]

• FMDBN:a first-order Markov dynamic Bayesian network classifier based on Gaussian density [6]

• KDTBC:dynamic tree Bayesian classifier based on Gaussian kernel density [6, 33]

• GDOBC:dynamic One-dependence [17] Bayesian classifier based on Gaussian density [33]

• KDOBC:dynamic One-dependence [17] Bayesian classifier based on Gaussian kernel density [6, 33]

• RNN: Recurrent Neural Network [41]

• LSTM: Long Short-Term Memory [42]

• GRU: Gated Recurrent Unit [43]

• DFBEC: Dynamic Full Bayesian Ensemble Classifier

Among these, the parameter configurations for RNN, LSTM and GRU are: (a) RNN, 1 hidden layer, units = 32, active_function = 'tanh', loss = ‘mean_squared_error’, optimizer = ‘rmsprop’, metrics = [‘accuracy’]; (b) LSTM: 1 hidden layer, units = 32, active_function = ‘relu’, loss = ‘mean_squared_error’, optimizer = ‘adam’, metrics = [‘accuracy’]; (c) GRU: 1 hidden layer, units = 32, active_function = 'tanh', loss = ‘nn.CrossEntropyLoss’, optimizer = ‘optim.SGD’, metrics = [‘accuracy’].

A statistical comparison of the classifiers’ performances over error rate (error rate = 1-accuracy) is conducted by taking the Friedman Test with the post-hoc Bonferroni-Dunn method and Wilcoxon Signed-Ranks Test [44]. The differences amongst the 10 classifiers’ performances are first examined via the Friedman Test, and the pairwise comparisons are then realized by the post-hoc Bonferroni-Dunn method, showing the critical value at a significance level of 0.05 to be 2.773. If the difference between average ranks for pairwise classifiers is greater than the critical value, then we say the performance of the two classifiers is significantly different. We then use the Wilcoxon Signed-Ranks Test to examine the difference between each pairwise comparison (other classifier vs. DFBEC classifier). The test results listed at the bottom of Table 1 show significant differences in classification error between DFBEC and other classifiers. Considering the overall average classification performance, the classification accuracy of DFBEC is 15.81%, 12.95%, 9.47%, 14.13%, 15.33%, 18.62%, 12.62%, 18.46% and 13.79% larger than the other 9 classifiers by simple calculation.

Table 1 Classification error rate of 10 classifiers on 45 time-series datasets

The classification error rates of DFBEC and the other classifiers are shown in Fig. 11 as scatter-plot graphs, where the coordinates of each point represent the error rates of the two compared classifiers. The points above each diagonal line show that the error rates of DFBEC are smaller than those of the given classifier, and the points below the diagonal line show that the error rates of DFBEC are greater than those of the given classifier.

Fig. 11

Scatter plot graphs of classification error rates. a DFBEC vs GDNBC, b DFBEC vs KDNBC, c DFBEC vs FMDBN, d DFBEC vs KDTBC, e DFBEC vs GDOBC, f DFBEC vs KDOBC, g DFBEC vs RNN, h DFBEC vs LSTM, i DFBEC vs GRU

From Fig. 11, we can clearly see that the classification error rates of DFBEC are smaller than those of the other classifiers. Overall, the results of significance tests of difference, average value comparison and scatter diagrams show that DFBEC has significant advantages over the other 9 classifiers in terms of classification error rate.

Classification is one kind of human concept learning based on computer simulation. In human concept learning, to make full use of sample information (fitting data), rote learning (data overfitting) should be avoided as much as possible, and flexible learning (generalization ability) should be promoted when there are relatively few references. In our research, multivariate Gaussian kernel function is used to estimate attribute joint density, and the smoothing parameters are optimized based on the configured tree (or forest), so that DFBEC can fit data well. In addition, on the premise of maintaining the accuracy of classification, we reduce the overfitting by taking the maximum value of the smoothing parameter configuration, and thus improve the generalization ability of DFBEC.

4.3 Influence of smoothing parameter changes on classification accuracy

The smoothing parameters determine the shape of the Gaussian function curve, so any change to the smoothing parameter will affect the fit accuracy of the classifier to the data. We choose 6 time-series datasets for experiments: the Dow_jones_index (DJI), Drink_glass_model_1 (DGM), Energydata_complete (EDC), ME_BTSC3 (MEB), Gold_ICP (GIC) and Fund_MTUNV (FMA). We use s1, …, s9, s10, …, s18, s19, …, s27, s28 forρ when they are 0.001, …, 0.009,0.01, …, 0.09,0, 1, …, 0.9,1, correspondingly. The experiments and analysis of that the influence of smoothing parameter changes on classification accuracy are carried out under both temporal synchronous and asynchronous situations. The influence of smoothing parameter changes on classification accuracy is shown in Fig. 12, where the horizontal axis represents the value of smoothing parameter, and the vertical axis represents the classification accuracy. To reduce the influence of initial configuration on smoothing parameter changes, in the asynchronous change situation, the initial values of the smoothing parameters are set to 1 for the 6 time-series datasets. In the asynchronous change situation, the smoothing parameters ρ₁₁, ρ₇, ρ₂₀, ρ₆, ρ₃ and ρ₁₉ are selected for the 6 indexes according to the sequence of the datasets, respectively.

Fig. 12

The influence of smoothing parameter changes on classification accuracy. a The influence of temporal synchronous changes, b The influence of temporal asynchronous changes

In Fig. 12, we find that the smoothing parameter changes on the 6 time-series datasets all have significant influence on DFBECs’ classification accuracies in both temporal synchronous and asynchronous situations. In the synchronous changes, the maximum classification accuracy differences are 23.01%, 29.20%, 25.66%, 33.63%, 23.01% and 12.39% (with an average of 24.48%); in the asynchronous changes, the maximum classification accuracy differences are 41.60%, 5.31%, 21.24%, 24.78%, 21.24% and 7.96% (with an average of 20.35%). The significance of the differences illustrates both that the smoothing parameters need to be optimized and the benefit of doing so.

4.4 Influence of the minimum and maximum smoothing parameter configurations on classification accuracy

In this part, we discuss the influence of the minimum and maximum smoothing parameter configurations on DFBECs’ classification accuracy. These experiments and analyses are carried out based on the 45 datasets from the UCI and the Wind database and are discussed under both the temporal synchronous and asynchronous situations. The experimental results are shown in Fig. 13, where the horizontal axis represents the number of datasets, and the vertical axis represents the classification accuracy.

Fig. 13

The influence of the minimum and maximum smoothing parameter configurations on classification accuracy. a The influence of synchronous optimizations, b The influence of asynchronous optimization

From both Fig. 13 (a) and (b), we can see that the classifiers under the maximum smoothing parameter configurations are more accurate than those under the minimum configurations in both synchronous changes and asynchronous changes, but especially for the asynchronous series. Among the 45 classification problems, in synchronous optimization, the classification accuracies for 23 out of 45 problems under the maximum configuration is greater than that under the minimum configuration, and the accuracies occur in 15 of the same problems. In asynchronous optimization, the classification accuracy of 39 problems under the maximum configuration is greater than that under the minimum configuration, and the accuracies occur in 3 of the same problems. The comparison results are shown in Table 2. For synchronous optimization and asynchronous optimization, the differences between the average classification accuracy of the maximum configuration and the minimum configuration are 1.78% and 4.84%, respectively.

Table 2 Comparison of classification accuracies under the maximum and minimum smoothing parameter configurations

We can conclude that, on the premise of maintaining the classification accuracy of the classifier, data overfitting can be reduced by selecting the maximum configuration of the smoothing parameter. This is especially important for the classification of small sample time-series data.

4.5 Anti-disturbance of DFBEC

Additionally, the anti-disturbance ability of DFBEC based on asynchronous optimization is analyzed by using the 45 time-series datasets, under the disturbance of that 20% of the attribute data are randomly changed within the range of the attribute value. The experimental results are shown in Fig. 14.

Fig. 14

The experimental results for anti-disturbance of DFBEC based on asynchronous optimization

After introducing noise into the attribute data, the classification accuracy for some time-series datasets decrease slightly, with an average decline of 0.012, which shows that DFBEC with the maximum smoothing parameter configuration has good anti-disturbance performance based on asynchronous optimization, and a similar conclusion can be drawn based on synchronous optimization.

5 Conclusions and future work

In this paper, we develop the DFBEC which is suitable for small sample time-series data by combining estimation of the multivariate Gaussian kernel function with a diagonal smoothing parameter matrix; the classification accuracy criterion of time-series progressiveness; the construction of smoothing parameter configuration tree (or forest) and classifier selection and averaging.

The smoothing parameters that shape the curve (or surface) of a Gaussian function have direct impact on the performance of a classifier. The smaller the value of the smoothing parameter and the steeper the density curve is, the better the fit between the classifier and data achieves, but the worse the generalization ability appears; and vice versa. To establish a small sample time-series data classifier, two problems must be solved: one is to make the classifier fit data well, and the other is to avoid data overfitting. The latter is the more difficult problem to solve. In our research, multivariate Gaussian kernel function is used to estimate attribute joint density, and the smoothing parameters are optimized based on the configured tree (or forest), enabling the DFBEC to fit the data most advantageously. On the premise of maintaining the accuracy of classification, overfitting is reduced by taking the maximum value of the smoothing parameter configuration, thus improving the generalization ability of DFBEC. By combining classifier selection and averaging results, the generalization of DFBEC is further improved.

The experimental results based on the UCI and Wind datasets show that the DFBEC is more accurate with good anti-disturbance ability in the turning point classifications with small sample time-series data compared with the other nine commonly used classifiers. However, the DFBEC is limited in that it is only suitable for the classification of small time-series data. We propose further work to expand DFBEC by adjusting the classification accuracy criterion from completely cumulative accurate into partially accurate, and thus make it more suitable for general time-series data classification.