Kernel mixture model for probability density estimation in Bayesian classifiers

Abstract

Estimating reliable class-conditional probability is the prerequisite to implement Bayesian classifiers, and how to estimate the probability density functions (PDFs) is also a fundamental problem for other probabilistic induction algorithms. The finite mixture model (FMM) is able to represent arbitrary complex PDFs by using a mixture of mutimodal distributions, but it assumes that the component mixtures follows a given distribution, which may not be satisfied for real world data. This paper presents a non-parametric kernel mixture model (KMM) based probability density estimation approach, in which the data sample of a class is assumed to be drawn by several unknown independent hidden subclasses. Unlike traditional FMM schemes, we simply use the k-means clustering algorithm to partition the data sample into several independent components, and the regional density diversities of components are combined using the Bayes theorem. On the basis of the proposed kernel mixture model, we present a three-step Bayesian classifier, which includes partitioning, structure learning, and PDF estimation. Experimental results show that KMM is able to improve the quality of estimated PDFs of conventional kernel density estimation (KDE) method, and also show that KMM-based Bayesian classifiers outperforms existing Gaussian, GMM, and KDE-based Bayesian classifiers.

1 Introduction

Bayesian classifiers is a commonly used alternative for classification problems by representing the discriminant functions using probabilistic descriptions. Except considering the attribute independency, estimating the class-conditional probability density function (PDF) of a finite continuous data sample is another fundamental problem when exploiting Bayesian classifiers for classification tasks (Sucar 2015), and it is also a prerequisite for implementing other probabilistic induction algorithms (Xiong et al. 2017a, b; Jeon and Taylor 2012).

In general, related density estimation methodologies can be summarized into the four categories: discretization, parametric density estimation, nonparametric kernel density estimation (KDE), and semi-parametric density estimation. The first approach is widely used in Bayesian multinomial network (BMN) (Castillo et al. 2012), in which all attributes are assumed to follow multinomial distributions and continuous attributes will be discretized according to the consequent loss of information (Yang and Webb 2009). This approach has been applied in a variety of Bayesian algorithms, such as the Naive Bayes (NB) (Bouckaert 2004), tree-augmented naive Bayes (TAN) (Jiang et al. 2012), and the general Bayesian networks (Bielza 2014). However, when dealing with continuous data with many intervals, discretization method has problems of overfitting and unstability (Hand and Yu 2001), making it complex to train an optimal BMN.

In the second approach, parametric normal density estimation (PNDE) method is commonly used by simply assuming that data sample is drawn from a Gaussian distribution, and the mean value and standard deviation can be obtained by using the maximum likelihood estimation (MLE) method. The computation cost in classification phase is quite low, thus it is suitable for large data samples (Domingos and Pazzani 1997). However, due to reasons, such as irregularity of data distribution and lack of training data, performance of PNDE method in practice is not satisfactory, making it incompetent in most real-world problems (John and Langley 2013).

Without assuming any predefined distribution, estimating continuous density using nonparametric kernel density estimation (KDE) method has been proved to be much more effective for Bayesian classifiers compared with the discretization and PNDE methods (John and Langley 2013; Pérez et al. 2009). The kernel density estimation method, also known as the Parzen window method, is a limiting form of the finite mixture model since its number of components equals to the total number of data points. In KDE, the target conditional probability is estimated by regressing the PDF using smooth kernel functions, and the window bandwidth is the key factor influencing the quality of estimated results. Usually, it is obtained by minimizing the mean integrated squared error (MISE) between the estimated density and true density (Dehnad 1986; Wang et al. 2013). The most successful way of selecting the optimal bandwidth of the kernel is the density derivative functionals (DDF) based methods (Heidenreich et al. 2010). However, when the number of data sample is N, the complexity of DDF methods is ${\mathcal {O}}(N^2)$, which is inefficient and even unpractical when N is too large (Raykar and Duraiswami 2006). A commonly used bandwidth selection method is Silverman’s rule of thumb (RoT) (Dehnad 1986), which is efficient and has been proved to effective in most real world applications (Pérez et al. 2009).

The high computation cost of employing the full data sample for density estimation limits the practicability of KDE for large data sample. Complexity reduction by reducing the scale of data sample is the main focus of KDE related studies. Scott and Sheather (1985) proposed binning strategy by replacing the original data points using bin centers, and the multivariate form of the binned kernel density method is discussed by Holmström (2000). Similar to the binning strategy, cluster centers also can be used as the reduced data in to reduce the complexity of Parzen window estimators, the related works include the branch and bound approach (Jeon and Landgrebe 1994), the weighted Parzen windows (Babich and Camps 1996) and self-organizing map (Holmström and Hämäläinen 1993). Girolami and He (2003) proposed a Reduced Set Density Estimator (RSDE) using a constrained straightforward quadratic optimization algorithm to find a condensed sample from the original sample. Since the k-means-like clustering requires a iterative process to find optimal clusters centroids, Schwander and Nielsen (2012, 2013) proposed a single-step clustering method to avoid iteration calculation, and quality of estimation results is guaranteed by Fisher–Rao metric or Kullback–Leibler divergence. Although the above works significantly improve the efficiency of KDE approach, the quality of estimation results remains unimproved.

As a semi-parametric density estimation approach, the finite mixture models (FMM) (Figueiredo and Jain 2002), such as the well known Expectation-Maximum (EM) algorithm based density estimation (Yin and Allinson 2001), can be applied to represent arbitrary complex PDFs by assuming data sample is drawn from a mixture of several independent components. Usually, FMM is suitable for estimating PDFs in unsupervised learning scenarios to discover clusters with similar distribution properties (Escobar and West 1995; Shen et al. 2013; Kayabol and Zerubia 2013). In unsupervised learning, clustering ensembles can be used to find clusters with arbitrary shape, and it has been proved to be more effective than single clustering algorithms (Topchy et al. 2004). The commonly used FMM model is Gaussian mixture model (GMM), which has been applied in estimating conditional probability in classification problems, and has been proved to more effective than simple PNDE methods (Reynolds and Rose 1995). However, the FMM based pdf estimation assumes that the components follows a certain distribution, e.g. Gaussian distribution, which may not be true for real world data. Wang et al. (2005) proposed an improved GMM model based on boosting, which is able to adjust the estimated results according to regional samples, thus the Gaussian distribution assumption is relieved.

1.1 Motivations and contributions

The estimated PDFs of the KDE method are obtained by minimizing the mean integrated squared error (MISE) to the histograms of the training samples, and this practice has been proved to be effective in producing flexible and continuous densities (Dehnad 1986). Calculating probabilities using above optimality criterion follows a basic assumption: the histogram is a discretization of the real PDF of the data sample. However, this estimation method still suffers from the inhomogeneous and irregular distributions of different regional data.

To illustrate the motivations of this paper, a simple example is given in Fig. 1, in which (a) is the contour plot of the original distributions of an artificial dataset with two independent features $x_1$ and $x_2$, and they are randomly generated by a mixture of two component subclasses. The samples of the two hidden subclasses are imbalanced, and the ratio is 2:1. The estimated KDE method are shown in Fig. 1b, c. The former one is obtained by combining the PDFs of estimation results of $x_1$ and $x_2$ using naive bayes rule, i.e. $p({\mathbf {x}})=p(x_1)p(x_2)$, and the latter one is the result of joint PDF of bivariate feature $p({\mathbf {x}}=[x_1,x_2])$.

Fig. 1

Example of estimating joint PDFs using KDE method, in which a the original distribution, b estimated results with naive Bayes assumption, and c estimated results with bivariate distribution

Fig. 2

Example of estimated PDFs on real-world EEG eyestate data obtained by using RoT-based KDE, in which a, b are histograms and estimated results of ‘AF3’ feature and ‘F3’ feature, respectively. The class of the two features are all ‘open’

From Fig. 1, we observe that the estimated PDF plotted in (b) is biased compared with the original distribution in (a), which indicates that the estimated PDFs for independent features may be undesirable in a Bayesian classifier. The results in (c) are much better than the one in (b), however, contour lines of hidden subclass 2 are still not reliable compared with the original data distribution. This result shows that the KDE method still has imperfections to deal with irregular data distributions, especially for estimating joint PDFs of independent features, thus it needs to be improved.

Another example is the estimated PDFs of real-world EEG eyestate data obtained by using RoT method, as shown in Fig. 2, in which (a) and (b) are the histograms and estimated results of ‘AF3’ feature and ‘F3’ feature, respectively. We can see that the PDF of ‘AF3’ feature is approximated to a Gaussian distribution, and the estimated result is very reasonable. However, When the target PDF is irregular and multimodal, as shown in (b), the estimated result is biased. This result show that although RoT is very efficient, its performance on complex PDFs is not acceptable and should be improved. On the other hand, existing related work mainly focuses on complexity reduction problems in kernel based density estimation. There is lack of an approach to improve of the quality of estimation results of KDE approaches while preserving acceptable efficiency (Wang et al. 2013).

In this paper, we intend to improve the the KDE-based PDF estimation method in Bayesian classifiers by using the FMM model. Different from conventional FMM models, we assume that the components are drawn by several unknown distributions. We present a new method called kernel mixture model (KMM) by considering components in different spatial regions. The proposed KMM method employs the simple RoT method to select bandwidth, and it achieves good performance in both effectiveness and efficiency. We regard the data sample belonging to one class as a mixture composed of several independent hidden subclasses with unknown distributions, and the k-means clustering algorithm is exploited to partition the data sample into several componential sub-sample sets. We develop a Bayesian framework to estimate the PDF under the framework of KMM, and propose a general three-step framework for estimating PDFs in Bayesian classifiers. Examples and experimental results will be provided to show the remarkable performance of the proposed method.

The rest of this paper is organized as follows: Sect. 2 give a review of existing probability density estimation methods and the Bayesian classifiers. Section 3 elaborated the proposed KMM algorithm. A three-step Bayesian classifier is proposed in Sect. 4. Experimental results along with the analysis are provided in Sect. 5. Finally, Sect. 6 concludes this paper.

2 Kernel density estimation and Bayesian classifiers

2.1 Kernel density estimation

The quality of estimated probability density function is an important factor influencing the performance of Bayesian classifiers. However, we always don’t consider which distribution is the most suitable one to fit the distributions of numerical features, and the most commonly used one is the Gaussian function, i.e. assume that data follows normal distribution, and this practice is necessary for efficiency considerations, especially for high dimensional data. Notations used in this paper is summarized in Table 1.

Table 1 Notations used in this paper

Suppose ${\mathbf {x}}$ is a d-dimensional vector, its multivariate Gaussian probability distribution of class $\omega$ is

$$\begin{aligned} p({\mathbf {x}}|\omega ) = \frac{1}{{(2\pi )}^{d/2} |\varvec{\varSigma }|^{1/2}}\exp \left\{ -\frac{1}{2}({\mathbf {x}}-\varvec{\mu })^T \varvec{\varSigma }^{-1}({\mathbf {x}}-\varvec{\mu })\right\} , \end{aligned}$$

(1)

where $\varvec{\mu }$ and $\varvec{\varSigma }$ denote the mean value vector and covariance matrix, respectively. $|\varvec{\varSigma }|$ denotes the determinant of $|\varvec{\varSigma }|$. When $d=1$, the above equation corresponds to the Gaussian distribution of a single variable.

Unfortunately, the distribution of a random variable is usually irregular and it can’t be perfectly drawn from one ideal parametric PDF, thus the mixture model has been applied, such as the Gaussian mixture model in Reynolds and Rose (1995). Another way to obtain more precise conditional probability is the well-known kernel density estimation (KDE) method, also called Parzen–Rosenblatt window method (Scott 2015), has been developed to estimate the non-parametric PDF of an random attribute. Suppose we have N d-dimensional samples ${\mathbf {X}}= [{\mathbf {x}}_{1},\ldots , {\mathbf {x}}_N]$ drawn from an unknown probability density function $f({\mathbf {x}})$, its smooth estimation is given by

$$\begin{aligned} \widehat{f}_{{\mathbf {H}}}({\mathbf {x}}) = \frac{1}{N }\sum _{i=1}^N {K}_{{\mathbf {H}}}\left( {\mathbf {x}}-{\mathbf {x}}_i \right) , \end{aligned}$$

(2)

where ${K}_{{\mathbf {H}}}(\cdot )$ is a non-negative kernel function, and ${K}_{{\mathbf {H}}}({\mathbf {x}}) = |{\mathbf {H}}|^{-1/2}{K}({\mathbf {H}}^{-1/2}{\mathbf {x}})$, parameter ${\mathbf {H}}$ is a $d\times d$ symmetric and positive definite bandwidth matrix which decides the smoothing degree of the estimated density function. Usually, the standard Gaussian kernel is used as the kernel function, and the above equation can be explicitly written as

$$\begin{aligned} \widehat{f}_{{\mathbf {H}}}({\mathbf {x}}) = \frac{1}{N(2\pi )^{d/2}|{\mathbf {H}}|^{1/2}}\sum _{i=1}^N \exp \left\{ -\frac{1}{2}({\mathbf {x}}-{\mathbf {x}}_i)^T {\mathbf {H}}^{-1}({\mathbf {x}}-{\mathbf {x}}_i)\right\} . \end{aligned}$$

(3)

The bandwidth matrix ${\mathbf {H}}$ has a critical influence on the precision of the estimated density function (Heidenreich et al. 2010), thus it needs to be assigned with proper values. Since the full matrix ${\mathbf {H}}$ has $d(d+1)/2$ values to be estimated, when d is relative large, obtaining the full matrix ${\mathbf {H}}$ is computationally expensive, even unpractical (Pérez et al. 2009). To guarantee effect of smoothing while improving the computation efficiency, we adopt the differential scaled approach (Simonoff 1997), in which ${\mathbf {H}}$ is simplified as a diagonal matrix ${\mathbf {H}}=\text {diag}(\lambda _{1},\ldots ,\lambda _{d})$. The above restricted parametrization enables different smoothing degrees for each coordinate direction, and how to select proper values for the diagonal matrix still needs to be carefully considered.

As aforementioned, ${\mathbf {H}}$ is obtained by using the MISE criterion, and using the computationally intensive DDF-based bandwidth selections method are not practical for Bayesian classifiers. A commonly used way is assuming that the target PDF is approximated to a Gaussian distribution, and calculate bandwidth $\lambda _{i}(1\le i\le d)$ according to Silverman’s rule of thumb (RoT) (Dehnad 1986), and the optimal bandwidth for normal kernel is given by

$$\begin{aligned} \displaystyle \lambda _i = \widehat{\sigma }_i \left( \frac{4}{(d+2) N} \right) ^{\frac{1}{d+4}}, \end{aligned}$$

(4)

where $\widehat{\sigma }_i$ is the estimated standard deviation of the ith predictor ${\mathbf {X}}^{(i)}$. The above rule is quite easy to implement and it performs well even when the density is not closely approximated to Gaussian distributions. However, when the target PDF is a complex multimodal distribution, estimated results of RoT is proved be not reliable compared with DDF-based methods (Heidenreich et al. 2010; Xu et al. 2015), thus there is a need to develop a RoT-based kernel method to improve the quality of KDE while preserving good efficiency.

2.2 Bayesian classifiers

The goal of a Bayesian classifier is knowing the posterior probability of each class, and according to the Bayes theorem, the posterior probability can be calculated via the combination of the two probability measures: prior probability and conditional probability. The former one can be easily obtained by calculating the each classs proportion in training samples, and the latter can be calculated by using a parametric or nonparametric probability density estimation methods.

Consider a classification problem with the frame of discernment $\varOmega = \left\{ \omega _1,\ldots ,\omega _c \right\}$. Let ${\mathbf {X}} = \left\{ {\mathbf {x}}_1,\ldots ,{\mathbf {x}}_N \right\}$ be the training samples, in which the $i^{th}$ feature vector is ${\mathbf {x}}_i = \left[ x_{i1},\ldots ,x_{id} \right]$. Given a new test instance ${\mathbf {x}} = [x_1, \ldots , x_d]$, the final decision can be made by choosing the class with the maximum overall posterior probability, as given by

$$\begin{aligned} \displaystyle d_g = \arg \max _{1\le i \le c} p(\omega _i | {\mathbf {x}}) . \end{aligned}$$

(5)

Define the prior probability of class $\omega _i$ as $P(\omega _i)$. By using the Bayes theorem, the overall posterior probability $p(\omega _i |{\mathbf {x}})$ can be calculated by

$$\begin{aligned} \displaystyle p(\omega _i | {\mathbf {x}}) = \frac{p({\mathbf {x}}|\omega _i )P (\omega _i)}{\sum _{j=1}^{c} p({\mathbf {x}}|\omega _j)P (\omega _j) } , \end{aligned}$$

(6)

where the denominator can be regarded as merely a normalization factor. The class-specific condition probabilities can be calculted by

$$\begin{aligned} p({\mathbf {x}}|\omega _j) = \prod _{i=1}^{d_1} p(x_i|{\mathbf {C}}_i,\omega _j)\prod _{t=d_1+1}^d p(x_i|\omega _j), \end{aligned}$$

(7)

where $d_1$ is the number of attributes with parent nodes (except the class node), and ${\mathbf {C}}_i$ denotes the parent nodes of attribute $x_i$. Except estimating the conditional PDFs, the above decomposition also requires us to find the structure of the network, thus structure learning is necessary in training a Bayesian classifier. In this paper, we consider the following three typical Bayesian classifiers: naive Bayes (NB), tree-augmented naive Bayes (TAN), and complete graph (CG). Fundamentals of the above three classifiers will be provided in the next subsections.

2.2.1 Naive Bayes

Training an optimal Bayesian Network has been proved to be a NP-hard problem and it is not efficient in practice (Chickering 2010), especially for features with high dimensions. The naive Bayes (NB) classifier is the most widely used version of Bayesian classifiers. It just simply assumes that the features are conditionally and statistically independent from each other, thus the calculation of joint conditional probability of the whole feature vector is greatly simplified (Rish 2001), as given by

$$\begin{aligned} \displaystyle p(\omega _i | {\mathbf {x}} ) = \beta P (\omega _i) \prod _{k=1}^{d}p(x_k|{\omega _i}) , \end{aligned}$$

(8)

where $\beta = 1/\sum _{j=1}^{c}p({\mathbf {x}}|\omega _j) P (\omega _j)$. Finally, the decision can be made by selecting the class with maximum posterior probability.

2.2.2 TAN

The conditional independent assumption in naive Bayes is not realistic for most real-world problems, thus learning the structure of Bayesian classifiers is unavoidable if we want to improve the performance of a naive Bayes classifier. However, as aforementioned, learning an optimal Baysian network is NP hard with high computation cost (Chickering 2010). A commonly used strategy to compromise the attribute dependency and computation efficiency in training Bayesian networks is imposing a restricted structure of the Bayesian network. A typical Bayesian classifier with restricted structure is the Tree-augmented naive Bayes (TAN) classifier (Friedman et al. 1997).

In TAN, the structure of a navie Bayes classifier can be extended by using directed arcs to represent attribute dependency, and a maximum weighted spanning tree is constructed by using Chow and Lius procedure (Chow and Liu 1968). TAN uses the conditional mutual information (Friedman et al. 1997), or Heckerman’s scoring variation metric (Heckerman et al. 1995), to quantify the dependency between two attributes. When conditional mutual information or scoring variation metric is obtained, it can be used as the weight of the edge of two connecting attributes, and a undirected weighted graph can be built. Subsequently, a undirected maximum weighted spanning tree can be constructed by using Chow–Liu tree algorithm (Chow and Liu 1968). Finally, directed edges from class labels to all attributes are added, and a TAN classifier is obtained.

2.2.3 Complete graph classifiers

As learning the optimal Bayesian network is unpractical, we can avoid it by simply construct a complete graph structure without cycles between the attributes. Therefore, for a d-dimensional data sample, an attribute can be assigned with up to $d-1$ parent nodes, except the class node. The above Bayesian network with complete graph are equivalent to the multivariate Parzen window (PW) classifiers, or multivariate parametric estimation based Bayesian classifiers (Babich and Camps 1996; Pérez et al. 2009). Implementing a PW classifier requires us to calculate the class-specific conditional probabilities by using multivariate kernel density estimation method, as given in Eq. (2). Also, for multivariate parametric estimation, we consider multivariate Gaussian distribution based PDF estimation, as defined in Eq. (1).

As the proposed KMM method adopts a FMM model, the structure of the corresponding Banyesian networks will be constructed in a hierarchy architecture. Except the general framework, modifications to the above tree typical Bayesian classifiers will also be introduced, as illustrated in Sect. 5.

3 Proposed kernel mixture model

Unlike the existing methods, we present a new way to estimate the probability density of the sample data by considering the statistical differences in spatial distributions of regional areas. To illustrate the proposed method, we firstly define the concepts of multifaceted feature and hidden subclass as follows.

Definition 1

Multifaceted feature. Let ${\mathbf {X}} = [{\mathbf {x}}_1, \ldots , {\mathbf {x}}_N]$ be the data sample, ${\mathbf {X}}$ is said to be multifaceted it can not be precisely drawn by any single PDF of a given distribution. We assume that the density function of a multifaceted attribute is a mixture of multiple density distributions. Particularly, in this paper the given data distribution of continuous numerical attributes is specified as the Gaussian distribution, since it is the most commonly used distribution in practice.

Definition 2

Hidden subclass (HSC). Suppose that ${\mathbf {X}} = [{\mathbf {x}}_1, \ldots , {\mathbf {x}}_N]$ are the data sample of some class $\omega$, and $\omega \in \varOmega$. If ${\mathbf {X}}$ is multifaceted if it can be drawn from a mixture of PDFs $p_{{\mathbf {X}}^1}({\mathbf {x}}),\ldots , p_{{\mathbf {X}}^{n}}({\mathbf {x}})$, in which ${\mathbf {X}}^1,\ldots ,{\mathbf {X}}^{n}$ are independent and mutually exclusive subsets of ${\mathbf {X}}$, i.e. ${\mathbf {X}} = {\mathbf {X}}^1 \cup \ldots \cup {\mathbf {X}}^{n}$ and ${\mathbf {X}}^p \subset {\mathbf {X}}, {\mathbf {X}}^p \cap {\mathbf {X}}^{q} =$ Ø  for any ${\mathbf {X}}^q \subset {\mathbf {X}}$. Denote the corresponding subclasses of the sub sample sets as $\left\{ {\omega }^1,\ldots ,{\omega }^{n}\right\}$, and they are called the hidden subclasses of $\omega$.

With the above two definitions, the proposed KMM model will be elaborated. The framework for density estimation considering hidden subclass will be developed. Also, examples will be provided to illustrate the proposed method.

Fig. 3

Framework of the proposed KMM method. In partitioning, the training data sample of class $\omega$ is divided into several clusters, and each cluster corresponds to a HSC. In structure leaning, the Bayesian network structure of the HSCs is computed. In estimation, give a test data, conditional probability of each HSC is computed by using conventional KDE method with the guide of obtained network structure. Finally, the conditional probabilities of HSCs are aggregated to obtain conditional probability of class $\omega$ by using Bayes rule

3.1 Kernel mixture model

Similar to FMM, we propose a kernel mixture model (KMM) in this paper, and its framework is depicted in Fig. 3. As KMM assumes that data sample of a class is a mixture of several mixtures of unknown distributions, the first step is to partition the sample data to several HSCs using class-specific clustering algorithm. Structure learning is conducted with the obtained HSCs, but not the original classes. Subsequently, basic multivariate KDE is applied to estimate the PDFs with the guide of the obtained Bayesian network structure. Posterior probabilities of HSCs belonging to one class will be aggregated by using Bayes Theorem. At last, decision can be made by choosing the one with maximum posterior probability. Detailed process of KMM will be illustrated in next subsections.

3.2 Partitioning

The results in Fig. 1 have shown that the estimation results of KDE is affected by the inhomogeneity and irregularity the sample data. By partitioning the data sample into different regions with similar distributions, the above imperfections of data distribution will be revealed. The clustering algorithms have been designed to divide unsupervised data into clusters with similar statistical properties, thus they can be exploited for the hidden subclasses partitioning process.

In this paper, we use the k-means clustering algorithms for conducting the partitioning process, the main reason is that it is applicable for small data samples. Also, it is efficient and effective in practice. Although the Expectation-Maximum (EM) algorithm is developed using probability induction process, we found that it has problem in estimating reliable standard deviation, or covariance matrix, for small data samples. Using clustering algorithms for unsupervised classification is a fundamental topic in machine learning, a detailed introduction can be found in Duda et al. (2012).

Again, suppose that we have N random samples ${\mathbf {X}} = [{\mathbf {x}}_1, \ldots , {\mathbf {x}}_N]$ belonging to some class $\omega$, but they are drawn by multi-modal probability density mixture, i.e. the random variable is multifaceted, suppose the hidden subclasses are $\omega ^1,\ldots ,\omega ^n$, and their corresponding samples are ${\mathbf {X}}^1,\ldots , {\mathbf {X}}^n$, in which ${\mathbf {X}}^i = [{\mathbf {x}}_1^i,\ldots ,{\mathbf {x}}_{N_i}^i]$ and $N=\sum _{i=1}^n N_i$. The prior probability of hidden subclass $\omega ^i$ can be easily obtained as $P(\omega ^i)= N_i/N$. Given a new observation ${\mathbf {x}}$, we can obtain n conditional probabilities $p({\mathbf {x}}|\omega ^1),$ $\ldots ,p({\mathbf {x}}|\omega ^n)$, then the conditional probability $p({\mathbf {x}}|\omega )$ can calculated by using the finite mixture model, as given by

$$\begin{aligned} \displaystyle p({\mathbf {x}}|\omega ) = \sum _{i=1}^{n} \alpha _i p({\mathbf {x}}|\omega ^i), \end{aligned}$$

(9)

where parameter $\alpha _i \ge 0$ and $\sum _{i=1}^{n}\alpha _i = 1$. After the partitioning process, the componential hidden subclasses will be known to us, the above equation can be rewritten as

$$\begin{aligned} \displaystyle p({\mathbf {x}}|\omega ) = \frac{\sum _{i=1}^{n}p({\mathbf {x}}|\omega ^i)P(\omega ^i)}{P(\omega )}, \end{aligned}$$

(10)

where $P(\omega )$ is the prior probability of class $\omega$. According the Bayes’ Theorem, the posterior probability can be calculated by

$$\begin{aligned} \displaystyle \begin{aligned} p(\omega |{\mathbf {x}})&= \frac{P(\omega )p({\mathbf {x}}|\omega )}{\sum _{\omega _j} p({\mathbf {x}}|\omega _j)}\\&= \beta \sum _{k=1}^n p({\mathbf {x}}|\omega ^k)P(\omega ^k), \end{aligned} \end{aligned}$$

(11)

where $\beta = 1/ \sum _{\omega _j} p({\mathbf {x}}|\omega _j)P(\omega _j)$ and $\omega _j \subseteq \varOmega$. By using the above equation, calculating the posterior probability has been changed to the problem of estimating the conditional probabilities of its member HSCs.

3.3 Structure learning

Learning the network structure is another essential process when training a Bayesian classifier. For naive Bayes classifier and the Parzen window classifier, structure learning is avoided. We also consider TAN classifier, as it is a popular Bayesian classifier balances the training efficiency and computational cost. In this paper, learning the structure of a TAN is achieved by using Chow–Liu tree algorithm (Chow and Liu 1968).

After the network structure of a TAN is obtained, we have to calculate the continuous conditional PDFs if one attribute node x is assigned with a parent node C. One can calculate the approximated continuous conditional PDFs by using a discretization operation, but information loss is unavoidable. We can calculate the continuous conditional PDFs by using Baye rule, as given by

$$\begin{aligned} p({x}|{C},\omega ) = \frac{p({x},{C}|\omega )}{p({C}|\omega )} \end{aligned}$$

(12)

As $p({x},{C}|\omega )$ and $p({C}|\omega )$ can be obtained by using the KDE-based estimation methods, and subsequently $p({x}|{C},\omega )$ can be calculated. More specifically, $p({x},{C}|\omega )$ can be obtain by using a bivariate KDE estimation method, as given in Eqs. (2) and (3). Note that when the denominator $p({C}|\omega )$ is closed to 0, using the above equation to calculate continuous conditional probabilities may produce biased results. A practical solution is to compensate a small scale value (for example $1\times 10^{-7}$) to the denominator to obtain more reasonable estimation results.

3.4 Estimation

We assume that distributions of HSCs are unknown to us, and use KDE for probability density estimation, and the estimated probability of hidden subclass $\omega ^i$ is

$$\begin{aligned} \widehat{f}_{{\mathbf {H}}_i}({\mathbf {x}}) = \frac{1}{N_i}\sum _{k=1}^{N_i} {K}_{{\mathbf {H}}_i} \left( {{\mathbf {x}}-{\mathbf {x}}_k^i}\right) , \end{aligned}$$

(13)

where ${\mathbf {H}}_i$ is the band width matrix of HSC $\omega ^i$. We shall see that the proposed KMM uses different ${\mathbf {H}}_i$ for different HSCs, while only one band width matrix ${\mathbf {H}}$ is used in convolutional KDE method, thus the proposed KMM has better adaptation ability to inhomogeneity and irregularity of data distributions.

Combined with Eq. (11), we have the estimated conditional probability, as given by

$$\begin{aligned} \displaystyle \begin{aligned} p({\mathbf {x}}|\omega )&= \frac{1}{P(\omega )}\sum _{i=1}^{n} \frac{P(\omega ^i)}{N_i}\sum _{k=1}^{N_i} {K}_{{\mathbf {H}}_i} \left( {{\mathbf {x}}-{\mathbf {x}}_k^i} \right) \\&= \frac{1}{NP(\omega )}\sum _{i=1}^{n} \sum _{k=1}^{N_i} {K}_{{\mathbf {H}}_i} \left( {{\mathbf {x}}-{\mathbf {x}}_k^i} \right) . \end{aligned} \end{aligned}$$

(14)

Since $P(\omega ^i)=N_i/N$, the corresponding posterior probability of class $\omega$ can be calculate by

$$\begin{aligned} \displaystyle \begin{aligned} p(\omega |{\mathbf {x}})&= \frac{\beta }{N}\sum _{i=1}^{n}\sum _{k=1}^{N_i} {K}_{{\mathbf {H}}_i} \left( {{\mathbf {x}}-{\mathbf {x}}_k^i} \right) . \end{aligned} \end{aligned}$$

(15)

Specifically, when using the Gaussian kernel function, the above equation can be explicitly written as

$$\begin{aligned} \displaystyle \begin{aligned} p({\mathbf {x}}|\omega )&=\frac{\beta }{N(2\pi )^{d/2}}\sum _{i=1}^{n}|{\mathbf {H}}_i|^{-\frac{1}{2}}\sum _{k=1}^{N_i} \exp \left\{ -\frac{1}{2}({\mathbf {x}}-{\mathbf {x}}_k^i)^T {\mathbf {H}}_i^{-1}({\mathbf {x}}-{\mathbf {x}}_k^i)\right\} \end{aligned} \end{aligned}$$

(16)

Actually, when the band width matrices of hidden subclasses are the same, i.e. ${\mathbf {H}}_1 = \cdots ={\mathbf {H}}_{N_i}$, Eq. (16) can be rewritten as

$$\begin{aligned} \displaystyle \begin{aligned} p({\mathbf {x}}|\omega )&= \frac{\beta }{N}\sum _{i=1}^{n}\sum _{k=1}^{N_i} {K}_{{\mathbf {H}}} \left( {{\mathbf {x}}-{\mathbf {x}}_k^i} \right) \\&= \frac{\beta }{N}\sum _{i=1}^{N} {K}_{{\mathbf {H}}} \left( {{\mathbf {x}}-{\mathbf {x}}_i} \right) , \end{aligned} \end{aligned}$$

(17)

which is equivalent to Eq. (2). We can see that, although the KDE method is able to estimate the approximate shape of any unknown PDF, it fails to consider the variations of band width matrices of hidden subclasses when an attribute has a finite mixture of multi-modal PDFs. When the data sample has irregular distributions, its global histogram is not a good choice for estimating its PDF. In this sense, finding functions close the global histogram is not a good way for probability density estimation tasks, and a better way is to find adaptive band width matrices for different regional data samples.

Another benefit of using FMM for PDF estimation is its natural property in relaxing the attribute independency assumption. Apparently, for two random variables, if both of them are divided into several HSCs, the independency between HSCs will be easier to be achieved compared with the original distributions.

3.5 Examples

We use the example given in Fig. 1 to illustrate the proposed method, and the estimation results of the proposed KMM method are depicted in Fig. 4. In Fig. 4a, the two features are assumed to be independent with each other, thus the joint PDF of the data sample is obtained by univariate KMM, i.e. $p({\mathbf {x}}|\omega )\propto P(\omega ^1)p(x_1|\omega ^1)p(x_2|\omega ^1) +P(\omega ^2) p(x_1|\omega ^2) p(x_2|\omega ^2)$. In Fig. 4b, the two features are assumed to be correlated with each other, thus the joint PDF of the data sample is obtained by multivariate KMM, i.e. $p({\mathbf {x}}|\omega )\propto P(\omega ^1)p({\mathbf {x}}|\omega ^1)+P(\omega ^2)p({\mathbf {x}}|\omega ^2)$. Also, the estimated results of the two features in Fig. 2 are shown in Fig. 5. To give quantified comparison result, the mean square errors (MSEs) of the estimation PDFs of KDE and the proposed KMM are also calculated, the results are shown in Table 2.

Fig. 4

Estimation results of the KMM method, joint PDFs in a, b are calculated by $p({\mathbf {x}}|\omega )\propto P(\omega ^1)p(x_1|\omega ^1)p(x_2|\omega ^1)+P(\omega ^2)p(x_1|\omega ^2)p(x_2|\omega ^2)$ and $p({\mathbf {x}}|\omega )\propto P(\omega ^1)p({\mathbf {x}}|\omega ^1)+P(\omega ^2)p({\mathbf {x}}|\omega ^2)$, respectively

Fig. 5

Example of estimated PDFs on real-world EEG eyestate data obtained by using KMM, HSC numbers in a and b are 3 and 6, respectively

Table 2 Comparison of MSEs of the estimated PDFs

We have the following observations:

(1) From Figs. 1 and 4, it can be seen that the proposed method has very significant improvement for calculating joint PDFs, as we can see the estimated PDFs in Fig. 4a (MSE: $7.035\times 10^{-12}$) is very close to the original distribution, but the results in Fig 1b (MSE: 0.0427) is apparently biased. Also, The proposed method has improvement for calculating joint PDFs of bivariate features. In Fig. 4b (MSE: $6.223\times 10^{-12}$), we can see contour lines of HSC 2 are more smooth compared with results in Fig. 11c (MSE: $7.871\times 10^{-12}$). Besides, when univariate KMM is used, the MSE of estimated results are smaller than multivariate KDE, which also demonstrate the effectiveness of the proposed method.

(2) From Figs. 2 and 5, it can be observed that, when the target PDF is irregular and multimodal, KMM can significantly reduce the MSE of KDE. For feature ‘F3’, the MSE is reduced from $1.40\times 10^{-4}$ to $3.87\times 10^{-6}$ when KMM is adopted. For feature ‘AF3’ that is not complex, the MSE is also reduced from $7.93\times 10^{-6}$ to $2.94\times 10^{-6}$, but not that significant like feature ‘F3’.

The above results show that, compared with KDE, KMM tend to be able produce more reliable results when estimating multidimensional PDFs with independent features, or complex PDFs with irregular and multimodal components. On the other hand, when the target is not very complex, or independent, KMM also may be more effective than KDE.

Table 3 Comparison of complexity

3.6 Complexity analysis

In this subsection, we analyze the time complexities of different probability density estimation methods, including Gaussian parametric density estimation (Gaussian), kernel density estimation (KDE), the Gaussian mixture model (GMM), and the proposed kernel mixture model (KMM). Suppose the used kernel function is Gaussian kernel function and clustering algorithm is k-means, the comparison results are listed in Table 3, in which d is the number of attribute, and t and n denote the iteration number of clustering process and the total number of hidden subclass, respectively. Note that in the training phase of KDE, we just have to estimate the standard deviation of each attribute, thus its complexity is ${\mathcal {O}}(Ndc)$. Since the clustering process is essential in the proposed KMM, the corresponding complexity ${\mathcal {O}}(Nn t)$ is added in the training phase.

It is easy to conclude that, compared with Gaussian and KDE methods, the proposed KMM algorithm has higher complexity in both training and classification processes, this is because a additional clustering process is needed in the train process, and the number of hidden subclasses are more than the explicit classes. Moreover, the training process has to be repeated several times to find the optimal HSC numbers. The complexity of the proposed KMM is N times of GMM in the classification phase. However, the complexity of KMM has the same order of magnitude as KDE in the classification phase, thus the efficiency of RoT is preserved, and it is acceptable if the performance can be improved.

4 KMM-based Bayesian classifiers

As aforementioned, the proposed KMM-based Bayesian classifier is divided into the following 3 steps: partitioning, structure learning, and estimation, and we call them P-step, S-step and E-step for short. In P-step, samples belonging to one class are partitioned into several hidden subclasses by using the k-means clustering algorithm, and the next S-step is conducted to learn network structure under the framework of the extended hidden subclasses. In E-step, when given a new test sample, the posterior probabilities of each hidden subclass will be firstly obtained, then they are aggregated to calculate the posterior probabilities of each real class in the frame of discernment.

Posterior probabilities can be obtained by using different Bayesian classification algorithms, we consider the following three typical Bayesian classifiers: naive Bayes, TAN, and CG.

(1) KMM-based Naive Bayes In the Naive Bayes scenario, i.e. subfeatures are mutually independent, we have

$$\begin{aligned} \begin{aligned} p(\omega _i | {\mathbf {x}} )&= \sum _{k=1}^{n_i} p\left( \omega _i^k | {\mathbf {x}} \right) \\&\propto \sum _{k=1}^{n_i} P \left( \omega _i^k\right) \prod _{j=1}^{d}p\left( x_j|{\omega _i^k}\right) . \end{aligned} \end{aligned}$$

(18)

The implementation of KMM-based Naive Bayes is easy to be achieved since there is no need to learn the network structure, as illustrated in Algorithm 1. Note that ${\mathbf {X}}_i (1\le i\le c)$ denotes the data sample of class $\omega _i$, and ${\mathbf {X}}_i^k (1\le i\le c,1\le k \le n_i)$ denotes the data sample of HSC $\omega _i^k$. After P-step, the conditional probabilities each subclasses $[p(x_j|{\omega _i^k})]_{i=1,\ldots ,n_i}$ can be estimated by using KDE methed, the posterior probability of $\omega _i$ can be directly calculated by using Eq. (18).

(2) KMM-based TAN In TAN, an attribute $x_j$ may be assigned with a parent attribute $C_j$, except the class node $\omega _i^k$. In this scenario, posterior probability can be calculated by

$$\begin{aligned} \begin{aligned} p(\omega _i | {\mathbf {x}} )&\propto \sum _{k=1}^{n_i} P \left( \omega _i^k\right) \prod _{j=1}^{d_1} p\left( x_j|C_j,{\omega _i^k}\right) \prod _{t=d_1+1}^d p\left( x_j|{\omega _i^k}\right) \\&\propto \sum _{k=1}^{n_i} P \left( \omega _i^k\right) \prod _{j=1}^{d_1} \frac{p\left( x_j,C_j|{\omega _i^k}\right) }{p\left( C_j|\omega _i^k\right) }\prod _{t=d_1+1}^d p\left( x_j|{\omega _i^k}\right) . \end{aligned} \end{aligned}$$

(19)

where $d_1$ is number of attributes with parent nodes. As illustrated in Algorithm 2, the implementation of KMM-based TAN is much more complex than KMM-based Naive Bayes. After P-step, we obtain the training samples of each HSC, and then the dependency matrix between the attributes is calculated by suing mutual information or Heckermans scoring variation metric. Subsequently, a maximum weighted spanning tree is constructed by using Chow and Liu’s procedure, and the network structure is obtained. With the obtained network structure, KDE is applied to estimate conditional probabilities of each HSC. Note that conditional probabilities of a node with a parent node can be calculated by (12). Finally posterior probability of each class can be aggregated by using Eq. (19).

(3) KMM-based CG In this scenario, PDFs are estimated using multivariate KMM method, thus the posterior probability can be calculated by

$$\begin{aligned} p(\omega _i | {\mathbf {x}} ) \propto \sum _{k=1}^{n_i} P \left( \omega _i^k\right) p\left( {\mathbf {x}}|{\omega _i^k}\right) . \end{aligned}$$

(20)

Similar to KMM-based NB, structure learning is avoided in KMM-based CG. After P-step, multivariate KDE estimation can be used to obtain conditional probabilities of each HSC, and posterior probability of each class can be computed by using Eq. (20). Implementation of KMM-CG is shown in Algorithm 3.

5 Experimental results

In this Section, experiments will be conducted to prove the effectiveness of the proposed KMM method. The experiments mainly include two parts: one is the test to show KMM is able to improve the quality of PDF estimation compared with KDE. In this test, two images will be used to estimating the PDFs of their grey-levels. Another one is the test to show the classification performance of the proposed KMM method in three typical Bayesian classifiers by using 20 benchmark datasets. Comparison results with other PDF estimation methods will also be provided. All the experiments are conducted in a laptop with Intel i7 2.4GHz CPU, 8G RAM, MATLAB 2017a, Win 10 system.

Fig. 6

The used gray-scale image data, in which a is the Lenna image and b is its histogram, c is the Cameraman image and d is its histogram

Fig. 7

Comparison of the estimated PDFs with Gaussian kernel functions, target image of a, b are Lenna and Cameraman, respectively. It can be seen that KMM achieves much better results compared with KDE. However, KMM may produce overfitted results, as we can see when $n_{h}=10$, results of some regional peaks are biased

Fig. 8

Comparison of ISEs with increasing HSC numbers, images used in a, b are Lenna and Cameraman, respectively

5.1 Experiment on PDF estimation

In this subsection, we show experimental results to demonstrate that the proposed KMM method is able to improve the quality of PDF estimation results of KDE method. The integrated squared error (ISE) is used for evaluating the estimation performance. Give data ${\mathbf {x}}$, the ISE is defined as

$$\begin{aligned} \text {ISE} = \int _{{\mathbf {x}}} \left( \tilde{p}({\mathbf {x}})-p({\mathbf {x}})\right) ^2 d{\mathbf {x}} \end{aligned}$$

(21)

where $\tilde{p}({\mathbf {x}})$ and $p({\mathbf {x}})$ are the estimated PDF and real PDF, respectively. To compare the ISEs of KMM and KDE, the task is set to estimate PDF of grey-scales of the Lenna image and Camearaman image. The size of the two images are all $512\times 512$, and the gray scale pixels have 256 grey levels (from 0–255), the images and their corresponding histograms are plotted in Fig. 6. Specifically, the ISE in this task can be calculated as

$$\begin{aligned} \text {ISE}=\sum _{i=0}^{255} \left( \sum _{k=1}^{n_h}p (\omega ^k)\tilde{p}(x_i|\omega ^k)-p(x_i)\right) ^2, \end{aligned}$$

(22)

where $x_i$ is the grey scale. Since different kernel functions produce different estimation results, the following three kernel functions are used: Gaussian, Triangle, and Epanechnikov. The RoT is used to obtain the bandwidth of the kernel functions. The estimated PDFs when HSCs numbers are 1, 5, 10 are shown Fig. 7. The ISEs of the estimation results are shown in Fig. 8. From the above figures, we have the following observations.

(1) When the target PDF is irregular and multimodal, the proposed KMM with a proper HSC number will greatly reduce the ISE of KDE. As we can see Fig. 5, when using the Gaussian kernel, the estimated PDFs of the KMM are more close to the histograms of the image compared with. Results of using triangle and epanechnikov kernel functions are similar to Gaussian kernel. For the Lenna image, when $n_h$ increases from 1 to 5, the average ISE of the three kernels gradually reduced from about $5\times 10^{-5}$ to $2\times 10^{-5}$. Similarly, for the Cameraman image, when KMM is used and $n_h=2$, the average ISE is reduced from about $14\times 10^{-4}$ to $3.5\times 10^{-4}$. Therefore, KMM is able to significantly improve the quality of estimation results of KDE.

(2) A too large HSC number may cause over-estimated results. It can be seen in Fig. 8a, when $n_h>5$, estimation results of triangle and epanechnikov kernels become more and more biased when $n_h$ is larger. Accordingly, we can see that some parts of the estimated PDFs when $n_h=10$ in Fig. 7a, b are slightly deviated from the real histograms, especially in the regions with slender peaks. Results in Fig. 8b are similar to Fig. 8a, as we can see ISE becomes higher when $n_h>2$.

A too large HSC number may cause the following two effects: One is that when $n_h$ becomes too large, the sample number of some clusters may be too small, and the estimated PDF of the corresponding HSC is not reliable due to the lack of sufficient sample number. Another one is that, although the sample number of some clusters is sufficient, they are densely distributed in a very small region, which makes the estimated results become unreliable since the calculation of bandwidth [see Eq. (4)] is more sensitive to the local variations of the HSC data samples.

(3) It seems that Gaussian kernel function outperforms the Triangle and Epanechnikov kernel functions. As shown in both Fig. 8a, b, the achieved minimum ISEs of Gassuain kernel are all lower than other two kernels.

Table 4 The used UCI datasets

5.2 Experiments on UCI datasets

The experiments in this subsection is conducted by using datasets from UCI machine learning repository. Firstly we show the results of how KMM effects the classification performance, then classification results 20 numerical datasets will be provided. Three typical Bayesian classifiers are used to provide different scenarios of PDF estimation, including NB, TAN, and CG, and they have been introduced in Sects. 3 and 5. In structure learning process of TAN, as suggested by Leray and Francois (2004), we use Heckerman’s scoring variation metric to quantify the dependency between two attributes, and unsupervised 10-bin discretization is used in the dependency calculation process. The experiment data used in this subsection are shown in Table 4.

5.2.1 Effect of KMM

For a classification task with c classes, if the maximum number of HSCs of each class is $n_{max}$, there will be $n_{max}^c$ possible assignments, hence finding the optimal solution via exhaustive searching is inefficient. As such, it is necessary to know how the number of HSCs influences the classification performance, which is helpful for us to develop a reasonable empirical strategy to efficiently select the number of HSCs.

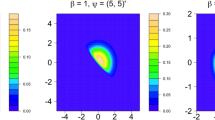
The banana data only has two attributes, which is suitable for visualizing how KMM influences the decision boundary. In this example, the KMM-CG classifier is used. To show the changes of decision boundaries, the HSC numbers of the two classes is set as [1,1], [5,5], [15,15], [25,25], and the corresponding results are depicted in Fig. 9a–d. Note that when HSC numbers are [1,1], it is actually the KDE-CG classifier.

Fig. 9

Decision boundaries of banana data obtained with different number of HSCs, there are two classes and the used classifier is KMM-CG, the HSC numbers of each class in a–d are [1,1], [5,5], [15,15], [25,25], respectively

Fig. 10

Classification accuracies with increasing HSC numbers, the HSC numbers of each class are all set as $n_{hsc}$. Datasets used in a–d are banana data, diabetes data, eyestate data, ionosphere data, respectively

From Fig. 9, we can see that when under-fitting happens in KDE, the KMM can be used to obtain proper-fitting results. When simple KDE is used, the produced decision boundary in (a) is under-fitted, while in (b) and (c), it can be observed that the decision boundaries become more complex and reasonable when HSC number is larger, the boundaries are obviously more discriminative. Accordingly, the training error becomes much lower. However, as shown in subfigure (d), when HSC number is too large, over-fitting will happen inevitably due to lack of sufficient sample number of some HSCs, or unreliable regional estimation results.

To further illustrate the effect of KMM, we show the classification accuracies with different HSC numbers on four benchmark datasets, as shown in Fig. 10, and we have the following observations.

(1) No matter which Bayesian classifier is used, it can be seen that KMM can improve the classification accuracy compared with KDE. For example, the classification accuracy of Banana data of KMM-NB is 15.9% higher than KDE-NB. However, it doesn’t mean that the performance of KMM will be surely better than KDE, on the contrary, results may be worse when KMM is used, as we can see the results of diabetes data, and dramatic accuracy decreasing happens from 75.8 to 70.2% when KMM-CG is used.

(2) The HSC number of each class should be properly selected, since a too large HSC number may cause over-fitting, especially for datasets with relative small sample number. We can see that the optimal HSC number for Diabetes data and Ionosphere data is 2 or 3, which is very small. For datasets with adequate sample numbers, a relative larger HSC number may produce better results. In this situation, an empirical rule for determining the number HSC is that: the optimal number of the hidden subclass is the one when the accuracy just reaches its maximum value. Although the performance remains almost the same in a wide range of relative larger hidden subclass numbers, it is suggested using the optimal number for efficiency consideration, since the computation complexity of KMM method is proportional to hidden subclass number.

Fig. 11

Comparison of time consumption with increasing HSC numbers, datasets used in a, b are waveform data and navigation data, respectively

To show the effect of HSC number on time efficiency, we use the waveform data and navigation data to test the time span of the whole classification process, and the results are shown in Fig. 11. Apparently, we can see that $n_h$ has critical influences on the KMM-TAN classifier. The reason is that, for a d-dimensional data with c class labels, the number correlation indices is $cd(d-1)/2$, thus the complexity is determined by the data dimension d. When KMM is used, the number of correlation indices becomes $n_h d(d-1)/2$, thus the time requirement will be higher than KDE.

It also can be observed that the KMM-NB and KMM-CG classifiers are not so sensitive to $n_h$. This is because the k-means algorithm is very efficient and converges fast even when the sample number is large.

5.2.2 Classification results

In this subsection, the following four PDF estimation methods will be examined: parametric density estimation using Gassian distribution (Gaussian), semi-parametric density estimation using Gassian mixture model (GMM), convolutional kernel density estimation (KDE), and the proposed kernel mixture model (KMM). In all tests, the commonly used Gaussian kernel is used as the kernel function for PDF estimation, and the bandwidth is determined by using Silverman’s RoT, as given in Eq. (4). All the results are obtained by 20 repetitions, except for the ISOLET data and MUSK2 data, and only 5 repetitions are conducted, since it is inefficient using TAN classifier on high dimensional data. In each test, 2/3 of the samples are randomly selected as the training data, and the remaining 1/3 samples are used as test data. The used training data and test data for each method are the same, thus the comparison results of different methods in each repetition are obtained on using the same data.

For the eyestate data, we find that it has 4 outliers, and they have been removed to improve the performance. For the skin data, each test is conducted by randomly selecting 15,000 data samples from the original data to improve the efficiency. For some data without enough training data (eg. the seeds data) for each HSC, the estimated covariance matrix is compensated with a small scale diagonal matrix ($1\times 10^{-3} {\mathbf {I}}$) to make it be a regular symmetrical positive determined matrix.

Table 5 Classification accuracy and standard deviation of NB classifier (%)

The used clustering algorithm is k-means, and the number of HSCs are selected from $\left\{ 2,3,\ldots ,15 \right\}$. As aforementioned, selecting proper number of HSCs is important for GMM and KMM based PDF estimation. We adopt a greedy search based strategy to find the optimal number of HSCs. More specifically, for a data with labels $\varOmega = \left\{ \omega _1,\ldots ,\omega _c \right\}$, at the beginning we fixed the number HSCs of all classes as 1. Then we find optimal HSC number for class $\omega _1$ with best performance. Next is $\omega _2$, and so on. Once the number of HSC of a class is obtained, it will be fixed until we find out all other classes’ HSCs numbers. Note that if the proposed KMM method has no improvement, one can just use the traditional KDE method for PDF estimation, and performance decreasing will be avoided. However, to distinguish the difference, at least one class label will be partitioned to two HSCs in each test if KMM is adopted.

Except classification accuracy, we also adopt the area under the ROC curve (AUC) (Hand and Till 2001) metric to evaluate the ranking performance of a Bayesian classifier. For a binary classification problem, the AUC equals to the probability that a randomly chosen positive example has higher ranking score than a randomly chosen negative example. A larger AUC value indicates that the classifier has stronger discriminating ability. Compared with classification accuracy metric, AUC metric is more reasonable for ranking classification performance on imbalanced data. The calculation process of AUC can be found in Hand and Till (2001).

Experimental results of classification accuracy with its standard deviation are shown in Tables 5, 6, and 7, and the corresponding used Beyesian classifiers are NB, TAN, and CG. In addition, AUC with its standard deviation of the above three tested classifiers are provided in Tables 8, 9, and 10, respectively. The best ranked method of each data set is highlighted with bold fonts. The average classification accuracy and AUC will also be provided. In addition, we count the total number of wins on the 20 datasets, as shown in the last row of each table.

Table 6 Classification accuracy and standard deviation of TAN classifier (%)

Table 7 Classification accuracy and standard deviation of CG classifer (%)

Table 8 AUC and standard deviation of NB classifier (%)

Table 9 AUC and standard deviation of TAN classifier (%)

Table 10 AUC and standard deviation of CG classifer (%)

Based on above results, we have following observations.

(1) The proposed KMM method is able to significantly improve the performance of KDE for different kinds of Bayesian classifiers. As shown in the above six tables, when using the KMM for PDF estimation, average classification accuracy of NB, TAN and CG have increased with 4.15, 2.26, and 3.45%, respectively, compared with KDE. Also, average AUC and the number of wins of KMM are all larger than the ones of KDE for all the three Bayesian classifiers. A similar observation is that GMM has much better performance compared with pure Gaussian method. These results prove that finite mixture model can be used to improve KDE-based PDF estimation in Bayesian classifiers, but not only the parametric Gaussian estimation method.

(2) The average performance of the proposed KMM is better than GMM method. This result is not surprised to us, since non-parametric PDF estimation methods are more flexible and adaptable to irregular data distributions. However, computation complexity of GMM is much lower, and GMM shows better classification accuracy for 6 wins when the classifier is CG. Therefor, it is still a competitive method to KMM.

(3) On average, GMM outperforms KDE, and KDE outperforms Gaussian. Although parametric Gaussian estimation is uncompetitive compared with KDE, but it can be strengthened as GMM, and performance can be greatly enhanced. Since GMM has lower computation complexity compared with KDE, therefore, it is a better choice for using GMM, but not KDE to improve the performance of Bayesian classifiers. However, as we have seen the proposed KMM has the best performance, and kernel-based density estimation is still a better choice than parametric estimation.

(4) As expected, average performance of KDE-TAN (average accuracy: 86.49%, average AUC: 94.76%) is better than KDE-NB (average accuracy: 84.74%, average AUC: 93.03%) . However, when KMM or GMM is adopted for PDF estimation. The average performance of KMM-TAN (average accuracy: 88.91%, average AUC: 95.85%) and KMM-NB (average accuracy: 88.89%, average AUC: 96.42%) are close with each other, and this phenomenon also exists between GMM-TAN (average accuracy:87.67%, average AUC: 90.00%) and GMM-NB (average accuracy: 87.82%, average AUC: 94.92%). This is because the partition (clustering) process in KMM and GMM divides the data sample of each class to different regional hidden subclasses, and the dependency between the original classes is relaxed. Therefore, Compared with KDE, considering the dependency will be more probable to be useless for improving performance of NB classifer if FMM is adopted for PDF estimation.

(5) KMM-based CG classifier achieves the best performance among the three Bayesian classifiers. Also, CG classifier significantly outperforms NB classifier and TAN, thus the CG classifier is the first choice for classification tasks. Besides, it is also more efficient compared with NB and TAN. Particularly, it is not to suggest using TAN for classification tasks with high-dimension data, since it is very inefficient, and the KMM-NB may achieve similar performance to KMM-TAN.

6 Conclusions

In this paper we have proposed a kernel mixture model for improving the reliability of probability density estimations in Bayesian classifiers. We introduced the basic concepts of hidden subclasses, and developed a KMM algorithm by using Bayesian inference. We proposed to use the k-means algorithm to improve the mixture model based conditional probability estimation. We also proposed a KMM based Bayesian classifiers, which is comprised of the following three steps: partitioning, structure learning and estimation. Application of the proposed to following three typical Bayesian classifiers are considered: including NB, TAN, and CG. Experimental results demonstrate the proposed KMM method significantly outperforms KDE method and parametric Gaussian method, and outperforms GMM method. Particulary, KMM-based CG classifier achieved the highest performance.

In this paper, we use k-means for the partitioning process, but not the EM algorithm, although it is developed by using a probability induction based process. The reason is that k-means is more efficient, and applicable for data with small data samples. Actually, we have also tested the performance of EM algorithm-based partitioning, and results show that its performance is lower than k-means. Therefore, it is suggested using k-means algorithm for the partitioning process. For dealing with classification problems with very high-dimensional data, it is suggested that a feature selection process is necessary to eliminate redundant features to improve computation efficiency and the reliability of estimated joint probabilities.

Future directions may include: (1) Find more suitable clustering algorithms for the KMM approach, or definitely find other alternatives for the hidden subclasses partitioning operation; (2) Design models to improve estimation quality or efficiency of KMM; (3) Apply the proposed KMM method in other probabilistic induction applications.