KNN-based least squares twin support vector machine for pattern classification

Abstract

The least squares twin support vector machine (LSTSVM) generates two non-parallel hyperplanes by directly solving a pair of linear equations as opposed to solving two quadratic programming problems (QPPs) in the conventional twin support vector machine (TSVM), which makes learning speed of LSTSVM faster than that of the TSVM. However, LSTSVM fails to discover underlying similarity information within samples which may be important for classification performance. To address the above problem, we apply the similarity information of samples into LSTSVM to build a novel non-parallel plane classifier, called K-nearest neighbor based least squares twin support vector machine (KNN-LSTSVM). The proposed method not only retains the superior advantage of LSTSVM which is simple and fast algorithm but also incorporates the inter-class and intra-class graphs into the model to improve classification accuracy and generalization ability. The experimental results on several synthetic as well as benchmark datasets demonstrate the efficiency of our proposed method. Finally, we further went on to investigate the effectiveness of our classifier for human action recognition application.

1 Introduction

Support vector machine [6] is a powerful method for pattern classification and regression. It has been successfully applied in a wide variety of real-world problems such as face recognition [28], voice classification [33], text categorization [20], bioinformatics [25] and civil engineering [27]. SVM is on the basis of Vapnik-Chervonekis (VC) dimension and structural risk minimization. Its basic idea is to find the optimal separating hyperplane between positive and negative samples which involves solving of a convex quadratic programming problem (QPP).

Researchers have made many improvements on the basis of SVM. For instance, Fung and Mangasrian [22] proposed proximal support vector machine (PSVM) for binary classification. This method generates two parallel hyperplanes for each class of data points. That is, each plane must be as close as possible to its class and as far as possible from other class. Following PSVM, Mangasrian and Wild [23] proposed generalized eigenvalue proximal SVM (GEPSVM) which does binary classification by obtaining two non-parallel hyperplanes. In this method, samples of each class are proximal to one of two non-parallel planes. Two non-parallel planes are obtained by solving the eigenvector corresponding to the smallest eigenvalue of a generalized eigenvalue problem.

Jayadeva et al. [12] proposed twin support vector machine (TSVM) for binary classification, inspired by GEPSVM. TSVM seeks two non-parallel hyperplanes such that each hyperplane is as close as possible to samples of its own class and as far as possible from samples of other class. The main idea is to solve two smaller QPPs rather than a single large QPP which makes training speed of TSVM four times faster than that of a standard SVM. The experimental results in [12] show the superiority of TSVM over SVM and GEPSVM on UCI datasets.

In the last decade, TSVM has been enhanced rapidly [8, 9, 13, 38]. Some improvements have been made to TSVM by researchers to obtain higher classification accuracy with lower computational time such as Least Squares Twin Support Vector Machine (LSTSVM), Twin Bounded Support Vector Machine (TBSVM), Weighted TwinSVM with local information (WLTSVM), Energy-based Least Squares TwinSVM (ELS-TSVM), Robust Energy-based Twin Support Vector Machines (RELS-TSVM), Angle-based Twin Support Vector Machine (ATSVM) and An Improved v-Twin Bounded Support Vector Machine (Iv-TBSVM) [15,16,17, 26, 31, 35, 37, 41, 42].

The major disadvantage of TSVM is that it fails to exploit the similarity information between any pair of samples that may be important for classification. Yi et al. [42] proposed WLTSVM which considers the similarity information between pairs of samples by finding the k-nearest neighbors for all the samples. This approach has three additional advantages over TSVM: (1) close or better classification accuracy compared to TSVM. (2) Different from TSVM, it considers marginal points of each class instead of all the data points. (3) It has only one penalty parameter.

Similar to TSVM, LSTSVM [17] fails to exploit the similarity information between any pair of samples. However, LSTSVM is simple, extremely fast and solves two systems of linear equations as opposed to solving two QPPs in TSVM. In this paper, we present an improvement on LSTSVM and embed the similarity information between pairs of samples into the optimization problems of LSTSVM based on k-nearest neighbor graph. The proposed method possesses the following advantages:

• 1. Similar to WLTSVM, the proposed method (KNN-LSTSVM) makes full use of similarity information between pairs of samples. That is, it uses k-nearest neighbor graph to characterize the intra-class compactness and inter-class separability, respectively. Based on this, KNN-LSTSVM achieves higher classification accuracy and better generalization ability.

• 2. Unlike WLTSVM, KNN-LSTSVM solves two systems of linear equations which leads to simple algorithm and less computational time. As a result, the proposed method does not need any external optimizer.

• 3. The LS-TSVM is more sensitive to the outliers. However, KNN-LSTSVM gives much less weight to the outliers. As a result, the final hyperplane is less sensitive to the outliers and noisy samples and is potentially robust.

Numerical experiments on several synthetic and benchmark datasets show that our KNN-LSTSVM obtains better classification ability in comparison with TSVM, WLTSVM and LSTSVM. We also explored the application of linear KNN-LSTSVM to human action recognition problem. It is the task of assigning a given video to one of action categories. Moreover, human action recognition has several challenges such as intra-class and inter-class variations, environment settings and temporal variations [30].

This paper is organized as follows. Section 2 briefly introduces SVM and TSVM. Section 3 gives the details of KNN-LSTSVM, including linear and non-linear cases. Section 4 discusses the experimental results on various datasets to investigate the effectiveness and validity of our proposed method. Finally, concluding remarks are given in Section 5.

2 Background

In this section, we briefly explain the basics of SVM and TSVM.

2.1 Support vector machine

Consider the binary classification problem with the training set T = {(x₁, y₁),...,(x_n, y_n)}, where are $x_{i} \in \mathbb {R}^{n}$ feature vectors in the n-dimensional real space and y_i ∈{− 1,1} are the corresponding labels. The idea is to find a separating hyperplane w^Tx + b = 0 where $w \in \mathbb {R}^{n}$ and $b \in \mathbb {R}$. Figure 1 shows geometric interpretation of standard SVM for a toy dataset.

Fig. 1

Geometric interpretation of standard SVM

Assume that all the samples are strictly linearly separable. Then, the optimal separating hyperplane is obtained by solving the following optimization problem.

$$ \begin{array}{lllllllllll} \min_{w}\frac{1}{2}{{\left\| w \right\|}^{2}} \\ \text{s.t. } {{y}_{i}}({{w}^{T}}{{x}_{i}}+b)\ge 1,\forall i \end{array} $$

(1)

The problem defined by (1) is called ’hard margin’ and the inequality constraint should be satisfied for all the samples. In real world scenarios, two classes are not often linearly separable. Therefore, an error occurs in satisfying the inequality for some samples. The slack variable added to the problem (2) to classify samples with some error. The problem (2) is modified as

$$ \begin{array}{lllllllllll} \min_{w}\frac{1}{2}{{\left\| w \right\|}^{2}}+C\sum\limits_{i = 1}^{n}{{{\xi }_{i}}} \\ \text{s.t. } {{y}_{i}}({{w}^{T}}{{x}_{i}}+b)\text{ }+{{\xi }_{i}}\ge 1,\forall i \end{array} $$

(2)

Where ξ_i is a slack variable associated with x_i sample and C is a penalty parameter. In this case, the classifier is known as soft margin. The Wolfe dual of (2) is given by

$$ \begin{array}{lllllllllll} \min_{\alpha} \frac{1}{2}\sum\limits_{i = 1}^{n}{\sum\limits_{j = 1}^{n}{{{\alpha }_{i}}{{\alpha }_{j}}{{y}_{i}}{{y}_{j}}{x_{i}^{T}}{{x}_{j}}-\sum\limits_{i = 1}^{n}{{{\alpha }_{i}}}}} \\ \text{s.t. } \sum\limits_{i = 1}^{n}{{{\alpha }_{i}}{{y}_{i}}= 0,\text{ }0\le {{\alpha }_{i}}\le C,\text{ }\forall i} \end{array} $$

(3)

Where $\alpha \in \mathbb {R}$ are Lagrange multipliers. The parameters of optimal separating hyperplane are given by

$$ \begin{array}{lllllllllll} w=\sum\limits_{i = 1}^{n}{\alpha_{i}^{*}{{y}_{i}}{{x}_{i}}} \end{array} $$

(4)

Where α^∗ is the solution of the dual problem (3). A new sample is classified as + 1 and -1 according to the decision function D(x) = sign(w^Tx + b). SVM can be extended in a simple manner to handle nonlinear kernels [36].

2.2 Twin support vector machine

Consider a binary classification problem of m₁ positive samples and m₂ negative samples (m₁ + m₂ = m). Suppose that samples in class + 1 are denoted by a matrix $A\in {{\mathbb {R}}^{{{m}_{1}}\times n}}$, where each row represents a sample. Similarly, the matrix $B\in {{\mathbb {R}}^{{{m}_{2}}\times n}}$ represents the samples of class -1. Unlike SVM, TSVM does classification using two non-parallel hyperplanes:

$$ {{x}^{T}}{{w}^{(1)}}+{{b}^{(1)}}= 0, {{x}^{T}}{{w}^{(2)}}+{{b}^{(2)}}= 0 $$

(5)

where ${{w}^{(1)}},{{w}^{(2)}}\in {{\mathbb {R}}^{n}}$ and ${{b}^{(1)}},{{b}^{(2)}}\in {\mathbb {R}}$. Each hyperplane is close to samples of one class and far from the samples of other class. Figure 2 shows geometric interpretation of standard TSVM for crossplane dataset.

Fig. 2

Geometric interpretation of standard TSVM

TSVM solves the following two QPPs for obtaining two non-parallel hyperplanes:

$$ \begin{array}{lllllllllll} \underset{w_{(1)} ,b_{(1)}}{\min} \qquad & \frac{1}{2}{{\left\| A{{w}^{(1)}}+{{e}_{1}}{{b}^{(1)}} \right\|}^{2}}+{{C}_{1}}{e_{2}^{T}}y \\ \text{s.t. } \qquad & -(B{{w}^{(1)}}+{{e}_{2}}{{b}^{(1)}})+y\ge {{e}_{2}}\text{ },y\ge 0 \end{array} $$

(6)

$$ \begin{array}{lllllllllll} \underset{w_{(2)} ,b_{(2)}}{\min} \qquad & \frac{1}{2}{{\left\| B{{w}^{(2)}}+{{e}_{2}}{{b}^{(2)}} \right\|}^{2}}+{{C}_{2}}{e_{1}^{T}}y \\ \text{s.t. } \qquad & (A{{w}^{(2)}}+{{e}_{1}}{{b}^{(2)}})+y\ge {{e}_{1}}\text{ },y\ge 0 \end{array} $$

(7)

where C₁, C₂ ≥ 0 are penalty parameters, e₁, e₂ are vectors of ones of appropriate dimensions. It can be noted that samples of one class appear in the constraints of each QPP. As a result, TSVM is almost four times faster than a standard SVM. By introducing Lagrange multipliers, the Wolf dual of QPPs (6) and (7) are represented as follows:

$$ \begin{array}{lllllllllll} \underset{\alpha}{\min} \qquad & \frac{1}{2}{{\alpha }^{T}}G{{({{H}^{T}}H)}^{-1}}{{G}^{T}}\alpha -{e_{2}^{T}}\alpha \\ \text{s.t. } \qquad & 0{{e}_{2}}\le \alpha \le {{C}_{1}}{{e}_{2}} \end{array} $$

(8)

$$ \begin{array}{lllllllllll} \underset{\beta}{\min} \qquad & \frac{1}{2}{{\beta }^{T}}P{{({{Q}^{T}}Q)}^{-1}}{{P}^{T}}\beta -{e_{1}^{T}}\beta \\ \text{s.t. } \qquad & 0{{e}_{1}}\le \beta \le {{C}_{2}}{{e}_{1}} \end{array} $$

(9)

where H = [A e], G = [B e], P = [A e] and Q = [B e], $\alpha \in {{\mathbb {R}}^{{{m}_{2}}}}$ and $\beta \in {{\mathbb {R}}^{{{m}_{1}}}}$ are Lagrangian multipliers. The two dual QPPs (8) and (9) have the advantage of bounded constraints and reduced number of parameters, implying that QPP (8) has only m₂ parameters and QPP (9) has only m₁ parameters.

The two non-parallel hyperplanes (5) can be obtained from the solution of QPP (8) and (9) by

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{lllllll} & {{w}^{(1)}} \\ & {{b}^{(1)}} \end{array}\right] &=& -{{({{H}^{T}}H)}^{-1}}{{G}^{T}}\alpha \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{lllllll} & {{w}^{(2)}} \\ & {{b}^{(2)}} \end{array}\right] &=& {{({{Q}^{T}}Q)}^{-1}}{{P}^{T}}\beta \end{array} $$

(11)

The matrices H^TH and Q^TQ are of size (n + 1) × (n + 1) where n ≪ m. Once the two hyperplanes (5) are obtained, a new sample is assigned to class i(i = + 1,− 1) depending on which of the two hyperplanes in (5) it is closer to

$$ Class\text{ }i\text{ }=\underset{j = 1,2}{arg\min}\,\,\text{ }\left| {{x}^{T}}{{w}^{(j)}}+{{b}^{(j)}} \right| $$

(12)

where |.| is perpendicular distance. The case of non-linear kernels is handled similar to linear kernels [12]. According to [42] TSVM has the following two limitations:

• It fails to exploit the similarity information between pairs of samples. Previous studies have shown that most of the samples are highly correlated [42]. Therefore, underlying similarity is crucial for data classification [4].

• In TSVM, hyperplane of each class should be far from all the samples of other class. Consequently, TSVM may misclassify margin points. By utilizing a few margin points from other class instead of all the samples, TSVM may achieve better result [42].

WLTSVM addressed these limitations by making full use of similarity information in terms of the data affinity [42].

3 KNN-based least squares twin support vector machine

In this section, we present our proposed method(KNN-LSTSVM) and explain its details. Section 3.1 discusses construction of weight matrices. Details of linear KNN-LSTSVM are given in Section 3.2. Proposed method extended to nonlinear kernels in Section 3.3.

3.1 Construction of weight matrices

The central idea of WLTSVM and proposed method is to give larger weights to the samples with high density and extract possible margin points from the samples of other class. In other words, the hyperplane yielded by KNN-LSTSVM fits the samples with high density and are far from the margin points of other class. Figure 3 shows the geometrical interpretation of LSTSVM and KNN-LSTSVM for both linear and Gaussian kernel. As shown in Fig. 3, the hyperplane of KNN-LSTSVM is less sensitive to outliers and noisy samples. On the other hand, the hyperplane of LSTSVM is close to the outliers of circle class, because the hyperplane is as close as possible to all the samples of its own class. In order to demonstrate the main idea of KNN-LSTSVM clearly, the perpendicular distance of one margin point is calculated for both classifiers in Fig. 3.

Fig. 3

The comparison of LSTSVM with KNN-LSTSVM

Similar to WLTSVM, a k-nearest neighbor graph is constructed as follows:

$$ W_{ij} = \left\{\begin{array}{lllllllllll} 1, & \text{if}\, x_{i} \in N\left( x_{j}\right)\ \text{or}\, x_{j} \in N\left( x_{i}\right) \\ 0, & \text{otherwise}. \end{array}\right. $$

(13)

where the set N(x_j) contains k-nearest neighbors of x_j and is given by: [4]

$$ N(x_{j}) = \{{x^{1}_{j}}, {x^{2}_{j}}, {\dots} , {x^{k}_{j}}\} $$

(14)

However, the graph W cannot reveal the discriminative structure in data [42]. Instead, a within-class graph W_w and between-class graph W_b are constructed to model the intra-class compactness and inter-class separability, respectively. The weight matrices W_w and W_b of class + 1 are respectively defined as:

$$ W_{w,ij} = \left\{\begin{array}{lllllllllll} 1, & \text{if}\, x_{i} \in N_{w}(x_{j})\ \text{or}\, x_{j} \in N_{w}(x_{i}) \\ 0, & \text{otherwise}. \end{array}\right. $$

(15)

$$ W_{b,ij} = \left\{\begin{array}{lllllllllll} 1, & \text{if}\, x_{i} \in N_{b}(x_{j})\, \text{or}\, x_{j} \in N_{b}(x_{i}) \\ 0, & \text{otherwise}. \end{array}\right. $$

(16)

where N_w(x_j) stands for k-nearest neighbors of x_j from same class and N_b(x_j) contains k-nearest neighbors of x_j from different class. The two sets N_w(x_j) and N_b(x_j) are respectively given by:

$$ N_{w}\left( x_{i}\right) = \{{x^{j}_{i}} \mid l({x^{j}_{i}}) = l(x_{i}), 1 \leq j \leq k \} $$

(17)

$$ N_{b}\left( x_{i}\right) = \{{x^{j}_{i}} \mid l({x^{j}_{i}}) \neq l(x_{i}), 1 \leq j \leq k \} $$

(18)

where l(x_i) denotes the class label of x_i. Clearly, $N_{w}(x_{i})\, \allowbreak \cap \, N_{b}(x_{i}) = \varnothing$ and N_w(x_i) ∪ N_b(x_i) = N(x_i). The distance between pairs of samples is measured by using the standard Euclidean metric. In order to find the margin points of class -1, the weight matrix W_{b, ij} is redefined as follows:

$$ f_{j} = \left\{\begin{array}{lllllllllll} 1, & \text{if}\, \exists i, W_{b,ij} \neq 0 \\ 0, & \text{otherwise}. \end{array}\right. $$

(19)

The weight of each sample in class + 1 is computed by

$$ {{d}_{j}}=~\underset{i = 1}{\overset{{{m}_{1}}}{\sum }}\,{{W}_{w,~ij}}~,~j = 1,2,{\ldots} ,~{{m}_{1}} $$

(20)

where d_j denotes the weight of x_j. The value of d_j shows how much dense x_j is. In other words, the number of neighbors with same label determines the weight of a sample.

3.2 Linear KNN-LSTSVM

Similar to WLTSVM, proposed method seeks a pair of non-parallel hyperplanes, each of which fits samples with high density and is far from the margin points of other class. However, KNN-LSTSVM modifies the primal problems of WLTSVM by replacing the inequality constraints with equality constraints and using the square of 2-norm slack variables. The solution of two modified primal problems requires solving two systems of linear equations as opposed to solving two QPPs in WLTSVM. Also note that modification of primal problems leads to extremely fast and simple method for obtaining two non-parallel hyperplanes. The modified primal problem of class 1 can be expressed as follows:

$$ \begin{array}{lllllllllll} \underset{w_{(1)} ,b_{(1)}}{\min} \qquad & \frac{1}{2}{{(A{{w}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}})}^{T}}D(A{{w}^{\left( 1 \right)}} +e{{b}^{\left( 1 \right)}}) \\ & +\frac{C}{2}{{y}^{T}}y \\ \text{s.t. } \qquad & -F(B{{w}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}})+y=Fe \end{array} $$

(21)

where $D=diag(d_{1},d_{2},\dots ,d_{m_{1}})$ and $F=diag(f_{1},f_{2},\dots ,\allowbreak f_{m_{2}})$ are the weight matrix of class + 1 and the margin points of class -1, respectively. Cleary, f_j is either 0 or 1 and d_i is greater than or equal to zero (d_i ≥ 0).

The modified primal problem (21) allows to substitute the equality constraints into the objective function, thus Lagrangian of (21) becomes:

$$ \begin{array}{lllllllllll} \underset{w_{(1)} ,b_{(1)}}{\min} L = \quad & \frac{1}{2}{{\left\| D(A{{w}^{(1)}}+{{e}}{{b}^{(1)}}) \right\|}^{2}} \\ & +{\frac{C}{2}}{{\left\|F(B{{w}^{(1)}}+{{e}}{{b}^{(1)}})+F{e} \right\|}^{2}} \end{array} $$

(22)

By taking partial derivative of (22) with respect to w⁽¹⁾ and b⁽¹⁾, gives:

$$ \begin{array}{lllllllllll} \frac{\partial L}{\partial w^{(1)}} = \ & {{A}^{T}}D(A{{w}^{\left( 1\right)}}+e{{b}^{\left( 1 \right)}} ) \\ & + C{{B}^{T}}F(B{{w}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}}+Fe)= 0e \end{array} $$

(23)

$$ \begin{array}{lllllllllll} \frac{\partial L}{\partial b^{(1)}} = \ & {{e}^{T}}D(A{{w}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}}) \\ & + C{{e}^{T}}F(B{{w}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}}+e)= 0 \end{array} $$

(24)

Next, combining (23) and (24) and solving for w⁽¹⁾ and b⁽¹⁾, leads to a system of linear equations which is expressed as follows:

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{ccccccccc} {{B}^{T}}FB\, & {{B}^{T}}Fe \\ {{e}^{T}}FB\, & {{e}^{T}}Fe \end{array} \right]\left[ \begin{array}{ccccccccc} {{w}^{\left( 1 \right)}} \\ {{b}^{\left( 1 \right)}} \end{array} \right]+~\frac{1}{C}\left[ \begin{array}{ccccccccc} {{A}^{T}}DA\, & {{A}^{T}}De \\ {{e}^{T}}DA\, & {{e}^{T}}De \end{array} \right]\left[ \begin{array}{ccccccccc} {{w}^{\left( 1 \right)}} \\ {{b}^{\left( 1 \right)}} \end{array} \right] \\ +~\left[ \begin{array}{ccccccccc} {{B}^{T}}Fe \\ {{e}^{T}}Fe \end{array} \right]= 0e. \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{ccccccccc} {{w}^{\left( 1 \right)}} \\ {{b}^{\left( 1 \right)}} \end{array} \right]=~{{\left[ \begin{array}{ccccccccc} {{B}^{T}}FB+~\frac{1}{C}{{A}^{T}}DA\, & {{B}^{T}}Fe+\frac{1}{C}{{A}^{T}}De\, \\ {{e}^{T}}FB+~\frac{1}{C}{{e}^{T}}DA\, & {{e}^{T}}Fe+\frac{1}{C}{{e}^{T}}De\, \end{array} \right]}^{-1}} \\ \times \left[ \begin{array}{ccccccccc} -{{B}^{T}}Fe \\ -{{e}^{T}}Fe \end{array} \right] \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{ccccccccc} {{w}^{\left( 1 \right)}} \\ {{b}^{\left( 1 \right)}} \end{array} \right]=~{{\left[ \begin{array}{ccccccccc} \left[ \begin{array}{ccccccccc} {{B}^{T}} \\ {{e}^{T}} \end{array} \right]F & \left[ \begin{array}{ccccccccc} B & e \end{array} \right]+~\frac{1}{C}\left[ \begin{array}{ccccccccc} {{A}^{T}} \\ {{e}^{T}} \end{array} \right]D\left[ \begin{array}{ccccccccc} A & e \end{array} \right] \end{array} \right]}^{-1}} \\ \times \left[ \begin{array}{ccccccccc} \left[ \begin{array}{ccccccccc} -{{B}^{T}} \\ -{{e}^{T}} \end{array} \right] & Fe \end{array} \right] \end{array} $$

(27)

By defining H = [A e] and G = [B e], the solution of minimization problem (21) becomes:

$$ \left[ \begin{array}{ccccccccc} {{w}^{\left( 1 \right)}} \\ {{b}^{\left( 1 \right)}} \end{array} \right] = -~{{({{G}^{T}}FG+\frac{1}{C}{{H}^{T}}DH)}^{-1}}{{G}^{T}}Fe $$

(28)

The modified primal problem of class -1 can be represented as follows:

$$ \begin{array}{lllllllllll} \underset{w_{(2)} ,b_{(2)}}{\min} \qquad & \frac{1}{2}{{(B{{w}^{\left( 2 \right)}}+e{{b}^{\left( 2 \right)}})}^{T}}Q(B{{w}^{\left( 2 \right)}}+e{{b}^{\left( 2 \right)}})+\frac{C}{2}{{y}^{T}}y \\ \text{s.t. } \qquad & P(A{{w}^{\left( 2 \right)}}+e{{b}^{\left( 2\right)}})+y=Pe \end{array} $$

(29)

where $Q=diag(q_{1},q_{2},\dots ,q_{m_{2}})$ and $P=diag(p_{1},p_{2},{\dots } \allowbreak ,p_{m_{1}})$ are the weight matrix of class -1 and the margin points of class + 1, respectively. Similar to F matrix, the p_j is either 0 or 1. In similar way, the solution of primal problem (29) can be obtained as follows:

$$ \left[ \begin{array}{ccccccccc} {{w}^{\left( 2 \right)}} \\ {{b}^{\left( 2 \right)}} \end{array} \right] = {{({{H}^{T}}PH+\frac{1}{C}{{G}^{T}}QG)}^{-1}}{{H}^{T}}Pe $$

(30)

The solutions of (28) and (30) involves two matrix inverses of size (n + 1) × (n + 1) where n is much smaller than the number samples of classes 1 and -1. Consequently, the learning speed of linear KNN-LSTSVM is extremely fast.

The decision function for assigning a class i(i = + 1,− 1) to a new sample x_i is defined as follows:

$$ D(x_{i}) = \left\{\begin{array}{lllllllllll} + 1, & \text{if \(|{{x}^{T}}{{w}^{(1)}}+{{b}^{(1)}}|\, < \, |{{x}^{T}}{{w}^{(2)}}+{{b}^{(2)}}| \)} \\ -1, & \text{otherwise}. \end{array}\right. $$

(31)

where |.| denotes perpendicular distance of a sample from the hyperplane. In summary, algorithm 3.1 shows the required steps for constructing linear KNN-LSTSVM classifier.

3.3 Non-linear KNN-LSTSVM

Following the same idea, the linear KNN-LSTSVM can be extended to non-linear version by considering the following kernel-generated surfaces instead of planes:

$$ K({{x}^{T}},~{{C}^{T}}){{u}^{\left( 1 \right)}}+{{b}^{\left( 1 \right)}}= 0 \text{ and } K({{x}^{T}},~{{C}^{T}}){{u}^{\left( 2 \right)}}+{{b}^{\left( 2 \right)}}= 0 $$

(32)

where $C=~\left [ \begin {array}{ccccccccc} A \\ B \end {array} \right ]$ and K is any arbitrary kernel function. Similar to linear version, the primal problems of linear KNN-LSTSVM can be modified in the same way with inequality constraints replaced by equality constraints as expressed in (33) and (34).

$$\begin{array}{@{}rcl@{}} \underset{u_{(1)} ,b_{(1)}}{\min} \quad && \frac{1}{2}{{(K(A,~{{C}^{T}}){{u}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}})}^{T}}D(K(A,~{{C}^{T}}){{u}^{\left( 1 \right)}} \\ && +e{{b}^{\left( 1 \right)}}) +\frac{C}{2}{{y}^{T}}y \\ \text{s.t. } \quad && -F(K(B,~{{C}^{T}}){{u}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}})+y=Fe \end{array} $$

(33)

$$\begin{array}{@{}rcl@{}} \underset{u_{(2)} ,b_{(2)}}{\min} \quad && \frac{1}{2}{{(K(B,{{C}^{T}}){{u}^{(2)}}+e{{b}^{(2)}})}^{T}}Q(K(B,{{C}^{T}}){{u}^{(2)}} \\ &&+e{{b}^{(2)}})+\frac{C}{2}{{y}^{T}}y \\ \text{s.t. } \quad && P(K(A,{{C}^{T}}){{u}^{(2)}}+e{{b}^{(2)}})+y=Pe \end{array} $$

(34)

where K(A, C^T) and K(B, C^T) are kernel matrices of sizes m₁ × m and m₂ × m respectively (m = m₁ + m₂). By substituting the constraints into objective function, The QPPs (33) and (34) become:

$$ \begin{array}{lllllllllll} \underset{u_{(1)} ,b_{(1)}}{\min}~ & \frac{1}{2}\left\|D(K(A,~{{C}^{T}}){{u}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}})\right\|^{2} \\ & +\frac{C}{2}\left\|F(K(B,~{{C}^{T}}){{u}^{\left( 1 \right)}}+e{{b}^{\left( 1 \right)}}+F{{e}})\right\|^{2} \end{array} $$

(35)

$$ \begin{array}{lllllllllll} \underset{u_{(2)} ,b_{(2)}}{\min}~ & \frac{1}{2}\left\|Q(K(B,~{{C}^{T}} ){{u}^{\left( 2 \right)}}+e{{b}^{\left( 2 \right)}})\right\|^{2} \\ & +\frac{C}{2}\left\|P(K(A,~{{C}^{T}} ){{u}^{\left( 2 \right)}}+e{{b}^{\left( 2 \right)}}+P{{e}})\right\|^{2} \end{array} $$

(36)

In a similar way, the solutions of QPPs (35) and (36) can be obtained as follows:

$$\begin{array}{@{}rcl@{}} \left[\begin{array}{ccccccccc} {{u}^{(1)}} \\ {{b}^{(1)}} \end{array} \right]= & -{({{S}^{T}}FS+\frac{1}{C}{{R}^{T}}DR)^{-1}}{{S}^{T}}Fe \end{array} $$

(37)

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{ccccccccc} {{u}^{(2)}} \\ {{b}^{(2)}} \end{array} \right]= & {({{R}^{T}}PR+\frac{1}{C}{{S}^{T}}QS)^{-1}}{{R}^{T}}Pe \end{array} $$

(38)

where $R=\left [ \begin {array}{ccccccccc} K(A,{{C}^{T}})\ & e \end {array} \right ]$ and $S=\left [ \begin {array}{ccccccccc} K(B,{{C}^{T}})\ & e \end {array} \right ]$. A new sample is classified in the same way as it is done in linear case. The decision function for non-linear case is given by:

$$ D(x) = \left\{\begin{array}{lllllllllll} + 1, & \text{if } |K(x,{C}^{T}){{u}^{(1)}}+{{b}^{(1)}}|\, \\ & < \, |K(x,{C}^{T}){{u}^{(2)}}+{{b}^{(2)}}| \\ -1, & \text{otherwise}. \end{array}\right. $$

(39)

It can be noted that the solution of non-liner KNN-LSTSVM requires inversion of matrix size (m + 1) × (m + 1) twice. However, using Sherman-Morrison-Woodbury (SMW) formula [10], the solution (37) and (38) can be solved using four inverses of smaller dimension than (m + 1) × (m + 1). The solution of (37) and (38) can be rewritten as:

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{ccccccccc} {{u}^{(1)}} \\ {{b}^{(1)}} \end{array} \right]&\,=\, & -(Y\!-Y{{R}^{T}}D{{(CI+RY{{R}^{T}}D)}^{-1}}RY){{S}^{T}}Fe \end{array} $$

(40)

$$\begin{array}{@{}rcl@{}} \left[ \begin{array}{ccccccccc} {{u}^{(2)}} \\ {{b}^{(2)}} \end{array} \right]&= & (Z\,-\,Z{{S}^{T}}Q{{(CI+SZ{{S}^{T}}Q)}^{-1}}SZ){{R}^{T}}Pe \end{array} $$

(41)

where Y = (S^TFS)^− 1 and Y = (R^TPR)^− 1. The matrix (S^TFS) and (R^TPR) might be positive semi-definite. Following [12], a regularization term εI, ε > 0 is introduced to Y and Z to avoid the possibility of the ill-conditioning of (S^TFS) and (R^TPR). This allows us to use SMW formula in finding Y and Z as

$$\begin{array}{@{}rcl@{}} Y&= & \frac{1}{\varepsilon }(I-{{S}^{T}}F{{(\varepsilon I+S{{S}^{T}}F)}^{-1}}S) \end{array} $$

(42)

$$\begin{array}{@{}rcl@{}} Z&= & \frac{1}{\varepsilon }(I-{{R}^{T}}P{{(\varepsilon I+R{{R}^{T}}P)}^{-1}}R) \end{array} $$

(43)

After using SMW formula, the solution of non-linear case requires two matrix inverses of size (m₁ × m₁) and two matrix inverses of size (m₂ × m₂). In summary, algorithm 3.2 shows the required steps for constructing non-linear KNN-LSTSVM classifier.

3.4 Discussion on KNN-LSTSVM

3.4.1 KNN-LSTSVM vs. LSTSVM

Compared with LSTSVM, KNN-LSTSVM incorporates KNN method into LSTSVM and embodies the similarity information between pairs of samples into the objective function. Therefore proposed method is less sensitive to the outliers and noisy samples than LSTSVM. Both algorithms solve a pair of linear equations instead of two QPPs. As a result, they have fast learning speed.

3.4.2 KNN-LSTSVM vs. WLTSVM

Both WLTSVM and KNN-LSTSVM find two non-parallel hyperplanes by making full use of similarity information. They also give weight to the samples and have noise suppression capability. However, KNN-LSTSVM needs to solve two systems of linear equations as opposed to solving two QPPs in WLTSVM. It implies that the proposed method is faster than WLTSVM.

4 Numerical experiments

To demonstrate the performance of our proposed KNN-LSTSVM, we conducted experiments on 14 datasets from UCI machine learning repository.¹ They are Australian, Bupa-Liver, Cleveland, Haber-man, HeartStatlog, Hepatits, Ionsphere, Monk3, Pima-Indian, Sonar, Titanic, Votes, WDBC and WPBC. Table 1 shows the characteristics of these datasets.

Table 1 The characteristics of benchmark datasets

Classification accuracy of each method is measured by standard 10-fold cross-validation. More specifically, each dataset is split into ten subsets randomly. One of those sets is reserved as a test set whereas the remaining data are considered for training. This process is repeated ten times until all of the ten subsets is tested [3].

4.1 Implementation details

All the methods were implemented in Python 3.6 programming language and ran on Windows 8 PC with Intel Core i7 6700K (4.0 GHZ) and 32.0 GB of RAM. In addition, NumPy package [40] was used for linear algebra operations and SciPy [14] package was employed for distance calculation and statistic functions. The solver is critical part of the code and is implemented in Cython² [2] which improves the training speed.

4.1.1 Optimizer

The proposed method solves two systems of linear equations for obtaining the hyperplanes. However, other algorithms such as standard SVM, standard TSVM and WLTSVM need an external optimizer for solving their QPPs problem. The clipDCD algorithm [29] was employed to solve the dual QPPs of these classifiers. This optimizer has simple formulation, fast learning speed and is easy-to-implement. It only solves one single-variable sub-problem according to the maximal possibility-decrease strategy [29]. The dual QPP of the standard SVM can be expressed as follows:

$$ \begin{array}{lllllllllll} \underset{\alpha}{\min} \qquad & \frac{1}{2} \alpha^{T}Q\alpha - e^{T}\alpha, \\ \text{s.t. } \qquad & 0 \leq \alpha \leq C. \end{array} $$

(44)

the clipDCD algorithm only updates one component of α at each iteration. More information on the convergence of this algorithm and theoretical proofs can be found in [29].

4.2 Parameters selection

The performance of TSVM and its extentions depend heavily on the choice of optimal parameters. Therefore, the grid search method is used to find the optimal parameters. Moreover, the Gaussian kernel function k(x_i, x_j) = exp(−∥x_i − x_j∥ ²/γ²) was only considered as it is often employed and yields great generalization performance. The penalty parameters in TSVM, WLTSVM, LSTSVM and KNN-LSTSVM are selected from set {2ⁱ∣i = − 10,− 9,…,9,10}. The Gaussian kernel parameter γ is selected from the set {2ⁱ∣i = − 15,− 14,…,5}. The neighborhood size k in WLTSVM and KNN-LSTSVM is chosen from the set {2,3,…,10}.

4.3 Synthetic datasets

To illustrate graphically advantage of our KNN-LSTSVM over LSTSVM, we conducted experiments on artificial Ripley’s datset [32] which contains 250 samples and checkerboard dataset [11] of 1000 samples. 70% of samples were selected randomly for training both algorithms. Figures 4 and 5 depict performance of KNN-LSTSVM and LSTSVM on Ripey’s and checkerboard dataset, respectively. It can be seen that KNN-LSTSVM obtains better separating hypersurface. This indicates that our proposed method significantly improves the classification performance of LSTSVM.

Fig. 4

The performance and decision boundary of KNN-LSTSVM and LSTSVM on Ripley’s dataset with Gaussian kernel

Fig. 5

The performance and decision boundary of KNN-LSTSVM and LSTSVM on checkerboard dataset with Gaussian kernel

4.4 Experimental results and discussion

Table 2 shows the averages and standard deviation of the test accuracies (in %) for the TSVM, WLTSVM, LSTSVM and KNN-LSTSVM on fourteen UCI benchmark datasets. In addition, the training time of each classifier is demonstrated (It should be noted that the training time of WLTSVM and KNN-LSTSVM include KNN finding). The optimal parameters of four algorithms used in the experiments are also shown in Table 2. From the experimental results, we can draw the following conclusions:

• 1. From the perspective of classification accuracy, our proposed method (KNN-LSTSVM) outperforms the other three algorithms. This result validates that the necessity of introducing similarity information within samples into the objective function which improves the accuracy of classifier.

• 2. In terms of computational time, LSTSVM is the fastest algorithm, because it solves two systems of linear equations. Even though two systems of linear equations are solved in our KNN-LSTSVM, KNN finding increases computing time. In comparison to WLTSVM, our proposed method costs shorter computational time as it inherits the advantage of LSTSVM which is solving a pair of linear equations rather than QPPs.

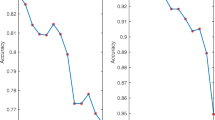
• 3. In order to show the effect of parameter k on the accuracy of KNN-LSTSVM, an experiment conducted on the Australian and Hepatits datasets. The value of k ranges from 2 to 30, and the step is 2. Figure 6 indicates the importance of selecting parameter k. The maximum accuracy appears when k is equal to 12. This implies that k = 12 is an optimal choice for the Australian dataset. For Hepatits dataset, the classification accuracy improves significantly as the value of k increases. Therefore, the choice of optimal parameter k is prominent.

• 4. In comparison with new non-parallel classifiers (i.e. RELS-TSVM [37] and Iv-TBSVM [41]), our KNN-LSTSVM has better classification ability as shown in Table 3. It obtains the lowest rank among new alogorithms. The results of RLES-TSVM and Iv-TBSVM were taken from [37] and [41], respectively. It should be noted that Iv-TBSVM solves two QPPs as opposed to solving a pair of linear equations in KNN-LSTSVM and RELS-TSVM. As a result, its learning speed is slower than least squares algorithms.

Table 2 Comparison of accuracy and training time for TSVM, WLTSVM, LSTSVM and KNN-LSTSVM

Fig. 6

Changes of accuracy with the growth of k

Table 3 The comparison of accuracy for KNN-LSTSVM, RELS-TSVM and Iv-TBSVM in the case of Guassian kernel

4.5 Statistical test

To further analyze the performance of four algorithms on fourteen UCI datasets as it was suggested in [7]. The Friedman test was used with corresponding post hoc tests which is proved to be a simple, nonparametric and safe. For this, the average ranks of four algorithms on accuracy for all datasets are calculated and listed in Table 4. Under the null hypothesis that all the algorithms are equivalent, one can compute the Friedman test according to (45):

$$ {\chi^{2}_{F}} = \frac{12N}{k(k + 1)}\left[\sum\limits_{j} {R^{2}_{j}} - \frac{k(k + 1)^{2}}{4} \right], $$

(45)

where $R_{j}=\frac {1}{N}{\sum }_{i}{r^{j}_{i}}$, and ${R^{j}_{i}}$ denotes the j-th of k algorithms on the i-th of N datasets. Friendman’s ${\chi ^{2}_{F}}$ is undesirably conservative and derives a better statistic

$$ F_{F} = \frac{(N - 1){\chi^{2}_{F}}}{N(k - 1) - {\chi^{2}_{F}}} $$

(46)

which is distributed according to the F-distribution with k − 1 and (k − 1)(N − 1) degrees of freedom. We can obtain ${\chi ^{2}_{F}} = 8.293$ and F_F = 3.198 according to (45) and (46). Where F_F is distributed according to F-distribution with (3, 39) degrees of freedom. The critical value of F(3,39) is 1.42 for the level of significance α = 0.25, similarly, it is 2.23 for α = 0.1 and 2.84 for α = 0.05. Since the value of F_F is larger than the critical value, there is significant difference between the four algorithms. Table 4 also illustrate that our KNN-LSTSVM is more valid than other three algorithms, because the average rank of KNN-LSTSVM is the lowest among other algorithms (Table 4).

Table 4 Average rank on classification accuracy of four algorithms

4.6 Experiments with NDC datasets

In this subsection, experiments were conducted on large datasets to compare computing time of KNN-LSTSVM with other three algorithms as the number of datapoints increase. Large datasets were generated using NDC Data Generator [24]. Table 5 shows the description of NDC datasets. For experiments with these datasets, the penalty parameters of all algorithms were fixed to be one (i.e, C = 1). The Gaussian kernel (RBF) was used with γ = 2^− 15 for non-linear case. The neighborhood size k is also 5 for all datasets. Table 6 shows the comparison of computing time for all four algorithms on NDC datasets with both linear and Gaussian kernel.

Table 5 The description of NDC datasets

Table 6 The comparison of computing time for four algorithms on NDC datasets

KNN-LSTSVM performed several orders of magnitude faster than WLTSVM on all datasets, because KNN-LSTSVM does not require any external optimizer whereas WLTSVM is implemented with clipDCD algorithm. While KNN-LSTSVM is fast, it is not as fast as LSTSVM which is evident from Table 6. LSTSVM obviously requires solving two systems of linear equations whereas KNN-LSTSVM requires KNN-finding plus solving two systems of linear equations. For non-linear test, a rectangular kernel [22] was employed using 10% of total datapoints. Results with reduced kernel indicate that LSTSVM and KNN-LSTSVM are much faster than TSVM and WLTSVM, because even with reduced kernel $(m \times \bar {m})$, TSVM and WLTSVM still require solving two QPPs of size m₁ and m₂.

In order to show the influence of parameter k on the computing time of KNN-LSTSVM, an experiment was conducted on the relatively large dataset, NDC-10K. As shown in the Fig. 7, the value of k does not influence the computing time for KNN-LSTSVM. In summary, results on NDC datasets reveal that our KNN-LSTSVM is suitable for medium and large problems.

Fig. 7

The changes of time with the growth of k on the NDC-10K dataset

4.7 Application in human action recognition

To further investigate the efficiency and robustness of our KNN-LSTSVM, we apply it into human action recognition which is one of the active research area in the field of computer vision and pattern recognition. It has a wide range of applications in surveillance video, automatic video retrieval and human computer interaction [1]. The difficulty of human action recognition problems may originate from several challenges such as illumination changes, partial occlusions, and intra-class variations [26].

An action is a sequence of body movements that may involves several body parts concurrently [5]. From the perspective of computer vision, the goal of human action recognition is to correctly classify the videos into its action category [1]. Major components of human action recognition system include action representation and classification.

4.7.1 Action representation

Sparse space-time features have been frequently used in human action recognition research which are extracted from 3-dimensional space-time volumes to represent and classify actions [1]. Space-time interest points are detected using Harris3D operator [18]. The Histogram of Oriented Gradient (HoG) and Optical Flow (HOF) were employed for action representation [19].

After extracting space-time features, the Bag of Video Words (BoVW) technique was applied which treats videos as documents and visual features as words. This technique proved its robustness to location changes and to noise. The visual words are constructed by utilizing K-means clustering [21] as it is the most popular algorithm to construct visual dictionary. Since the total number of features is very large to use for clustering, a subset of 10⁵ features were selected randomly. The number of clusters is set to 4000 which has shown empirically to produce good results. The resulted clusters are equivalent to the visual words. Finally, the word frequency histogram are computed and used as video sequence representation.

4.7.2 KTH dataset

In Section 4.7, the experiments are carried out on KTH dataset which was introduced by Schuldt et al. [34] and is one of the most popular human activity dataset. It contains six types of human actions (boxing, hand clipping, hand waving, jogging, running and walking) performed by 25 people in four different scenarios including outdoor, indoor, changes in clothing and variations in scale. The dataset consists of 2391 sequences where the background is homogeneous in all cases. Figure 8 shows several examples frames corresponding to different types of action.

Fig. 8

Examples of sequences corresponding to different types of actions from KTH dataset

4.7.3 Results and discussion

Due to the limited number of persons in the KTH dataset, the leave-one-person-out is used where each run uses 24 persons for training and one person for testing. Then, the average of the results is calculated to give the final recognition rate.

For experiment with KTH dataset, our linear KNN-LSTSVM was extended to handle multi-class problems based on One-versus-All (OVA) strategy. For K-class classification problem, the linear OVA KNN-LSTSVM solves K-linear equations and determines K non-parallel hyper planes, one for each class [39]. Table 7 shows a comparison between our KNN-LSTSVM and other classifiers on KTH dataset. The result shows that our proposed method has the highest mean accuracy among other algorithms. This further validates the effectiveness of our KNN-LSTSVM in real-world application.

Table 7 Mean accuracy rates of different methods on KTH dataset

5 Conclusion

Motivated by both LSTSVM and WLTSVM, we present a novel algorithm, i.e, the KNN-based least squares twin support vector machine. Similar to WLTSVM, our new algorithm takes full advantage of similarity information within each samples by KNN method before classification which improves prediction accuracy. Furthermore, the proposed method not only inherits the advantage of LSTSVM algorithm, which owns low computational time by solving linear equations, but also addresses the shortcoming of outlier sensitivity and noise tolerance in LSTSVM. The experimental results reveal that KNN-LSTSVM outperforms other three algorithms in terms of classification accuracy. The computational result on NDC datasets also indicates that KNN-LSTSVM is faster than WLTSVM and can handle large-scale classification problems. We also investigated the application of linear KNN-LSTSVM to human action recognition. The comparison of experimental results against linear LSTSVM show that linear KNN-LSTSVM has better classification ability on KTH dataset. The subject of our future work is to find effective methods which improves KNN-LSTSVM in terms of learning speed and memory consumption.