Bi-objective sequence optimization in reliability problems with a matrix-analytic approach

Abstract

The redundancy allocation problem (RAP) is an intriguing area in the field of reliability optimization to which a lot of research has been devoted in recent years. In this paper, a bi-objective model is developed for RAP with a heterogeneous backup scheme and a mixed redundancy strategy. Elimination of the lower bound estimation and the exact calculation of the reliability of the mixed strategy forms one of the most striking features of the proposed model. Investigating the optimal sequence of components in each subsystem, the study modifies a non-dominated sorting genetic algorithm (NSGA-II), as a powerful multi-objective evolutionary one, to solve the proposed bi-objective model. Two numerical examples will then be used to verify the efficiency of the model in achieving enhanced system reliability. Finally, the results of Pareto optimal set are used to demonstrate that the assumptions made enable the proposed model to improve system reliability by offering various structures while simultaneously considering system limitations.

1 Introduction

All high-tech engineering fields are nowadays witnessing a growing need for ingenious system structure designs that are capable of dealing with problematic and elaborate reliability analysis. Given the fact that the reliability of a product is mainly affected by the decisions made in the system design process (O’Connor & Kleyner, 2012) and, further, that enhanced system reliability is a costly decision, optimization of system reliability requires principles to be employed in the design process that consider not only the total budget available but the associated limitations as well. A useful technique used in this process comes under the rubric of reliability optimization problem (ROP) that might be realized through one of four general approaches: i) procuring redundant units in parallel, ii) enhancing component reliability, iii) a mixture of these two approaches, and iv) reassignment of interchangeable components (Chambari et al., 2012). The first approach, known as the Redundancy Allocation Problem (RAP), is a popular topic in the field a brief description of which follows.

In RAPs, the policy of using redundant components is known as the redundancy strategy that comes in the two conventional types of active and standby. The standby redundancy strategy has the three cold, warm, and hot sub-types. A detailed description of the different kinds of cold strategy may be found in Refs. (Levitin et al., 2013a; Tavakkoli-Moghaddam et al., 2008). A general redundancy strategy, called the mixed strategy, was recently introduced by Ardakan and Hamadani (2014). This new strategy not only outperforms its rival conventional active and standby strategies but also subsumes them as its special cases (Abouei Ardakan et al., 2016; Guilani et al., 2020).

Generally speaking, all the redundant components in a standby strategy are sequentially activated by a switching system. Detection of a faulty unit and the subsequent switching to a substitute one in the standby strategy may be accomplished by either of two mechanisms. The first type of mechanism (T1) involves a continuous detecting system with a reliability of $\rho (t)$, while in the second type (T2), the switch is activated whenever needed so that the failure of the switch occurs with a constant probability of $\rho$ (Kuo & Prasad, 2000).

Previous studies were mainly focused on optimizing the single objective redundancy allocation problem (SORAP) mostly formulated based on identical components under either an active or a standby strategy (Ardakan et al., 2015). A considerable interest has been recently shown in the multi-objective redundancy allocation problem (MORAP). Kulturel-Konak et al. (2003) were among the first to employ a Tabu Search (TS) algorithm for solving the RAP with the multiple objective functions of minimizing system cost and weight as well as maximizing system reliability. A number of studies have been devoted to improvement of system reliability of the MORAP under both active and cold-standby strategies (Chambari et al., 2012; Garg & Sharma, 2013; Liang & Lo, 2010; Okafor & Sun, 2012; Safari, 2012; Soylu & Ulusoy, 2011; Wang et al., 2009). However, the main limitation in most of these studies, however, is that they considered a predetermined active or standby redundancy strategy and tried to enhance system reliability by finding better structures. In a recent study, Ardakan et al. (2015) proposed a new mathematical model of the MORAP and introduced for the first time the mixed strategy in a bi-objective RAP context aimed at maximizing system reliability and minimizing system cost.

A major advance in dealing with RAPs is their classification into the two main categories of homogeneous ones, in which all the components employed in each system (or subsystem) are identical in type, and the heterogeneous ones, in which one type of component can be replaced by different types of functionally-equivalent components. It is worth mentioning that all the papers reviewed in this study were found to have investigated homogeneous systems. Among the first works to deal with a heterogeneous backup scheme, one can refer to (Amari & Dill, 2009; Cha et al., 2008) that focused primarily on warm standby systems. Several studies also entertained the opportunity of accomplishing reliable systems in RAP with heterogeneous (i.e., mixed) components (RAPMC) (Hsieh & Yeh, 2012; Sadjadi & Soltani, 2012; Soltani et al., 2014, 2015; Yeh, 2014; Zhao et al., 2015; Zhuang & Li, 2015). The main shortfall in the mentioned papers is that they employed an active strategy, in which the sequence of components has no bearing on system reliability. In contrast, Cha et al. (2008), Amari and Dill (2009), Zhai et al. (2015), and Levitin et al. (2013a) studied the warm strategy in the standby mode with a perfect switching system and considered the impact of sequencing components on system reliability. Also, Levitin et al. (2013b) studied the optimal standby component sequencing problem (SESP) with a perfect switching system for the cold-standby strategy. Moreover, in the pioneering studies of the RAPMC, Kim and Kim (2017a) and Kim (2018) proposed a novel method based on the Markov theory to calculate the reliability of a system with heterogeneous components in the cold-standby redundancy strategy with an imperfect switching system. A summary of the most important studies in the literature and a comparison with the present study is shown in Table 1.

Table 1 Summary of the previous important studies

As already mentioned in Table 1, all the above papers in the RAPMC studied the single-objective model. The present paper is, however, different in that it is focused on the effect of component ordering on the reliability of a system with the mixed strategy. Furthermore, the model proposed in this case is a bi-objective one that aims to accomplish a comprehensive analysis of both system cost and system reliability. This approach will expectedly be of much interest to system designers due to the potential impacts component sequencing might have on both system cost and its reliability. Additionally, the reliability function in the present study is formulated based on the continuous-time Markov chain (CTMC) model, which calculates the exact reliability of the RAPMC with a mixed strategy in a timely manner. According to Chern (1992), the RAP belongs to the NP-hard class of optimization problems, for whose solution meta-heuristic algorithms have been commonly used in the literature. Accordingly, a modified version of the well-known multi-objective algorithm, called NSGA-II, is used in the present study for solving the problem.

The rest of the paper is organized as follows. Section 2 reviews the mixed redundancy strategy as a superior one used in this work. A new methodology is outlined in Sect. 3 for evaluating system reliability in a RAPMC with a mixed strategy using the CTMC model. Section 4 provides an overview of the NSGA-II meta-heuristic algorithm as the solution method employed. Section 5 presents the analysis of a popular RAP as a case study and, finally, conclusions are presented in Sect. 6.

Notation
$i, j$	Subsystem and component indicators, respectively	${R}_{S}\left(t\text{,} \, seq\right)$	System reliability at time t regarding the defined sequence
$\rho \left(t\right), \rho$	Switch reliability at time t and constant switch reliability, respectively	expm	Matrix exponential function
${T}_{sys}$	System lifetime	$\overrightarrow{1}$	Column vector for which all entries are equal to unity
${n}_{{A}_{i}}$, ${n}_{{S}_{i}}$	Number of active and standby components in subsystem i, respectively	$\oplus , \oplus$	Kronecker tensor product and Kronecker tensor sum, respectively
${n}_{i}$	Redundancy level of subsystem i	Nstart	Number of the first population generated
${Z}_{i}$	Index of component choice applied for subsystem i	Maxiter	Final iteration of the meta-heuristic algorithm
${Y}_{j,i}$	Index of component choice used for position j of subsystem i	$C,W$	Maximum total system cost and weight, respectively
${{\varvec{O}}}_{A}$, ${{\varvec{O}}}_{S}$	Arrangement vector of components in active and standby strategies, respectively	$\alpha , \beta$	Penalty coefficients
${\lambda }_{j}$	Failure rate of component j
${\mathbb{S}}$	Continuous phase-type distribution set of state spaces	Nomenclature
${\mathbb{S}}_{T}$, ${\mathbb{S}}_{A}$	Transient and absorbing set of state spaces, respectively	CTMC	Continuous-time Markov chain
${{\varvec{\pi}}}_{i}$	Initial state probability distribution	RAPMC	Redundancy allocation problem with mixed components
Q	Infinitesimal generator matrix	TRM	Transition rate matrix
D	Transition rate matrix	TTF	Time-to-failure
d	Absorbing rate matrix	PHD	Phase-type distribution
Ix	Identity matrix of size x	NSGA-II	Non-dominated sorting genetic algorithm II
m	Cardinal number of ${\mathbb{S}}_{T}$	TPM	Transition probability matrix
${m}_{i,d}$	Cardinal number of the transient set of state spaces in the switch/fault detector of subsystem i	MORAP	Multi-objective redundancy allocation problem
${r}_{i\text{,}j}\left(t\right)$	Reliability of component j in subsystem i	SORAP	Single-objective redundancy allocation problem

2 Mixed strategy

As already explained, the mixed strategy is a general form subsuming both the conventional active and standby strategies. Assuming that subsystem i under a mixed redundancy strategy comprises various levels of active and standby redundant components denoted by ${n}_{{A}_{i}}$ and ${n}_{{S}_{i}}$, the redundancy level (${n}_{i}$) in this subsystem is then considered as a decision variable that can be computed by ${n}_{i}={n}_{{A}_{i}}+{n}_{{S}_{i}}$. Given the assumption that heterogeneous components may be employed in each subsystem, it will be necessary to consider a sequence according to which these components are activated. In this study, the orders in subsystem i for the active and standby components are denoted by ${O}_{{A}_{i}}$ and ${O}_{{S}_{i}}$, respectively. Thus, to achieve both objectives of maximizing system reliability and minimizing its cost, the components will need to be properly ordered and convenient redundancy levels be defined.

Coit (2003) was among the first to explore the link between reliability of the cold-standby strategy and that of the active strategy in a given subsystem as mainly affected by redundancy level. The fact is that both the strategies have their own strengths and weaknesses both of which are shared by a strategy formed as a combination of the two. Such a combined strategy, referred to in the present paper as the mixed strategy (Ardakan et al. 2015), may be applied to subsystems in order to improve the overall system performance. Figure 1 provides a detailed schematic of a sample structure of a heterogeneous series–parallel system under a mixed strategy, where the green and white cells indicate active and cold-standby components, respectively, and the number in each cell implies the component type. The proposed system in this series–parallel structure will work until all subsystems are operating, and only one online component in each subsystem is needed to have such subsystem.

Fig. 1

A sample structure of a heterogeneous system with the mixed redundancy strategy

In the mixed strategy, all the ${n}_{{A}_{i}}$ primary components are simultaneously activated in subsystem i at time zero while the subsystem is capable of satisfactory operation with only one component in operation. At the failure of the last active component, the switching mechanism replaces the failed component with the first standby one according to a predetermined order. As a result, the subsystem fails in a perfect switching case when the ${n}_{i}^{th}$ malfunction occurs.

All types of redundancy strategies are based on the assumptions that each subsystem contains at least one active component (i.e., ${n}_{{A}_{i}}\ge 1$) and that there is no limit on the number of cold-standby units (i.e., ${n}_{{S}_{i}}\ge 0$). Table 2 lists the five redundancy strategies derived on the basis of these assumptions. Clearly, the mixed strategy as a generalized form of both the active and standby ones yields structures that offer a more flexibility pleasing to system designers.

Table 2 Types of redundancy strategies

According to Ref. (Ardakan et al. 2015), exact calculation of reliability for a system under the mixed strategy is a complicated and time-consuming process. A lower bound formulation is, therefore, proposed as in Eq. (1) for calculating the reliability of a subsystem with identical components under a mixed strategy, albeit the calculation is still complex and time-consuming.

$$\begin{aligned} R_{{ik_{i} ,Mixed}} (t;\;n_{Ai} ;\;n_{{sk_{i} }} ) & = \left( {1 - (1 - r_{{ik_{i} }} (t))^{{n_{Ai} }} } \right) + \rho_{i} (t)\int\limits_{0}^{t} {r_{{ik_{i} }} (t - u) \times f_{{ik_{i} }}^{{Max,n_{Ai} }} (u)du} \\ & \quad + \rho_{i} (t)\sum\limits_{j = 1}^{{n_{{sk_{i} }} - 1}} {\int\limits_{0}^{t} {\int\limits_{{t_{1} }}^{t} {r_{{ik_{i} }} (t - u) \times f_{{ik_{i} }}^{(j)} (u - t_{1} ) \times f_{{ik_{i} }}^{{Max,n_{Ai} }} (t_{1} )dudt_{1} } } } \\ \end{aligned}$$

(1)

where ${f}_{i{k}_{i}}^{(j)}$ represents the probability density function for the $j{\text{th}}$ failure in subsystem i when a component of type ${k}_{i}$ is used and ${f}_{i{k}_{i}}^{Max, {n}_{Ai}}$ is the probability density function for the maximum failure times of ${n}_{Ai}$ number of independent and identical components in subsystem i when a type ${k}_{i}$ is utilized.

The major drawback Ardakan and Hamadani (2014) found with Eq. (1) was that it could just be used for calculating the lower bound of the whole system reliability. They also claimed that the equation could have been more useful if it were able to handle subsystems with non-identical components. To overcome these inadequacies, Guilani et al. (2020) proposed an exact reliability formulation for the mixed strategy, which calculated system reliability based on a matrix analytic method. This approach, which can also be used for systems with heterogeneous components, is adopted in the present study for the exact calculation of system reliability, a detailed description of which follows.

3 Exact calculation of system reliability

The mathematical formulation proposed for calculating the exact reliability of a system under a mixed strategy with heterogeneous components is an innovative alternative to that presented in Ardakan et al. (2015). Of particular interest in this model is the short time it takes to calculate the exact reliability value of a system with heterogeneous backup scheme under a mixed strategy. Moreover, the model is capable of considering a sequence according to which the components are activated.

From a reliability point of view, possible states and transitions form the two main parts of a Markov model, with states representing the current working component(s) and transitions representing the connection paths among the states. A simplified view of a Markov model for a non-repairable system with two states is presented in Fig. 2, where the system can shift from State 1 to State 2 through a given transition path.

Fig. 2

A simple illustration of a Markov model for a non-repairable two-unit system

3.1 Individual reliability

Previous studies of the problem commonly considered an exponential distribution for the time-to-failure (TTF) of components. This leads to the following formulation for the reliability of component j in subsystem i at a given time t:

$${r}_{i,j}\left(t\right)=\mathrm{exp}(-{\lambda }_{ij}t)$$

(2)

where $\lambda$ represents failure rate.

3.2 Subsystem reliability

In the present paper, a structured continuous-time Markov chain (CTMC) model is developed for the exact calculation of each subsystem’s reliability. In this case, the TTF of subsystem i with n_i components can be modeled based on a continuous phase-type distribution (PHD) supported by a set of state spaces ${\mathbb{S}}_{i}=\{{{\mathbb{S}}_{i}}_{T},{{\mathbb{S}}_{i}}_{A}\}$. The set ${\mathbb{S}}_{i}$ is composed of ${m}_{i}+1$ finite and countable states, whereas the set of transient states ${{\mathbb{S}}_{i}}_{T}=\left\{1.2.\dots .{m}_{i}\right\}$ contains ${m}_{i}$ states as phases and the absorbing set of states ${{\mathbb{S}}_{i}}_{A}=\left\{A\right\}$ contains one as either the absorbing or the final state. In the proposed reliability model, the state transitions among all ${n}_{i}$ components capture the deterioration process of subsystem $i$. Accordingly, failure in the subsystem is interpreted by entering the absorbing state. In this regard, the TTF of a particular unit may be analyzed using a random variable of PHD as PH(${\varvec{\uppi}}, \mathbf{D}$), where ${\varvec{\uppi}}$ is the initial state probability distribution and D is a square matrix of size $m$ containing the transition rates among the phases. In addition, the infinitesimal generator, Q, of the CTMC model can be expressed as in (3):

$$\mathbf{Q}=\left[\begin{array}{cc}\mathbf{D}& \mathbf{d}\\ 0& 0\end{array}\right]$$

(3)

where d is a column vector of entering rates into absorbing states. Based on the fundamental PHD features, Eqs. (4–6) below can be derived as the probability density, cumulative distribution, and reliability functions, respectively, for a given component at time $t$ (Latouche & Ramaswami, 1999).

$$f(t) = \left\{ {\begin{array}{*{20}l} {\pi_{{{\mathbb{S}}_{A} }} ,} \hfill & {for\;t = 0} \hfill \\ {{{\varvec{\uppi}}}{\text{expm}}({\mathbf{D}}t){\mathbf{d}},} \hfill & {for\;t > 0} \hfill \\ \end{array} } \right.$$

(4)

$$F(t) = \pi_{{{\mathbb{S}}_{A} }} + 1 - {{\varvec{\uppi}}}{\text{expm}}({\mathbf{D}}t)\overrightarrow {{\mathbf{1}}} ,\quad for\;t \ge 0$$

(5)

$$R(t) = 1 - F(t) = {{\varvec{\uppi}}}{\text{expm}}({\mathbf{D}}t)\overrightarrow {{\mathbf{1}}} ,\quad for\;t \ge 0$$

(6)

where the initial probability at which the system starts in a failed state is denoted by ${\pi }_{{S}_{A}}$. In all cases, this variable is taken to be ${\pi }_{{S}_{A}}=0$.

3.3 Mixed redundancy strategy formulation

A subsystem with $n$ components and a mixed strategy combines both conventional strategies, where ${n}_{A}$ components are in operation and ${n}_{S}=n-{n}_{A}$ components are kept immune from operational stress. Additionally, when all the initially launched components fail, the standby components are sequentially put into operation in a predetermined order. Across these sequential activations, a switching system is needed to sense and detect a failing component and to substitute it with a standby one (Ardakan & Hamadani, 2014). In this study, the first type of switching mechanism (T1) is employed with an exponentially distributed TTF.

As a matter of fact, the working conditions of each component and switch indicate the states of the CTMC reliability model; hence, the following two situations may be envisioned based on the switch operating conditions.

Situation 1: The switching system of subsystem i functions properly. The subsystem, therefore, operates properly until the last redundant unit fails. In this case, the lifetime of a system with ${n}_{A}$ active and ${n}_{S}$ cold-standby redundant units is given by:

$$T_{sys} = Max\left( {T_{j} ;j \in n_{A} } \right) + \mathop \sum \limits_{{k \in n_{S} }} T_{k}$$

where the term $Max\left({T}_{j};j\in {n}_{A}\right)$ expresses the lifetime of the initially launched components and the term ${\sum }_{k\in {n}_{S}}{T}_{k}$ denotes that of the cold-standby units. System failure occurs by the time all the n components reach their absorbing states. This requires, then, an infinitesimal generator matrix to cover all the possible combinations of states in the active units for the term $Max\left({T}_{j};\;j\in {n}_{A}\right)$; this yields the relation ${\mathbf{Q}}_{A}={\oplus }_{j\epsilon }{{n}}_{A}{\mathbf{Q}}_{j}$. Thus, the matrix format of ${\mathbf{Q}}_{sys}$ may be modeled as follows:

$${\mathbf{Q}}_{{\text{A}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{{\text{A}}} } & {{\mathbf{d}}_{{\text{A}}} } \\ 0 & 0 \\ \end{array} } \right],{\mathbf{Q}}_{sys} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{A} } & {{\mathbf{d}}_{A} {{\varvec{\uppi}}}_{k = 1} } & {} & {} & {} &\vline & {} \\ {} & {{\mathbf{D}}_{k = 1} } & {{\mathbf{d}}_{k = 1} {{\varvec{\uppi}}}_{k = 2} } & {} & {} &\vline & {} \\ {} & {} & {{\mathbf{D}}_{k = 2} } & {{\mathbf{d}}_{k = 2} {{\varvec{\uppi}}}_{k = 3} } & {} &\vline & {} \\ {} & {} & {} & \ddots & \ddots &\vline & {} \\ {} & {} & {} & {} & {{\mathbf{D}}_{{k = n_{S} }} } &\vline & {{\mathbf{d}}_{{k = n_{S} }} } \\ \hline {} & {} & {\mathbf{0}} & {} & {} &\vline & 0 \\ \end{array} } \right]\,$$

(7)

where ${\mathbf{d}}_{\mathrm{A}} \;\mathrm{and}\;{\mathbf{D}}_{\mathrm{A}}$ are intensity vectors to absorbing state and the sub-transition rate matrix (TRM) among the transient states for active components, respectively; ${\mathbf{D}}_{\mathrm{k}}, {\mathbf{d}}_{\mathrm{k}},\mathrm{ and }{{\varvec{\uppi}}}_{\mathrm{k}}$ are the intensity vectors to absorbing state, TRM among transient states, and the initial probability distribution vector for cold-standby components, respectively.

As mentioned earlier, the TTFs for all the components are taken in this study to be exponentially distributed; hence, ${\mathbf{D}}_{\mathrm{k}}=-{\lambda }_{k}, {\mathbf{d}}_{\mathrm{k}}={\lambda }_{k},\mathrm{ and }{{\varvec{\uppi}}}_{\mathrm{k}}=[1]$.

Situation 2: In this case, the switching system of subsystem i is in a failure state. Subsystem i, therefore, functions properly until the failure of either the last active component or an online standby one. In other words, the possibility for replacing a failed online component with a new one is not available. As a result, system failure occurs upon either of two events: first, by the time all the ${n}_{A}$ primary components reach their absorbing states (i.e., ${\mathbf{d}}_{A}$), or second, when an activated cold-standby component fails (i.e., ${\mathbf{d}}_{k\in {n}_{S}}$). Consequently, ${\mathbf{Q}}_{sys}$ in this situation may be formulated as in (8) below:

$${\mathbf{Q}}_{sys} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{A} } & {} & {} & {} & {} &\vline & {{\mathbf{d}}_{A} } \\ {} & {{\mathbf{D}}_{k = 1} } & {} & {} & {} &\vline & {{\mathbf{d}}_{k = 1} } \\ {} & {} & {{\mathbf{D}}_{k = 2} } & {} & {} &\vline & {{\mathbf{d}}_{k = 2} } \\ {} & {} & {} & \ddots & {} &\vline & \vdots \\ {} & {} & {} & {} & {{\mathbf{D}}_{{k = n_{S} }} } &\vline & {{\mathbf{d}}_{{k = n_{S} }} } \\ \hline {} & {} & {\mathbf{0}} & {} & {} &\vline & 0 \\ \end{array} } \right]\,$$

(8)

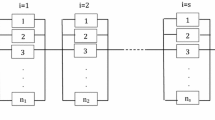
The proposed formulation can be illustrated with a simple example of a subsystem with four non-identical components. Such a subsystem will have the four different redundant structures shown in Fig. 3. To cover all the possible combinations for the proposed exact model, the structure with two active and two standby components (i.e., the second subsystem in Fig. 3) is selected for discussion. This subsystem is under a mixed redundancy strategy. The related states of the CTMC model for this structure are coded as follows:

• State S_A = All the active components are online;

• State S_i = Only component i is online;

Fig. 3

Different types of redundancy strategies in a subsystem with four components

Absorbing State = The final state of the CTMC method, which implies system failure.

As explained earlier, the mechanism might be in either of two situations based on the functioning states of the switching system. The infinitesimal generator of the structure assumed in Situation 1 is expressed by Eq. (9). The evidence from this matrix implies perfect operation of the switching system such that the system operates up to the failure of the last redundant component.

$$Q_{i,1} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{i,1} } & {{\mathbf{d}}_{i,1} } \\ {\mathbf{0}} & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \lambda_{1} - \lambda_{2} } & {\lambda_{1} } & {\lambda_{2} } & {} & {} &\vline & {} \\ {} & { - \lambda_{2} } & {} & {\lambda_{2} } & {} &\vline & {} \\ {} & {} & { - \lambda_{1} } & {\lambda_{1} } & {} &\vline & {} \\ {} & {} & {} & { - \lambda_{3} } & {\lambda_{3} } &\vline & {} \\ {} & {} & {} & {} & { - \lambda_{4} } &\vline & {\lambda_{4} } \\ \hline {} & {} & {\mathbf{0}} & {} & {} &\vline & 0 \\ \end{array} } \right]$$

(9)

The schematic view of the Markov model for this situation is presented in Fig. 4.

Fig. 4

State transitions in Situation 1

Accordingly, the infinitesimal generator matrix for Situation 2 may be outlined as in (10) below.

$$Q_{i,2} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{i,2} } & {{\mathbf{d}}_{i,2} } \\ {\mathbf{0}} & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \lambda_{1} - \lambda_{2} } & {\lambda_{1} } & {\lambda_{2} } & {} & {} &\vline & {} \\ {} & { - \lambda_{2} } & {} & {} & {} &\vline & {\lambda_{2} } \\ {} & {} & { - \lambda_{1} } & {} & {} &\vline & {\lambda_{1} } \\ {} & {} & {} & { - \lambda_{3} } & {} &\vline & {\lambda_{3} } \\ {} & {} & {} & {} & { - \lambda_{4} } &\vline & {\lambda_{4} } \\ \hline {} & {} & {\mathbf{0}} & {} & {} &\vline & 0 \\ \end{array} } \right]$$

(10)

This matrix indicates that the switching mechanism has failed and that the system functions properly until the failure of the current online components; this is depicted in Fig. 5.

Fig. 5

State transitions in Situation 2

As noted above, in the CTMC model, the operation state of subsystem i is affected by the operation states of both the switching system and the components. This calls for a method to determine the overall transition rate matrix (TRM) of subsystem i by integrating the infinitesimal generator matrices of both situations. For this purpose, the transition probability matrices (TPM), ${\mathbf{P}}_{\mathrm{T}}$ and ${\mathbf{P}}_{\mathrm{A}}$, are introduced. ${\mathbf{P}}_{\mathrm{T}}$ is the one used for retaining the current state of the components when the state transition occurs in the switch while ${\mathbf{P}}_{\mathrm{A}}$ is used to imply that the state of the switch has already arrived at an absorbing state and that the transition happens only in the online component(s). The relationship between ${\mathbf{P}}_{\mathrm{T}}$ and ${\mathbf{P}}_{\mathrm{A}}$ can be established by an identity matrix of size 2, such that ${\mathbf{P}}_{\mathrm{T}}+{\mathbf{P}}_{\mathrm{A}}={\mathbf{I}}_{2}$.

$${\mathbf{P}}_{{\text{T}}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ \end{array} } \right],\,\,\,\,\,\,\,\,\,{\mathbf{P}}_{{\text{A}}} = \,\left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 1 \\ \end{array} } \right]$$

The sub-TRM ${\mathbf{D}}_{i}^{T}$ in subsystem i for the integrated situation can be determined using Eq. (11):

$$\begin{aligned} {\mathbf{D}}_{i}^{T} & = {\mathbf{P}}_{{\text{T}}} \otimes {\mathbf{D}}_{1} + {\mathbf{Q}}_{switch} \otimes {\mathbf{I}}_{{{\mathbf{D}}_{1} }} + {\mathbf{P}}_{{\text{A}}} \otimes {\mathbf{D}}_{2} \\ & = {\mathbf{I}}_{{{\mathbf{D}}_{switch} }} \otimes {\mathbf{D}}_{1} + {\mathbf{Q}}_{switch} \otimes {\mathbf{I}}_{{\mathbf{D}}} + {\mathbf{P}}_{{\text{A}}} \otimes \left( {{\mathbf{D}}_{2} - {\mathbf{D}}_{1} } \right) \\ & = {\mathbf{Q}}_{switch} \oplus {\mathbf{D}}_{1} + {\mathbf{P}}_{{\text{A}}} \otimes \left( {{\mathbf{D}}_{2} - {\mathbf{D}}_{1} } \right) \\ \end{aligned}$$

(11)

where, the term ${\mathbf{P}}_{\mathrm{T}}\otimes {\mathbf{D}}_{1}+{\mathbf{Q}}_{switch}\otimes {\mathbf{I}}_{{\mathbf{D}}_{1}}$ calculates the possible transitions of the integrated phases of the components while the switch is functioning, ${\mathbf{I}}_{{\mathbf{D}}_{1}}$ is an identity matrix of size sub-TRM ${\mathbf{D}}_{1}$, and the sub-TRM for describing the mechanism in Situation 2 is expressed by ${\mathbf{P}}_{\mathrm{A}}\otimes {\mathbf{D}}_{2}$. Furthermore, the initial probability vector for subsystem i is indicated by ${{\varvec{\pi}}}_{i}^{T}=[{{\varvec{\pi}}}_{1},{{\varvec{\pi}}}_{2}]$. It was assumed in this model that subsystem i never starts with a failed switching system; therefore, ${{\varvec{\pi}}}_{2}=0$ and, consequently, ${{\varvec{\pi}}}_{i}^{T}=[{{\varvec{\pi}}}_{1},0]$. As a result, Eq. (6) would seem to imply that the subsystem’s reliability, ${R}_{i}(t)$, for a mixed redundancy strategy with a heterogeneous backup scheme may be determined using Eq. (12):

$$R_{i} \left( t \right) = {\varvec{\pi}}_{i}^{T} {\text{expm}}\left( {{\mathbf{D}}_{i}^{T} .t} \right)\vec{1},\quad for\;t \ge 0$$

(12)

3.4 Fundamental assumptions

It is assumed in this study that the system is of the 1-out-of-n:G type in which at least one operating component is needed in each subsystem to discharge the mission successfully. It is further assumed that each subsystem involves n parallel components with ${n}_{A}$ active and ${n}_{S}$ cold-standby units, where $n={n}_{A}+{n}_{S}$. The active components start operation at time zero, while the cold-standby ones come into operation sequentially by an imperfect switching mechanism.

In addition, the following assumptions are made in the analysis of the problem:

• (i) The components have TTFs that are independently distributed.

• (ii) Mission time is predetermined and cannot be changed during the mission.

• (iii) The sequence of components is fixed.

• (iv) An imperfect switching system of the first type (T1) is considered with exponentially distributed TTFs.

• (v) The switching and restoration times of components are negligible.

• (vi) The possibility of using non-identical components in each subsystem is available.

• (vii) The switching system and components are non-repairable.

4 Solution method: non-dominated sorting genetic algorithm II (NSGA-II)

Rooted in biological genetics, Genetic Algorithm (GA), as one of the most well-known evolutionary algorithms, was first introduced by Holland (1975). Combining an elitist archive and the rules for adaptation assignment transformed the fast non-dominated sorting genetic algorithm (NSGA-II) into an effective multi-objective evolutionary algorithm (Deb et al. 2002) that was chosen as one of the most practical solution methods for solving reliability problems (dos Santos Coelho, 2009; Konak et al. 2006; Salazar et al. 2006). Herein, the proposed NP-hard problem is also solved using NSGA-II.

Using a fast non-dominated sorting procedure, the algorithm assigns ranks to individuals in a population of size N. This ranking method attaches special importance to the good individual as an attempt to generate a multitude of such solutions. Diversity in NSGA-II is provided throughout the crowding distance designated by points of the same rank. The value of this index is directly related to the crowd in the solution space. Therefore, the point with the highest crowding distance is selected from among a group of those with the same rank and using the index, thus, avoids the focus on limited regions of the search space. NSGA-II is clearly a convenient meta-heuristic method for obtaining Pareto optimal sets (Chambari et al., 2012; Safari, 2012). The related pseudo code and flowchart are represented in Figs. 6 and 7, respectively.

Fig. 6

NSGA-II procedure

Fig. 7

NSGA-II flowchart

Fig. 8

Encoded representation of a chromosome

• 1. Design the chromosome. In order to decrease the CPU time, the size of the chromosome is compacted to a matrix of size $Max\left({n}_{i}\right)\times S$, in which $Max({n}_{i})$ represents the maximum allowable redundancy level for all the subsystems and $S$ is the total number of subsystems. Each column of the matrix represents a subsystem, and the value of the element in each column indicates the component type in that subsystem. It must be mentioned that the proper values for ${n}_{A}$ and ${n}_{S}$ in each subsystem are optimally determined by the proposed algorithm rummages through the available combinations in search of the best choice among them. The matrix elements are coded numbers representing the component choices from Table 7. Clearly, the element 0 in a chromosome means no components are selected. Figure 8 shows the chromosome structure of the system represented in Fig. 1, where $Max\left({n}_{i}\right)=4$ and $S=14$..

In order to shrink the solution space of the proposed model, the size of the chromosome was reduced. This reduction is made by removing the decision variable of redundancy strategy from the chromosome. By doing so, the possible redundancy strategies are identified based on other remained variables (i.e., type of the component, and the total number of components in each subsystem), and the reliabilities of all possible redundancy strategies are calculated and compared. For instance, consider the fourth subsystem in Fig. 8, where four components with the sequence of {1,4,1,4} are selected. Consequently, four different redundancy strategies can be fitted to this subsystem as Ac, St, M1, and M2 strategies. The subsystem reliabilities under all four different redundancy strategies are calculated and then the best one is selected. This procedure of comparison is implemented in the objective function of NSGA-II algorithms.

As shown in Fig. 8, the first subsystem ($i=1$) consists of three parallel components including one of type 2 and two of type 3 ordered in the sequence 2, 3, 3. The element 0 in the last entry means that no components are chosen. Hence, decoding the component types according to Table 7 yields the reliability sequence [0.93, 0.91, and 0.91] for this subsystem. Finally, the algorithm chooses the best redundancy strategy with the highest reliability value considering these three components and their sequence. For example, Fig. 1 shows that the algorithm chooses the mixed strategy for the first subsystem with ${n}_{A1}=2,$ and ${n}_{S1}=1$, or consider the fourth subsystem where a cold-standby strategy with ${n}_{A4}=1$, and ${n}_{S4}=3$ and a sequence of 1–4-1–4 is selected.

• 2. Generate ${N}_{start}$ chromosomes randomly as the initial population.

• 3. Evaluate the fitness function (ff) of the population. The ff is defined as the summation of the objective functions and a dynamic penalty function expressed as the associated infeasibility. Consequently, by performing an infeasible solution, a penalty value is applied to both objective functions. Effecting penalty values in ff reduces the probability for infeasible solutions selected in the remaining algorithm processes, while the feasibility of the final solution is guaranteed. For optimizing the considered problem, two objective functions as maximizing the system reliability, and minimizing the system cost are considered. Also, two constraints as cost and weight limitations are granted in this mathematical model. All regarded equations of the considered problem will be expressed further in Sect. 5.2. Equation (13) describes the penalty function. A penalty coefficient is applied to the amount of infeasibility and considered in the objective function in case of constraint violation. For example, the following relations are derived for cost and weight penalties, respectively:

  $$\begin{aligned} cost\;penalty & = \alpha \times \max \left( {0,system \;cost - maximum \;budget} \right) \\ weight \;penalty & = \beta \times {\text{max}}\left( {0,system\; weight - maximum\; allowable\; weight} \right) \\ ff & = 1 - Total\; Reliability + penalty \;for\; the\; violation \;of\; cost\; limitation \\ & \quad + penalty \;for \;the\; violation\; of\;weight\; limitation \\ \end{aligned}$$

  (13)

• 4. Select the candidate chromosomes for mutation and crossover operations. In this algorithm, the tournament procedure, which involves running several tournaments among the chromosomes, is performed on the population to select the candidate chromosomes. Further information can be found in Ref. (Ardakan & Hamadani, 2014).

• 5. Apply the crossover procedure by selecting two chromosomes as parents to produce new ones as offspring. This procedure allows for the inheritance of some basic features of the parent strings by the offspring. Each iteration of the crossover procedure leads to the selection of two parents to generate four offspring. The two premium chromosomes out of the six now available will be moved to the next step (i.e., mutation procedure). The proposed NSGA-II uses two crossover operators identified as the uniform and the max–min functions. In the max–min crossover, a rank-based selection scheme is adopted on parents’ chromosomes to mark the best and the worst subsystems according to their reliability values and all the genes thus marked are exchanged with the same genes in the other parent. This type of crossover operator is presented in Fig. 9. Further information on this operation may be obtained from Refs. (Ardakan & Hamadani, 2014; Gholinezhad & Hamadani, 2017).

• 6. Apply the mutation procedure to one chromosome selected; this procedure results in the slightest changes in the chromosome structure while maintaining solution diversity. The procedure is meant to avoid premature convergence to a local optimum but to facilitate irregular jumps in the solution space. In this version of NSGA-II, the three simple, max–min, and sort functions are utilized as the mutation procedures. Throughout the max–min mutation, the best and the worst subsystems in terms of reliability value are changed randomly (Fig. 10). The sort mutation then sorts all the components in each subsystem in decreasing order of reliability values such that the most reliable component of subsystem i is located in the first position of the arrangement, and so on. Figure 11 details this function by assuming a direct relationship between component reliability and its index.

• 7. Apply the selection procedure that compares the new offspring with the current population, selects the superior one, and discards the remaining. The selected population is transferred to the next iteration.

• 8. Return to step 4 to start a new iteration.

• 9. Stop the algorithm after running $Ma{x}_{iter}$ iterations.

Fig. 9

Max–min crossover operator

Fig. 10

Max–min mutation operator

Fig. 11

Sort mutation operator

5 Numerical experiments

In this section, two numerical examples are presented to illustrate the proposed contributions. The first example addresses the idea of optimal sequencing of components in a bi-objective problem and explains the application of the proposed CTMC method to sequence optimization. The second numerical example, which is a well-known benchmark problem, focuses on developing an improved Pareto optimal set by applying the modified NSGA-II.

5.1 Sequence optimization

The heterogeneous components allowed in a parallel subsystem instigate the idea of optimal component sequencing. In the recent numerical example, all the combinations of four components in a parallel subsystem are analyzed to determine the impacts of component sequencing on both subsystem reliability and total purchasing cost. This yields the set of five components with different reliabilities and different purchasing costs as reported in Table 3. The objective functions of the problem try to minimize the subsystem cost and to maximize its reliability, taking into account a cost limitation of 130 units. Moreover, four components at most are allowed to be allocated to the subsystem. Table 4 reports the five different component choices with their corresponding purchasing costs.

Table 3 Input data of the first numerical example

Table 4 Details of component choices

According to Table 4, just two out of the five choices (i.e., choices 2 and 3) are considered as feasible sets due to the assumed limitation on cost. In other words, there are two feasible sets for allocation to this subsystem. In this situation, the sequence with the maximum reliability should be defined for both feasible sets by trying all the possible combinations of the orders. Considering a mission time of 100 time units and an imperfect switching system with a reliability of ${\rho }_{i}\left(100\right)=0.99$, one obtains subsystem reliability values, ${R}_{s}$, for all the available component orders of sets 2 and 3 reported in Tables 5 and 6, respectively. The first two components in each sequence, marked in bold typeface in these Tables, represent active units while the rest are cold-standby ones. According to Table 5, the ${R}_{s}$ values for the first feasible set vary from 0.997235 to 0.998041 while those for the second feasible set, and also reported in and Table 6, vary from 0.997993 to 0.999036 under the mixed redundancy strategy. The results obtained clearly provide an insight into the impact of component ordering on reliability. Furthermore, it is seen that the ${R}_{s}$ values for the first and second feasible sets will be equal to 0.988 and 0.994 when using an active strategy; hence, the superiority of the mixed strategy over the active one with respect to the reliability values gained.

Table 5 System reliability for set #2

Table 6 System reliability for set #3

It may be noted in Tables 5 and 6 that it is only the order of the standby components that affects subsystem reliability value while that of active ones has no effect. As an example, ${R}_{s}$ remains unaffected when the order of active components in the sequence 2,3,4,5 is changed to 3,2,4,5, whereas ${R}_{s}$ value changes as a result of changing the order of the cold-standby components from 2,3,4,5 to 2,3,5,4. The reason that might be claimed for this is that the switching system activates the first cold-standby component after all the online ones fail. In other words, the switching system activates the first cold-standby component when all the active ones have reached their maximum lifetimes regardless of their sequence.

Another point worth noting in Tables 5 and 6 is that the maximum ${R}_{s}$ values recorded for the first and second feasible sets are equal to 0.998041 and 0.999036 and that the corresponding sums of purchasing costs are 110 and 120, respectively. This allows the system designer to choose his preferred sequence for either maximizing system reliability or minimizing system cost. Figure 12 illustrates the Pareto optimal set of this numerical example. The most remarkable result to emerge from the example is that considering the problem in a bi-objective mode is crucial for system designers since what they find as the best system structure will not be achieved unless a tradeoff is made between the priorities assigned to system reliability and system cost.

Fig. 12

The Pareto optimal set of the first numerical example

From the viewpoint of system reliability, attaining the maximum possible value for ${R}_{s}$ in the presence of an imperfect switching mechanism presupposes a method to sort the components in a decreasing order of their reliability values. For example, the maximum possible value of ${R}_{s}$ reported in Table 6 is obtained when the components are sorted as in the sequences 1,3,4,5 and 3,1,4,5. These results support the rules previously reported by Kim (2018) and Levitin et al. (2013b).

5.2 Benchmark problem

In order to confirm the superiority of the proposed heterogeneous backup scheme in the mixed redundancy strategy over the previously studied MORAP, a popular test problem is considered that was originally introduced by Fyffe et al. (1968) and widely studied elsewhere (Chambari et al., 2012; COIT, 2001, 2003; Safari, 2012; Tavakkoli-Moghaddam et al. 2008). This test problem contains a series–parallel system with 14 subsystems. The input data for the components of each subsystem such as cost, weight, and reliability are reported in Table 7. In this table, the characteristics of component $j$ in subsystem $i$ such as reliability (${r}_{ij}$), cost (${c}_{ij}$) and weight (${w}_{ij}$) are reported. For example, there are three component choices available for the second subsystem. It means, just these mentioned components with the specified characteristics can be allocated to the second subsystem. Furthermore, it is assumed that unlimited supply of each component are available and the limitations are on the cost and weight of the system.

Table 7 Input data of the benchmark problem

The problem also has the two objective functions of maximizing system reliability and minimizing system cost subject to constraints on system weight (W ≤ 170) and system cost (C ≤ 130). Furthermore, an imperfect switching mechanism with a reliability of 0.99 at 100 time units is considered for each subsystem, which permanently monitors system performance in order to remove failed components and replace them with new ones (T1). It is finally assumed that six components can at most be allocated to each subsystem (${n}_{Max,i}=6$). Based on the assumptions made in Subsection (3.4), the mathematical model for this MORAP will be as follows:

$${\text{Max}}\,R_{S} (t,seq) = \prod\limits_{i = 1}^{S} {R_{i} (t,seq_{i} )}$$

(14)

$$\min \,C_{S} (seq) = \sum\limits_{i = 1}^{S} {{\text{cost}}(seq_{i} )}$$

(15)

$$\begin{aligned} & {\text{Subject to:}} \\ & \sum\limits_{i = 1}^{S} {{\text{cost}}(seq_{i} ) \le C} \\ \end{aligned}$$

(16)

$$\sum\limits_{i = 1}^{S} {{\text{weight}}(seq_{i} ) \le W}$$

(17)

$$\begin{array}{*{20}l} {{\text{card}}(O_{{A_{i} }} ) \ge 1} \hfill & {i = 1,...,S} \hfill \\ {seq_{i} = \{ O_{{A_{i} }} ,O_{{S_{i} }} \} \;{\text{set}}\,{\text{of}}\,{\text{integer}}\,{\text{numbers}},} \hfill & {i = 1,...,S} \hfill \\ \end{array}$$

(18)

Equation (14) as the first objective function of the model is meant to improve system reliability by maximizing it and the exact reliability of each subsystem is calculated using Eq. (12). The second objective function, Eq. (15), aims to minimize system cost considering the two practical cost and weight constraints the maximum values for which are calculated from Eqs. (16) and (17), respectively. The size of the set is measured by the function card(.); Eq. (18), therefore, guarantees that at least one active component is allocated to each subsystem. Finally, the arrangement of the components in subsystem i is denoted by $se{q}_{i}$, which includes the orders of both active, ${O}_{{A}_{i}}$, and cold-standby, ${O}_{{S}_{i}}$, components.

A considerable progress has been made by various researchers regarding the different structures that can be obtained for this series–parallel problem. The first study on RAP solved a version of this problem with an active redundancy and achieved a system reliability of 0.9700 (Fyffe et al., 1968). Also, its solution with a cold-standby strategy yielded a system reliability of 0.9863 (COIT 2001). It was suggested in (Coit, 2003) that the choice of the redundancy strategy be treated as a decision variable, a suggestion that proved useful since its implementation raised system reliability to 0.9875. Many attempts have been made toward improving system reliability of RAPs in the single objective mode via modifying the meta-heuristic algorithms available, yielding system reliability values as high as 0.9875 (Chambari et al., 2012, 2013; Coit, 2003; Safari, 2012; Tavakkoli-Moghaddam et al., 2008). In a recent study of the problem in its bi-objective mode, Ardakan et al. (2015) investigated the RAP with identical components under a mixed redundancy strategy to obtain a system reliability of 0.99233.

Based on try and error procedure, the algorithm parameters were in this study set to ${N}_{start}=500$, $Ma{x}_{Iter}=300$, $Mutation rate=0.2$, and $Crossover rate=0.25$. As mentioned in Sect. 4, in this study, the uniform and max–min operators are used in crossover process, and the simple, max–min, and newly developed sort operators are implemented for mutation process. In uniform crossover operator, %80 genes of selected subsystem are nominated to perform the function. This amount in simple and max–min mutation operators for each selected subsystem is %30. Regarding the stochastic nature of the proposed NSGA-II, four trials were performed on each problem to ensure the standard deviation was negligible and that a good Pareto front would be reported. Figure 13 illustrates these four independent runs and provides the details of the randomly generated initial population and the ultimate population as a Pareto front provided by the modified NSGA-II for each independent run. It may be noted that the different initial populations lead to almost the same Pareto fronts. This phenomenon is the graphical representation of the capability and robustness of the modified NSGA-II for solving the proposed RAP. Run #4 is randomly selected among the four runs and the progress changes in the Pareto front as a result of the iterations for this run are depicted in Fig. 14. Table 8 lists some of the data on Run #4.

Fig. 13

Four independent runs of the modified NSGA-II for solving the benchmark problem

Fig. 14

Progress changes in Pareto front for different iterations in Run #4

Table 8 The top five non-dominated solutions of Run #4 with the highest reliability values

To save space, only five detailed structures out of the forty-five Pareto optimal set alternatives are reported in Table 8. In this table, the sequence order and preferred strategy of each subsystem is reported, where St, M1 and M2 stand for cold-standby, and Mixed strategy with one and two standby components, respectively. The structure of each solution is based on input data reported by Table 7. Discovering the component reliability is same as chromosome decoding, which explained earlier in Sect. 4. The structures in Table 8 might yield improved flexibility in the system design process because a specific system with desirable levels of reliability and cost is created in each case. Since these alternatives are non-dominated populations, the designer is free to choose the ideal solution from among them based on the reliability improvement or cost reduction achieved. For instance, if the designer selects the first solution, a system with a cost of 112 units and a reliability of 0.984636 obtains, whereas choosing the third option leads to a system with a cost decreased to 110 units and a system reliability equal to 0.983881. Moreover, in the benchmark problem it is assumed that a subsystem can be designed with any combination of components. The 4th subsystem of the structure #4 in Table 8 reveals this situation. According to Table 7, there are three component choices as {1,2,3} for this specific subsystem. Also, based on benchmark’s assumption, i.e. ${n}_{Max,i}=6$, there are ${3}^{6}$ different combinations for this subsystem. After applying the proposed NSGA-II, the sequence {3,3,1} has been selected among all the potential choices. So, in this subsystem, a combination of homogeneous and heterogeneous components is utilized. Hence, the proposed method of combination, makes the system designer more flexible to opt the desired structure.

There is indeed no guarantee that a better solution is obtained using the multi-objective optimization method rather than the single-objective one. However, the structures obtained in this study were found to outperform those obtained even in previous instances of the single-objective problem, this may be attributed to the two contributions of the new approach: I) using a new redundancy strategy with a heterogeneous backup scheme, and II) taking account of component sequencing. It is worthwhile noting that some of the results reported in recent publications had been obtained based on the lower bound formula with non-exponential components (Ardakan et al., 2015; Coit, 2003; Fyffe et al., 1968; Safari, 2012; Tavakkoli-Moghaddam et al., 2008). In order to make a fair comparison between the results of the present study and those reported in other premium studies, all the reported structures were recalculated using the proposed exact CTMC method (i.e., Eq. 12) with an exponential TTF (Kim & Kim, 2017b). Run #4 yielded three solutions out of the 45 non-dominated populations that led to system reliabilities better than the value of 0.98382 reported in Ardakan et al. (2015). The Pareto optimal set thus obtained is presented in Fig. 15. Comparison of the present results with those previously reported (Fig. 15) confirms not only the superiority of the newly proposed redundancy strategy with non-identical components but the utility of the modified solution algorithm as well.

Fig. 15

A graphical comparison of non-dominated solutions obtained in Run #4 versus reported in the literature

In multi-objective problems, the decision maker (DM) has to select a particular solution as the final one from among those in the Pareto optimal set. A number of methods have been developed to help DMs find their most desirable solution. In this paper, the L₂-norm criteria (Ardakan et al., 2015; Kasprzak & Lewis, 2000; Safari, 2012) and the minimum distance selection method (TMDSM) (Dammak & El Hami, 2019; Sun et al., 2011) were used to select the most satisfactory point and to illustrate the good performance of the modified algorithm toward diversifying the Pareto optimal set when compared with those reported in similar works (Ardakan et al., 2015; Kasprzak & Lewis, 2000; Safari, 2012).

In order to apply the L₂-norm criteria, all the objective functions have to be in their minimizing mode. Hence, the objective of maximizing system reliability needs to be changed into minimizing system unreliability. Run #4 yields the 45 non-dominated solutions reported in Table 9 along with their corresponding L₂ norms. It seems almost all the DM has to do is to look for the solution with the minimum L₂ value and select it as the best alternative. Accordingly, the L₂ norm of the best solution in Run #4 from the DM’s viewpoint is solution No. 35, for which L₂ = 0.28898 that is smaller than those reported elsewhere as in (Ardakan et al., 2015; Safari, 2012).

Table 9 Non-dominated solutions in Run #4 together with the corresponding L₂ norms

Another conventional approach to find the most satisfactory point (termed the “knee point”) is the TMDSM that measures the distance from each solution point to an “utopia point” obtained based on the optimal values of each individual objective. The method then selects the minimum distance among them and, finally, converts the maximizing reliability objective function to one of minimizing unreliability in order to be consistence with the results reported in similar studies. A schematic view of this method is shown in Fig. 16.

Fig. 16

The knee point on the Pareto optimal set

The knee point thus obtained, corresponding to the 35^th solution in Table 9, has the shortest distance to the utopia point and presents a tradeoff among the competing cost and reliability objectives.

A Pearson correlation coefficient (PCC) significance test was conducted to confirm statistically the tradeoff between the objective function values of the Pareto frontier points. PCC measures the strengths of the linear correlation (i.e., ${\rho }_{X,Y}$) between two given variables, X and Y, here denoted by cost and reliability, respectively. For the points reported in Table 9, the PCC was obtained as ${\rho }_{X,Y}=0.7684$. A hypothesis test checks the significance of the correlation obtained, in which the null and the alternative hypotheses are determined as follows:

$$\left\{\begin{array}{c}{{\mathrm{H}}_{0}{:}\; \rho }_{X,Y}=0\\ {{\mathrm{H}}_{a}{:}\; \rho }_{X,Y}\ne 0\end{array}\right.$$

The probability value is P_value = 0.000. By assuming the 5% level of significance, the ${\rho }_{X,Y}$ obtained is significant since the P_value is smaller than the significance level; hence, the null hypothesis is rejected.

Based on the result obtained from the hypothesis test, a system designer can consider a tradeoff between reliability and cost values. As an instance, comparison of the knee point and the first point in Table 9 reveals that the cost increases by 43.6% (from 78 to 112) in response to a 3.2% enhancement in reliability value (from 0.9544 to 0.9846).

Table 10 compares the solution with the maximum system reliability obtained in Run #4 and those reported elsewhere. The results in this Table highlight the advantages of both the mixed redundancy strategy with a heterogeneous backup scheme and the component sequencing. According to Table 10, the best solution for this benchmark problem is a system with a reliability of 0.984636 (obtained in the present study).

Table 10 Comparisons of the present study and those reported in the literature

Regarding the redundancy type of each subsystem, the model selected the mixed redundancy strategy for six subsystems and the cold-standby strategy for the other eight. It may be noted that subsystems 7 and 13 utilized heterogeneous components. Moreover, each of these two subsystems had one primary and one offline component, which means that the cold-standby and the mixed strategies behaved similarly for these two subsystems. Furthermore, the components in these subsystems were arranged in a decreasing order of component reliability. This is while a substantial reduction in cost was also achieved in this case when compared with that in the premium study (Ardakan et al., 2015). As expected, considering orders of non-identical components in the mixed strategy led to higher reliability values and lower system costs, which is of vital importance to high-tech system designers (Zio, 2007).

6 Conclusion

The mixed redundancy strategy with a heterogeneous backup scheme was investigated for the multi-objective redundancy allocation problem (MORAP). Two objective functions of maximizing system reliability and minimizing system cost were considered for the problem. Maximizing system reliability was modeled using the continuous-time Markov chain (CTMC) method that is sensitive to the sequencing of components. In addition, the exact value of system reliability in the mixed strategy was calculated using the CTMC method. The proposed non-linear integer programming mathematical model was tested on a well-known benchmark problem. A modified version of the NSGA-II meta-heuristic algorithm was employed as the solution for the problem at hand categorized with the NP-hard class of reliability optimization problems. The numerical results obtained revealed the advantages of utilizing heterogeneous components for improving the overall system reliability. In addition, the findings of the present study lent support to the idea of considering the sequencing of standby components in a mixed strategy to enhance the reliability of each subsystem. The final Pareto optimal set was found to suggest several courses of action to help designing complex high-tech industrial machines with structures of various levels of system reliability and system costs.

To further our research, one can apply the CTMC method to components with non-exponential TTFs. The suggested problem would become more challenging if non-identical components with an Erlang TTF are used in each subsystem. Finally, the effect of time dependent reliability in the mixed strategy will worth exploring when the CTMC method is employed, as was first explored in Ref. (Abouei Ardakan et al., 2017).