1 Introduction

Crashworthiness is of primary interest in automotive industry to ensure structural integrity of vehicle and more importantly the safety of occupant in the event of the crash (Kurtaran et al. 2002). Over the past two decades, finite element analysis (FEA) based optimization has been developed as an effective tool to seek a best possible crashworthiness design for a full vehicle or components (Avalle et al. 2002; Duddeck 2008; Fang et al. 2005; Forsberg and Nilsson 2006; Gu et al. 2001; Hou et al. 2008; Jansson et al. 2003; Liao et al. 2008a, b; Marklund and Nilsson 2001; Redhe et al. 2002). Since impact modeling involves highly nonlinear mechanics, a sensitivity analysis may be rather challenging. Thus, such surrogate techniques as response surface method (RSM) and its variation (Kurtaran et al. 2002; Liao et al. 2008a, b) have been exhaustively adopted in this respect (Yang et al. 2005a).

To date, substantial studies on crashworthiness design have been focused on deterministic optimization, in which all the design variables and parameters involved are assumed to be certain and there is no variability in the simulation outputs. However, most real-life engineering problems involve some degree of uncertainty in loading conditions, material properties, geometries, manufacturing precision and actual usage, etc. It must be noted that usually a deterministic optimization tends to push a design toward one or more constraints until the constraints become active, thereby leaving very little or no room for tolerances in modeling, uncertainties, and/or manufacturing imperfections. In addition, optimization algorithms search for a “peak” solution, where even subtle perturbation in design variables and parameters can result in substantial loss of performance, making an “optimum” less meaningful or even misleading. Consequently, deterministic optimal design obtained without consideration of those uncertainties could lead to unreliable design.

To take into account various uncertainties, a number of non-deterministic methods have been developed over the last two decades, which can be classified into probability based design optimization (PBDO) and non-probability based design optimization (NPBDO). The reliability-based design and robust based design are two typical PBDO methods (Zang et al. 2005). The former estimates the probability distribution of the system in terms of known probability distributions of the stochastic parameters, and is predominantly used for risk analysis by computing the failure probability of a system (Doltsinis and Kang 2004; Doltsinis et al. 2005; Siddall 1984; Zang et al. 2005). The latter improves the quality of a product by minimizing the effect of variations on system responses. Unlike the reliability design, the robust design optimizes the mean performance and minimize its variation, while satisfying given probabilistic constraints (Zang et al. 2005).

There has been some published work available about PBDO for vehicle crashworthiness optimization. For example, Yang, Gu and their co-workers (Gu et al. 2001; Koch et al. 2004; Yang et al. 2000; Youn et al. 2004) proposed a reliability-based design and six sigma-based robust optimization for vehicle side impact. Youn et al. (2004) developed a reliability-based optimization by integrating the hybrid mean value approach with RSM to improve side impact crashworthiness of vehicle.

NPBDO is mainly based on Taguchi philosophy, which incorporates the mean and variability in the design so that variation and mean of performance can be optimized (Kovach et al. 2008). Often, a dual response surface approach is adopted to model these two quantities in an optimization framework (Sun et al. 2010a; Vining and Myers 1990; Youn and Choi 2004) as:

$$ \left\{ {{\begin{array}{ll} {\min} \hfill & {\tilde {y}_\sigma } \hfill \\ {s.t.} \hfill & {\tilde {y}_\mu =T} \hfill \\ \end{array} }} \right. $$
(1)

where \(\tilde {y}_\mu\) denotes the mean response, \(\tilde {y}_\sigma\) is its standard deviation (SD), T is the constraint of mean value. To avoid the zero-bias presented in the mean constraint, Lin and Tu (1995) proposed a mean square error (MSE) approach as:

$$ \min \,\,\,\emph{MSE}=\tilde {y}_\sigma ^2 +\left( {\tilde {y}_\mu -T} \right)^2 $$
(2)

which allows a certain bias, and the resulted process variance would be less than or, at most, equal to the variance in Eq. 1, thereby achieving a better (or at least equal) result.

Most existing robust design problems have concerned with single objective optimization. While real-life engineering problems are typically characterized by a number of quality and/or performance indices, some of which could be conflicting with each other. To address such a multiobjective robust optimization problem, some attempts have been made. For instance, Koksoy et al. (Koksoy 2006; Koksoy and Yalcinoz 2006) adopted the mean square error criterion for optimizing several different objectives. Gunawan and Azarm (2005) presented a multiobjective robust method for measuring multiple sensitivities of design variation and then use such measure to obtain a set of robust Pareto solutions. Kovach et al. (2008) proposed a physical programming model for experiment-based multiobjective robust design by linking RSM to a multi-response robust design problem. Yang et al. (Yang and Chou 2005; Yang et al. 2005b) solved a multi-response robust problem by constructing proper dual response surfaces firstly, then transforming the dual-response problem into a standard non-linear programming formulation, and finally obtaining a robust design by using a so-called scatter-search method. Kapur and Cho (1996) also developed a multi-response technique by minimizing the deviation from the target and maximizing the robustness to noise. Shimoyama et al. (2005) developed a multiobjective design for a design problem of welded beams. Kim and Lin (1998) adopted the dual RS model for mathematical programming formulation in the fuzzy optimization with a goal to maximize the lowest degree of satisfaction.

However, there have been few reports available regarding multiobjective robust crashworthiness for vehicle design studies despite their practical value. This paper aims to tackle this problem by exploring how uncertainties, different sigma criteria and different emphases on mean and deviation components affect the Pareto optimum.

2 Surrogate model for robust design

A conventional RSM has focused on the mean value of response Y without considering variance. However, only constructing mean response model may not be adequate and an optimization could become even meaningless (Yeniay et al. 2006). While DRSM allows constructing two models: one for the mean (μ) and another for the standard deviation (σ), as:

$$ \left\{ {{\begin{array}{l} y_\mu =\tilde {y}_\mu +\varepsilon _u =\sum\limits_{\emph{v}=1}^V {b_{\emph{v}} \phi _{\emph{v}}} ({\rm {\bf x}})+\varepsilon _\mu \\ y_\sigma =\tilde {y}_\sigma +\varepsilon _\sigma =\sum\limits_{\emph{w}}^W {c_{\emph{w}} \psi _{\emph{w}} } ({\rm {\bf x}})+\varepsilon _\sigma \\ \end{array} }} \right. $$
(3)

where y μ and y σ denotes, respectively, the mean and standard deviation of the true responses from FEA, \(\tilde{y}_\mu\) and \(\tilde{y}_\sigma\) the RS models for the mean and standard deviation, ε μ and ε σ the modeling errors, \({\bf x} = [x_{1}, x_{1},{\ldots}x_{n}]^{\rm T}\) denotes the design variables, \(b_{\emph{v}}(\emph{v} = 1,{\ldots},V)\) is the \(\emph{v}^{\rm th}\) unknown coefficient corresponding to the \(\emph{v}^{\rm th}\) basis function \(\varphi_{\emph{v}}\) (x), \(c_{\emph{w}}(\emph{w} = 1,{\ldots},W)\) is the \(\emph{w}^{\rm th}\) unknown coefficient corresponding to the \(\emph{w}^{\rm th}\) basis function \(\psi_{\emph{w}}\) (x). In theory, the basis function can be in any form. In most cases, the polynomial functions have proven fairly effective for both the mean and standard deviation responses. For example, a quadratic polynomial dual RS model can be given as,

$$ \left\{ {{\begin{array}{l} \tilde {y}_\mu =b_0 +\sum\limits_{e=1}^n {b_e} x_e +\sum\limits_{e=1}^n {b_{ee} x_{ee}^2 } +\sum\limits_{e<f}^n {b_{ef} x_e x_f } +\varepsilon _\mu \\ \tilde {y}_\sigma =c_0 +\sum\limits_{e=1}^n {c_e } x_e +\sum\limits_{e=1}^n {c_{ee} x_{ee}^2 } +\sum\limits_{e<f}^n {c_{ef} x_e x_f } +\varepsilon _\sigma \\ \end{array} }} \right. $$
(4)

where the unknown coefficients b and c can be determined by means of the least square method. Specifically, If the FEA results \({\rm {\bf y}}_\mu =\big[{y_\mu ^{(1)} ,y_\mu ^{(2)} ,\cdots ,y_\mu ^{(P)}}\big]^{\rm T}\) and \({\rm {\bf y}}_\sigma =\big[{y_\sigma ^{(1)} ,y_\sigma ^{(2)} ,\cdots ,y_\sigma ^{(P)}}\big]^{\rm T}\) are obtained at m selected sample design points (m ≥ V and m ≥ W), the total squared errors between the analysis and dual RS model are computed as:

$$ \left\{ {{\begin{array}{l} E_\mu ({\rm {\bf b}})=\sum\limits_{i=1}^m {\varepsilon _{\mu _i }^2 =\sum\limits_{i=1}^m {\left[ {y_\mu ^{(i)} -\sum\limits_{v=1}^V {b_{\emph{v}} \phi _{\emph{v}} ({\rm {\bf x}}_i )} } \right]^2} } \\ E_\sigma ({\rm {\bf c}})=\sum\limits_{i=1}^m {\varepsilon _{\sigma _i }^2 =\sum\limits_{i=1}^m {\left[ {y_\sigma ^{(i)} -\sum\limits_{w=1}^W {c_{\emph{w}} \psi _{\emph{w}} ({\rm {\bf x}}_i )} } \right]^2}} \\ \end{array} }} \right. $$
(5)

or in the matrix forms as:

$$ \left\{ {{\begin{array}{l} E_\mu ({\rm {\bf b}})={\boldsymbol\varepsilon} _\mu ^T {\boldsymbol\varepsilon} _\mu =\left( {{\rm {\bf y}}_\mu -{\rm {\boldsymbol \upvarphi }}_\mu {\rm {\bf b}}} \right)^{\rm T}\left( {{\rm {\bf y}}_\mu -{\rm {\boldsymbol \upvarphi }}_\mu {\rm {\bf b}}} \right) \\ E_\sigma ({\rm {\bf c}})={\boldsymbol\varepsilon} _\sigma ^T {\boldsymbol\varepsilon} _\sigma =\left( {{\rm {\bf y}}_\sigma -{\boldsymbol\Psi} _\sigma {\rm {\bf c}}} \right)^{\rm T}\left( {{\rm {\bf y}}_\sigma -{\boldsymbol\Psi} _\sigma {\rm {\bf c}}} \right) \\ \end{array} }} \right. $$
(6)

where \({\boldsymbol\upvarphi}_{\mu}\) and \({\boldsymbol\Psi}_{\sigma}\) are the matrices consisting of basis functions evaluated at these selected design points, respectively, as:

$$\begin{array}{rll} {\rm {\boldsymbol\upvarphi }}_\mu &=&\left[\!\! {{\begin{array}{ccc} {\phi _1 ({\rm {\bf x}}_1 )} \hfill & \cdots \hfill & {\phi _V ({\rm {\bf x}}_1 )} \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\phi _1 ({\rm {\bf x}}_m )} \hfill & \cdots \hfill & {\phi _V ({\rm {\bf x}}_m )} \hfill \\ \end{array} }} \!\!\right],\notag \\ {\boldsymbol\Psi} _\sigma &=&\left[\!\! {{\begin{array}{*{20}c} {\psi _1 ({\rm {\bf x}}_1 )} \hfill & \cdots \hfill & {\psi _W ({\rm {\bf x}}_1 )} \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\psi _1 ({\rm {\bf x}}_m )} \hfill & \cdots \hfill & {\psi _W ({\rm {\bf x}}_m )} \hfill \\ \end{array} }} \!\!\right]\end{array}$$
(7)

By minimizing E μ (b) and E σ (c) in Eq. 6,

$$ \left\{ {{\begin{array}{@{}l} \displaystyle \frac{\partial E_\mu ({\rm {\bf b}})}{\partial {\rm {\bf b}}}=-2{\rm {\boldsymbol \upvarphi }}_\mu ^{\rm T} {\rm {\bf y}}_\mu +2{\rm {\boldsymbol\upvarphi }}_\mu ^{\rm T} {\rm {\bf b}}=0 \\[10pt] \displaystyle \frac{\partial E_\sigma ({\rm {\bf c}})}{\partial {\rm {\bf c}}}=-2{\boldsymbol\Psi} _\sigma ^{\rm T} {\rm {\bf y}}_\sigma +2{\boldsymbol\Psi} _\sigma ^{\rm T} {\rm {\bf c}}=0 \\ \end{array} }} \right. $$
(8)

the coefficient vectors of the dual RS model are obtained as,

$$ \left\{ {{\begin{array}{@{}l} {\rm {\bf b}}=({\rm {\boldsymbol\upvarphi }}_\mu ^{\rm T} {\rm {\boldsymbol\upvarphi }}_\mu )^{-1}{\rm {\boldsymbol\upvarphi }}_\mu ^{\rm T} {\rm {\bf y}}_\mu \\[6pt] \hfill {{\rm {\bf c}}=({\boldsymbol\Psi }_\sigma ^{\rm T} {\boldsymbol\Psi} _\sigma )^{-1}{\boldsymbol\Psi} _\sigma ^{\rm T} {\rm {\bf y}}_\sigma } \\ \end{array} }} \right. $$
(9)

The flowchart of constructing the dual response surface is presented in Fig. 1.

Fig. 1
figure 1

The flowchart of constructing dual response surface model

Full size image

The choice of sample points can substantially influence the accuracy of the dual RS model. In this paper, the Optimal Latin Hypercube sampling (OLHS) method is adopted to explore the design space for its proven efficiency (Sun et al. 2010a; b; c). It is critical to validate the fitness of the dual model when the dual RS model is constructed. The error in the dual RS model can be caused by the selection of basis functions, selection of sampling points and the least squares (Hou et al. 2008). To evaluate the predictive ability of the dual RS model, a simple relative error (RE) can be evaluated as

$$ RE=\frac{y({\rm {\bf x}})-\tilde {y}({\rm {\bf x}})}{y({\rm {\bf x}})} $$
(10)

where \(\tilde {y}({\rm {\bf x}})\) represents the result of mean or standard deviation response from the dual RS model, y(x) denotes the corresponding FEA result.

Alternatively, statistical techniques such as analysis of variance can be used to check the fitness of a dual RS model to identify the main effects of design variables on the responses. The major statistical measures used for evaluating dual RS model fitness can include

$$ F=\frac{( {{\it SST}-{\it SSE}} )/p}{{\it SSE}/({m-p-1})} $$
(11)
$$ R^2=1-\frac{\it SSE}{\it SST} $$
(12)
$$ R_{\it adj}^2 =1-\frac{({1-R^2}) ({m-1})}{m-p-1} $$
(13)
$$ \emph{RMSE}=\sqrt {\frac{\it SSE}{m-p-1}} $$
(14)

where p is the number of inconstant terms in the mean or standard deviation response of dual RS model. SSE and SST are calculated, respectively, as follows,

$$ \emph{SSE}=\sum\limits_{i=1}^m {({y_i -\tilde {y}_i})^2} $$
(15)
$$ \emph{SST}=\sum\limits_{i=1}^m {(y_i -\bar {y}_i )^2} $$
(16)

where\(\bar {y}_i\) is the mean value of y i .

Note that these parameters are not completely independent on each other (Fang et al. 2005; Wang and Shan 2007). Generally speaking, the larger the values of R 2 and \(R_{\it adj}^2\), and the smaller the value of RMSE; the better the fitness. When the number of design variables is large, it is more appropriate to look at \(R_{\it adj}^2\), because R 2 will keep increasing as increase in the number of terms, while \(R_{\it adj}^2\) actually decreases if unnecessary terms are added to the model.

3 Multiobjective robust optimization method

Robust optimization aims at developing a solution that is insensitive to variations of the nominal design and is feasible in an uncertainty range around the nominal design. As shown in Fig. 2, the x-axis represents the uncertain parameters, including design variables (control factors) and noise factors (uncontrollable factors), while the vertical axis represents the objective function f(x) to be minimized. Of these three solutions 1, 2, and 3 pointed, Solution 3 is considered robust as a variation of ±Δx in design variables does not alter the objective function too much and maintains the solution within the design constraint when the design variable is perturbed. Although Solution 2 is also within the design space when the design variable varies in ±Δx, the perturbation causes a larger change in objective function. Solution 1 is highly sensitive to the parameter perturbation and usually cannot be recommended in practice, though it has the best mean value of all the three solutions.

Fig. 2
figure 2

Schematic of robust optimization design

Full size image

Despite the importance of determining robust solution to a single objective, development of a multiobjective robust optimization for sophisticated engineering problems is more significant from practical point of view (Koksoy 2008; Koksoy and Yalcinoz 2006; Yang et al. 2005b). To cope with this problem, this paper presents a multi-objective robust optimization procedure that is constructed by integrating dual response surface model, sigma criteria and multi-objective particle swarm optimization.

3.1 Sigma criteria for robustness

In order to quantify the robustness of a design, different sigma criteria are introduced to measure performance variability. The term “sigma” refers to standard deviation, σ, which is a measure to the distribution of a set of data around the mean value, μ. This property can be used to describe the known randomness of variables and parameters that influence system responses, thereby measuring variability of objective performances. Performance variations can be characterized in terms of different standard deviations from the mean performance (Koch et al. 2004). Traditionally, many companies adopt ±3σ as variation criterion, where 99.73% of the variation is within specification limits. Recently, some industries have been advocating the zero product defects, though it could cost substantially more from design and production perspectives. In this paper, we use ±6σ as performance variation criterion to ensure a higher level of acceptable quality. Nevertheless, other sigma level (e.g. ±3σ) will be also explored herein to investigate its effects on the multiobjective robust design.

3.2 Multiobjective robust optimization mathematical model

A general multiobjective optimization problem can be formulated as:

$$ \left\{ {{\begin{array}{@{}lll} {\min} \hfill & {\left\{ {f_1 ({\rm {\bf x}}),f_2 ({\rm {\bf x}}),\cdots ,f_K ({\rm {\bf x}})} \right\}} \hfill & \hfill \\ {s.t.} \hfill & {g_j ({\rm {\bf x}})\le 0,} \hfill & {j=1,2,\cdots ,J} \hfill \\ \hfill & {{\rm {\bf x}}_L \le {\rm {\bf x}}\le {\rm {\bf x}}_U } \hfill &\hfill \\ \end{array} }} \right. $$
(17)

where f 1(x), f 2(x), ⋯ ,f K (x) are the K objective functions, g j (x) denotes the j th constraint, J is the number of constraints, x L and x U denote the lower and upper bounds of design variable x, respectively. Obviously, this formulation does not take into account the perturbation induced by parameter uncertainties. For this reason, a corresponding multiobjective robust optimization model can be formulated as:

$$ \left\{ {{\begin{array}{*{20}c} {\min } \hfill & {\left\{ {f_1 \left( {Y_{\mu 1} ({\rm {\bf x}}),Y_{\sigma 1} ({\rm {\bf x}})} \right),\;f_2 \left( {Y_{\mu 2} ({\rm {\bf x}}),Y_{\sigma 2} ({\rm {\bf x}})} \right),}\right.}\\[6pt] &{\left.{\cdots ,\,f_K \left( {Y_{\mu K} ({\rm {\bf x}}),Y_{\sigma K} ({\rm {\bf x}})} \right)} \right\}} \hfill \\[6pt] {s.t.} \hfill & {g_{\mu j} ({\rm {\bf x}})+\eta g_{\sigma j} ({\rm {\bf x}})\le 0} \hfill \\[6pt] \hfill & {{\rm {\bf x}}_L +\eta {\rm {\bf x}}_\sigma \le {\rm {\bf x}}_\mu \le {\rm {\bf x}}_U -\eta {\rm {\bf x}}_\sigma } \hfill \\ \end{array} }} \right. $$
(18)

where Y μ1 (x),Y μ2 (x), ⋯ ,Y μK (x) and Y σ1 (x),Y σ2 (x), ⋯ ,Y σK (x) are the mean values and standard deviations of these K objectives, respectively, g μj (x) and g σj (x) are the mean and standard deviation of the j th constraint, vectors x μ and x σ are the mean and standard deviation of x, respectively, η is design level of sigma, e.g. η = 6 denotes a six sigma design.

Objective vector in (18) often includes different types of mathematical components, in which some require maximization, some require minimization, and others seek for specific target. For this reason, three different robust objective functions are formulated as follows:

Case 1—Minimization  The design aims to minimize the mean of response and the objective function is expressed as:

$$ f_I \left( {Y_{\mu I} ({\rm {\bf x}}),Y_{\sigma I} ({\rm {\bf x}})} \right)=\lambda Y_{\mu I}^2 ({\rm {\bf x}})+(1-\lambda )Y_{\sigma I}^2 ({\rm {\bf x}}) $$
(19)

where λ denotes the weight to emphasize either mean or standard deviation.

Case 2—Maximization  The design aims to maximize the mean of response and the objective function is formulated as:

$$ f_I \left( {Y_{\mu I} ({\rm {\bf x}}),Y_{\sigma I} ({\rm {\bf x}})} \right)=-\lambda Y_{\mu I}^2 ({\rm {\bf x}})+(1-\lambda )Y_{\sigma I}^2 ({\rm {\bf x}}) $$
(20)

Case 3—Target  The design aims to force the mean of response to a specific target and the objective function is given by:

$$ f_I \left( {Y_{\mu I} ({\rm {\bf x}}),Y_{\sigma I} ({\rm {\bf x}})} \right)=\lambda \left( {Y_{\mu I} ({\rm {\bf x}})-Y_{\mu I}^\ast } \right)^2+(1-\lambda )Y_{\sigma I}^2 ({\rm {\bf x}}) $$
(21)

where \(Y_{\mu I}^\ast \) denotes the target for the Ith objective mean.

The multiobjective particle swarm optimization (MOPSO) has drawn some attention recently because it exhibits a relatively fast convergence and well-distributed Pareto front compared with other multiobjective optimization algorithms, such as NSGA, PEAS et al (Liu et al. 2007; Raquel and Naval 2005). Hence, we adopt MOPSO to solve multiobjective robust optimization here. The more details about MOPSO can be found in Raquel and Naval (2005).

4 Demonstrative example for vehicle crashworthiness design

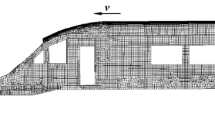
We used a full-scale FE model of a National Highway Transportation and Safety Association (NHTSA) vehicle to demonstrate the multiobjective robust optimization algorithm. The FE model of the vehicle was obtained from the public domain at: www.ncac.gwu.edu/archives/model/index.html. It has a total mass of 1,373 kg. Note that the front part of the car absorbs the most impact energy and the rear part of the car nearly does not deform much in the case of full frontal impact. Therefore an adaptive mesh was generated as in Fig. 3, whose accuracy has been verified in literature (Craig et al. 2005), thus it is considered appropriate for the design optimization herein.

Fig. 3
figure 3

Full-scale finite element model of Taurus

Full size image

4.1 Design objectives and variables

When car crashing occurs, it is expected that most of impact energy is absorbed by the vehicle structure to reduce risk to occupants. However, increase in energy absorption capacity often leads to unwanted increase in structural weight. In other words, energy absorption and lightweight can conflict with each other and we have to impose the optimum in a Pareto sense. Furthermore, the deceleration history typically used as an indicator of impact severity, where deceleration peak should be restricted to a certain level, for instance, 40 g (g = 9.81 m/s2) for crashworthiness design. Thus, the energy absorbed by car parts and structural weight of vehicle are chosen as the objectives, while the peak acceleration as constraint in this paper.

The vehicle front end structures are important structural components for their roles on the energy absorption. Following a variable screen analysis (Craig et al. 2005), we found that the thicknesses of different parts of the frontal frame have a more significant effect on energy absorption and deceleration of the vehicle (Liao et al. 2008a; b). Thus the thicknesses (t 1, t 2 and t 3) of different parts are selected as design variables in a range of 1 and 2 mm (Fig. 4). The material properties, such as Young’s modulus E, density ρ, yielding stress σ y can be affected by rolling process, and thus are chosen as random parameters, whose fluctuation are in the ranges of E = (198, 202 GPa), \(\rho = (7\text{,}700, 7\text{,}900~{\rm kg/m}^{3})\), and σ y  = (213, 217 MPa), respectively.

Fig. 4
figure 4

Design variables

Full size image

4.2 Multiobjective robust optimization model

OLHS and orthogonal design are integrated to perform DoE analysis. The noise factors sampled with orthogonal design are arranged in an outer array with the sample points of 4, and control factors sampled with OLHS are arranged in an inner array with the sample points of 16. Experiments in the inner array are repeated at 4 points corresponding to the outer array to simulate the variability due to the uncertainties of the three noise factors, making the total number of simulations equals to 64. Although increasing sample points for outer array could better populate the space of random variables, the total DoE numbers would increase by 16 times of the sample points for the outer array in our case. Thus to compromise the sampling precision with computational cost, we adopted 4 sample points for the outer array herein.

For crash simulation, we used LSDYNA970 (LS-DYNA 2003) in a personal computer with 1.7 GHz Pentium 4 with 2 GB RAM. A single simulation of 100 ms frontal impact takes approximately three hours. The arrangement of cross design matrix and FEA parameters are given in Table 1. The mean and standard deviation of each response are summarized in Table 2.

Table 1 The arrangement of cross product arrays and FEA results
Full size table
Table 2 The results of the mean and standard deviation
Full size table

Based upon the results in Table 2, the dual RS models of energy absorption U and deceleration peak a are constructed in the quadratic polynomials. Due to the mass M is a linear function of the part thickness, the dual RS models of mass M are formulated linearly. Finally, the three dual RS models are obtained as follows, respectively:

$$\begin{array}{rll} U_\mu &=&72.4996+2.8178366t_1 -0.0778410t_1^2 \\ &&+\,3.7901860t_2 +6.0060214t_2^2 +52.005026t_3 \\ &&-\,17.599580t_3^2 +1.2718916t_1 t_2 -0.5211597t_1 t_3 \\ &&-\,30.982883t_2 t_3 +11.034587t_2 t_3^2 \end{array}$$
(22)
$$\begin{array}{rll} U_\sigma &=&-17.2556+5.9578145t_1 +1.2958929t_1^2 \\ &&+\,24.621994t_2 -9.1443553t_2^2 +9.2728728t_3 \\ &&-\,2.7655915t_3^2 -12.398747t_1 t_2 +5.1793939t_1 t_2^2 \\ &&-\,0.3385413t_1^2 t_2^2-2.6668789t_1 t_3 +1.2851342t_1 t_3^2 \\ &&-\,4.0883178t_2 t_3 +1.4172815t_2^2 t_3 \end{array}$$
(23)
$$\begin{array}{rll} M_\mu &=&0.00392497+4.9603440t_1 \\ &&+\,4.4474721t_2 +4.7437340t_3 \end{array}$$
(24)
$$\begin{array}{rll} M_\sigma &=&-0.00199024+0.0470143t_1 \\ &&+\,0.0436218t_2 +0.0459824t_3 \end{array}$$
(25)
$$\begin{array}{rll} a_\mu &=&48.3807-8.4035115t_1 +4.0333016t_1^2 \\ &&-\,17.774059t_2 +4.2845324t_2^2 \\ &&-\,11.547927t_3 +4.3592314t_3^2 \\ &&+\,4.7775756t_1 t_2 +4.5825734t_2 t_3 \end{array}$$
(26)
$$\begin{array}{rll} a_\sigma &=&8.01313-15.839609t_1 +6.5481072t_1^2 \\ &&-\,14.431725t_2+7.3179605t_2^2 -2.1630359t_3 \\ &&+\,0.3434967t_3^2 +25.189906t_1 t_2 -11.487322t_1 t_2^2 \\ &&-\,9.8933289t_1^2 t_2+4.4144716t_1^2 t_2^2 +2.3720314t_1 t_3 \\ &&-\,1.0131037t_1^2 t_3 +1.0550853t_2 t_3 \\ &&-\,0.6444463t_2^2 t_3 \end{array}$$
(27)

It is essential to evaluate the accuracies of such surrogate models obtained. In this paper, the R 2, \(R^{2}_{\rm adj}\), and max(RE) measures are used to evaluate the accuracy of these dual RS models of objective and constraint functions. max(RE) is obtained by randomly generating five extra sampling points in the design space. The error results are listed in Table 3. It needs to point out that in this case the inclusion of relatively small constant terms in Eqs. 24 and 25 can make the modelling accuracy higher. Obviously, the accuracies of the dual response models are adequate and allow us to carry out the design optimization properly.

Table 3 Error analysis of response surface models
Full size table

After introducing the sigma criterion (η = 3, 6, respectively herein), the multiobjective robust optimization is thus formulated as:

$$ \left\{ {{\begin{array}{*{20}l} {\min :} & {(f_1 ,f_2 )} & \\[6pt] & {f_1 =-\lambda U_\mu ^2 +(1-\lambda )U_\sigma ^2 } & \\[6pt] & {f_2 =\lambda M_\mu ^2 +(1-\lambda )M_\sigma ^2 } & \\[6pt] {s.t.} & {a_\mu +\eta a_\sigma \le 40} & \\[6pt] & {t_i^L +\eta t_{\sigma i} \le t_{\mu i} \le t_i^U -\eta t_{\sigma i} ,} &{(i=1,2,3)} \\ \end{array} }} \right. $$
(28)

4.3 Optimization results and discussion

We first used MOPSO-CD to solve the deterministic multiobjective optimization problem without considering the perturbations of design variables and parametric noise with inertial weight w = 0.4, acceleration constants C 1 = C 2 = 0.5, population size a = 100; and external archive A = 50. The optimal Pareto fronts with the 10, 30, 50, 80, 100 and 200 generations are respectively plotted in Fig. 5, which indicate that the 100 generations converged fairly stably and is considered adequate.

Fig. 5
figure 5

Pareto optimal front of MOPSO-CD with different generations

Full size image

In order to take into account the uncertainties, the design variables are assumed to distribute normally, whose standard deviations are given as [0.01, 0.01, 0.01] from typical manufacturing tolerance. Figure 6 gives the Pareto optimal fronts for different sigma levels. Although the profiles of the Pareto fronts keep similar in the different sigma levels, whose ranges change fairly evidently compared with that in the deterministic case. All the Pareto optimal fronts are obtained with the same population size (100) and number of generations (100). Every point represents one Pareto optimal solution in different cases, which elucidate the trade-off between mass M and energy absorption U. It is shown that these two objective functions strongly compete with each other: the more the mass, the higher the energy absorption. Consequently, if the decision maker wishes to emphasize more on the energy absorption of the structures, the mass must be compromised and become heavier, and vice versa. More importantly, a higher sigma level indicates that the perturbations of the design variables and parametric noise have a lower probability to violate constraint. This is to say that the Pareto becomes more stable. However, the objective functions must sacrifice more, as compared in Fig. 6. In addition, a greater standard deviation (i.e. a wider range of random parameters) could lead to a bigger gap between different sigma levels (e.g. 3 and 6 sigma).

Fig. 6
figure 6

Pareto optimal front for different sigma levels

Full size image

Figure 7 presents the optimal Pareto fronts for the deterministic multiobjective optimization (λ = 1) and the means of robust multiobjective optimizations with λ = 0.01 and λ = 0.1, respectively. It is interesting to note that the consideration of randomness of the parameters leads to sacrifice of Pareto optimum, i.e. the robust solution is farther to the origin in the Pareto space than the deterministic counterpart. Figure 8 gives the optimal Pareto fronts of standard deviation in the multiobjective robust optimizations with λ = 0.01 and λ = 0.1. The ranges and shapes of the Pareto optimal front change with variation of λ as compared to the deterministic case. The smaller the λ (i.e. less emphasis on the mean objective), the higher the robustness of the objective functions (see Fig. 8, where the deviation is much smaller). However, the mean objective functions are worse (see Fig. 7, where the Pareto front moves farther). Hence, compromise must be made between the robustness and nominal performance in practice. The optimized Pareto set, which takes into account the perturbations of the design variables and noise parameters, does not violate the constraint, as in Fig. 9.

Fig. 7
figure 7

Comparison of Pareto optimal fronts in the deterministic optimization, and robust optimizations with λ = 0.01 and λ = 0.1 (with the six-sigma criterion)

Full size image
Fig. 8
figure 8

Pareto optimal front of standard deviation for the multiobjective robust optimizations with λ = 0.01 and λ = 0.1 (with the six-sigma criterion)

Full size image
Fig. 9
figure 9

The trend of α μ  + 6α σ to optimal Pareto set

Full size image

Although the Pareto-set can provide designer with a large number of design solutions for their decision-make in the beginning of design stage, decision must be made for the most satisfactory solution (termed as “knee point”) from Pareto-set finally. Conventionally, the most satisfactory solution is often decided by the weight method which aggregates many objectives into a single cost function in terms of weighted average to emphasize their relative importance. However, it can be difficult to assign proper weight to each objective. In this paper, we present the minimum distance selection method (TMDSM), mathematically given as below, which allows us determining a most satisfactory solution from Pareto-set,

$$ \min \,\,D=\left( {\sum\limits_{\tau =1}^K {\left( {f_{c\tau } -\min \left( {f_\tau ({\rm {\bf x}})} \right)} \right)^d} } \right)^{\frac{1}{d}} $$
(29)

where K is the number of the objective components, f cτ is the τ th objective value in the c th Pareto solution, d = 2, 4, 6,..., D is the distance from knee point to an “utopia point” that is given by the optimal values of each individual objective (refer to Fig. 10), which are normally not attainable in practice with presence of conflicting objectives.

Fig. 10
figure 10

The knee point on the Pareto front having the shortest distance from utopia point

Full size image

The deterministic knee point and robust knee point are obtained to use TMDSM from the Pareto-sets, respectively. The results are summarized in Table 4 to compare with the baseline model. It can be seen that the deterministic design and robust design can improve the performance of vehicle. However, the optimal result of the deterministic multiobjective optimization lies on the margin of design space, thus the reliability is low. Comparing x D with x R, the mean objective performance of x D is better than that of x R, but the robustness of x D is worse than that of x R. The optimal results of the deterministic design and robust design are also verified by additional FEM simulations. In terms of %error, these two optimal results of approximations have sufficient accuracies, which demonstrate the effectiveness of DRSM optimization method presented.

Table 4 Comparison of deterministic, robust multiobjective optimizations and baseline design
Full size table

5 Conclusions

Following widely available reports on either multiobjective deterministic optimization or single robust optimization of crashworthiness designs, this paper presented a multiobjective robust optimization for vehicle design by using dual response surface model and sigma criteria, which allows taking into account the effects of system uncertainties on different objectives. The adoption of a new multiobjective particle swarm optimization algorithm no longer requires formulating a single cost function in terms of weight average or other means of combining multiple objectives. The procedure proved fairly effective in a full-scale vehicle crashing model, where energy absorption and weight are taken as the objectives, while the peak deceleration as the constraint. The example demonstrated that the multiobjective particle swarm optimization generates the Pareto points fairly efficient and evenly. The comparison of Pareto optimums between the deterministic design and robust design clearly indicated that improvement in the robustness must sacrifice the Pareto optimum of mean objectives. For this reason, a weight factor can be prescribed to balance the importance between deterministic design and robust design. The more the emphasis on robustness (a higher sigma level), the worse the objective means. The example showed that the energy absorption and weight of the car were improved, at the same time; the robustness of the design is enhanced.