1 Introduction

The redundancy allocation problem (RAP) is a combinatorial optimization problem with multiple resource constraints aimed at improving the system reliability. The RAP was first introduced by Misra and Ljubojevic [16]. RAPs are generally formulated as nonlinear integer problems and usually characterized by a considerable computational complexity.

A series–parallel RAP consists of a set of sub-systems which are connected in series where it is possible to select multiple component choices and redundancy levels in parallel in each sub-system. The components of each sub-system may be either binary- or multi-state [10, 30]. The entire system may also consist of either two or multiple states. Binary systems are assumed to be either functional or non-functional [21]. However, a real system may go through several states ranging from full performance to complete failure carrying out infinite partial performances during its service time. That is, the state of a real system may be either downgraded or improved during its service time depending on several factors such as aging, maintenance, and workload. The transition between the states can be modeled using stochastic and Markov processes.

In a multi-state series–parallel system, two different types of redundancy strategies may be considered. The first one occurs when the components of the system are binary state, but each type of component may have a different nominal performance level. In this case, the system performance depends on the performance levels of the selected components and on these components being functional or non-functional. The second type of redundancy strategy applies to systems with multi-state components where the system performance is completely determined by the states of the selected components [21]. In this paper, we consider this second type of redundancy problem for multi-state series–parallel systems.

RAPs and their extensions are NP-hard problems [2]. A wide range of solution procedures including heuristics and meta-heuristics [1, 5, 12, 13, 17–19, 22, 23, 25, 29], hybrid methods [3, 20, 24], and multi-objective optimization [7] have been proposed to solve these problems. Yu and Gen [28] provided a comprehensive review of the genetic algorithm (GA) approaches that have been used to solve various reliability optimization problems in the literature.

To solve multi-objective system reliability optimization problems, Li et al. [11] proposed a procedure consisting of two steps: (1) generating non-dominated solutions using a multi-objective evolutionary algorithm; (2) clustering similar solutions by means of a self-organizing map and identifying the most efficient solutions by data envelopment analysis. Khalili-Damghani and Amiri [7] proposed a hybrid approach to solve binary-state multi-objective reliability RAPs. Their approach combines the efficient epsilon-constraint with the multi-start partial bound enumeration algorithm and data envelopment analysis.

In this paper, a multi-objective mixed-integer nonlinear programming is proposed to solve repairable multi-state multi-objective RAPs (RMMRAPs).

A RMMRAP is a series–parallel system where components are allowed to go through several performance states. We assume that one can select multiple component choices and redundancy levels in parallel in each sub-system. The performance of a component may deteriorate or improve based on minor and major failures and repairs, respectively. The partial failure/repair model is parameterized by a Markov process.

RMMRAPs are based on practical real-world problems and, as such, have many practical implications. However, to the best of our knowledge, so far they have not been adequately studied in the RAP literature.

Due to conflicting objective functions, we use a multi-objective decision-making method to solve the proposed RMMRAP model. Generating non-dominated solutions on the Pareto front is an insightful way to study the problem since it imposes no restriction on the priorities of the objective functions. Thus, a customized version of the NSGA-II method is introduced to generate a set of non-dominated solutions on the Pareto front for RMMRAP instances. The performance of the proposed NSGA-II method on several benchmark instances is compared with that of an epsilon-constraint method using a set of well-known multi-objective comparison metrics.

The paper proceeds as follows. Section 2 provides some preliminaries including: a brief introduction to the principles of multi-objective decision making, the basic NSGA-II method, and the component availability analysis using a Markov process. Section 3 introduces and describes the proposed RMMRAP, the customization of the epsilon-constraint method, and a customized version of the NSGA-II method. Test problems, software implementation, and comparison metrics are presented in Sect. 4. The results obtained for the test problems are reported and discussed in Sect. 5. Finally, Sect. 6 concludes and suggests future research directions.

2 Preliminaries

A multi-objective decision-making (MODM) problem considering minimum objective functions can be presented as follows [6]:

$$\left\{ {\begin{array}{*{20}l} {\hbox{min} \quad f(x)} \hfill \\ {s.t.\quad x \in S = \left\{ {x \in \left. {R^{n} } \right|F\left( x \right) \le b,x \ge 0} \right\}} \hfill \\ \end{array} } \right.$$
(1)

where f(x) represents a finite number of objective functions, F(x) ≤ b represents a finite number of constraints, S is the feasible solution space, and x is the n-vector of decision variables, n ∊ Z +.

The type and the timing of the preference articulations play a central role in the decision-making process. MODM solution procedures have been classified into four groups [6]. In particular, Hwang and Masud [6] showed that when assuming posterior preference information on the priority of objective functions, it is desirable to generate non-dominated solutions on the Pareto front of MODM problem.

Mavrotas [15] introduced the efficient epsilon-constraint method which is an improved version of a classical non-dominated solution generation method known as the epsilon-constraint method. The efficient epsilon-constraint method has been widely used to solve MODM problems [7, 8, 17, 26].

2.1 Non-dominated sorting genetic algorithm (NSGA-II) method

The NSGA-II method, initially introduced by Deb et al. [4], is a well-known multi-objective evolutionary algorithm. This method combines different techniques such as elitism, fast non-dominated sorting, and diversity maintenance along with the Pareto-optimal front and has been widely and successfully employed to solve several engineering, management, and combinatorial optimization problems. Details regarding the structure of the standard NSGA-II algorithm can be found in Deb et al. [4].

2.2 Component performance and availability

According to the general Markov model for a generic multi-state system introduced by Lisnianski and Levitin [14], any component h in the multi-state system can have k h different states corresponding to different performance levels belonging to the set \(g_{h} = \left\{ {g_{h,1} , \ldots ,g_{{h,k_{h} }} } \right\}\). The indexing of the set g h reflects the performance level of the component h, that is:

$$\forall l,q = 1, \ldots ,k_{h} ,\quad l < q\quad \leftrightarrow \quad g_{h,l} < g_{h,q} .$$
(2)

The current state of the component h and the corresponding value of the component performance level G h (t) at any instant t are random variables. G h (t) takes values in g h , that is, G h (t) ∊ g h . Thus, given an operational time period [0, T], the evolution of the performance level G h (t) of component h follows a discrete-state continuous-time Markov stochastic process.

Lisnianski and Levitin [14] model deals with minor and major failures and repairs of components. Given a generic repairable multi-state component h, a minor failure causes a downgrading from a state q to the adjacent lower state q − 1, while a major failure causes a downgrading from a state q to a state l < q − 1. Similarly, a minor repair implies a return of the component from a state l to the adjacent higher state l + 1, while a major repair a return of the component from a state l to a state q > l + 1.

The state probabilities p q (t), with q = 1, …, k h , define the probabilities that at the instant t > 0 the component h will be in state q and can be obtained from the following system of differential equations.

$$\begin{aligned} & \frac{{{\text{d}}p_{{k_{h} }} \left( t \right)}}{{{\text{d}}t}} = \mathop \sum \limits_{l = 1}^{{k_{h} - 1}} \mu_{{l,k_{h} }} p_{l} \left( t \right) - p_{{k_{h} }} \left( t \right)\mathop \sum \limits_{l = 1}^{{k_{h} - 1}} \lambda_{{k_{h} ,l}} \\ & \frac{{{\text{d}}p_{q} \left( t \right)}}{{{\text{d}}t}} = \mathop \sum \limits_{l = q + 1}^{{k_{h} }} \lambda_{l,q} p_{l} \left( t \right) + \mathop \sum \limits_{l = 1}^{q - 1} \mu_{l,q} p_{l} \left( t \right) - p_{q} \left( t \right)\left( {\mathop \sum \limits_{l = 1}^{q - 1} \,\lambda_{q,l} + \mathop \sum \limits_{l = q + 1}^{{k_{h} }} \mu_{q,l} } \right)\quad {\text{for}}\quad 1 < q < k_{h} \\ & \frac{{{\text{d}}p_{1} \left( t \right)}}{{{\text{d}}t}} = \mathop \sum \limits_{l = 2}^{{k_{h} }} \lambda_{l,1} p_{l} \left( t \right) - p_{1} \left( t \right)\mathop \sum \limits_{l = 2}^{{k_{h} }} \mu_{1,l} \\ \end{aligned}$$
(3)

where

  • \(p_{{k_{h} }} (0) = 1,p_{{k_{h} - 1}} (0) = \cdots = p_{1} (0) = 0\) are the initial conditions representing the fact that at time t = 0 the component h is new, that is, the component h is in state k h where no failure has occurred yet;

  • μ l, q is the repair rate from state l to state q, where l, q = 1, …, k h and l < q;

  • λ q, l is the failure rate from state q to state l, where l, q = 1, …, k h and l < q;

If D is a given demand level, that is, a reference component performance level, the acceptable states for the component h are all states q such that g h,q+1 ≥ D > g h,q . This leads to the definition of instantaneous availability of component h which is calculated as follows [28]:

$$A_{h} \left( t \right) = \mathop \sum \limits_{e = q + 1}^{{k_{h} }} p_{e} \left( t \right) .$$
(4)

Equation (4) says that the instantaneous availability of component h at time t is given by the sum of all the state probabilities of the component from state q + 1 to state k h . That is, at a given demand level D, A h (t) calculates the probability of component h going through all working states which allow the component to meet the minimum required performance level.

3 Modeling RMMRAPs

Repairable multi-state multi-objective redundancy allocation problems (RMMRAPs) consist of series–parallel systems experiencing repairs, partial failures, and component degrading through time. RMMRAPs comprise configuring multiple components and redundancy levels in each sub-system while evaluating multiple objectives (i.e., availability and cost). In RMMRAPs, the performance of a component depends on its state and may decrease/increase due to minor and major failures/repairs which are modeled by a Markov process.

The proposed RMMRAP model is based on the following main assumptions.

  • Multi-objectives (i.e., availability and cost) are considered for planning the RMMRAPs.

  • All components are assumed to go through several states from perfect performance to complete failure.

  • All components are assumed to be repairable.

  • The performance level is a discrete-state continuous-time Markov stochastic process.

  • Cost and weight of all components are assumed to be known, deterministic, and time independent.

  • The availability of each component is assumed to be time dependent.

  • The demand level is assumed to be constant and hence time independent.

  • There are several redundant component choices within a sub-system.

  • The redundancy strategy is assumed to be active.

  • The total number of components in each sub-system is bounded.

  • Final designs must conform to the cost, weight, and availability constraints.

The main notations used in the proposed RMMRAP are listed below:

m :

Number of sub-systems

i :

Index for the sub-systems, i = 1, 2, …, m

n i :

Total number of components used in sub-system i

h :

Index for the components of subsystem i, h = 1, 2,…, n i

j :

Index for the component types in each sub-systems, j = 1, 2,…,n

D :

Demand level

A ij (t):

Availability of a component of type j in sub-system i at the time t

c ij :

Cost of a component of type j in sub-system i

w ij :

Weight of a component of type j in sub-system i

A s(t):

Overall availability of the series–parallel system at time t

C s :

Overall cost of the series–parallel system

A o :

System-level constraint: lower bound limit for availability (a number between 0 and 1)

C o :

Overall cost allowed by the system

W o :

Overall weight allowed by the system

a i :

Number of available component choices for sub-system i

x ij :

Number of components of type j used in sub-system i

n max :

Maximum number of components allowed to be in parallel

\(n_{\hbox{min} }\) :

Minimum number of components allowed to be in parallel

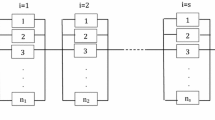
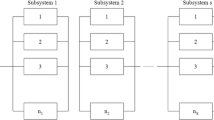
Figure 1 provides the schematic view of a series–parallel system whose sub-systems consist of repairable multi-state components, displaying the decision variables of the proposed RMMRAP model and the solution encoding that will be used to solve the model with NSGA-II.

Fig. 1
figure 1

Proposed framework

Full size image

More precisely, the proposed model considers a series–parallel system formed of m subsystems (Fig. 1a). Each sub-system i consists of n i components which are allowed to be of n different types (Fig. 1b). Thus, a generic hth component is assigned a type j, where j = 1, …, n, and it is assumed to have the same states as the rest of the components of the same type. That is, the possible states for a component and the corresponding performance levels depend on the type of the component (Fig. 1c).

Through time, any component in any sub-system goes through minor and major failures and repairs while the demand level D is kept constant. Figure 1d represents the state-space diagram for a repairable multi-state component. The state probabilities and the availability of a component are calculated as in Lisnianski and Levitin [14] (see Sect. 2.2) and extended to the corresponding component type. That is, A h (t) = A h′(t) = A ij (t) whenever h and h′ are two components of type j in sub-system i.

The multi-objective model proposed for the RMMRAP is the following:

$${\text{Max}}\quad A_{\text{s}} (t) = \mathop \prod \limits_{i = 1}^{m} \left( {1 - \mathop \prod \limits_{j = 1}^{{a_{i} }} \left( {1 - A_{ij} \left( t \right)} \right)^{{x_{ij} }} } \right)$$
(5)
$${\text{Min}}\quad C_{\text{s}} = \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \cdot c_{ij}$$
(6)
$$\begin{aligned} &s.t. \hfill \\ &\mathop \prod \limits_{i = 1}^{m} \left( {1 - \mathop \prod \limits_{j = 1}^{{a_{i} }} \left( {1 - A_{ij} \left( t \right)} \right)^{{x_{ij} }} } \right) \ge A_{o} , \hfill \\ \end{aligned}$$
(7)
$$\mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \cdot c_{ij} \le C_{o} ,$$
(8)
$$\mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \cdot w_{ij} \le W_{o} ,$$
(9)
$$\mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \le n_{\hbox{max} } ;\quad i = 1, 2, \ldots ,m;$$
(10)
$$\mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \ge n_{\hbox{min} } ;\quad i = 1, 2, \ldots ,m ;$$
(11)
$$x_{ij } \in Z^{ + } ; \quad i = 1, 2, \ldots ,m; \quad j = 1, \ldots , n.$$
(12)

Objective functions (5) and (6) seek to optimize the system availability and system cost, respectively. In particular, objective function (5) calculates the availability of a series–parallel system which consists of m sub-systems and, in each sub-system i, it is possible to configure in parallel a number x ij of components of type j, for every j varying from 1 (the sub-system is formed of at least one type of components) to a predetermined value a i . Constraint (7) specifies the lower bound for the system availability. Constraints (8) and (9) place an upper bound on the system cost and weight, respectively. Constraints (10) and (11) state the minimum and maximum number of components allowed in each sub-system. Constraint (12) defines the decision variables to be positive integers.

The right-hand side of constraint (7) represents the system lower bound limit for availability. Clearly, introducing constraint (7) imposes the model to seek configurations which have at least an availability value greater than or equal to A o. In our model, the value A o is assumed to be given, but it could alternatively be customized and set through managerial insights for different systems. Form an optimization viewpoint, the direct consequence of introducing constraint (7) is that the proposed Model (5)–(12) seeks preferred solutions among all the non-dominated solutions on the Pareto front of the RMMRAPs. Thus, it is first necessary to generate a desired section of the Pareto front from the final non-dominated solution set of Model (5)–(12).

3.1 Handling RMMRAP using the epsilon-constraint method

Model (5)–(12) is transformed into Model (13)–(19) using the efficient epsilon-constraint method proposed by Mavrotas [15].

$${\text{Max}}\quad Z = \mathop \prod \limits_{i = 1}^{m} \left( {1 - \mathop \prod \limits_{j = 1}^{{a_{i} }} \left( {1 - A_{ij} \left( t \right)} \right)^{{x_{ij} }} } \right) - \varepsilon \times \frac{{S_{\text{c}} }}{{r_{\text{c}} }}$$
(13)
$$\begin{aligned} &s.t. \hfill \\ &\mathop \prod \limits_{i = 1}^{m} \left( {1 - \mathop \prod \limits_{j = 1}^{{a_{i} }} \left( {1 - A_{ij} \left( t \right)} \right)^{{x_{ij} }} } \right) \ge A_{o} , \hfill \\ \end{aligned}$$
(14)
$$\mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \cdot c_{ij} + S_{\text{c}} = C_{o} - (C_{0} - C_{l} ) \times e_{2} ,$$
(15)
$$\mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \cdot w_{ij} \le W_{o} ,$$
(16)
$$\mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \le n_{\hbox{max} } ;\quad i = 1, 2, \ldots ,m;$$
(17)
$$\mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \ge n_{\hbox{min} } ;\quad i = 1, 2, \ldots ,m;$$
(18)
$$x_{ij } \in Z^{ + } ;\quad i = 1, 2, \ldots ,m;\quad j = 1, \ldots , n.$$
(19)

where C l is the minimum cost allowed by the system, S c is the slack variable of the cost objective function, r c is the range of the cost objective function, e 2 is a parameter belonging to the interval [0, 1], and ɛ is a very small positive constant value.

Note that the term \(\frac{{S_{\text{c}} }}{{r_{\text{c}} }}\) in Eq. (13) is to be minimized due to the negative multiplier before it. Also, r c is the range of the cost objective function and is a fixed parameters. Thus, Model (13)–(19) aims at reducing the value of S c in the second term of objective function (13). As a consequence, given the presence of S c in Eq. (15), the cost of the system will be as near as to the upper bound of cost in Eq. (15). This will lead to stronger efficient solutions in terms of cost objective function while maximizing the availability of the system expressed by Eq. (13). Moreover, note that the term \(\frac{{S_{\text{c}} }}{{r_{\text{c}} }}\) in Eq. (13) normalizes the slack variable of the cost objective function. Since both \(0 \le \frac{{S_{\text{c}} }}{{r_{\text{c}} }} \le 1\) and \(0 \le A_{0} \le \prod\nolimits_{i = 1}^{m} {\left( {1 - \prod\nolimits_{j = 1}^{{a_{i} }} {\left( {1 - A_{ij} \left( t \right)} \right)^{{x_{ij} }} } } \right) \le 1}\) hold true, adding \(\mathop \prod \nolimits_{i = 1}^{m} \left( {1 - \mathop \prod \nolimits_{j = 1}^{{a_{i} }} \left( {1 - A_{ij} \left( t \right)} \right)^{{x_{ij} }} } \right)\) and \(- \varepsilon \times \frac{{S_{\text{c}} }}{{r_{\text{c}} }}\) is meaningful (as both these terms vary in the same range).

Finally, it must be noted that the simultaneous use of constraints (14) and (15) together with the objective function in Eq. (15) may lead to some infeasibility issues in Model (13)–(19). Fortunately, the efficient epsilon-constraint method proposed by Mavrotas [15] has a key advantage with respect to the classic epsilon-constraint method, that is, it can recognize infeasible loops and break them. So, no extra computational efforts are imposed to the model when considering Eqs. (14)–(15).

More formally, consider the parametric Model (13)–(19) to be solved using a predetermined step size for e 2. In the first iteration, e 2 is set equal to zero. Hence, the term C o − (C 0 − C l) × e 2 is equal to C o. As the iterations go on, the value of e 2 increases and, consequently, the value of the term C o − (C 0 − C l) × e 2 decreases form C o toward C l. The decreasing behavior of the right-hand side of constraint (15) may lead to some infeasibilities in Model (13)–(19) when incorporating the role of constraint (14). Indeed, constraint (14) imposes the model to generate configurations that have an availability higher than A 0, while in each iteration the model is also imposed to generate a solution with smaller total cost, as the C o − (C 0 − C l) × e 2 is decreasing while iterations go on. Using the efficient epsilon-constraint method, when the model is recognized infeasible due to such a conflict of constraints, the next iterations are discarded, as they cannot improve the right-hand side of constraint (15). So, no extra computational efforts are imposed to the model.

3.2 Customizing NSGA-II for RMMRAP

In this section, a customized version of NSGA-II, initially introduced by Deb et al. [4], is structured to solve the proposed RMMRAP.

3.2.1 Solution encoding

As for any other evolutionary algorithm, a feasible solution to the proposed RMMRAP is represented by a chromosome, while a population can be interpreted as a set of feasible solutions. Thus, to correctly encoding a solution, a chromosome must be a string of genes signifying the available components in all the sub-systems.

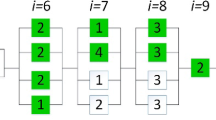
Figure 2 shows a schematic representation of the chromosome used to encode the solution to RMMRAP. This chromosome is composed of m sub-strings one per each sub-system. The first a 1 genes represent the first sub-system, the next a 2 genes represent the second sub-system, and so on. The sub-string of genes corresponding to the sub-system i will be referred to as chromosome i.

Fig. 2
figure 2

Structure of the proposed chromosome

Full size image

3.2.2 Determining the initial population

The size of the initial population is generated randomly to be 50. After generating the initial population, each chromosome is checked for feasibility based on the minimum and maximum number of components allowed in each sub-system.

3.2.3 Handling the constraints

In order to handle the constraints of the RMMRAP, a combination of the modification and penalty strategies is employed.

3.2.3.1 Penalty strategy

Constraints (7)–(9) are handled by incorporating a penalty strategy. Two sets of violation values are calculated for each chromosome i. The first set of violations has an effect on the availability objective, while the second one has an effect on the cost objective.

The first set of violations relative to chromosome i is given by:

$$AV_{i1} = {\text{Max}}\left\{ {A_{o} - \mathop \prod \limits_{i = 1}^{m} \left( {1 - \mathop \prod \limits_{j = 1}^{{a_{i} }} \left( {1 - A_{ij} } \right)^{{x_{ij} }} } \right),0} \right\}$$
(20)
$$CV_{i1} = {\text{Max}}\left\{ {\frac{{\mathop \sum \nolimits_{i = 1}^{m} \mathop \sum \nolimits_{j = 1}^{{a_{i} }} x_{ij} \cdot c_{ij} }}{{C_{o} }} - 1,0} \right\}$$
(21)
$$WV_{i1} = {\text{Max}}\left\{ {\frac{{\mathop \sum \nolimits_{i = 1}^{m} \mathop \sum \nolimits_{j = 1}^{{a_{i} }} x_{ij} \cdot w_{ij} }}{{W_{o} }} - 1, 0} \right\}$$
(22)

where AV i1, CV i1, and WV i1 are, respectively, the violation values for the availability, cost, and weight of chromosome i relative to the first objective. Therefore, the availability objective is dynamically penalized as follows:

$$A_{si}^{{\prime }} = A_{si} - \left( {\hbox{max} \left\{ {AV_{i1} ,CV_{i1} ,WV_{i1} } \right\} \times it} \right)$$
(23)

where \(A_{si}^{\prime }\) is the penalized availability function for the violated chromosome i and it is the iteration number. The second set of violations is relative to chromosome i is given by:

$$AV_{i2} = {\text{Max}}\left\{ {A_{o} - \mathop \prod \limits_{i = 1}^{m} \left( {1 - \mathop \prod \limits_{j = 1}^{{a_{i} }} \left( {1 - A_{ij} } \right)^{{x_{ij} }} } \right),\;0} \right\} \times M$$
(24)
$$CV_{i2} = {\text{Max}}\left\{ {\mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \cdot c_{ij} - C_{o} ,0} \right\}$$
(25)
$$WV_{i2} = {\text{Max}}\left\{ {\mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{a_{i} }} x_{ij} \cdot w_{ij} - W_{o} ,0} \right\}$$
(26)

where AV i2, CV i2, and WV i2 are, respectively, the violation values of the availability, cost, and weight of chromosome i for the second objective. Hence, the cost objective is dynamically penalized as follows:

$$C_{si}^{{\prime }} = C_{si} + \left( {\hbox{max} \left\{ {AV_{i2} ,CV_{i2} ,WV_{i2} } \right\} \times it} \right)$$
(27)

where C′ si is the penalized cost function for the violated chromosome i and it is the iteration number.

3.2.3.2 Modification strategy

Constraints (10) and (11) are handled using the modification strategy. The chromosomes violating the condition \(n_{\hbox{min} } \le \sum\nolimits_{j = 1}^{{a_{i} }} {x_{ij} } \le n_{\hbox{max} }\), for i = 1, …, m, are modified by using the methods proposed by Khalili-Damghani et al. [9]. This modification strategy allows to determine which one of the component types of the violated chromosome i should be pruned by introducing a cost–benefit heuristic. Following again Khalili-Damghani et al. [9], a cost–benefit ratio is associated with each component type of the proposed RMMRAP model. This ratio is obtained dividing the availability of the component type by the sum of its cost with its weight, that is:

$${\text{Ratio}}_{ij} \left( t \right) = \frac{{A_{ij} \left( t \right)}}{{c_{ij} + w_{ij} }}.$$
(28)

The components with a lower \({\text{Ratio}}_{ij} (t)\) have a higher pruning priority, while the components with a higher \({\text{Ratio}}_{ij} (t)\) have a higher adding priority in the case of a shortage. That is, after ordering all the ratios from the lowest to the highest one, the redundant components are those whose ratios are at the top of the list while the components corresponding to ratios at the bottom of the list can be used to supply a shortage of components.

3.2.4 Fitness function and non-dominated ranking

The fitness functions are calculated based on the penalized objective functions. All the solutions in a population are assigned a rank according to a non-dominated ranking procedure: Assign Rank 1 to non-dominated solutions; omit these solutions from the population; assign Rank 2 to other non-dominated solutions; omit these solutions; and so on until when all the solutions in the current population receive a rank.

3.2.5 Genetic operators

3.2.5.1 Crossover operator

Double-point crossover is applied based on a predefined cross-rate. In the double-point crossover, two different points between 1 and the chromosome length minus 1 are selected randomly. Parents are divided into three separate parts by these two points. Each child is formed based on a selection of a mid-piece from one of the parents and two other pieces from the other parent.

3.2.5.2 Mutation operator

First, an initial step size is determined. A binary random number is then generated. If the generated number is one, the step size is added to the value of the selected gene for mutation. Otherwise, the step size is subtracted from the value of the selected gene. In this method, an exception is intended to avoid a negative number for the values of genes. If the value of the selected gene for mutation is zero, then the step size will be added regardless of the random number value.

3.2.6 Stopping criterion

In the proposed customized version of NSGA-II, the number of iterations works as the stopping criterion.

4 Test problems, software implementation, and comparison metrics

Thirty test RMMRAP instances belonging to three classes of test problems, namely small-size, medium-size, and large-size problems, have been used to test the performance of the proposed algorithm. The efficient epsilon-constraint and the proposed NSGA-II methods have been implemented on all instances and their performances compared using multi-objective metrics.

4.1 Test problems

The characteristics of the test instances are reported in Table 1.

Table 1 Test problem configuration
Full size table

These characteristics have been simulated using uniform probability density functions. U[a, b] in Table 1 means that the associated parameters have been generated using a uniform distribution function with parameters a and b.

4.2 Software–hardware implementation

The test instances have been simulated with MS-Excel. The LINGO software was used to code the efficient epsilon-constraint method, while the proposed customized version of NSGA-II was coded using the MATLAB software. All codes were run on a laptop with MS-Windows 8.0, with 4 GB of RAM and 1.8 GHz Core i7 CPU.

4.3 Comparison metrics

In order to analyze and compare the accuracy and the diversity of the epsilon-constraint and the NSGA-II methods with respect to the Pareto front of the RMMRAP, several metrics proposed by Yu and Gen [28] have been used [i.e., number of non-dominated solutions (NNSs), error ratio (ER), generational distance (GD), and spacing metric (SM)]. The interested reader may refer to Khalili-Damghani and Amiri [7], Khalili-Damghani et al. [9], and Tavana et al. [27] for a detailed review of these metrics. Moreover, the reference set (RS) was retrieved for all runs since the real Pareto front cannot be achieved through direct enumeration for the test problems. The RS contains the non-dominated solutions for all the methods in all the runs. We performed 20 runs for each method and retrieved a suitable estimation of the RS.

5 Results

The results are presented in three subsections. The first subsection presents the results obtained when calculating the availability of the components. The second subsection discusses the results relative to a single run of the NSGA-II and epsilon-constraint methods for all test problems comparing them to the RS. The third subsection describes the results obtained for the computational CPU time for the NSGA-II and epsilon-constraint methods.

5.1 Results for the availability values of components

The differential Eq. (3) is coded in MATLAB for each component. The availability graphs of the components are plotted and illustrated in Fig. 3.

Fig. 3
figure 3

Availability graphs for the components in the test problems

Full size image

As shown in Fig. 3, the availability value of each component takes the maximum value at time zero and decreases over time. This is due to the fact that the components are in their best state at the start time. As time goes on, the components become less available due to component aging, until their availability becomes constant. This component behavior can be observed in all the test problems.

5.2 Results of the proposed NSGA-II and epsilon-constraint methods

In this subsection, the result of the customized NSGA-II and the epsilon-constraint methods is presented for all test problems.

5.2.1 Results for the small-size test problems

The solutions generated for the small-size test problems by implementing the proposed customized version of NSGA-II and the epsilon-constraint method together with the RS are represented in Fig. 4, while the corresponding accuracy and diversity metrics are displayed in Table 2.

Fig. 4
figure 4

Pareto front for the small-size test problems

Full size image
Table 2 Comparison metrics for the test problems
Full size table

Relative to the small-size test problems, Table 2 shows that the NNS for the NSGA-II method is much higher than the NNS for the epsilon-constraint method. That is, the number of non-dominated solutions generated by the NSGA-II method is higher than that generated by the epsilon-constraint method. The ER measure is zero for the customized NSGA-II method and much smaller than the ER measure for the epsilon-constraint method. The zero value obtained for ER when implementing NSGA-II indicates the fact that the NSGA-II method allows for a complete convergence of the solutions toward the Pareto front in the considered small-size test problems. The GD value in the NSGA-II method not only is much smaller than the GD value in the epsilon-constraint method, but equals zero. Therefore, the distance between the Pareto front/RS and the solution set generated in the customized NSGA-II method is minimal. The SM value in the NSGA-II method is zero and much smaller than that in the epsilon-constraint method, which means that the non-dominated solutions obtained by the NSGA-II method are considerably more uniformly distributed than those obtained by the epsilon-constraint method.

5.2.2 Results for the medium-size test problems

The solutions generated for the medium-size test problems for the NSGA-II and the epsilon-constraint methods together with the RS are represented in Fig. 5, while the corresponding accuracy and diversity metrics are displayed in Table 2.

Fig. 5
figure 5

Pareto front for the medium-size test problems

Full size image

As given in Table 2, in the medium-size case, the NNS for the customized NSGA-II method is significantly higher than the NNS for the epsilon-constraint method. The ER in the NSGA-II is very low compared to the ER in the epsilon-constraint method. The GD value in the customized NSGA-II method is considerably smaller than the GD value in the epsilon-constraint method. The SM measure in the NSGA-II is very small in comparison with the SM measure in the epsilon-constraint.

5.2.3 Results for the large-size test problems

Figure 6 represents the solutions generated for the large-size test problems for the NSGA-II and the epsilon-constraint methods together with the RS. The accuracy and diversity metrics for the large-size test problems are displayed again in Table 2.

Fig. 6
figure 6

Pareto front for the large-size test problems

Full size image

The epsilon-constraint method was unable to solve the problem for the large-size instances. Therefore, the graph of Fig. 6 and the comparison metrics of Table 2 show solutions and values relative only to the NSGA-II method. Although the NNS for the NSGA-II method for the large instances is low, the GD and the SM metrics are acceptable. The GD measure shows that the distance between the solution sets obtained by the NSGA-II method and the RS is very small. Finally, the SM value shows that the non-dominated solutions obtained by the NSGA-II are diverse.

5.3 Computational CPU time

Table 3 reports the average CPU time of the test problems for the NSGA-II method. The NSGA-II was run ten times and the average computing time reported.

Table 3 CPU time for the customized NSGA-II
Full size table

Table 4 presents the average CPU time of the test problems for the epsilon-constraint method. The CPU time in the epsilon-constraint method consists of two average time calculations. The first average time corresponds to the time needed for solving the differential equations using the MATLAB software, and the second average time accounts for the time necessary to solve the problem with the LINGO software.

Table 4 CPU time for the epsilon-constraint method
Full size table

It must be observed that a comparison of the computational CPU time between the two methods is not feasible. In fact, in order to solve the problem with the epsilon-constraint method, we must first solve the differential equations in MATLAB. Thus, considering that some time is needed to change from one software to the other, the real time for solving the test problems is actually larger than the sum of the times which are presented in Table 3. In addition, although the sum of the average times for the epsilon-constraint method is less than the corresponding times for NSGA-II method for the small and medium-size test problems, the NNS for the epsilon-constraint method is very small while the other accuracy and diversity metrics for the large-size test problems are not even acceptable.

6 Conclusions and future research direction

We proposed a multi-objective mixed-integer nonlinear programming to solve repairable multi-state multi-objective redundancy allocation problems (RMMRAPs). Despite being among the extensions of RAPs which are the closest to real-life availability engineering problems, to the best of our knowledge, this class of problems has not been receiving the adequate attention in the RAP literature.

A customized version of the NSGA-II method was introduced in order to generate a set of non-dominated solutions on the Pareto front for RMMRAPs. Several test instances were designed and simulated to compare the proposed NSGA-II method to an epsilon-constraint method on several benchmark instances by using a set of well-known multi-objective comparison metrics. The Pareto front was generated for all instances together with a reference set (RS) using both solution procedures based on several runs. The performance of both solution procedures was compared with the RS using diversity and accuracy metrics.

The proposed customized version of the NSGA-II method showed better accuracy and diversity when compared to the epsilon-constraint method. In particular, although the total computational times for the epsilon-constraint method were less than the corresponding times for NSGA-II method for small- and medium-size test problems, the NNS obtained by the epsilon-constraint method was very small and the other accuracy and diversity metrics for large-size test problems were not even acceptable.

Future work may include the selection of other redundancy strategies such as hot-standby or cold-standby strategies in place of the active redundancy strategy addressed in this study. Furthermore, additional objective functions (e.g., weight) could be considered in future formulations of the problem. Considering dynamic and different demand levels of performance could also provide interesting extensions of the model proposed in this study.