Complex dynamical behaviors in a memcapacitor–inductor circuit

Abstract

In this present contribution, a simple chaotic oscillator based on a memcapacitor with only one equilibrium point is reported. The proposed oscillator consists of an inductor (only storage element) and a nonlinear active memcapacitor which is the key component responsible for the complex behaviors exhibited by the circuit. The resulting mathematical model is a simple jerk-type equation system that is easy to manipulate both analytically and numerically. The numerical results reveal the emergence of a plethora of phenomena such as period-doubling bifurcations, antimonotonicity, offset-boosting, and multistability giving rise to several kinds of coexisting attractors among which the coexistence of six stable states. The PSpice investigations confirm the real feasibility of the proposed circuit. The complexity of the phenomena and behaviors observed make the particularity of the proposed memcapacitor–inductor circuit and thus constitutes an enriching contribution in nonlinear dynamics.

1 Introduction

The existence of the memristor as the fourth electronic component having a memory next to the resistor, capacitance, and inductor was deduced in 1971 by Chua [1]. Many applications in nonlinear circuits have been realized through the memristor in the growing interest of nonlinear science [2,3,4,5,6]. Later in 2009, Di Vental et al. formally defined the three pinch hysteresis loops of each element combining two consecutive state variables when an alternative source is applied to them, notably the current–voltage for the memristor, charge–voltage for the memcapacitor and current-flux for the meminductor [7]. Several works on chaotic oscillations based on the memristor have been investigated. Memristor models are used to replace the nonlinear negative resistance of the Chua circuit with that of the quadratic, cubic, piecewise linear model [8,9,10]. Using some models derived from HP memristor a chaotic circuit was explored in [11, 12]. In 2016, an application in cryptography was analyzed using a chaotic system based on the memristor [13]. In the same year, an optimal synchronization on a memristor circuit was investigated [14]. Unlike the memristor, few works have been investigated with the memcapacitor and the meminductor. Notably, some dynamic systems based on memcapacitor and meminductor are designed and studied through mathematical models [15,16,17,18], and equivalent circuits [19,20,21,22,23,24,25]. The smooth cubic nonlinearities used for memcapacitor and meminductor are proposed respectively by Fitch et al. [15], and Yuan et al. [26]. Very recently in 2019, a chaotic oscillator based on memcapacitor and meminductor has been proposed and investigated [27]. In that same year, Yuan et al. also proposed a new model of memcapacitor and its corresponding circuit used in a chaotic oscillator explored analytically and experimentally [28]. The previous works present simple chaotic circuits having at least three components. Another simple chaotic system based on meminductor was also proposed in 2017 by Birong et al. [29], whose authors investigated the complete dynamics.

Very recently, Ngoumkam and Kengne have proposed a minimal three-term chaotic Jerk system consisting of two linear terms and single hyperbolic sine nonlinearity. The authors have shown that the system can exhibit a coexistence of six different solutions for a set of parameters of the system [30]. Tchinga et al., in their work proposed the simplest chaotic circuit of Hartley’s oscillator family consisting of two components including an inductor and a JFET [31]. They also reported a simple autonomous chaotic oscillator with five jerky type components, considered to be the simplest of its kind, using a single operational amplifier [32]. In these works [27, 28], the authors have not carried out detailed dynamic studies. Very recently, Joshi and his collaborators presented a simple oscillator which can be both chaotic and hyperchaotic with a sine hyperbolic nonlinearity [33]. The authors also presented a simple Jerk system with hyperbolic sine nonlinearity which can be either from the category of hidden attractors or self-excited attractors according on the nature of the equilibrium points [34]. As a result, Joshi and Ranjan proposed a new simple chaotic oscillator consisting of a single operational amplifier with tank circuit to generate a chaotic waveform [35].

Since the challenge nowadays is to propose oscillators that are very simple both in their circuits and their equations, and presenting complex dynamic behaviors, in this paper a simple circuit consisting of an inductor and a memcapacitor that can exhibit a plethora of dynamic phenomena is proposed. This work is original and highlights the following innovations:

• (a) The proposed circuit is simple, consisting only of an inductor and a nonlinear active memcapacitor;The proposed circuit is simple, consisting only of an inductor and a nonlinear active memcapacitor;

• (b) The proposed circuit although simple, presents chaos and very complex dynamic behaviors including antimonotonicity, offset-boosting, multistability, and many others;

• (c) The mathematical model resulting from the proposed circuit is a simple jerk-type equation system that is easy to manipulate both analytically and numerically;

• (d) Multistability gives rise to the coexistence of two, three, four, and even six attractors, which is usually difficult to find in 3D jerk systems.

Considering the standard for the publication of new chaotic systems mentioned by Sprott in 2011 [36], the new proposed system satisfies all the three publication criteria and for this purpose enriches the literature on dynamic circuits and systems based on controlled-charge memcapacitor. The rest of this article is organized as follows: in Sect. 2, the mathematical model of a charge-controlled memcapacitor is proposed and used for designing a simple chaotic oscillator. Based on the mathematical model of the proposed circuit, its dynamics analysis is performed. Basic properties of the system are explored analytically in Sect. 3. In Sect. 4, bifurcation diagrams, Lyapunov stability diagrams for an overall system view, antimonotonicity, and multistability are investigated and explored. PSpice studies are explored in Sect. 5 for the validation of the proposed circuit and finally, a conclusion of the work in Sect. 6.

2 Memcapacitor model and a simple memcapacitor-based chaotic circuit

2.1 Memcapacitor model

In accordance with the general definition reported in Ref. [7], the charge-controlled memcapacitor is described as:

$$ \left\{ {\begin{array}{*{20}l} {v_{m} (t) = C^{ - 1} \left( {\sigma_{m} (t)} \right)q_{m} (t),} \hfill \\ {\dot{\sigma }_{m} (t) = q_{m} (t),} \hfill \\ \end{array} } \right. $$

(1)

where $v_{m} (t)$ is the voltage across the memcapacitor, $q_{m} (t)$ the charge passing through the memcapacitor at time $t$, $\sigma_{m} (t)$ the integral of $q_{m} (t)$, and $C^{ - 1}$ the inverse memcapacitance. In this paper, we define $C^{ - 1}$ according to the charge $q_{m} (t)$ and the non-linear element $\sigma_{m} (t)$ as follow:

$$ C^{ - 1} = \frac{{A_{1} }}{{q_{m} }}\sigma_{m} (t) + A_{2} \sigma_{m}^{4} (t) - A_{3} , $$

(2)

By substituting Eq. (2) in Eq. (1), we obtain the expression of the proposed memcapacitor model which is described as follows (time dependence was intentionally omitted for simplicity):

$$ \left\{ {\begin{array}{*{20}l} {v_{m} = \left( {\frac{{A_{1} }}{{q_{m} }}\sigma_{m} + A_{2} \sigma_{m}^{4} - A_{3} } \right)q_{m} ,} \hfill \\ {\dot{\sigma }_{m} = q_{m} ,} \hfill \\ \end{array} } \right. $$

(3)

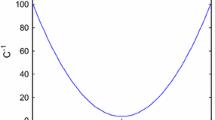
where $A_{1}$, $A_{2}$, and $A_{3}$ are positive real constants. In order to test the property of this proposed memcapacitor, we set $A_{1} = 1$, $A_{2} = 0.1$, $A_{3} = 1$ and $q_{m} (t) = U\sin (2\pi ft)$, by varying the frequency ($f$), amplitude ($U$) and initial conditions ($\sigma_{m} (0)$). The simulation results of the $v_{m} - q_{m}$ hysteresis curve are illustrated in Fig. 1. From this Fig. 1, a pinched hysteresis loop and a hysteresis collapse with increasing frequency ($f$), amplitude ($U$) and initial conditions ($\sigma_{m} (0)$) of the alternating voltage source are clearly observed and the considered memcapacitor faithfully respects the conditions described in [7], these curves conform to the definition of the negative memcapacitor's characteristics [37].

Fig. 1

$q_{m} - v_{m}$ hysteresis loop of the novel memcapacitor in different situation: a for f = 0.1 Hz, f = 0.5 Hz, and f = 1.5 Hz, b for U = 2 v, U = 3 v, and U = 5 v; c for $\sigma_{m} (0) = 1$, $\sigma_{m} (0) = 3$, and $\sigma_{m} (0) = 5$. Obtained for the fixed parameters $A_{1} = 1$, $A_{2} = 0.1$, and $A_{3} = 1$

2.2 A simple memcapacitor-based chaotic circuit

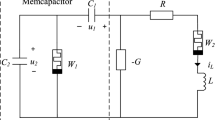
Based on the proposed memcapacitor model in Eq. (3), a simple chaotic oscillator consisting of an inductor and a memcapacitor is designed as shown in Fig. 2. Since the memcapacitor is the central element of the proposed circuit as responsible for the autonomy and also the complex behavior of the system thanks to its nonlinearity; it constitutes the only active element [38]. By applying Kirchhoff's laws to the circuit of Fig. 2 and taking the charge $q_{m}$ on the memcapacitor, the current $i$ through the inductor and the internal state variable $\sigma_{m}$ of the memcapacitor as state variables, the following differential equations of the circuit are obtained:

$$ \begin{aligned} & \frac{{d\sigma_{m} }}{dt} = q_{m} , \\ & \frac{{dq_{m} }}{dt} = i, \\ & \frac{di}{{dt}} = - \frac{r}{L}i - \frac{1}{L}v_{m} , \\ \end{aligned} $$

(4)

where $v_{m} = A_{1} \sigma_{m} + A_{2} \sigma_{m}^{4} q_{m} - A_{3} q_{m}$.

Fig. 2

The proposed memcapacitor-based chaotic oscillator where $r$ is the internal resistance of the inductor

Considering $x_{1} = \sigma_{m}$, $x_{2} = q_{m}$, $x_{3} = i$, $\alpha = \frac{{A_{3} }}{L}$, $\gamma = \frac{r}{L}$, $\beta = \frac{{A_{1} }}{L}$ and $\rho = \frac{{A_{2} }}{L}$, we obtain

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} ,} \hfill \\ {\dot{x}_{2} = x_{3} ,} \hfill \\ {\dot{x}_{3} = \alpha x_{2} - \gamma x_{3} - \beta x_{1} - \rho x_{2} x_{1}^{4} ,} \hfill \\ \end{array} } \right. $$

(5)

where $\alpha$, $\beta$, $\gamma$, and $\rho$ represent the system setting parameters (all are positive) and the dot represents differentiation with respect to time. By using simple mathematical rules, Eq. (5) can be written into the following simple jerk form

$$ \dddot x = \alpha \dot{x} - \gamma \ddot{x} - \beta x - \rho \dot{x}x^{4} $$

(6)

3 Basic dynamical characteristic

3.1 Dissipativity and symmetry

The necessary condition to study the dissipation of our model (5) is expressed by the following equation [39,40,41]:

$$ \nabla V = \frac{{\partial \dot{x}_{1} }}{{\partial x_{1} }} + \frac{{\partial \dot{x}_{2} }}{{\partial x_{2} }} + \frac{{\partial \dot{x}_{3} }}{{\partial x_{3} }} = - \gamma $$

(7)

Since $\gamma$ is a positive constant, the volume contraction rate Eq. (7) is always negative and the system (5) is dissipative. From Eq. (7), all trajectories are confined to space whose volume is zero [42] and, therefore, existing attractors can be chaotic.

Another important property is the symmetry, because it provides additional information about the dynamic behavior of the system. By performing the transformation $\left( {x_{1} ,\,x_{2} ,\,x_{3} } \right) \leftrightarrow \left( {x_{1} ,\, - x_{2} ,\, - x_{3} } \right)$ on the system (5), the solution remains the same. It implies that the system (5) is symmetric about the coordinate $x_{2}$ and $x_{3}$.

3.2 Stability of equilibrium point

To study the stability of equilibrium [43] point amounts to determine this point which is obtained by solving the system equation $\dot{x}_{1} = \dot{x}_{2} = \dot{x}_{3} = 0$ in order to know if it is stable or unstable. The only equilibrium point is the origin $E_{0} = \left( {0,\,0,\,0} \right)$. The Jacobian matrix of the system (5) around the fixed point $E_{0}$ is defined by:

$$ J = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ { - \beta } & \alpha & { - \gamma } \\ \end{array} } \right] $$

(8)

whose characteristic equation is:

$$ \lambda^{3} + \gamma \lambda^{2} - \alpha \lambda + \beta = 0 $$

(9)

According to the Routh–Hurwitz criterion, the characteristic Eq. (9) is an opposite sign, therefore, the equilibrium point $E_{0}$ is always unstable whatever the set of system parameters’. For the range of system parameters $\alpha = 1$, $\beta = 0.5$, and $\rho = 1$, the eigenvalues, as well as the stability of fixed point are summarized in Table 1. In light of the results of Table 1, the eigenvalues, solutions of characteristic Eq. (9) are obtained in the form:

$$ \begin{aligned} \lambda_{1} & = - \eta \\ \lambda_{2,3} & = \vartheta \pm i\varphi \\ \end{aligned} $$

(10)

with positive constants $\eta$ and $\vartheta$. We note that $\lambda_{1}$ is real negative whereas the complex conjugate eigenvalues $\lambda_{2}$ and $\lambda_{3}$ are all real positive roots. Therefore, the fixed point $E_{0}$ is unstable saddle-focus equilibrium and the existing attractors can be classified as self-excited attractors [44, 45].

Table 1 Eigenvalues and stability of equilibrium point with fixed parameter $\alpha = 1$, $\beta = 0.5$, and $\rho = 1$

4 Numerical simulations and dynamical behaviors

4.1 Bifurcation analysis and route to chaos

The system (5) is solved numerically using the standard four order Runge–Kutta algorithm and the largest Lyapunov exponent the Wolf algorithm [46] at $\Delta t = 10^{ - 3}$ s. The system reveals a complex and varied dynamic that reflects the bifurcation diagrams in Fig. 3(a) and their corresponding largest Lyapunov exponents of Fig. 3(b). It can be seen from Fig. 3 that chaos is obtained by period-doubling followed by a symmetry restoration when the parameter β is considered as a bifurcation control parameter. Two sets of data are superimposed and the color difference (blue by increasing the values of β and green by decreasing the values of the same parameter β) is observed to illustrate the symmetry property of the system. A good correspondence of periodicity of the system is observed on the bifurcation diagram and the largest Lyapunov exponent of Fig. 3. The transition to chaos is illustrated by the phase portraits in Fig. 4 when we consider the bifurcation diagram or the graph of Lyapunov exponent in green. In light of Fig. 4, the color difference (magenta and green) simply shows the asymmetrical behaviors. The attractors in blue are obtained when the symmetry of the system is restored.

Fig. 3

Bifurcation diagrams a showing local maxima of the coordinate $x_{1}$ versus β and the corresponding largest b of Lyapunov exponents plotted in the range $0.28 \le \beta \le 1$ for $\alpha = 1$, $\gamma = 0.5$ and $\rho = 1$

Fig. 4

Phase portraits showing routes to chaos in the system for varying the control parameter $\beta$: a period-1 limit cycle for $\beta = 1$, b period-2 limit cycle for $\beta = 0.9$, c period-4 limit cycle for $\beta = 0.885$, d asymmetric chaos for $\beta = 0.8$, e symmetric chaos for $\beta = 0.7$, f period-3 limit cycle for $\beta = 0.56$, g symmetric chaos for $\beta = 0.4$, and h period-1 limit cycle for $\beta = 0.3$. Initial conditions $(x_{1} (0),\;x_{2} (0),\;x_{3} (0))$ are $\left( {0,\; \pm \;1,\;0} \right)$ for a–d and $\left( {0,\;1,\;0} \right)$ for e–h

The other parameters of the system in particular γ and α are also considered as bifurcation control parameters in a great interest to observe their influences on the dynamic behavior of the system. Thus, the bifurcation diagrams of Figs. 5(a) and 6(a) are obtained by plotting the local maxima of the state variable $x_{1}$ as a function of γ and α respectively. The corresponding graphs of Lyapunov exponents are shown in Figs. 5(b) and 6 (b) showing a good agreement between the periodicity of bifurcation diagrams. Moreover, striking phenomena are observed when a parameter $a$ is introduced on the second line of the system (5). Note that this parameter $a$ represents an intrinsic property that is highlighted during the design of the emulator circuit of the memcapacitor (see Sect. 5). Interesting behaviors are observed when it considered as a bifurcation control. Thus Fig. 7(a) shows two superimposed bifurcations diagrams obtained by varying the bifurcation control parameter $a$ in the range $1 \le a \le 12$ (see caption of Fig. 7). The corresponding graphs of Lyapunov exponents in Fig. 7(b) justify the correspondence between periodicity and the transition to chaos.

Fig. 5

Bifurcation diagrams a showing local maxima of the coordinate $x_{1}$ versus $\gamma$ and the corresponding largest b of Lyapunov exponents plotted in the range $0.35 \le \gamma \le 0.75$ for $\alpha = 1$, $\beta = 0.7$ and $\rho = 1$

Fig. 6

Bifurcation diagrams a showing local maxima of the coordinate $x_{1}$ versus $\alpha$ and the corresponding largest b of Lyapunov exponents plotted in the range $1 \le \alpha \le 4.5$ for $\gamma = 0.8$, $\beta = 2$ and $\rho = 1$

Fig. 7

Bifurcation diagrams a showing local maxima of the coordinate $x_{1}$ versus $a$ and their corresponding largest b of Lyapunov exponents plotted in the range $1 \le a \le 12$ for $\alpha = 1$, $\gamma = 0.5$, $\beta = 0.7$ and $\rho = 1$

Note that the color difference in Fig. 7 highlights both the symmetry and hysteresis behaviors of the system that will be exploited in the following sections. With regard to Figs. 5, 6 and 7, the same transition towards the chaos of Fig. 3 is observed when considering γ, α, and $a$ as bifurcation control parameters.

4.2 Lyapunov stability diagrams of the proposed system

It is always interesting to have a global idea of the dynamic behavior of a chaotic system for a better analysis of the system by studying the influence of one parameter on another. In the same line, we decided to study the influence of the different bifurcation control parameters presented previously. To better understand the type of dynamic behavior of the system (5), the Lyapunov exponent bands are enabled each time to characterize the different observed behaviors. Thus, Fig. 8(a) shows the effect of the parameter β on the parameter γ for the choice of the other parameters $\alpha = 1$ and $\rho = 1$ where the type of the dynamic behavior is a function at the same time both of the color and the value of the correspondence of the Lyapunov exponent. In light of the Lyapunov stability diagram of Fig. 8(a), the blue shadings correspond to the periodic attractors (negative Lyapunov exponents), the cyan marks attractors of high periodicity and more and more attractors of strong chaoticity for the data in dark red. When keeping set the parameters $\alpha = 1$, $\beta = 0.7$, and $\rho = 1$; the influence of the parameter $a$ on γ is also observed in Fig. 8(b) which is strongly dominated by the high periodicity behaviors. The limit cycles of period-1 are weakly observed for this set of parameters in blue, the periodicity increases in cyan until the chaotic behavior represented by the other colors. Similarly, the influence of the parameters $a$ and β in Fig. 8(c) which presents a situation opposite to that of Fig. 8(b) because the periodic behavior dominates the chaotic one by the strong cyan coloration. The rest of parameters are $\alpha = 1$, $\gamma = 0.5$, and $\rho = 1$.

Fig. 8

Standard Lyapunov stability diagrams a, b, and c in the $\left( {\gamma ,\,\beta } \right)$, $\left( {a,\,\gamma } \right)$, and $\left( {a,\,\gamma } \right)$ plane obtained by scanning upward the values of control parameters where Lyapunov exponents are unable to discriminate individual behaviors. (Color figure online)

Let us note that this way of representation is very important for the good control of the dynamic behavior of the system (5) and even for practical studies on the choice of the parameters of the system while having an idea on the dynamic behavior. In the literature, these Lyapunov stability diagrams are used namely in [47, 48].

4.3 Multistability and offset boosting

Unlike the bifurcation diagram and the largest of Lyapunov exponent where a so-called bifurcation parameter is varied for a qualitative analysis, there is an unusual and striking phenomenon which is obtained by varying only the initial conditions for the same set of given parameter's system and commonly called multistability or coexistence of several stable states (attractors). Each attractor that coexists corresponds to a single initial condition given and it is in this sense that we have explored in literature different types of attractors (fixed point, periodic, quasi-periodic, chaotic, and hyperchaotic) that coexist [49]. Considering the bifurcation diagram of Fig. 3, hysteresis windows are observed in the $0.285 \le \beta \le 0.208$ and $0.83 \le \beta \le 0.86$ ranges. It is obvious that there is a coexistence of two different attractors in the first zone and when the bifurcation diagram of Fig. 3 is widened in the second range as in Fig. 9, a coexistence of several kings of four types of attractors of different natures only by varying only the initial conditions (see Fig. 13). Similarly, when widening the bifurcation diagram and the graph of Lyapunov exponents of Fig. 6 in the range $4.23 \le \alpha \le 4.50$, a coexistence of three symmetrical solutions are observed, including the bifurcation like sequence of local maxima of $x_{1}$ versus the initial conditions $x_{1} (0)$ (keeping the other initial variables $x_{2} (0) = 2$, $x_{3} (0) = 5$) of Fig. 10(a). We can have a coexistence of two chaotic attractors with a periodic attractor of period-1 (see Fig. 14) or a coexistence of two periodic attractors with a chaotic attractor ($\alpha = 4.44$ for example).

Fig. 9

Highlighting the hysteresis window of the bifurcation diagrams of Fig. 3 (a) and their corresponding largest b of Lyapunov exponents plotted in the range $0.83 \le \beta \le 0.86$ showing the different types of coexistences

Fig. 10

a Bifurcation like sequence showing local maxima of the coordinate $x_{1}$ versus initial state $x_{1} (0)$ plotted in the range 0.4 ≤ $x_{1} (0)$ ≤ 1.2 while keeping $\alpha = 4.49$, $\, x_{2} (0) = 2$, and $x_{3} (0) = 5$; enlargement of bifurcation diagrams b of Fig. 5 and their corresponding largest c of Lyapunov exponents plotted in the range $4.23 \le \alpha \le 4.5$ showing the region in which the system experiences the coexistence of three symmetrical attractors

In the same line, a coexistence of six asymmetric solutions is obtained when widening the bifurcation diagram of Fig. 7 as illustrated in Fig. 11(a) and for a set of initial values of Fig. 11(b), the zoom of the bifurcation diagram of Fig. 11(c) is shown where three branches of different bifurcations can be easily observed in accordance with the initial conditions of Fig. 11(b) a sample of this coexistence of six attractors is presented in Fig. 16.

Fig. 11

a Enlargement of bifurcation diagrams a of Fig. 7 in the range $7 \le a \le 8.9$ showing the region in which the system develops the coexistence of six asymmetrical attractors; Bifurcation like sequence b showing local maxima of the coordinate $x_{1}$ versus initial state $x_{2} (0)$ plotted in the range 0.15 ≤ $x_{2} (0)$ ≤ 0.4 while keeping $a = 7.42$, $\, x_{1} (0) = 0.0$, and $x_{3} (0) = 0.0$; Enlargement of the bifurcation diagrams c of Fig. 10(b) in the interval $7.355 \le a \le 7.538$ showing the zone of coexistence of six asymmetrical solutions

To illustrate the different coexistence mentioned above, Fig. 12 shows a coexistence of two symmetrical attractors (chaotic in (a) with a limit cycle of period-1 in (b)) for $\beta = 0.3$. The coexistence of four asymmetric attractors are illustrated in Fig. 13 where we respectively have four chaotic attractors of Fig. 13(${\text{a}}_{{1}}$) and (${\text{b}}_{{1}}$) for $\beta = 0.8425$, two chaotic attractors (${\text{a}}_{2}$) with two periodic attractors of period-3 (${\text{b}}_{2}$), and finally a coexistence of four periodic attractors (of period-4 (${\text{a}}_{3}$) and period-3 (${\text{b}}_{3}$)). Other works whose authors also show the coexistence of four different attractors are investigated in [50, 51].

Fig. 12

Phase portraits illustrating the coexistence of two symmetric attractors (chaotic (a) and cycle limit of period-1 (b)) obtained for the set parameters $\beta = 0.3$, $\alpha = 1$,$\gamma = 0.5$, and $\rho = 1$. Initial conditions are $\left( {0,\;0.4,\;0} \right)$ and $\left( {0,\;1,\;0} \right)$ respectively

Fig. 13

Phase portraits illustrating the coexistence of four different types of attractors obtained for the fixed set $\alpha = 1$,$\gamma = 0.5$, $\rho = 1$,$\, x_{1} (0) = 0.0$, and $x_{3} (0) = 0.0$: four different chaotic attractors for $\beta = 0.8425$, $x_{2} (0) = \pm 0.4$ (a₁) and $x_{2} (0) = \pm 0.7$ (b₁); two chaos with two limit cycles of period-3 for $\beta = 0.85$, $x_{2} (0) = \pm 0.4$ (a₂) and $x_{2} (0) = \pm 0.7$ (b₂); two limit cycles of period-5 with two limit cycles of period-3 $\beta = 0.8526$, $x_{2} (0) = \pm 0.4$ (a₃) and $x_{2} (0) = \pm 0.7$ (b₃)

More interestingly, a coexistence of three symmetrical attractors and their correspondence densities spectral of frequency is presented in Fig. 14 where in (a) a limit cycle of period-1 coexists with two chaotic attractors (b) and (c) (for more detail see caption of the figure). Each attractor of Fig. 14 corresponds to a space that it magnetizes in the phase space of the initial conditions. Thus, cross-section of a basin of attraction (all of the initial conditions that give rise to one or another attractor) is presented in Fig. 15 in the $\left( {x_{1} (0),\,x_{2} (0)} \right)$, $\left( {x_{1} (0),\,x_{3} (0)} \right)$, and $\left( {x_{2} (0),\,x_{3} (0)} \right)$ planes of the initial conditions where each color corresponds to a coexisting attractor of Fig. 14 (see caption of Fig. 15).

Fig. 14

Phase portraits in the ($x_{1} ,\,x_{2}$) plan and their corresponding spectral power density obtained for the parameters of the system $\beta = 2$,$\gamma = 0.8$, $\rho = 1$, and $\alpha = 4.49$ illustrating the coexistence of three symmetrical solutions: a limit cycle of period-1 with two different chaotic attractors (b, c). Initial conditions are $\left( {0.8,\,2,\,5} \right)$,$\left( {0.5,\,2,\,5} \right)$, and $\left( {0.6,\,2,\,5} \right)$ respectively

Fig. 15

Cross sections of basins of attraction for $x_{3} (0) = 0$, $x_{2} (0) = 0$, and $x_{1} (0) = 0$ respectively, showing the influence of each attractors of Fig. 14 where the blue basin represents the periodic attractor, those in green and yellow the different chaotic attractors, and the red areas denote the unbounded dynamics obtained for the same set of parameters in Fig. 14

Figure 16 shows the coexistence of the six attractors and their corresponding frequency diagrams where we can easily distinguish the periodicity of each attractor. This figure presents four periodic attractors (a) and (b) that coexist with the other two chaotic (c) for a set of system parameters $\alpha = 1$, $\beta = 0.7$ $\gamma = 0.5$, $\rho = 1$, and $a = 7.42$ but by varying only the initial condition $x_{2} (0)$. Several works also explores the coexistence of six solutions in the literature [52, 53].

Fig. 16

Phase portraits in the ($x_{1} ,\,x_{2}$) plan and their corresponding spectral power density obtained for the parameters of the system $\beta = 0.7$, $\alpha = 1$, $\gamma = 0.5$, $\rho = 1$, and $a = 7.42$ illustrating the coexistence of six asymmetrical solutions: a two limits cycle of period-5, b two limits cycle of period-6, with two chaotic attractors c. Initial conditions are $\left( {0,\,0.375,\,0} \right)$,$\left( {0,\,0.15,\,0} \right)$, and $\left( {0,\,0.8,\,0} \right)$ respectively

Another form of coexistence of the attractors is offset boosting [54, 55] which is obtained by varying a single parameter $k$ added to the state variable $x_{1}$ ($x_{1} + k$). Note that this parameter is not added to hazard and the only condition of its existence is that when a state variable of the system appears on a single line as in [56], it is possible that this system develops the phenomenon of offset boosting. Only the variable $x_{1}$ can be booster and thus, for discrete values of $k$, we have attractors of the same nature that appear in a staggered way. An example of this phenomenon is presented in Fig. 17 where the chaotic attractor has seen booster on several positions (see caption of the figure for the details).

Fig. 17

Offset boosting of the chaotic attractor for varying the control parameter k: in ($x_{1} ,\,x_{2}$) and ($x_{1} ,\,x_{3}$) planes for $k = - 2$ (blue), $k = 0$ (green), and $k = 2$ (magenta). Others parameters are $\alpha = 1$, $\beta = 0.8$, $\gamma = 0.5$, and $\rho = 1$

4.4 Antimonotonicity

Next to the multistability which is a strange and unpredictable phenomenon, it exists to the other which is obtained by appearance followed by the spontaneous disappearance of the periodic bubbles of bifurcations. This birth followed by the disappearance of the bifurcation bubbles is called antimonotonicity and is explored in several works namely in [57]. This new phenomenon is observed in our system (5) and illustrated in Fig. 18 for different discrete values of the parameter $\alpha$ considering $\beta$ as the bifurcation control parameter (see caption of Fig. 18). To justify the existence of the phenomenon of antimonotonicity observed in our system, we explore the discrete first return map dynamics. From the positions of two critical return points $C_{1}$ and $C_{2}$ consecutive to $t = t_{n}$ and $t = t_{n + 1}$, we have drawn the diagram of Fig. 19$\left( {M_{n + 1} (x_{2} ) = f(M_{n} (x_{2} ))} \right)$. Note that the points $C_{1}$ and $C_{2}$ respectively justify the apparition and destruction of periodic bubble bifurcations [58, 59].

Fig. 18

Bifurcation diagrams (showing the phenomenon of antimonotonicity) obtained by plotting the local maxima of the state variable $x_{1}$ as a function of the control parameter $\beta$: period-2 bubble for $\alpha = 0.47$; period-4 bubble for $\alpha = 0.48$; period-8 bubble for $\alpha = 0.482$; four chaotic bubbles for $\alpha = 0.485$; two chaotic bubbles for $\alpha = 0.488$; Full Feigenbaum remerging tree at $\alpha = 0.5$. The rest of fixed parameters are $\gamma = 0.5$ and $\rho = 1$

Fig. 19

First-return map of the maxima of the coordinate $x_{2}$. This map is indicative of one-dimensional maps with two critical points confirming the occurrence of antimonotonicity in the proposed memcapacitor oscillator. The parameters are: $\alpha = 0.5$, $\beta = 0.34$, $\gamma = 0.5$, and $\rho = 1$

5 Circuit diagram and PSpice results

The purpose of this section is to propose a simple electronics circuit in order to validate the correctness of the proposed model [60]. Since there is no standard memcapacitor circuit in the literature, building an equivalent memcapacitor circuit is a big challenge. In Fig. 20, the memcapacitor-based circuit simulation model is designed, where the proposed charge-controlled memcapacitor is presented by the dotted block. The circuit components of Fig. 20 are in others the operational amplifiers ${U}_{1}A$ to ${U}_{1}D$ and ${U}_{2}A$ of the integrated circuits $TL084$, capacitors ${C}_{1}$ and ${C}_{2}$, the real inductance L with its internal resistance $r$, the resistors $R$ and ${R}_{i}$ for $i = \left\{ {1\,\,to\,3} \right\}$, and the multipliers defined by ${M}_{1}$, ${M}_{2}$, and ${M}_{3}$. A symmetric voltage of ± 15 V serves to supply the circuit components. By exploiting the Kirchhoff laws, the differential system describing the dynamics of the circuit of Fig. 20 is obtained as follows:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{d\upsilon_{{C_{1} }} }}{dt} = \frac{1}{RC}\upsilon_{{C_{2} }} ,} \hfill \\ {\frac{{d\upsilon_{{C_{2} }} }}{dt} = \frac{1}{RC}R_{0} i_{L} ,} \hfill \\ {\frac{{di_{L} }}{dt} = - \frac{r}{L}i_{L} - \frac{1}{L}v_{m} ,} \hfill \\ \end{array} } \right. $$

(11)

where $v_{m} = - R\left( { - \frac{1}{{R_{2} }}\upsilon_{{C_{1} }} + \frac{1}{{R_{3} }}\upsilon_{{C_{2} }} - \frac{1}{{R_{1} }}\upsilon_{{C_{1} }}^{4} \upsilon_{{C_{2} }} } \right)$.

Fig. 20

Circuit realization of the memcapacitor-based chaotic oscillator

To implement the proposed oscillator conveniently, we introduce the scaling factor $RC$. Thus, by carrying out the variable change $t = \tau RC$, system (11) becomes:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{d\upsilon_{{C_{1} }} }}{d\tau } = \upsilon_{{C_{2} }} } \hfill \\ {\frac{{d\upsilon_{{C_{2} }} }}{d\tau } = R_{0} i_{L} } \hfill \\ {\frac{{di_{L} }}{d\tau } = - \frac{rRC}{L}i_{L} - \frac{{R^{2} C}}{{LR_{2} }}\upsilon_{{C_{1} }} + \frac{{R^{2} C}}{{LR_{3} }}\upsilon_{{C_{2} }} - \frac{{R^{2} C}}{{LR_{1} }}\upsilon_{{C_{1} }}^{4} \upsilon_{{C_{2} }} } \hfill \\ \end{array} } \right. $$

(12)

where $\upsilon_{{C_{1} }}$ and $\upsilon_{{C_{2} }}$ are the voltages across the capacitors $C_{1}$ and $C_{2}$; $i_{L}$ the current of the inductor$L$. With the following variable change $C_{1} = C_{2} = C$, $X_{1} = \upsilon_{{C_{1} }}$, $X_{2} = \upsilon_{{C_{2} }}$, $X_{3} = i_{L}$, $\alpha = \frac{{R^{2} C}}{{LR_{3} }}$, $\gamma = \frac{rRC}{L}$, $\beta = \frac{{R^{2} C}}{{LR_{2} }}$, $\rho = \frac{{R^{2} C}}{{LR_{1} }}$, and $a = R_{0}$( the added parameter of Sect. 4) the dynamics of the electronic circuit of Fig. 20 and the one of Fig. 2 are equivalents.

The circuit diagram of Fig. 20 is simulated by PSpice software and the complex behaviors are carried out through the phase portraits. For the choice of the resistors ${R}_{1}=25\Omega$ and ${R}_{2}=13K\Omega$, we obtain the asymmetric chaotic attractors of Fig. 21. For the resistors ${R}_{1}=50\Omega$ and ${R}_{2}=11K\Omega$, we obtain the symmetric chaotic attractors of Fig. 22 on different planes of the system’s coordinate. In light of Figs. 21 and 22, a good agreement is observed between the behaviors obtained by PSpice simulations of the left column and those obtained by the numerical resolution of the right column. Obtaining these chaotic behaviors confirms the feasibility of the proposed model, which is justified by the concordance between the results obtained.

Fig. 21

Asymmetric chaotic attractor in the different planes obtained by PSpice simulations for ${\mathrm{R}}_{1}=25\Omega$ and ${\mathrm{R}}_{2}=13\mathrm{ k\Omega }$. The initial conditions ($\upsilon_{{C_{1} }} (0),\,\upsilon_{{C_{2} }} (0),\,\,i_{L} (0)\,$) are (0.1, 0, 0)

Fig. 22

Symmetric chaotic attractor in the different planes obtained by PSpice simulations for ${\mathrm{R}}_{1}=50\Omega$ and ${\mathrm{R}}_{2}=11\mathrm{ k\Omega }$. The initial conditions ($\upsilon_{{C_{1} }} (0),\,\upsilon_{{C_{2} }} (0),\,\,i_{L} (0)\,$) are (0.1, 0, 0)

6 Conclusion

A novel mathematical model of charge-controlled memcapacitor and its corresponding circuit emulator is introduced in this paper. Based on this model, a simple chaotic oscillator is proposed and studied in detail. The simplicity of the circuit and the complexity of the dynamic behavior are the particular characteristics of the proposed model. The entire dynamics of the system has been explored giving rise to a plethora of phenomena including multistability (through the coexistence of several types of dynamic behavior), antimonotonicity, and offset boosting. For the validation and the feasibility of the model, a circuit realization has been carried out via PSpice simulations whose results are in good agreement. This discovery enriches for this purpose the literature on dynamic systems in general and the family of oscillators based on the charge-controlled memcapacitor, in particular by rich, varied and complex results.