Quantum-inspired evolutionary algorithm for analog test point selection

Abstract

An important problem that arises in fault diagnosis of analog circuit for fault dictionary technique is the test point selection, which is known to be NP-hard. This paper develops a mathematical optimization model for analog test point selection (ATPS) problem and proposes a novel method to solve it based on quantum-inspired evolutionary algorithm (QEA). The proposed method uses the solution produced by the inclusive algorithm to initialize Q-bit individuals and presents a new fitness function to search the global minimum test point set. In addition, an approach for dynamically determining the magnitude of rotation angle is introduced to accelerate the convergent speed. The efficiency of the proposed algorithm is proven by one practical analog circuit example and a group of statistical experiments. Results show that the proposed algorithm, compared with other methods, finds the global minimum set of test points more efficiently and more accurately.

1 Introduction

With the broad application and increasing complexity of analog circuit, methods for fault diagnosis of analog circuits have gained much attention. It is usually classified into two categories with simulation-before-test (SBT) and simulation-after-test (SAT). Probabilistic and fault dictionary techniques fall into SBT, whereas optimization, fault verification, and parameter identification techniques fall into SAT [1]. Fault dictionary technique is the most popular and practical method applied to diagnose catastrophic faults in analog circuits [2]. It mainly includes three important phases: fault dictionary construction, test point selection, and fault diagnosis. This paper deals with the second phase.

The problem of analog test point selection (ATPS) aims to find the least number of test points that can isolate all given faults. This problem has been proven to be NP-hard and the global minimum set of test points can only be guaranteed by exhaustive search which is only applicable to small-size analog circuits [3, 4]. Up to now, a lot of researches have been studied in this area. Varghese et al. [5] proposed a heuristic method to find an optimum set of test points based on the concept of confidence level. Hochwald and Bastian [6] introduced the concept of ambiguity sets and developed logical rules to select test points. Lin and Elcherif [2] proposed two heuristic methods for test point selection based on the integer-coded dictionary. Prasad and Babu [3] proposed two new inclusive strategies and one efficient polynomial-time algorithm to generate the minimum set using integer code sorting. An entropy-based approach, using entropy index (EI) as a criterion to choose test points, was proposed by Starzyk and Lin [4]. Its complexity was proven to be less than that of polynomial-time algorithms. More recent studies by Yang et al. [7, 8] transformed the test point selection problem into a directed acyclic graph search problem, and made use of information theoretic entropy to guide graph search.

All above mentioned methods belong to greedy algorithm, which is less time consuming, but rarely find the global optimum solution. Recently, two intelligent optimization algorithms have been applied to solve this problem and demonstrated with promising performance, such as genetic algorithm (GA) [9] and discrete particle swarm optimization (DPSO) [10]. GA has excellent global search ability, whereas it has disadvantage of slow convergence. On the contrary, DPSO converges quickly, but it easy gets trapped into local optima. Therefore, an algorithm with less time consumption and high global searching ability is needed.

In 2002, Han et al. [11] proposed quantum-inspired evolutionary algorithm (QEA), which is a novel evolutionary algorithm based on principles and concepts of quantum computing, such as superposition, interference and entanglement. Compared with traditional evolutionary algorithm, QEA can more easily achieve the right balance between exploration and exploitation. In QEA, probabilistic representation is employed to define an individual, called Q-bit individual, which has a better characteristic of maintaining population diversity than other counterparts such as binary, numeric and symbolic. Therefore, QEA can explore whole search space with a relative small population size. In the last decade, QEA attracted a lot of attention and has successfully been applied to knapsack problem [11], unit commitment problem [12, 13] and multiple-fault diagnosis [14].

This paper is devoted to applying QEA to solve ATPS problem and proposes an efficient QEA-based ATPS method (QEA-ATPS). Section 2 first summarizes the integer-coded dictionary approach and then formulates the ATPS problem. The principle of QEA is described in Sect. 3. In Sect. 4, the proposed QEA-APTS method is elaborated on. Section 5 demonstrates the efficiency of QEA-APTS method through one practical circuit and statistical experiments. The comparison results with other methods are also listed in this section. Finally, the conclusions follow in Sect. 6.

2 Problem formulations

2.1 Integer-coded dictionary

We start first by describing the integer-coded dictionary, which was first proposed by Lin and Elcherif [2] and subsequently researched by Prasad and Babu [3]. During the before-test stage, the circuit under test (CUT) is simulated for all assumed fault states (including fault-free case $f_{0}$) and the corresponding responses (voltage values in general) at each test point are stored. Table 1 presents the fault dictionary for a hypothetical CUT with five potential fault states $f_{1} - f_{5}$ and four test points $n_{1} - n_{4}$.

Table 1 Fault dictionary

Integer-coded dictionary is a two dimensional integer matrix. Its rows represent all anticipated faults (including fault-free condition), while its columns represent all available test points. For each test point, all faults are divided into several ambiguity sets base on their voltage values, and then a specific integer code is assigned to each ambiguity set which is defined as any two faulty conditions that fall into the same ambiguity set if the gap between the voltage values produced by them is less than 0.7 V [6]. Table 2 shows an integer-coded dictionary derived from Table 1. The detailed description of integer-coded dictionary technique can be found in the literature [2].

Table 2 Integer-coded dictionary

2.2 Optimization model

Let ${\mathbf{F}} = \left\{ {f_{0} ,f_{1} , \ldots,f_{m} } \right\}$ be the set of all potential faults, ${\mathbf{N}} = \left\{ {n_{1} ,n_{2} , \ldots ,n_{n} } \right\}$ be the set of available test points, ${\mathbf{D}} = \left( {d_{ij} } \right)_{{\left( {m + 1} \right) \times n}}$ be the relevant integer-coded dictionary of CUT, where subscript $m$ is the number of potential faults and $n$ is the number of test points.

Let ${\mathbf{N}}_{s} = \left\{ {n_{{s_{1} }} ,n_{{s_{2} }} , \ldots ,n_{{s_{k} }} } \right\} \subseteq {\mathbf{N}}$ be a subset of ${\mathbf{N}}$, ${\mathbf{D}}_{is} = \left( {d_{{is_{1} }} ,d_{{is_{2} }} , \ldots ,d_{{is_{k} }} } \right)$ be the signature of fault $f_{i}$ formed from ${\mathbf{N}}_{s}$, where $s_{j} \in \left\{ {1,2, \ldots ,n} \right\}\left( {j = 1,2, \ldots ,k} \right)$.

If fault $f_{i}$ and any other one fault $f_{j}$, we always have ${\mathbf{D}}_{is} \oplus {\mathbf{D}}_{js} = 1$, then the fault $f_{i}$ is diagnosable by ${\mathbf{N}}_{s}$. Where notation $\oplus$ is “exclusive OR” calculation and employed to compare the difference between ${\mathbf{D}}_{is}$ and ${\mathbf{D}}_{js}$; if the corresponding elements of ${\mathbf{D}}_{is}$ and ${\mathbf{D}}_{js}$ are all identical, then the result is 0, otherwise 1.

Denote ${\mathbf{F}}_{s}$ by the set of faults diagnosed by ${\mathbf{N}}_{s}$, that is

$$ {\mathbf{F}}_{s} = \left\{ {f_{i} \left| {f_{i} \in {\mathbf{F}},\sum\limits_{{\forall f_{j} \in F}} {{\mathbf{D}}_{is} \oplus {\mathbf{D}}_{js} = m} } \right.} \right\} $$

(1)

Based on the above description, ATPS problem is then formulated as

$$ \left\{ \begin{array}{l} \hbox{Min} \left| {{\mathbf{N}}_{s} } \right| \\ s.t.{ |}{\mathbf{F}}_{s} | = |{\mathbf{F}}| \\ \end{array} \right. $$

(2)

where, $| \cdot |$ is the cardinality of set. Thus, the problem of using the minimum number of test points to isolate all faults is equivalent to distinguish all rows of integer-coded dictionary by minimum number of columns.

3 QEA

QEA is a population-based probabilistic evolutionary algorithm, which integrates the concepts from quantum computing to enhance conventional evolutionary algorithms. QEA is characterized by using Q-bit representation to initialize population, making binary solutions from Q-bit individuals by observation and taking Q-gate as a variation operator to update Q-bit individuals.

In QEA, the smallest information unit is called Q-bit, which is defined as follow

$$ q = \left[ \begin{gathered} \alpha \hfill \\ \beta \hfill \\ \end{gathered} \right] $$

where $\alpha$ and $\beta$ are a pair of complex numbers, which satisfy $\left| \alpha \right|^{2} + \left| \beta \right|^{2} = 1$. The modulus $\left| \alpha \right|^{2}$ and $\left| \beta \right|^{2}$ give the probability that a Q-bit will collapse to state “0” and “1”, respectively. The states of a Q-bit may be in “0” state, in “1” state or in any superposition of the two.

A Q-bit individual with a string of $k$ Q-bits is defined as

$$ {\user2{q}} = \left[ \begin{gathered} \alpha_{1} \hfill \\ \beta_{1} \hfill \\ \end{gathered} \right. \, \left| \begin{gathered} \, \alpha_{2} \hfill \\ \, \beta_{2} \hfill \\ \end{gathered} \right. \, \left| \begin{gathered} \ldots \hfill \\ \ldots \hfill \\ \end{gathered} \right. \, \left. {\left| \begin{gathered} \, \alpha_{k} \hfill \\ \, \beta_{k} \hfill \\ \end{gathered} \right.} \right] $$

(3)

where $\left| {\alpha_{i} } \right|^{2} + \left| {\beta_{i} } \right|^{2} = 1,i = 1,2, \ldots ,k$. The merit of Q-bit representation is that a Q-bit individual with $k$ Q-bits can represent all $2^{k}$ possible binary solutions in search space probabilistically. Therefore, QEA requires only a small population size to provide good population diversity.

To evaluate each Q-bit individual’s fitness and find the desired solution, all Q-bit individuals need to be transformed into binary solutions by observation. When a Q-bit $\left[ {\alpha_{i} ,\beta_{i} } \right]^{T}$ is observed, its corresponding binary character $a_{i}$ is determined by comparing $\left| {\beta_{i} } \right|^{2}$ to a uniformly distributed number $Rnd$ in [0, 1] for $i = 1,2, \ldots ,k$, i.e.

$$ a_{i} = \left\{\begin{array}{ll} 1, & Rnd < \left| {\beta _{i} } \right|^{2} \\ 0, & otherwise \\\end{array}\right. $$

Thus, a binary solution ${\user2{A}} = \left[ {a_{1} ,a_{2} , \ldots ,a_{k} } \right]$ can be obtained after all Q-bits in ${\user2{q}}$ have been observed.

A Q-gate is a variation operator of QEA to drive Q-bit individuals toward better solutions. Its function is similar to crossover and mutation operations in GA. There are several Q-gates, such as not gate, controlled not gate, rotation gate, hadamard gate, etc. [11]. Among them, rotation gate is the most poplar one and widely employed in QEA. The rotation gate $U\left( {\Updelta \theta_{i} } \right)$ and the update operation are given as follows

$$U(\Delta \theta _{i} ) = \left[ {\begin{array}{cc} {\cos (\Delta \theta _{i} )} & { - \sin (\Delta \theta _{i} )} \\ {\sin (\Delta \theta _{i} )} & {\cos (\Delta \theta _{i} )} \\\end{array}} \right] $$

(4)

$$ \left[ \begin{gathered} \alpha_{i}^{\prime } \hfill \\ \beta_{i}^{\prime } \hfill \\ \end{gathered} \right] = U\left( {\Updelta \theta_{i} } \right)\left[ \begin{gathered} \alpha_{i} \hfill \\ \beta_{i} \hfill \\ \end{gathered} \right] $$

(5)

In which, $\Updelta \theta_{i}$ is the rotation angle of the ith Q-bit in ${\mathbf{q}}$ toward either 0 or 1 state, $\left[ {\alpha_{i}^{\prime } ,\beta_{i}^{\prime } } \right]^{T}$ is the ith Q-bit of the updated Q-bit individual. In [11], rotation angle is determined through a pre-defined lookup table as shown in Table 3, and the value of $\theta$ is set to be $0.01\pi$ for solving knapsack problem.

Table 3 Example of lookup table for determining rotation angle

In Table 3, $a_{i}$ and $b_{i}$ are the ith binary control variables in solution ${\mathbf{A}}$ and the best solution ${\mathbf{B}}$, respectively; $f\left( \cdot \right)$ represents the fitness function.

4 QEA application to ATPS problem

QEA has been demonstrated its better performance on many practical optimization problem, but it hasn’t been used in the domain of ATPS. In the following, we elaborate on the proposed QEA-ATPS algorithm from three particular aspects.

4.1 Initialization of Q-bit individuals

Initialization is an important step of QEA. At the beginning, a population of Q-bit individuals $\user2{Q}(t) = [\user2{q}_{1}^{t} ,\user2{q}_{2}^{t} , \ldots ,\user2{q}_{G}^{t} ]$ is initialized. Where, $G$ is the population size, and $t$ is the generation counter. In original QEA, $\alpha_{i}^{0}$ and $\beta_{i}^{0}$, $i = 1,2, \ldots ,n$, of all $\left. {{\mathbf{q}}_{j}^{0} = {\mathbf{q}}_{j}^{t} } \right|t = 0,j = 1,2, \ldots ,G$, are initialized with ${1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }}$; for ATPS problem, it means that all combinations of test points are initialized with the same probability, i.e. $1/2^{n}$. In [15], the authors have verified that the initialization of Q-bit individuals with appropriate values can accelerate the convergence speed and advance solution accuracy. In this section, a novel initialization method is proposed by employing the solution produced by the inclusive algorithm in [3].

Assuming that the solution generated by the inclusive algorithm is ${\mathbf{X}}_{0} = \left[ {x_{1} ,x_{2} , \ldots ,x_{i} , \ldots ,x_{n} } \right]$, where, if the ith test point $n_{i}$ is selected, $x_{i}$ is equivalent to 1; otherwise, $x_{i}$ is 0. From computation experience, the inclusive algorithm, though less time consuming, usually produces a local optimum solution. Therefore, taking advantage of information in $X_{0}$, the values of Q-bits can be initialized properly to represent the promising search space with small distance to the global optimum solution. For this reason, two special expressions of Q-bits are proposed in (6) and (7). If there are $L$($1 \le L \le G$) Q-bit individuals need to be initialized in this way, the $l$th ($l = 1,2, \ldots ,L$) Q-bit individual ${\mathbf{q}}_{l}$ can be initialized by replacing the states “1” and “0” in $X_{0}$ with the following $Q_{l} \left( 1 \right)$ and $Q_{l} \left( 0 \right)$, respectively.

$$ Q_{l} \left( 1 \right) = \left[ \begin{gathered} \alpha_{l} \left( 1 \right) \hfill \\ \beta_{l} \left( 1 \right) \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \, \sqrt {\frac{{\left( {0.5 - 2\delta } \right)}}{L - 1}\left( {l - 1} \right) + \delta } \hfill \\ \sqrt {1 - \frac{{\left( {0.5 - 2\delta } \right)}}{L - 1}\left( {l - 1} \right) - \delta } \hfill \\ \end{gathered} \right] $$

(6)

$$ Q_{l} \left( 0 \right) = \left[ \begin{gathered} \alpha_{l} \left( 0 \right) \hfill \\ \beta_{l} \left( 0 \right) \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \sqrt {1 - \frac{{\left( {0.5 - 2\delta } \right)}}{L - 1}\left( {l - 1} \right) - \delta } \hfill \\ \, \sqrt {\frac{{\left( {0.5 - 2\delta } \right)}}{L - 1}\left( {l - 1} \right) + \delta } \hfill \\ \end{gathered} \right] $$

(7)

where $\delta$, $0 < \delta \ll 1$, is the minimum probability of state 1(or 0). Based on the definition of (6) and (7), $Q_{l} \left( 1 \right)$ is a Q-bit whose probability for it to be “1” is larger than the probability for it to be “0”. The contrary is also true for Q-bit $Q_{l} \left( 0 \right)$. Therefore, when ${\mathbf{q}}_{l}$ is observed, $X_{0}$ has a higher probability to appear. Besides, in order to make the initial population of Q-bit individuals sufficiently diversified to enlarge the search area, the other Q-bit individuals ($G - L$) are initialized in original way. Parameters $\delta$ and $L$ have a direct impact on maintaining diversity of the initial population. However, the ideal values of the two are difficult to determine; a rough but simple way is to set: $\delta = 0.01$ and $L = G/2$.

4.2 Fitness function

A candidate solution group ${\mathbf{P}}\left( t \right) = \left[ {{\mathbf{X}}_{1}^{t} ,{\mathbf{X}}_{2}^{t} , \ldots ,{\mathbf{X}}_{G}^{t} } \right]$ is formed after all Q-bit individuals in $Q\left( t \right)$ are observed. To evaluate the quality of each solution ${\mathbf{X}}_{j}^{t} = \left[ {x_{j1}^{t} ,x_{j2}^{t} , \ldots ,x_{jn}^{t} } \right]$($j = 1,2, \ldots ,G$), a new fitness function $f({\mathbf{X}}_{j}^{t} )$ is proposed in (8) according to (2). It is defined as the sum of two parts. The first one, i.e., $\left( {n - NT} \right)/\left( {m + n + 1} \right)$ evaluates the rate of test point reduction, and the second part, i.e. $\gamma \cdot \hbox{max} \left( {0,1 - S/\left( {m + 1} \right)} \right)$ is a penalty term.

$$ f\left( {{\mathbf{X}}_{j}^{t} } \right) = \frac{n - NT}{m + n + 1} - \gamma \cdot \hbox{max} \left( {0,1 - \frac{S}{m + 1}} \right) $$

(8)

where, $NT$ is the number of test points contained in ${\mathbf{X}}_{j}^{t}$, $S$ is the number of isolated fault states, and $\gamma$ is the penalty factor. If ${\mathbf{X}}_{j}^{t}$ is a feasible solution, i.e. $S/\left( {m + 1} \right) = 1$, then the value of $f\left( {{\mathbf{X}}_{j}^{t} } \right)$ is only determined by the first part. Otherwise, if ${\mathbf{X}}_{j}^{t}$ is not a feasible solution, i.e. $S/\left( {m + 1} \right) < 1$, then $f\left( {{\mathbf{X}}_{j}^{t} } \right)$ is mainly determined by the second parts if $\gamma$ is large enough. In this paper, $\gamma$ is assigned as $m + 1$.

4.3 Update operation

The conventional rotation gate requires a pre-specified lookup table to determine the rotation angle $\Updelta \theta_{ji}^{t}$ at generation $t$ for updating the $i$th Q-bit of ${\mathbf{q}}_{j}^{t}$, where $i = 1,2, \ldots ,n$, $j = 1,2, \ldots ,G$. One equivalent method for determining rotation angle is given in (9).

$$ \Updelta \theta_{ji}^{t} = \theta^{t} \times \left\{ {\chi \times \left( {b_{i} - x_{ji}^{t} } \right)} \right\} $$

(9)

where $\theta^{t}$ is the magnitude of $\Updelta \theta_{ji}^{t}$ and the term in brace determines the sign of $\Updelta \theta_{ji}^{t}$. $\chi$ is obtained by comparing the fitness value of current solution ${\mathbf{X}}_{j}^{t}$ with the best solution ${\mathbf{B}}$ as follows

$$\chi = \left\{ {\begin{array}{ll} 0 & {f({\bf X}_{j}^{t}) \ge f({\bf B})} \\ {sign(\alpha ^{t}_{{ji}} \beta ^{t}_{{ji}})} & {otherwise}\\\end{array}} \right.$$

(10)

where $sign\left( \cdot \right)$ is the sign function. In general, $\theta^{t}$ is designed in compliance with the application problem, and has an effect on both the speed of convergence and the quality of solution. If it is too big, the solutions may diverge or converge prematurely to local optima. On the contrary, if it is too small, the algorithm may converge slowly. Therefore, the proper selection of $\theta^{t}$ is of great importance. Here, we make $\theta^{t}$ decrease monotonously from $\theta_{\hbox{max} }$ to $\theta_{\hbox{min} }$ along with iterations, but not a fixed value. It is presented as follows:

$$ \theta^{t} = \theta_{\hbox{min} } + \left( {\theta_{\hbox{max} } - \theta_{\hbox{min} } } \right) \times \frac{T - t}{T} $$

(11)

where $T$ is the maximum iteration number. This approach can more easily balance the global and local search ability, i.e. with a larger value at the beginning for better exploration and a small value at the end for better exploitation. The values of $\theta_{\hbox{max} }$ and $\theta_{\hbox{min} }$ are determined experimentally. After determining the rotation angle, the update operation is performed as below:

$$ \left[ \begin{array}{c} \alpha_{ji}^{t + 1} \\ \beta_{ji}^{t + 1} \\ \end{array} \right] = \left[ \begin{array}{c} \cos \left( {\Updelta \theta_{ji}^{t} } \right) - {\text{sin}}\left( {\Updelta \theta_{ji}^{t} } \right) \\ { \sin }\left( {\Updelta \theta_{ji}^{t} } \right) \, \cos \left( {\Updelta \theta_{ji}^{t} } \right) \\ \end{array} \right]\left[ \begin{array}{c} \alpha_{ji}^{t} \\ \beta_{ji}^{t} \\ \end{array} \right] $$

(12)

4.4 Procedure of QEA-ATPS algorithm

The procedure of QEA-ATPS algorithm is summarized as shown in Fig. 1.

Fig. 1

Procedure of QEA-ATPS algorithm

The time complexity of QEA-ATPS method is dominated by the step of evaluating ${\mathbf{P}}\left( t \right)$ due to the fact that $m > n$ is usually true. Based on the fitness function (8), when evaluating each solution ${\mathbf{X}}_{j}^{t}$ ($j = 1,2, \ldots ,G$), we need to check the number of fault states that can be isolated, i.e. $S$. This can be transformed into a sorting problem and the time complexity is $O\left( {m\log m} \right)$ by using some efficient sorting algorithms such as quick sort and heap sort [3]. So the total time complexity of QEA-ATPS method is $O\left( {TGm\log m} \right)$.

5 Experiments

5.1 Example on practical analog circuit

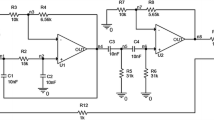
The experiment is implemented on an active filter circuit as shown in Fig. 2. This is cited by many literatures [3, 4, 8–10] as a benchmark circuit. A sinusoidal wave with amplitude of 4 V and frequency of 1 kHz is used as test stimulus. 19 CUT fault states ($f_{0}$ for nominal case and $f_{1} ,f_{2} \ldots ,f_{18}$ for potential catastrophic faults), and 11 test points marked in Fig. 2 are considered. The voltage values at all nodes for different faulty conditions are obtained by Pspice. The integer-coded dictionary is constructed by the method described in Sect. 2.1 and the result is presented in Table 4.

Fig. 2

Example analog filter

Table 4 Integer-coded dictionary for the analog filter

In the initialization step, the inclusive algorithm (the algorithm 3 combined with inclusive strategy 3 in [3]) is carried out and the resultant solution is ${\mathbf{X}}_{0} = [1,0,0,1,1,0,1,1,1,0,1]$. Based on ${\mathbf{X}}_{0}$, the initial population is initialized. After that, the QEA-ATPS algorithm is executed with the following parameters: $\theta_{\hbox{max} } = 0.05\pi$, $\theta_{\hbox{min} } = 0.01\pi$, $G = 20$ and $T = 30$. As a result, the solution with the highest value of fitness has been found in the 3rd generation, and the best solution is

$$ X_{opt} = \left[ {1,0,0,0,1,0,0,0,1,0,1} \right] $$

So the optimum set of test points found by QEA-ATPS is $\left\{ {n_{1} ,n_{5} ,n_{9} ,n_{11} } \right\}$, which is identical with the sets that were obtained from the methods described in [3, 4, 8–10].

The performance of the proposed QEA-ATPS algorithm is influenced by the parameters $\theta_{\hbox{max} }$ and $\theta_{\hbox{min} }$. In general, the value from $0.001\pi$ to $0.05\pi$ for the magnitude of rotation angle is recommended, although it is designed according to the specific application [11]. In order to find the optimum combination of rotation angles (i.e., $\theta_{\hbox{max} }$ and $\theta_{\hbox{min} }$), we take $\theta_{\hbox{max} }$ from $\left\{ {0.05\pi ,0.04\pi ,0.03\pi } \right\}$, $\theta_{\hbox{min} }$ from $\left\{ {0.001\pi ,0.006\pi ,0.01\pi } \right\}$. Therefore, there are nine different combinations of parameters needed to be considered. For each one, 100 runs are conducted with following two cases: case 1) $G = 20$ and $T = 30$; case 2) $G = 10$ and $T = 20$, respectively.

For case 1, the QEA-ATPS algorithm achieves 100 % of success and the average convergent iterations are listed in the second row of Table 5. While for case 2, the percentages of success are given in the third row of Table 5. Based on the Table 5, $\theta_{\hbox{max} }$ and $\theta_{\hbox{min} }$ are selected as $0.05\pi$ and $0.01\pi$, respectively.

Table 5 The results for different combination of $\theta_{\hbox{max} }$ and $\theta_{\hbox{min} }$

To validate the efficiency of QEA-ATPS algorithm, other three algorithms are compared including: QEA, GA [9] and MDFDSPO [10]. Besides the above two cases, a new case, named case 3) $G = 30$ and $T = 50$, is also considered. The magnitude of rotation angle for QEA is set as: $\theta = 0.01\pi$. Other parameters of GA and MDFDPSO are the same as that used in [9] and [10]. Similarly, under the condition of each case, 100 independent runs are implemented for each algorithm. The results of percentage of success are listed in Table 6.

Table 6 Percentages of success for all methods

As indicated in Table 6, for case 3, all three algorithms achieve 100 % of success, while for other two cases, as the values of $G$ and $T$ decrease, the percentage of success is accordingly reduced. Especially for case 2, all algorithms can not make sure to find optimum solution, but compared with other three algorithms, QEA-ATPS is more robust and has a higher probability to find optimum solution. In order to compare the convergent properties of the methods, we taking case 3 as an example and give the comparison results as shown in Table 7.

Table 7 Convergent properties of the methods for case 3

From Table 7, QEA-ATPS has a fast convergence speed, with the average running time equal to 0.32 s, which is less than MDFDPSO and only about half and fifth of QEA and GA, respectively. The conclusion from Tables 6 and 7 is that QEA-ATPS outperforms GA, MDFDPSO and QEA both in terms of solution accuracy and speed of convergence.

5.2 Statistical experiments

In the former example, the proposed QEA-ATPS algorithm has been demonstrated its better performance. However, there is no theoretical proof can be given to demonstrate the optimality (except for exhaustive search method) of our method, so it must be tested statistically on a large number of integer-coded dictionaries in order to check its efficiency and accuracy. Here, statistical experiments are carried out on 100 integer-coded dictionaries randomly generated. Each dictionary is created for a hypothetic CUT with 100 simulated faults, 30 test points and 5 ambiguity sets for each test point. Every randomly created dictionary has been browsed exhaustively for all possible combinations of three (minimum theoretical quantity necessary to achieve 100 % fault isolation for the considered dictionaries), four, and five test points. Only dictionaries that have global optimum at five points have been added to the benchmark set.

For comparison, other four alternative approaches, including GA [9], MDFDPSO [10], EI-based algorithm [4], heuristic graph search [8], have also been examined on the same benchmark set, respectively. In this experiment, the parameters $G$ and $T$ for QEA-ATPS is set as: $G = 30$ and $T = 50$. The obtained statistical results for the examined approaches are presented in Tables 8 and 9.

Table 8 The solution accuracy of the compared methods

Table 9 The average running time of each method

As can be seen from Table 8 and 9, the proposed QEA-ATPS algorithm, together with GA and MDFDPSO, can always find the optimum solutions (effectiveness 100 %), but the QEA-ATPS algorithm take the shortest average running time (1.43 s) among them. For the last two greedy algorithms, i.e., EI and Heuristic graph search, reach only 54 % and 30 % of global minimum sets, respectively, although the time consumptions are radically lower than that used for the first three methods. Therefore, through statistic experiment, the proposed method also reveals its very high effectiveness and accuracy and is demonstrated to be superior to other methods.

6 Conclusions

The ATPS problem remains an important problem in fault diagnosis of analog circuit, to the best of our knowledge, but it hasn’t been formulated. The current paper just fills this blank. In addition, an effective QEA-ATPS algorithm for solving ATPS problem has been developed. The attractiveness of this algorithm lies in two aspects: the utilization of the solution produced by inclusive algorithm to initialize population and dynamically adjustment the magnitude of rotation angle. These two measures make the algorithm more easily find the global minimum set in a very short time. Experiments show that the solution generated by QEA-ATPS algorithm is more accurate than that of EI and Heuristic graph search methods and that its efficiency is higher than that of GA and MDFDPSO methods. Therefore, it is a good solution to optimize analog test point selection. Further enhancement of the method will be concentrated on using a more accurate greedy method to initialize population, for example EI [4].