1 Introduction

Currently the use of composite material in prosthetic applications is on the rise due to the need to create structures with high performance and low weight, in addition to including advantageous mechanical properties. Scholz et al. [1] showed that composite materials provide excellent biocompatibility, being very convenient for the design of prostheses. In the literature, the composite material has been largely used in prosthetic applications [2,3,4,5] generating a decreased mass and increasing the structural performance.

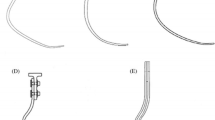
Studies estimate that there are seven million people worldwide suffering from lower limb amputations. One factor to consider is the long size of these bones compared to others, moreover, lower limbs are generally more unprotected to impacts [3, 6]. For this reason, tubes for prostheses have been manufactured with the intention of replacing a body fragment aimed at ensuring the movement. This way, devices using composite material are required to increase strength, decrease cost and mass, as depicted in Fig. 1.

Fig. 1
figure 1

Tube manufactured in epoxy/carbon composite material for transtibial prosthesis (Taken from [7])

Full size image

An efficient alternative often used in the aerospace industry to further reduce the mass and consequently the cost with material is the dropping-off of plies along the length of the laminate, known as drop-off or blending [8].

A habitual composite structure with drop-off is divided into several panels (longitudinal direction) with stacked plies (transversal direction), beginning with thick panel and ending with thin panel, as shown in Fig. 2. Furthermore, the laminate with drop-off presents taper section, where the plies dropped are located [9].

Fig. 2
figure 2

Nomenclature of a structure with 4 drop-offs (Taken from 9)

Full size image

The dropping-off of the plies can cause the stresses concentration in the region near the drop-off and failures that directly affect the structural performance [10, 11]. Meanwhile, depending on the drop-off location these unwanted situations can be contained or reduced. For a typical laminate with drop-offs is possible to consider two main variables responsible for drop-off location, which is ply and panel position.

Shim [12] mentions that the main difficulties encountered in works involving structures with ply drop-off are: i) the large number of possibilities for ply drop-off location in a single structure and ii) the influence that the ply drop-off location has about the strength of the laminate composite. It can be affirmed that the drop-off location is a key question in any analysis involving laminate structure.

The composite material with drop-off has been very useful in aeronautical applications [13,14,15] and wind industry [16,17,18]. However, studies considering applications in hybrid tubes for lower limb prosthesis are limited and poorly explored. In addition, many studies considered the behavior of structures with drop-off in relation to mass and failure [19, 20]. According to [10], the literature on buckling and vibration analyses involving laminate structures with drop-off is limited, which may increase interest in the research.

That way, in this paper the drop-off location will be analyzed considering two continuous design variables related to panel position (X1 and X2) and two discrete design variables related to ply position (Y1 and Y2). Furthermore, a categorical variable will determine the type of laminate fiber, hybrid (CFRP/GFRP) or not (only CFRP). The laminate behavior with drop-offs will be investigated in relation to static and dynamic conditions.

The optimization will be employed with the intention of determining a better drop-off location in a prosthetic tube aiming to create a meta-model that can assist in future projects involving structures with drop-off. The structural optimization will be carried out using Design of Experiments (DOE) with Factorial Design and Response Surface Methodology (RSM), and then applied the SunFlower Optimization algorithm (SFO). One of the great advantages of DOE is the limited number of experiments for analyses with several variables [21, 22]. The DOE is very common in the studies with composite materials [23,24,25,26], in the meantime, is scarce in the studies on the optimization of laminate with drop-offs. Also, this method is the most commonly used for approximation concepts [26, 27].

In this study, the DOE contributed to the creation of a meta-model, once you have a set of equations well-defined can successfully represent the real model. In addition, this approach can offer guidelines for the designers in relation to order of importance of the manufacture variables and better drop-offs location.

It is important to highlight that the most common approach for optimizing laminate with drop-off is to use evolutionary algorithms, such as the Genetic algorithm (GA) [28,29,30,31,32,33]. Meanwhile, in this study, the SFO algorithm was chosen due to its relevance and also due to the fact it is a recent and new metaheuristic created between the years of 2019 and 2020 [34]. Initial studies were conducted considering different algorithms, such as Particle Swarm Optimization (PSO) [35,36,37], Ant Colony Optimization (ACO) [38,39,40], and GA [41,42,43], and SFO demonstrated superior results.

2 Theoretical Background

2.1 Rules for Modeling of the Composite Structure with Drop-offs

There are numerous rules for manufacture structures with drop-off arising from industrial knowledge. Some important rules are exposed in this paper and considered in the design of the composite tube for lower limb prosthesis, other rules can be found in [9].

  • Symmetry: stacking sequence should be symmetric about the midplane;

  • Balance: stacking sequence should be balanced, same number + θ and –θ plies when θ is different to that of 0º and 90º;

  • Contiguity: it is not allowed more than two plies of the same orientation stacked together;

  • 10% rule: it is mandatory in the minimum 10% of oriented plies with angles 0°, ± 45° and 90°;

  • Damtol: it is not permitted to have ply fibers oriented at 0º on the laminate’s lower and upper surfaces;

  • Covering: plies localized in lower and upper surfaces should not be dropped;

  • Max-stopping: it is not accepted more than two plies stopped at the same addition of thickness;

  • Maximum taper slope: the taper angle should not exceed 7º.

These rules are intended to prevent unwanted failure, such as delamination and cracking, and high stress concentrations. In addition, these rules provide structural integrity and manufacturability of the structures.

2.2 Tsai-Wu Failure Criterion

The Tsai-Wu failure criterion is able to analyze the failure mechanisms in anisotropic material, being considered very appropriate due to approximation with experimental data [44]. In this criterion, the knowledge about strength parameters and stresses it possible to establish whether the structure will fail or not. According to Tsai-Wu failure criterion if Eq. (1) is countered, the failure occurs [45]:

$${F}_{11}{\sigma }_{1}^{2}+{F}_{22}{\sigma }_{2}^{2}+{F}_{66}{\tau }_{12}^{2}+{F}_{1}{\sigma }_{1}+{F}_{2}{\sigma }_{2}+{F}_{12}{\sigma }_{1}{\sigma }_{2}\le 1$$
(1)

where F11, F22, F66, F1, F2, F12 are the strength parameters and σ1, σ2, τ12 are the stresses (normal and shear).

Here, the failure index is used to reveal the tube performance related to failure in compression and torsion, but these axial and transverse efforts suffered by tube used in lower limb prostheses. Many scientific works implemented Tsai-Wu failure criterion for analyze the failure and avoid collapse of the structure with drop-off [17, 27, 46,47,48,49,50].

2.3 Linear and Nonlinear Buckling Model

2.3.1 Numerical Buckling Model

The linear buckling analysis is able to reveal the buckling load or bifurcation point for perfect structures where there are small deformations generating conservative results. For structures with large deformations it is recommended to use nonlinear analysis due the structures suffering geometric modifications and consequently respond nonlinearly [51, 52]. Using the FEM, the linear buckling analysis is considered simpler and has low computational cost [51].

The linear buckling analysis is more useful for presuming the theoretical buckling load that will be used as convergence criterion in the nonlinear buckling analysis. In the FEM for determinate the linear buckling load is necessary to encompass the effect of the differential stiffness into the linear stiffness matrix, mathematically, the Eigenvalue analysis is required, as shown in Eq. (2) [51].

$$\left(\left[\mathrm{K}\right]+\lambda \left[{\mathrm{K}}_{\mathrm{d}}\right]\right)\left\{\boldsymbol{\upphi}\right\}\left\{0\right\}$$
(2)

where [K] indicates the linear stiffness matrix, [\({K}_{d}\)] the differential stiffness matrix, the ϕ represents buckling mode shapes (eigenvector) and λ is eigenvalue of the system. The eigenvalue can be considered the bifurcation point provided the value of the load applied in the structure is unitary.

The nonlinear buckling analysis is used to achieve realistic results, in which the critical load is set out by progressive increasing the load applied until the structure becomes unstable.

Considering an elastic system limited to a conservative loading, when the stability is lost, the linear stiffness matrix [K] becomes singular and symmetrical. Then, the nonlinear buckling load can be found using Eq. (3):

$${K}_{T}\left(u\right)\Delta u-\Delta F\left(u\right)=\left\{0\right\}$$
(3)

where \({K}_{T}\) represents the tangent stiffness matrix, (u) is the increment step, \(\Delta u\) and \(\Delta F\) are respectively the displacement and the load.

As the nonlinear buckling analysis considers the linear critical load as convergence criterion your value must always be less than linear buckling load. Then, a previous analysis about linear buckling is required to begin the nonlinear buckling analysis [51].

2.4 Design of Experiments

The statistical study implemented in this paper encompasses strategies of experimentation, as factorial design and RSM, in which a data set is collected and examined in providing meaningful conclusions [53].

The factorial design is responsible for establishing the main effects and their significance level. These effects are created by the change between the levels of variables that influence in the response. Thereby, the interactions could be represented by a linear regression model, as shown in Eq. (4) [53]:

$$y={\beta }_{0}+{\beta }_{1}{x}_{1}+{\beta }_{2}{x}_{2}+{\beta }_{12}{x}_{1}{x}_{2}+e$$
(4)

where y is the response variable of the issue under study, the β is a model constant, x1 and x2 are the factors and e the random error term.

The factorial design allows distinguishing the importance between the variables that interfere in the response highlighting the relevant aspects and decreasing the amount of experiments using an approximation function of first-order. If necessary, the variables that prove to have curvature could be refined using second-order model through of a RSM, as shown in the Eq. (5):

$$y={\beta }_{0}+\sum_{i=1}^{k}{\beta }_{i}{x}_{i}+\sum_{i=1}^{k}{\beta }_{ii}{x}_{i}^{2}+\sum_{i<j}0\sum {\beta }_{ij}{x}_{i}{x}_{j}+e$$
(5)

According to [54], the second-order model represents very well problems in the response surface. The procedure developed in RSM uses a fitted surface which allows equivalent approximations of a real system. The inclusion of the quadratic terms, as can be seen from Eq. (5), is considered the main difference in relation to factorial design and RSM. This term is responsible for level of the variables and optimization of responses [53].

An analysis of variance (ANOVA) is used to reveal the significance level and curvature parameters that can be represented by the addition of an interaction term in a first-order model, making it possible to determine the model fit of the system [53, 55]. The ANOVA analyzes the variables through a p-value that is defined as the probability of observing a given value of the test statistic. Traditionally, a p-value less than 0.05 represents that there is a statistically significant difference between the means of the groups composed by the response and design variables. Now, if the p-value is not less than 0.05, it is possible to conclude that there is not sufficient evidence to affirm that there is a statistically significant difference between the means of the groups [56].

The analysis of variance consists of equating the expected mean squares to their observed values and solving the variance components, where the quality of fit is determined through the coefficient of determination, indicated by R2, as shown in Eq. (6) [53]:

$${R}^{2}=\frac{{SS}_{model}}{{SS}_{total}}$$
(6)

where SSmodel is the sum of model squares and SStotal is the sum of total squares. The sum of squares revealed the measure of variation or deviation from the mean in relation to the model and total variation. The value of R2 above 90% demonstrates that the model clarifies the variability of fitted data [53, 56].

3 Methodology

3.1 Finite Element Model Description for Composite Tubes with Drop-offs

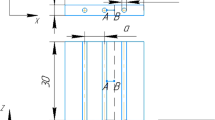
A typical hollow tubular laminate is modeled by stacked plies considering different orientations for the fiber angles, such as [45º/90º/90º/-45º/0º]s indicated by [9] that it satisfies the design rules. The tube with drop-offs used in prosthesis is designed considering the dimensions of 0.30 m in height and diameter of 0.03 m [57]. The ply thickness varied according to the type of fiber, in addition to the conventional material (carbon/epoxy) was considered a hybrid material (carbon/epoxy/glass). For the hybrid tube, in the outer plies is used carbon fiber and in the inner plies the glass/epoxy material. While that for the non-hybrid tube is only employed carbon/epoxy material. The carbon/epoxy material properties were obtained from experimental tests, while the glass/epoxy composite material properties can be found in [58], both composite material properties together with the failure parameters can be shown in Table 1.

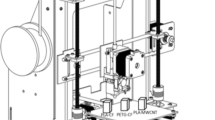
Table 1 Properties of composite materials considering failure criterion
Full size table

All the numerical models used in this study were created in Ansys® software on a personal computer with an Intel® 5 processor, 5 GB of memory, and a 1 TB hard drive and were evaluated through FEM using an element type shell with 8 nodes and 6 degrees of freedom in each node. The time spent for each static analysis involving the Tsai-Wu failure criterion was on average 1 min and 37 s, for modal analyses around of 3 min and 12 s, linear buckling analyses around of 3 min and 9 s, and nonlinear buckling was on average 11 min and 19 s. A mesh convergence study was done to evaluate the quality of the mesh, where the same simulations were carried out with a finer mesh and compare the results. The feasible optimal mesh was discretized each line in fragments considering 20 elements in each line of the structure, resulting in the total number of 8002 elements and 24,162 nodes. Furthermore, rigid bodies were created in the ends aiming to apply the boundary conditions. In one of the tube ends was applied a loading (compression or torsion), whereas the other was clamped without any kind of translation and rotation movement, as shown in Fig. 3. In order to obtain reliable results, the applied load in compression was 4480 N, the equivalent to 450 kg, and torsion moment 7.1 N.m, both considering failure mechanisms. The loads were established by [57], and this is the Standard responsible for structural tests in lower limb prosthesis.

Fig. 3
figure 3

Tubular geometry for prosthesis: a thickness of plies; b Rigid body in the free end for applied loading and c Rigid body in the clamped-end

Full size image

In this manner, in accordance with the different combinations for drop-offs location generated on the DOE, numerical simulations were carried out and structural performance was obtained, then the response variables were identified. In the numerical approaches using the FEM were considered modal, eigen buckling and structural analyses for obtaining response variables in relation to natural frequency, buckling load, mass and failure index, respectively.

Firstly, the simulation was carried out with tube without drop-offs e posteriorly a tube with drop-offs, being the drop-off located in any region along the length of the tube. The main purpose in this analysis is proving the reduction in the structural mass when the drop-off is inserted into laminate considering the hybrid and non-hybrid structure. The hybrid tube with drop-offs presented a decreasing in the mass of 70% in relation to hybrid tube without drop-offs, already the non-hybrid tube with drop-offs allowed to decrease the mass in 80% due the carbon fiber is lighter than glass fiber. In view of this, the drop-off in tubular geometry can provide a considerable reduction in structural mass.

Another important response variable is the failure index obtained with Tsai-Wu failure criterion. Here, the failure is evaluated in two conditions, torsion and compression, considering that these situations will likely be suffered by prosthesis. Due to the fact of the failure in compression to be more common and often, the same is illustrated in Figs. 4 and 5 considering non-hybrid and hybrid tubes.

Fig. 4
figure 4

Non-hybrid tubes considering failure in compression for drop-offs located in a X1 = 0.06, Y1 = 2, X2 = 0.18 e Y2 = 3, b X1 = 0.12, Y1 = 2, X2 = 0.18 e Y2 = 3, c X1 = 0.06, Y1 = 4, X2 = 0.18 e Y2 = 3, d X1 = 0.12, Y1 = 4, X2 = 0.18 e Y2 = 3, e X1 = 0.06, Y1 = 2, X2 = 0.24 e Y2 = 3, f X1 = 0.12, Y1 = 2, X2 = 0.24 e Y2 = 3, g X1 = 0.06, Y1 = 4, X2 = 0.24 e Y2 = 3, h X1 = 0.12, Y1 = 4, X2 = 0.24 e Y2 = 3, i X1 = 0.06, Y1 = 2, X2 = 0.18 e Y2 = 5, j X1 = 0.12, Y1 = 2, X2 = 0.18 e Y2 = 5, k X1 = 0.06, Y1 = 4, X2 = 0.18 e Y2 = 5, l X1 = 0.12, Y1 = 4, X2 = 0.18 e Y2 = 5, m X1 = 0.06, Y1 = 2, X2 = 0.24 e Y2 = 5, n X1 = 0.12, Y1 = 2, X2 = 0.24 e Y2 = 5, o X1 = 0.06, Y1 = 4, X2 = 0.24 e Y2 = 5, p X1 = 0.12, Y1 = 4, X2 = 0.24 e Y2 = 5 e q X1 = 0.09, Y1 = 3, X2 = 0.21 e Y2 = 4

Full size image
Fig. 5
figure 5

hybrid tubes considering failure in compression for drop-offs located in a X1 = 0.06, Y1 = 2, X2 = 0.18 e Y2 = 3, b X1 = 0.12, Y1 = 2, X2 = 0.18 e Y2 = 3, c X1 = 0.06, Y1 = 4, X2 = 0.18 e Y2 = 3, d X1 = 0.12, Y1 = 4, X2 = 0.18 e Y2 = 3, e X1 = 0.06, Y1 = 2, X2 = 0.24 e Y2 = 3, f X1 = 0.12, Y1 = 2, X2 = 0.24 e Y2 = 3, g X1 = 0.06, Y1 = 4, X2 = 0.24 e Y2 = 3, h X1 = 0.12, Y1 = 4, X2 = 0.24 e Y2 = 3, i X1 = 0.06, Y1 = 2, X2 = 0.18 e Y2 = 5, j X1 = 0.12, Y1 = 2, X2 = 0.18 e Y2 = 5, k X1 = 0.06, Y1 = 4, X2 = 0.18 e Y2 = 5, l X1 = 0.12, Y1 = 4, X2 = 0.18 e Y2 = 5, m X1 = 0.06, Y1 = 2, X2 = 0.24 e Y2 = 5, n X1 = 0.12, Y1 = 2, X2 = 0.24 e Y2 = 5, o X1 = 0.06, Y1 = 4, X2 = 0.24 e Y2 = 5, p X1 = 0.12, Y1 = 4, X2 = 0.24 e Y2 = 5 e q X1 = 0.09, Y1 = 3, X2 = 0.21 e Y2 = 4

Full size image

The tube with drop-offs proved to be reliable with all failure index values smaller than 1. In most cases, the region close to the drop-off on the tubes demonstrated a slight increase in the intensity of the stress associated with failure, as can be seen in Figs. 4 and 5. This is due to the fact that the drop-off region stimulates stress concentrations [9]. The increase in the intensity of stress can be noted by an amendment in the color scale in each tubular structure, as can be seen in Figs. 4 and 5. For non-hybrid tapered tubes, the failure index values suffered an increase in the region close to the second drop-off in cases (c), (d), (g) and (h) and in the region close to both drop-offs in cases (a), (b), (e), (f), (i), (j), (m) and (n). For the cases (k), (l), (o) and (p), the use of drop-off in the non-hybrid tubular structures did not cause changes in failure index values. The intensity of stress remained stable, as can be confirmed in Fig. 4. A reason for this can be justified due to the tubular structure being manufactured only with carbon fabric, considered the strongest material. Furthermore, the most continuous plies, which were not dropped, had their fibers oriented at 90º in the same direction as the load, generating an increase in the laminate strength. However, when these plies oriented at 90º are dropped, as can be seen in cases (a), (b), (e) and (f) in Figs. 4 and 5, the failure index values have a significant increase in the posterior region to the second drop-off, and therefore the color scale of these structures is changed, generating higher failure index values.

The panel and ply design variables are represented by X and Y, respectively. Where X1 and X2 correspond to the first and second panel in which the drop-off is located, while Y1 and Y2 the first and second ply dropped. The values for the failure index considering a hybrid tube with drop-offs can be assessed afterwards in Table 3 on the second column that presents the failure in compression.

Again, the insertion of the drop-off in hybrid tubular structures caused changes in the intensity of stress in a manner similar to the non-hybrid tubular structures, except for the cases (k), (l), (o) and (p), where the failure index values had a smooth increase in the region close to the second drop-off. This fact is expected due to the second ply dropped being manufactured with carbon fiber, which provides a reduction in the structural strength. It is worth remembering that the hybrid structures have only two plies manufactured in carbon fiber (external plies), while the non-hybrid structures are fully manufactured in carbon fiber.

Once the failure index has proven to be so useful for determining the reliability of a structure composite with drop-offs, it is important to investigate other unwanted situations that can occur in a thin laminate that can influence the structural performance, such as buckling phenomenon.

For hybrid tubes with drop-offs the maximum critical load found in linear buckling analysis realized in this study was around 31kN and for non-hybrid tubes with drop-offs was around 22kN, being these loads much greater than the load applied of 4480 N. In order to achieve accurate results in relation to maximum buckling load, nonlinear analyses were generated considering the linear buckling load as criterion for stopping interactions. The nonlinear analyses revealed low buckling loads than the calculated in linear buckling, nevertheless, none of both were less than the compression load applied. Considering the nonlinear buckling analysis for a hybrid tubes with drop-offs the maximum buckling load achieved was 22.203kN. Then, to maintain stability of the hybrid tube with drop-offs is necessary to apply load less than nonlinear buckling load, higher loading than this, beginning the process buckling in the structure, as can been seen in Fig. 6.

Fig. 6
figure 6

Nonlinear analysis for hybrid tube with drop-offs considering the maximum buckling load

Full size image

However, for a hybrid tubular structure with drop-offs used in lower limb prostheses the maximum buckling load representing almost five times the load applied. In the case of non-hybrid tubes, the maximum buckling load found is 16.173kN, as depicted in Fig. 7, almost four times greater than the compression load applied in the tubular structure. Therefore, it is proved that the load applied in compression will not cause buckling in the tubular structures with drop-offs and, additionally, a higher loading could be applied with security on the structures so that the same will not suffer buckling.

Fig. 7
figure 7

Nonlinear analysis for non-hybrid tube with drop-offs considering the maximum buckling load

Full size image

Indeed, a buckling load greater for hybrid tube compared to non-hybrid tube was expected due to the glass fiber being thicker than carbon fiber. Furthermore, the hybrid tubes are only composed of two carbon layers and the remainder is glass. In this way, the end area where the load is applied tends to be greater.

The results about all response variables obtained in numerical simulation using the FEM can be viewed in the next section in Tables 3, 5, and 6 that represent the structural response in the last five columns.

3.2 Factorial Design

The first step of the statistical approach is based on factorial design considering 4 variables both with 2 levels, as depicted in Table 2.

Table 2 Design variables considering the respective levels
Full size table

In the factorial design was considered only the hybrid tube due their unusual structure. Posteriorly in the RSM, the non-hybrid tube will be analyzed together with the hybrid tube. That way, the factorial design was created generating 17 different runs for hybrid tubes with drop-offs with 5 response variables: Tsai-Wu failure criterion in relation to torsion and compression, 1st natural frequency, mass and buckling load, as can be seen in Table 3. The last run represents the center point where the component proportions are the averages of the vertex proportions in the design space.

Table 3 Experimental matrix for factorial design of the hybrid tubes with drop-offs
Full size table

The factorial design enables to investigate which design variables is relevant in the tube behavior in relation to the response variables, besides to identifying the curvature for the development of the RSM that will be discussed in the next section.

4 Results and Discussion

The results obtained by ANOVA model were examined by the coefficient of determination represented by R2 and their derivations, such as adjusted coefficient of determination (R2adj) that reflects the number of predictors in the regression model and predicted coefficient of determination (R2(pred)) responsible by indicate how well the regression model predicts response considering new data. In this context, Table 4 presents the R2 results for each response variable considering the hybrid tube.

Table 4 Results of the R2 considering the response variables for hybrid tubes with drop-offs
Full size table

It can be inferred, that the Tsai-Wu failure criterion in compression and buckling load responses ensure an excellent quality of fit indicating how well the model fits the data for the hybrid tube with drop-offs. The mass response showed low fit with R2 less than 70%, one explanation is that the mass values often were the same or changed very little in relation to drop-off location. In relation to curvature, all response variables have achieved curvature less than 0.05 (p-value), enabling the refinement of these responses by quadratic model. According to [53], the model terms are more realistic when p-value is less than 0.05, who demonstrated that there is a significant association between the design and response variables.

According to factorial design results, a RSM was created considering the two responses more significant, as Tsai-Wu failure criterion in compression and buckling load, aiming for a reduced number of runs. The mass response variable had a lower quality of fit with an R2 of around 68%, being retired from the experimental design of the RSM and consequently, the optimization process. That way, a design matrix was created considering the same design variables used in factorial design, but a categorical variable denoted hybrid was taken together with axial points, generating a total of 60 runs, as depicted in Tables 5 and 6.

Table 5 Design matrix created to analyze the response surface (part I)
Full size table
Table 6 Design matrix created to analyze the response surface (part II)
Full size table

Proceeding in a similar manner, the RSM realized an ANOVA aiming to confirm the quality of fits obtained by factorial design, depicted in Tables 7 and 8. While that, the relevance of variables can be seen in Fig. 8 with Pareto charts considering the Tsai-Wu failure criterion and buckling load response variables.

Table 7 Results of the ANOVA for Tsai-Wu failure criterion in compression
Full size table
Table 8 Results of the ANOVA for buckling load
Full size table
Fig. 8
figure 8

Pareto charts considering the effects: a Tsai-Wu failure criterion in compression and b nonlinear buckling load

Full size image

Clearly, the Tsai-Wu failure criterion and buckling load represent high predictive capability, as long as the R2 above 95%, as shown in the ANOVA results in Tables 7 and 8. The p-value generated by ANOVA for the Tsai-Wu failure criterion demonstrated that there exists a statistically significant relationship between the Y1, X2, Y2 and hybrid design variables with this response variable. The X2 design variable did not demonstrate any relation to response variables, their p-value being above 0.005, as can be confirmed by Table 7. While for the buckling load response variable, the Y1, Y2 and hybrid design variables had p-value less than 0.005, demonstrating the significance between design and response variables, as depicted in Table 8. In this case, the X1 and X2 design variables demonstrated that there is no significance between the design and response variables. As can be observed for both response variables, the X2 design variable related to the second drop-off position on the panel had a p-value above 0.005, demonstrating that this variable is not significant for the failure criterion and buckling load responses.

These important results show that the Y1, Y2, hybrid design variables and their interactions present a noticeable influence in the drop-off location, interfering directly in the all response variables. The X2 variable and their interactions with the Y2 variable demonstrated relevance for the buckling load response variable with p-value lower than 0.05. Therefore, it can be stated that the statistically relevant variables in relation to the drop-offs were ply position and hybrid, as depicted in Pareto charts, being the drop-off location in panel with little relevance.

The following second-order model was formulated using the ANOVA based on the significant response variables distinguishing between hybrid and non-hybrid tube, as depicted in Eqs. (7) to (10).

$$\begin{array}{l}{TW}_{C}\left(HYBRID\right)=0.1056+0.027\ {\mathrm{X}}_{1}+0.01920\ {\mathrm{Y}}_{1}+0.511\ {\mathrm{X}}_{2}-0.07661\ {\mathrm{Y}}_{2}\\\qquad\qquad\qquad\qquad\quad -\ 0.151\ {\mathrm{X}}_{1}*{\mathrm{X}}_{1}-0.005342\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{1}-1.233\ {\mathrm{X}}_{2}*{\mathrm{X}}_{2}\\\qquad\qquad\qquad\qquad\quad +\ 0.008196\ {\mathrm{Y}}_{2}*{\mathrm{Y}}_{2}+0.00000\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{1} +\ 0.001\ {\mathrm{X}}_{1}*{\mathrm{X}}_{2}\\\qquad\qquad\qquad\qquad\quad -\ 0.00004\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{2}+0.00005\ {\mathrm{Y}}_{1}*{\mathrm{X}}_{2}+0.002042\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{2}\\\qquad\qquad\qquad\qquad\quad -\ 0.00005\ {\mathrm{X}}_{2}*{\mathrm{Y}}_{2}\end{array}$$
(7)
$$\begin{array}{l}{TW}_{C}=0.1466+0.027\ {\mathrm{X}}_{1}+0.01590\ {\mathrm{Y}}_{1}+0.518\ {\mathrm{X}}_{2}-0.08182\ {\mathrm{Y}}_{2}\\\qquad\quad\ -0.151\ {\mathrm{X}}_{1}*{\mathrm{X}}_{1}-0.005342\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{1}-1.233\ {\mathrm{X}}_{2}*{\mathrm{X}}_{2}\\\qquad\quad\ +\ 0.008196\ {\mathrm{Y}}_{2}*{\mathrm{Y}}_{2}+0.00000\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{1}+0.001\ {\mathrm{X}}_{1}*{\mathrm{X}}_{2}\\\qquad\quad\ -\ 0.00004\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{2}+0.00005\ {\mathrm{Y}}_{1}*{\mathrm{X}}_{2}+\ 0.002042\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{2}\\\qquad\quad\ -\ 0.00005\ {\mathrm{X}}_{2}*{\mathrm{Y}}_{2}\end{array}$$
(8)
$$\begin{array}{l}\lambda \left(HYBRID\right)=-23526+38393\ {\mathrm{X}}_{1}-12961\ {\mathrm{Y}}_{1}-40858\ {\mathrm{X}}_{2}+23840\ {\mathrm{Y}}_{2}\\\qquad\qquad\qquad\quad\ -\ 37658\ {\mathrm{X}}_{1}*{\mathrm{X}}_{1}+2677\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{1}+294383\ {\mathrm{X}}_{2}*{\mathrm{X}}_{2}\\\qquad\qquad\qquad\quad\ +\ 2271\ {\mathrm{Y}}_{2}*{\mathrm{Y}}_{2}-369\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{1}+17228\ {\mathrm{X}}_{1}*{\mathrm{X}}_{2}\\\qquad\qquad\qquad\quad\ +\ 1552\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{2}+517\ {\mathrm{Y}}_{1}*{\mathrm{X}}_{2}+69\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{2}\\\qquad\qquad\qquad\quad\ -\ 13819\ {\mathrm{X}}_{2}*{\mathrm{Y}}_{2}\end{array}$$
(9)
$$\begin{array}{l}\lambda =-23450+37082\ {\mathrm{X}}_{1}-13422\ {\mathrm{Y}}_{1}-54915\ {\mathrm{X}}_{2}+23627\ {\mathrm{Y}}_{2}\\\qquad -\ 237658\ {\mathrm{X}}_{1}*{\mathrm{X}}_{1}+2677\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{1}+294383\ {\mathrm{X}}_{2}*{\mathrm{X}}_{2}\\\qquad +\ 2271\ {\mathrm{Y}}_{2}*{\mathrm{Y}}_{2}-369\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{1}+\ 17228\ {\mathrm{X}}_{1}*{\mathrm{X}}_{2}\\\qquad +\ 1552\ {\mathrm{X}}_{1}*{\mathrm{Y}}_{2}+517\ {\mathrm{Y}}_{1}*{\mathrm{X}}_{2}+69\ {\mathrm{Y}}_{1}*{\mathrm{Y}}_{2}\\\qquad -\ 13819\ {\mathrm{X}}_{2}*{\mathrm{Y}}_{2}\end{array}$$
(10)

Based on the equations of regression mentioned above, it has become possible to create a meta-model that determines the relationship between the responses and the combinations of design variable levels. Furthermore, the regression model allows creating quadratic surface plots that illustrate the relationship between the fitted response and two variables, as shown in Figs. 9 and 10.

Fig. 9
figure 9

Surface plot of the Tsai-Wu failure criterion considering all the variables that influence on the drop-off location

Full size image
Fig. 10
figure 10

Surface plot of the nonlinear buckling load considering all the variables that influence on the drop-off location

Full size image

The surface plots are very efficient for indicating the fitted responses considering the optimum region where is localized the minimum point for Tsai-Wu failure criterion and the maximum point for buckling load, as can be seen in Fig. 9 for a non-hybrid tube and Fig. 10 for a hybrid tube. It is possible to see that the behavior for failure criterion in the hybrid and non-hybrid tube is very similar in case (a) and (b), already for the cases (c) and (d) there is a small difference, as shown in Fig. 9. In relation to the buckling load, all the cases revealed a small difference, as depicted in Fig. 10. The cases (a) and (b) tend to be more parabolic than in other cases for failure criterion response, while for buckling load all cases tend to be a little linear, as can be seen in Fig. 10.

In order to provide solutions to several problems new evolutionary algorithms began to be built up from GA, such as PSO, ACO and currently the SFO. This new algorithm created by [34] is based on the behavior of sunflowers in the search from the sun. The sunflower with best fitness is chosen as the sun that will provide orientation for the other sunflowers. Once sunflowers are oriented from the sun, they will reproduce and move toward the optimal point. This algorithm has already been used in many studies [59,60,61].

The SFO considers main three biological operators: i) Pollination rate which defines the percentage of the population who will pollinate, ii) survival rate corresponds to the sunflowers that move toward the sun and iii) mortality rate represents the percentage of sunflowers that no survive because they are further from the sun.

In order to satisfy the design requirements, a multiobjective optimization is developed using SFO algorithm aiming at the best drop-offs location that maximize the buckling load and minimize the failure index. Firstly, once the meta-model was obtained considering a composite tube with drop-offs, could be formulated the constrained nonlinear optimization problem. The optimization problem is depicted in Eqs. (11) to (20).

$$i\mathit{)}\ Minimize\ {\mathrm{TW}}_{\mathrm{C}}\left(\mathbf{x}\right)$$
(11)
$$ii\mathit{)}\ Maximize\ \lambda \left(\mathbf{x}\right)$$
(12)
$$iii\mathit{)}\ Minimize\ {\mathrm{TW}}_{\mathrm{C}}\left(\mathbf{x}\right)\ \&\ Maximize\ \lambda \left(\mathbf{x}\right)$$
(13)
$$\mathrm{Subject\ to}:\mathrm{ g}\left(\mathrm{x}\right): {\mathbf{x}}^{\mathrm{T}}\mathbf{x}\le \alpha$$
(14)
$$0.06\le {\mathrm{x}}_{1}\le 0.12$$
(15)
$$2\le {\mathrm{x}}_{2}\le 4$$
(16)
$$0.18\le {\mathrm{x}}_{3}\le 0.24$$
(17)
$$3\le {\mathrm{x}}_{4}\le 5$$
(18)
$${\mathrm{x}}_{5}=\left\{\mathrm{no},\ \mathrm{yes}\right\}$$
(19)
$$\mathbf{x}=\left\{{\mathrm{x}}_{1},{\mathrm{x}}_{2},{\mathrm{x}}_{3},{\mathrm{x}}_{4},{\mathrm{x}}_{5}\right\}$$
(20)

where now the ply position is represented by x2 and x4 and hybrid categorical variable by x5, meanwhile, the limits laid in the statistical approach are the same. The problem was tackled according to three different optimization backgrounds: i) Tsai-Wu failure index mono-objective optimization (Eq. (11)), ii) buckling load mono-objective optimization (Eq. (12)) and iii) both response multiobjective optimization (Eq. (13)). In all optimization cases, a nonlinear constrained spherical equation is incorporated to ensure that the optimal always is in the viable region (Eq. (14)). The lateral limits are defined according to Eqs. (15) to (19). It is important to note that decision variables x1 and x3 are continuous, x2 and x4 are discrete and x5 is categorical.

This way, we can optimize the better drop-offs location using the SFO algorithm, being the main parameters used in this algorithm depicted in Table 9.

Table 9 Main parameters using the Sunflower optimization algorithm
Full size table

The maximum number of iterations was defined as stopping criterion. The results of the multi-objective optimization were exposed using a Pareto front composed of non-dominated solutions. In this study, there are two conflicting cases (objectives), i.e., buckling load and TWC, especially by considering the 5th design variable (hybrid categorical variable) which gives the information if the structure must be hybrid or not. In this sense, the optimization considered the responses alone in a mono-objective optimization and subsequently in a multi-objective optimization considering both responses at the same time, can be seen in Tables 10 and 11.

Table 10 Mono-objective optimization
Full size table
Table 11 Multi-objective optimization
Full size table

Complementarily, Figs. 11 and 12 show the convergence curves for the two mono-objective cases studied. It is observed that the problem converged properly and the parameters used in the optimizer were adequate.

Fig. 11
figure 11

Optimization converge results for the case I (buckling): objective function (a) and decision variables (b)-(f)

Full size image
Fig. 12
figure 12

Optimization converge results for the case 2 (Tsai-Wu): objective function (a) and decision variables (b)-(f)

Full size image

The results obtained by mono-objective and multi-objective optimization demonstrated the better drop-off location, where in both the cases the dropping-off of 4 and 5 plies together with a hybrid tube have generated higher buckling load and less failure index, as can be seen in Tables 10 and 11. It is important to note that the hybrid variable (x5) has proven be very significant for the tube allowing most promising results.

The Pareto front considers that it is impossible to improve an objective without making the other worse. Then this method provides a set of optimal solutions where the better conditions for both objectives are met as far as possible. In other words, in a multi-objective optimization process, an objective must be attended to in a manner that the other objective is slightly impaired. The set of points belonging to the optimal solution found with SunFlower algorithm can be seen in the optimal Pareto front in Fig. 13. A small range was obtained from the combination of five design variables where one of these is categorical (composite hybrid or not). The physical characteristics of the presented problem contributed to this phenomenon. It could be concluded that the optimal point is tight.

Fig. 13
figure 13

Optimal solution found using Pareto front considering the failure index and buckling load responses

Full size image

To further analyze, the Pareto front determines a set of feasible points, which in this case, are represented by hybrid CFRP/GFRP tube. The knee point is considered as the point with greatest convexity that often is located on the middle of the curve and represents the best combination simultaneous between the responses of the objective function [62, 63]. The optimal solution can be found on the knee point due to convexity, as can be seen in Fig. 13. The points located at the ends of the curve correspond to the points known as Nadir that also symbolize optimal parameters considering the mono-optimization [64]. The Nadir 1 point represents the optimal result aimed at minimizing TW, while the Nadir 2 point represents maximizing buckling loading. The mono and multi-objective optimization considering the better drop-off location is represented by Pareto front, whereas can be seen in Table 12.

Table 12 Multi-objective optimization considering Pareto front
Full size table

For the Nadir and Knee points the best results were considered a hybrid tube, as depicted in Table 12, another fact important was the dropping-off of 5 ply for the second drop-off was considered as the most suitable, due to the 4 ply has already been dropped in x1. According to panel position, the first drop-off located in the beginning of the tube and second drop-off at the end provide better results related to buckling load and failure index, as can be seen in Tables 10, 11, and 12, even though panel position does not interfere on the responses. The buckling load and failure index responses for the Nadir and knee points were advantageous provided that, have indicated a buckling load much higher than the load applied and a failure index lower than 1.

For this purpose, optimized response variables provide the better drop-off location considering the design and categorical variables. The dropping-off of 4 and 5 plies are more favorable when the aim is minimizing the TWc and maximizing λ, individually. For buckling load and failure index are most convenient the drop-offs located nearest to ends of the tube, drop-offs located in the middle of the tube generate reduction in the buckling load. Figure 14 highlights the optimal drop-off location considering the longitudinal position design variable for a hybrid tubular structure.

Fig. 14
figure 14

Optimal tubular structure with a total length of 0.3 m considering the fourth ply dropped at 0.1 m and the fifth ply at 0.24 m, respectively

Full size image

Hence, the results confirm that inserting drop-offs on the tubular laminate provides drastic reduction on the structural mass and can provide benefits when the better location is achieved. Furthermore, the tube with drop-offs proved to be adequate for the use in prostheses because of their high-level reliability in relation to failure index and buckling load.

5 Conclusions

In this study, the results related to better drop-off location in a tube used in prosthesis for lower limb were obtained by DOE using the factorial design, RSM and SFO with Pareto front. Firstly, combinations between design variables were elaborated in factorial design and analyzed using the FEM aiming to provide the responses in relation to failure index, buckling load, mass and 1st natural frequency. Additionally, a meta-model using the DOE was executed to determine the variables that have the most influence on the drop-offs location and, together with SFO, optimize these variables in search of the better drop-off location. The most important conclusions can be drawn:

  • The use of a composite laminate with drop-offs afforded the reduction of mass, besides creating a unique format for a tubular geometry used in prosthesis.

  • The R2 greater than 90% for Tsai-Wu failure criterion and buckling load revealed great fits demonstrating how well the data were to the fitted model. That way, the meta-model created in this study allowed quick analyses with a reliability of 90%. In relation to mass, the R2 presented value less than 70% noting that the model does not explain very well the variability of this data. A reason for this is because many times the mass was the same, independent of drop-offs location on the tube. That way, the mass response variable was not considered in optimization process.

  • For the variables that determine the drop-offs location, only the hybrid, Y1 and Y2 variables and their interactions had significant effects for both response variables. The X2 variable and their interactions with variables mentioned above presented significance related to buckling load response. Hence, the ply variable becomes more relevant together with the hybrid variable. The X1 and X2 variables that represent the longitudinal position were seen as variables without statistical significance.

  • The main effects of the variables demonstrated important parameters in the manufacturing of tubes with drop-offs used in prostheses for lower limb, where higher buckling load and low failure index are achieved with the dropping-off of last plies and a hybrid tube.

  • The optimization using SFO with Pareto front led to a simultaneous optimization of the Tsai-Wu failure criterion and buckling load responses generating adequate values for design variables, where the better drop-off location was found dropped the fourth and fifth plies on the longitudinal length between 0.10 m and 0.11 m.