Stacking sequence optimization and blending design of laminated composite structures

Abstract

The stacking sequence optimization problem for multi-region composite structures is studied in this work by considering both blending and design constraints. Starting from an initial stacking sequence design, unnecessary plies can be removed from this initial design and layer thicknesses of necessary plies are optimally determined. The existence of each ply is represented with discrete 0/1 variables and ply thicknesses are treated as continuous variables. A first-level approximate problem is constructed with branched multipoint approximate functions to replace the primal problem. To solve this approximate problem, genetic algorithm is firstly used to optimize discrete variables, and meanwhile, a blending design scheme is proposed to generate a blended structure. Starting from the thinnest region, this scheme shares all layers of current thinnest region with its adjacent regions. For non-shared layers in the adjacent regions, local mutation is implemented to add or delete plies to make them efficient designs. The whole process is repeated until the blending rule is satisfied. After that, a second-level approximate problem is built to optimize the continuous variables of ply thicknesses for retained layers. Those procedures are repeated until the optimal solution is obtained. Numerical applications, including a two-patch panel and a corrugated central cylinder in a satellite, are conducted to demonstrate the efficacy of the optimization strategy.

1 Introduction

With their high specific stiffness and strength, laminated composites have gained widespread applications in a large spectrum of sectors, like aerospace, automotive, and marine structures. Optimal designs of such composite structures, where the fiber orientations, layer thickness, stacking sequence, and the number of plies can be simultaneously optimized, are extensively conducted to fully explore their potentials (Pai et al. 2003; Walker and Smith 2003; Lopez et al. 2009; Rocha et al. 2014). For traditional design, in which the fiber orientations are limited to a set of options, such as 0, ± 45, and 90°, and the ply thickness is usually fixed as a constant, the optimization problem is full of discreteness, and the size of search space is exponentially dependent on the number of plies, making it much more challenging compared with conventional materials (Yang et al. 2016).

Due to the discrete nature, evolutionary algorithms (EAs), especially genetic algorithms (GAs), are widely adopted to address laminate stacking sequence optimization problems (Venkataraman and Haftka 1999; Ghiasi et al. 2009). However, EAs always come at highly computational consumptions, requiring dramatic function evaluations for structural responses. For this reason, approximation concepts, like response surface methods, are employed to reduce the computational costs. With the use of response surfaces, the number of required of structural analyses can be decreased to some extent, but as the number of design variables increases, the cost to build response surfaces becomes prohibitive (Irisarri et al. 2011). Lamination parameters are thus introduced as intermediate variables and can significantly reduce the number of design variables (Todoroki and Sekishiro 2008). Generally, lamination parameter strategies are restricted to global structural responses, such as stiffness, and inverse problems have to be solved to obtain the number of plies, layer thicknesses, and orientations (Ghiasi et al. 2009; Bruyneel 2006). A further review of the topic on optimum stacking sequence design of composite materials can be found in the literature by Ghiasi et al. (Ghiasi et al. 2009).

Practical structures, e.g., aircraft wings, are often divided into multiple panels or regions. For such kind of multi-region composite structures, their thicknesses are often tailored for lowest weight and best performance, bringing mismatch of stacking sequences and stiffness variations between adjacent regions. This incompatibility between regions often breaks the load path, thus easily causing stress concentration in tapers (Jing et al. 2015), and in the meantime, with the loss of structural integrity, which results from layer discontinuity on adjacent regions (known as blending problem), it makes the structure difficult to manufacture (Curry et al. 1992; Poon et al. 1994; Irisarri et al. 2014). So, both blending rule, which imposes the layer continuity of any two regions that are connected together, and design constraints should be considered simultaneously (Liang and Chen 2003; Panesar and Weaver 2012).

The term, blending, was firstly introduced by Kristinsdottir et al. (2001) in their work to ensure manufacturability of multiple regions and accommodate load variations across them. By designing a 12-region sandwich keel panel, the results showed that blended panel was more practical. In the works of Soremekun et al. (2002), Liu et al. (2011, 2015), and Jing et al. (2015), the shared-layer blending (SLB) technique was used to design blended laminates, which was based on the plies of the thinnest region required by all the regions. A series of optimization methods were developed by introducing the concept of guide-based blending (Adams et al. 2003, 2004, 2007; Van Campen et al. 2008; Seresta et al. 2007; IJsselmuiden et al. 2009; Zein and Bruyneel 2015). With the use of a template stacking sequence as a guide, the regions having the same number of plies are identical in stacking sequence designs. Zein et al. (2016) demonstrated that those two methods have some restrictions on the possible choices of stacking sequences, and they presented an algorithm in terms of constraint satisfactory programming to satisfy the blending rule, showing its advantage over the other two methods. By considering both blending and design rules, many of the optimizers that were used in those literatures are EAs, GAs in particular. As mentioned earlier, those methods are computationally expensive, and this makes them not suitable for large-scale engineering problems of composite structure optimizations (Jing et al. 2015). Additionally, some gradient-based methods are also proposed for ply-drop optimization, like the approximation strategy in Peeters and Abdalla (2016), while most of the gradient-based optimization methods are only applicable for variable-stiffness composite structures, which have curvilinear fiber paths (Hao et al. 2018). In the present work, we focus on the optimization of composite structures constituted of a combination of several straight-fiber layers.

In recent studies (Chen et al. 2013; An et al. 2015a, b), the authors have developed a two-level multipoint approximation method for stacking sequence optimization, and some design and manufacturing constraints are considered. Starting from an initial design of stacking sequence, unnecessary plies can be removed from this initial design and layer thicknesses of necessary plies are optimally determined. The existence of each ply is represented with discrete 0/1 variables and ply thicknesses are treated as continuous variables. A branched multipoint approximate function is firstly used to make the primal problem explicit, and the first-level approximate problem is constructed involving mixed discrete and continuous variables. To solve this approximate problem, GA is used to optimize discrete variables so that necessary and unnecessary plies in the initial stacking sequence design are decided, and ply thicknesses of necessary layers are optimized with a second-level approximate problem, which can be efficiently solved with dual method. After removing the unnecessary plies from the initial design and rounding the ply thicknesses of necessary layers, the optimal design of stacking sequence is obtained. In the optimization process, no intermediate variables are introduced. With benchmark studies and engineering applications, this method has shown good efficiency, and many near optimal solutions can be easily obtained to provide designers as options. However, this method has no capability in dealing with blending rules in multi-region composite structures.

Thus, in this work, we improve and extend the two-level multipoint approximation method to tackle the stacking sequence optimization problem of composite structure under both design and blending rules. For each individual in GA, it represents a stacking sequence design, but this design may not necessarily satisfy the blending rule. So, to make it a blended structure, all layers of current thinnest region are shared with its adjacent regions, and for the non-shared layers in the adjacent regions, local mutation is implemented to add or delete some plies to make them efficient designs. The whole process is repeated until the individual satisfies the blending rule, and we incorporate it into the procedure of GA. Here, we refer to this scheme as shared-layer and mutation (SLM) method. It should be noted that it is different from the existing shared-layer blending (SLB) method, which imposes that the layers of the thinnest region are shared by all the regions. Illustrative example is given to show the process of generating a blended structure with the proposed SLM method, and it is also verified with numerical applications.

The rest of this paper is organized as follows. In the next section, some design and manufacturing constraints, including the blending rule, are given. On the basis of an initial stacking sequence design, the optimization problem is formulated in Section 3. Section 4 is focused on the presentations of the two-level multipoint approximation method as well as the proposed SLM blending scheme. Two numerical applications, a two-patch design from the literature and a practical engineering design from the industrial department, are presented in Section 5, demonstrating the efficiency of the developed method, which is then followed by some concluding remarks in Section 6.

2 Design and manufacturing constraints

In order to generate a manufacturable design which also has good mechanical behaviors, both design and manufacturing constraints should be considered in the design process of composite structures. Some of those design rules that are cited in this work are listed as follows.

• The available choices of fiber orientations are limited to a permissible set of angles, such as 0, ± 45, and 90°.

• The ply thickness should be integral multiples to the fixed basic ply thickness.

• Symmetric sequences are the first choice. If possible, the stacking sequence should be symmetric about the mid-plane.

• If possible, the stacking sequence should be a balanced design, which means the same number of + θ and − θ plies (θ ≠ 0°, 90°).

• To alleviate matrix cracking problems, maximum four contiguous plies with the same fiber orientation are allowed (Zein et al. 2016). When the symmetric constraint is also involved, a maximum of two plies is allowed at the symmetry plane.

• The blending manufacturing is defined as the continuity of layers between two adjacent regions (Jing et al. 2015). This states that if there are two adjacent regions A and B and A has more plies than B, then the plies of B are a subset of the ones of A.

• Considering mechanical properties, structural responses, such as strength, buckling, and stiffness, also need to be treated as constraints in the design process.

Above are some of the design constraints that are considered in the present work, and how to achieve them in the design of composite structures is presented in the following two sections. For more considerations like limiting the number of plies and proportions of each orientation (Irisarri et al. 2014), they are not discussed in this paper and will be the focus of our future work.

3 Basic idea of optimization strategy and problem formulation

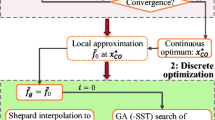
The basic idea of stacking sequence optimization is described in this section, without considering the blending rule. It is based on an initial design of stacking sequence. Considering manufacture constraints, the orientations for each ply are chosen from the set of permissible angles, like 0, ± 30, ± 45, ± 60, and 90°. Starting from this initial stacking sequence design, unnecessary plies can be removed from it and necessary layers are kept in the laminate. In the meantime, layer thicknesses for the necessary plies are optimally designed as continuous variables. Finite element (FE) method is used for structural analysis in the optimization process, and in order to keep the FE model unchanged during the optimization, layer thicknesses for unnecessary plies are represented with a very small value. So, the final design consists of both necessary and unnecessary plies, but it is expected that the physical behavior of the composite structure is solely controlled by the necessary plies, meaning that the mechanical properties of a structure consisting of only necessary plies are almost the same as those of a structure containing both necessary and unnecessary plies. This assumption has been always accepted in topology optimization design of truss structures and continuum structures (An and Huang 2017). So, after optimization, by removing unnecessary plies from the initial stacking sequence design and rounding ply thicknesses for the necessary layers to meet the requirement that the ply thickness should be integral multiples to the fixed basic ply thickness, the optimal stacking sequence is then obtained. Using the initial design of [(0/± 45/90)₂]s as an example, an overview of the basic idea for the optimization strategy is presented in Fig. 1.

Fig. 1

An illustrative example to show the basic idea of the optimization method

According to the basic idea, it removes plies from the initial design. Even though layer thicknesses for the retained plies can be increased after continuous variable optimization, there exists upper limit on the number of layers with the same ply angle. That is caused by the upper bound of continuous ply thickness variables, which are given from the consideration of four-ply contiguity constraint. Care should be taken when choosing the number of plies in the initial design. From our experiences, it is found that for a good exploration of the design space, about 20% of the plies should be removed from the initial design. If a lower number of plies are removed at the end of the optimization, a higher number of plies in the initial design should be used. In our previous works (Chen et al. 2013; An et al. 2018a), we have shown that the approach can find reasonable solutions when varying the number of plies and the sequences of ply angles in the initial design.

As described above, we should decide which layers are necessary and which are not, i.e., deciding the presence/absence of each ply in the initial stacking sequence design. Here, we use discrete 0/1 variables to represent the absence or presence of each ply. If the discrete variable equals 1, this means that related ply is necessary and it is kept. The ply thickness of this necessary layer can be continuously optimized within given lower and upper bounds. When the discrete variable takes the value of 0, it means that ply is unnecessary and can be deleted from the initial design. The ply thickness of this unnecessary layer is represented with a small value in the optimization process. Assuming that the number of design regions is m, the optimization problem is formulated as follows:

$$ \Big\{{\displaystyle \begin{array}{lll} find& \begin{array}{l}X={\left\{{x}_{11},{x}_{12},\cdots, {x}_{1{n}_1},\cdots, {x}_{k1},{x}_{k2},\cdots, {x}_{k{n}_k},\cdots, {x}_{m1},{x}_{m2},\cdots, {x}_{m{n}_m}\right\}}^T\\ {}\kern1.3em ={\left\{{x}_1,{x}_2,\cdots, {x}_i,\cdots, {x}_n\right\}}^T\\ {}\alpha ={\left\{{\alpha}_{11},{\alpha}_{12},\cdots, {\alpha}_{1{n}_1},\cdots, {\alpha}_{k1},{\alpha}_{k2},\cdots, {\alpha}_{k{n}_k},\cdots, {\alpha}_{m1},{\alpha}_{m2},\cdots, {\alpha}_{m{n}_m}\right\}}^T\\ {}\kern1.1em ={\left\{{\alpha}_1,{\alpha}_2,\cdots, {\alpha}_i,\cdots, {\alpha}_n\right\}}^T\end{array}& \\ {}\min & f\left(X,\alpha \right)& \\ {}s.t.& {g}_j\left(X,\alpha \right)\le 0& j=1,\cdots, {J}_0\\ {}& {\alpha}_i{x}_i^L+\left(1-{\alpha}_i\right){x}_i^b\le {x}_i& \\ {}& {x}_i\le {\alpha}_i{x}_i^U+\left(1-{\alpha}_i\right){x}_i^b& \\ {}& {\alpha}_i=0\kern0.8000001em or\kern0.6em {\alpha}_i=1& i=1,\cdots, n\end{array}} $$

(1)

where X is a vector for continuous ply thickness variables, x_i is an element of X, ${x}_i^L$ and ${x}_i^U$ are the lower and upper bounds on x_i, respectively, and ${x}_i^b$ is a small value ($0.01{x}_i^L$ in this work) to represent the thickness value of an unnecessary ply; α is the discrete 0/1 variable vector, and α_i denotes the presence (1) or absence (0) of the i-th ply; n_k is the number of plies in the k-th design region, n is the total number of plies in the initial stacking sequence design of all design regions, and $\sum \limits_{k=1}^m{n}_k=n$;f(X, α) is the objective function, g_j(X, α) is the j-th constraint regarding structural responses, and J₀ is the number of such constraints. Considering the four-ply contiguity constraint and the restriction on the manufacturing process that the thickness of one layer cannot be less than the basic ply thickness t_p, the lower and upper bounds on continuous ply thickness variables are given as ${x}_i^L={t}_p$ and ${x}_i^U=4{t}_p$, respectively.

For the k-th design region, a domain is defined for the necessary layers, involving the discrete variables (which take the value of 1) and their associated continuous variables, as expressed below:

$$ {D}_k=\left\{\left({\alpha}_{ke},{x}_{ke}\right)|{\alpha}_{ke}=1,{x}_{ke}^L\le {x}_{ke}\le {x}_{ke}^U\right\}\kern2.4em e=1,...,{n}_k\kern0.9000001em k=1,...,m $$

(2)

where ${x}_{ke}^L$ and ${x}_{ke}^U$ are the lower and upper bounds on the e-th ply thickness variable x_ke. So D_k is a domain containing all retained discrete and continuous variables for the k-th region. Let k and l be two connected zones. According to the definition of the blending rule in Section 2, if region k has more plies than region l, then the plies of l are a subset of the ones of k, satisfying the constraint as follows:

$$ {D}_l\subseteq {D}_k $$

(3)

Section 4.3 describes the method on how to achieve this blending constraint. Additionally, as for the symmetry constraint, it can be achieved by optimizing one half of the laminate, and the other half is then obtained symmetrically. When considering the balanced design requirement, the ply thickness variables of adjacent + θ and − θ plies are enforced to link together.

4 Optimization method

As the primal problem (PP) is always implicit and contains mixed variables, it is very difficult to be solved with common mathematical programming methods. The two-level multipoint approximation method developed in our previous work is introduced to solve this problem, which is briefly described in this section. The objective of the present work is how to design a blended structure. So, the main contribution of this work is to propose a blending scheme and combine the scheme with the two-level approximation method to efficiently design composite structures, and the proposed blending design scheme is elaborated in Section 4.3.

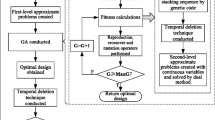
The main procedure of the improved optimization method is firstly described. After conducting finite element analysis (FEA) on the initial design, the first-level approximate problem is constructed with the use of branched multipoint approximate functions, so that the primal problem is made explicit. This approximate problem still contains mixed variables. GA is then employed to optimize discrete 0/1 variables and generate blended structures. When calculating the individual fitness in GA, a second-level approximate problem, which can be efficiently solved by dual method, is built to optimize retained continuous ply thickness variables. After executing all operators in GA, an optimal solution with the best individual fitness is selected from the population, and convergence criterion is then checked on this solution. If the problem is not converged, FEA is conducted on this design point, i.e., the current optimal solution obtained from GA, and the analysis results are used for constructing the first-level approximate problem. The whole process is repeated until the convergence criterion is satisfied, and the optimal design for the primal problem is then obtained. The global optimization strategy is shown in Fig. 2. In the following, the components encompassed with a dotted box in Fig. 2 are introduced in detail.

Fig. 2

Schematic overview of the global optimization strategy

4.1 The first-level approximate problem

As the primal problem is always implicit with regard to design variables, branched multipoint approximate (BMA) functions are used to make it explicit (Chen et al. 2013). In the p-th stage, i.e., after the p-th structural analysis is completed, the first-level approximate problem is formulated as follows:

$$ \Big\{{\displaystyle \begin{array}{lll}\min & {f}^{(p)}\left(X,\alpha \right)& \\ {}s.t.& {g}_j^{(p)}\left(X,\alpha \right)\le 0& j=1,\cdots, {J}_1\\ {}& {\alpha}_i{x}_{i(p)}^L+\left(1-{\alpha}_i\right){x}_i^b\le {x}_i& \\ {}& {x}_i\le {\alpha}_i{x}_{i(p)}^U+\left(1-{\alpha}_i\right){x}_i^b& \\ {}& {\alpha}_i=0\kern0.8000001em or\kern0.6em {\alpha}_i=1& i=1,\cdots, n\end{array}} $$

(4)

$$ {x}_{i(p)}^U=\min \left\{{x}_i^U,{\tilde{x}}_{i(p)}^U\right\} $$

(5)

$$ {x}_{i(p)}^L=\max \left\{{x}_i^L,{\tilde{x}}_{i(p)}^L\right\} $$

(6)

where f^(p)(X, α) and g_j(p)(X, α) are the approximate objective and constraint functions, respectively, created in the p-th stage; J₁ is the number of active constraints related to the primal problem in (1); ${\tilde{x}}_{i(p)}^U$ and ${\tilde{x}}_{i(p)}^L$ are the move limits of x_i at the p-th stage. For a unified formulation, the approximate functions f^(p)(X, α) and g_j(p)(X, α) are represented with the BMA function w^(p)(X, α), as shown below:

$$ {w}^{(p)}\left(X,\alpha \right)=\sum \limits_{t=1}^H{\tilde{w}}_t\left(X,\alpha \right)\bullet {h}_t\left(X,\alpha \right) $$

(7)

where

$$ {\tilde{w}}_t\left(X,\alpha \right)=w\left({X}_t,{\alpha}_t\right)+\sum \limits_{i=1}^n\varDelta {w}_{i,t}\left(X,\alpha \right) $$

(8)

$$ \varDelta {w}_{i,t}\left(X,\alpha \right)=\Big\{{\displaystyle \begin{array}{ll}\frac{1}{r_{o,t}}\frac{\partial w\left({X}_t,{\alpha}_t\right)}{\partial {x}_i}{x}_{i,t}^{1-{r}_{o,t}}\left({x}_i^{r_{o,t}}-{x}_{i,t}^{r_{o,t}}\right)& \kern0.5em if\kern0.2em {\alpha}_i=1\kern0.4em \\ {}\frac{1}{r_{m,t}}\frac{\partial w\left({X}_t,{\alpha}_t\right)}{\partial {x}_i}\left(1-{e}^{-{r}_{m,t}\left({x}_i-{x}_{i,t}\right)}\right)& \kern0.5em if\kern0.2em {\alpha}_i=0\end{array}} $$

(9)

$$ {h}_t\left(X,\alpha \right)=\frac{{\overline{h}}_t\left(X,\alpha \right)}{\sum \limits_{l=1}^H{\overline{h}}_l\left(X,\alpha \right)},\kern0.5em t=1,\cdots, H $$

(10)

$$ {\overline{h}}_l\left(X,\alpha \right)=\prod \limits_{\begin{array}{l}s=1\\ {}s\ne l\end{array}}^H{\left(X-{X}_s\right)}^T\left(X-{X}_s\right) $$

(11)

and X_t or α_t is the t-th known design point, h_t(X, α) is a weighted function, and H is the number of design points to be counted with the upper bound H_max. When the number of known points is larger than H_max, only the last H_max points obtained are taken into account (in this work, H_max = 5). In (9), the exponents r_o,t and r_m,t (t = 1,…,H) are adaptive parameters used to control the non-linearity of the approximation. When t = 1,…,H-1, r_o,t and r_m,t can be obtained by using the least-squares parameter estimation (Chen et al. 2013).

In addition, it should be pointed out that this approximate function is essentially different from the common response surface functions. That is because the response surface needs to be built with sampling points before the optimization starts, while this multipoint approximate function is built in the optimization process. The sampling points, or design points, are only from the iteration process, and each iteration can only produce one design point, which can be clearly observed in Fig. 2.

Even though the primal problem has been made explicit, the first-level approximate problem still involves both continuous and discrete variables. If GA is directly used and the continuous and discrete variables are encoded simultaneously, the scale of design variables and the computational costs could become tremendous. Thus, a layered optimization strategy is introduced: discrete 0/1 variables are optimized with GA in the external layer and continuous variables are optimized in the internal layer by using the dual method, which could significantly reduce the gene code length in GA meanwhile improving the optimization efficiency as well as accuracy.

4.2 GA to optimize discrete 0/1 variables

The discrete variable described in (1) {α₁, α₂, ⋯, α_n}^T takes the value of 1 or 0 to represent the existence or absence of each ply in the initial design. Accordingly, one string of genes, i.e., str = α₁α₂⋯α_n, is used in GA. After the random generation of an initial population, the GA procedure is conducted following the fitness calculation for each individual in the population. We assume that the number of individuals in the population is N, and the maximum generation number is given as MaxG.

As GA is an unconstrained optimization method, problems with constraints need to be transformed into unconstrained ones. Thence, based on the adaptive scheme in (Liu et al. 2012), a constrained minimization problem using an exterior penalty function is first established for the S-th individual:

$$ {F}_1=\Big\{{\displaystyle \begin{array}{ll}{\phi}^{n_c}\left\{{f}^{(p)}\left({X}_S,{\alpha}_S\right)-\left\langle {f}^{(p)}\left(X,\alpha \right)\right\rangle \varepsilon |\max \left\{{g}_1^{(p)}\left({X}_S,{\alpha}_S\right),\cdots, {g}_{J_1}^{(p)}\left({X}_S,{\alpha}_S\right)\right\}|\right\}& \kern0.3em \mathrm{if}\;\left({X}_S,{\alpha}_S\right)\;\mathrm{is}\kern0.17em \mathrm{feasible},\\ {}{\phi}^{n_c}\left\{{\overline{f}}^{(p)}\left(X,\alpha \right)+\left\langle {f}^{(p)}\left(X,\alpha \right)\right\rangle \left[{\left(1+\sum \limits_{j=1}^{J_1}\frac{{\overline{g}}_j^{(p)}}{\sum \limits_{l=1}^{J_1}{\overline{g}}_l^{(p)}}{g}_j^{(p)}\left({X}_S,{\alpha}_S\right)\right)}^2-1\right]\right\}& \kern0.4em \mathrm{otherwise}.\end{array}} $$

(12)

where

$$ {\overline{f}}^{(p)}\left(X,\alpha \right)=\Big\{{\displaystyle \begin{array}{ll}{f}^{(p)}\left({X}_S,{\alpha}_S\right)& \kern0.3em \mathrm{if}\;{f}^{(p)}\left({X}_S,{\alpha}_S\right)>\left\langle {f}^{(p)}\left(X,\alpha \right)\right\rangle, \\ {}\left\langle {f}^{(p)}\left(X,\alpha \right)\right\rangle & \kern0.4em \mathrm{otherwise}.\end{array}} $$

(13)

and 〈f^(p)(X, α)〉 represents the average value of the objective function over the current population, ${\overline{g}}_j^{(p)}$ is the violation of the j-th constraint averaged over the current population, f^(p)(X_S, α_S) and ${g}_j^{(p)}\left({X}_S,{\alpha}_S\right)$ are the objective and constraint values with respect to the optimal continuous values X_S under a given configuration α_S, and all of these values will be obtained by solving the second-level approximate problem which will be detailed in Subsection 4.4; ϕ = (10/9)^0.5 is used to enforce the four-ply contiguity constraint (Le Riche and Haftka 1995), and n_c is the number of same-orientation plies in excess of four contiguously same orientation layers; ε is a small fraction of the maximum constraint to be subtracted from the objective to discriminate between multiple designs with the same objective value, all of which satisfy all the constraints. This composite function, F₁, is then appended to the individual fitness function F₂, which is to be maximized as

$$ {F}_2={\left(1-\frac{F_1-\min \left({F}_1\right)}{\max \left({F}_1\right)-\min \left({F}_1\right)}\right)}^{\chi } $$

(14)

where χ is an exponent for normalization (χ = 2 in this work).

When the fitness calculation is completed, a simulated roulette wheel selection method is used as the reproduction operator, followed by crossover and mutation operations. A one-point crossover method is adopted, and a simple mutation method is used as the mutation operator. In this work, a method with adaptive crossover probability (P_c) and variable mutation probability (P_m) (An et al. 2018b) is used as follows:

$$ {P}_{\mathrm{c}}=\Big\{{\displaystyle \begin{array}{ll}{P}_{\mathrm{c}1}-\frac{\left({P}_{\mathrm{c}1}-{P}_{\mathrm{c}2}\right)\left({F}^{\prime }-{F}_{\mathrm{ave}}\right)}{F_{\mathrm{max}}-{F}_{\mathrm{ave}}}& {F}^{\prime}\ge {F}_{\mathrm{ave}},\\ {}{P}_{\mathrm{c}1}& {F}^{\prime }<{F}_{\mathrm{ave}}.\end{array}}\kern0.5em $$

(15)

$$ {P}_{\mathrm{m}}={P}_{\mathrm{m}\mathrm{i}}{\left(\frac{P_{\mathrm{m}\mathrm{f}}}{P_{\mathrm{m}\mathrm{i}}}\right)}^{\frac{G-1}{MaxG-1}} $$

(16)

where F_max is the maximum fitness value in the current population, F_ave is the average fitness value among the current population, and F^′ is the larger fitness value of the solutions to be crossed; P_mi is the initial probability of mutation and P_mf is the final probability of mutation; G is the current generation number. In addition, we set P_c1 = 0.9, P_c2 = 0.6, P_mi = 0.1, and P_mf = 0.001.

The GA is executed sequentially by using the operations above. It does not stop until the number of evolution generations reaches the maximum generation number, i.e., MaxG, which is preset.

4.3 Blending design scheme

For each individual in GA, it represents a stacking sequence design, but this design may not satisfy the blending rule. Here, we use a structure consisting of four regions as an example to show this possibility, as shown in Fig. 3. The initial stacking sequences for the four regions are given as [0/± 45/90/0/90]s, and a possible design in the population of GA could be [0]s, [90₂]s, [± 45/90]s, and [0₂/90]s for regions I, II, III, and IV, respectively, which obviously does not satisfy the blending rule. In Fig. 3, we use the color of dark gray to represent the removed layers which may be unnecessary. Actually, those unnecessary layers are represented with small values of ply thicknesses. Next, we present a blending scheme, termed as shared-layer and mutation (SLM) method, to make each individual in GA satisfy the blending rule.

Fig. 3

A structure having three regions and a possible design in GA. a A structure consisting of four regions. b Initial stacking sequence design for four regions. c A possible design in the population of GA violating blending rule

First of all, all regions are divided into two groups, i.e., groups A and B. Here, group A represents the regions with the mark of “current thinnest zone,” and the elements in group B are the regions without such thinnest marks. Based on those two groups, the main procedure of the proposed blending scheme is described as follows:

• Step 0 In the beginning, all regions are in group B, meaning that all regions are not marked as “current thinnest zone.”

• Step 1 Find the thinnest region in group B. This region is then marked as “current thinnest zone,” and it becomes an element of group A. So, this region is transferred from group B to group A.

• Step 2 All layers of this current thinnest region are shared with its adjacent regions that are in group B. If its adjacent regions are not in group B, which means those regions are in group A and have been marked as “current thinnest zone,” the layers will not be shared with them. After sharing all layers of the thinnest region to its adjacent regions, the number of necessary layers in those adjacent regions becomes larger or at least keeps unchanged. If the design problem has restrictions on the number of layers, this treatment will cause constraint violation; when the problem is to minimize the structural mass, which is proportional to the number of plies, this treatment will keep this region away from an optimal design. So, step 3 follows to avoid such condition to some extent.

• Step 3 In those adjacent regions, for the non-shared layers that are necessary in the initial design as well as the removed layers which are unnecessary ones, local mutation is conducted on them to delete or add plies so that efficient designs for those regions are possibly produced. As the treatment of sharing layers to the adjacent regions possibly causes the result that the number of necessary layers is increased, the probability of mutation on the non-shared and necessary layers (0.2 in this work), which means deleting plies from the initial stacking sequence design, is recommend to be a bit larger than the probability of mutation on the removed layers (0.1 in this work), which means unnecessary plies are turned into necessary ones and more layers are added as a result.

All the steps described above (except step 0) are repeated until group B is empty. This is the procedure to generate a blending structure, and we refer to it as shared-layer and mutation (SLM) method, the flowchart of which is given in Fig. 4.

Fig. 4

The flowchart of the proposed SLM blending scheme

The proposed SLM method is used to turn the design that is shown in Fig. 3 to be a blended one, the procedure of which is presented in Fig. 5, showing how this method works step by step. From the above descriptions for the SLM method as well as the illustrative example in Fig. 5, it should be noted that the successful implementation of this technique is based on the premise that the initial stacking sequences for any adjacent regions should be the same. This scheme is incorporated into the process of GA to generate blended structures, which can be seen from the optimization flowchart that will be presented in Subsection 4.5.

Fig. 5

An illustrative example to turn an individual in GA into a blended design. a Initialization—all regions are in group B (step 0). b Find the thinnest zone in B and move it from B to A (step 1). c Share all layers of the current thinnest region with its adjacent regions that are in B (step 2). d Local mutation in these adjacent regions (step 3). e Find the thinnest zone in B and move it from B to A (step 1). f Share all layers of the current thinnest region with its adjacent regions that are in B (step 2). g Local mutation in these adjacent regions (step 3). h Find the thinnest zone in B and move it from B to A (step 1). i Share all layers of the current thinnest region with its adjacent regions that are in B (step 2). j Local mutation in these adjacent regions (step 3). k Find the thinnest zone in B and move it from B to A (step 1)

4.4 The second-level approximate problem to optimize continuous ply thicknesses

After the blending structure is produced, the ply thicknesses of retained layers are optimized as continuous variables to obtain the final optimal stacking sequence design.

For each individual design that satisfies the blending rule, the discrete variables in the first-level approximate problem are fixed as α_s. Continuous ply thickness variables, whose corresponding discrete variables are zero, cannot be changed and they are fixed with small values. So, only those continuous variables that are associated with the necessary layers are left in the first-level approximate problem. Considering that the number of retained continuous variables is usually more than the number of active constraints, it is reasonable to use the dual method to solve that problem. However, the first-level approximate problem is still in a complex form, and we cannot easily get a clear relationship between design variables and dual variables. Thus, a second-level approximate problem that can be solved by the dual method is established to approach the optimum of the first-level approximate problem. For more common use, the objective and constraint functions in the first-level approximate problem are expanded into the linear Taylor series with respect to the continuous variables and their reciprocal variables, respectively. Thence, the second-level approximate problem is constructed in a variable separable form, with which the dual method can be effectively used. Under a given discrete variable vector of α_s, this approximate problem in the q-th step is formulated as follows:

$$ \Big\{{\displaystyle \begin{array}{lll} find& \tilde{X}=\left\{{\tilde{x}}_1,\cdots, {\tilde{x}}_I\right\}& \\ {}\mathit{\min}& {\tilde{f}}^{(q)}\left(\tilde{X},{\alpha}_s\right)={f}^{(p)}\left({\tilde{X}}_{(q)},{\alpha}_s\right)+\sum \limits_{i=1}^I\frac{\partial {f}^{(p)}\left({\tilde{X}}_{(q)},{\alpha}_s\right)}{\partial {\tilde{x}}_i}\left({\tilde{x}}_i-{\tilde{x}}_{i(q)}\right)& \\ {}s.t.& {\tilde{g}}_j^{(q)}\left(\tilde{X},{\alpha}_s\right)={g}_j^{(p)}\left({\tilde{X}}_{(q)},{\alpha}_s\right)-\sum \limits_{i=1}^I{\tilde{x}}_{i(q)}^2\frac{\partial {g}_j^{(p)}\left({\tilde{X}}_{(q)},{\alpha}_s\right)}{\partial {\tilde{x}}_i}\left(\frac{1}{{\tilde{x}}_i}-\frac{1}{{\tilde{x}}_{i(q)}}\right)\le 0& j=1,\cdots, {J}_2\\ {}& {\overline{x}}_{i(q)}^L\le {\tilde{x}}_i\le {\overline{x}}_{i(q)}^U& i=1,\cdots, I\end{array}} $$

(17)

$$ {\overline{x}}_{i(q)}^U=\min \left\{{x}_{i(p)}^U,{\tilde{x}}_{i(q)}^U\right\} $$

(18)

$$ {\overline{x}}_{i(q)}^L=\max \left\{{x}_{i(p)}^L,{\tilde{x}}_{i(q)}^L\right\} $$

(19)

where $\tilde{X}$ is the continuous ply thickness variable vector related to the necessary layers and I is the number of those retained continuous variables; ${\tilde{f}}^{(q)}\left(\tilde{X},{\alpha}_s\right)$ is the objective function at the q-th step; ${\tilde{g}}_j^{(q)}\left(\tilde{X},{\alpha}_s\right)$ is the constraint function, and J₂ is the number of the retained constraints; ${\tilde{x}}_{i(q)}^U$ and ${\tilde{x}}_{i(q)}^L$ are the move limits of ${\tilde{x}}_i$ at the q-th step, and ${\overline{x}}_{i(q)}^U$ and ${\overline{x}}_{i(q)}^L$ are the upper and lower bounds on ${\tilde{x}}_i$. The dual problem for the second-level approximate problem can be stated as follows:

$$ \Big\{{\displaystyle \begin{array}{lll}\mathit{\operatorname{Max}}& l\left(\lambda \right)=\underset{\tilde{X}\in R\left(\tilde{X}\right)}{\min}\left[{\tilde{f}}^{(q)}\left(\tilde{X},{\alpha}_s\right)+\sum \limits_{j=1}^{J_2}{\lambda}_j{\tilde{g}}_j^{(q)}\left(\tilde{X},{\alpha}_s\right)\right]& \\ {}s.t.& {\lambda}_j\ge 0,\kern0.5em j=1,\cdots, {J}_2& \end{array}} $$

(20)

where $R\left(\tilde{X}\right)=\left\{{\tilde{x}}_i|{\overline{x}}_{i(q)}^L\le {\tilde{x}}_i\le {\overline{x}}_{i(q)}^U,\kern0.6em i=1,\cdots, I\right\}$. The relationship between the continuous design variables and the dual variables can be established as:

$$ {\tilde{x}}_i=\Big\{{\displaystyle \begin{array}{ll}{\overline{x}}_{i(q)}^L& {\overline{x}}_i<{\overline{x}}_{i(q)}^L\\ {}{\overline{x}}_i& {\overline{x}}_{i(q)}^L\le {\overline{x}}_i\le {\overline{x}}_{i(q)}^U\\ {}{\overline{x}}_{i(q)}^U& {\overline{x}}_i>{\overline{x}}_{i(q)}^U\end{array}}\kern0.5em i=1,\cdots, I $$

(21)

where

$$ {\overline{x}}_i=\Big\{{\displaystyle \begin{array}{cc}\sqrt{x_i^{\prime }}& {x}_i^{\prime}\ge 0\\ {}0& {x}_i^{\prime }<0\end{array}} $$

(22)

$$ {x}_i^{\prime }=-\frac{\sum \limits_{j=1}^{J_2}{\lambda}_j{\tilde{x}}_{i(q)}^2\frac{\partial {g}_j^{(p)}\left({\tilde{X}}_{(q)},{\alpha}_s\right)}{\partial {\tilde{x}}_i}}{\frac{\partial {f}^{(p)}\left({\tilde{X}}_{(q)},{\alpha}_s\right)}{\partial {\tilde{x}}_i}} $$

(23)

The dual problem in (20) can be solved by using the variable metric method (BFGS algorithm). After finding the optimal solution λ^∗, the second-level approximate problem can be easily solved through (21).

With the use of GA and solving the second-level approximate problem with dual method, the optimal design variables (X^∗ and α^∗) are found. The ply thickness variables X^* need to be rounded to make them integer multiples of the basic ply thickness, and plies corresponding to a discrete variable of 0 are deleted.

4.5 Optimization flowchart

The flowchart of the optimization method described above is presented in Fig. 6, which can be seen as a detailed representation of the global optimization strategy that is shown in Fig. 2.

Fig. 6

Flowchart of the optimization method

Once again, it should be pointed out that the adopted multipoint approximation function is gradually established well with the known design points that are obtained from the iteration process, and the number of required structural analysis is thus equal to the iteration number. So, it is quite different from the common response surface functions which need to be built by conducting structural analyses among a series of testing points before starting the optimization. Moreover, it can be seen that by replacing a series of structural analyses for function evaluations in the GA, the first-level approximate problem is solved to achieve these evaluations, while structural and sensitivity analyses are mainly used for establishing the first-level approximate problem. Consequently, computational costs are reduced significantly.

5 Numerical applications

Numerical applications are conducted in this section to illustrate the feasibility and efficiency of the optimization strategy in dealing with stacking sequence optimization and blending design of composite structures. The first example is to optimize a two-patch panel structure from the literature (Irisarri et al. 2011) so that the effectiveness of the proposed method is verified. Moreover, a corrugated central cylinder in a satellite is optimally designed to test its performance in addressing practical engineering problems. All calculations in this section are completed in a computer with CPU3.30 GHz/RAM8.00G.

5.1 A two-patch panel

The first example deals with a two-patch panel from the literature (Irisarri et al. 2011). It was also studied in our previous work, but the blending constraint was not taken into account in the design process (An et al. 2015a). The structure consists of three laminates, and the exterior two laminates have the same design, as shown in Fig. 7. This structure is simply supported on its edges and all four external edges remain straight. The composite material properties are as follows: the elastic modulus of E₁₁ = 138 GPa and E₂₂ = 11 GPa, a shear modulus of 6.5 GPa, Poisson’s ratio of 0.28, and a density of 1600 kg/m³. The basic ply thickness is t_p = 0.125 mm.

Fig. 7

Geometry and loading of the considered two-patch panel

The structural mass is minimized and the critical buckling factor, λ_b, is considered the design constraint, which should be greater than or equal to 0.61. All laminates are assigned with the same stacking sequence design [(− 45/45/90/0)₅]s. The constraints described in Section 2 are all considered except the balanced design requirement. The population size and the maximum generations are set as 200 and 100, respectively. After many repeated runs, several of the optimization results are listed in Table 1, together with the result from Irisarri et al. (2011). It can be seen that this strategy is effective in dealing with stacking sequence optimization and blending design of composite structures, and meanwhile, as GA is adopted, which is a stochastic process, more near optimal designs can be achieved, providing options for the designer. Additionally, the considered design requirements are all satisfied in the optimal solutions, but the result from the literature violates the four-ply contiguity constraint near the mid-plane for the exterior laminate. The number of required finite element analysis (FEA) is always smaller than that of the literature, showing a good efficiency. Figure 8 shows the critical buckling failure modes for the initial design and the optimization result of case 1. For the initial design, the critical bucking factor is around 5.09. As both exterior and interior laminates have the same stacking sequences, the critical buckling failure mode appears as a whole. As for the optimized design, the interior laminate has fewer plies than the exterior one, and the buckling pattern is mainly presented on the interior laminate as a result.

Table 1 Optimal designs for the considered two-patch panel

Fig. 8

Buckling modes for the initial design and the optimization result of Case 1. a Initial design. b Optimization result for case 1

By varying the number of population size and generation, the computational performance is evaluated in terms of computational cost and practical reliability. In this study, the computational cost is calculated from the average number of structural analyses by performing 200 independent optimization runs, and the practical reliability is defined as the fraction of the 200 runs producing a practical optimum. Here, the practical optima are designed as the feasible designs within 2t_p-ply’s weights for one half of the exterior/interior laminate of the global optimum, when we assume that the result from the literature is the global optimum solution. After 200 repeated optimization runs in each pair of population size and generation, the performance comparisons are listed in Table 2. It can be seen that the proposed method has a high practical reliability, i.e., over 0.98, and the required structural analysis can be reduced to some extent when larger population sizes and generations are given. For example, when both the population size and maximum generation numbers are given as 50, the computational cost is around 13.94, and it is reduced to 12.51 when both population size and generation numbers are set as 200. Meanwhile, there is also a similar tendency for the standard deviation of computational cost, i.e., the standard deviation values are decreasing when both population sizes and generations are increasing.

Table 2 Computational performance with different population sizes and generations

5.2 A corrugated central cylinder in a satellite

The second application considers a corrugated central cylinder in a satellite, and Fig. 9 shows its whole structure. It consists of two main parts of components: a carbon cylinder part and a conic shell part made of aluminum, and two parts are connected with an end-frame, through which mechanical joints of bolting are used to connect them together. The carbon cylinder part is composed of three sections, and the cross-sections for each section are in corrugated shapes, which can be seen in Fig. 10. As marked in Fig. 11, each corrugation is divided into four parts. The elastic modulus for the composite materials are E₁₁ = 230 GPa and E₂₂ = 7.29 GPa. The shear modulus is 8.22 GPa with Poisson’s ratio of 0.3, and the material density is 1600 kg/m³. The strength limits are X_T = 1800 MPa, X_c = 780 MPa, Y_T = 30 MPa, Y_c = 130 MPa, and S = 126 MPa, where X_T and X_c are the tensile and compressive stress limits in the longitudinal direction, respectively, Y_T and Y_c are the tensile and compressive stress limits in the transverse direction, respectively, and S is the shear stress limit. The basic single ply thickness is t_p = 0.08 mm. The finite element method is adopted for structural analysis, and the bottom of the conic shell is fixed as the boundary condition.

Fig. 9

Analysis model for the corrugated composite central cylinder

Fig. 10

Cross-sections for the corrugated composite central cylinder

Fig. 11

Composition parts for each corrugation

Without consideration of blending rule, the cylinder was optimally designed in the previous work (An et al. 2016). Here, the blending requirement is considered in the optimization design process. The stacking sequences in each part of the corrugation are treated as design variables. In the current design stage, the concerned structural responses include the fundamental frequency, f₁, the critical buckling factor, λ_b, and the margin of strength safety. The critical buckling factor is calculated under the launch condition load that the overloading is 9.15 g in the transverse direction and 1.5 g in the longitudinal direction, respectively. Meanwhile, the margin of safety (MS) for composite plies is obtained when the Hoffman criterion is used. The failure index (FI) for the Hoffman criterion is:

$$ FI=\frac{\sigma_1^2}{X_{\mathrm{T}}\cdot {X}_{\mathrm{c}}}+\frac{\sigma_2^2}{Y_{\mathrm{T}}\cdot {Y}_{\mathrm{c}}}+\frac{\sigma_1{\sigma}_2}{X_{\mathrm{T}}\cdot {X}_{\mathrm{c}}}+\frac{\sigma_{12}^2}{S^2}+\left(\frac{1}{X_{\mathrm{T}}}-\frac{1}{X_{\mathrm{c}}}\right){\sigma}_1+\left(\frac{1}{Y_{\mathrm{T}}}-\frac{1}{Y_{\mathrm{c}}}\right){\sigma}_2 $$

(24)

where σ₁ and σ₂ are the ply longitudinal stress and transverse stress, respectively, and σ₁₂ is the ply shear stress. MS is calculated as:

$$ MS=\frac{1}{\sqrt{FI}}-1 $$

(25)

The fundamental frequency of the structure should not be lower than 18 Hz, and the critical buckling factor should be equal to or more than 3. The margin of safety for the composite plies should be greater or equal to 1.

With the objective to minimize the structural mass, this cylinder is optimized using the proposed scheme in the present work. Starting from two cases of different initial stacking sequence designs in different sections (i.e., case A and case B), the optimization calculations are conducted. All the constraints stated in Section 2 are considered. As the same stacking sequences are given for each part, the initial designs for both cases are blended designs for each section. Considering the balanced requirement, the ply thickness variables of adjacent + 45° and − 45° plies, or + 60° and − 60°plies, are enforced to be linked together. In GA, the population size and the maximum generation numbers are given as 300 and 200, respectively.

After 20 repeated optimization runs, one feasible result in each case is selected with the lowest mass value among those runs, as listed in Tables 3 and 4. Rational results are obtained even with different initial stacking sequences, and both results satisfy the considered design and manufacturing constraints. Each section has been formed as a blending design. It is known that plies with 90° perform badly in the axial direction, as can also be observed from the material properties, so no plies with 90° are introduced in this cylinder in order to strengthen the mechanical properties in the axial direction. Considering the launch condition load that the overloading is 9.15 g in the transverse direction and 1.5 g in the longitudinal direction, respectively, the optimization results are dominated by ± 45° plies. For cases A and B, the numbers of required plies in different sections/parts may be different. For some parts, like parts 2–4 in lower section, case A has more plies than case B, but it has fewer plies in other parts, like part 4 in middle section and part 1 in lower section. Consequently, they have the same mass in the results. Tables 3 and 4 also give the optimization result from our previous work (An et al. 2016), where the blending rule was not considered. When considering the blending rule, the design space is narrowed, so the obtained structural masses in cases A and B are a bit heavier than the results in the previous work. Moreover, as stated in step 3 of how to generate a blended structure, the treatment of sharing layers to the adjacent regions possibly causes the result that the number of necessary layers is increased. Even though we have imposed a larger probability of local mutation to remove plies on the non-shared and necessary layers, this is a random process and the number of piles can be possibly increased or decreased as a result. Compared with the non-blended design, this has caused slight differences on the thickness distribution. For instance, the thickness distribution for case A in the upper section is a bit different.

Table 3 Optimization result for case A

Table 4 Optimization result for case B

In addition, less than 20 structural analyses are consumed during the entire process, and the time cost for optimization is less than 1 h, showing that this proposed scheme can efficiently supply rational solutions for practical engineering problems. The objective iteration histories for both cases are plotted in Fig. 12. For both cases, it can be seen that there is an increase after one iteration and then goes down to reach the convergence. This increase is caused by the approximation accuracy of the first-level approximate problem as well as the move limits. When there is only one known design point, i.e., the initial design, the accuracy of the first-level approximate problem is not very high and the active constraints in this problem are not located in the real constraint boundaries. Besides, the values of the move limits are quite large at the beginning stage. Therefore, some increase may be produced in the mass just after one iteration. After several iterations, the number of known design points becomes larger, and the accuracy of the first-level approximate problem is improved. Meanwhile, the values of the move limits become gradually smaller when the iteration continues. Thus, the convergence may become more stable after several iterations.

Fig. 12

Objective iteration histories

6 Conclusions

The previously proposed two-level multipoint approximation method for laminate stacking sequence optimization is extended in this work by involving blending rule. Starting from a given initial stacking sequence design, the optimization problem is formulated, and the first-level approximate problem is created to make the primal problem explicit. GA is then used to decide the presence and absence of each ply in the initial design, and in order to generate a blended structure, a shared-layer and local mutation method is proposed to turn each individual in GA to satisfy the blending rule. The ply thicknesses for retained layers are then optimally decided as continuous variables by solving a second-level approximate problem. Thence, the optimal stacking sequences are achieved, satisfying considered both design and manufacturing constraints. The optimization strategy is then verified by using two numerical applications. The efficacy of this method is tested by varying the population sizes and generations. Rational solutions can also be obtained with different initial stacking sequence designs. All those optimization calculations show that this method has a good efficiency, and meanwhile, many practical optima can be achieved to provide designers as options. The application in a satellite cylinder also shows that the presented method can efficiently solve practical engineering problems.