1 Introduction

Central configurations play an important role in the study of the Newtonian \(n\)-body problem. Given a initial position of a central configuration in \(\mathbb{R}^{3}\) with zero initial velocity, the \(n\) particles accelerate toward the center of mass in such a way that the configuration collapses homothetically. If we have initial positions of a central configuration in \(\mathbb{R}^{2}\) and proper initial velocities, each particle will traverse an elliptical orbit around the center of mass as in the Kepler problem and the configuration remains similar to the initial configuration throughout the motion, varying only in size.

Finding all central configurations is challenging in the field of celestial mechanics. They are completely known only for \(n=2,3\) and for configurations in \(\mathbb{R}^{1}\) and \(\mathbb{R}^{n-1}\) for all \(n\). For \(n=2\), every configuration of two bodies is central. Counting up to rotations and translations, we obtain one central configuration. For \(n=3\), there are five central configurations. Three of them are collinear configurations found by Euler and the others are the equilateral triangle discovered by Lagrange. Considering \(n\) bodies in \(\mathbb{R}^{1}\), there are \(\frac{n!}{2}\) central configurations [18]. On the other hand, the only central configuration in \(\mathbb{R}^{n-1}\) is when the \(n\) bodies form a regular simplex [23].

For \(n>3\), only limited results are known about central configurations in \(\mathbb{R}^{\ell}\), where \(1<\ell<n-1\). For \(n=4\), Hampton and Moeckel [16] proved the finiteness of central configurations in \(\mathbb{R}^{2}\) for any choices of four positive masses. For \(n=5\) with generic choices of masses, the finiteness of central configurations in \(\mathbb{R}^{2}\) was proved by Albouy and Kaloshin [2], and the finiteness of central configurations in \(\mathbb{R}^{3}\) was proved by Hampton and Jensen [15]. For \(n>5\), we do not even know if the number of central configurations is finite. Smale’s 6-th problem in the list of his 18 mathematical problems for the 21 century [24] asked if the number of central configurations in \(\mathbb{R}^{2}\) is finite for all \(n\). It is still open for \(n>5\).

Even in the cases of 4 bodies in \(\mathbb{R}^{2}\) and 5 bodies in \(\mathbb{R}^{3}\), we do not have exact counts for the numbers of central configurations for all systems where finiteness are proved. Restricted cases where some of the masses are zero and/or some of the non zero masses are equal are among the few successful examples. There are two kinds of restricted cases for some of the masses being zero. One is when only one of the masses equals to zero, called the restricted \((n+1)\)-body problem. Another is when all but one of the masses approach zero and considering the limiting central configurations. This is called the \((1+n)\)-body problem.

The restricted \((2+1)\)-body problem is well studied and also has five central configurations as in the 3-body problem. The number of central configurations of the restricted \((3+1)\)-body problem in \(\mathbb{R}^{2}\) is shown numerically to be \(8,9\) or 10 [1, 20, 22]. The results are recently proved in [3, 4]. To our understanding, the paper in [4] is among the few dealing with the counting problems where masses are also on the bifurcation curve. They prove rigorously that, on the bifurcation curve, there are nine central configurations.

In this paper, we generalize the case of equal masses of the restricted \((4+1)\)-body problem in \(\mathbb{R}^{3}\) and consider two special cases, where one mass parameter is involved. We use different approach to count the numbers of central configurations and obtain \(3,4,5\) and \(2,3,4\) for the zero mass on different lines of symmetry. In particular, the numbers of such central configurations are four and three at the bifurcation points.

The cases of the \((1+n)\)-body problems are first considered by Maxwell when studying the rings of Saturn. For such problems, we have one dominant mass, assuming 1, and \(n\) small masses, \(\mu_{i}\varepsilon\). Let \(\varepsilon \rightarrow 0\) and consider the limiting central configurations. Such central configurations have the body of the dominant mass at the center of a circle in \(\mathbb{R}^{2}\) which passes through the bodies of infinitesimal masses [9]. There are two central configurations of the \((1+2)\)-body problem, one is collinear and the other one is the equilateral triangle [10].

The \((1+3)\)-body problem is studied in [5, 6]. In [5], the special cases of \(\mu_{1}=\mu_{2}\) are considered. There numerical evidences shows the number of central configurations varies from 5 to 7. In [6], the general cases are studied and generic results of 5 or 7 central configurations are proved, while cases on the bifurcation curve are still in lack of rigorous proofs. It turns out that rigorous counts at two bifurcation points in the case of \(\mu_{1}=\mu_{2}\) are missing. In this paper, we use our method to show that, in the special cases of \(\mu_{1}=\mu_{2}\), the number of central configurations are indeed \(5,6\), or 7. In particular, at two bifurcation points, the numbers of central configurations are five and six.

In this paper, some computations involve Groebner basis and resultants, which are exact symbolic computations. We use Mathematica 10, to perform such computations. We also use Mathematica to count roots of integral polynomials of one variable by its implemented command “CountRoots” that always give accurate answers as explained in [8]. Therefore, all of our arguments in this paper are rigorous. In [26], we provide a link for Mathematica notebooks containing results of our computations.

2 Two Restricted Problems and Main Results

The Newtonian \(n\)-body problem studies the dynamics of \(n\) particles with masses \(m_{i}>0\) and positions \(q_{i}\in\mathbb{R}^{d}\), moving according to the Newton’s laws of motion:

$$ m_{j}\ddot{q}_{j}=\sum _{i \neq j}{}\frac{m_{i}m_{j}(q_{i}-q_{j})}{\|q_{i}-q_{j}\|^{3}}, \quad 1 \leq j \leq n. $$
(1)

Definition 1

A configuration \((q_{1},\ldots,q_{n})\in \mathbb{R}^{dn}\setminus\triangle\) is central if there exists \(\lambda<0\) such that

$$ \lambda(q_{j}-c)=\sum_{i \neq j}{} \frac{m_{i}(q_{i}-q_{j})}{\|q_{i}-q_{j}\|^{3}}, \quad 1 \leq j \leq n, $$
(2)

where \(c=\frac{1}{M} (m_{1}q_{1}+\cdots+m_{n}q_{n} )\), \(M=m_{1}+\cdots+m_{n}\), and \(\triangle= \lbrace q_{i}=q_{j}, i \neq j \rbrace \).

2.1 A Restricted \((4+1)\)-Body Problem in \(\mathbb{R}^{3}\)

Let five particles have masses \(m_{1},\ldots,m_{4}>0\) and \(m_{5}=0\). The four particles with positive masses form a central configuration by themselves according to (2). Considering the central configuration in \(\mathbb{R}^{3}\), we obtain a regular tetrahedron [23]. Fixing \(q_{1},\dots,q_{4}\) in \(\mathbb{R}^{3}\) such that the length of the sides of the regular tetrahedron is 1 and assuming the total mass \(M=1\), without lost of generality, we obtain \(\lambda=-1\) in (2). The equation in (2) for the zero mass become \(\partial_{x}G=\partial_{y}G=\partial_{z}G=0\), where

$$G=\frac{1}{2}\|q_{5}-c\|^{2}+\dfrac{m_{1}}{\|q_{5}-q_{1}\|}+ \dfrac{m_{2}}{\|q_{5}-q_{2}\|}+\dfrac{m_{3}}{\|q_{5}-q_{3}\|}+\dfrac{m_{4}}{\|q_{5}-q_{4}\|}. $$

By the identity,

$$\|q_{5}-c\|^{2}-\sum_{i=1}^{4}m_{i} \|q_{5}-q_{i}\|^{2}=\|c\|^{2}-\sum _{i=1}^{4}m_{i} \|q_{i}\|^{2}, $$

we change the coordinate of \(q_{5}\) to \(r_{i}=\|q_{5}-q_{i}\|\) for \(i=1,\dots,4\). So, we obtain

$$G=\frac{1}{2}\bigl(m_{1}r_{1}^{2}+m_{2}r_{2}^{2}+m_{3}r_{3}^{2}+m_{4}r_{4}^{2} \bigr)+\frac{m_{1}}{r_{1}}+\frac{m_{2}}{r_{2}}+\frac{m_{3}}{r_{3}}+ \frac{m_{4}}{r_{4}}+C, $$

for some constant \(C\) depending on \(c\). With new coordinates, we impose a restriction for the mutual distances of five points in \(\mathbb{R}^{3}\) given by the Cayley–Menger determinant below [19]. Therefore, we have the equation below for \(r_{1},r_{2},r_{3},r_{4}\).

$$\left \vert \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&1&1&1&1&1\\ 1&0&1&1&1&r_{1}^{2}\\ 1&1&0&1&1&r_{2}^{2}\\ 1&1&1&0&1&r_{3}^{2}\\ 1&1&1&1&0&r_{4}^{2}\\ 1&r_{1}^{2}&r_{2}^{2}&r_{3}^{2}&r_{4}^{2}&0 \end{array}\displaystyle \right \vert =F=0. $$

Now we find the critical points of \(G\) restricted to \(F=0\). By the Lagrange multiplier technique, we obtain the following equations for a multiplier \(\omega\).

$$ \begin{aligned} \partial_{r_{i}}G&=\omega \partial_{r_{i}}F,\quad \forall i=1,2,3,4,\\ F&=0. \end{aligned} $$
(3)

Eliminating \(\omega\) and clearing the denominators, we obtain polynomial systems from (3).

For the case of equal masses, we have the following results [17, 21].

Proposition 1

When \(m_{1}=m_{2}=m_{3}=m_{4}\), there are 5 central configurations for the zero mass locating at the line with \(r_{i}=r_{j}\), and \(r_{k}=r_{\ell}\), for distinct \(i< j, k<\ell\) in \(\{1,2,3,4\}\). There are 4 central configurations for the zero mass locating at the line with \(r_{i}=r_{j}=r_{k}\) for \(i< j< k\) in \(\{1,2,3,4\}\). If the zero mass is not on any of the 7 lines of symmetry, there are no central configurations.

To generalize the problem, we consider two special cases. The first case is when \(m_{1}=m_{3}=k\), \(m_{2}=m_{4}=\frac{1}{2}-k\). In this case, we consider \(r_{1}=r_{3}=x\) and \(r_{2}=r_{4}=y\) for simplicity. The second case is when \(m_{1}=m_{2}=m_{3}=k,\ m_{4}=1-3k\). In this case, we consider \(r_{1}=r_{2}=r_{3}=x\) and \(r_{4}=y\).

For the first case, we have the following system.

$$ \left \{ \textstyle\begin{array}{rcl} f_{1}&=& (1-2k)x^{3}-(2-4k)x^{5}+(2-4k)x^{3}y^{2}-2ky^{3}\\ &&{}-4kx^{2}y^{3}-(1-4k)x^{3}y^{3}+2x^{5}y^{3}+4ky^{5}-2x^{3}y^{5},\\ f_{2}&=& 3-4x^{2}+4x^{4}-4y^{2}-8x^{2}y^{2}+4y^{4}. \end{array}\displaystyle \right . $$
(4)

Theorem 1

The system (4) has 3, 4, and 5 positive zeros in \((0,\alpha)\cup(\frac{1}{2}-\alpha,\frac{1}{2})\), at \(k=\alpha,\frac{1}{2}-\alpha\), and in \((\alpha,\frac{1}{2}-\alpha)\), respectively, where \(\alpha\) is approximately 0.226696. Therefore, in the restricted \((4+1)\)-body problem in \(\mathbb{R}^{3}\), there are \(3,4\), or 5 central configurations for the zero mass on the line of symmetry shown in Fig. 1 when \(m_{1}=m_{3}, \ m_{2}=m_{4}\).

Fig. 1
figure 1

\(m_{1}=m_{3}\), \(m_{2}=m_{4}\)

Full size image

For the second case, we have the following system.

$$ \left \{ \textstyle\begin{array}{rcl} f_{3} &=& (1-3k)x^{3}-(1-3k)x^{5}+(1-3k)x^{3}y^{2}-ky^{3}\\ &&{} -3kx^{2}y^{3}-(1-4k)x^{3}y^{3}+x^{5}y^{3}+3ky^{5}-x^{3}y^{5},\\ f_{4} &=& 3-6x^{2}+3x^{4}-2y^{2}-6x^{2}y^{2}+3y^{4}, \\ f_{5} &=& -1 + (-1 + x^{2}) z. \end{array}\displaystyle \right . $$
(5)

Note that in system (5), we impose an extra variable \(z\) and the equation \(f_{5}\) to remove the singularities when \(x=1\), where the zero mass particle collides with the particle of mass \(1-3k\).

Theorem 2

The system (5) has 2, 3, and 4 zeros with positive \(x,y\) coordinates in \((0,\beta)\), at \(k=\beta\), and in \((\beta,\frac{1}{3})\), respectively, where \(\beta\) is approximately 0.246659. Therefore, in the restricted \((4+1)\)-body problem in \(\mathbb{R}^{3}\), there are \(2,3\), or 4 central configurations for the zero mass on the line of symmetry shown in Fig. 2 when \(m_{1}=m_{2}=m_{3}\).

Fig. 2
figure 2

\(m_{1}=m_{2}=m_{3}\)

Full size image

Remark 1

In Theorem 1, the number of central configurations 5 is obtained as in Proposition 1 by letting \(k=\frac{1}{4}\). Similarly, in Theorem 2, the number of central configurations 4 is obtained as in Proposition 1 by letting \(k=\frac{1}{4}\).

2.2 The \((1+3)\)-Body Problem in \(\mathbb{R}^{2}\)

Now, let \(q_{i}=(x_{i},y_{i})\in\mathbb{R}^{2}\) and \(r_{i,j}=\|q_{i}-q_{j}\|\) be the distance between particles \(i\) and \(j\). Let \(\triangle_{i,j,k}\) denote the oriented area of the triangle with vertices \(q_{i},q_{j}\), and \(q_{k}\). That is,

$$\triangle_{i,j,k}=\frac{1}{2} \left \vert \textstyle\begin{array}{c@{\quad}c@{\quad}c} x_{i}&y_{i}&1\\ x_{j}&y_{j}&1\\ x_{k}&y_{k}&1 \end{array}\displaystyle \right \vert . $$

We have the following characterization for non collinear central configurations [14].

Proposition 2

Let \((q_{1},\ldots,q_{n})\in \mathbb{R}^{2n}\setminus\triangle\) be a non collinear planar configuration. Then (2) are satisfied if and only if

$$\sum_{k=1,k\neq i,j}^{n}m_{k} \triangle_{i,j,k}\biggl(\frac{1}{r_{ik}^{3}}-\frac{1}{r_{jk}^{3}}\biggr)=0,\quad 1 \leq i < j \leq n. $$

Let \((q_{1}(\epsilon),q_{2}(\epsilon),q_{3}(\epsilon),q_{4}(\epsilon))\) be a central configuration of the planar 4-body problem, with \(m_{1}=\mu_{1}\epsilon, m_{2}=\mu_{2}\epsilon, m_{3}=\mu_{3}\epsilon, m_{4}=1\). If the limit of each \(q_{i}(\epsilon)\) exists as \(\epsilon\) approaches zero such that none of the two limiting positions collide, we call the limiting configuration a non-collision central configuration of the planar \((1+3)\)-body problem. We have the following well known results [9].

Proposition 3

All the central configurations of the planar \((1+n)\)-body problem lie on a circle centered at the particle with positive mass.

To find the non-collision central configurations of the planar \((1+3)\)-body problem, we can apply Proposition 2 and let \(\epsilon\) approaches zero. By Proposition 3 we can then use, without lost of generality,

$$q_{1}=\biggl(\frac{1-r_{3}^{2}}{1+r_{3}^{2}},\frac{2r_{3}}{1+r_{3}^{2}}\biggr),\qquad q_{2}=\biggl(\frac{1-r_{4}^{2}}{1+r_{4}^{2}},\frac{2r_{4}}{1+r_{4}^{2}}\biggr),\qquad q_{3}=(-1,0),\qquad q_{4}=(0,0) $$

in the limiting equations. Here we consider \(\mu_{1}=\mu_{2}=1\) and \(\mu_{3}=k>0\). Also, we impose two more variables \(r_{1},r_{2}\) such that \(\frac{1}{r_{1}^{2}}=1+r_{3}^{2}\), and \(\frac{1}{r_{2}^{2}}=1+r_{4}^{2}\). Then, we obtain the following system with four equations, four variables, and one parameter.

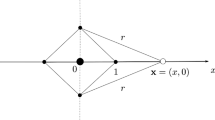
$$ \left \{ \textstyle\begin{array}{rcl} f_{6} &=& r_{1} r_{3}^{2} r_{4} - 8 r_{1} r_{2}^{3} r_{3}^{2} r_{4} - 2 r_{1} r_{3} r_{4}^{2} + 16 r_{1} r_{2}^{3} r_{3} r_{4}^{2} + r_{1} r_{4}^{3} - 8 r_{1} r_{2}^{3} r_{4}^{3}\\ && + k(1 - 8 r_{1}^{3} r_{2}^{3} r_{3}^{3} + r_{3} r_{4} + 24 r_{1}^{3} r_{2}^{3} r_{3}^{2} r_{4} - 8 r_{1}^{3} r_{2}^{3} r_{3}^{4} r_{4} - 24 r_{1}^{3} r_{2}^{3} r_{3} r_{4}^{2} \\ &&{} + 24 r_{1}^{3} r_{2}^{3} r_{3}^{3} r_{4}^{2} + 8 r_{1}^{3} r_{2}^{3} r_{4}^{3} - 24 r_{1}^{3} r_{2}^{3} r_{3}^{2} r_{4}^{3} + 8 r_{1}^{3} r_{2}^{3} r_{3} r_{4}^{4}) ,\\ f_{7} &=& r_{2} r_{3} - 8 r_{1}^{3} r_{2} r_{3} + r_{1} r_{4} - 8 r_{1} r_{2}^{3} r_{4} , \\ f_{8} &=& 1 - r_{1}^{2} - r_{1}^{2} r_{3}^{2}, \\ f_{9} &=& 1 - r_{2}^{2} - r_{2}^{2} r_{4}^{2}. \end{array}\displaystyle \right . $$
(6)

The geometric meanings of \(r_{3},r_{4}\) are the \(y\)-coordinates of the points of intersection between the \(y\)-axis and the line segments connecting \(q_{3}\) and \(q_{1}, q_{2}\), respectively. Denote the intersection points by \(p_{1}\) and \(p_{2}\). Then \(r_{1}\) and \(r_{2}\) are the inverse of the lengths of the hypotenuse of the triangles \(p_{1}q_{3}q_{4}\) and \(p_{2}q_{3}q_{4}\), respectively. Figure 3 shows the geometry. The goal here is to count the number of common zeros of the system (6) with \(0< r_{1},r_{2}<1\) and \(r_{3}>r_{4}\) without lost of generality. (Note that it is easy to see there are no common zeros for \(r_{1}=1\) or \(r_{2}=1\) if \(0< k\).)

Fig. 3
figure 3

The \(1+3\) body problem

Full size image

Theorem 3

The system (6) has 5, 6, and 7 zeros with \(0< r_{1},r_{2}<1\) and \(r_{3}>r_{4}\) in \((0,a)\cup [ b, \infty )\), at \(s=a\), and in \((a,b)\), respectively, where \(a,b\) are approximately 0.89616 and 1.42385. Therefore, for the planar \((1+3)\)-body problem with two equal infinitesimal masses, there are \(5,6\), or 7 central configurations.

Remark 2

In [6], the number of central configurations 5 or 7 on \((0,\infty) \setminus \{a,b\}\) are proved rigorously. As in [5], only numerical evidences are given for the numbers of central configurations at \(a\) and \(b\).

3 Counting Algorithm

In this section, we present our method of counting real common zeros of a parametric polynomial system \(\mathcal{F}=\lbrace f_{1},\ldots,f_{n} \rbrace\), where \(f_{i}\in \mathbb{Q} [ k ] [ x_{1},\ldots,x_{n} ]\). Here \(\mathbb{Q} [ k ]\) is the domain of the coefficients.

We define the specialization at a point \(r \in \mathbb{R}\). It is a ring homomorphism \(\varphi^{r}: \mathbb{Q} [ k ] [ x_{1},\ldots,x_{n} ] \rightarrow \mathbb{R} [ x_{1},\ldots,x_{n} ]\) such that \(\varphi^{a}(f)\) is the real polynomial after substituting the parameter with the value \(r\) in \(f\). We denote \(\varphi^{r}(f)=f^{r}\) and \(\varphi^{r}(\mathcal{F})=\lbrace f^{r} \vert f\in \mathcal{F} \rbrace=\mathcal{F}^{r}\).

The enumeration problem of the system ℱ is to count the number of common zeros in \(\mathcal{X}\) of \(\mathcal{F}^{r}\) for all \(r \in \mathcal{P}\). Here \(\mathcal{X}= \lbrace x \in \mathbb{R}^{n}| \ p_{1}(x)>0,\dots,p_{\ell}(x)>0 \rbrace\), where \(p_{j}\) are polynomials with integral coefficients and \(\mathcal{P}\) is an open interval in ℝ, called the parameter space. (For example, if \(n=2\), \(p_{1}=x_{1}, \ p_{2}=x_{2}\), and \(\mathcal{P}=(0,\infty)\), we are to count the common zeros of the system in the first quadrant for all positive parameters.) To do so, we proceed as the following.

  1. 1.

    View ℱ in \(\mathbb{Q} [x_{1},\ldots,x_{n},k]\) and compute the Groebner basis \(\mathcal{G}\) of ℱ with a block order.

  2. 2.

    View \(\mathcal{G}\) in \(\mathbb{Q}(k) [ x_{1},\ldots,x_{n} ]\), where \(\mathbb{Q}(k)\) is the field of rational polynomials in \(k\), and compute the Hermite matrices \(H_{j}:=H(\mathcal{F},P_{j})\) for all \(P_{j}\), where \(P_{j}\) is any product of a subset from \(\lbrace p_{1},\dots,p_{\ell} \rbrace\). There are \(2^{\ell}\) of them including of the product of no polynomials \(P_{0}:=1\).

  3. 3.

    From \(H_{0}\), we obtain all points \(a \in \mathcal{P}\) where the number of real zeros of ℱ may change. Those points are zeros of a polynomial \(g\), called the bifurcation polynomial, which is the numerator of \(H_{0}\).

  4. 4.

    Call the zeros \(a_{i}\) of \(g\) the bifurcation points and pick a rational sample point \(a \in (a_{i},a_{i+1})\). Use Hermite root counting theorem to count the number of zeros in \(\mathcal{X}\) by computing signatures of \(H(\mathcal{F}^{a},P_{j})\) for all \(j\).

    The number of zeros in \(\mathcal{X}\) is a constant in \((a_{i},a_{i+1})\) if \(p_{j}\neq 0\) for all \(j\) at the common zeros. Therefore, generic results are obtained. Next, we focus on parameters at the bifurcation points \(a_{i}\)’s. Let \(H_{j}^{i}:=H(\mathcal{F}^{a_{i}},P_{j})\) and \(d\) be the dimension of \(H_{j}\).

  5. 5.

    For each \(a_{i}\) and \(H_{j}\), obtain the rank \(r_{i,j}\) of \(H_{j}^{i}\) from the principal minors of \(H_{j}\). For each \(H_{j}\), denote the leading principal minors of order \(t\) by \(D_{j,t}\). It turns out \(D_{j,t}^{a_{i}}=0\) for all \(t>r_{i,j}\), if \(r_{i,j}< d\).

  6. 6.

    For each \(a_{i}\), we pick an interval \((a_{i\ell},a_{ir})\) containing it such that, for all \(j\) and \(t \leq r_{i,j}\), if \(D_{j,t}\) is not identically equal to zero, then there is no zeros in \((a_{i\ell},a_{ir})\) and there is only one zero, \(a_{i}\), of \(D_{j,t}\) for all \(t>r_{i,j}\), if \(r_{i,j}< d\).

  7. 7.

    For each \(a_{i}\) and \(H_{j}\), compute the number of sign changes \(v_{i,j}\) in the list \(\lbrace 1,D_{j,1}^{b_{i}},\dots, D_{j,r_{i,j}}^{b_{i}}\rbrace \), where \(b_{i}\) can be either \(a_{li}\) or \(a_{ri}\).

  8. 8.

    Obtain the signatures of \(H_{j}^{i}\) from \(v_{i,j}\) and \(r_{i,j}\) by the Jacobian theorem and compute the number of common zeros in \(\mathcal{X}\) of \(\mathcal{F}^{a_{i}}\) again by Hermite root counting theorem.

Remark 3

By Hermite root counting theorem, we not only count the common zeros of \(\mathcal{F}^{a_{i}}\) in \(\mathcal{X}= \lbrace x \in \mathbb{R}^{n}| \ p_{1}(x)>0,\dots,p_{\ell}(x)>0 \rbrace\). We also obtain the numbers of common zeros in any of the region \(\lbrace \ (-1)^{m_{1}}p_{1}>0,\dots,(-1)^{m_{\ell}}p_{\ell}>0 \rbrace\) among the \(2^{\ell}\) “quadrants”.

In the following two subsections, we present tools we used. Moreover, we focus on showing that our counting method is rigorous.

3.1 Steps from \((1)\) to \((4)\): on Finding the Bifurcation Polynomial

Given any polynomial ring over ℚ, a finite set of polynomials in it, a total ordering on monomials, we can symbolically manipulate the given set of polynomials and output the Groebner basis, another finite set of polynomials, which has many good properties [11]. They generate the same ideal and hence share the same set of common zeros. For certain orders on monomials, the Groebner base are much easier to solve than the original system.

Consider the quotient algebra \(A\) over the filed ℂ of the ideal generated by the polynomials, a Groebner basis can verify if the polynomial system has finitely many complex common zeros by showing the dimension of \(A\) as a vector space over ℂ is finite. In this case, the dimension gives an upper bound to the number of zeros. Moreover, we can obtain a basis of \(A\) and an algorithm to express any element in \(A\) with this basis. Therefore, it becomes possible to compute the Hermite matrix that is used to count the number of real roots.

Definition 2

Let \(\mathcal{F}= \lbrace f_{1},\ldots,f_{n} \rbrace\subset \mathbb{Q} [ x_{1},\ldots,x_{n} ]\), \(I= \langle \mathcal{F} \rangle \), \(p \in \mathbb{Q} [ x_{1},\ldots,x_{n} ]\) and \(A= \mathbb{R} [ x_{1},\ldots,x_{n} ]/I\) with a basis \(\lbrace b_{1},\ldots, b_{m} \rbrace \), the Hermite matrix, denoted by \(H(\mathcal{F},p)\), is the \(m\times m\) real symmetric matrix with entries \(\mathit{Trace} ( L (pb_{i}b_{j} ) )\), where \(L (pb_{i}b_{j} )\) is the linear map on \(A\) defined by the left multiplication with \(pb_{i}b_{j}\).

Hermite root counting method is given in the following proposition [7]. In [26], we provide a Mathematica notebook containing the implementation of our efficient algorithm outputting \(H ( \mathcal{F}, p )\) given \(\mathcal{F}, p\) and a Groebner basis of ℱ.

Proposition 4

Matrix rank of \(H ( \mathcal{F}, p )\) equals to the number of complex roots of ℱ with \(p \neq 0\). Signature of \(H ( \mathcal{F}, p )\) equals to the number of real roots with \(p>0\) minus the number of real roots with \(p<0\).

If we are to count real roots in \(\mathcal{X}= \lbrace x \in \mathbb{R}^{n}| \ p_{1}(x)>0,\dots,p_{\ell}(x)>0 \rbrace\), where \(p_{j}\) are polynomials, we need to compute \(2^{\ell}\) Hermite matrices \(H(\mathcal{F},P_{j})\) for all \(P_{j}\), where \(P_{j}\) is any product of a subset from \(\lbrace p_{1},\dots,p_{\ell} \rbrace\), including of the product of elements in the empty set \(P_{0}=1\). Then solving a linear system of \(2^{\ell}\) variables, we obtain the numbers of real roots in all of the \(2^{\ell}\) regions \(\lbrace \ (-1)^{m_{1}}p_{1}>0,\dots,(-1)^{m_{\ell}}p_{\ell}>0 \rbrace\).

In our situations, parameters are involved. Extra cares should be taken into consideration. Given \(\mathcal{F}=\lbrace f_{1},\ldots,f_{n} \rbrace \subset \mathbb{Q} [ k ] [ x_{1},\ldots,x_{n} ]\), a polynomial system with coefficients in the domain \(\mathbb{Q} [ k ]\). The first goal is to compute a set of polynomials \(\mathcal{G}\) in \(\mathbb{Q} [ k ] [ x_{1},\ldots,x_{n} ]\) such that the specialization at any point \(r \in \mathbb{R}\), \(\mathcal{G}^{r}\) is a Groebner basis for \(\mathcal{F}^{r}\) in \(\mathbb{R} [ x_{1},\ldots,x_{n} ]\). Here, we adopt the following proposition to achieve this goal for almost all \(r \in \mathbb{R}\) [13].

Proposition 5

View \(\mathcal{F}\subset \mathbb{Q} [ x_{1},\ldots,x_{n},k ]\), consider any total ordering where any monomial involving one of the \(x_{i}\) ’s is greater than all monomials in \(k\), called a block order, and compute a Groebner basis \(\mathcal{G}= \lbrace g_{1},\dots,g_{s} \rbrace\) of ℱ with this order. Using the total ordering on the variables \(x_{1},\dots,x_{n}\) of the block order, we find the leading terms \(\lbrace h_{1},\dots,h_{s} \rbrace \subset \mathbb{Q} [ k ]\) of \(\mathcal{G}\) in \(\mathbb{Q} [ k ] [ x_{1},\ldots,x_{n} ]\). If \(h_{i}^{r}\neq 0\) for all \(i\), then \(\mathcal{G}^{r}\) is a Groebner basis of \(\mathcal{F}^{r}\).

Next, we will compute \(H(\mathcal{F}^{r},p)\) for all such \(r\) where \(h_{i}^{r}\neq 0\) for all \(i\). We use the following results whose proofs can be found in [25].

Proposition 6

View \(\mathcal{G}\) obtained in Proposition  5 as a set in \(\mathbb{Q}(k) [ x_{1},\ldots,x_{n} ]\) and consider ℱ in \(\mathbb{Q}(k) [ x_{1},\ldots,x_{n} ]\). Then \(\mathcal{G}\) is a Groebner basis of ℱ in \(\mathbb{Q}(k) [ x_{1},\ldots,x_{n} ]\). Hence, we can compute the hermite matrix \(H ( \mathcal{F}, p )\) on the algebra \(A\) over the field \(\mathbb{Q}(k)\). \(H ( \mathcal{F}, p )\) is a symmetric matrix with entries in \(\mathbb{Q}(k)\), whose denominators can only contain factors \(h_{i}\) ’s in Proposition  5. We have the specialization \(\varphi^{r}(H ( \mathcal{F}, p ))=H ( \mathcal{F}^{r}, p )\) for all \(r\) where \(h_{i}^{r}\neq 0\) for all \(i\).

Then, we compute the bifurcation polynomial \(g\) of the system ℱ. Theoretically, the bifurcation polynomial is defined as the polynomial containing the projection of the common zeros of \(\lbrace \mathcal{F},J \rbrace\) in \(\mathbb{C} [ x_{1},\ldots,x_{n},k ]\), where \(J\) is the Jacobian determinant of ℱ, into the parameter space \(\mathcal{P}\) in ℝ. Those points of projection in the parameter space are called the bifurcation points. One approach to compute \(g\) is to compute a Groebner basis of \(\lbrace \mathcal{F},J \rbrace\) with a certain order to eliminate the variables \(x_{1},\ldots,x_{n}\). We will not use this method because the computations of such Groebner basis usually require much more computer memories then we have. Instead, we use the following method [25].

Proposition 7

Consider the hermite matrix \(H ( \mathcal{F}, p )\) in \(\mathbb{Q}(k)\) obtained in Proposition  6 and \(p=1\). If the determinant of \(H ( \mathcal{F}, 1 )\) in \(\mathbb{Q}(k)\) is not identically equal to zero. Then the zero set of the numerator \(g\) contains the bifurcation points. Therefore, we call such \(g\) the bifurcation polynomial.

3.2 Steps from \((5)\) to \((8)\): on Counting at the Bifurcation Points

Assume the bifurcation polynomial \(g\) has real zeros \(\lbrace a_{1},\dots,a_{w} \rbrace\) in the parameter space \(\mathcal{P}\). We will also use the Hermite root counting method to count the number of common zeros of \(\mathcal{F}^{a_{i}}\) in \(\mathcal{X}\). Since \(a_{i}\)’s are only know implicitly, we can not compute \(\varphi^{a_{i}}(H(\mathcal{F},p))\) nor \(H(\mathcal{F}^{a_{i}},p)\) directly to obtain the signatures. However, as long as \(a_{i}\) is not a zero for any of the \(h_{j}\)’s in Proposition 5, we have \(\varphi^{a_{i}}(H(\mathcal{F},p))=H(\mathcal{F}^{a_{i}},p)\) by Proposition 6. In fact, \(\varphi^{r}(H(\mathcal{F},p))=H(\mathcal{F}^{r},p)\) in a small closed interval \([ a_{\ell i},a_{r i} ]\) containing \(a_{i}\). We will pick such interval that is small enough for us to obtain the signatures of \(\varphi^{a_{i}}(H(\mathcal{F},p))\). The critical tool is the Jacobian theorem in the following [12].

Proposition 8

Let \(H\) be a \(d\times d\) real symmetric matrix and \(D_{i}\) for \(i=1,\dots,d\) be the leading principal minors of \(H\) of order \(i\). That is, \(D_{i}\) is the determinant of the sub matrix \(H^{i}\) of \(H\), where \(H_{s,t}^{i}=H_{s,t}\) for \(1\leq s,t \leq i\). Assume \(H\) has rank \(r\).

  1. 1.

    If \(D_{i}\neq 0\) for all \(i\leq r\), then the signature of \(H\) is \(r-2v\), where \(v\) is the number of variation of sign in the sequence \(1,D_{1},\dots,D_{r}\).

  2. 2.

    If in the sequence \(1,D_{1},\dots,D_{r}\neq 0\), there are zeros but not three in succession, then the signature of \(H\) can be determined by \(r-2v\) omitting the zero \(D_{k}\) if \(D_{k-1}D_{k+1}\neq 0\) and, in the cases of \(D_{k}=D_{k+1}=0\), setting the number of variation in the sequence \(D_{k-1},D_{k},D_{k+1},D_{k+2}\) to be 1 if \(D_{k+2}D_{k-1}<0\) and to be 2 if \(D_{k+2}D_{k-1}>0\).

  3. 3.

    If there are three consecutive zeros in \(D_{1},\dots,D_{r-1}\), then the signs of the non zero \(D_{k}\) ’s do not determined the signature.

  4. 4.

    If \(D_{r}=0\), the signs of the non zero \(D_{k}\) ’s do not determined the signature.

According to the Jacobian theorem, we only consider cases when \(H(\mathcal{F},p)\) does not have more than two consecutive zero polynomials in the sequence of its leading principal minors. Also, in applying the Jacobian theorem, it is critical to find the rank first. We list the following facts about ranks.

Definition 3

Let \(H\) be a \(d\times d\) real matrix. A minor of order \(i\leq d\) is the determinant of the \(i \times i\) sub matrix \(M\) of \(H\), where \(M_{s,t}=H_{s,t}\) for \(s,t \in \lbrace 1,\dots,d \rbrace\). The largest among the orders of the non-zero minors generated by \(H\) is the rank.

From the definition, it is easy to see the following facts. We omit the proofs.

Proposition 9

Let \(H\) be a \(d\times d\) real symmetric matrix and \(D_{i}\) for \(i=1,\dots,d\) be the leading principal minors of \(H\) of order \(i\). Let \(M^{d-1}\) be the matrix of order \(d-1\), where \(M_{s,t}^{d-1}=H_{s,t}\) for \(s,t \in \lbrace 1,\dots,d-2,d \rbrace\). Let \(M_{d-1}\) denote the determinant of \(M^{d-1}\). We have the following.

  1. 1.

    If \(D_{d}\neq 0\), then the rank of \(H\) is \(d\).

  2. 2.

    If \(D_{d}=0, \ D_{d-1}\neq 0\), then the rank of \(H\) is \(d-1\).

  3. 3.

    If \(D_{d}=D_{d-1}=M_{d-1}=0, \ D_{d-2}\neq 0\), then the rank of \(H\) is \(d-2\).

Now, we return to the goal of computing the signature of \(\varphi^{a_{i}}(H(\mathcal{F},p))\), where \(a_{i}\) a zero of the bifurcation polynomial \(g\) and is not a zero for any of the \(h_{j}\)’s in Proposition 5. Using Proposition 9, we obtain the ranks for the Hermite matrices considered in this paper involving the parameter \(k\). It remains to compute the numbers of variation of sign in the sequences of leading principal minors.

Suppose the rank is \(r\), \(D_{r}^{a_{i}}\neq 0\), and there are no three or more consecutive zero polynomials in \(D_{1},\dots,D_{r-1}\). A small interval \([ a_{i \ell },a_{i r} ]\) containing \(a_{i}\) can be found easily satisfying that there is no zeros for the non zero \(D_{k}\)’s for all \(k=1,\dots,r-1\) in \([ a_{i \ell},a_{ir} ]\). Then the sign of the non zero \(D_{k}^{a_{i}}\) agrees with that of \(D_{k}^{a_{i \ell }}\) or \(D_{k}^{a_{i r}}\).

3.3 Challenging Parts and Other Remarks

Remark 4

To apply our approach, ℱ need to meet some requirements.

  1. 1.

    In step \((1)\), the Groebner basis \(\mathcal{G}\) in \(\mathbb{Q} [x_{1},\ldots,x_{n},k ]\) should be computable.

  2. 2.

    In step \((3)\), determinant of \(H ( \mathcal{F}, 1 )\) in \(\mathbb{Q}(k)\) is not identically equal to zero.

  3. 3.

    For steps \((5)\) to \((8)\), the \(H_{j}\)’s having entries \(\mathbb{Q}(k)\) and defined in the step \((2)\) can not have three or more consecutive zero polynomials in the sequences of their leading principal minors up to the order of rank. And the leading principal minors of the order of rank are not zero polynomials.

  4. 4.

    For steps \((5)\) to \((8)\), \(a_{i}\), a zero of the bifurcation polynomial \(g\), is not a zero for any of the \(h_{j}\)’s in Proposition 5.

    In fact, any zero of a \(h_{j}\) in the parameter space should be handle differently, for in Proposition 7, which is proved by Proposition 6 in [25], did not consider such points. It is even possible to obtain bifurcation points from them.

Remark 5

The orders on monomials can be determined by a matrix with row \(\mathbf{w}_{\mathbf{i}}\)’s. Given two monomials \(\mathbf{x}_{\mathbf{1}},\mathbf{x}_{\mathbf{2}}\) with exponent vectors \(\alpha\) and \(\beta\), we have \(\mathbf{x}_{\mathbf{1}}>\mathbf{x}_{\mathbf{2}} \) if \(\mathbf{w}_{\mathbf{1}}\cdot \alpha>\mathbf{w}_{\mathbf{1}}\cdot \beta\). If \(\mathbf{w}_{\mathbf{1}}\cdot \alpha=\mathbf{w}_{\mathbf{1}}\cdot \beta\), we compare \(\mathbf{w}_{\mathbf{2}}\cdot \alpha\) with \(\mathbf{w}_{\mathbf{2}}\cdot \beta\). Repeat the procedure until we find which one is larger. In this paper, we use the following matrix for variables \(x_{1},\ldots,x_{n},k\).

$$\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1&1&\cdots&1&1&0\\ 1&1&\cdots&1&0&0\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ 1&1&\cdots&0&0&0\\ 1&0&\cdots&0&0&0 \\ 0&0&\cdots&0&0&1 \end{array}\displaystyle \right ] $$

This is a block order. Its restriction on \(x_{j}\)’s is the order determined by the upper left \(n \times n\) block called the graded reverse lexicographical order (or grevlex order). According to [11], for some operations, the grevlex ordering is the most efficient for computation. Therefore, we use this order as one of the block.

Remark 6

In step \((6)\), we use the implemented command “CountRoots” of Mathematica 10 to count roots of integral polynomials of one variable. This command is based on [8]. In the introduction of this paper, the authors commented that “Unlike numerical methods the algorithm will always terminate with correct results.”

Remark 7

In our work, we simply use the command “Det” of Mathematica to compute leading principal minors in one variable. For system (6), the order of \(H\) is 104 and we need to compute \(104\times 8\) leading principal minors. It took us almost three months to have them all computed. The results are provided in [26].

4 The \((4+1)\)-Body Problem

4.1 Counting Zeros for System (4)

The following results give a whole picture of the numbers of zeros in each quadrant when the parameters are in \((0,\frac{1}{2})\). So, Theorem 1 is proved.

Proposition 10

For system (4), we obtain the bifurcation polynomial \(g^{4}\) in the Appendix . There are 4 zeros of \(g_{4}\) in \((0,\frac{1}{2})\). The neighbour points in the step \((6)\) of our method are given in the Table  1. The ranks and sign variations of the neighbour and the bifurcation points are given in Table  2. Finally, the numbers of real roots in four quadrants for those points are given in Table  3.

Table 1 Neighbors of the zeros of \(g^{4}\) in \((0,\frac{1}{2})\)
Full size table
Table 2 Ranks and sign variations for the system (4)
Full size table
Table 3 Numbers of zeros of the system (4)
Full size table

Proof

We have \(\mathcal{F}=\lbrace f_{1},f_{2}\rbrace \subset \mathbb{Q} [x,y,k ]\). Using the block order in Remark 5, we obtain \(\mathcal{G}=\lbrace g_{1},g_{2},g_{3},g_{4}\rbrace\) with leading coefficients \(\lbrace 4,4,4,16\rbrace \subset \mathbb{Q} [k ]\). Using \(\mathcal{G}\), we find a basis \(\lbrace 1,y,y^{2},y^{3},y^{4},y^{5},y^{6},y^{7},y^{8},x,xy,xy^{2},xy^{3},xy^{4},xy^{5},xy^{6},x^{2},x^{2}y,x^{2}y^{2},x^{2}y^{3}, x^{2}y^{4}, x^{2}y^{5},x^{2}y^{6},x^{3},x^{3}y, x^{3}y^{2},x^{3}y^{3},x^{3}y^{4} \rbrace\) for the algebra \(A= \mathbb{Q}(k) [ x,y ]/ \langle \mathcal{F} \rangle\). So, the dimension of \(A\) is 28 and there are at most 28 complex zeros for all \(k\).

Computing four Hermite matrices, \(H_{0}=H(\mathcal{F},1),H_{1}=H(\mathcal{F},x),H_{2}=H(\mathcal{F},y),H_{3}=H(\mathcal{F},xy)\) with \(\mathcal{G}\), we find the determinant of \(H(\mathcal{F},1)\) is not identically equal to zero. So, we obtain the bifurcation polynomial \(g^{4}\) from the numerator. Using “CountRoots”, we isolate four real roots \(a_{1},a_{2},a_{3},a_{4}\) of \(g^{4}\) in \((0,\frac{1}{2})\).

Computing \(28\times 4\) leading principals minors, we find \(a_{1},a_{2},a_{3},a_{4}\) are also roots of the numerator of the determinants of \(H_{1},H_{2},H_{3}\). And, all the leading principals minors of order 27 do not have \(a_{1},a_{2},a_{3},a_{4}\) as their zeros. Therefore, by Proposition 9, \(H_{j}^{i}\) has rank \(r_{i,j}=27\) for all \(i,j\).

Choosing neighbour points of \(a_{i}\)’s as in Table 1, we use “CountRoots” to verify the requirements in the step \((6)\) in Sect. 3. Therefore, the numbers \(v_{i,j}\) of variation of signs in the step \((7)\) are obtained in Table 2.

Finally, using Table 2 to obtain signatures, and solving linear systems in four variables, we obtain Table 3. For example, in Table 2 at \(k=a_{1}\), \(r_{1,j}=27, v_{1,0}=10, v_{1,1}=13, v_{1,2}=12, v_{1,3}=13\), signatures, \(r_{1,j}-2v_{1,j}\), are \(7,1,3,1\).

Let \(s_{1}, s_{2}, s_{3}, s_{4}\) denote the number of real roots \((x,y)\) with the signs \((+,+)\), \((+,-)\), \((-,+)\), \((-,-)\), respectively. We get

$$\begin{aligned} 7 =&s_{1}+s_{2}+s_{3}+s_{4},\\ 1 =&s_{1}+s_{2}-s_{3}-s_{4},\\ 3 =&s_{1}-s_{2}+s_{3}-s_{4},\\ 1 =&s_{1}-s_{2}-s_{3}+s_{4}. \end{aligned}$$

Therefore, we obtain \((s_{1},s_{2},s_{3},s_{4})=(3,1,2,1)\) as in Table 3. Note that, for all \(k\), \(x=0\) or \(y=0\) are not zeros. Therefore, the number of roots at each quadrants is a constant in each \((a_{i},a_{i+1})\) interval. So, Table 3 give the numbers of roots in each quadrant of the system (4) for all parameters in \((0,\frac{1}{2})\). □

4.2 Counting Zeros for System (5)

The following results give a whole picture of the numbers of zeros when the parameters are in \((0,\frac{1}{3})\). So, Theorem 2 is proved.

Proposition 11

For system (5), we obtain the bifurcation polynomial \(g^{5}\) in the Appendix . There are 3 zeros of \(g^{5}\) in \((0,\frac{1}{3})\). The neighbour points in the step \((6)\) of our method are given in the Table  4. The ranks and sign variations of the neighbour and the bifurcation points are given in Table  5. Finally, the numbers of real roots in four quadrants for those points are given in Table  6.

Table 4 Neighbors of the zeros of \(g^{5}\) in \((0,\frac{1}{3})\)
Full size table
Table 5 Ranks and sign variations for the system (5)
Full size table
Table 6 Numbers of zeros of the system (5)
Full size table

Proof

Now \(\mathcal{F}=\lbrace f_{3},f_{4},f_{5}\rbrace \subset \mathbb{Q} [x,y,z,k ]\). Using the block order in Remark 5, we obtain \(\mathcal{G}=\lbrace g_{1},\dots,g_{14}\rbrace\), where the non constant leading coefficients in \(\mathbb{Q} [k ]\) are

$$\left \{ \textstyle\begin{array}{rcl} h_{2} &=& 9 k^{2} (-1+3 k) (-6193005856+34523341224 k-88164313884 k^{2}\\ &&{}+179027640450k^{3} -296194349727 k^{4}+292634913915 k^{5}\\ &&{}-135093148569 k^{6}+22052144295 k^{7}),\\ h_{5} &=& c_{5}k,\\ h_{9} &=& c_{9}(-1+3 k)^{3} (-485-162 k+243 k^{2}),\\ h_{10} &=& c_{10}(-1+3 k)^{2},\\ h_{11} &=& c_{11}(-1+3 k), \end{array}\displaystyle \right . $$

for some integers \(c_{5},c_{9},c_{10},c_{11}\). There is no zeros in \((0,\frac{1}{3})\) for all \(h_{j}\)’s above.

Using \(\mathcal{G}\), we find a basis \(\lbrace 1,z,z^{2},z^{3},z^{4},y,yz,yz^{2},yz^{3},y^{2},y^{2}z,y^{2}z^{2},y^{3},x,xz,xz^{2},xz^{3}, xy,xyz, xyz^{2},xy^{2},x^{2},x^{2}y,x^{3} \rbrace\) for the algebra \(A= \mathbb{Q}(k) [ x,y,z ]/ \langle \mathcal{F} \rangle\). So, the dimension of \(A\) is 24 and there are at most 24 complex zeros for all \(k\).

Computing four Hermite matrices, \(H_{0}=H(\mathcal{F},1),H_{1}=H(\mathcal{F},x),H_{2}=H(\mathcal{F},y),H_{3}=H(\mathcal{F},xy)\) with \(\mathcal{G}\), we find the determinant of \(H(\mathcal{F},1)\) is not identically equal to zero. So, we obtain the bifurcation polynomial \(g^{5}\) from the numerator. Using “CountRoots”, we isolate three real roots \(a_{1},a_{2},a_{3}\) of \(g^{5}\) in \((0,\frac{1}{3})\).

Computing \(24\times 4\) leading principals minors, we find \(a_{1},a_{2},a_{3}\) are also roots of the numerator of the determinants of \(H_{1},H_{2},H_{3}\). And, all the leading principals minors of order 23 do not have \(a_{1},a_{2},a_{3}\) as their zeros. Therefore, by Proposition 9, \(H_{j}^{i}\) has rank \(r_{i,j}=23\) for all \(i,j\).

Choosing neighbour points of \(a_{i}\)’s as in Table 4, we use “CountRoots” to verify the requirements in the step \((6)\) in Sect. 3. Therefore, the numbers \(v_{i,j}\) of variation of signs in the step \((7)\) are obtained in Table 5.

Finally, using Table 5 to obtain signatures, and solving linear systems in four variables, we obtain Table 6. Note also, for all \(k\), \(x=0\) or \(y=0\) are not zeros. Therefore, the number of roots at each quadrants is a constant in each \((a_{i},a_{i+1})\) interval. So, Table 6 give the numbers of roots in each quadrant of the system (5) for all parameters in \((0,\frac{1}{3})\). □

5 The \((1+3)\)-Body Problem

5.1 Counting Zeros for System (6)

The following results give a whole picture of the numbers of zeros for positive parameters. So, Theorem 3 is proved.

Proposition 12

For system (6), we obtain the bifurcation polynomial \(g^{6}\) in the Appendix . There are 11 zeros of \(g^{6}\) in \((0,\infty)\). For \(a_{2}\) to \(a_{10}\), our method is applied. The neighbour points in the step \((6)\) are given in the Table  7. The ranks and sign variations of the neighbour and the bifurcation points are given in Table  8. Finally, the numbers of real roots in the eight orthants for those points are given in Table  9.

Table 7 Neighbors of 10 zeros of \(g^{6}\) in \((0,\infty)\)
Full size table
Table 8 Ranks and sign variations for the system (6)
Full size table
Table 9 Numbers of zeros of the system (6)
Full size table

For \(a_{1}\), it is a zero for some \(h_{j}\) in as remarked in Sect. 3.3. Our method does not apply. We will show it is not a bifurcation point. That is, the number of real zeros is a constant in the neighbourhood of this point, which is given from the results for \(a_{2\ell}\).

For \(a_{11}=10\), it is again a zero for some \(h_{j}\). We can just substitute \(k\) with 10 to obtain a system in ℚ. We can use Hermite root counting theorem directly for this system to obtain the numbers of zeros. It is also recorded in Table 9. Same approached is applied to the sample point 100 on the right hand side of \(a_{11}\).

Note there is a extra bifurcation point that is not obtain form \(g^{6}\) in our method. That is when \(k=4\). This point of bifurcation explains why the numbers of zeros are not the same for \(k=a_{9,r}\) and \(k=a_{10\ell}\). It is again a zero for some \(h_{j}\) in as remarked in Sect. 3.3. We can again substitute \(k\) with 4 to obtain a system in ℚ and count roots directly. The results are also recorded in Table 9.

Proof

Now \(\mathcal{F}=\lbrace f_{6},f_{7},f_{8},f_{9}\rbrace \subset \mathbb{Q} [r_{1},r_{2},r_{3},r_{4},k ]\). Using the block order in Remark 5, we obtain \(\mathcal{G}=\lbrace g_{1},\dots,g_{59}\rbrace\). Non constant factors in the leading coefficients that contain positive zeros are \(k-4,k-10,-312+1896 k+530 k^{2}+588 k^{3}+101 k^{4}+31 k^{5}+k^{6}\). They have zeros \(4,10\), and approximately 0.156489. These three points will be considered separately.

Using \(\mathcal{G}\), we find a basis for the algebra \(A= \mathbb{Q}(k) [ r_{1},r_{2},r_{3},r_{4} ]/ \langle \mathcal{F} \rangle\). They are \(\{1,\, r_{4},\, r_{4}^{2},\, r_{4}^{3},\, r_{4}^{4},\, r_{4}^{5},\, r_{4}^{6},\, r_{3}, r_{3} r_{4}, r_{3} r_{4}^{2}, r_{3} r_{4}^{3}, r_{3} r_{4}^{4}, r_{3} r_{4}^{5}, r_{3}^{2}, r_{3}^{2} r_{4}, r_{3}^{2} r_{4}^{2}, r_{3}^{2} r_{4}^{3}, r_{3}^{3}, r_{3}^{3} r_{4}, r_{3}^{3} r_{4}^{2}, r_{3}^{4}, r_{3}^{4} r_{4},\, r_{3}^{5},\, r_{2},\, r_{2} r_{4},\, r_{2} r_{4}^{2},\, r_{2} r_{4}^{3},\, r_{2} r_{4}^{4}, r_{2} r_{4}^{5}, r_{2} r_{3}, r_{2} r_{3} r_{4}, r_{2} r_{3} r_{4}^{2}, r_{2} r_{3} r_{4}^{3}, r_{2} r_{3}^{2}, r_{2} r_{3}^{2} r_{4}, r_{2} r_{3}^{2} r_{4}^{2}, r_{2} r_{3}^{3}, r_{2} r_{3}^{3} r_{4}, r_{2}^{2},\, r_{2}^{2} r_{4},\, r_{2}^{2} r_{3},\, r_{2}^{2} r_{3} r_{4}, r_{2}^{2} r_{3}^{2}, r_{2}^{2} r_{3}^{2} r_{4}, r_{2}^{2} r_{3}^{3}, r_{2}^{3}, r_{2}^{3} r_{4}, r_{2}^{3} r_{3}, r_{2}^{3} r_{3} r_{4}, r_{2}^{3} r_{3}^{2}, r_{2}^{4}, r_{2}^{4} r_{4}, r_{2}^{4} r_{3}, r_{2}^{5}, r_{1}, r_{1} r_{4},\, r_{1}r_{4}^{2},\, r_{1} r_{4}^{3},\, r_{1} r_{4}^{4},\, r_{1} r_{3},\, r_{1} r_{3} r_{4}, r_{1} r_{3} r_{4}^{2}, r_{1} r_{3} r_{4}^{3}, r_{1} r_{3}^{2}, r_{1} r_{3}^{2} r_{4}, r_{1} r_{3}^{2} r_{4}^{2}, r_{1} r_{2}, r_{1} r_{2} r_{4}, r_{1} r_{2} r_{4}^{2}, r_{1}r_{2}r_{3}, r_{1} r_{2} r_{3} r_{4},\, r_{1} r_{2} r_{3} r_{4}^{2},\, r_{1} r_{2} r_{3}^{2},\, r_{1} r_{2} r_{3}^{2} r_{4}, r_{1} r_{2}^{2}, r_{1} r_{2}^{2} r_{4}, r_{1} r_{2}^{2} r_{3}, r_{1} r_{2}^{2} r_{3} r_{4}, r_{1} r_{2}^{2} r_{3}^{2}, r_{1} r_{2}^{3}, r_{1} r_{2}^{3} r_{4}, r_{1}^{2},\, r_{1}^{2} r_{4},\, r_{1}^{2} r_{4}^{2},\, r_{1}^{2} r_{4}^{3},\, r_{1}^{2} r_{3},\, r_{1}^{2} r_{3} r_{4},\,r_{1}^{2} r_{3}r_{4}^{2},\, r_{1}^{2} r_{2},\, r_{1}^{2} r_{2} r_{4}, r_{1}^{2} r_{2} r_{4}^{2}, r_{1}^{2} r_{2} r_{3}, r_{1}^{2} r_{2} r_{3} r_{4}, r_{1}^{2} r_{2}^{2}, r_{1}^{2} r_{2}^{2} r_{4}, r_{1}^{2} r_{2}^{2} r_{3}, r_{1}^{2} r_{2}^{3}, r_{1}^{3}, r_{1}^{3} r_{4}, r_{1}^{3} r_{4}^{2}, r_{1}^{3} r_{3}, r_{1}^{3} r_{3} r_{4}, r_{1}^{3} r_{2}, r_{1}^{3} r_{2} r_{4} \}\). Therefore, the dimension of \(A\) is 104 and there are at most 104 complex zeros for all \(0< k \neq 0.156489\dots,4,10\).

For this system, we are interest in common zeros with \(0< r_{1},r_{2}<1\) and \(r_{3}>r_{4}\). Therefore, we need to compute \(2^{3}\) Hermite matrices, \(H_{j}=H(\mathcal{F},P_{j})\)’s, where \(P_{j}\) is a product of any subset from \(\lbrace p_{1}=\frac{1}{4} - (r_{1} - \frac{1}{2})^{2},p_{2}=\frac{1}{4} - (r_{2} - \frac{1}{2})^{2}, p_{3}=r_{3}-r_{4}\rbrace\), including of \(P_{0}=1\).

We find the determinant of \(H_{0}\) is not identically equal to zero. So, we obtain the bifurcation polynomial \(g^{6}\) from the numerator. Using “CountRoots”, we isolate eleven real roots \(a_{1},\dots,a_{11}\) of \(g^{6}\) in \((0,\frac{1}{3})\). Here, \(a_{1}=0.156489\dots\) and \(a_{11}=10\) are the two zeros of some leading terms of \(\mathcal{G} \) mentioned above. So, we use our method in Sect. 3 to count zeros only at \(a_{2},\dots,a_{10}\).

We separate zeros into three groups. The first group is \(\lbrace a_{4},a_{8},a_{10}\rbrace\). They are zeros of \(g^{6}\) of multiplicity 1. The second group is \(\lbrace a_{2},a_{3},a_{5},a_{6}\rbrace\). They are zeros of multiplicity 2. The third group is \(\lbrace a_{7},a_{9}\rbrace\). They are zeros of multiplicity 3.

We find all \(a_{i}\)’s are zeros of the determinants of \(H_{j}\) for all \(j\). Let \(D_{j,w}\) be the leading principal minors of \(H_{j}\) of order \(w\) and \(M_{j,103}\) be the principal minor of \(H_{j}\) of order 103 as the definition of \(M_{d-1}\) in Proposition 9 form \(H\).

For all \(a_{i}\)’s in the first group, \(D_{j,103}^{i}\neq 0\) for all \(j\). Therefore, by Proposition 9, ranks \(r_{i,j}=103\) for \(i=4,8,10\) and all \(j\). For all \(a_{i}\)’s in the second and third groups, \(D_{j,103}^{i}=M_{j,103}^{i}=0\) for all \(j\), and \(D_{j,102}^{i}\neq 0\) for all \(j\). Therefore, by Proposition 9, ranks \(r_{i,j}=102\) for \(i=2,3,5,6,7,9\) and all \(j\).

Choosing neighbour points of \(a_{i}\)’s as in Table 7, we use “CountRoots” to verify the requirements in the step \((6)\) in Sect. 3. Therefore, the numbers \(v_{i,j}\) of variation of signs in the step \((7)\) are obtained in Table 8. Finally, using Table 8 to obtain signatures, and solving linear systems in eight variables, we obtain Table 9. Note also, for all \(k>0\), zeros of \(p_{1}, p_{2}\) or \(p_{3}\) are not common zeros for ℱ. The number of common zeros at each orthant is a constant in each \((a_{i},a_{i+1})\) interval for all \(i=1,\dots,10\).

The number of zeros at 4 and 10 and a sample point \(100>10\) are obtained by applying Hermite root counting theorem for systems in \(\mathcal{Q} [r_{1},r_{2},r_{3},r_{4} ]\). For the point \(a_{1}=0.156489\dots\), which is a zero of \(-312+1896 k+530 k^{2}+588 k^{3}+101 k^{4}+31 k^{5}+k^{6}\), we will show that is it not a real bifurcation point. Therefore, the number of zeros at that point and in the interval \((0,a_{1}]\) agree with that at \(a_{2\ell}\).

Denote the resultant of \(f,g\) with respect to the variable \(x\) by \(\mathit{Res}(f,g,x)\). Here are our computations. Project common zeros of \(\mathcal{F} \subset \mathbb{Q} [r_{1},r_{2},r_{3},r_{4},k ]\) into the \(r_{1},r_{3},r_{4}\) space by computing \(f_{10}=\mathit{Res}(f_{6},f_{9},r_{2}),\ f_{11}=\mathit{Res}(f_{7},f_{9},r_{2}),\ f_{12}=\mathit{Res}(f_{8},f_{9},r_{2})^{\frac{1}{2}}\). Project common zeros of \(\lbrace f_{10},f_{11},f_{12} \rbrace \subset \mathbb{Q} [r_{1},r_{3},r_{4},k ]\) into the \(r_{3},r_{4}\) space by computing \(f_{13}=\mathit{Res}(f_{10},f_{12},r_{1}),\ f_{14}f_{15}^{2}=\mathit{Res}(f_{11},f_{12},r_{1})\).

Project common zeros of \(\lbrace f_{13},f_{14} \rbrace \subset \mathbb{Q} [r_{3},r_{4},k ]\) into the \(r_{4}\) space by computing \(\mathit{Res}(f_{13},f_{14},r_{3})=c(1+r_{4}^{2})f_{16}f_{17}f_{18}f_{19}\). Also, project common zeros of \(\lbrace f_{13},f_{15} \rbrace \subset \mathbb{Q} [r_{3},r_{4},k ]\) into the \(r_{4}\) space by computing \(\mathit{Res}(f_{13},f_{15},r_{3})=f_{20}f_{21}\).

If there is a \(k\) such that the Jacobian of ℱ with respect to \(r_{1},r_{2},r_{3},r_{4}\) is zero at the common zero, than the projection onto the \(r_{4}\) space must be a zero of multiplicity greater than one [25]. Therefore, at least one of the polynomial from \(f_{16},\dots,f_{21}\) has such zero of multiplicity greater than one. Let \(f_{i+6}=\mathit{Res}(f_{i},\frac{df_{i}}{dr_{4}},r_{4})\), for \(i=16,\dots, 21\).

Finally, we find that \(\mathit{Res}(f_{i},-312+1896 k+530 k^{2}+588 k^{3}+101 k^{4}+31 k^{5}+k^{6})\neq 0\), for all \(i=22,\dots, 27\). So, any zero of \(-312+1896 k+530 k^{2}+588 k^{3}+101 k^{4}+31 k^{5}+k^{6}\) is not a bifurcation point. □