Patterns in bifurcation levels of the integral manifolds of the N body problem

Abstract

In the N-body problem, it is classical that there are conserved quantities of center of mass, linear momentum, angular momentum, and energy. The level sets ${\mathfrak {M}}(c,h)$ of these conserved quantities are parameterized by the angular momentum c and the energy h, and are known as the integral manifolds. A long-standing goal has been to identify the bifurcation values, especially the bifurcation values of energy for fixed non-zero angular momentum, and to describe the integral manifolds at the regular values. Alain Albouy identified two categories of singular values of energy: those corresponding to relative equilibria, referred to as “finite bifurcations”; and those corresponding to “bifurcations at infinity”, and provided an algorithm for identifying all possible values of each. This requires identifying all central configurations for the N bodies and all sub-collections of the bodies. Using available data on central configurations for 10 or fewer equal masses, we apply Albouy’s analysis to enumerate all singular values, and study the patterns of “finite” vs. “infinite” bifurcations. In particular, we show that the conjecture that all bifurcations at infinity occur at energy levels less in magnitude than the finite bifurcations is false.

1 Introduction

This work continues the investigation of the integral manifolds of the spatial N-body problem. The integral manifolds are the level sets of the classical conserved quantities of energy, angular momentum, linear momentum, and center of mass. In the spatial problem, they form a family of $(6N - 10)$-dimensional manifolds. Their structure depends on the values $m_1, \ldots m_N$ of the masses, the angular momentum $\vec {c} \in {\mathbb {R}}^3$, and energy h. Typically, the dependence on the masses is not displayed explicitly, and the integral manifolds are viewed as a parameterized family ${\mathfrak {M}}(c,h)$. However, a global rescaling can be applied, mapping ${\mathfrak {M}}(c,h)$ homeomorphically to ${\mathfrak {M}}(\frac{c}{\sqrt{\lambda }}, \lambda h)$. Moreover, there is a rotational symmetry, so that we may, without loss, take $\vec {c} = c{\hat{k}}$. That is, for non-zero angular momentum, the topology of ${\mathfrak {M}}(c,h)$ depends only on the single parameter $c^2 h$. In this work, we will view c as fixed at a non-zero value, so that ${\mathfrak {M}}(c,h)$ can be viewed as a one-parameter family of level sets of the energy $H(x, v) = \sum _{i = 1}^N m_i v_i^2 - U(x)$ on a manifold of fixed angular momentum, center of mass and center of linear momentum. The submanifold with all positions and velocities confined to the $x-y$ plane is invariant under the laws of motion, and is referred to as the planar integral manifold ${\mathfrak {m}}(c,h)$. Unless specified otherwise, the phrase “integral manifold” will refer to the spatial manifold ${\mathfrak {M}}(c,h)$.

In this setting, the questions of interest for the global behavior are:

• Identify the bifurcation values of h—the energy levels at which the topology of ${\mathfrak {M}}(c,h)$ changes.

• At the regular values of h between those bifurcation values, describe ${\mathfrak {M}}(c,h)$.

• Use that global description to provide insights into the global dynamics of the N-body problem.

The starting point for this program is [1]. There, Albouy produced necessary conditions for an energy level h to be a bifurcation value for ${\mathfrak {M}}(c,h)$. Those conditions are specified in Sect. 3. At the moment, it suffices to take note of two observations:

• As the angular momentum manifolds are not compact, singular values can occur either as critical values of H restricted to the angular momentum manifold; or as limiting values of sequences on the angular momentum manifold that are unbounded, with the tangential component of $\nabla H$ along the angular momentum manifold tending to zero. The former are referred to as “finite bifurcations” and the latter as “bifurcations at infinity”¹

• For a given set of masses $m_1, \ldots m_N$, Albouy’s results can be viewed as providing an algorithm that identifies all singular values. That algorithm requires knowledge of the full set of planar central configurations [13, 14], both for the given set of masses and for all of its subsets.

While central configurations have been intensively studied, at present, the identification of a complete set of central configurations has only been rigorously established for three arbitrary masses, or four, five, six, or seven equal masses [2, 12]. For eight, nine, and ten equal masses, computer searches have identified families of central configurations that are widely believed to be the complete set [4]. Many of these families have been shown rigorously to indeed be central configurations [12], but it has not yet been established that all of the families identified are central configurations, nor that the list is complete.

There is an important distinction between the finite bifurcations and the bifurcations at infinity. The former are simply critical points of the energy function on the manifold of constant angular momentum. These are the relative equilibria: solutions to the N-body problem that rotate uniformly about their center of mass. As such, they are of profound importance in the N-body problem. In particular, their role in bifurcation theory for the integral manifolds is clear. When viewed as critical points of the energy function, if the relative equilibria are non-degenerate, the topology of the integral manifold can be expected to change in a straightforward manner a la Morse theory. Moreover, that Morse-theoretic behavior can be read off from the corresponding behavior of the planar submanifold [11], over which we have considerable control [8, 15, 16]. The non-compactness of the integral manifolds is a complicating factor in this, but not a significant obstacle.

The situation for bifurcations at infinity is quite different. As the name suggests, these are not actually points on the angular momentum manifold. Instead, they are “limiting“ arrangements sequences of positions and velocities in which the positions diverge to infinity while preserving constant angular momentum, doing so in a way that the total energy remains finite and converges, while the energy gradient becomes parallel to the angular momentum gradient in the limit. Albouy showed that these can be realized as follows:

• Partition the N particles into $k \le N$ clusters.

• For each non-trivial cluster, give the particles the $x-y$ positions of a central configuration, and the $x-y$ velocities to create a relative equilibrium for that cluster’s subset of masses.

• Adjust the scaling to ensure that all of the clusters have a common Lagrange multiplier $\lambda _z$, and that the clusters’ angular momenta sum to the specified total angular momentum.

• Assign each cluster a different z-position value and 0 velocity along the z-axis.

• Finally, create a sequence by multiplying the z-positions by values $\lambda _n$ that diverge to infinity, while holding all other values constant.

The net effect of this is to create a sequence with constant angular momentum that diverges to infinity in position (specifically, in the z-coordinate). As it does so, each cluster “feels“ the less and less of the potential of other clusters, while within the cluster, it “feels“ like a relative equilibrium (i.e., a critical point of energy). That is, while the sequence diverges in position, its energy converges to a finite value and the gradient of energy converges to zero.

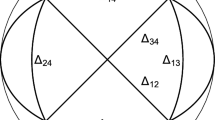
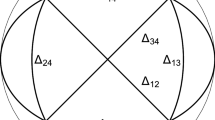
Unlike finite bifurcations, whose structure as relative equilibria has a clear dynamic significance, there is no direct dynamic interpretation of the bifurcations at infinity. Further, the types of bifurcations that can occur at such energy levels are qualitatively different than those corresponding to finite bifurcation values, and do not appear to lend themselves to a Morse-theoretic analysis [10]. On the other hand, the two types of bifurcations do share the property that identifying bifurcation values for a given set of masses requires identifying all possible central configurations for those masses, and for all sub-clusters of those masses. To illustrate this, consider the energy values for three and four equal masses, displayed in Table 1. The shapes of the corresponding central configurations (for finite bifurcations) or critical sequences (for bifurcations at infinity) are shown in Fig. 1

Table 1 Singular values of energy for three and four equal masses

Fig. 1

Central configurations and critical sequences for 3 and 4 masses

Observe that there are no bifurcations for positive energy, and that as energy grows in magnitude from 0 to $-\infty$, all of the bifurcations at infinity occur first, then all of the finite bifurcations. Also, observe that all of the bifurcation values for $N = 3$ of either type have corresponding bifurcations at infinity for four masses. In the case of three arbitrary masses, generically, both the binary cluster and the collinear configuration bifurcation levels split into three levels, with all of the binary (i.e., infinite bifurcations) remaining at energy levels with magnitude less than the Lagrange configuration’s energy level [7].

This leads to the following questions:

• For arbitrary masses, do all of the bifurcations at infinity occur at energy levels of lower magnitude than those of the finite bifurcations?

• If the pattern does not hold for arbitrary masses, does it do so in the case of equal masses?

In either case, an affirmative answer would indicate that all of the changes to ${\mathfrak {M}}(c,h)$ at infinity occur before any of the finite bifurcations. In this scenario, the analysis of the integral manifolds divides into two parts: the energy range containing all of the bifurcations at infinity; and the energy range containing all of the finite bifurcations. In particular, the latter set is identical to the set of bifurcation values of the planar manifold, and the Morse-theoretic analysis of the planar manifold can be translated to the spatial manifold. A negative answer would indicate that the changes to the topology are potentially quite complex, with changes at the boundary and in the interior mixed together. In particular, the ability to exploit the reduction to the planar manifold is compromised, if not eliminated.

In this note, we examine the available evidence to test these questions.

2 Results

As noted, three arbitrary masses, all bifurcations at infinity occur at lower magnitude energies than the finite bifurcations. However, even at $N = 4$, this pattern does not hold for all masses, as the following result shows.

Theorem 2.1

Consider a four-body system with masses (1, 1, 1, m). There is a finite bifurcation at energy level $-\frac{9}{2} (1+m \sqrt{3}) ^2$ and a bifurcation at infinity at energy level $-\frac{25}{4}$. For $m < \frac{5 -3\sqrt{2}}{3\sqrt{6}}$, the finite bifurcation occurs at an energy level of lower magnitude.

Fig. 2

Bifurcation energy levels

This result depends very much on the disparity in the masses, leaving the possibility that the pattern of bifurcations at infinity occurring at lower magnitude might remain intact for equal masses. We tested this by applying Albouy’s algorithm to Ferrario’s set of central configurations. We find that:

• For $N \le 7$ equal masses (i.e., the range for which the set of central configurations has been rigorously established), all infinite bifurcation energy levels have smaller magnitude than any finite bifurcation energy levels.

• For $N = 8$ equal masses, all infinite bifurcation energy levels have smaller magnitude than any known finite bifurcation energy levels.

• For $N = 9, 10$ equal masses, there are confirmed infinite energy levels $h_i$ and confirmed finite energy levels $h_f$ with $| h_f | < | h_i|$. In particular, let $x_c(N)$ denote the family of collinear central configurations with N particles of mass 1, and let $x_g(N, m)$ denote the family of central configurations with N particles of mass 1 at the vertices of a regular N-gon and a mass m at the center, with both configurations normalized, so that $x_c^2(N) = x_q^2(N, m) = 1$. Then, $U(x_g(N,1)) < U(x_c(N))$ for $N = 8, 9$.

3 Methods

We apply Albouy’s algorithm for identifying singular values to Ferrario’s set of central configurations. Albouy’s algorithm is set out in detail in [1] and [9, Sect. 3]. Briefly, to find all singular values of energy for N equal masses of mass m, the steps in the algorithm are:

• (1) Take all possible integer partitions $n_1, \ldots , n_k$ of N.

• (2) For each $n_i$, identify all planar central configuration families $x_{\sigma _i}$ of $n_i$ particles and scale each, so that when $n_i > 1$, $m x^2_{\sigma _i} = 1$. If $n_i = 1$, take $x_{\sigma _i} = \vec {0}$.

• (3) For each $x_{\sigma _i}$, let $U_i(x_{\sigma _i})$ be the potential energy of $x_{\sigma _i}$. If $n_i = 1$, take $U_i(x_{\sigma _i}) = 0$.

• (4) Then, the corresponding singular value of energy is $\frac{-1}{2c^2} \left( \sum _i U^{2/3}_i(x_{\sigma _i}) \right) ^3$.

The case $k = 1$ (i.e., when there is a single central configuration consisting of all N particles) correspond to the finite bifurcations; the partitions with $k >1$ correspond to the bifurcations at infinity. Note that, by adding an additional cluster with one element in it, every partition of N masses generates a partition of $N+1$ masses with $k > 1$. That is, every singular energy level for N masses, whether of finite type or infinite type, is a singular value of infinite type for $N+1$ masses.

Theorem 2.1 is a straightforward application of this process. The finite bifurcation with energy $-\frac{9}{2}(1 + m \sqrt{3})$ corresponds to the four-body central configuration with particles of mass 1 at the vertices of an equilateral triangle and the particle with mass m at the center of the triangle. The bifurcation at infinity corresponds to the partition with the three particles of mass 1 forming a collinear central configuration in one cluster, and the particle of mass m by itself in a second cluster. In this case, the energy level is simply that of the collinear configuration, namely $-\frac{25}{4}$.

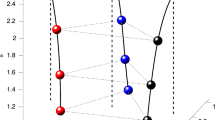
Applying this process to the collection of configurations identified by Ferrario produces the results shown in Fig. 2, with $ln(-h)$ plotted for the maximum and minimum-energy levels of the finite bifurcations and bifurcations at infinity. For $N = 8, 9, 10$, we need to address the fact that not all of the central configurations identified in [4] have been confirmed. For the maximum energy levels (of both the finite and infinite bifurcations), this is not an issue: the collinear configurations have maximum energy levels. For the minima, we note that for $N = 8$ and $N = 10$, the minimum-energy central configurations identified by Ferrario have a symmetry that allows us to verify that they are in fact central configurations. For $N = 9$, the regular octagon with a mass at the center has $U(x_g(8,1)) = 86.0943$, while the minimum-energy configuration identified by Ferrario has $U_{\min } = 85.9007$. That is, the patterns of finite vs. infinite bifurcations are the same whether we include all of Ferrario’s configurations or restrict to those that have been confirmed.

4 Discussion

For three arbitrary masses and four equal masses, we saw that all bifurcations at infinity occur at energy levels of smaller magnitude than any finite bifurcations. Those patterns break down almost immediately. Theorem 2.1 shows that for as few as four masses, disparities in the mass ratios can be exploited to invert the ordering of the bifurcations. It is expected that this pattern will persist for any number of masses.

For equal masses, the pattern persisted briefly, but broke down at nine equal masses. For $N = 8, 9$, the N-body collinear central configuration has greater potential energy than the regular $(N+1)$-gon. We conjecture that this remains true for all $N \ge 8$.

Proving that either of these patterns holds for all N confronts a challenge. We observe that, for fixed N and fixed masses $m_1, \ldots m_N$, the collinear central configurations appear to have the largest potential of all N-body central configurations. This in turn implies that the bifurcation at infinity for $N+1$ particles with the largest energy will occur at the collinear central configurations with N masses.

The challenge is, there is no expression for the potential energy of the collinear central configurations with N equal masses, and only weak estimates. In principle, a lower bound on the energy level might suffice, but even that is difficult to obtain. First, since $x_{c}(N)$ is the minimizer of U along the collinear configurations, the potential at any collinear central configuration is an upper bound on $U(x_{c}(N))$, not a lower bound. Second, even for equal masses, there is little known about the relative spacing of the masses along the line for $x_{c}(N)$. While Buck [3] provides some information about the relative spacing of the outermost particles vs. the innermost, and Lindstrom [6] provides an asymptotic estimate of the mass distribution as the number of particles goes to infinity, we do not have sufficient information about the relative spacing to produce a useful lower bound on $U(x_{c}(N))$.

In conclusion, we observe that the separation between bifurcations at infinity and finite bifurcations does not hold as N grows, with the implication that the topological changes corresponding to the bifurcations are more complex than current examples indicate. We can conjecture that the mixing of bifurcations at infinity and finite bifurcations persist. Then, we conjecture that:

• For equal masses and for all N, $U(x_c(N))$ is an increasing function of N, with $U(x_c(N)) > U(x_p(N))$ for all planar central configurations of N equal masses.

• It follows immediately that, for N equal masses, the largest energy level corresponding to a bifurcation at infinity is $\frac{-1}{2c^2} U^2(x_c(N-1))$

• For $N \ge 8$, $U(x_c(N)) > U(x_g(N,1))$, which implies that for all $N \ge 9$, there is an overlap between energy levels of bifurcations at infinity and finite bifurcations.

• For all N, for m sufficiently small, $U(x_c(N)) > U(x_g(N,m))$.

The key to verifying these conjectures lies in producing an effective lower bound on the energy level of the collinear central configurations.