1 Introduction

The Newtonian \(n\)-body problem studies the dynamics of \(n\) particles with masses \(m_{i}>0\) and positions \(q_{i}\in\mathbb{R}^{d}\), moving according to the Newton’s laws of motion:

$$ \ddot{q}_{j}=\sum_{i \neq j}{} \frac{m_{i}(q_{i}-q_{j})}{\|q_{i}-q_{j}\| ^{3}}, \quad 1 \leq j \leq n. $$
(1)

Definition 1

A configuration \((q_{1},\ldots,q_{n})\in\mathbb{R}^{dn}\setminus \Delta\) is central if \(\exists \lambda<0\) with

$$ \lambda(q_{j}-c)=\sum_{i \neq j}{} \frac{m_{i}(q_{i}-q_{j})}{\| q_{i}-q_{j}\|^{3}}, \quad1 \leq j \leq n, $$
(2)

where \(c=\frac{1}{M} (m_{1}q_{1}+\cdots+m_{n}q_{n} )\), \(M=m_{1}+\cdots+m_{n}\), and \(\Delta= \lbrace q_{i}=q_{j}, i \neq j \rbrace\).

Given a central configuration in \(\mathbb{R}^{2}\) as the initial position and proper initial velocity, the \(n\) particles rotate around the center of mass \(c\) with a fixed angular speed. For this reason, a central configuration in \(\mathbb{R}^{2}\) is also called a relative equilibrium. Given any central configuration in \(\mathbb {R}^{3}\) and zero initial velocity, the \(n\) particles accelerate toward \(c\) in such a way that the configuration collapses homothetically.

One of the famous problems about central configurations is Smale’s 6-th problem for the 21-st century [23]: “Is the number of relative equilibria finite for all \(n\)?” The problem is open for \(n>6\). For \(n=2\), there is one class of relative equilibrium up to rotations, translations, and dilations (with different \(\lambda\)). For \(n=3\), there are five classes found by Euler and Lagrange. For \(n=4\), the number is between 32 and 8472, found by Hampton and Moeckel [14]. For \(n=5\), the problem is solved for almost all masses by Albouy and Kaloshin [1].

Enumeration problems for \(n>3\) are far from complete. Solving such problems means to find complete classifications of the masses according to the numbers of classes of central configurations. Usually, restricted cases where some of the masses are zero or cases where symmetries are imposed are considered.

In this paper, we consider central configurations from two different sets of problems. The first one is the planar \((3+1)\)-body problem. Some studies of central configurations on this problem can be found in [3–5, 11, 15, 17, 19, 22]. The bifurcation curve is rigorously characterised in [4, 5] and the enumeration problem of central configurations on such curve is also studied in [5]. We revisit this problem and obtain new findings on the bifurcation curve where two positive masses are equal.

The second set consists of two cases that are considered in [16]. One is the planar 4-body problem with two equal masses which have an axis of symmetry containing two other masses. The other is the spatial 5-body problem with three equal masses at the vertices of an equilateral triangle and two other masses on the line passing through the center of the triangle and being perpendicular to the plane containing it. Other related studies can be found in [2, 10, 20]. The bifurcation curves are rigorously studied in [16]. They all contain an unique singular point. Bifurcations at the singular points on a bifurcation curve can be interesting. We provide rigorous counts at those two bifurcation points.

As in [25], our approach is to reduce the problems to solving parametric polynomial systems with one parameter. In [25], we purposed an algorithm using Groebner basis and Hermite’s root counting method to count the numbers of real zeros for all parameter, including the bifurcation points. However, the algorithm in [25] becomes infeasible by directly applying to all three problems mentioned above.

While Groebner bases provide powerful tools in studying polynomial systems, whether one can obtain them or not plays the critical role in this approach. In using Hermite’s root counting method, the key computation comes from computing many determinants of matrices with symbolic entries. Whether such computation can terminate in a reasonable period of time also determines the feasibility of our algorithm. In this paper, we provide an improved version of our algorithm in the sense that an alternative way of computing the required Groebner basis is provided when the old method does not apply, and that much time is saved in computing all the required determinants.

Our paper is arranged as follow. In Sect. 2, we present the counting algorithm. Main results on central configurations are in the next two sections. In Sect. 3, our studies about the planar \((3+1)\)-body problem will be presented. In Sect. 4, we focus on a symmetrical 4-body problem and a symmetrical 5-body problem. In Sect. 5, some of the detailed computations will be given. Our symbolic computations are performed in the Computer Algebra System, Mathematica 10. The Mathematica notebook containing all the implementations of our algorithm and computations can be found in [26].

2 Counting Algorithm

Given a polynomial system \(\mathcal{F}=\lbrace f_{1},\ldots,f_{n} \rbrace\) in variables \(x_{1},\dots,x_{m}\) with coefficients in \(\mathbb {Z} [ s ]\), and a bifurcation polynomial \(g \in\mathbb {Z} [ s ]\) with a irrational zero \(\beta\), our goal is to find the number of common real zeros of \(\mathcal{F}^{\beta}\) in an open set \(\mathcal{X}= \lbrace x \in\mathbb{R}^{m}\mid p_{1}(x)> 0,\dots ,p_{\ell}(x)> 0 \rbrace\), where \(p_{j} \in\mathbb{Z} [ x_{1},\dots ,x_{m} ]\) and \(\mathcal{F}^{\beta}\) denotes the real polynomial system obtained from substituting \(s\) with \(\beta\) in all \(f_{i}\)’s. Here is the outline of the algorithm.

  1. (1)

    Compute \(G=\lbrace g_{1},\ldots,g_{t} \rbrace\in\mathbb {Z} [ s ] [ x_{1},\dots,x_{m} ]\) from ℱ such that \(G^{s}\) is a Groebner basis of \(\mathcal{F}^{s} \) for almost all \(s\), including \(\beta\).

  2. (2)

    Compute the Hermite matrices \(H_{j}:=H(\mathcal {F},P_{j})\) for all \(P_{j}\), where \(P_{j}\) is any product of a subset from \(\lbrace p_{1},\dots,p_{\ell} \rbrace\), including \(P_{1}:=1\), using \(G\).

  3. (3)

    Compute \(r\) leading principal minors of \(H_{j}\) for all \(j=1,\dots,2^{\ell}\), where \(r\) is the dimension of the matrix \(H_{j}\) in \(\mathbb{Q}(s)\) using Gaussian elimination.

  4. (4)

    Compute ranks and signatures of \(H_{j}^{\beta}\) for all \(j\) by nearby points using principal minors and the Jacobian theorem, respectively.

  5. (5)

    Compute the solution of a linear system obtained from signatures to find the number of common real zeros by Hermite’s root counting theorem.

Buchberger’s algorithm [6] produces, from a given polynomial system, another system with the same set of common zeros that has many good properties [9]. Such algorithm has been implemented in Mathematica as the command GroebnerBasis. In [25], we compute the required generic Groebner basis using a method that is based on [12]. Here, we use an alternative method provided in [9] for the systems in Sect. 4.

Hermite’s root counting theorem uses the Hermite matrices to obtain information on numbers of common roots of a polynomial system [7]. The Hermite matrices are symmetric matrices that come from the quotient algebra over the ideal generated by the polynomials. They are symmetric matrices over the underground field and the signatures of real Hermite matrices count the numbers of real roots. It is a collaborated work from Moeckel and the author in [24] that implementing an algorithm using a Groebner basis to compute the Hermite matrices.

The Jacobian theorem is used in computing the signatures of the Hermite matrices. It uses the ranks and the numbers of sign variations in the list of leading principal minors. There are \(r2^{\ell}\) leading principal minors. Computing them costs the most part of the time required in all of the computations, since we compute determinants of matrices with symbolic matrices. In [25], we simply use the \(\mathit{Det}\) commend from Mathematica and it totally costs three months in computing all the leading principal minors for a system with \(r=104,\ell =3\). In this paper, with the algorithm using the idea from Gaussian elimination (see Sect. 5.1.3 for details), it costs only three days for a system with \(r=140,\ell=3\).

The rank of a matrix can be defined as the largest among the orders of the non-zero minors generated by the matrix. At the bifurcation point \(\beta\), suppose the rank of the Hermite matrix is \(r-w\) for some \(w>0\). As in [25], we use only principal minors to find \(w\) in the cases of \(w<3\), which also saves some time for not going through all the required minors from the definition. As in [25], all problems in this paper are the cases of \(w<3\).

At the bifurcation point \(\beta\), sign variations in the list of the leading principal minors are determined by its nearby rational points. In doing so, we find an interval with rational endpoints containing \(\beta\) such that all the leading principal minors of orders smaller \(r-w\) contain no zeros in such interval. This can be done using methods of isolating zeros for univariate polynomials. In our computations, we use the implemented command CountRoots of Mathematica. This command is based on [8]. In the introduction of this paper, the authors commented that “Unlike numerical methods the algorithm will always terminate with correct results.”

Since computing the Groebner basis in the first step is critical and the \(r2^{\ell}\) leading principal minors are required, the preprocessing of applying our algorithm is to find a polynomial system from which one can compute such Groebner basis so that the computed Hermite matrices (with parameter) have as small dimension as possible. As a result of applying our algorithm, we not only count the common zeros of \(\mathcal{F}^{\beta}\) in \(\mathcal{X}\), but also obtain the numbers of zeros in any of the region \(\lbrace \pm p_{1}>0,\dots,\pm p_{\ell}>0 \rbrace\) among all the \(2^{\ell}\) “quadrants”.

3 The Planar \((3+1)\)-Body Problem

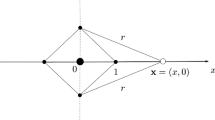
Let four particles have masses \(m_{1},m_{2},m_{3}>0\) and \(m_{4}=0\). The three particles with positive masses form a central configuration by themselves according to Eqs. (2). Considering the central configuration in \(\mathbb{R}^{2}\) for three bodies, we obtain an equilateral triangle [21]. Fixing \(q_{1},q_{3},q_{3}\) in \(\mathbb {R}^{2}\) such that the length of the sides of the equilateral triangle is 1 and assuming the total mass \(M=1\), without loss of generality, we obtain \(\lambda=-1\) in Eqs. (2). The equations in (2) for the zero mass \(q_{4}=(x,y)\) become \(\partial_{x}G=\partial _{y}G=0\), where

$$G=\frac{1}{2}\|q_{4}-c\|^{2}+\dfrac{m_{1}}{\|q_{4}-q_{1}\|}+ \dfrac{m_{2}}{\|q_{4}-q_{2}\|}+\dfrac{m_{3}}{\|q_{4}-q_{3}\|}. $$

By the identity,

$$\|q_{4}-c\|^{2}-\sum_{i=1}^{3}m_{i} \|q_{4}-q_{i}\|^{2}=\|c\|^{2}-\sum_{i=1}^{3}m_{i}\|q_{i} \|^{2}, $$

we change the coordinates of \(q_{4}\) to \(r_{i}=\|q_{4}-q_{i}\|\) for \(i=1,2,3\). So, we obtain

$$G=\frac{1}{2}\bigl(m_{1}r_{1}^{2}+m_{2}r_{2}^{2}+m_{3}r_{3}^{2}\bigr)+ \frac{m_{1}}{r_{1}}+\frac{m_{2}}{r_{2}}+\frac{m_{3}}{r_{3}}+C, $$

for some constant \(C\). With the new coordinates, we impose a restriction for the mutual distances of four points in \(\mathbb{R}^{2}\) given by the Cayley-Menger determinant [18]. Therefore, we have the following equation for \(r_{1},r_{2},r_{3}\).

$$F= \begin{vmatrix} 0&1&1&1&1\\ 1&0&1&1&r_{1}^{2}\\ 1&1&0&1&r_{2}^{2}\\ 1&1&1&0&r_{3}^{2}\\ 1&r_{1}^{2}&r_{2}^{2}&r_{3}^{2}&0 \end{vmatrix} =0. $$

Now, we find the critical points of \(G\) restricted to \(F=0\). By the Lagrange multiplier technique, we obtain the following equations for a multiplier \(\omega\).

$$ \begin{aligned} \partial_{r_{i}}G&=\omega\partial_{r_{i}}F,\quad \forall i=1,2,3,\\ F&=0. \end{aligned} $$
(3)

Eliminating \(\omega\) and clearing the denominators, we obtain a polynomial system from (3). Note that the system is homogeneous of degree one in the masses \(m_{1},m_{2},m_{3}\). Normalizing the total mass gives us a system with two parameters. From Eqs. (3), Barros and Leandro obtained the following results in [4, 5].

Theorem 1

The bifurcation set is a simple, closed, analytic curve. There are 8 and 10 central configurations outside and inside the curve, respectively. Moreover, there are 9 central configurations on the curve when \(0.37< r_{i}\leq0.58\).

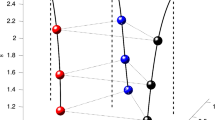
When testing the parameters \((m_{1},m_{2},m_{3})=(1,1,s)\) for some \(s\) with nearby points of \(0.27168\dots\), we obtain 8 positive zeros, including the one with \((r_{1},r_{2}){\approx}(0.70269,0.70269)\), at \(s=0.2716\) and 10 positive zeros, including the three with \((r_{1},r_{2})\approx (0.70266,0.70266)\), \((0.70351,0.70181)\), \((0.70181,0.70351)\), at \(s=0.2717\). This suggests that, at the point \(s=0.27168\dots\), the system experiences a pitchfork bifurcation instead of a saddle-note bifurcation. Figure 1 demonstrates such bifurcation from \(s=0.5\) to 0.2. Therefore, it suggests there are 8 central configurations at that bifurcation point. In fact, this is the first main result in this paper.

Fig. 1
figure 1

Pitchfork bifurcation of the \((3+1)\)-body problem: \(s=0.5,0.29,0.2\)

Full size image

Theorem 2

There are three points on the bifurcation curve obtained in [5], where there are exactly 8 central configurations. Each one corresponds to one of the intersection points of the bifurcation curve with the line \(m_{i}=m_{j}\).

After eliminating \(\omega\) and clearing the denominators from systems (3), we substitute \((m_{1},m_{2},m_{3},r_{3})\) with \((1,1,s,\frac{1}{r_{3}})\) and clear the denominators. We obtain the system \(\lbrace dh_{1},dh_{2},(r_{1}-r_{2})dh_{3},dh_{4}\rbrace\). After substituting \(r_{3}\) with \(\frac{1}{r_{3}}\) again and clearing the denominators, we obtain the system \(\lbrace h_{1},h_{2},(r_{1}-r_{2})h_{3},h_{4}\rbrace\) which splits into system one \(\lbrace h_{1},h_{2},r_{1}-r_{2},h_{4}\rbrace\) and system two \(\lbrace h_{1},h_{2},h_{3},h_{4}\rbrace\). (See Appendix.)

System one becomes \(\lbrace k_{1},k_{2}\rbrace\) after letting \(r_{1}=r_{2}=x,r_{3}=y\), where \(k_{1}=(1+y^{2})sx^{3}-sx^{5}-(1+2x^{2})y^{3}+(1-s)x^{3}y^{3}+(2+s)x^{5}y^{3}+2y^{5}-(2+s)x^{3}y^{5}\) coming from \(h_{1}\) and \(h_{2}\), and \(k_{2}=-1+2x^{2}-x^{4}+y^{2}+2x^{2}y^{2}-y^{4}\) coming from \(h_{4}\).

Let \(r_{1}=r_{2}=x,r_{3}=y\) in \(h_{3}\). We obtain \(3 x^{2} k_{3}\), where \(k_{3}=1 - 3 x^{2} + 2 x^{5} + y^{2}\). Therefore, when \(r_{1}=r_{2}>0\), system two becomes \(\lbrace k_{1},k_{2},k_{3}\rbrace\). Note that \(k_{2},k_{3}\) do not involve the parameter \(s\). It is easy to see that \(k_{2}=k_{3}=0\) has an unique positive zero \((x,y)\approx (0.702665,0.3723266)\). Form \(k_{1}\), we obtain an unique positive \(s\approx0.27168\) where system two has that unique positive zero. Computing a Groebner basis from \(k_{1},k_{2},k_{3}\) in the variables \(x,y,s\), we obtain \(g_{1}\in \mathbb{Z} [ s ]\) of degree 18 that contains \(0.27168\dots\) as a zero.

In conclusion, only when \(s=0.27168\dots\) does system two \(\lbrace h_{1},h_{2},h_{3},h_{4}\rbrace\) contain positive zeros of \(r_{1}=r_{2}=x,r_{3}=y\) and such zero is unique as \((x,y)\approx (0.702665,0.372326)\). Obviously, all common zeros of \(k_{1},k_{2},k_{3}\) are common zeros of \(k_{1},k_{2}\). Therefore, at such parameter, the unique zero \((x,y)\approx(0.702665,0.372326)\) is also a zero of system one.

From [17], we see that system one has 4 positive common zeros at \(0.27168\dots\). If we can show that system two has 5 positive zeros, we obtain that the system \(\lbrace h_{1},h_{2},(r_{1}-r_{2})h_{3},h_{4}\rbrace\) has totally \(3+1+4=8\) zeros. The summand \(3+1\) comes from system one, \(1+4\) comes from system two, and the common summand 1 comes from the shared unique zero with \(r_{1}=r_{2}\).

Lemma 1

The system \(\lbrace h_{1},h_{2},h_{3},h_{4}\rbrace\) has exactly 5 zeros with \(r_{1},r_{2},r_{3}>0\) at \(s_{1}= 0.27168\dots\), that is a zero of \(g_{1}\in \mathbb{Z} [ s ]\) of degree 18.

4 The Symmetrical 4-Body and 5-Body Problems

In this section, we consider the symmetrical central configurations, \((2,d)\)-cc’s, defined in [16]. They consist of point masses in \(\mathbb{R}^{d}\) such that \(m_{1},m_{2}\) are on a fixed line passing through and being perpendicular to a \((d-1)\)-dimensional hyperplane at the center of a regular simplex of dimension \(d-1\) contained in it where all remaining equal masses (all assuming 1) are at the vertices of the simplex. It is shown in [16] that there are finitely many \((2,d)\)-cc’s for all \(d>1\). In particular, for \(d=2,3\), there are more refined results.

Theorem 3

For both the \((2,2)\)-cc and \((2,3)\)-cc’s problems, the bifurcation sets in the \((m_{1},m_{2})\) plane contain two curves in the first quadrant. They are symmetric to each other with respect to the line \(m_{1}=m_{2}\) and intersect at an unique point on such line (say at \(s_{2},s_{3}>1\) for \(d=2,3\), respectively). They divide the first quadrant into four open connected components containing \((0,0),(0,\infty),(\infty,\infty )\), or \((\infty,0)\) as one of their boundary points, where there are \(5,3,1,3\) central configurations, respectively. Among them in each case, precisely one is convex.

When considering the special cases of \(m_{1}=m_{2}\), we obtain two corollaries.

Corollary 1

For the planar 4-body problem with two pairs of equal masses which have an axis of symmetry containing one pair of them, there are generically \(2,4\) concave central configurations.

Proof

Let two pairs of equal masses be 1 and \(s\). We call masses on the axis of symmetry \(m_{1},m_{2}\). If \(0< s<\frac{1}{s_{2}}\), we have 4 concave central configurations with \(m_{1}=m_{2}=s\). Since \(m_{1}=m_{2}\), the number 4 is reduced to 2 by symmetry. If \(s_{2}< s\), we have no concave central configurations with \(m_{1}=m_{2}=s\) but again 2 concave central configurations with \(m_{1}=m_{2}=1\). For \(\frac{1}{s_{2}}< s< s_{2}\) and \(s\neq1\), we have 2 concave central configurations with \(m_{1}=m_{2}=s\) and 2 concave central configurations with \(m_{1}=m_{2}=1\). At \(s=1\), the number is reduced to 2 by symmetry. □

Corollary 2

For the spatial 5-body problem with three equal masses at the vertices of an equilateral triangle and two equal masses on the line passing through the center of the triangle and being perpendicular to the plane containing it, there are generically \(0,2\) concave central configurations.

Proof

Let three equal masses at the vertices of an equilateral triangle be 1 and two equal masses on the line be \(s\). For \(0< s< s_{3}\), we have 4 concave central configurations. Since two masses on the line are equal, the number 4 is reduced to 2 by symmetry. For \(s_{3}< s\), there are no concave central configurations. □

In the first corollary, there are two bifurcation points, \(s_{2}\) and \(\frac{1}{s_{2}}\). In the second corollary, there is only one, \(s_{3}\). All of them come from the singular points on the bifurcation sets that are on the line of \(m_{1}=m_{2}\) described in Theorem 3. We will identify \(s_{2},s_{3}\) (find polynomials \(g_{2}\) and \(g_{3}\) containing each as one of the zeros, respectively) using a different method than that in [16] and count the numbers of concave central configurations at them with our algorithm.

Here, in stead of using Eqs. (2) directly, we use the Laura-Andoyer equations [13] that are equivalent to Eqs. (2).

4.1 The Symmetrical 4-Body Case

For \(i=1,\dots,4\), let \(q_{i}=(x_{i},y_{i})\in\mathbb{R}^{2}\) and \(r_{ij}=\|q_{i}-q_{j}\|\) be the distance between particles \(i\) and \(j\). Let \(\Delta_{i,j,k}=(q_{i}-q_{j})\wedge(q_{i}-q_{k})\), twice the oriented area defined by the triangle with vertices at \(q_{i},q_{j}\), and \(q_{k}\). We have the following six equations for non-collinear central configurations formed by \(q_{1},\dots,q_{4}\).

Proposition 1

For non-collinear 4 bodies in \(\mathbb{R}^{2}\), Eqs. (2) are satisfied if and only if

$$\sum_{k=1,k\neq i,j}^{4}m_{k} \Delta_{i,j,k}\biggl(\frac {1}{r_{ik}^{3}}-\frac{1}{r_{jk}^{3}}\biggr)=0,\quad 1 \leq i < j \leq4. $$

In our case, let \((m_{1},m_{2},m_{3},m_{4})=(1,1,s,s)\) and \(q_{1}=(-\frac{1}{2},0),q_{2}=(\frac{1}{2},0),q_{3}=(0,a),q_{4}=(0,b)\). Since we consider concave configurations, we assume \(a>b>0\). Then the six equations are reduced to the following two.

$$ \textstyle\begin{cases} a(1-(\frac{1}{4}+a^{2})^{-\frac{3}{2}})+(\frac{a}{2}-\frac{b}{2})(-(a-b)^{-3}+(\frac{1}{4}+b^{2})^{-\frac{3}{2}})s=0,\\ b(1-(\frac{1}{4}+b^{2})^{-\frac{3}{2}})+(\frac{b}{2}-\frac{a}{2})(-(a-b)^{-3}+(\frac{1}{4}+a^{2})^{-\frac{3}{2}})s=0. \end{cases} $$
(4)

Let \(r_{1}=a\), \(r_{2}=b\), \(r_{3}^{-2}=\frac{1}{4}+a^{2}\), \(r_{4}^{-2}=\frac{1}{4}+b^{2}\). We obtain the system \(\lbrace f_{1},f_{2},f_{3}=-4 + r_{3}^{2} + 4 r_{1}^{2} r_{3}^{2},f_{4}=-4 + r_{4}^{2} + 4 r_{2}^{2} r_{4}^{2} \rbrace\), where \(f_{1},f_{2}\) come from (4). (See Appendix.)

Lemma 2

The system \(\lbrace f_{1},f_{2},f_{3},f_{4}\rbrace\) has 1 zero with \(r_{1}>r_{2}>0\) at \(s= 1.002713329\dots\), a zero of \(g_{2}\in \mathbb{Z}[s]\) of degree 136. It has 2 such zeros for all \(1.00271332 \leq s< 1.002713329\dots\) and 0 such zeros for all \(1.002713329\dots< s\leq1.00271333\).

Since the system \(\lbrace f_{1},f_{2},f_{3},f_{4}\rbrace\) experiences a bifurcation at the parameter \(s=1.002713329\dots\) according to the lemma above, we identify \(s_{2}= 1.002713329\dots\) in Theorem 3 for \(d=2\) due to the uniqueness of bifurcation point. The unique zero with \(r_{1}>r_{2}>0\) for the system \(\lbrace f_{1},f_{2},f_{3},f_{4}\rbrace\) at \(s_{2}\) gives a 4-body concave central configuration as shown on the left side of Fig. 2. Together with Corollary 1, we obtain the following.

Fig. 2
figure 2

Concave 4-body and 5-body central configurations at the bifurcation points

Full size image

Theorem 4

For the planar 4-body problem with two pairs of equal masses which have an axis of symmetry containing one pair of them, there are \(2,3,4\) concave central configurations.

4.2 The Symmetrical 5-Body Case

For \(i=1,\dots,5\), let \(q_{i}=(x_{i},y_{i},z_{i})\in\mathbb{R}^{3}\) and \(r_{ij}=\|q_{i}-q_{j}\|\) be the distance between particles \(i\) and \(j\). Let \(\Delta_{i,j,\ell,k}=(q_{i}-q_{j})\wedge(q_{i}-q_{\ell})\cdot (q_{i}-q_{k})\), six times the oriented volume defined by the tetrahedron with vertices at \(q_{i},q_{j},q_{\ell}\) and \(q_{k}\). We have the following thirty equations for non-planar central configurations formed by \(q_{1},\dots,q_{5}\).

Proposition 2

For non-planar 5 bodies in \(\mathbb{R}^{3}\), Eqs. (2) are satisfied if and only if

$$\sum_{k=1,k\neq i,j,\ell}^{5}m_{k} \Delta_{i,j,\ell,k}\biggl(\frac {1}{r_{ik}^{3}}-\frac{1}{r_{jk}^{3}}\biggr)=0,\quad 1 \leq i,j,\ell\leq 5, i< j, \ell\neq i,j. $$

In our case, let \((m_{1},m_{2},m_{3},m_{4},m_{5})=(1,1,1,s,s)\) and \(q_{1}=(\frac{1}{\sqrt{3}},0,0)\), \(q_{2}= (-\frac{1}{2\sqrt{3}},\frac {1}{2},0)\), \(q_{3}=(-\frac{1}{2\sqrt{3}},-\frac {1}{2},0)\), \(q_{4}=(0,0,a)\), \(q_{5}=(0,0,b)\). Since we consider concave configurations, we assume \(a>b>0\). Then the thirty equations are reduced to the following two.

$$ \textstyle\begin{cases} \frac{3}{2}a(1-(\frac{1}{3}+a^{2})^{-\frac{3}{2}})+(\frac{a}{2}-\frac{b}{2})(-(a-b)^{-3}+(\frac{1}{3}+b^{2})^{-\frac{3}{2}})s=0,\\ \frac{3}{2}b(1-(\frac{1}{3}+b^{2})^{-\frac{3}{2}})+(\frac{b}{2}-\frac{a}{2})(-(a-b)^{-3}+(\frac{1}{3}+a^{2})^{-\frac{3}{2}})s=0. \end{cases} $$
(5)

Let \(r_{1}=a\), \(r_{2}=b\), \(r_{3}^{-2}=\frac{1}{3}+a^{2}\), \(r_{4}^{-2}=\frac {1}{3}+b^{2}\). We obtain the system \(\lbrace f_{5},f_{6},f_{7}=-3 + r_{3}^{2} + 3 r_{1}^{2} r_{3}^{2},f_{8}=-3 + r_{4}^{2} + 3 r_{2}^{2} r_{4}^{2} \rbrace\), where \(f_{5},f_{6}\) come from (5). (See Appendix.)

Lemma 3

The system \(\lbrace f_{5},f_{6},f_{7},f_{8}\rbrace\) has 1 zero with \(r_{1}>r_{2}>0\) at \(s= 1.068821203\dots\), a zero of \(g_{3}\in \mathbb {Z} [ s ]\) of degree 136. It has 2 such zeros for all \(1.0688212 \leq s< 1.068821203\dots\) and 0 such zeros for all \(1.068821203\dots< s\leq1.0688213\).

Since the system \(\lbrace f_{5},f_{6},f_{7},f_{8}\rbrace\) experiences a bifurcation at the parameter \(s= 1.068821203\dots\) according to the lemma above, we identify \(s_{3}= 1.068821203\dots\) in Theorem 3 for \(d=3\) due to the uniqueness of bifurcation point. The unique zero with \(r_{1}>r_{2}>0\) for the system \(\lbrace f_{5},f_{6},f_{7},f_{8}\rbrace\) at \(s_{3}\) gives a 5-body concave central configuration as shown on the right side of Fig. 2. Together with Corollary 2, we obtain the following.

Theorem 5

For the spatial 5-body problem with three equal masses at the vertices of an equilateral triangle and two equal masses on the line passing through the center of the triangle and being perpendicular to the plane containing it, there are \(0,1,2\) concave central configurations.

5 Proofs of the Lemmas

In this section, we present some details in proving Lemmas 1 and 2. Situations for Lemma 3 are very similar to that in Lemma 2. Therefore, we skip the details for Lemma 3 here. All the computations can be found in [26].

5.1 Proof of Lemma 1

Since the system \(\lbrace h_{1},h_{2},h_{3},h_{4} \rbrace\in\mathbb {Z} [ s ] [ r_{1},r_{2},r_{3} ]\) contains zeros \((r_{1},r_{2},r_{3})=(0,\pm1,\pm1), (\pm1,0,\pm1),(1,1,0),(-1,1,0)\), and \((1,-1,0)\), for all \(s\), we remove them by introducing three more variables \(r_{4},r_{5},r_{6}\) and adding three equations \(h_{5}=r_{1}r_{4}-1\), \(h_{6}=r_{2}r_{5}-1\), \(h_{7}=r_{3}r_{6}-1\) to the system.

5.1.1 Step 1: Generic Groebner Basis

In this case, we still can use the method provided in [25] for computing a generic Groebner basis. Consider \(\mathcal{F}=\lbrace h_{1},\dots,h_{7} \rbrace\in\mathbb{Z} [ r_{1},\dots,r_{6},s ]\) and use the monomial order specified by the following matrix to compute a Groebner basis in \(\mathbb{Z} [ r_{1},\dots,r_{6},s ]\),

$$\begin{bmatrix} 1&1&1&1&1&1&0\\ 1&1&1&1&1&0&0\\ 1&1&1&1&0&0&0\\ 1&1&1&0&0&0&0\\ 1&1&0&0&0&0&0 \\ 1&0&0&0&0&0&0 \\ 0&0&0&0&0&0&1 \end{bmatrix} . $$

We obtain \(G\) that contains 68 polynomials. Collecting the leading coefficients of \(G\) when polynomials in it are viewed as in \(\mathbb{Z} [ s ] [ r_{1},\dots,r_{6} ]\) with the restriction of the order to \(r_{1},\dots,r_{6}\), called the Graded Reverse Lex Order [9], we obtain 68 polynomials in \(\mathbb{Z} [s]\). None of them vanish for \(s>0\). Therefore, \(G^{s}\) is a Groebner basis of \(\mathcal{F}^{s}\in\mathbb{C} [ r_{1},\dots,r_{6} ]\) for all \(s>0\) [25].

5.1.2 Step 2: Hermite Matrices

Now, consider \(G \in\mathbb{Q}( s ) [ r_{1},\dots,r_{6} ]\). It is also a Groebner basis of ℱ viewed as a system \(\mathbb {Q}( s ) [ r_{1},\dots,r_{6} ]\) with respect to the Graded Reverse Lex Order of \(r_{1},\dots,r_{6}\) [24]. Therefore, we compute eight Hermite matrices \(H(\mathcal{F},1)\), \(H(\mathcal{F},r_{1})\), \(H(\mathcal{F},r_{2})\), \(H(\mathcal{F},r_{3})\), \(H(\mathcal{F},r_{1}r_{2})\), \(H(\mathcal{F},r_{1}r_{3})\), \(H(\mathcal{F},r_{2}r_{3})\), and \(H(\mathcal{F},r_{1}r_{2}r_{3})\). All are \(140\times140\) symmetric matrices with entries in \(\mathbb{Q}( s )\).

5.1.3 Step 3: Leading Principal Minors

For each \(140\times140\) Hermite matrix, denoted by \(H^{140}\), we need to compute 140 leading principal minors. They are the determinants, denoted by \(M_{i}\), of the square matrix obtained from taking the first \(i\) rows and columns from \(H^{140}\) for \(i=1,\dots,140\).

Initialize \(a^{140}=b^{140}=H^{140}_{1,1}\). For \(j\) decreasing from 140 to 2, recursively define \(a^{j-1}=H^{j-1}_{1,1},b^{j-1}=b^{j}a^{j-1}\), where \(H^{j-1}\) is defined as the \((j-1)\times(j-1)\) matrix through taking the second to \(j\)-th rows and columns from \(\hat{H}^{j}\), the \(j\times j\) matrix obtained from \(H^{j}\) by clearing \(H^{j}_{i,1}\) for all \(i=2,\dots,j\) with \(a^{j}\). If \(a^{j}\neq0\) for all \(j\), the algorithm will not stop until the last \(b^{j}\) (that is \(b^{1}\)) is defined. Since adding any multiple of the first row to others does not change the determinants, we obtain \(M_{i}=b^{141-i}\) for \(i=1,\dots,140\).

Remark 1

For \(H(\mathcal{F},r_{1})\) and \(H(\mathcal{F},r_{2})\), we add the 4-th row to the first row and do the same for columns and then switch rows \(2,3\) and do the same for columns to obtain new \(H^{140}\) in order to satisfy \(a^{j}\neq0\) for all \(j\). For \(H(\mathcal{F},r_{1}r_{3})\) and \(H(\mathcal{F},r_{2}r_{3})\), we add the 5-th row to the first row and do the same for columns and then switch rows \(2,4\) and do the same for columns to obtain new \(H^{140}\) for the same reason.

It turns out that, for all eight \(H^{140}\)’s, \(M_{140}\) contains the polynomial \(g_{1}\) of degree 18 that has \(s_{1}=0.27168\dots\) as a zero, while no other \(M_{i}\)’s have \(g_{1}\) as a factor. These implies that ranks of \(H^{140}\) is 139 at \(s=s_{1}\) (and 140 for \(s\) nearby \(s_{1}\)).

5.1.4 Step 4: Signatures

Let \(a_{\ell}=0.271686396\) and \(a_{r}=0.271686397\). We verify that the numerator of \(M_{140}\) contains an unique zero and the numerators of \(M_{i}\) contain no real zeros on \([ a_{\ell},a_{r} ]\) for \(i<140\). At \(s=a_{\ell}\), the numbers of sign variations in the lists of \(\lbrace1,M_{1},\dots,M_{140} \rbrace\) are \(63,67,67,69,71,69,69,69\) for \(H(\mathcal{F},1),\dots,H(\mathcal {F},r_{1}r_{2}r_{3})\), respectively. At \(s=a_{r}\), the numbers of sign variations are \(62,66,66,68,70,68,68,68\). Therefore, at \(s=s_{1}\), the numbers of sign variations are \(62,66,66,68,70,68,68,68\) (in the lists of \(\lbrace1,M_{1},\dots,M_{139} \rbrace\)). Then, the signatures are computed from the formula \(r-2v\), where \(r\) is the rank and \(v\) is the number of sign variations in the list of \(\lbrace1,M_{1},\dots,M_{r} \rbrace\). At \(s=s_{1}\), the signatures are \(15,7,7,3,-1,3,3,3\).

5.1.5 Step 5: Linear System

Let \(x_{1}, \ldots, x_{8}\) denote the numbers of real roots of \(\mathcal{F}^{s_{1}}\) such that \((r_{1},r_{2},r_{3})\) has the signs \((+,+,+), \ldots, (-,-,-)\), respectively. We solve the following linear system and get \(x_{1}=5\).

$$\begin{aligned} 15&=x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}+x_{7}+x_{8},\\ 7&=x_{1}+x_{2}+x_{3}+x_{4}-x_{5}-x_{6}-x_{7}-x_{8},\\ 7&=x_{1}+x_{2}-x_{3}-x_{4}+x_{5}+x_{6}-x_{7}-x_{8},\\ 3&=x_{1}-x_{2}+x_{3}-x_{4}+x_{5}-x_{6}+x_{7}-x_{8},\\ -1&=x_{1}+x_{2}-x_{3}-x_{4}-x_{5}-x_{6}+x_{7}+x_{8},\\ 3&=x_{1}-x_{2}+x_{3}-x_{4}-x_{5}+x_{6}-x_{7}+x_{8},\\ 3&=x_{1}-x_{2}-x_{3}+x_{4}+x_{5}-x_{6}-x_{7}+x_{8},\\ 3&=x_{1}-x_{2}-x_{3}+x_{4}-x_{5}+x_{6}+x_{7}-x_{8}. \end{aligned} $$

Therefore, there are 5 zeros of \(\lbrace h_{1},h_{2},h_{3},h_{4},r_{1}r_{4}-1,r_{2}r_{5}-1,r_{3}r_{6}{-}1\rbrace\) with \(r_{1},r_{2},r_{3}{>} 0\). So, for the system \(\lbrace h_{1},h_{2},h_{3},h_{4\rbrace}\), there are 5 positive zeros.

5.2 Proof of Lemma 2

Here, we study \(\lbrace f_{1},f_{2},f_{3},f_{4} \rbrace\in\mathbb{Z} [ s ] [ r_{1},r_{2},r_{3},r_{4} ]\) and find \(s_{2}>1\), where there is a bifurcation.

5.2.1 Step 1: Generic Groebner Basis

Unfortunately, the method used in [25] as shown in Sect. 5.1.1 does not work. We cannot compute the desired generic Groebner basis with that method. Instead, we apply the following method that is provided in [9] of Sect. 6.3 as exercises. It can be proved through the definition of a Groebner basis. We omit the proof here.

Proposition 3

Let \(\mathcal{F}=\lbrace p_{1},\dots,p_{n} \rbrace\subset\mathbb{Q}(s ) [ x_{1},\dots,x_{m} ]\) consisting of monic polynomials in some order, \(G=\lbrace g_{1},\dots,g_{t} \rbrace\) be the reduced Groebner basis of ℱ in \(\mathbb{Q}( s ) [ x_{1},\dots ,x_{m} ]\) in that order, and \(d \in\mathbb{Z} [ s ]\) be the least common multiple of all denominators in \(p_{i}\) ’s and \(g_{j}\) ’s. Let \(\tilde{p_{i}}\) and \(\tilde{g_{j}}\) be polynomials in \(\mathbb{Z} [ x_{1},\dots,x_{m},s ]\) obtained from \(p_{i}\) and \(g_{j}\) by clearing denominators, respectively, and \(\langle\tilde {\mathcal{F}} \rangle\) be the ideal in \(\mathbb{Q} [ x_{1},\dots ,x_{m},s ]\) generated by \(\tilde{p_{i}}\) ’s. If \(d\tilde{g_{j}} \in \langle\tilde{ \mathcal{F}} \rangle\) for all \(j=1,\dots,t\), then \(G^{a}\) is a Groebner basis of \(\mathcal{F}^{a}\) in \(\mathbb{C} [ x_{1},\dots,x_{m} ]\) for all \(a \in\mathbb{C}\) with \(d\neq0\). (Recall that \(G^{a}\) and \(\mathcal{F}^{a}\) are the systems in \(\mathbb {C} [ x_{1},\dots,x_{m} ]\) obtained from substituting \(s\) with \(a\in\mathbb{C}\) in all polynomials in \(G\) and ℱ, respectively.)

Now, fixing the Graded Reverse Lex Order in \(r_{1},r_{2},r_{3},r_{4}\), we have our monic system \(\lbrace p_{1}=\frac{f_{1}}{(-2)},p_{2}=\frac {f_{2}}{(-s)},p_{3}=\frac{f_{3}}{4},p_{4}=\frac{f_{4}}{4} \rbrace\) in \(\mathbb{Q}( s ) [ r_{1},r_{2},r_{3},r_{4} ]\). So, \(\tilde {p_{i}}=f_{i}\). Applying the option RationalFunctions in assigning the domain of coefficients in Mathematica, we compute the Groebner basis of the monic system in \(\mathbb{Q}( s ) [ r_{1},r_{2},r_{3},r_{4} ]\). (In fact, we compute from \(\lbrace f_{1},f_{2},f_{3},f_{4} \rbrace\).)

By default, the output is a semi reduced Groebner basis obtained from the reduced Groebner basis after clearing denominators [9]. Therefore, we indeed obtain \(\tilde{g_{j}}\)’s. (There are 42 of them.) The reduced Groebner basis \(G\) is the set \(\lbrace\frac{\tilde{g_{1}}}{L_{i}},\dots,\frac{\tilde{g_{42}}}{L_{42}} \rbrace\), where \(L_{j}\) is the leading coefficient of \(\tilde{g_{j}}\) in \(\mathbb {Z} [ s ]\) with respect to the Graded Reverse Lex Order in \(r_{1},r_{2},r_{3},r_{4}\). Therefore, \(d\) is the least common multiple of \(L_{i}\)’s and \(-2,-s,4,4\).

Then, we compute \(GB\), the Groebner basis of \(\lbrace f_{1},f_{2},f_{3},f_{4} \rbrace\) in \(\mathbb{Q} [ r_{1},r_{2},r_{3},r_{4},s ]\) with Graded Reverse Lex Order in \(r_{1},r_{2},r_{3},r_{4},s\). We verify \(d\tilde{g_{j}}\in\langle\tilde {\mathcal{F} }\rangle\) by finding the remainders to be zeros after applying PolynomialReduce in dividing \(d\tilde{g_{j}}\) with \(GB\). For \(s>0\), it is easy to see \(d\neq0\) except at \(s=0.25,1,1.2939\dots,1.5436\dots,2\). Therefore, \(G^{s}\) is a Groebner basis of \(\mathcal{F}^{s}\) in \(\mathbb{C} [ r_{1},r_{2},r_{3},r_{4} ]\) for almost all \(s>0\).

5.2.2 Step 2: Hermite Matrices

Since \(G\) is computed as the Groebner basis in \(\mathbb{Q}(s) [r_{1},r_{2},r_{3},r_{4} ]\), we again can compute Hermite matrices in \(\mathbb{Q}(s)\). (In fact, we compute Hermite matrices using \(\lbrace\tilde{g_{1}},\dots,\tilde{g_{42}} \rbrace\) which is also a Groebner basis in \(\mathbb{Q}(s) [ r_{1},r_{2},r_{3},r_{4} ]\).) In order to find zeros with \(r_{1}>r_{2}>0\), we need to compute four Hermite matrices, \(H(\mathcal{F},1),H(\mathcal {F},r_{1}-r_{2}),H(\mathcal{F},r_{2})\), and \(H(\mathcal {F},r_{2}(r_{1}-r_{2}))\). All are \(102\times102\) symmetric matrices with entries in \(\mathbb{Q}( s )\).

5.2.3 Step 3: Leading Principal Minors

As in Sect. 5.1.3, we compute 408 leading principal minors using the idea that is similar to the Gaussian elimination. For the matrix \(H(\mathcal{F},r_{1}-r_{2})\), we add the 4-th row to the first row and do the same for columns and then switch rows \(2,3\) and do the same for columns in order to satisfy \(a^{j}\neq0\) for all \(j\) (See Sect. 5.1.3 for the definition of \(a^{j}\).) For \(H(\mathcal{F},r_{2})\), we switch rows \(1,2\) and do the same for columns.

Numerical observations suggest the bifurcation point is at \(s= 1.002713329\dots\), a zero of \(g_{2}\in\mathbb{Z}(s)\) of degree 136. Here, \(g_{2}^{2}\) is a factor of four \(M_{102}\) (see section \(5.1.3\) for similar definitions for \(M_{i}\)), \(g_{2}\) is a factor of four \(M_{101}\), and \(g_{2}\) is not a factor for all \(M_{i}\) with \(i<101\).

To determine the ranks at \(s= 1.002713329\dots\), we need to consider principal minors, denoted by \(M^{101}\), of order 101 obtained from deleting the 101-th row and column. All four of them contain \(g_{2}\) as a factor. Together with information on \(M_{i}\)’s, we conclude that the ranks at \(s= 1.002713329\dots\) of four Hermite matrices are 100 [25]. For nearby \(s\), the ranks are 102.

5.2.4 Step 4: Signatures

Let \(a_{\ell}=1.00271332\) and \(a_{r}=1.00271333\). We verify that numerators of both \(M_{102}\) and \(M_{101}\) contain an unique zero and numerators of \(M_{i}\) contain no real zeros on \([ a_{\ell},a_{r}]\) for \(i<101\). At \(s=a_{\ell}\), the numbers of sign variations in the lists of \(\lbrace1,M_{1},\dots,M_{102} \rbrace\) are \(46,50,52,52\) for \(H(\mathcal{F},1),H(\mathcal {F},r_{1}-r_{2}),H(\mathcal{F},r_{2}),H(\mathcal {F},r_{2}(r_{1}-r_{2}))\), respectively. At \(s= a_{r}\), the numbers of sign variations are \(46,50,51,51\). Therefore, at \(s=1.002713329\dots\), the numbers of sign variations are \(46,50,51,51\) (in the lists of \(\lbrace1,M_{1},\dots,M_{100} \rbrace\)).

Therefore, at \(s=a_{\ell}\), the signatures are \(10,2,-2,-2\); at \(s=a_{r}\), the signatures are \(10,2,0,0\); at \(s=1.002713329\dots\), the signatures are \(8,0,-2,-2\). In fact, signatures for \(a_{\ell }< s<1.002713329\dots\) are the same as that at \(a_{\ell}\) and signatures for \(1.002713329\dots< s< a_{r}\) are the same as that at \(a_{r}\).

5.2.5 Step 5: Linear System

Let \(x_{1}, x_{2}, x_{3}, x_{4}\) denote the numbers of real roots with \(r_{1}>r_{2}>0\), \(\mathrm{Min} \lbrace r_{1}, 0\rbrace>r_{2}\), \(\mathrm{Max} \lbrace r_{1}, 0\rbrace< r_{2}\), and \(r_{1}< r_{2}<0\), respectively. At \(s=1.002713329\dots\), we solve the system below and obtain \(x_{1}=1\).

$$\begin{aligned} 8&=x_{1}+x_{2}+x_{3}+x_{4},\\ 0&=x_{1}+x_{2}-x_{3}-x_{4},\\ -2&=x_{1}-x_{2}+x_{3}-x_{4},\\ -2&=x_{1}-x_{2}-x_{3}+x_{4}. \end{aligned} $$

Therefore, there is exactly 1 zero of \(\lbrace f_{1},f_{2},f_{3},f_{4} \rbrace\) at \(s=1.002713329\dots\) with \(r_{1}>r_{2}>0\). Similar, for all \(a_{\ell}\leq s<1.002713329\dots \), we find there are 2 such zeros. For all \(1.002713329\dots < s\leq a_{r}\), we find there are 0 such zeros.