A Three-Dimensional Statistical Volume Element for Histology Informed Micromechanical Modeling of Brain White Matter

Abstract

This study presents a novel statistical volume element (SVE) for micromechanical modeling of the white matter structures, with histology-informed randomized distribution of axonal tracts within the extracellular matrix. The model was constructed based on the probability distribution functions obtained from the results of diffusion tensor imaging as well as the histological observations of scanning electron micrograph, at two structures of white matter susceptible to traumatic brain injury, i.e. corpus callosum and corona radiata. A simplistic representative volume element (RVE) with symmetrical arrangement of fully alligned axonal fibers was also created as a reference for comparison. A parametric study was conducted to find the optimum grid and edge size which ensured the periodicity and ergodicity of the SVE and RVE models. A multi-objective evolutionary optimization procedure was used to find the hyperelastic and viscoelastic material constants of the constituents, based on the experimentally reported responses of corpus callosum to axonal and transverse loadings. The optimal material properties were then used to predict the homogenized and localized responses of corpus callosum and corona radiata. The results indicated similar homogenized responses of the SVE and RVE under quasi-static extension, which were in good agreement with the experimental data. Under shear strain, however, the models exhibited different behaviors, with the SVE model showing much closer response to the experimental observations. Moreover, the SVE model displayed a significantly better agreement with the reports of the experiments at high strain rates. The results suggest that the randomized fiber architecture has a great influence on the validity of the micromechanical models of white matter, with a distinguished impact on the model’s response to shear deformation and high strain rates. Moreover, it can provide a more detailed presentation of the localized responses of the tissue substructures, including the stress concentrations around the low caliber axonal tracts, which is critical for studying the axonal injury mechanisms.

Introduction

Human brain white matter consists mainly of long myelinated and unmyelinated axonal fibers extending from soma into the deep structures such as corpus callosum, corona radiata, and brain stem. Diffuse axonal injury (DAI), characterized by stretching or shear straining of axons and impairment of axoplasmic transport, is considered as a main cause of damage to the white matter. It has been reported to lead to a wide array of symptoms, from permanent disability to coma and death, as a result of subsequent swelling and neuropathologic changes in the tissue.7,11,38

DAI involves a multi-scale damage mechanism; the macroscopic large deformations in the tissue result in microscopic localized injuries mainly in the so called “injury triad”, i.e., the lobar white matter (including corona radiata), the corpus callosum, and the dorsolateral quadrant of the rostal brainstem adjacent to the superior cerebellar peduncle.40 Hence, understanding and prognosis of the effects of DAI requires an in-depth knowledge of the mechanical behavior of the white matter at both the macroscopic and microscopic levels. Micromechanical modelling of the white matter can help to gain a deeper insight into the mechanical response of tissue to various mechanical stimuli, in macroscopic and microscopic scales.

A large number of fiber-reinforced micromechanical models of the white matter have been developed by researchers to account for the anisotropic and heterogamous microstructure of tissue.1,17,18,22,41,46 These models represent the white matter as a composite of axonal fibers embedded in an extra-cellular matrix (ECM). The constitutes are usually modeled as hyperplastic materials, with their material constants characterized based on the experimental results of compressive, tensile, and shear oscillatory tests.6,35,41,44

The currently available micromechanical models of the white matter can capture the homogenized (macroscopic) direction-dependent mechanical behavior of the tissue relatively well. However, they are not often capable of realizing the localized microscopic responses required for investigation of the damage mechanisms, due to being based on simplified microstructures. As the histological studies4 have shown, the axonal fibers not only have different volume fractions in different parts of the white matter, but also their calibers and orientations change substantially within each specific structure. This highly heterogeneous microstructure is thought to be responsible for the inter-regional and intra-regional heterogeneity of the mechanical behavior of white matter, reported by previous studies.6,26,35,43 In fact, the discrepancy of the experimental observations while testing the whole tissue samples19,22,44 is also thought to be at least in part a result of the randomized intra-regional microstructure of the white matter.17

In a recent study,46 we showed that the degree of the injury predicted by a computational model of the DAI is highly dependent on the assumed microstructure. For a realistic prediction of the strain/stress levels in the tissue substructures, the model should consider the detailed architecture of the axons within the ECM, accounting for their non-uniform and randomized distributions of the diameters and orientations. The previous statistical micromechanical models of the white matter45,46 have only accounted for the probabilistic distribution of axonal calibers within the ECM. The purpose of this study is to develop a more comprehensive statistical histology-informed micromechanical model of the tissue and investigate the effects of axonal architecture on the localized responses of the substructures. The corrected embedded element technique (EET)45 is used to create a statistical volume element (SVE) of the white matter based on the findings of the diffusion weighted imaging (DWI), diffusion tensor imaging (DTI), fiber tractography, and scanning electron microscopy (SEM) studies in the literature. A simplistic RVE with hexagonal arrangement of axonal fibers within the ECM is also developed for comparison of the results. A sensitivity analysis in conducted to find the optimum edge and mesh size for both models. The hyper-viscoelastic material properties of the ECM and axonal fibers are characterized, for both models, by using a multi-objective evolutionary optimization procedure to fit the homogenized stress responses onto the experimental curves. The validity of the optimally characterized models is assessed by comparing the predicted homogenized responses of the white matter structures with the experimental data reported for different loading rates and scenarios. The models are then used to investigate the homogenized tissue behavior, as well as the associated localized responses of the axonal fibers, under quasi-static and dynamic loadings. The results help to understand the importance of the fiber architecture on the localized responses of the white matter substructures and provide a deeper insight into the axonal damage mechanism due to the DAI at the microscopic level. Furthermore, by linking such model with a macro-mechanical model of the human brain in a multiscale framework, it would be possible to predict the axonal responses to the external loads more accurately.

Methods

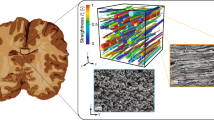
Despite the routine simplifications employed in micromechanical models, in general, the axonal architecture is extremely complicated within the white matter (Fig. 1). This complicated architecture involves randomized and diverse distributions of the axonal calibers, densities, and orientations in different tissue structures.33,47 The probability distribution functions obtained from the results of the experimental measurements, e.g., SEM, and DWI, may be utilized to characterize this randomized architecture. Based on the electron micrographs from various structures of the white matter, three morphological levels of random microstructure have been utilized in this study. First, the white matter is considered to have a variable spatial fiber density, in view of the SEM cross-sectional micrographs (Figs. 1a and 1b) which show a random distribution of axonal fiber locations within the tissue. Secondly, the calibers of the axonal fibers are assumed to be variable, considering the same micrographic data (Fig. 1b) which demonstrates substantial changes of the axon calibers even amongst adjacent tracts. This assumption is also supported by some recent studies9 which reported that axonal calibers can further fluctuate in space and time due to the organelles and activity-dependent mechanisms. Thirdly, the axons are assumed to have variable orientations within bundles of neural tracts, based on the SEM longitudinal micrographs (Fig. 1c) and Fractional Anisotropy (FA) data extracted from DTI.13

Figure 1

Electron micrographs showing the diverse architecture of myelinated axons in white matter structures: (a) cross section of splenium of corpus callosum (adapted with permission from Pesaresi et al.33); (b) cross section of brainstem (adapted with permission from Javid et al.18); (c) longitudinal section of corpus callosum (adapted with permission from Zemmoura et al.47).

Data Acquisition and Processing

MR and diffusion weighted images (DWIs) were obtained from a 25-year-old male volunteer using a 3T Siemens TrioTIM scanner. The MR images included 176 slices with 1 mm slice thickness (TR/TE = 6700/5.5 ms, 1 mm in plane resolution, 256 × 256 mm FOV). The DWIs were captured by using the single shot imaging pulse sequence with gradient sectors in 12 directions and $b{\text{-value}} = 1000\, {\text{s}}/{\text{mm}}^{2}$, and included 88 slices with 2 mm slice thickness (${\text{TR/TE }} = 8900/100\, {\text{ms}}$, $2 {\text{mm }}$ in plane resolution). The white matter was separated from the rest of the brain by implementing thresholding and segmentation techniques. Explore DTI was utilized to register DTI data onto T1 images and extract the 4D diffusion tensors for all voxels of the white matter24 (Figs. 2a and 2b). The results were verified by using Freesurfer.36 The voxels of three target structures, i.e. corpus callosum and corona radiata were marked and extracted from the white matter by means of a semi-automatic brain atlas27 (Fig. 2c). The main axonal orientation corresponding to the highest eigenvalue of the dispersion tensor in each voxel was expressed in terms of the angle θ with respect to the dominant fiber direction in the structure (e.g., X-axis for corpus callosum) as shown in Fig. 2d.

Figure 2

Schematic illustration of DTI data extraction for a typical structure of the white matter, i.e., corpus callosum: (a) fiber tractography map for all voxels within the white matter; (b) segmentation and marking of corpus callosum structure; (c) extraction of voxels; (d) a voxel with the main axonal orientation expressed in terms of the angle θ with respect to the X-axis.

Statistical Volume Element Construction

The statistical volume element, constructed in this study, was a cubic lattice consisting of a random distribution of axons (with main orientation along x direction), within the ECM (Fig. 2a). The axonal density was assigned by using the volume fraction $V_{\text{f}}$, defined as the ratio of the fiber volume to the SVE volume as in (1):

$$V_{\text{f}} = \frac{\pi }{{4a^{2} }} \mathop \sum \limits_{i = 1}^{N} d_{i}^{2}$$

(1)

where a is the lattice edge length and $d_{i}$ represents the diameter of the ith cylindrical fiber. A three-step randomization procedure was adopted to create a fiber architecture with random position, caliber and orientation. At the first step, unidirectional cylindrical axons of the same caliber ($1.9 \,\mu {\text{m}}$) were positioned one-by-one at random positions on the YZ-plane of the unit cell. Subsequently, the axonal calibers were randomized by using a cumulative density function (CDF). To this purpose, the CDF proposed by Sepehrband et al.37 was used which describes the density of axonal calibers by a gamma distribution function parameterized in terms of a shape factor, k and a scale factor, τ (Fig. 3a):

$$F\left( {x;k,\tau } \right) = \frac{{\gamma \left( {k, \frac{x}{\tau }} \right)}}{\varGamma \left( k \right)}$$

(2)

where $\gamma \left( {k, \frac{x}{\tau }} \right)$ is the lower incomplete gamma function defined in Eq. (3).

$$\gamma \left( {k, \frac{x}{\tau }} \right) = \mathop \smallint \limits_{0}^{{\frac{x}{\tau }}} t^{k - 1} e^{ - t} {\text{d}}t$$

(3)

Figure 3

Construction of the statistical volume element: (a, b) cumulative distribution functions of axonal calibers and orientations of a typical structure of white matter, i.e. corpus callosum, based on the experimental data reported by Sepehrband et al.37 and DTI analysis of this study, respectively; (c) spherical components of the orientation vector p assigned to the axons contained in the SVE model; (d) symmetrical RVE with simple uniform axonal architecture; (e) histology-informed SVE with random position, caliber, and orientation of axons.

Finally, while keeping the random positions and calibers of the axons, the orientations of axons were randomized by using another CDF, obtained from analyzing the main orientations of all DTI voxels within the structure under study, using a method similar to the one described for axonal calibers. An exponential fit in the form of $F\left( {x;\lambda } \right) = 1 - e^{ - \lambda x}$, with $\lambda = 0.076$ as the rate parameter, was used to describe the CDF (Fig. 3b). In order to introduce the probabilistic distribution of axonal orientations into the model, the orientation vector p, characterized by two spherical angles θ and ϕ, was assigned to the axons contained in the SVE (Fig. 3c). The angle θ between the main axonal orientation (X-axis) and vector p was assigned based on the DTI analysis, while the angle ϕ between Z-axis and the projection of the orientation vector p onto the YZ-plane was assumed to be normally distributed between zero and 360 degrees. A minimum myelin sheath of $0.05 \mu {\text{m}}$ was considered to satisfy impenetrability and overlapping. The procedure of positioning axons in the SVE continued until the desired portion of the lattice was filled, i.e., the specified volume fraction was achieved. The periodicity of the SVE was preserved throughout the process by using DIGIMAT 2017.0. The resulting SVE, and a simple hexagonal symmetrical RVE, considered as the benchmark, are shown in Figs. 3d and 3e.

Material Modeling

The white matter has been shown to be a heterogeneous and anisotropic material.44 Also, under large deformation, the brain tissue has been reported to display incompressible hyperelastic behavior.25,26,35,39 The hyperelastic mechanical behavior of axons and the ECM can be described using OGDEN-type strain energy density function10 (SEDF) as (4):

$$W = \frac{2\mu }{{\alpha^{2} }} \left( {\lambda_{1}^{\alpha } + \lambda_{2}^{\alpha } + \lambda_{3}^{\alpha } - 3} \right) + \frac{1}{D}\left( {J - 1} \right)^{2}$$

(4)

where $\lambda_{i} \left( {i = 1,2,3} \right)$ are the principal stretches, $\mu$ indicates the shear modulus, D is a material constant related to the bulk modulus,$\alpha$ is a material constant, and J is the determinant of the deformation gradient tensor. By assuming incompressibility $\left( {J = 1} \right)$ for both fiber and ECM, the SEDF may be re-written for axon and the ECM as (5) and (6), respectively:

$$W_{\text{axon}} = \frac{{2\mu_{\text{axon}} }}{{\alpha_{\text{axon}}^{2} }} \left( {\lambda_{1}^{{\alpha_{\text{axon}} }} + \lambda_{2}^{{\alpha_{\text{axon}} }} + \lambda_{3}^{{\alpha_{\text{axon}} }} - 3} \right)$$

(5)

$$W_{\text{ECM}} = \frac{{2\mu_{\text{ECM}} }}{{\alpha_{\text{ECM}}^{2} }} \left( {\lambda_{1}^{{\alpha_{\text{ECM}} }} + \lambda_{2}^{{\alpha_{\text{ECM}} }} + \lambda_{3}^{{\alpha_{\text{ECM}} }} - 3} \right)$$

(6)

In addition, it has been shown that the material constant α is not sensitive to the test direction.29 Therefore, assuming α_Axon= α_ECM= α, three independent material constants, i.e., $\mu_{\text{axon}}$, $\mu_{\text{ECM}}$, and α, would be sufficient to characterize the hyperelastic properties of the white matter constituents.46

Moreover, it has been reported that the white matter exhibits viscoelastic behavior, mainly through its changing mechanical response at different strain rates.28,35,44 The rate dependent response of the tissue can be realized by defining the strain energy function in the form of a convolution integral.34,35 By using Prony series approximation, the time dependent shear relaxation moduli of the white matter constitutes, i.e., $\mu_{\text{axon}} \left( t \right)$ and $\mu_{\text{ECM}} \left( t \right)$, are described as in (7) and (8).18

$$\mu_{\text{axon}} \left( t \right) = \mu_{\text{axon}}^{0} \left[ { 1 - \mathop \sum \limits_{i = 1}^{M} g_{{i,{\text{axon}}}} \left( {1 - \exp \left( { - \frac{t}{{\tau_{{i,{\text{axon}}}} }}} \right)} \right)} \right]$$

(7)

$$\mu_{\text{ECM}} \left( t \right) = \mu_{\text{ECM}}^{0} \left[ { 1 - \mathop \sum \limits_{i = 1}^{M} g_{{i,{\text{ECM}}}} \left( {1 - \exp \left( { - \frac{t}{{\tau_{{i,{\text{ECM}}}} }}} \right)} \right)} \right]$$

(8)

where M is the number of terms in the Prony series, $g_{i}$ and $\tau_{i}$ are the material-dependent coefficients, and $\mu_{\text{axon}}^{0}$ and $\mu_{\text{ECM}}^{0}$ represent the instantaneous shear moduli of axon and ECM, respectively. For a two-term Prony series, one can define the instantaneous moduli in terms of the equilibrium moduli, i.e., $\mu_{\text{axon}}^{e}$ and $\mu_{\text{ECM}}^{e}$, and Prony constants, as in (9) and (10),

$$\mu_{\text{axon}}^{0} = \frac{{\mu_{\text{axon}}^{e} }}{{1 - \left( {g_{{1,{\text{axon}}}} + g_{{2,{\text{axon}}}} } \right)}}$$

(9)

$$\mu_{\text{ECM}}^{0} = \frac{{\mu_{\text{axon}}^{e} }}{{1 - \left( {g_{{1,{\text{ECM}}}} + g_{{2,{\text{ECM}}}} } \right)}}$$

(10)

where the equilibrium shear moduli of the axon and ECM are the same as those of the hyperelastic models, i.e., (5) and (6), under quasi-static loading. Therefore, having the equilibrium shear moduli from the hyperelastic models, a set of Prony constants, i.e., $g_{1}$, $g_{2}$, $\tau_{1}$, and $\tau_{2}$, is sufficient to characterize the viscoelastic properties of each of the axon and ECM.

Application of Embedded Element Technique

The embedded element technique was applied to the SVE and RVE models by superimposing the guest domain (axons) onto the host domain (ECM), creating independent grids, and coupling the translational degrees of freedom in the superimposed regions (Fig. 4). The stiffness redundancy of the models was corrected by subtracting the shear modulus of the ECM from that of the axons in the fiber domain,45 as (11):

$$\mu_{\text{axon}}^{*} = \mu_{\text{axon}} - \mu_{\text{ECM}}$$

(11)

where $\mu_{\text{axon}}^{*}$ is the corrected shear modulus for axonal tracts in the EET method. The axonal fibers were modeled by using 4-node tetrahedron linear hybrid elements (C3D10H in ABAQUS 6.14), and the ECM by 8-node linear brick hybrid elements (C3D8RH), considering the incompressibility assumption. The symmetricity of the mesh on the opposite nodes of the models was maintained by applying face partitioning for host and guest domains, separately.

Figure 4

Applying the EET method to the SVE: (a) superimposing the guest domain (axons) onto the host domain (ECM); (b) the mesh with independent grids for host and guest domains.

Application of Periodic Boundary Conditions

Periodic boundary conditions (PBC) were applied to enforce deformation and stress continuity within the models, by using a set of algebraic equations which equalized the deformations on the opposite faces of each of the SVE and RVE.17 Considering a deformation gradient field, $F_{ij}( i,j = 1,2,3)$, acting on the unit cell, the PBC were applied on each pair of nodes on two opposite faces of $S_{ + x}$ and $S_{ - x}$ perpendicular to the X-axis, as (12) to (14):

$$u_{{S_{ + x} }} - u_{{S_{ - x} }} - L\left( {F_{11} - 1} \right) = 0$$

(12)

$$v_{{S_{ + x} }} - v_{{S_{ - x} }} - {{L }}F_{12} = 0$$

(13)

$$w_{{S_{ + x} }} - w_{{S_{ - x} }} - {{L }}F_{13} = 0$$

(14)

where L is the characteristic length of the unit cell, and u, $v$, and $w$ represent the nodal displacements in X, Y and Z directions, respectively. By applying a similar approach, six equations were derived for edge nodes and nine equations for each corner node. The resulting constraints were applied to the models by using a custom Python script in ABAQUS 6.14-1. The application of the PBC was facilitated by the EET as the girds were independent in host and guest domains, providing identical elemental sizes, shapes, and distributions. The continuity of stress (traction boundary conditions) was verified by conducting a series of simulations which ensured the symmetry of stress contour on the opposite faces of the RVE and SVE models.14

Material Characterization

The hyperelastic constants of the axonal fibers and the ECM were found using a multi-objective optimization procedure. Assuming that the tissue is subjected to quasi-static large deformation in both axonal and transverse directions, simultaneously, the cost functions were defined as the deviations of the homogenized responses of the tissue and the experimental data in the axonal and transverse directions. The choice of two cost functions from two sets of experimental data (tests at two different directions) has proven to provide more precise results regarding the hyperelastic material model.23 An evolutionary optimization procedure, based on the imperialist competitive algorithm,3 was then used to search for the best hyperelastic material constants which minimized the cost functions.

The flowchart of the optimization procedure is shown in Fig. 11 in Appendix. The domain of the material parameters were set to $\mu_{\text{axon}} \in \left[ {100 2000} \right]$, $\mu_{\text{ECM}} \in \left[ {0 500} \right]$, and $\alpha \in \left[ {0 10} \right],$ considering the values reported in the literature.5,29,46 The algorithm was run with an assimilation coefficient of $\gamma = 0.3$ and the initial population of 100 sets of variables ($100 \times 3$ array), among which 10 of the most powerful solutions were selected as imperialists in the first decade (iteration), forming 10 initial empires. The cost functions, ${\text{CF}}_{\perp }$ and ${\text{CF}}_{\parallel }$, were formulated as the sum of the coefficient of determination (R²) and the root mean square error (RMSE) of stress values, between every two set of data points, to account for deviations of both the patterns and the values of the resulting curves from the experimental data, respectively, as (15) and (16):

$${\text{CF}}_{\parallel } = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {\frac{{S_{\parallel ,i}^{\text{Mod}} - S_{\parallel ,i}^{\text{Exp}} }}{{S_{\parallel ,i}^{\text{Exp}} }}} \right)^{2} } + \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {S_{\parallel ,i}^{\text{Mod}} - S_{\parallel ,i}^{\text{Exp}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {S_{\parallel ,i}^{\text{Exp}} - \overline{{S_{\parallel }^{\text{Exp}} }} } \right)^{2} }}$$

(15)

$${\text{CF}}_{\bot } = \sqrt {\frac{1}{N}\mathop \sum \limits_{{{\text{i}} = 1}}^{\text{N}} \left( {\frac{{S_{{\bot ,{\text{i}}}}^{\text{Mod}} - S_{{\bot ,{\text{i}}}}^{\text{Exp}} }}{{S_{{\bot ,{\text{i}}}}^{\text{Exp}} }}} \right)^{2} } + \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{N}} \left( {S_{{\bot ,{\text{i}}}}^{\text{Mod}} - S_{{\bot ,{\text{i}}}}^{\text{Exp}} } \right)^{2} }}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{N}} \left( {S_{{\bot ,{\text{i}}}}^{\text{Exp}} - \overline{{S_{\bot }^{\text{Exp}} }} } \right)^{2} }}$$

(16)

where ${\text{CF}}$ is the cost function, N in the number of data points in the stress curve,$S$ is the nominal stress, and the subscript indices $\parallel$ and $\bot$ stand for the axonal and transverse directions, respectively. The superscripts Mod and Exp stand for the corresponding values obtained by the models and the experiments, and I is the index of summation. The average stress of the experimental curve is described by (17):

$$\overline{{\sigma^{\text{Exp}} }} = \frac{{\sum\nolimits_{i = 1}^{N} {\sigma_{i}^{\text{Exp}} } }}{N}$$

(17)

The stop condition, yielding the optimal set of parameters, was defined as a single remaining empire with a total cost of $0 \le {\text{CF}}_{\parallel } , {\text{CF}}_{\perp } \le 0.2$. In this case, the resulting optimal parameters were checked to be within the pre-assumed initial range and the process was terminated. Otherwise, it continued to create a new set of parameters and the competitive algorithm was repeated until the stop condition was satisfied. In order to ensure that the global optimum solutions are achieved, a sensitivity analysis was conducted to verify the independence of the optimal solutions from the upper and lower bounds of the parameters.

A similar approach was adopted to optimize the viscoelastic material constants of each of the axon and ECM. The optimal hyperelastic constants from the previous optimization step were used as equilibrium moduli, and the algorithm searched for optimal Prony constants, i.e., $g_{1}$, $g_{2}$, $\tau_{1}$, and $\tau_{2}$. The domain of these constants were set to $g_{1} ,g_{2} \in \left[ {0 1} \right]$ and $\tau_{1} ,\tau_{2} \in \left[ {0 1000} \right]$ for both the axon and ECM constituents, considering the data reported in the literature.6,18,31 The cost functions were also defined similar to that of the hyperelastic characterization, i.e., (10) and (11), as the sum of R² and RMSE between every two sets of data points of the model-predicted and experimental relaxation curves.

Volume Averaging

In order to characterize the overall mechanical behaviors of the SVE and RVE, volume averaging of stresses and strains was performed by using an ABAQUS user subroutine which integrated the nodal stresses and strains over the volume of the unit cells.15 Equations (18) and (19) were used to estimate the volume-averaged values of the outputs17:

$$\bar{\sigma }_{ij} = \frac{1}{V}\mathop \smallint \limits_{V} \sigma_{ij} \left( {x,y,z} \right)dV$$

(18)

$$\bar{\varepsilon }_{ij} = \frac{1}{V}\mathop \smallint \limits_{V} \varepsilon_{ij} \left( {x,y,z} \right)dV$$

(19)

where V is the volume of the unit cell, $\bar{\sigma }_{ij}$ and $\bar{\varepsilon }_{ij}$ represent the volume-averaged values of the stress and strain, and $\sigma_{ij}$ and $\varepsilon_{ij}$ are average nodal stresses and strains, respectively.

Results

In order to examine the effect of the mesh size on the responses of the SVE and RVE models, they were subjected to a quasi-static extension of λ = 1.3 in the axonal direction (X-axis in Fig. 3) while changing the number of nodes from 3000 to 35,000, approximately. The axonal volume fraction of the models was set to $V_{\text{f}} \approx 50\%$ and their edge size to 6 μm. The overall tissue response was studied in terms of the homogenized stresses, computed based on the averaging method described in 2–7 sections (Fig. 5a). In addition, the localized responses were investigated in terms of the normalized maximum stress, i.e. σ_max/σ_ave as shown in Fig. 5b. The results indicated that both the local and overall tissue responses were almost independent from the grid when the elements were sufficiently fine. However, while the homogenized tissue responses converged for both models at almost 18,000 nodes, the local responses of the SVE were more sensitive to the grid size level; the normalized maximum stress σ_max/σ_ave within the SVE required a higher number of nodes (almost 27,000 nodes) to converge, while this measure flattened at 12,000 nodes for the RVE. Moreover, the SVE model converged to higher fractions of local stress than the RVE model ($\sigma_{ \hbox{max} } /\sigma_{\text{ave}} \approx 4$ compared to $\sigma_{ \hbox{max} } /\sigma_{\text{ave}} \approx 2$), while its homogenized Cauchy stress converged to relatively lower values (almost 10%). This behavior was not unexpected as the dispersion of axonal orientations in the guest domain caused a lower equivalent stiffness in the tissue along the X-axis. Based on the results, the RVE and SVE models were meshed using almost 18,000 and 27,000 nodes, respectively.

Figure 5

Sensitivity analysis of the overall and local responses of the RVE and SVE models for a hypothetical white matter structure with $V_{\text{f}} \approx 50\%$: (a, b) the effect of the grid size; (c, d) the effect of the edge length.

The minimum edge size was also investigated in a parametric study by subjecting the RVE and SVE models to the same loading conditions as in the mesh sensitivity analysis. While the mesh size of the RVE and SVE was fixed at the optimum, their lattice edge size was changed from 4 to 30 μm. The number of axons and the approximate volume fraction of the guest domain of the models are shown in Table 1. The effect of the edge size on the average stress and localized maximum/average stress are shown in Figs. 5c and 5d. As expected, the homogenized response of the RVE model was almost independent of the lattice edge size, with marginal local variations in the maximum stress. However, both the homogenized and local responses of the SVE model experienced considerable variations with the change of the edge length. The minimum acceptable edge length increased with the microstructural randomness level, demanding a larger SVE model (${\text{Edge size}} = 20 \mu {\text{m}}$) compared to the RVE model (${\text{Edge size}} = 12 \mu {\text{m}}$) to stabilize the tissue homogenized and local behaviors against the microstructural variations.

Table 1 The number of axons (N) and the estimated volume fraction (V_f) of 24 realizations of the RVE and SVE models for edge size sensitivity analysis.

The hyperelastic material properties of each of the axonal fibers and the ECM were characterized by fitting the homogenized response of the SVE and RVE models of corpus callosum to quasi-static axonal and transverse loading, onto the experimental results reported by Budday et al.5 The volume fraction was set to $V_{\text{f}} = 0.3$ for both models to represent the average volume fraction reported for the tissue, based on histological observations.22 The optimization procedure converged for the RVE and SVE models after 36 and 68 iterations with total runtimes of 2.1 and 6.5 h (for all iterations), respectively, on a PC with 8 CPUS and 12 GB of RAM. The optimal hyperelastic constants, as well as the ones proposed by some previous studies, are shown in Table 2. The corresponding values of the objective functions, ${\text{CF}}_{\perp }$ and ${\text{CF}}_{\parallel }$, are also depicted. A series of sensitivity analyses were conducted to ensure the independence of the converged values from the choice of the initial set of parameters, upper and lower bounds, and initial number of imperialists in the optimization algorithm. The response of the models are compared with the experimental data used in the optimization procedure41 in Figs. 6a and 6b.

Table 2 The optimal hyperelastic material constants of white matter constituents obtained for the RVE and SVE models of the present study compared with the values reported by two previous studies.

Figure 6

The overall responses of the RVE and SVE models of white matter structures to quasi-static extension in comparison with the experimental data in the literature: (a) corpus callosum in longitudinal direction; (b) corpus callosum in transverse direction; (c) corona radiata in longitudinal direction. The experimental data of (c) was not used in the characterization procedure.

In order to examine the validity of the hyperelastic SVE and RVE models and the corresponding material constants, the predictions for the mechanical behavior of another white matter structure, i.e., corona radiata, was compared with the experimental data in the literature. The volume fraction was set to $V_{\text{f}} = 35{{\% }}$, based on the SEM observations for corona radiata22 The homogenized responses of the models under quasi-static longitudinal extension were compared with the experimental results reported by Budday et al.5 (2017a), as shown in Fig. 6c. The results are indicated in terms of the nominal stress to match those of the experiments. There was a good agreement between the predicted and the experimental stress curves for corona radiata with normalized RMSEs less than 5 and 7% for the RVE and SVE models, respectively.

The validity of the characterized hyperelastic SVE and RVE models was further investigated by analyzing the mechanical response of the white matter structures to shear. The SVE and RVE models of corpus callosum, with $V_{\text{f}} = 30{{\% }},$ were subjected to quasi-static shear strains of 0 to 0.2 (small deformation regime) in YZ and XZ planes. The shear strains were applied to the models in the directions $\gamma_{32}$ and $\gamma_{31}$ where the first subscript denotes the normal vector of the face that is shifted by shear, and the second subscript denoted the direction that the face is shifted. The predicted homogenized shear stresses $\overline{{S_{32} }}$ and $\overline{{S_{31} }}$ are compared with the experimental data reported by Budday et al.6 in two simple shear modes in Fig. 7. The results indicated a considerable difference between the responses of the two models, with the SVE displaying a substantially better agreement with the experimental data in YZ-plane (Fig. 7a). Moreover, unlike the RVE model, the SVE model could well capture the higher stiffness of the tissue in the YZ-plane observed in the experiments.

Figure 7

The overall responses of the RVE and SVE models of corpus callosum to quasi-static shear strains in (a) YZ and (b) XZ planes compared with the experimental data not used in the characterization procedure.

The localized responses of the hyperelastic RVE and SVE models subject to 10% quasi-static longitudinal extension, are shown in Figs. 8a and 8b. The longitudinal extension caused a non-uniform distribution of local stresses in the SVE model, unlike the RVE, due to the probabilistic distribution and orientation of axonal fibers. The localized stresses predicted by the SVE model were almost two times higher than those of the RVE model. A similar behavior was observed for the localized responses of the models to 20% shear strain (Figs. 8c and 8d). The non-uniform pattern of the stress contours in the SVE model included higher stress concentrations around smaller axons, up to 3 times the average stress.

Figure 8

Deformed configurations and contour plots of stress distribution in axonal fibers and ECM: (a, b) normal stress in RVE and SVE models of corpus callosum subjected to 10% quasi-static longitudinal extension, respectively; (c, d) shear stress in RVE and SVE models of corpus callosum subjected to a 20% shear in the YZ plane, respectively (also displayed separately for host and guest domains). The stress is indicated in MPa.

The viscoelastic material properties of each of the axonal fibers and the ECM were characterized by fitting the homogenized response of the SVE and RVE models of corpus callosum to dynamic loading, onto the experimental relaxation curves reported by Budday et al.5 At each run, a sudden shear strain of $\gamma = 0.2$ was applied to each model in the XZ-plane and held for 100 s. The resulting homogenized shear stress response of the model was then compared to the experimental data to calculate the cost functions. The optimal hyperelastic constants from Table 1 were used as equilibrium moduli, and the algorithm searched for optimal Prony constants. The procedure converged after 36 and 42 iterations (with one single empire left) after a total runtime of 5.3 and 11 h and the final value of cost function 0.253 and 0.122 for the RVE and the SVE, respectively (Table 3). The change in the cost function was less than $10^{ - 7}$ in the last three iterations for both models. The relaxation time was reduced from 300 s (experimental curve) to 100 s to reduce the computational cost of the optimization procedure (Fig. 9). The resulting relaxation curves of the viscoelastic RVE and SVE models were within the standard deviations of the experimental curve, with the SVE displaying a better agreement with the experimental results.

Table 3 Optimal viscoelastic constants for microstructural constituents of the RVE and SVE models.

Figure 9

Optimized shear relaxation responses of the RVE and SVE models compared to the reference experimental curve.5

The validity of the characterized viscoelastic SVE and RVE models was investigated by analyzing the mechanical responses of two white matter structures to different loading rates. The characterized models of corpus callosum and corona radiata were subjected to 50% tensile strain in the main axonal direction at three strain rates of 0.5/s (low), 5/s (medium), and 30/s (high) and the resulting tensile stresses were compared with the experimental results reported by Jin et al.44 for the same structures. The model-predicted and experimental results in terms of the nominal tensile stress at 50% strain are compared in Fig. 10. Both the RVE and the SVE models overestimated the tissues’ responses at all strain rates, with the SVE model displaying a relatively better agreement with experimental results; the deviations of the RVE and SVE model predictions from the experimental results of corpus callosum and corona radiata were 49 and 54%, and 28 and 26%, respectively, in average (Fig. 10).

Figure 10

Average nominal stresses at 50% tensile strain predicted by the RVE and SVE models in comparison with the experimental data from Jin et al. at three strain rates for (a) corpus callosum (b) corona radiata.

Discussion

In order to understand the axonal injury mechanism of the white matter and determine the injury thresholds, it is necessary to develop sophisticated models of the tissue in which the detailed microstructure is considered. This study presented, for the first time, a statistical volume element model of the white matter structures, with histology-informed randomized architecture of the axonal tracts within the ECM. The previous micromechanical models of the white matter lack such detailed histology information; in the most detailed model so far46 only the variations in axon calibers was taken into account. Our more sophisticated hyper-viscoelastic micromechanical model enables capturing the homogenized mechanical behavior of the white matter structures in different loading rates and scenarios, i.e., extension and shear, and provides a more realistic presentation of the localized stresses within the tissue substructures to study the axonal damage mechanisms due to the DAI at the microscopic level.

The hyperelastic material constants obtained in our study for the axons and the ECM, by characterizing the histology-informed, i.e., SVE, model of the white matter structures, is considerably different from the ones suggested by previous studies (Table 2). In particular, the shear modulus of the axon was approximately three times the value proposed by Meany29 and 25% lower than that suggested by Yousefsani et al.46 However, this discrepancy is not surprising considering the insufficiencies involved in previous studies. First of all, most previous investigations have characterized the material properties of the axons and the ECM based on the experimental data from tests in a single (mostly axonal) direction.20,32 Such characterization has been reported to yield unrealistic results as the relatively large number of parameters make the problem redundant.23,45 As Latorre et al.23 concluded, the hyperelastic material model of fiber-reinforced biomaterials such as the human brain should not be characterized with tensile tests only; other tests (preferably in alternative directions) are also required.

Moreover, some authors20,32 have considered the shear modulus of ECM to be three times softer than axonal fibers, i.e. $\mu_{\text{ECM}} = \mu_{\text{axon}} /3$, based on the oscillatory shear test results of Arbogast and Margulies2 (1997). However, these experimental results are not applicable to large deformations and are limited to the small deformation regime. The results of our characterized SVE model (Table 2) suggest the ratio of the long-term (equilibrium) shear moduli to be $\mu_{\text{axon}} /\mu_{\text{ECM}} \approx 7.5$ which is between the ratio suggested by Yousefsani et al.46 i.e. $\mu_{\text{axon}} /\mu_{\text{ECM}} \approx 13$, and that reported by Meany (2003),29 i.e. $\mu_{\text{axon}} /\mu_{\text{ECM}} \approx 3$.

Finally, material characterization has been performed based on rather simplified micromechanical models of the white matter in previous studies. Most previous micromechanical models lacked histology information of any kind; they either used a straight single fiber embedded within the ECM,18 or a hexagonal arrangement of the aligned fibers.1 The rare histology-informed models, on the other hand, were based on insufficient histological data; they considered the statistical distribution of axonal fibers either for positions,1 or for calibers,45,46 neglecting the effects associated with the randomized fiber orientations. This is particularly important as previous studies42 have shown that the degree of injury that is predicted by a computational model of DAI is highly dependent on the incorporation of the axonal orientation information.

The results of our study indicate a good agreement between the homogenized responses of the characterized SVE and RVE models of the corona radiata and corpus callosum under quasi-static extension with the experimental data in the literature (Figs. 6c and 6d). Considering the fact that the experimental data of corona radiata (Fig. 6c) were not seen by our model (i.e. not used in the optimization of the hyperelastic constants), these results suggest that both the SVE and RVE micromechanical models provide good estimations for the mechanical behavior of the white matter under quasi-static extension. The results also suggest that the models can capture the effect of the axonal volume fraction on the mechanical response of the white matter structures; as Figs. 6a and 6c illustrate, the stress predicted for the corona radiata at the same stretch level is higher than that predicted for corpus callosum. This observation is in good agreement with the findings of experimental studies in the literature.6,44

Despite the similar response of the SVE and RVE models to quasi-static extension in the axonal direction, the homogenized response of the models to shear strain involved considerable deviations, with the former model displaying a significantly closer response to the experimental data under shear in the YZ-plane (Fig. 7). This result indicates that the performance of our histology-informed micromechanical model of the white matter is not limited to a specific loading scenario, unlike the RVE of this study and the previously published models. In fact, one might conclude that the hyperelastic micromechanical model of the white matter presented in this study is indeed valid, and the corresponding optimal material constants provide good estimations for the mechanical behavior of the tissue constituents under quasi-static loading.

The important effect of the randomized fiber orientations, implemented in this study, on the homogenized behavior of the white matter structures might be recognized more clearly if the results of our study are compared with those of the previous statistical models. For instance, Yousefsani et al.46 have validated their histology-informed RVE (based on non-uniform caliber distribution only) with the experimental data in extension and reported a good agreement. However, their optimal material properties are close to the data obtained in our study for the RVE, but not the SVE model (Table 2); their model would predict a homogenized response to shear strain similar to our RVE model, which demonstrates large deviations from the experimental results (Fig. 7). Considering the randomized orientations of axonal fibers within the ECM seems an essential requirement for the micromechanical models of the white matter in order to capture the actual mechanical behavior of the tissue in quasi-static extension and shear, simultaneously.

The results of this study for the localized responses of the white matter structures to quasi-static extension (Figs. 8a and 8b) and shear (Figs. 8c and 8d), indicate that they are affected greatly by the microstructure assumed for the tissue. The SVE model, with a randomized distribution of the axonal fibers’ positions, calibers and orientations, resulted in a highly fluctuating distribution of stresses, with substantially higher local stresses around axonal tracts with lower calibers. This observation is not surprising considering the larger localized stress concentration that are produced in the SVE model with a non-uniform axonal architecture, and suggest that such sophisticated model is critical for micromechanical modeling of the brain white matter when studying the axonal injury mechanism due to DAI.

The viscoelastic material constants obtained in our study for the axons and the ECM, by characterizing the RVE and SVE models, provided reasonably good agreement with the reference experimental data, particularly for the SVE (Fig. 9). Based on our results (Table 3), the instantaneous moduli are 5.5 to 6 times the equilibrium moduli for both the axons and the ECM. We could not find comparable data in the literature for human brain tissue. However, Javid et al.18 reported ratios of 3.3 and 4 times for the instantaneous and equilibrium moduli of the axons and the ECM of the porcine brain, respectively, which are in the same order of our results.

The characterized viscoelastic RVE and SVE models of the corpus callosum and corona radiata were validated against the experimental results reported by Jin et al.44 for the same structures (Fig. 10). In general, both models overestimated the homogenized responses of the tissues, particularly at high strain rates. However, the predictions of the SVE model were in better agreement with the experimental results (average deviation: 27%) in comparison with those of the RVE model (average deviation: 52%). In fact, for almost all six cases we studied, the SVE model responses lay within the standard deviation of the experimental data (Fig. 10), which suggests that the SVE model can provide a reasonably good representation of the viscoelastic behavior of the brain white matter structures. Moreover, the SVE model predicted the homogenized stress in the corona radiata to be 2 and 49% higher than corpus callosum at 0.5/s and 30/s, respectively. This prediction is consistent with the previous observations that the heterogeneity of mechanical properties between regions are most apparent at the shorter time frames, i.e. for rapid events rather than slower crushing head injuries,34 and provides a further evidence for the validity of the SVE model. Nevertheless, it should be noted that Jin et al.44 performed their experiments in two axonal and transverse directions and reported no clear directional dependence, which is inconsistent with the findings of more recent studies.6

There are some limitations in the current study that need to be addressed in future investigations. First of all, we assumed periodicity and ergodicity characteristics for the microstructure of the specific structures of the white matter studied, i.e. corpus callosum and corona radiata. While the axonal architecture is considered to be more or less unchanging in different regions of each of these structures, a more sophisticated model might consider the heterogeneity of the axonal fiber arrangements in more details. In particular, we applied the main eigenvector of DTI and CDF of orientations of DTI voxels to the SVE, while the latter represents the fiber bundles orientation in the macroscopic level. More specific and detailed micromechanical models of the white matter structures might use the fiber orientation distribution data obtained from advanced diffusion MRI, such as multi-shell multi-directions diffusion, to represent the axon orientation distribution in the microscopic level. In addition, the ECM may be considered as a heterogeneous microstructure by itself, considering its constituents of glial cells and lipid tissue veined with capillaries.

Furthermore, we used the corrected embedded element technique to account for the stiffness redundancy at the locations where the matrix and fibers overlap. However, when coupled to macroscale models and subjected to body force accelerations, the mass redundancy of the model might be also important and need correction. In such multi-scale framework, the external loading on the head is used as the initial conditions for the macro-mechanical model and the predicted deformation gradient tensor at each material point provides the periodic boundary conditions for the corresponding SVE/RVE of the micromechanical model for detailed analysis of the injury pathways.8,12,21 Finally, in this study we focused on the tensile and shear behaviors of the white matter structures, considering the fact the axonal damage and rupture, as a result of DAI, are often associated with the tensile and shear loads, as the prevailing modes of failure in the tissue’s microstructure. In such loading conditions, the ratio of the tensile stress (maximum principal stress) to the compressive stress (pressure) is more than 1000, neglecting the effect of compressive mechanical behavior of the tissue on the results. For a more generalized model of the white matter structures, the tensile-compressive switch behavior of the axonal tracts might be considered by using the tension-compression asymmetry in OGDEN30 or Holzapfel16 material models.

Appendix

The flowchart of the optimization procedure is shown in Fig. 11.

Figure 11

Flowchart of the optimization procedure, based on the imperial competitive algorithm. $\mu_{\text{axon}} , \mu_{\text{ECM}},$ α are material constants of OGDEN hyperelastic model. Also, ${\text{CF}}_{\perp}$ and ${\text{CF}}_{\parallel }$ stand for the cost functions defined as the deviations of the model and experimental responses in the transverse and axonal directions, respectively.