Isogeometric analysis of multi-patch solid-shells in large deformation

Abstract

In the context of isogeometric analysis (IGA) of shell structures, the popularity of the solid-shell elements benefit from formulation simplicity and full 3D stress state. However some basic questions remain unresolved when using solid-shell element, especially for large deformation cases with patch coupling, which is a common scene in real-life simulations. In this research, after introduction of the solid-shell nonlinear formulation and a fundamental 3D model construction method, we present a non-symmetric variant of the standard Nitsche’s formulation for multi-patch coupling in association with an empirical formula for its stabilization parameter. An selective and reduced integration scheme is also presented to address the locking syndrome. In addition, the quasi-Newton iteration format is derived as solver, together with a step length control method. The second order derivatives are totally neglected by the adoption of the non-symmetric Nitsche’s formulation and the quasi-Newton solver. The solid-shell elements are numerically studied by a linear elastic plate example, then we demonstrate the performance of the proposed formulation in large deformation, in terms of result verification, iteration history and continuity of displacement across the coupling interface.

Graphic Abstract

In the context of isogeometric analysis (IGA), after introduction of the solid-shell nonlinear formulation and a fundamental 3D model construction method, we present a non-symmetric variant of the standard Nitsche’s formulation for multi-patch coupling in association with an empirical formula for its stabilization parameter. An selective and reduced integration scheme is also introduced to address the locking syndrome. In addition, the quasi-Newton iteration format is derived as solver, together with a step length control method. The second order derivatives are totally neglected by the adoption of the non-symmetric Nitsche’s formulation and the quasi-Newton solver. The performance of the proposed formulation in large deformation is demonstrated by several examples.

1 Introduction

Shell structure plays an important role in industry, biomechanics (e.g. heart valve [1]), architecture and various kinds of daily products. Finite element method (FEM) based shell elements are necessary in structural simulations [2, 3]. However corresponding elements are usually derived from shell theories, e.g. Kirchhoff-Love theory for thin shells and Reissner-Mindlin theory for thick shells, due to the fact that the shell thickness dimension is much smaller than the other two dimensions of the shell mid-surface. Meshing the shell model by 3D solid blocks and calculating by 3D solid elements seems to be an alternative way, however using solid elements for thin shells is highly restricted to limited computational resources. In cases of thin or mid-thick shells, there should be sufficient elements along the thickness direction to capture the mechanical behavior, and the element length ratio should be close to one in order to keep good element performance. In FEM achieving simultaneously both requirements mentioned above would increase the computational effort heavily [4].

With the introduction of isogeometric analysis (IGA) by Hughes et al. in 2005  [5], both a seamless integration between the computer-aided design (CAD) and the analysis as well as a systematic construction of high-order basis functions become possible within a single robust paradigm [6], Kirchhoff-Love shell element and Reissner-Mindlin shell element are developed rapidly and applied widely in this framework. However, there exist several drawbacks of the shell elements.

• (1) The 3D shell structure is modeled by its mid-surface, which explains the name “degenerated shell”. According to the shell kinematics definition, the 3D displacement field is reconstructed by the nodal displacement degrees of freedom (DoFs), nodal rotational DoFs and outward normal vectors attached to the mid-surface nodes (control points) [7]. The nonlinear formulation together with, e.g. patch coupling [8] or contact problems, becomes complex due to the need of special treatment of the field reconstruction process.

• (2) The need of patch coupling raises naturally from the fact that shell structures are usually made upon multiple parts of CAD models in realistic scenarios. The Mortar method [9, 10], Nitsche’s method [11] and unfitted method [12] are widely adopted, however for patch coupling of a shell structure with different type of structures, the evaluation of the interfacial integrals would increase computational complexity. For example, in order to couple one shell mid-surface with another 3D solid structure, we need to determinate Gauss points for both sides of the coupling interfaces [13].

• (3) These shell-theory based elements depend on the degenerated representation of a shell into its mid-surface, the transverse stress (i.e. stress through the thickness direction) is neglected according to the plane stress assumption [14], or in other explanation, the strain energy corresponding to the stress perpendicular to the mid-surface is ignored to improve numerical conditioning [15]. This makes the elements inapplicable for contact simulations.

In the present research, we adopt the solid-shell elements, which are simply 3D solid elements, to simulate shell structures. As said by Bischoff et. al [16]: “Owing to increasing computer capacity on the one hand and higher demands in practice on the other hand, a strong indication to go three-dimensional can be currently recognized. In other words, even thin-walled structures are simulated by three-dimensional solid-type elements, allowing inclusion of higher-order effects not represented by classical theories for thin-walled structures”. The idea was originally proposed in 1998 by Hauptmann and Schweizerhof [17], where the usage of the solid-shell elements in traditional FEM was systematically studied. In some applications such as [18, 19] similar solid-like shell elements that derived from 3D continuum mechanics were adopted. In the framework of IGA, solid-shell elements and locking phenomenon were studied in [20,21,22,23]. Generally, the solid-shell elements have the following potential advantages.

• (1) Containing only displacement DoFs, the nonlinear formulation of the solid-shell elements is rather simple as classical solid elements.

• (2) The shell structure is modeled by 3D solids, making the patch coupling treatment straightforward.

• (3) No plane stress assumption is made, the deformation behavior through the thickness direction is treated the same as the other two directions, the solid-shell elements are capable to present complete 3D stress state, and thus are potentially suitable for contract problems [24].

However, before putting solid-shell elements into actual usage, we believe that several aspects of solid-shell elements in IGA need to be further studied. Firstly, the performance of the elements needs to be systematically studied, especially for the treatment of locking phenomena when one computes thin shells. Regarding the nonlinear formulation of solid-shell elements, effective and efficient multi-patch coupling formulation and its iterative format are still required. In this paper, we briefly introduce the nonlinear solid-shell element formulation in Sect. 2, then propose a simple way to generate the 3D-solid model from a shell mid-surface in Sect. 3. The Nitsche method for patch coupling, isogeometric discretion, and quasi-Newton solver are adopted in Sect. 4. In Sect. 5, fundamental questions of sold-shell elements are studied by a single patch plate problem in linear elasticity. Several numerical studies in Sect. 6 are carried out to illustrate the performance of the solid-shell elements. Conclusions are given in Sect. 7.

2 Brief introduction on solid-shell element formulation

Denote the initial configuration of a shell structure as $\varOmega$. One material point $\mathbf {X}$ on reference configuration $\varOmega$ is related to one material point $\mathbf {x}$ on current configuration through the mapping $\varvec{\varphi }$. The displacement is then the change between two frames

$$\begin{aligned} \mathbf {x} = \varvec{\varphi }(\mathbf {X}) = \mathbf {X} + \mathbf {u}(\mathbf {X}). \end{aligned}$$

(1)

The deformation gradient is derived as

$$\begin{aligned} {\mathbf {F}}({\mathbf {u}}) = {\nabla }_{\mathbf {X}} ({\mathbf {x}}) = {\mathbf {I}} + {\nabla }_{\mathbf {X}} ({\mathbf {u}}), \end{aligned}$$

(2)

where ${\nabla }_\mathbf{X }$ denotes the gradient in the initial configuration. Consider the Total-Lagrange formulation, the Green strain tensor is given as

$$\begin{aligned} {\mathbf {E}} = \frac{1}{2}({\mathbf {F}}^\mathrm{T} {\mathbf {F}} - {\mathbf {I}}) = \frac{1}{2} ( {\nabla }_{\mathbf {X}} {\mathbf {u}} + {\nabla }_{\mathbf {X}}^\mathrm{T} {\mathbf {u}} + {\nabla }_{\mathbf {X}}^\mathrm{T} \mathbf {u} \, {\nabla }_{\mathbf {X}} {\mathbf {u}} ). \end{aligned}$$

(3)

It should be noted that the idea of solid-shell elements simply consists in using 3D solid elements to simulate plates and shells, thus no plane stress assumption is made herein.

For hyperelastic material considered in this research, the second Piola-Kirchhoff (PK2) stress is computed by

$$\begin{aligned} \mathbf {S} = \frac{\partial W(\mathbf {E})}{\mathbf {E}}, \end{aligned}$$

(4)

where $W(\mathbf {E})$ is the strain energy density. Particularly we consider the St. Venant-Kirchhoff material, then

$$\begin{aligned} \begin{aligned} W(\mathbf {E})&= \frac{1}{2} \, \mathbf {E} : \mathbf {D} : \mathbf {E}, \\ \mathbf {S}&= \mathbf {D} : \mathbf {E}, \end{aligned} \end{aligned}$$

(5)

in which $\mathbf {D}$ is the constitutive tensor of isotropic material. The potential energy is written as

$$\begin{aligned} \varPi (\mathbf {u}) = \int _{\varOmega } W(\mathbf {E}) \, \mathrm{d}X - \varPi ^{\text {ext}}, \end{aligned}$$

(6)

in which $\varPi ^{\text {ext}}$ is the potential for the external work, made by the body force, traction force or gravity force for instance.

Define the directional derivative of a quantity A (with respect to $\mathbf {u}$) in direction $\delta \mathbf {u}$ as

$$\begin{aligned} \mathcal {D}A(\mathbf {u})[\delta \mathbf {u}] = \lim _{\epsilon \rightarrow 0} \frac{A(\mathbf {u}+\epsilon \delta \mathbf {u})-A(\mathbf {u})}{\epsilon }, \end{aligned}$$

(7)

then the weak formulation reads

$$\begin{aligned} \mathcal {D}\varPi (\mathbf {u})[\delta \mathbf {u}] = 0. \end{aligned}$$

(8)

Note that the Dirichlet conditions are omitted for simplification. More details can be found in Chapter 5 of Ref. [25], and Chapter 3 of Ref. [26], in spite of some differences between shape functions adopted in IGA and in FEM.

3 Construct a 3D solid model from a shell mid-surface

Fig. 1

Degenerated shell geometry description. The full 3D shell is constructed by its mid-surface $\mathbf {S}(\xi ,\eta )$ and thickness t along the mid-surface normal $\mathbf {n}$

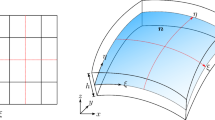
The simulation of a shell usually begins from its mid-surface sketch. In IGA framework, leveranging the superiority of non-uniform rational B-splines (NURBS) in drawing curved surfaces, the shell mid-surface is natually represented as shown in Fig. 1. The mid-surface is generated by tensor product of two sets of NURBS basis functions $R_{i,p}$ and $R_{j,q}$, and corresponding control points $\mathbf{P} ^{\text {mid}}_{ij}$ as [27]

$$\begin{aligned} \mathbf {S}^{\text {mid}}(\xi ,\eta ) = \sum _{i=1}^n \sum _{j=1}^m R_{i,p}(\xi ) R_{j,q}(\eta ) \mathbf{P} ^{\text {mid}}_{ij}. \end{aligned}$$

(9)

Define the Greville abscissae [28] in parametric space of the mid-surface as $(\bar{\xi }_i,\bar{\eta }_j)$, where

$$\begin{aligned} \bar{\xi }_i = \frac{\xi _{i+1}+\ldots +\xi _{i+p}}{p}, \quad \bar{\eta }_j = \frac{\eta _{j+1}+\ldots +\eta _{j+q}}{q}, \end{aligned}$$

(10)

and they typically give a stable interpolation [29]. According to the assumption that the distance between the top-surface and the mid-surface along the normal direction is half of the thickness t, we have

$$\begin{aligned} \big \Vert \mathbf {S}^{\text {top}}(\bar{\xi }_i,\bar{\eta }_j) - \mathbf {S}^{\text {mid}}(\bar{\xi }_i,\bar{\eta }_j)\big \Vert = \frac{t}{2}, \end{aligned}$$

(11)

additionally let $\mathbf {n}=(\mathbf {n}_x,\mathbf {n}_y,\mathbf {n}_z )^\mathrm{T}$ be the normalized outward normal vector at point $(\bar{\xi }_i,\bar{\eta }_j)$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {S}^{\text {top}}_x(\bar{\xi }_i,\bar{\eta }_j) - \mathbf {S}^{\text {mid}}_x(\bar{\xi }_i,\bar{\eta }_j) = \frac{t}{2}\mathbf {n}_x(\bar{\xi }_i,\bar{\eta }_j), \\ \mathbf {S}^{\text {top}}_y(\bar{\xi }_i,\bar{\eta }_j) - \mathbf {S}^{\text {mid}}_y(\bar{\xi }_i,\bar{\eta }_j) = \frac{t}{2}\mathbf {n}_y(\bar{\xi }_i,\bar{\eta }_j), \\ \mathbf {S}^{\text {top}}_z(\bar{\xi }_i,\bar{\eta }_j) - \mathbf {S}^{\text {mid}}_z(\bar{\xi }_i,\bar{\eta }_j) = \frac{t}{2}\mathbf {n}_z(\bar{\xi }_i,\bar{\eta }_j). \end{array}\right. } \end{aligned}$$

(12)

In this way we arrive at a system of linear equations by collocating at $(\bar{\xi }_i,\bar{\eta }_j)$, and then we solve for $\mathbf {P}^{\text {bot}}$. Control points for the bot-surface are obtained by the fact that $\mathbf {P}^{\text {mid}} = (\mathbf {P}^{\text {top}}+\mathbf {P}^{\text {bot}}) / 2$. This procedure is illustrated in Fig. 2.

Fig. 2

Distance between Greville points (blue cross) on the top-surface and the mid-surface is t/2. Then the control points on the top-surface are obtained by a system of linear equations

The 3D solid representation needs a set of B-spline basis functions along the thickness, denoted by $N(\zeta )$. As a starting point the $N(\zeta )$ is built as simple as possible, later algorithms could be adopted to insert knots or elevate orders. To generate $N(\zeta )$ the knot vector is set to be

$$\begin{aligned}{}[0,0,0,1,1,1], \end{aligned}$$

(13)

implying that $N_{k,r}$ with $k=1,2,3$ and order $r=2$. Then we perform a tensor product using the basis functions for the mid-surface $R(\xi ), R(\eta )$ and for the thickness $N(\zeta )$, and corresponding control points as

$$\begin{aligned} \mathbf {S}(\xi ,\eta ,\zeta ) = \sum _{i=1}^n \sum _{j=1}^m \sum _{k=1}^z R_{i,p}(\xi ) R_{j,q}(\eta ) N_{k,r}(\zeta ) \mathbf{P} _{ijk}, \end{aligned}$$

(14)

see Fig. 3 for illustration.

Fig. 3

Full 3D solid-shell representation. The solid model is generated by the help of the basis functions along the thickness direction, $N(\zeta )$, and corresponding control points

To transfer the mid-surface to 3D solid representation, the thickness t of the shell is needed, however for simplicity, in the present study we assume that the shell thickness t is constant. For a shell with a non-constant thickness function $t(\xi ,\eta )$, the method presented above would still work if sufficient number of sampling points are used. In addition, the presented study could treat the trimmed features by solving an additional linear equations correspond to the trimmed curves on the shell mid-surfaces. Such extension will be considered for further investigation.

4 Isogeometric multi-patch treatment and quasi-Newton solver

The Nitsche’s method was originally proposed in order to imply displacement boundary conditions [30]. In the context of IGA, its applications cover a wide range of boundary conditions implementation as well as domain decomposition problems and contact problems. Apostolatos et al. [31] did a comparison among the popular coupling methods and the results indicated the Nitsche type formulation is robust. Nguyen et.al. [13] employed the Nitsche’s method to couple 2D and 3D patches in linear elasticity. Guo and Ruess [32] used the Nitsche’s method to glue Kirchhoff-Love shell models and blended shell models, their further research [33] introduced the parameter-free non-symmetric Nitsche’s formulation for thin shells even with trimmed features by the finite cell method (FCM), the choice of the element-wise stabilization parameter was also discussed. In Ref. [34], Guo et al. extended the above techniques to real applications for Kirchhoff-Love shells by the STEP exchange format, the linearization process are given in the Newton-like form and some derivatives are given in appendix therein. Hu et.al. [11] proposed a general Nitsche’s framework to cover a various kinds of formulation variants and applications. Du et.al. [35] put the Nitsche’s method into hyperelastic applications and used the classical Newton-Raphson method to perform the linearization process. In this section, the Nitsche’s method is simply adopted as a patch coupling technique, except for a new empirical formula for the stabilization parameter. Moreover, we adopt the quasi-Newton method, together with other techniques, as the solver to avoid the linearization and more importantly, to avoid all the second order derivatives when considering the non-symmetric variant of the Nitsche’s formulation, and finally achieve a fully linearization-free formulation.

4.1 Non-symmetric Nitsche’s formulation for multi-patch coupling

Assume the initial domain $\varOmega$ is decomposed into two sub-domains $\varOmega ^m$, with the superscript $m=1,2$ indicating the corresponding variables on $\varOmega ^1$ and $\varOmega ^2$ respectively. The Nitsche’s method adds the coupling energy into the weak form of the problem [11]. Based on the single-patch formulation in Eq. (8), we have

$$\begin{aligned} \mathcal {D}\varPi (\mathbf {u})[\delta \mathbf {u}] + \text {Nitsche contribution} = 0, \end{aligned}$$

(15)

in which, the Nitsche’s contribution for multi-patch coupling is inserted as an energy-conjugate pair, made upon of displacement gap $\llbracket \mathbf {u} \rrbracket = \mathbf {u}^{1}-\mathbf {u}^{2}$ and average traction force $\langle \mathbf {P}(\mathbf {u}) \rangle = \left[ \mathbf {P}(\mathbf {u}^1) -\mathbf {P}(\mathbf {u}^2) \right] /2$ along the coupling interface $\varGamma _c$ between $\varOmega ^1$ and $\varOmega ^2$. $\mathbf {P}$ stands for the first Piola-Kirchhoff (PK1) stress and $\mathbf{N }$ is the outward normal to $\varGamma _c$. Then the modified weak form reads

$$\begin{aligned} \begin{aligned}&\int _{\varOmega } \mathbf {S} : \mathcal {D} \mathbf {E} [\delta \mathbf {u}] \, \mathrm{d}X - \int _{\varGamma _c} \llbracket \delta \mathbf {u} \rrbracket \cdot \langle \mathbf {P}(\mathbf {u}) \rangle \cdot \mathbf {N}^1 \,\mathrm{d}S \\&\qquad \qquad - \theta \int _{\varGamma _c} \llbracket \mathbf {u} \rrbracket \cdot \langle \mathbf {P}(\delta \mathbf {u}) \rangle \cdot \mathbf {N}^1 \,\mathrm{d}S + \int _{\varGamma _c} \gamma \llbracket \delta \mathbf {u} \rrbracket \cdot \llbracket \mathbf {u} \rrbracket \,\mathrm{d}S \\&\quad = \mathbf {f}^{\text {ext}} , \end{aligned} \end{aligned}$$

(16)

in which $\mathbf {f}^{\text {ext}} = \mathcal {D} \varPi ^{\text {ext}} [\delta \mathbf {u}]$ stands for the external force vector, $\theta$ is the Nitsche parameter, $\gamma$ is the stabilization parameter and it is normally required to be a large number.

The Nitsche parameter $\theta$ acts as a controller of system matrix symmetry and dependency on $\gamma$ [11]. When $\theta =1$, the standard Nitsche’s formulation is recovered, the obtained stiffness matrix is symmetric, and usually the stabilization parameter $\gamma$ is estimated by a generalized eigenvalue problem of the coupled interfaces [32], or a couple of generalized eigenvalue problems defined element-wise along the coupled interfaces [33]. This could be time-consuming especially for nonlinear problems that need iterations with configuration changing. When $\theta =-1$, we get the so-called skew-symmetric formulation, one remarkable advantage is that the formulation is parameter-free for linear boundary conditions and has less dependency on $\gamma$ for nonlinear boundary conditions. For simplicity we adopt $\theta =0$, in this way the third term of Eq. (16) is neglected, and the directional derivative of $\mathbf {P}$ is also dropped, therefore it finally leads to a non-symmetric formulation.

4.2 Isogeometric discretization

Assuming that, by the help of the method illustrated in Sect. 3, we generate a full-3D solid model from its mid-surface description as

$$\begin{aligned} \begin{aligned} \mathbf {S}(\xi ,\eta ,\zeta )&= \sum _{i=1}^n \sum _{j=1}^m \sum _{k=1}^z R_{i,p}(\xi ) R_{j,q}(\eta ) N_{k,r}(\zeta ) \mathbf{P} _{ijk} \\&= \sum _a R_a \mathbf {P}^a. \end{aligned} \end{aligned}$$

(17)

Define h as the mesh size associated to this parametrization, then similarly as above, we approximate the displacement field by

$$\begin{aligned} \mathbf {u}^h(\xi ,\eta ,\zeta ) = \sum _a R_a \mathbf {u}^a, \end{aligned}$$

(18)

where $\mathbf {u}^a=(u_x^a, u_y^a, u_z^a)^\mathrm{T}$ is the displacement vector attached to each control point $\mathbf {P}^a$. Taking the IGA approximation into the system leads to a non-linear formulation (with respect to displacement $\mathbf {u}^h$), which needs to be iteratively solved in Sect. 4.3.

We calculate the stabilization parameter $\gamma$, inspired by Refs. [36, 37], with a little modification of the Gismo implementation in Ref. [38] by multiplying the Young’s modulus E

$$\begin{aligned} \gamma = 4E(p+1)(p+d)\left( \frac{1}{h_1}+\frac{1}{h_2}\right) , \end{aligned}$$

(19)

where p is the maximum order of basis functions, d denotes the domain dimension, and $h_1$ and $h_2$ are mesh sizes of elements on both sides of the interface $\varGamma _c$. To our experience, this stabilization parameter plays an important role not only for stiffness matrix conditioning, but also for coupling conditions applying. It should be large enough for initialization, in order to effectively glue patches, then the self-correcting property of the quasi-Newton iterations, which will be introduced below, can lead this large number to a proper value. Otherwise, if the parameter $\gamma$ is not large enough at first, the system will be easier to converge but the interface cannot be glued tightly.

4.3 Quasi-Newton solver

Firstly let us briefly review the classical Newton-Raphson solver. Following the Newton-Raphson format, the linearization of a nonlinear IGA formulation [39] reads

$$\begin{aligned} \mathcal {D}^2\varPi (\mathbf {u}^h)[\delta \mathbf {u}^h, \varDelta \mathbf {u}^h] = -\mathcal {D}\varPi (\mathbf {u}^h)[\delta \mathbf {u}^h], \end{aligned}$$

(20)

where $\mathcal {D}\varPi (\mathbf {u}^h)[\delta \mathbf {u}^h]$ (respectively $\mathcal {D}^2\varPi (\mathbf {u}^h)[\delta \mathbf {u}^h, \varDelta \mathbf {u}^h]$) is the first (respectively second) order directional derivative of $\varPi (\mathbf {u}^h)$. Therefore the linearization of the multi-patch IGA formulation is derived as

$$\begin{aligned} \begin{aligned}&\int _{\varOmega } \mathcal {D} \mathbf {S} [\varDelta \mathbf {u}^h] : \mathcal {D} \mathbf {E} [\delta \mathbf {u}] \, \mathrm{d}X + \int _{\varOmega } \mathbf {S} : \mathcal {D}^2 \mathbf {E} [\delta \mathbf {u}^h, \varDelta \mathbf {u}^h] \, \mathrm{d}X \\&\qquad \quad - \int _{\varGamma _c} \llbracket \delta \mathbf {u} \rrbracket \cdot \langle \mathbf {P}(\varDelta \mathbf {u}^h) \rangle {\cdot } \varvec{N}^1 \,\mathrm{d}S {+} \gamma \int _{\varGamma _c} \llbracket \delta \mathbf {u}^h \rrbracket \cdot \llbracket \varDelta \mathbf {u}^h \rrbracket \,\mathrm{d}S \\&\quad = \; \mathbf {f}^{\text {ext}} -\int _{\varOmega } \mathbf {S} : \mathcal {D} \mathbf {E} [\delta \mathbf {u}] \, \mathrm{d}X + \int _{\varGamma _c} \llbracket \delta \mathbf {u}^h \rrbracket \cdot \langle \mathbf {P}(\mathbf {u}^h) \rangle \cdot \mathbf {N}^1 \,\mathrm{d}S \\&\qquad \quad - \gamma \int _{\varGamma _c} \llbracket \delta \mathbf {u}^h \rrbracket \cdot \llbracket \mathbf {u}^h \rrbracket \,\mathrm{d}S . \end{aligned} \end{aligned}$$

(21)

In general the tangent system can be summarized as

$$\begin{aligned} \mathbf {K}_T(\mathbf {u}_i) \cdot \varDelta \mathbf {u}_{i+1}= \mathbf {R}(\mathbf {u}_i), \end{aligned}$$

(22)

where $\mathbf {K}_T$ stands for the tangent stiffness matrix, residual $\mathbf {R}$ denotes the unbalanced force vector. In each iteration we solve the above tangent system then update the solution by $\mathbf {u}_{i+1} = \mathbf {u}_i + \varDelta \mathbf {u}_{i+1}$.

However, the Newton-Raphson solver for Nitsche formulation of large deformation problem requires additional improvements for sold-shell elements. Infact, from numerical experiment, the following issues are observed.

• (1) The Newton-Raphson solver needs to linearize the nonlinear system, as shown in Eq. (21), this is complex in formulation derivation and code implementation, especially after the introduction of the Nitsche’s method [8].

• (2) In each iteration we need to solve the linearized system (see Eq. (22)), which is time consuming no matter using iterative nor direct solvers.

• (3) From our experience the solid-shell formulation solving by the Newton-Raphson solver is sometimes difficult to converge, especially in cases of thin shells. This is also noticed in commercial FEM software ABAQUS with the error “too many attempts made for this increment”.

In discontinuous Galerkin (DG) method [40, 41] , regarding Eq.(16), (a) the 3rd term is dropped because this term is only used for symmetrizing the system but has no effect on consistency, and (b) the second order derivative of the 2nd term (i.e. the 3rd term in Eq. (21)) is neglected to save computational effort, because it is small compared to the stabilized jump term. By the above two simplifications the derivatives of $\mathbf {P}$ are avoided. The Nitsche’s formulation can be simplified in a similar way.

In our implementation, we adopt the quasi-Newton solver, which uses the similar tangent system structure as the Newton-Raphson solver but with an approximated tangent stiffness matrix $\tilde{\mathbf {K}}$,

$$\begin{aligned} \tilde{\mathbf {K}} (\mathbf {u}_i) \cdot \varDelta \mathbf {u}^h_{i+1}= \mathbf {R}(\mathbf {u}_i), \end{aligned}$$

(23)

and it is initialized by

$$\begin{aligned} \begin{aligned}&\tilde{\mathbf {K}}_0 = s \cdot \mathbf {K}_{linear} = s \cdot ( \int _{\varOmega } \varvec{\sigma } : \mathcal {D} \varvec{\varepsilon } [\delta \mathbf {u}] \, \mathrm{d}X \\&\qquad \quad - \int _{\varGamma _c} \delta \mathbf {u} \cdot \langle \varvec{\sigma }(\mathbf {u}) \rangle \cdot \mathbf {N}^1 \,\mathrm{d}S + \int _{\varGamma _c} \gamma \delta \mathbf {u} \cdot \mathbf {u} \,\mathrm{d}S ), \end{aligned} \end{aligned}$$

(24)

in which s is a scaling factor, which is recommended to be $s=16$ due to the fact that in a large deformation problem the geometry deformation, rather than the structure deformation, may dominate and absorb too much energy, and the model behaves more rigid than in the linear case. Then we recover the linear stiffness by setting the max step length as $s_a<s_{max}=16$.

Next, the inverse of $\tilde{\mathbf {K}}$ is directly updated by the Broyden-Fletcher-Goldfarb-Shanno (BFGS) formula. The quasi-Newton solver algorithm is outlined in Algorithm 1, and the Illinois algorithm for line search is outlined in Algorithm 2, from which the following features of the solver are addressed.

• (1) The quasi-Newton solver only needs to evaluate the right-hand-side residual vector $\mathbf {R}(\mathbf {u}^h)$, no need to linearize the formulation.

• (2) The approximated tangent stiffness matrix $\tilde{\mathbf {K}}$ is initialized by the linear elasticity problem, then the BFGS formula, which is believed to have self-correcting property, allows us to directly update the inverse of $\tilde{\mathbf {K}}$.

• (3) With the step length control [42] and stability check [43], the solver behaves more tolerance w.r.t. the shell thickness and element length ratio.

It is worth mention that, after using the non-symmetric Nitsche’s formulation, the obtained stiffness matrix becomes non-symmetric. Indeed, this is a drawback of the proposed method, compared to the standard and symmetric Nitsche one, in terms of matrix storage and matrix equation solving. It may take more computer resources and computational effort. However, by the help of the quasi-Newton method, the drawback coming from the non-symmetric Nitsche’s formulation is almost avoided: once the inverse of the non-symmetric stiffness matrix is calculated in the quasi-Newton initialization step, for the rest steps only matrix multiplications are required. Theoretically, the quasi-Newton solver could achieve superlinear convergence, compared to (local) quadratic convergence of the Newton-Raphson solver, which means the quasi-Newton method usually needs more iterations to converge, yet quasi-Newton iterations are distinctly less expensive: the cost per Newton-Raphson iteration is $O(n^3)$ plus computing the tangent stiffness matrix by second-order derivatives, while the cost per quasi-Newton is only $O(n^2)$. Moreover, although not used in this research, the so-called limited-memory BFGS (L-BFGS) method [44] could be further adopted to save computer storage.

5 Numerical study of solid-shell elements in linear elasticity

Fig. 4

Plate model subjected to uniform pressure $p_z$, only 1/4 plate is modeled

Before calculating numerical examples in Section 6, in this section we limit the problem in single-patch linear elasticity state. Consider a simple plate model subjected to uniform pressure $p_z$. The length of the plate is fixed to be $L=1$ and the thickness t various from 0.1 to 0.001, as shown in Fig. 4, and we set the load varies proportionally to $t^3$ as $p_z = -10(100t)^3$. For the plate problem with various thickness, firstly we compute the reference solutions at the central point A by commercial FEM software ABAQUS using $500 \times 500$ S4R elements (4-node doubly curved thin or thick shell elements with reduced integration, hourglass control and finite membrane strains), except for $t=0.1$ we use $50\times 50\times 10$ C3D8R elements (8-node linear bricks with reduced integration and hourglass control). The thickness t, applied pressure $p_z$, and corresponding reference solution $u_z^{\text {ref}}(A)$ are shown in Table 1.

Table 1 Reference solution $u_z^{\text {ref}}(A)$ and corresponding thickness t and applied pressure $p_z$ for the plate problem in Fig. 4

According to the conclusions in Ref. [45], for thin plates/shells, in IGA framework it is sufficient to adopt a single layer of solid elements of order 2 through the thickness direction. However, for extremely thin plates/shells, when one single layer of elements through the thickness is adopted, it is still necessary to limit the element length ratio to a small number (in ABAQUS the default criteria limit for the aspect ratio is 10¹). Thus for various element length ratios $\gamma$, the quality (condition number $\kappa$) of the stiffness matrix is studied. The number of elements is fixed as $4\times 4 \times 1$ in direction $\xi$, $\eta$ and $\zeta$ respectively, and the thickness t is changed gradually to obtain different element length ratios. The numerical experiment setup and results are shown in Table 2, and then plotted in Fig. 5. For a given system of linear equations, the condition number of its coefficient matrix describes the “sickness” of the system. The slope is about 1 despite for order differences, meaning that the condition number will become n times larger if the aspect ratio becomes n times smaller with other settings remaining unchanged. It is noticed there is a slope increment for length ratio larger than 200. Increasing orders of elements on the mid-surface layer only slightly decreases the condition number, nevertheless the computational time increases a lot for higher order elements since the basis functions are calculated recursively. Based on the considerations above, in the following studies the orders of elements are restricted as $(p,q,r)=(2,2,2)$, with only one single layer of elements along the thickness direction.

Table 2 Condition numbers $\kappa$ ($\times 10^{10}$) of stiffness matrix of the plate model with various element length ratios $\gamma$. The mesh is fixed as $4\times 4 \times 1$ in direction $\xi$, $\eta$ and $\zeta$ respectively

Fig. 5

Condition numbers $\kappa$ of stiffness matrix of the plate model with various element length ratios $\gamma$

For plates that are not extremely thin, for instance $t=0.1$ and $t=0.05$, more than one layer of solid elements can be used, so as to keep the element length ratio closed to one. In these cases using solid-shell elements performs similarly to normal 3D solid elements, and the results are acceptable, as shown in Table 3. For thin plates, such as $t=0.01, 0.005, 0.001$, as stated before only one single layer of elements is employed. Figure 6 indicates that one single layer of elements is effective to capture the mechanical deformation, because even for one single layer of elements there are 3 control points and corresponding 3 B-spline basis functions of order 2 through the thickness direction. As shown in Table 4, when the mesh $2\times 2\times 1$ is used for $t=0.001$ the element length ratio even reaches to 250, and the problem is still calculable. The convergence curves are plotted in Fig. 7a. When the meshes are refined, the curve of $t=0.001$ becomes flat, because of the slight mismatch of the refined results and the reference value : the refined results are slightly smaller than the reference value, this is verified in the partial enlarged figure in Fig. 7b. Is is also a common situation as in our previous research [7] when calculating thin shells by Reissner-Mindlin shells. More importantly it is noticed that shear locking occurs for thin plates with coarse meshes.

Table 3 Normalized solutions $u_z(A)/u_z^{\text {ref}}(A)$ for the plate model with thicknesses $t=0.1, 0.05$

Fig. 6

Solution field $u_z$ drawn on deformed configuration, plate thickness $t=0.01$. Here $10\times 10\times 1$ 3D solid elements of $(p,q,r)=(2,2,2)$ are used

Table 4 Normalized solutions $u_z(A)/u_z^{\text {ref}}(A)$ for thin plate model with thicknesses $t=0.01, 0.005, 0.001$. Only one single layer of elements through the thickness direction is used

Fig. 7

Results of $u_z(A)$ for the plate problem, shear locking occurs for thin plate with coarse meshes. (a) Convergence performance. (b) Partial enlarged

The above calculations are implemented by traditional Gaussian numerical integration with $(p+1)\times (q+1)\times (r+1)$ quadrature points for solid elements of order (p, q, r). The full Gaussian integration scheme as well as the proposed integration scheme are demonstrated in Fig. 8. For the common Gaussian integration, since we limit the order as $(p,q,r)=(2,2,2)$, the quadrature points are distributed as $3\times 3\times 3$. In the book [15] a simple reduction of the dimension in the thickness direction seems to be effective, thus in the middle of Fig. 8, we illustrate a simple reduced integration scheme, in which $2\times 2\times 2$ quadrature points are employed. A similar scheme is adopted in Timoshenko beam element [46], however this scheme is proved to be unable to alleviate locking effectively for this research. In our proposed scheme, the corner elements, boundary elements, and inner elements are treated differently, as shown on the right side of Fig. 8, this selective and reduced integration scheme is inspired by Ref. [14]. It is worth noting that the proposed scheme is equivalent to assuming the strain distribution as in the $\bar{B}$ method [7], but it is more convenient to be implemented. Fig. 9 shows the numerical results obtained by the full Gaussian integration and the proposed selective and reduced integration. The results indicate that the proposed scheme is able to alleviate locking phenomena and improve numerical accuracy especially for coarse mesh, although slightly rank-deficiency occurs. In Fig. 9b we show the convergence curves, the results by our method have distinctly better convergence performance, especially for extreme thin plate with thickness $t=0.001$.

Fig. 8

Common Gaussian integration $3\times 3\times 3$ for $(p,q,r)=(2,2,2)$, the normal simple reduced integration scheme $2\times 2\times 2$, and the proposed scheme illustrated in a typical cube

Fig. 9

Results of $u_z(A)$ for the plate problem with respect to elements per side on the mid-surface layer. RI means the proposed selective and reduced integration scheme. (a) Normalized results. (b) Convergence performance

6 Numerical examples

According to the observations above and also in [45], in the following examples the orders of elements are restricted as $(p,q,r)=(2,2,2)$, and only one single layer of elements along the thickness direction is used.

6.1 Plate made by two-patches in nonlinear elasticity

Firstly we test the solid-shell element performance in the context of nonlinear elasticity by the same simply supported square plate example in Fig. 4. The plate model is built by two identical patches, the maximum load is set to be $p_{\text {max}} = 10^6 \times p_z$. Figure 10 shows the contour plot of the plate deflection for thickness $t=0.05$ and $t=0.005$ using mesh $4 \times 2 \times 1$ for each of the two patches, the elements of one patch are colored by green wire frame and white for the other patch. It should be noted that for the second example the element length ratio is 25 : 25 : 1, but the solid-shell elements still respond well since there are 3 control points describing the thickness deformation in cooperating with 3 basis functions of order 2.

Fig. 11 describes the iteration history. It is observed that stagnation or oscillation happens during iterations but convergence can be achieved by the coefficient settings provided in Algorithm 1 and Algorithm 2. Although taking more iterations than the Newton-Raphson solver, in each quasi-Newton iteration huge computational resource is saved by approximating the tangent stiffness matrix instead of directly computing its inverse. To our experience, if the stabilization parameter in Eq. (16) is not large enough, the interface coupling conditions cannot be fully applied, the system may converge with a small gap along the coupling interface. The interface deflection plotted in Fig. 12 indicates the effectiveness of the Nitsche’s formulation as well as the proposed stabilization parameter in Eq. (19). The corresponding data for the above observation is provided². Figure 13 shows the load-displacement curves for plate thickness $t=0.005$, obtained by mesh $8 \times 8 \times 1$ for single patch and $8\times 4 \times 1$ for each of the two patches. Under this mesh discretization the Nitsche coupling of two patches gets similar results as one single patch.

Fig. 10

Contour plot of deflection field of the plate problem in large deformation, $p=p_{\text {max}}$. (a) Thickness $t=0.05$. (b) Thickness $t=0.005$

Fig. 11

Residual-iteration curves for the simply supported square plate in the geometrically nonlinear case, $p=p_{\text {max}}$. (a) Thickness $t=0.05$. (b) Thickness $t=0.005$

Fig. 12

Interface deflection along the coupling interface for the simply supported square plate in the geometrically nonlinear case, $p=p_{\text {max}}$. (a) Thickness $t=0.05$. (b) Thickness $t=0.005$

Fig. 13

Load-displacement curves ($p/p_{\text {max}}=f(u)$) for the simply supported square plate of thickness $t=0.005$ in the geometrically nonlinear case

6.2 Pinched cylinder

Figure 14 shows the 1/8 mid-surface model of the pinched cylinder problem. This structure experiences both shear and membrane locking, the proposed reduced integration scheme is numerically studied in linear case, and the element performance is slightly improved as indicated in Fig. 15.

Fig. 14

Pinched cylinder. One eighth of the mid-surface is modeled. The red filled squares are corresponding control points

Fig. 15

Normalized results of $u_z(C)$ for the pinched cylinder problem in linear elasticity

For the nonlinear case, the model is split into two identical patches, as shown in Fig. 16, and the nonlinear force $F_{nl}$ is $10^6$ times of the linear force $F_{lin}$. In Fig. 17 we draw the load-displacement curves under mesh $16 \times 16$, it is noted that the curve is nearly linear, the reason is that the cylinder belongs to developable structures and with this loading the structure is mainly dominated by inextensional deformations, also known as bending deformations [16]. Contour plot of displacement distribution by ABAQUS S4R elements and present solid-shell elements are presented in Fig. 18. Figure 19 illustrates the iteration history and interface deflection curves, it is worth noting that if we relax the convergence criteria the iteration system could be terminated earlier.

Fig. 16

Solid model of the pinched cylinder made by two patches. The left patch is shown in green line frame

Fig. 17

Load-displacement curves ($p/p_{\text {max}}=f(u)$) for the pinched cylinder problem in large deformation

Fig. 18

Contour plot of vertical displacement field of the pinched cylinder in large deformation, $F_{nl}=10^6 \times F_{lin}$. (a) ABAQUS S4R elements. (b) Present solid-shell elements $4 \times 8 \times 1 \times 2$ patches

Fig. 19

Iteration history and interface deflection curves for the pinched cylinder problem in the geometrically nonlinear case, $p=p_{\text {max}}$. (a) Residual-iteration and displacement-iteration. (b) Interface deflection

6.3 Pinched hemisphere with a hole

As the last example, we compute the pinched hemisphere with a hole, see Fig. 20. To eliminate the rigid body motion we fix the topmost left corner in the z direction. Severe membrane and shear locking is further enhanced by mesh distortion for this example [7]. Figure 21 shows that the results by the proposed reduced integration rule.

Fig. 20

Pinched hemisphere with hole. One fourth of the mid-surface is modeled. The red filled squares are corresponding control points

Fig. 21

Normalized results of $u_x(D)$ for the pinched hemisphere problem in linear elasticity

For the nonlinear case, the nonlinear force $F_{nl}$ is 100 times of the linear force $F_{lin}$. In Fig. 22 we cut the shell into 2 patches, The load-displacement curves are illustrated in Fig. 23, in which the reference values are provided in Ref. [47], and our results are calculated by mesh $16 \times 16$. As shown in Fig. 24 the solid-shell elements achieve good deformation response, compared with ABAQUS S4R elements. Moreover, for this severe locking shell problem the quasi-Newton solver went through more ups and downs than previous examples, but finally converged at nearly 1300 iterations, as illustrated in Fig. 25(a). Once again if we relax the convergence criteria, the iteration convergence could be achieved much earlier with similar results. Figure 25(b) proves the effectiveness of the proposed stabilization parameter for the non-symmetric Nitsche’s formulation.

Fig. 22

Solid model of the pinched hemisphere made by two patches. The left patch is shown in green line frame

Fig. 23

Load-displacement curves ($p/p_{\text {max}}=f(u)$) for the pinched hemisphere in large deformation

Fig. 24

Contour plot of vertical displacement field of the pinched hemisphere in large deformation, $F_{nl}=100 \times F_{lin}$. (a) ABAQUS S4R elements. (b) Present solid-shell elements $\times 4 \times 8 \times 1 \times 2$ patches

Fig. 25

Iteration history and interface deflection curves for the pinched hemisphere problem in the geometrically nonlinear case, $p=p_{\text {max}}$. (a) Residual-iteration and displacement-iteration. (b) Interface deflection

7 Conclusions

In this paper, we compute shell structures in isogeometric framework by solid-shell elements, couple patches by the Nitsche’s method, and solve the nonlinear system by the quasi-Newton method.

• 1) Solid elements are adopted to simulate thick or thin shells. The solid-shell elements suffer from locking, this problem is addressed by a selective and reduced integration scheme, in which elements in different positions are treated differently, in order to improve the elements softness and alleviate locking as much as possible. The numerical results of the solid-shell elements are similar to the ABAQUS S4R elements.

• 2) The quasi-Newton method is introduced as solver, the system takes more iterations to converge than classical Newton-Raphson solver, but the computational effort is reduced for each iteration due to the fact that the inverse of the approximated tangent stiffness matrix is directly updated by the BFGS formula. Moreover with the introduction of step length control and stability check, the iterations behave more robust. The non-symmetric Nitsche’s coupling formulation combined with the quasi-Newton solver allow us to achieve a linearization-free formulation, i.e. no need to calculate derivatives.

• 3) The non-symmetric version of the Nitsche’s method is employed for patch coupling of solid-shell elements. With the Nitsche parameter $\theta =0$ the coupling formulation is simplified by dropping the derivative of the PK1 stress $\mathbf {P}$. Instead of solving for the stabilization parameter $\gamma$ by a generalized eigenvalue problem along the coupled interface, a straightforward formula is also proposed based on the Young’s modulus and element mesh sizes. Using the non-symmetric Nitsche’s formulation, the obtained stiffness matrix loses its symmetry, but we believe that the concern about computational resources can be resolved by the quasi-Newton method.

Our further research directions include the accuracy of the stress through thickness direction of solid-shell elements, as well as methods to further alleviate locking. It could be also appealing and challenging to study further extensions, for instance trimmed surfaces and local refinement.