1 Introduction

Low order, Lagrangian-based, finite elements are often affected by spurious strains or stresses which lead to an overestimation of the stiffness matrix. As a consequence, an underestimation of the nodal variables appears, this behavior being referred to as locking. Through the years, several strategies were devised in order to eliminate (or at least alleviate) the occurrence of locking phenomena.

Among such techniques one can mention mixed pressure-displacement formulations [1–4], reduced and selective reduced integration [5–12], \(\bar{\mathrm {B}}\) [13] and \(\bar{\mathrm {F}}\) methods [14, 15] and Enhanced Assumed Strain (EAS) methods [16–28]. Another methodology developed to eliminate transverse shear locking in Lagrangian finite elements is known as the Assumed Natural Strain (ANS) approach. This technique was firstly implemented by Hughes and Tezduyar [29] for Mindlin plates and, later on, for shell elements by Dvorkin and Bathe [30]. The ANS method consists in interpolating the strain field at a set of points, known as tying points, whose strain terms will replace, in a weighted manner, the standard strain values coming from the quadrature points. This technique has been widely applied for the improvement of Lagrangian-based elements [7, 31–35].

In the last years, significant research effort has been employed in the development of the so-called solid-shell class of elements. The main goal of these elements is to combine the advantages of both solid and shell elements. This type of formulation is particularly attractive because only displacement degrees-of-freedom are used in its kinematic description, allowing to automatically account for 3D constitutive relations (e.g., plasticity) and obtain, as a consequence, a correct prediction of thickness changes in shell-like structures. Solid-shell elements also present strong advantages in numerical simulations involving double-sided contact, due, again, to the correct modelling of the stress and strain fields through the thickness direction. In addition, due to the absence of rotational degrees-of-freedom, the coupling with other solid elements in the mesh is straightforward and, most importantly, there is no need to elaborate update procedures in nonlinear geometric formulations.

Nevertheless, this class of elements is also affected by locking pathologies when considering incompressible materials, high length-to-thickness ratios and/or when modeling curved structures. Relevant finite element solid-shell formulations are described in [25, 26, 31, 34, 36–38], and references therein.

The concept of isogeometric analysis (IGA) was introduced in the pioneer work of Hughes et al. [39]. In IGA, the functions used to describe the CAD geometry (such as Non-Uniform Rational B-Splines—NURBS) are also employed, in an isoparametric fashion, for the approximation of the unknown fields, leading to an exact geometry representation.

Since the introduction of IGA, it has been shown that the high regularity properties of the employed functions lead in many cases to superior accuracy per degree of freedom with respect to standard FEM (see, e.g., [40–42]). However, it is well-known that NURBS-based element formulations are not free from locking pathologies. This can be seen, for instance, in the work of Echter and Bischoff [43] where the performance of classical finite elements with NURBS based elements was compared. In this work, convergence rates were analyzed, as well as the appearance of transverse shear and membrane locking. The authors concluded that the higher order continuity of the NURBS basis can significantly improve the quality of the numerical results. Nevertheless, the authors also state that the use of linear, quadratic or cubic basis functions can still lead to results that are not locking-free.

Therefore, the alleviation of pathologies such as volumetric, shear or membrane locking in NURBS-based elements is still an open issue. Elguedj et al. [44] employed the \(\bar{\mathrm {B}}\) and \(\bar{\mathrm {F}}\) projection methods to avoid volumetric locking in small and large deformation elasticity and plasticity problems in high-order solid NURBS elements. This projection methodology consists in splitting the volumetric and deviatoric components of the strain displacement/deformation gradient matrix, calculating then a new volumetric counterpart in a projected space of one order lower than the displacement space. Due to the higher inter-element continuity in the IGA formulation, this projection must be performed at the patch level. Numerical results show that the methodology is able to obtain good convergence rates and numerical solutions. It was also shown that the \(\bar{\mathrm {F}}\) method can alleviate shear locking for quadratic and higher-order basis functions. Taylor [45] proposed a formulation based on a three-field variational structure for the analysis of near incompressible solids in the large deformation regime. It is shown that the formulation where displacements, mean stress and volume variables are independently approximated may be used to efficiently solve this kind of problems. Cardoso and Csar de S [46] combined the enhanced assumed strain (EAS) method with isogeometric analysis to alleviate volumetric locking in 2D elastic problems. The choice of the EAS parameter was motivated by a subspace analysis of the incompressible deformation subspace [23]. However, this formulation requires a stabilization term to prevent spurious solutions arising when higher-order NURBS polynomials are employed.

Focusing specifically in the alleviation of shear locking, Echter and Bischoff [43] have extended the Discrete Shear Gap (DSG) method to NURBS-based beam elements. Beiro da Veiga et al. [47] implemented an isogeometric collocation method for straight planar Timoshenko beams, based on a mixed formulation scheme and leading to a shear locking-free formulation, which has been extended to spatial rods by Auricchio et al. [48]. Bouclier et al. [49] investigated the use of selective reduced integration and the \(\bar{\mathrm {B}}\) strain projection methods as means of alleviating shear and membrane locking in planar curved beams. More recently, the same authors [50] employed this methodology to alleviate locking pathologies in 2D solid elements for the analysis of both thick and thin beams. In addition, a simple extension to 3D NURBS based solid-shell elements was also presented. That work highlights the fact that reduced integration may be used to alleviate locking for solid-shell elements only in the quadratic case.

In the scope of plate/shell elements, Echter and et al. [51] have proposed a hierarchic family of isogeometric shell formulations. Although being based on a non-mixed concept, these methods are able to remove transverse shear and curvature thickness locking. Membrane locking is, in this case, alleviated by means of the DSG method or, alternatively, by a hybrid-mixed formulation based on a two-field Hellinger-Reissner variational principle (displacements and stress fields). To alleviate shear locking in Reissner-Mindlin plate elements, Thai et al. [52] have implemented a stabilization technique that consists in modifying the shear terms of the constitutive matrix. Hosseini et al. [53] proposed a solid-like shell element, a class of shell elements characterized by possessing only displacement degrees of freedom, but shell kinematics. In order to obtain a complete 3D representation of the shell, the authors employ NURBS/T-Splines basis functions to parametrize the mid-surface and linear Lagrange shape functions in the thickness direction. Benson et al. [54] proposed a quadratic rotation-free isogeometric shell formulation with a \(2\times 2\) reduced integration. The authors reported a significant reduction in the computational costs. In a later work, Benson et al. [55] also proposed an isogeometric quadratic blended shell formulation. The authors concluded that the use of uniformly reduced integration in isogeometric shell elements leads to a computationally efficient formulation.

Following the pursuit of locking-free isogeometric formulations, but based on an entirely distinct and innovative approach, in the present work the authors extend the ANS method to alleviate locking pathologies in NURBS-based solid-shell elements.

This study is organized in the following way: in Sect. 2 the basic principles behind isogeometric analysis are presented, followed by the description of the proposed ANS method in the scope of IGA in Sect. 3 and in Sect. 4 a set of numerical examples are presented in order to asses the performance of the proposed formulation. Finally, in Sect. 5 the main conclusions of the current study are presented.

2 NURBS for isogeometric analysis

In this section a brief introduction to B-Splines and NURBS is given. The interested reader is referred to [56] and references therein for further details.

2.1 B-Splines

Consider the representation of a B-Spline curve given by

$$\begin{aligned} \mathbf {C}(\xi ) = \sum _{i=1}^{n} N_{i,p}(\xi ) \mathbf {B}_i \end{aligned}$$
(1)

where \(\mathbf {B}_i\), with \(i=1,2,...,n\), are the control points and \( N_{i,p}\) are piecewise polynomial functions, known as B-Splines basis functions of order \(p\). Piecewise linear interpolations of the control points leads to the so-called control polygon.

Let \(\varXi = \left[ \xi _1, \xi _2,..., \xi _{n+p+1}\right] \) be a non-decreasing sequence of real numbers, known as a knot vector, where \(\xi _i\) is the ith knot. The interval defined by two subsequent knots is known as a knot span. The knot vector divides the parameter space into knot spans or elements. A given knot is said to have multiplicity \(m\) if it is repeated \(m\) times inside the knot vector. Also, a knot vector is considered to be open if the first and last knots have multiplicity \(m = p+1\).In an open knot vector, the basis functions are interpolatory at the ends of the parametric space. A knot vector is considered as uniform if the knots are equally spaced and non-uniform otherwise. More details on the B-Spline parameterization can be found in [56].

2.2 Basis functions

Using the Cox-de Boor recursion formula, the ith B-Spline basis function can be defined as

$$\begin{aligned} N_{i,0}(\xi ) =\left\{ \begin{array}{l@{\quad }l} 1 &{} \mathrm {if}~\xi _i \le \xi < \xi _{i+1} \\ 0 &{} \mathrm {otherwise} \end{array} \right. , \end{aligned}$$
(2)

for polynomial order zero, and

$$\begin{aligned} N_{i,p} (\xi )&= \frac{\xi -\xi _i}{\xi _{i+p} -\xi _i} N_{i,p-1}(\xi ) \nonumber \\&\quad +\frac{\xi _{i+p+1} - \xi }{\xi _{i+p+1} - \xi _{i+1}} N_{i+1,p-1}(\xi ) \end{aligned}$$
(3)

otherwise (i.e. for \(p \ge 1\)). The convention \(\frac{0}{0} = 0\) is adopter herein [56].

2.3 B-Splines surface and volume

A tensor product B-Spline surface can be defined as

$$\begin{aligned} \mathbf {S}\left( \xi ,\eta \right) = \sum _{i=1}^n \sum _{j=1}^m N_{i,p} \left( \xi \right) M_{j,q}\left( \eta \right) \mathbf {B}_{i,j}, \end{aligned}$$
(4)

where \(\mathbf {B}_{i,j}\) is now the control net. In the previous equation, \(N_{i,p} \left( \xi \right) \) and \(M_{j,q}\left( \eta \right) \) are the univariate B-Spline basis functions of order \(p\) and \(q\), corresponding to the knot vectors \(\varXi = \left[ \xi _1, \xi _2,...,\xi _{n+p+1}\right] \) and \(H = \left[ \eta _1, \eta _2,...,\eta _{m+q+1}\right] \), respectively.

In an analogous way, one can define a tensor product B-Spline volume. Given a control lattice \(\mathbf {B}_{i,j,k}\) and knot vectors \(\varXi = \left[ \xi _1, \xi _2,...,\xi _{n+p+1}\right] \), \(H = \left[ \eta _1, \eta _2,...,\eta _{m+q+1}\right] \) and \(Z = \left[ \zeta _1, \zeta _2,...,\zeta _{k+r+1}\right] \), a B-Spline volume (solid) can be expressed as

$$\begin{aligned} \mathbf {V}\left( \xi ,\eta , \zeta \right) = \sum _{i=1}^n \sum _{j=1}^m \sum _{k=1}^l N_{i,p} \left( \xi \right) M_{j,q}\left( \eta \right) L_{k,r}\left( \zeta \right) \mathbf {B}_{i,j,k}.\nonumber \\ \end{aligned}$$
(5)

2.4 Refinement

B-Spline basis can be enriched without changing the studied geometry and its parametrization. In computer aided design (CAD), the refinement can be performed by knot insertion and degree elevation. These two methods are closely related to h- and p-refinement in the traditional finite element analysis (FEA) [40]. However, the use of B-Spline basis allows for a new type of refinement known as k-refinement. For a more in-depth explanation of the different refinement techniques, the reader is referred to the work of Cottrell et al. [42]. Efficient algorithms for the knot insertion and order elevation procedures, among many others, can be found in Piegl and Tiller [56].

2.5 Non-uniform rational B-Splines

Despite being a powerful tool, B-Spline are not able to represent some geometries, such as circles and ellipsoids. However, this problem can be circumvented by employing a generalized form of B-Splines known as Non-Uniform Rational B-Splines (NURBS). NURBS provide a precise mathematical form capable of representing common analytical shapes such as lines, planes, conic curves, free-form curves, quadric and sculptured surfaces that are used in computer graphics and CAD [57].

A generic NURBS curve of order \(p\) can be defined as

$$\begin{aligned} \mathbf {C}\left( \xi \right) = \sum _{i=1}^{n} R_{i}^p\left( \xi \right) \mathbf {B}_i \end{aligned}$$
(6)

where \(R_{i}^p\left( \xi \right) \) are the rational basis functions. These functions are defined as

$$\begin{aligned} R_{i}^p\left( \xi \right) = \frac{N_{i,p}\left( \xi \right) w_i}{W\left( \xi \right) } = \frac{N_{i,p}\left( \xi \right) w_i}{\sum _{j=1}^n N_{j,p}\left( \xi \right) w_j}, \end{aligned}$$
(7)

where \(N_{i,p}\left( \xi \right) \) is the ith basis function of order \(p\) and \(w_i\) are the weights. The choice of appropriate values of the weights \(w_i\) allows for a proper representation of different types of curves, such as circular arcs. In an analogous way, it is possible to define the NURBS basis functions for surfaces and volumes as

$$\begin{aligned} R_{i,j}^{p,q}\left( \xi ,\eta \right) = \frac{N_{i,p}\left( \xi \right) M_{j,q}\left( \xi \right) w_ {i,j}}{\sum _{\hat{i}=1}^n \sum _{\hat{j}=1}^m N_{\hat{i},p}\left( \xi \right) M_{\hat{j},q}\left( \eta \right) w_{\hat{i},\hat{j}}} \end{aligned}$$
(8)

and

$$\begin{aligned}&R_{i,j,k}^{p,q,r}\left( \xi ,\eta ,\zeta \right) \nonumber \\&\quad =\frac{N_{i,p}\left( \xi \right) M_{j,q}\left( \xi \right) L_{k,r}\left( \xi \right) w_ {i,j,k}}{\sum _{\hat{i}=1}^n \sum _{\hat{j}=1}^m \sum _{\hat{k}=1}^l N_{\hat{i},p}\left( \xi \right) M_{\hat{j},q}\left( \eta \right) M_{\hat{k},r}\left( \zeta \right) w_{\hat{i},\hat{j},\hat{k}}},\nonumber \\ \end{aligned}$$
(9)

respectively.

The structure of IGA and FEM codes is very similar. Aside from the data input and results output, the major change is in the computation of the basis functions and derivatives, which will replace the classical finite element shape functions. A detailed procedure on how to employ B-Splines and NURBS basis functions in the context of Isogeometric Analysis, and its relation with FEM, can be found in the book by Cottrell et al. [40].

3 Assumed Natural Strain method for isogeometric analysis

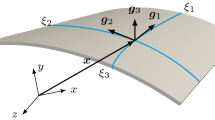
In the small strain regime, the strain at each integration point, in the covariant frame, can be expressed as

$$\begin{aligned} \varepsilon _{ij}^c\left( \xi ,\eta ,\zeta \right) = \frac{1}{2} \left( \frac{\partial \mathbf {u}}{\partial \xi _i} \mathbf {g}_j + \frac{\partial \mathbf {u}}{\partial \eta _j} \mathbf {g}_i \right) , \end{aligned}$$
(10)

where \(\xi _1 = \xi \), \(\xi _2 = \eta \) and \(\xi _3 = \zeta \) are the natural element coordinate system. The covariant base vectors are given as \(\mathbf {g}_i=\frac{\partial \pmb {x}}{\partial \xi _i}\). Equation (10) can be also expressed in matrix form as

$$\begin{aligned} \pmb {\varepsilon }^c \left( \xi ,\eta ,\zeta \right) = \mathbf {B}^c\left( \xi ,\eta ,\zeta \right) {\hat{{\upmu }}}, \end{aligned}$$
(11)

in which \(\mathbf {B}^c\left( \xi ,\eta ,\zeta \right) \) is the standard compatible strain-displacement matrix in the covariant frame computed at each integration point, while \({\hat{{\upmu }}}\) corresponds to the vector of displacement degrees-of-freedoms at the control points (control variables).

The key idea behind the ANS method consists of selecting a set of tying points that will replace the standard integration points for the calculation of the strain components. In standard Lagrange elements, after calculating the strain-displacement matrix at the tying points, a set of interpolation functions are used to associate the tying points with the integration point. This procedure leads to assumed covariant strain components. In the NURBS-based ANS formulation presented herein, the classic interpolation functions are replaced by a projection matrix. To alleviate locking effects and avoid numerical instabilities in the formulation, the choice of the tying points is of extreme importance.

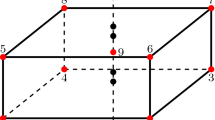
With the intent of more clearly exposing the proposed methodology, a quadratic NURBS element will be taken as an example. Following the original work of Bucalem and Bathe [58] for Lagrangian basis functions, the selection of the tying points for the second-order element is given in Fig. 1. To define the ANS strain displacement matrix in the context of IGA, a set of local bivariate basis functions must be created.

Fig. 1
figure 1

Representation of the tying points for the integration of \(\varepsilon _{\xi \xi }\) and \(\varepsilon _{\xi \zeta }\) (left), \(\varepsilon _{\eta \eta }\) and \(\varepsilon _{\eta \zeta }\) (center) and \(\varepsilon _{\xi \eta }\) (right)

Full size image

Consider the example with four second-order elements as presented in Fig. 2. In this figure, the integration points (circles) and the tying points (triangles) for the interpolation of \(\varepsilon _{\xi \xi }\) and \(\varepsilon _{\xi \zeta }\) strain components in the top left element are represented. The univariate basis functions coming from the knot vectors that define the mesh are depicted as the global space. For each element, it is also possible to define two local knot vectors that will be used to define the local space. These new knot vectors are open and contain only one non-zero knot span. It is important to note that the basis functions along the \(\xi \) direction is of one order lower than the one along the \(\eta \) direction, due to the fact that a lower number of tying points is considered in the latter.

Fig. 2
figure 2

Global and local spaces for the quadratic NURBS element

Full size image

Following the work of Bucalem and Bathe [58], the choice of the tying points is closely related to the order of the quadrature employed in the finite element formulation. In the current work, following classical 3D solid Lagrangian formulations, we define full integration when \((p+1)\), \((q+1)\) and \((r+1)\) quadrature points are used in a finite element for the \(\xi \), \(\eta \) and \(\zeta \)-directions, respectively: For the \(\varepsilon _{\xi \xi }\) and \(\varepsilon _{\xi \zeta }\) components, the points from a one-order lower Gaussian quadrature are employed in the \(\xi \)-direction, while the points corresponding to full Gaussian integration are employed in the \(\eta \)-direction. An analogous reasoning is performed for the \(\varepsilon _{\eta \eta }\) and \(\varepsilon _{\eta \zeta }\) components of the strain-displacement operator. For the in-plane component \(\varepsilon _{\xi \eta }\), the points from a one-order lower Gaussian integration scheme are considered. By applying the same reasoning, the presented methodology can be easily extended to higher-order basis functions.

The assumed strain field can then be expressed as

$$\begin{aligned} \pmb {\varepsilon }^{ANS} \left( \xi ,\eta ,\zeta \right) = \mathbf {N}^T \left( \xi ,\eta \right) \bar{\pmb {\varepsilon }}^c \left( \hat{\xi },\hat{\eta },\zeta \right) , \end{aligned}$$
(12)

where \(\mathbf {N}\) arises from the tensor product of the local basis functions calculated at each conventional integration point. In the previous equation, \(\bar{\pmb {\varepsilon }}^c \small \big (\hat{\xi },\hat{\eta },\zeta \big )\) is the compatible strain field calculated in the local space, while \(\hat{\xi }\), \(\hat{\eta }\), and \(\zeta \) are the tying point coordinates. Using the notation presented in Fig. 2, the vector \(\mathbf {N}\) can be expressed as

$$\begin{aligned} \mathbf {N} \left( \xi ,\eta \right)&= \left[ \bar{N}_{3,2}^k \bar{M}_{2,1}^k \; \bar{N}_{2,2}^k \bar{M}_{2,1}^k \; \bar{N}_{1,2}^k \bar{M}_{2,1}^k \; \bar{N}_{3,2}^k \bar{M}_{1,1}^k \;\right. \nonumber \\&\left. \bar{N}_{2,2}^k \bar{M}_{1,1}^k \; \bar{N}_{1,2}^k \bar{M}_{1,1}^k \right] ^T, \end{aligned}$$
(13)

where \(\bar{N}_{i,2}^k\) and \(\bar{M}_{j,1}^k\) are the local univariate NURBS basis functions calculated at the current integration point \(k\). It is then possible to project the local compatible strain field \(\bar{\pmb {\varepsilon }}^c \big (\hat{\xi },\hat{\eta },\zeta \big )\) onto the global space, leading now to a global compatible strain field \(\pmb {\varepsilon }^c \big (\hat{\xi },\hat{\eta },\zeta \big )\), by performing the following operation

$$\begin{aligned} \pmb {\varepsilon }^{c} \left( \hat{\xi },\hat{\eta },\zeta \right) = \mathbf {M} \left( \hat{\xi },\hat{\eta }\right) \bar{\pmb {\varepsilon }}^c \left( \hat{\xi },\hat{\eta },\zeta \right) , \end{aligned}$$
(14)

where \(\mathbf {M}\left( \hat{\xi },\hat{\eta }\right) \) is a projection matrix, with number of rows and columns equal to the number of tying points, obtained from the tensor product of the local basis function calculated at each tying point. The projection matrix for the tying point set given in Fig. 2 is, for example, expressed as

$$\begin{aligned}&\mathbf {M} \left( \hat{\xi },\hat{\eta }\right) \nonumber \\&\quad = \begin{bmatrix} \bar{N}_{3,2}^1 \bar{M}_{2,1}^1&\bar{N}_{2,2}^1 \bar{M}_{2,1}^1&\bar{N}_{1,2}^1 \bar{M}_{2,1}^1&\bar{N}_{3,2}^1 \bar{M}_{1,1}^1&\bar{N}_{2,2}^1 \bar{M}_{1,1}^1&\bar{N}_{1,2}^1 \bar{M}_{1,1}^1\\ \bar{N}_{3,2}^2 \bar{M}_{2,1}^2&\bar{N}_{2,2}^2 \bar{M}_{2,1}^2&\bar{N}_{1,2}^2 \bar{M}_{2,1}^2&\bar{N}_{3,2}^2 \bar{M}_{1,1}^2&\bar{N}_{2,2}^2 \bar{M}_{1,1}^2&\bar{N}_{1,2}^2 \bar{M}_{1,1}^2\\ \bar{N}_{3,2}^3 \bar{M}_{2,1}^3&\bar{N}_{2,2}^3 \bar{M}_{2,1}^3&\bar{N}_{1,2}^3 \bar{M}_{2,1}^3&\bar{N}_{3,2}^3 \bar{M}_{1,1}^3&\bar{N}_{2,2}^3 \bar{M}_{1,1}^3&\bar{N}_{1,2}^3 \bar{M}_{1,1}^3\\ \bar{N}_{3,2}^4 \bar{M}_{2,1}^4&\bar{N}_{2,2}^4 \bar{M}_{2,1}^4&\bar{N}_{1,2}^4 \bar{M}_{2,1}^4&\bar{N}_{3,2}^4 \bar{M}_{1,1}^4&\bar{N}_{2,2}^4 \bar{M}_{1,1}^4&\bar{N}_{1,2}^4 \bar{M}_{1,1}^4\\ \bar{N}_{3,2}^5 \bar{M}_{2,1}^5&\bar{N}_{2,2}^5 \bar{M}_{2,1}^5&\bar{N}_{1,2}^5 \bar{M}_{2,1}^5&\bar{N}_{3,2}^5 \bar{M}_{1,1}^5&\bar{N}_{2,2}^5 \bar{M}_{1,1}^5&\bar{N}_{1,2}^5 \bar{M}_{1,1}^5\\ \bar{N}_{3,2}^6 \bar{M}_{2,1}^6&\bar{N}_{2,2}^6 \bar{M}_{2,1}^6&\bar{N}_{1,2}^6 \bar{M}_{2,1}^6&\bar{N}_{3,2}^6 \bar{M}_{1,1}^6&\bar{N}_{2,2}^6 \bar{M}_{1,1}^6&\bar{N}_{1,2}^6 \bar{M}_{1,1}^6\\ \end{bmatrix},\nonumber \\ \end{aligned}$$
(15)

where \(\bar{N}_{i,p}^t\) and \(\bar{M}_{j,q}^t\) are the local univariate NURBS basis functions calculated at the tying point \(t\). In the work of Bucalem and Bathe [58], the local basis functions \(\bar{N}\) and \(\bar{M}\) are chosen as Lagrange polynomials such that they are interpolatory at the corresponding tying point and zero at the other tying points. In that case, the projection matrix \(\mathbf {M}\big (\hat{\xi },\hat{\eta }\big )\) would simply be the identity matrix. Since Bzier functions are not interpolatory, the same approach cannot be applied in the present work.

Combining Eqs. (12) and (14) leads to the final form of the ANS

$$\begin{aligned} \pmb {\varepsilon }^{ANS} \left( \xi ,\eta ,\zeta \right) \!=\! \mathbf {N}^T \left( \xi ,\eta \right) \mathbf {M}^{-1} \left( \hat{\xi },\hat{\eta }\right) \pmb {\varepsilon }^c \left( \hat{\xi },\hat{\eta },\zeta \right) , \end{aligned}$$
(16)

which yields the following expression for \(\mathbf {B}^{ANS}\)

$$\begin{aligned} \mathbf {B}^{ANS}\left( \xi ,\eta ,\zeta \right) = \mathbf {N}^T \left( \xi ,\eta \right) \mathbf {M}^{-1} \left( \hat{\xi },\hat{\eta }\right) \mathbf {B}^c\left( \hat{\xi },\hat{\eta },\zeta \right) ,\nonumber \\ \end{aligned}$$
(17)

to be properly inserted in place of \(\mathbf {B}^c\) for the strain definition in the variational formulation.

The interpolation based on the tying points, for the NURBS-based formulation, is independent of the element-based (natural) \(\zeta \) coordinate. This is typical for shell formulations, and is adopted in the present work for trivariate NURBS constructions, leading to a so-called solid-shell concept, whose counterpart in FEM can be seen, for instance, in references [25, 34]. The algorithmic procedure to calculate the ANS strain-displacement matrix can be seen in Table 1.

Table 1 General algorithm for the Enhanced Assumed Strain method in NURBS-based formulations
Full size table

Since linear NURBS elements yield the same results as linear Lagrange elements, the lowest order element that can take advantage of NURBS basis functions is the quadratic element, which will be the focus of the present study. Nevertheless, the extension to higher-order solid-shell elements is straightforward. This is an advantage of the present locking-alleviation methodology when compared to \(\bar{\mathrm {B}}\) and EAS formulations.

Finally, it is also worth mentioning that the procedure to implement the ANS method in NURBS-based formulations presented herein is entirely performed at the element level. As a consequence, this strategy would allow for an easier implementation within available commercial finite element codes, in combination with a Bézier extraction approach, as proposed by Borden et al. [59]

4 Numerical examples

In this section, several numerical examples are presented in order to assess the performance of the proposed methodology. All tests are performed in the linear elastic range, and standard Gaussian quadrature is employed. In the following, we focus in particular on the performance of a quadratic NURBS solid-shell finite element based on the presented ANS formulation, which is referred to as H2ANS. In all numerical examples, the proposed formulation is compared with quadratic and cubic NURBS-based solid and Kirchhoff-Love shell elements. Whenever possible, other NURBS-based shell results available in the literature are also presented, for comparison purposes. In this section, we adopt the following nomenclature for the different employed formulations:

  • Hn: Solid NURBS element of degree n with compatible strains;

  • KLn: Kirchhoff-Love shell element of degree n, as proposed by Kiendl et al. [60];

  • 3p-HS: Quadratic 3-parameter Kirchhoff-Love shell element with Hybrid Stress modification of membrane part, as proposed by Echter et al. [51];

  • 3p-DSG: Quadratic 3-parameter Kirchhoff-Love shell element with Discrete Strain Gap modification of membrane part, as proposed by Echter et al. [51];

  • 5p-stand(-DSG): Quadratic 5-parameter Reissner–Mindlin shell element with Discrete Shear Gap modification of membrane part, as proposed by Echter et al. [51];

  • 5p-hier(-HS): Quadratic 5-parameter Reissner–Mindlin shell element with hierarchic difference vector and with Hybrid Stress modification of membrane part, as proposed by Echter et al. [51].

In particular, the proposed numerical experiments consist of the study of a straight and a curved cantilever beam, as well as of the solution of the well-known “shell obstacle course”, proposed by Belytschko et al. [61] as a set of benchmarks for the assessment of shell analysis procedures.

4.1 Straight cantilever beam

In this first example, a straight beam clamped at one end is subjected to a vertical load \(F\) at its free end, as it can be seen in Fig. 3. From Bernoulli beam theory, the strain energy \(U\) is given as

$$\begin{aligned} U = \frac{2F^2L^3}{Ewt^3}, \end{aligned}$$
(18)

where \(E\) is the Young’s modulus, while \(L\), \(w\), and \(t\) are the beam length, width, and thickness, respectively. By expressing the results in terms of the strain energy, it is possible to assess the accuracy of the stress and strain fields present in the structure.

Fig. 3
figure 3

Scheme of the straight beam problem

Full size image

In a first case, the convergence of the formulations is analyzed for a beam of \(L=100.0\) and \(w=t=1.0\). The material properties are taken as \(E=1000.0\) and \(\nu =0.0\) (\(\nu \) classically being the Poisson’s ratio). The problem is discretized with only one element along the width and thickness directions. The results for the normalized strain energy versus the number of elements along the length direction are presented in Fig. 4. It can be seen that the proposed H2ANS formulation is able to obtain the reference solution, even when considering a very coarse mesh. The results are superior to those attained by quadratic solid and Kirchhoff-Love shell elements. The results for cubic formulations are not reported due to the fact a cubic polynomial interpolation is in this case enough to reproduce the exact solution.

Fig. 4
figure 4

Normalized strain energy versus mesh density for the straight cantilever beam problem with a constant slenderness of 100.0

Full size image

In the second case, a mesh of eight elements is considered, and the problem is studied for different beam thickness values. As the beam becomes thinner, transverse shear locking effects will be triggered, making this example a valuable tool for evaluating the capability of a given formulation to alleviate this kind of locking.

The results for the normalized strain energy versus slenderness are presented in Fig. 5. The proposed formulation is able to obtain good results for both thick and thin beams, demonstrating a very low sensitivity to shear locking effects. As expected, as the thickness of the beam decreases, the results for the standard quadratic NURBS solid element tend to deteriorate. It can also be seen that the KL2 formulation is free from shear locking. We moreover highlight that when higher slenderness ratios are considered, the stiffness matrices resulting from the solid elements become ill-conditioned, leading to difficulties when solving the global system of equations. This situation is not detected when shell elements are instead used.

Fig. 5
figure 5

Normalized strain energy versus beam slenderness for the straight cantilever beam problem for a eight NURBS element mesh

Full size image

4.2 Curved cantilever beam

In this example, a curved beam, consisting of a quarter of a circle, is clamped at one end and subjected to a transversal load at the free end. Due to the curvature of the beam, membrane locking will be the predominant phenomena [51]. In addition, when solid (or solid-shell) elements are used to model the curved profile, curvature thickness (trapezoidal) locking may also be present. The structure, depicted in Fig. 6, has a radius \(R = 10.0\) and a width \(w = 1.0\). A Young’s modulus of \(1000.0\) and a Poisson’s ratio of \(0.0\) are considered. The load is given as a function of the thickness \(t\), as \(F = 0.1t^3\). From Bernoulli beam theory the radial displacement can be computed to be 0.942 [51]. The problem is discretized using ten NURBS elements, with only one element through the thickness and width directions.

Fig. 6
figure 6

Scheme of the curved cantilever beam problem

Full size image

The results for the radial displacement as the beam slenderness \(R/t\) is increased are presented in Fig. 7. It can be seen that, although the proposed formulation is not locking free, it is able to significantly improve the behavior of the standard quadratic NURBS solid element. The performance of H2ANS is also superior to the quadratic Kirchhoff-Love shell element. In fact, H2 and KL2 formulations suffer from locking, even when considering a moderately thin shell. Cubic elements present a better overall performance, although not being completely locking-free.

Fig. 7
figure 7

Displacement versus slenderness for the curved cantilever beam problem (1)

Full size image

In Fig. 8, the proposed formulation is also compared with the shell formulations presented in [51]. The results obtained by H2ANS are very close to those attained by the 5p-stand-DSG shell element. Echter et al. [51] justify the deterioration of the results obtained by the 5p-stand-DSG element through shear locking effects. However, as seen in the previous example, since the presently proposed formulation is free from shear locking, the authors believe that the decrease of the H2ANS performance as the slenderness of the beam increases may be related to curvature thickness locking. As observed in [51], the 3p-DSG and 3p-HS formulations are instead completely locking-free.

Fig. 8
figure 8

Displacement versus slenderness for the curved cantilever beam problem (2)

Full size image

4.3 Shell obstacle course I—Scordelis–Lo roof

In this example, introduced by Scordelis and Lo [62], a cylindrical shell supported by rigid diaphragms in the curved edges is subjected to a volume force (self-weight). The geometry of the problem is presented in Fig. 9 and the dimensions of the structure are: radius \(R=25.0\), length \(L=50.0\), thickness \(t=0.25\). The magnitude of the volume force is given as \(\rho g = 360\), where \(\rho \) is the specific mass and \(g\) is the gravity acceleration constant. The elastic properties are given by \(E = 4.32\times 10^8\) and \(\nu = 0.0\). Due to symmetry conditions, only a quarter of the structure is modeled.

Fig. 9
figure 9

Schematic representation of the Scordelis–Lo roof problem (\(1/4\) of the whole structure is shown)

Full size image

The vertical displacement of the midpoint of the free edge (point D in the figure) is numerically computed and compared with the reference solution of \(0.3024\), and the results are presented in Fig. 10. The proposed H2ANS formulation is able to obtain good results and a very fast convergence, significantly improving the behavior of the conventional formulation (H2 element). In fact, it can be seen that the results from H2ANS are similar to those obtained by cubic solid and Kirchhoff-Love shell elements.

Fig. 10
figure 10

Displacement of the midpoint of the free edge for the Scordelis–Lo roof

Full size image

4.4 Shell obstacle course II—full hemispherical shell

The full hemispherical shell represented schematically in Fig. 11 is another well-known benchmark to assess the performance of shell elements. In this problem, a hemisphere of radius \(R = 10.0\) and thickness \(t = 0.04\) is subjected to a pair of opposite concentrated loads applied at antipodal points of the equator. The equator edge is considered to be free. Due to symmetry conditions, only one quarter of the structure needs to be modeled, as seen in the figure. The magnitude of the load is \(F = 1.0\) and the material parameters are given as \(E = 6.825 \times 10^7\) and \(\nu = 0.3\). The reference radial displacement at point A is \(u = 0.0924\).

Fig. 11
figure 11

Full hemispherical shell problem setup (\(1/4\) of the whole structure is shown)

Full size image

In Fig. 12, the results for the radial displacement at point A versus the number of control points per side is presented. Once again, the proposed H2ANS formulation is able to obtain good results and convergence, being superior to quadratic solid and Kirchhoff-Love shell elements, and comparable to those with higher order interpolations.

Fig. 12
figure 12

Radial displacement of point A for the full hemispherical shell problem

Full size image

4.5 Shell obstacle course III—pinched cylinder

As a last example, the pinched cylinder with end diaphragms subjected to a pair of concentrated loads is presented. The cylinder has radius \(R=300.0\), length \(L=600.0\), thickness \(t=3.0\). A schematic representation can be seen in Fig. 13. The concentrated loads have a magnitude of \(1.0\). The material properties are given as \(E = 3.0 \times 10^6\) and \(\nu =0.3\). Due to symmetry, only one eight of the structure is modeled. The reference solution for the radial displacement at the loaded point is given as \(u = 1.8248 \times 10^{-5}\).

Fig. 13
figure 13

Schematic representation of the pinched cylinder problem (\(1/8\) of the whole structure is shown)

Full size image

The results for the different formulations are presented in Fig. 14. The H2ANS formulation gives again better results than those obtained with quadratic elements, even if, in this case, not as good as those obtained with cubic elements.

Fig. 14
figure 14

Radial displacement for the pinched cylinder problem

Full size image

It is important to remark that, in all considered cases, the proposed H2ANS solid-shell formulation results in strongly enhancing the performance of a standard H2 quadratic element, alleviating the presence of locking and leading to results similar to those attained by a cubic element, at a significantly lower computational cost.

5 Conclusions

In the current work, an extension of the ANS method is for the first time proposed for solid-shell NURBS-based elements in order to alleviate locking effects. The methodology is based on a projection using a set of local basis functions. The numerical results for the proposed formulation show that it can efficiently alleviate locking pathologies such as shear and membrane locking. In fact, in most of the presented numerical examples, the proposed quadratic formulation is able to attain results and convergence rates similar to those obtained with cubic solid and Kirchhoff-Love shell elements, showing in any case clearly superior performance with respect to standard quadratic solid and shell formulations. Moreover, its significantly lower computational cost with respect to cubic solid formulations makes it an interesting and cost-effective tool for the analysis of shell-like structures, in particular when 3D nonlinear constitutive relations (e.g., plasticity) have to be included or when double-sided contact has to be taken into account. Another advantage of the proposed procedure is the fact that it is entirely performed at the element level, rather than at the patch level, making it easier to be implemented within available commercial finite element codes. Moreover, it is to be remarked that, although the present formulation is here implemented for quadratic solid-shell NURBS element, its extension to higher order approximations is straightforward, for both solid-shell and shell elements. Finally, a similar procedure could be easily implemented within the framework of finite strains; the extension of the presented formulation to nonlinear (both from the kinematical and the constitutive point of view) solid-shell models will be the subject of future research.